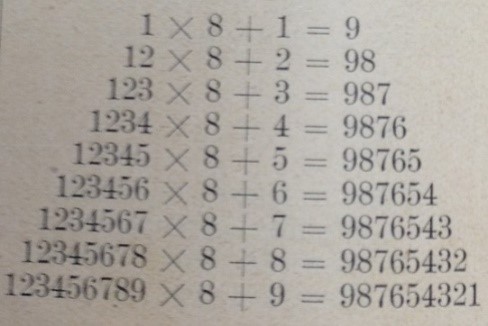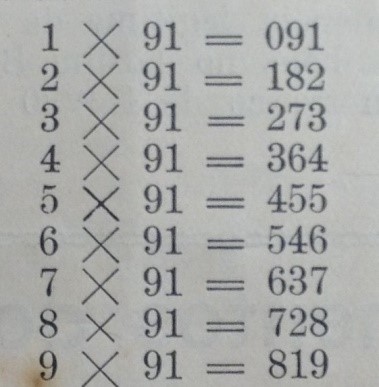1 Introdução
Este artigo tem por objetivo analisar as edições da revista O ECHO, com ênfase nas curiosidades matemáticas presentes na mesma. Trata-se de um recorte do estudo iniciado durante a elaboração da tese O ensino da aritmética nas escolas paroquiais católicas e no Ginásio Nossa Senhora da Conceição de São Leopoldo nos séculos XIX e XX sob a ótica dos Jesuítas (BRITTO, 2016), e aprofundado no estágio Pós-Doutoral no Programa de Pós-graduação em Ensino de Ciências e Matemática (PPGECIM), da Universidade Luterana do Brasil (ULBRA), tendo como questão norteadora a Matemática veiculada pelos Jesuítas em escolas católicas brasileiras no século XX.
Os trabalhos desenvolvidos pelas Ordens religiosas que chegaram ao Rio Grande do Sul (RS) após a segunda metade do século XIX deixaram relevantes contribuições. Dentre essas Ordens, estão os Jesuítas, que, por meio de trabalhos missionários, inicialmente, junto às colônias de imigrantes alemães católicos e, posteriormente, com a criação de uma rede de ginásios e seminários, contribuíram para a formação da juventude gaúcha. Dentre os educandários criados pela Ordem, destaca-se o Colégio Anchieta, com sede em Porto Alegre/RS.
A revista O ECHO foi editada pelo Colégio Anchieta, por meio da Typographia do Centro, localizada em Porto Alegre, no período entre abril de 1914 e dezembro de 1931. A partir de 1932, a revista passa a ser denominada O ECO, devido à reforma ortográfica1. O público-alvo do ECHO era a comunidade escolar e a mocidade católica brasileira, pois, segundo os editores, havia revistas para os diferentes públicos na época, exceto para os jovens estudantes. O periódico apresentava cultura geral e valores católicos, por isso era uma revista destinada para os jovens católicos.
Como o tema desta investigação se insere na História da Educação Matemática no RS, seu aporte metodológico está fundamentado na história cultural a partir da perspectiva de Chartier (1990). Para investigar a revista O ECHO, foram realizadas visitas ao acervo particular do professor Luiz Osvaldo Leite2, em Porto Alegre, onde se encontram as edições. Ao pesquisar cada edição, compilaram-se os excertos relacionados à Matemática para posterior análise à luz do referencial teórico-metodológico.
No estudo da Matemática na revista O ECHO, além do referencial teórico-metodológico são apresentadas características da revista e uma análise das curiosidades matemáticas ali presentes.
2 A história cultural como aporte teórico-metodológico
A história cultural se ocupa com a pesquisa e representação de determinada cultura em dado período e lugar, como: relações familiares, língua, tradições, religião, arte e algumas ciências. Segundo Chartier (1990), uma questão desafiadora para a história cultural é o uso que as pessoas fazem dos objetos que lhes são distribuídos ou modelos que lhes são impostos, uma vez que há sempre uma prática diferenciada na apropriação dos objetos colocados em circulação. Nessa perspectiva, pode-se dizer que a imprensa pedagógica, aqui representada pela revista O ECHO, foi um veículo para a circulação de ideias que traduziam valores e comportamentos que se desejava ensinar – a prática religiosa católica – postas em convergência com outras estratégias políticas e culturais no RS.
Conforme Chartier (1990), as noções complementares de práticas e representações são úteis para examinar os objetos culturais produzidos, os sujeitos produtores e receptores de cultura, os processos que envolvem a produção e a difusão cultural, os sistemas que dão suporte a esses processos e sujeitos e as normas a que se conformam as sociedades através da consolidação de seus costumes. Para a produção de uma revista, como O ECHO, foram movimentadas determinadas práticas culturais e também representações, sem contar que a própria revista, depois de produzida, difundia novas representações e contribuía para a produção de novas práticas.
Para Chartier (1990), as práticas culturais que aparecem na construção de uma revista são tanto de ordem autoral (modos de escrever, pensar ou expor o que será escrito), como editoriais (reunir o que foi escrito para constituí-la em revista), ou ainda artesanais (a construção da revista na sua materialidade). Da mesma forma, quando um redator se põe a escrever uma revista, ele se conforma a determinadas representações do que deve ser uma revista, a certas representações concernentes aos temas por ele desenvolvidos. Este redator também poderá se tornar criador de novas representações que encontrarão no devido tempo uma ressonância maior ou menor no circuito do leitor ou na sociedade mais ampla.
A leitura de uma revista também gera práticas criadoras, podendo produzir concomitantemente práticas sociais. Essa leitura poderá ser individual ou coletiva, e o seu conteúdo poderá ser imposto ou rediscutido. A partir da leitura e da difusão da revista, poderão ser geradas inúmeras representações novas sobre os temas que a atravessam, que em alguns casos poderão passar a fazer parte das representações coletivas. De acordo com Chartier (1990), a história cultural tem por principal objeto identificar o modo como “em diferentes lugares e momentos uma determinada realidade cultural é construída, pensada, dada a ler, por diferentes grupos sociais” (CHARTIER, 1990, p. 17), o que está fortemente relacionado à noção de representação.
Serra (2010) complementa que o trabalho com revistas educacionais, na perspectiva da história cultural:
Possibilita a reconstrução histórica das práticas específicas desenvolvidas pelos autores, como também permite redesenhar os leitores visados por tais práticas, portanto a importância do estudo dos periódicos na sua materialidade. A partir do próprio impresso é possível recompor os projetos específicos como estratégias que visam a públicos leitores característicos (SERRA, 2010, p. 25).
Segundo Valente (2007), pensar os saberes escolares como elementos da cultura escolar, realizar o estudo histórico da matemática escolar, exige que se devam considerar os produtos dessa cultura no ensino de Matemática, que deixaram traços que permitem o seu estudo, como a revista O ECHO, principal fonte documental desta investigação.
3 A revista O ECHO e sua história
Desde que retornaram ao RS, em 1842, os Jesuítas concentraram suas atividades missionárias no processo de instrução do povo gaúcho, em particular nas colônias de imigrantes alemães. Segundo Rambo (1994), as escolas paroquiais estiveram sob o comando da Ordem por, aproximadamente, 70 anos, orientando os professores paroquiais e melhorando a qualidade do ensino nessas colônias de imigrantes.
Devido à necessidade de formar padres e professores para essas comunidades, a Ordem criou, em São Leopoldo/RS, o Colégio Conceição3. Nos anos seguintes, floresce uma rede de ginásios dos Jesuítas em importantes cidades do Rio Grande do Sul e Santa Catarina, alavancando o processo de instrução na região sul do Brasil.
No ano de 1890, surge o Colégio Anchieta de Porto Alegre. Mantido e dirigido pelos padres da Companhia de Jesus, foi fundado como um simples colégio. No princípio, com a denominação de Colégio dos Padres, era destinado somente a meninos, sendo dividido em duas seções: alemã e brasileira. A preocupação máxima não era com a alfabetização, mas com a orientação moral e religiosa de seus alunos. (O ECO, 1965).
Em 1897, ainda como externato do Colégio Conceição, o Colégio muda de nome, passando a se chamar São José. A denominação que o faria entrar para história do RS, como Colégio Anchieta, aconteceu em 1901, em homenagem ao Padre José de Anchieta, um fiel intérprete e seguidor da espiritualidade de Santo Inácio de Loyola, fundador da Congregação dos Jesuítas. Em 1903, passa a ser externato do Ginásio Nossa Senhora da Conceição. Segundo Leite (2005), em 1908, como estabelecimento independente, o Anchieta foi equiparado ao Colégio Dom Pedro II. Já em 1911, torna-se estabelecimento autônomo devido à reforma ocasionada pela Lei Orgânica do mesmo ano. A partir de 1942, a denominação do colégio passou a ser Colégio Anchieta.
Complementa-se que, “após 1963, com o início da transferência dos alunos para o novo prédio, adotou-se o princípio da coeducação, com rapazes e moças estudando lado a lado, quando a tradição nos colégios confessionais mantinha a separação dos sexos”. (COLÉGIO ANCHIETA, 1990, p. 47). O Colégio Anchieta ainda está em funcionamento e completará, este ano, 129 anos de atividades junto à comunidade porto-alegrense.
Em 1914, no seu sétimo ano de atividade de forma independente, o Anchieta, como é conhecido, passa a editar a revista O ECHO, destinado à mocidade brasileira, abordando temas pertinentes em suas diferentes épocas de circulação. Sua publicação aconteceu pela Typographia do Centro, localizada em Porto Alegre, no período entre abril de 1914 e dezembro de 1931. A partir de 1932, a revista passa a ser denominada O ECO, devido à reforma ortográfica. Segundo Leite (2018), a designação do nome da revista O ECHO se dá:
No sentido de que os ensinamentos ressoassem fortemente, produzissem eco nos jovens, nas famílias, em toda a população católica. Para os seus precursores, todos de origem alemã, essa deveria ter o mesmo efeito do eco produzido nos Alpes da Europa, onde em sua maioria tiveram sua infância. Nesses locais, os pastores caminhavam pelas montanhas e ao chamarem seus animais produziam sons, através de instrumentos que ecoavam por toda a região, sendo algo típico que a população costumava a ouvir. (LEITE, 2018, informação verbal4).
A revista ECHO tinha circulação mensal, destinada à comunidade escolar, principalmente à mocidade estudiosa, conforme inscrição na capa das revistas publicadas, reunindo diversos temas. De acordo com Leite (2018), o corpo de redatores era constituído por um diretor e colaboradores, que enviavam artigos para as edições da revista O ECHO. Na Figura 1, apresentam-se capas da revista investigada em diferentes períodos, inicialmente com a denominação O ECHO, vigente até dezembro de 1931, e depois sob a denominação O ECO.
Nas duas primeiras décadas, a capa da revista apresentou poucas alterações. Já nos anos seguintes, verificaram-se alterações com certa frequência, apresentando, por exemplo, imagem de colégios pelo país (objetivando buscar novos assinantes), personagens da história do Brasil, esportes, profissões, pontos turísticos do Brasil, entre outros.
Há um número de revistas de diversas espécies: revistas para todos sem distincção de classe, e revistas especiaes para as diversas classes de pessoas. Há revistas jurídicas, há revistas médicas, há revistas commerciaes e industriaes, há revistas marítimas e militares, há revistas eclesiásticas, até para a infância há não sei quantas revistas infantis. Só a mocidade não tem um a revista própria, uma revista feita especialmente para ella. É uma lacuna por demais sensível e que urge preencher. Pois, essa classe poderosa em número, essa classe a que se dá tal importância que é chamada esperança da pátria, será admissível que careça de uma vantagem de que gozam os outros? Eis a origem do “ECHO”: nasceu da necessidade evidente de ter também a mocidade uma revista própria, exclusivamente sua. (O ECHO, 1915, p. 1)5.
Editada, inicialmente, a cada vinte e cinco dias, com o primeiro número em fevereiro e o último em novembro de cada ano, a revista totalizava 12 edições por ano. Uma das revistas, normalmente a última do ano, abrangia dois números, já que em janeiro ela não era editada em virtude das férias escolares. A 1ª edição foi registrada em abril de 1914:
Sahiu á luz o 1º número do O ECHO, revista mensal illustrada, na qual além de muitos colaboradores competentes que, em suas columnas, se dedicaram aos interesses da mocidade estudiosa do Brasil, os próprios alunos debaixo da direção de seus mestres, se estréam no manejo da pena. No suplemento “Echos dos Collegios” trocam os jovens escriptores impressões e notícias que particularmente affectam a vida internas dos collegios. (RELATÓRIO ANCHIETA, 1914, p. 28).
Cada edição era a continuação da anterior, inclusive na paginação, sendo que durante o ano eram publicadas de 350 a 430 páginas. O ano representava um volume, destacado em números romanos, e o mês representava um número natural. Os diferentes exemplares traziam artigos escritos e muitas gravuras, sendo sua estruturação semelhante em todas as edições. Nos 40 primeiros anos, a edição tinha um formato de 16 cm x 24 cm. Já em 1963, a revista ficou maior, com formato 32 cm x 23 cm, passando a ter circulação bimestral.
Nos artigos escritos na revista O ECHO, são apresentados poemas, notícias, reflexões de padres e professores, conferências, variedades, anedotas, contos, publicações de premiações de alunos por redação ou por competição esportiva, anúncios de propagandas, ciências, invenções, artes, astronomia, reforma da língua portuguesa, descobertas, sendo que, após 1950, começam a aparecer artigos direcionados à prática esportiva, como futebol, basquetebol, entre outros. Nesses artigos, também há ilustrações, como fotografias de colégios, imagens de papas, padres, alunos, ex-alunos, personagens da história do Brasil, santos da Igreja Católica, paisagens, ilustrações de textos, cenários de guerra, futebol e humor.
Para este artigo, foram examinados os exemplares da revista O ECHO, desde sua primeira publicação, em abril de 1914, até dezembro de 1931, totalizando 216 edições mensais.
4 A Matemática na revista O ECHO
Ao analisar as 216 edições da revista O ECHO, os excertos constituídos por enigmas, charadas matemáticas, curiosidades, situações problemas, entre outros, foram destacados. Em diversas edições da revista, observou-se a presença de fragmentos que trazem curiosidades matemáticas, que são o objeto de análise deste artigo.
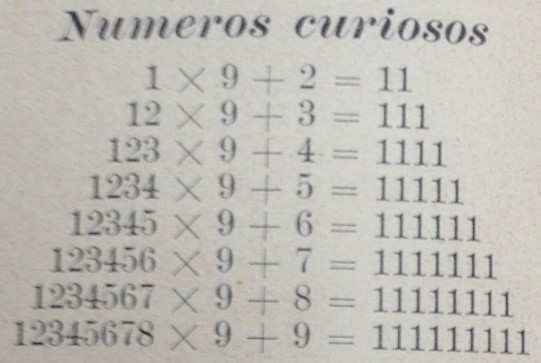
Na primeira edição da revista O ECHO, observa-se uma multiplicação curiosa envolvendo o enfileiramento dos 9 primeiros números do sistema decimal, com exceção do 8, conforme excerto mostrado na Figura 2:
O excerto apresentado na Figura 2 traz uma curiosidade numérica que envolve o produto do número 12345679 (observe que é um número formado pelos algarismos de 1 a 9, exceto o 8) pelos múltiplos de 9, compreendidos entre 9 e 81, resultando sempre em número com nove algarismos repetidos. Nota-se que o algarismo que se repete é o próprio multiplicador dividido por 9, ou seja:
12345679 x 9 = 111111111 (9 ÷ 9 = 1)
12345679 x 18 = 222222222 (18 ÷ 9 = 2)
12345679 x 27 = 333333333 (27 ÷ 9 = 3)
12345679 x 36 = 444444444 (36 ÷ 9 = 4)
12345679 x 45 = 555555555 (45 ÷ 9 = 5)
12345679 x 54 = 666666666 (54 ÷ 9 = 6)
12345679 x 63 = 777777777 (63 ÷ 9 = 7)
12345679 x 72 = 888888888 (72 ÷ 9 = 8)
12345679 x 81 = 999999999 (81 ÷ 9 = 9)
No excerto mostrado na Figura 3, observa-se outro resultado numérico interessante envolvendo a soma dos nove algarismos do sistema decimal. Num primeiro momento, iniciando por 9 e, a seguir, por 1. Somando-se todos esses números, obtém-se o 45.
A curiosidade consiste em subtrair os números obtidos quando descritos em ordem decrescente (minuendo) pelo descrito em ordem crescente (subtraendo). O resultado dessas subtrações consiste nos nove algarismos do sistema decimal, logo, ao somá-los, o resultado igualmente será 45.
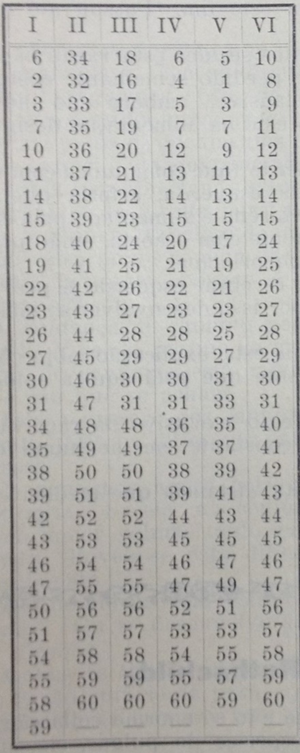
Já a Figura 4 traz uma tabela envolvendo os números naturais de 1 a 60. Pede-se a uma pessoa que pense num número qualquer de 1 a 60 e informe em que coluna o número se encontra na tabela. A partir da resposta dada, responde-se o número que foi pensado. Para isso, bastará somar os números da segunda linha das colunas onde o número pensado se encontra. Se a pessoa pensou no número 22, por exemplo, esse número se encontra nas colunas I, III e IV. Então, os números da segunda linha dessas colunas são: 2, 16 e 4, cuja soma que é 22 e resulta no número pensado.
O excerto, apresentado na Figura 4, é uma curiosidade matemática que explora a adivinhação de números entre 1 e 60 e exige a interação e a atenção entre os envolvidos, explorando o pensamento matemático de forma lúdica. A localização de cada número nas colunas está associada à sua representação no sistema de numeração de base 2. Por exemplo:
a). 1810 = 010012, pois 18 = 0 x 20 + 1 x 2¹ + 0 x 2² + 0 x 2³ + 1 x 24. Logo, o número 18 se encontra na 1ª coluna da tabela, que corresponde ao 2, e na 3ª coluna, que corresponde ao 16, pois 2 + 16 = 18.
b). 6010 = 0011112, pois 60 = 0 x 20 + 0 x 2¹ + 1 x 2² + 1 x 2³ + 1 x 24 + 1 x 25. Portanto, o número 60 se encontra 2a, 3a, 4a e 6a colunas da tabela, que correspondem a 32, 16, 4 e 8, respectivamente, resultando na soma 60.
As curiosidades apresentadas no Quadro 1 envolvem os números 37 e 3367. No primeiro caso, ao multiplicar o 37 por 3, 6, 9 12, 15, 18, 21, 24, isto é, aumentando sempre 3, obteremos um número com três algarismos repetidos. De forma mais surpreendente é o resultado da multiplicação de 3367 por 33, 66, 99, 132, 165, 185, 231, 264 e 297, ou seja, por um fator ao qual se soma para a multiplicação seguinte, o número 33. Assim, obteremos como resultado um número com seis algarismos iguais.
A primeira curiosidade envolve uma multiplicação entre o número 37 e os múltiplos de 3 compreendidos entre 3 e 27. O excerto descrito no Quadro 1 apresenta os nove produtos possíveis. Observa-se que cada produto pode ser obtido, rapidamente, ao se dividir o múltiplo de 3 por 3 e se repetir o quociente obtido três vezes lado a lado. Por exemplo:
a) 37 x 3 = 111 3 ÷ 3 = 1. Três vezes o 1 lado a lado = 111.
b) 37 x 15 = 555 15 ÷ 3 = 5. Repete-se o 5 três vezes = 555.
c) 37 x 24 = 888 24 ÷ 3 = 8. Três vezes o 8 lado a lado = 888.
Complementa-se que a soma dos algarismos repetidos de cada produto é igual ao multiplicador do qual ele se originou, ou seja:
Na segunda curiosidade numérica apresentada no Quadro 1, multiplica-se o número 3367 pelos múltiplos de 33 compreendidos entre 33 e 297. Observa-se que cada produto pode ser obtido, de forma prática, ao se dividir o múltiplo de 33 por 33 e se repetir o quociente obtido seis vezes lado a lado. Por exemplo:
a) 3367 x 33 = 111111 33 ÷ 33 = 1. Repete-se o 1 seis vezes = 111111.
b) 3367 x 132 = 444444 132 ÷ 33 = 4. Seis vezes o 4 lado a lado = 444444.
c) 3367 x 297 = 999999 297 ÷ 33 = 9. Repete-se o 9 seis vezes = 999999.
Verifica-se ainda que a soma dos algarismos repetidos de cada produto, dividida pelo respectivo quociente dos múltiplos de 33, é igual a 6, total de algarismos repetidos em cada resultado. Ou seja:
a). 66 x 3367 = 2 x 33 x 3367 = 222222 2 + 2 + 2 + 2 + 2 + 2 = 12 ÷ 2 = 6.
b). 165 x 3367 = 5 x 33 x 3367 = 555555 5 + 5 + 5 + 5 + 5 + 5 = 30 ÷ 5 = 6.
Ressalta-se que as duas curiosidades descritas no Quadro 1 evidenciam a preocupação dos editores do ECHO em desenvolver, na mocidade estudiosa, habilidades para o cálculo escrito e mental.
Na Figura 4, apresenta-se uma curiosidade em que, multiplicando-se o número 9 por 1, depois por 12, logo por 123, a seguir por 1234 e assim sucessivamente, até 12345678, acrescentando ao grupo anterior os algarismos 5, 6, 7 e 8 e somando ao resultado os números 2, 3, 4, 5, 6, 7, 8 e 9, respectivamente, o resultado será composto só de algarismos 1.
A curiosidade apresenta oito resultados interessantes, a partir de multiplicações por 9 e somas de 2 a 9, sendo que os resultados são números com todos os algarismos iguais a 1. Observa-se que a quantidade de algarismos 1 coincide com a parcela que é adicionada a cada produto, sendo que o aumento gradativo do número de algarismos do resultado está relacionado ao aumento de um algarismo, em ordem crescente (2 a 8), no primeiro fator das multiplicações.
Na curiosidade apresentada na Figura 5, os resultados são obtidos ao substituir o fator 9 da curiosidade ilustrada na Figura 4 pelo fator 8, começando a soma com 1 e não com 2, até terminar com 9.
Nessa curiosidade numérica, observam-se nove multiplicações por 8 e somas crescentes de 1 a 9, sendo que a quantidade de algarismos do resultado de cada cálculo é igual à parcela que está sendo adicionada ao produto. Verifica-se também que há o aumento de um algarismo, em ordem crescente (2 a 9), no primeiro fator das multiplicações e o aumento de um algarismo, em ordem decrescente (8 a 1), nos resultados finais de cada expressão numérica.
Outra curiosidade numérica encontrada na revista O ECHO envolve o número 91. Ao multiplicar 91, sucessivamente, por 1, 2, 3, 4, 5, 6, 7, 8 e 9, obtém-se os resultados ilustrados na Figura 6.
Na curiosidade observada na Figura 6, observa-se que os 1º e 3º algarismos de cada produto aumentam sucessivamente de 0 a 8 e de 1 a 9, respectivamente, ao passo que o 2º algarismo diminui sucessivamente de 9 a 1.
O desafio matemático apresentado na Figura 7 evidencia o conhecimento matemático explorado através de situações numéricas envolvendo as operações de multiplicação e adição. Ressalta-se que, nesse caso, o número 123456789 é multiplicado por um múltiplo de 9 e somado a um múltiplo de 10.
O excerto apresentado na Figura 7 traz outra curiosidade numérica. Envolve o produto do número 123456789 por múltiplos de 9, compreendidos entre 9 e 81, somados, respectivamente, aos múltiplos de 10, compreendidos entre 10 e 90, resultando sempre em número com dez algarismos repetidos. Ressalta-se que quando somamos os 10 algarismos, obtemos o múltiplo de 10 somado à multiplicação do 123456789 pelo múltiplo de 9.
No recorte apresentado na Figura 8, observa-se uma curiosidade que utiliza o conhecimento matemático para identificar o dia e mês de nascimento de uma pessoa.
Na atividade proposta, observam-se os procedimentos para resolução seguidos de exemplo que auxilia o leitor em sua compreensão. A lógica apresentada na atividade pode ser decifrada por meio de uma expressão algébrica. Nessa expressão, usa-se a incógnita x para o dia de nascimento e a incógnita y para o mês de nascimento. Seguindo as etapas de resolução sugeridas pelos editores da revista, chega-se à seguinte expressão algébrica (1):
Para encontrarmos o dia e o mês de nascimento, substitui-se o x da expressão obtida pelo dia de nascimento, multiplicando-o por cem e somando-o com y, que corresponde ao mês de nascimento. Por exemplo, se uma pessoa nasceu no dia 22 de maio, teremos x = 22 e y = 5. Substituindo os valores na expressão 100x + y, obtém-se 100.22 + 5 = 2205, em que 22 é o dia de nascimento e 5 é o mês de nascimento.
Na sequência, apresentam-se duas situações problemas ou quebra-cabeças, localizados na revista O ECHO, em que o redator destaca que sua solução pode ser resolvida somente por gente esperta, conforme descrito no Quadro 2:
Resolvendo o problema descrito no Quadro 2, considerando o sistema monetário brasileiro atual, apresentam-se duas possíveis soluções:
1) O problema pode ser resolvido com base no teorema do resto da divisão de um número por outro. Dividindo 50, 30 e 10 pela série dos números primos, encontramos na divisão por 7 os restos 1, 2 e 3, e como quocientes 7, 4 e 1, solução que resolve a questão, pois, vendendo 7 laranjas a R$ 1,00, por exemplo, o 1º irmão terá recebido R$ 7,00, o 2º irmão, R$ 4,00 e o 3º irmão, R$ 1,00; e vendendo o restante a R$ 3,00 cada fruta, teremos:
1º irmão: R$ 7,00 + R$ 3,00 = R$ 10,00.
2º irmão: R$ 4,00 + R$ 3,00 ∙ 2 = R$ 10,00.
3º irmão: R$ 1,00 + R$ 3,00 ∙ 3 = R$ 10,00.
2) Na outra solução possível, considera-se que os vendedores de laranja efetuaram suas operações por diferentes preços, vendendo, cada um, quantidades diferentes de cada vez. Supondo que os preços sejam x e y e que as quantidades vendidas ao preço de x foram a, b e c, as quantidades vendidas ao preço de y, foram: 10 – a, 30 – b e 50 – c. Então temos (2) ou (3), onde (4):
Como se vê, estamos diante de um caso de indeterminação e, por isso, podemos atribuir quaisquer valores para a, b e c, contando que as quantidades que substituírem estes símbolos estejam em progressão aritmética, como estão os valores 10, 30 e 50, cuja razão é 20.
Assim, se a = 1 e b = 24, c será igual a 47.
Substituindo as quantidades representadas por a, b e c por esses valores numéricos, temos uma nova equação (5):
Assim, (6):
Pode-se atribuir a y um valor qualquer, porque temos uma equação com duas incógnitas. Fazendo-se y = R$ 1,38, por exemplo, o valor de x, será (7):
Os preços procurados serão, respectivamente, R$ 0,18 e R$ 1,38 por laranja.
De acordo com o estabelecido, os vendedores obtiveram o seguinte resultado:
O 1º irmão, que tinha 10 laranjas, vendeu 1 laranja por R$ 0,18 e 9 laranjas por R$ 1,38, o que resulta em R$ 12,42 e totaliza R$ 12,60 na venda final.
O 2º irmão, que tinha 30 laranjas, vendeu 24 laranjas a R$ 0,18, que dá R$ 4,32, e 6 laranjas a R$ 1,38, resultando em R$ 8,28, totalizando R$ 12,60 na venda.
O 3º irmão, que tinha 50 laranjas, vendeu 47 laranjas a R$ 0,18, obtendo R$ 8,46 e 3 laranjas a R$ 1,38, juntando R$ 4,14, perfazendo R$ 12,60 no total da venda.
Com a equação (8) podemos dar ao problema todas as soluções que quisermos, bastando, para isso, variar os valores de a, b, c e y.
No Quadro 3, descreve-se o outro problema proposto na revista O ECHO:
Analisando o problema descrito no Quadro 3, pode-se solucioná-lo da seguinte forma:
Seja x o número das vezes que Procópio jogou. Então a soma das entradas (S) será:
S = 4 + (4 + 1) + (4 + 2) ++... + [4 + (x – 1)]. Aplicando a fórmula da soma da progressão aritmética, temos (9):
A última entrada é: 4 + (x – 1) = x + 3; portanto, o sêxtuplo da última entrada será:
6 ∙ (x + 3) = 6x + 18. Representando este sêxtuplo, como diz o problema, a soma das entradas, temos a equação (10):
Resolvendo a equação de 2º grau obtida, encontramos x = 9 e x = -4. Como o segundo valor é negativo, não serve como solução para o problema. Logo, Procópio jogou 9 vezes.
Finaliza-se o estudo da Matemática na revista O ECHO com uma curiosidade relacionada à História da Matemática em que o redator fala da Álgebra e de sua evolução ao longo dos séculos, conforme descrito no Quadro 4:
O excerto descrito no Quadro 4 conta um pouco da evolução histórica da Álgebra. Observa-se que muitas coisas que hoje nos parecem evidentes são resultado de um trabalho de muitos séculos e de muitas tentativas, fato esse que se verifica com a maior parte dos elementos que constituem a cultura moderna.
Com as curiosidades numéricas apresentadas neste artigo, os editores da revista buscavam despertar o interesse e a curiosidade da mocidade estudiosa, contribuindo para a circulação da revista e a formação da juventude católica nos colégios onde a mesma circulava.
5 Considerações finais
A partir do referencial da história cultural, investigou-se a revista ilustrada O ECHO, com ênfase nas curiosidades matemáticas veiculadas em suas 216 edições, no período entre abril de 1914 e dezembro de 1931. Essa revista foi editada pelo Colégio Anchieta por meio da Typographia do Centro, de Porto Alegre.
O público-alvo da revista O ECHO era a comunidade escolar e a mocidade católica brasileira, pois, segundo os editores, havia revistas para os diferentes públicos na época, exceto para os jovens estudantes. A ideia consistia em inserir algo que contemplasse todas as vozes, do sábio, do narrador, do colega jovial, do historiador, do jornalista, do religioso, tudo isso para a vida da mocidade estudiosa, por meio de textos, histórias, informações e curiosidades, enfatizando os aspectos morais, religiosos e a formação em geral.
Com relação à matemática, constatou-se que os editores da revista traziam enigmas e charadas, valorizando o raciocínio lógico do leitor com desafios a serem solucionados, premiando os leitores que enviassem soluções corretas. As curiosidades matemáticas encontradas na revista estão relacionadas a diferentes conteúdos matemáticos envolvendo Aritmética e Álgebra com foco no desenvolvimento de habilidades para o cálculo escrito e mental, resolução de problemas e História da Matemática.
O estudo histórico sobre as curiosidades matemáticas na revista O ECHO permitiu um adentramento na cultura escolar, num lugar e num tempo determinados, contribuindo assim para a História da Educação Matemática. Aponta-se a possibilidade de pesquisas que explorem as contribuições desta revista em outras áreas do conhecimento. Esta pesquisa terá sua continuidade com a investigação da Matemática na revista O ECO, cuja edição aconteceu de 1932 até 1969.