Introdução^*

Recorrentemente tem sido apontada a necessidade de a escola se adaptar ao novo mundo tecnológico em que as crianças desde tenra idade estão imersas e dominam. Nesse sentido, as escolas têm sido apetrechadas com diferentes recursos tecnológicos e tem sido feito um investimento na formação dos professores para a integração da tecnologia em suas práticas. No entanto, existe uma tendência para focar a atenção mais na tecnologia como ferramenta do que no modo como ela pode ser utilizada para ensinar importantes ideias (^{MISHRA; KOEHLER, 2006}), salientando-se que incorporar a tecnologia aos processos educativos apenas como complemento não é suficiente. A criação e implementação de ambientes de aprendizagem que tirem partido da tecnologia emergente requerem que os professores sejam detentores de um conhecimento aprofundado não só sobre a Matemática que ensinam mas também das ferramentas tecnológicas disponíveis e do seu potencial para explorar ideias matemáticas, assim como dos aspectos pedagógicos relacionados com o ensino e a aprendizagem da Matemática com tecnologia (^{MISHRA; KOEHLER, 2006}; ^{KIM, 2016}). O modelo teórico de Technological Pedagogical Content Knowledge (TPACK) (^{MISHRA; KOEHLER, 2006}) tem sido explorado como possibilidade de reconhecimento dos saberes de que os professores necessitam para uma efetiva integração da tecnologia ao ensino. Tal requer da formação inicial uma ponderação importante sobre a preparação para o ensino da Matemática com auxílio das tecnologias (^{NIESS, 2012}).

Na componente didática do curso de formação inicial de professores de Matemática para o 3º ciclo do ensino básico e ensino secundário¹ da Universidade de Lisboa, temos procurado promover o conhecimento dos futuros professores sobre o uso de tecnologias digitais no ensino da Matemática, sendo dada também particular atenção à perspectiva do ensino exploratório, em que se assume a necessidade de propor aos alunos tarefas desafiadoras, como problemas, investigações ou explorações, e de envolvê-los ativamente nas aulas, nomeadamente através da promoção da discussão coletiva das suas ideias matemáticas a partir da atividade realizada (^{PONTE et al., 2017}). Assim, este estudo tem com o objetivo compreender que conhecimentos profissionais evidenciam futuros professores de Matemática, no que diz respeito à integração das tecnologias digitais na planificação de aulas de Matemática, na perspectiva do ensino exploratório. Assumindo-se o modelo teórico de desenvolvimento de TPACK² do professor de Matemática (^{NIESS et al., 2009}), formulou-se a seguinte questão de investigação: que nível de desenvolvimento de TPACK revelam futuros professores de Matemática no que refere às dimensões do currículo, aprendizagem e ensino quando planificam aulas numa perspectiva de ensino exploratório?

Enquadramento teórico

O TPACK

A tecnologia, particularmente a tecnologia educacional, tem-se consolidado como um importante recurso enriquecedor das práticas pedagógicas, influenciando a Matemática que é ensinada e o modo como a aprendizagem dos alunos pode ser potenciada (^{NCTM, 2000}; ^{AMTE, 2006}). Por isso, os professores de Matemática têm sido encorajados a usar a tecnologia para melhorar a aprendizagem dos seus alunos.

Esta crescente ênfase na utilização da tecnologia no ensino e aprendizagem tornou possível e necessário o desenvolvimento de modelos para representar o conhecimento do professor, para uma integração efetiva da tecnologia no ensino de tópicos específicos. É nesse sentido que ^{Mishra e Koehler (2006)} desenvolveram o modelo teórico de TPACK, que integra e enfatiza as complexas interações entre três domínios desse conhecimento – conteúdo, pedagogia e tecnologia – quando aquelas têm lugar em contextos de sala de aula. O modelo TPACK tem influenciado significativamente a investigação sobre a integração da tecnologia na educação matemática, nomeadamente como base teórica para estruturar a conceptualização e a prática da formação inicial de professores e para investigar como os futuros professores adquirem esse conhecimento (^{NIESS et al., 2009}).

Com o propósito de guiar e avaliar o desenvolvimento do TPACK, ^{Niess et al. (2009)} propõem o Modelo de Desenvolvimento do TPACK do Professor de Matemática. Este modelo assenta na descrição de um processo sequencial de crescimento de cinco níveis, para a integração por parte dos professores de uma tecnologia particular que eles ainda não tenham explorado no ensino e aprendizagem da Matemática:

• 1..Reconhecer (conhecimento): se os professores são capazes de usar a tecnologia e reconhecer o seu alinhamento com o conteúdo matemático, mas ainda não a integram no ensino e aprendizagem da Matemática;

• 2..Aceitar (persuasão): quando os professores tomam uma atitude favorável ou desfavorável relativamente ao ensino e aprendizagem da Matemática com tecnologia adequada;

• 3..Adaptar (decisão): quando os professores se envolvem em atividades que os levam à decisão de adotar ou rejeitar o ensino e a aprendizagem da Matemática com tecnologia adequada;

• 4..Explorar (implementação): se os professores integram ativamente uma tecnologia adequada no ensino e na aprendizagem da Matemática;

• 5..Avançar (confirmação): se os professores avaliam os resultados da decisão de integrar tecnologia adequada no ensino e na aprendizagem da Matemática.

A Figura 1 apresenta uma descrição visual dos níveis acima descritos, nos quais os professores se envolvem à medida que desenvolvem o seu conhecimento e compreensão dos modos de integrar as múltiplas dimensões do conhecimento – conteúdo, pedagogia e tecnologia. O conhecimento descrito como TPACK, caracterizado por permitir o envolvimento ativo dos professores na orientação da aprendizagem dos seus alunos com tecnologia apropriada, emerge à medida que o conhecimento da tecnologia se amplia e começa a intersectar-se com o conhecimento didático, que integra pedagogia e conteúdo (^{NIESS et al., 2009}).

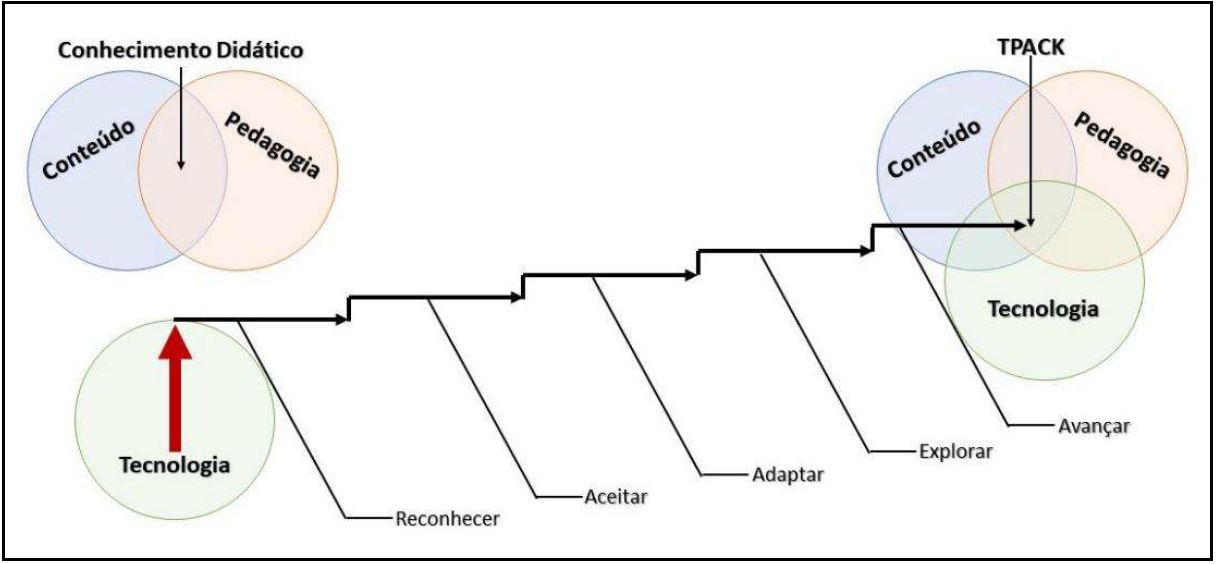
Fonte: Adaptada de ^{Niess et al. (2009}, p. 10).

Figura 1 – Descrição visual dos níveis de integração da tecnologia 

O modelo fornece, igualmente, contexto para os constructos do conhecimento do professor associados ao TPACK, estando estruturado em quatro temas principais: (i) Currículo e Avaliação, centrado no tratamento curricular do conteúdo matemático quando se ensina com tecnologia e na forma como o conteúdo será avaliado; (ii) Aprendizagem, focado nas conceções do professor em relação à aprendizagem dos alunos quando usam tecnologia; (iii) Ensino, centrado nas abordagens e metodologias de ensino, assim como na gestão do ambiente de sala de aula quando integra a tecnologia; e (iv) Acesso, referente ao uso, às limitações à integração e à disponibilidade da tecnologia na sala de aula. Os descritores dos temas e níveis deste modelo (dos quais se apresenta uma adaptação no Anexo A) permitem usá-lo para analisar o desenvolvimento do TPACK dos professores, por exemplo, a partir da planificação ou implementação de situações de aprendizagem (^{NIESS et al., 2009}).

A formação inicial do professor e o TPACK

^{Ponte e Chapman (2008}, p. 223) salientam que “[...] a formação de futuros professores de Matemática é um processo complexo que envolve muitos elementos que interagem entre si”. Por exemplo, ^{Albuquerque et al. (2006)} e ^{Ponte (2012)} salientam que um professor de Matemática necessita ter conhecimento relativo à natureza da Matemática, aos conteúdos matemáticos, aos objetivos curriculares, à forma de apresentar as ideias de modo a que sejam aprendidas pelos alunos, à forma como os alunos compreendem e aprendem os conteúdos matemáticos e à gestão da sala de aula.

Vários autores também se têm pronunciado sobre o conhecimento necessário ao professor para responder aos desafios e exigências de uma educação matemática no século XXI, significativamente transformada pelo uso de tecnologias digitais (^{ALBUQUERQUE et al., 2006}; ^{MISHRA; KOEHLER, 2006}; ^{NIESS, 2012}; ^{VOOGT; ROBLIN, 2012}). É por isso fundamental que a formação inicial de professores de Matemática assegure que todos os “professores em formação tenham oportunidades de adquirir os conhecimentos e experiências necessários para incorporar a tecnologia no contexto do ensino e da aprendizagem da Matemática” (^{AMTE, 2006}, p. 1).

Para ^{Niess (2012}, p. 332), “o reconhecimento e a aceitação do TPACK como o conhecimento que os professores necessitam para o ensino, exige que os formadores de professores repensem o design da preparação para o ensino da Matemática com tecnologias”, pelo que a formação dos futuros professores deve incluir nas suas unidades curriculares mais estratégias promotoras do conhecimento tecnológico, proporcionando-lhes experiências na integração da tecnologia em articulação com a Matemática e a Pedagogia. Estas experiências devem desafiar os futuros professores a considerar o impacto da tecnologia na aprendizagem da Matemática, preparando-os para planear e implementar situações de aprendizagem tendo em conta o conteúdo específico a ensinar, as características específicas dos alunos e as vantagens e limitações do uso da tecnologia (^{LEUNG, 2017}).

Em relação ao desenvolvimento do TPACK, ^{Mouza (2016)} identificou, a partir de uma revisão de literatura, três abordagens que têm sido seguidas na formação inicial de professores: (i) inclusão de uma disciplina de autoformação em tecnologia; (ii) estratégias de formação inseridas dentro de uma disciplina de educação tecnológica ou dentro de uma disciplina de didática ou metodologia; e (iii) estratégias de formação implementadas no contexto de todo o programa de formação. No entanto, ^{Mishra e Koehler (2006)} argumentam que a opção mais comum na formação dos professores no uso da tecnologia, com a qual se adquire habilidades de aplicação universal e conhecimentos básicos no uso de distintas tecnologias, tem-se revelado bastante problemática, dado o ritmo acelerado das mudanças tecnológicas, o inapropriado/incompleto design do software e a ênfase no quê, e não no como. Este enfoque leva os professores frequentemente a se considerarem mal preparados para o uso da tecnologia na sua prática docente (^{CHAI; KOH; TSAI, 2013}), pelo que se tem verificado uma tendência para usar abordagens caraterizadas por incorporar questões pedagógicas neste tipo de disciplina ou por levar as preocupações sobre o ensino com tecnologia para as disciplinas de pedagogia e metodologia que estruturam a formação inicial de professores.

A planificação na formação inicial

A elaboração de planos de aula é uma prática formativa corrente e com longa tradição na formação de professores de Matemática, uma vez que esta é considerada um dos meios para o FP desenvolver o conhecimento didático necessário para assumir, no futuro, o seu papel como docente. De facto, num estudo realizado por ^{Prescott, Bausch e Bruder (2013)}, a análise de planos de aulas que pretendiam ser exemplares revelou-se um bom indicador do conhecimento didático [Pedagogical Content Knowledge, no original] dos FPs.

Contudo, esta atividade do professor é, por vezes, conotada com uma perspectiva racionalista do ensino, orientada por um modelo linear de planificação, constituindo-se como sequência de passos previamente determinados (^{JOHN, 2006}). Tal tipo de planificação assenta na definição de um conjunto restrito de objetivos de aprendizagem comuns a todos os alunos, a partir do currículo prescrito, e independentes dos contextos em que o ensino ocorre. No entanto, a atividade de planificação do ensino na formação do professor não deve ser encarada apenas como uma aprendizagem em torno da elaboração de planos de aula (o produto final) mas como um processo complexo de tomada de decisão, em que estão envolvidos múltiplos fatores e no qual é necessário levar em conta a natureza negociada da aprendizagem (^{JOHN, 2006}).

Numa perspetiva de ensino exploratório que rompe com a lógica de transmissão de conhecimentos do professor para o aluno, que em geral os FPs experimentaram na sua própria escolarização, a atividade de planificação torna-se ainda mais exigente, na medida em que é necessário não só selecionar boas tarefas, que promovam uma atividade significativa para os alunos, como concetualizar um novo papel para o professor e os alunos (^{CANAVARRO; OLIVEIRA; MENEZES, 2014}). Um plano para uma aula com essas características deve ser um guião que contemple diversas ações dos vários intervenientes e as suas possíveis interações, em torno da realização de uma ou mais tarefas matemáticas. Nesse contexto, há que considerar o que se espera da atividade dos alunos, nomeadamente prevendo as estratégias que venham a delinear na resolução da tarefa e as dificuldades que possam enfrentar (^{PONTE; QUARESMA; MATA PEREIRA, 2015}), assim como o professor pode apoiar os alunos e tirar partido da sua atividade para construir novo conhecimento matemático.

No entanto, a planificação detalhada de aulas nesta perspectiva constitui um desafio mesmo para professores experientes, em particular no que diz respeito à antecipação das estratégias dos alunos na resolução das tarefas propostas (^{OLIVEIRA; CARVALHO, 2014}). Num estudo com FPs de Matemática, ^{Taylan (2016)} também refere que tal aspecto se mostra deficitário nos planos que eles elaboraram, a par de outros, tais como a formulação de objetivos para a aula e questões a colocar aos alunos, apesar de terem sido considerados ao longo do processo formativo, o que evidencia que este é um campo que merece a atenção da formação.

No que diz respeito à planificação de aulas centradas no uso da tecnologia, esta exige que o FP pense com detalhe em diversos aspectos que se ligam à articulação do conteúdo da aula e às características do recurso, podendo constituir uma experiência formativa importante, que lhe permita perceber com maior profundidade as suas potencialidades e limitações para o ensino (^{LEUNG, 2017}). A elaboração de um plano de aula assente na exploração de uma tecnologia pode justamente ajudar a romper com a falsa noção de linearidade associada à planificação e impelir o FP a repensar como se exploram os conceitos visados, assim como a identificar e estabelecer objetivos de maior nível de complexidade para os alunos. Ainda assim, ^{Ainley, Pratt e Hansen (2006)} chamam a atenção para o que designam como “paradoxo da planificação”, que pode surgir quando os professores pretendem propor tarefas que visam atingir determinados objetivos de aprendizagem, mas que acabam por se tornar pouco interessantes para os alunos, em face de uma situação em que propõem tarefas desafiadoras aos alunos, mas através das quais se torna mais difícil atingir os objetivos de aprendizagem definidos. Tal paradoxo pode surgir também quando são propostas tarefas a serem exploradas com a tecnologia no quadro do ensino exploratório, particularmente para os FPs que não têm experiência nestes campos.

Finalmente, ao pensar com grande detalhe, por exemplo, nas estratégias dos alunos para a resolução de uma tarefa com a tecnologia e nas suas eventuais dificuldades e no modo como o professor pode lidar com elas, o FP poderá também ganhar maior confiança no momento em que levar à prática o plano, apesar da natureza sempre imprevisível do processo de ensino e aprendizagem. A reflexão associada à própria elaboração do plano de aula, quando realizada colaborativamente com os seus pares ou formadores, particularmente após a lecionação da aula (^{MUTTON; HAGGER; BURN, 2011}), pode constituir também um elemento chave no desenvolvimento do TPACK do FP.

Contexto do estudo

O estudo que apresentamos realizou-se no contexto de duas unidades curriculares (UCs) da área de Didática da Matemática, no Mestrado em Ensino da Matemática para o 3º ciclo do ensino básico e ensino secundário, tendo sido lecionadas pelas duas primeiras autoras nos 2º e 3º semestres do curso, em 2016. Estas UCs (Didática da Matemática II [DMII] e Metodologia do Ensino da Matemática [MEM]) visam promover reflexão e discussão sobre questões fundamentais do currículo de Matemática, do seu ensino e aprendizagem e da prática profissional do professor, fornecendo aos FPs instrumentos para análise e interpretação da prática letiva dos professores. O trabalho em sala de aula assumiu um caráter eminentemente colaborativo por parte dos oito FPs que as frequentaram e promoveu discussões coletivas, favorecendo a adoção de uma abordagem exploratória. Para além disso, no que respeita ao desenvolvimento do TPACK dos FPs, as duas UCs seguiram uma abordagem global de introdução de estratégias de formação promotoras de um conhecimento tecnológico integrado.

Na UC de DMII, na temática do ensino e aprendizagem de Estatística, proporcionaram-se oportunidades para os FPs desenvolverem conhecimento sobre como ensinar investigações estatísticas com tecnologia, realizando uma investigação com recurso a software específico de Estatística. Foram discutidas as principais orientações didáticas para o ensino de Estatística, particularmente as investigações estatísticas em aula, o modo como as ferramentas tecnológicas podem apoiar o raciocínio estatístico e como os seus alunos poderiam realizar investigações estatísticas, incluindo as suas dificuldades e o modo como poderiam ajudá-los a ultrapassá-las. Após o término das aulas, os FPs realizaram, em grupo, um trabalho para avaliação, que consistiu na seleção/adaptação de uma tarefa (investigação ou outra) visando a promoção das aprendizagens dos alunos no tema da Estatística e na elaboração de um plano de aula, enquadrado curricularmente, que definia o modo como a tarefa seria trabalhada em aula, recorrendo a um recurso tecnológico à sua escolha. Os planos integraram, entre outros elementos, os objetivos que procuram atingir, o(s) método(s) de trabalho a implementar na sala de aula, as possíveis estratégias e dificuldades dos alunos na resolução da tarefa e os papéis do professor e do aluno. A tarefa e o respetivo plano de aula foram complementados com uma reflexão dos FPs, por meio da qual fundamentaram as opções tomadas na elaboração dos seus planos de aula.

Na UC de MEM, o foco do trabalho foi a análise dos modos de desenvolvimento do currículo, no que respeita às opções pedagógicas e didáticas e à consideração de alternativas e tomada de decisões nos diferentes momentos do processo de ensino e aprendizagem, nomeadamente promovendo a capacidade dos FPs em analisar, selecionar e conceber tarefas matemáticas e selecionar e promover o uso de recursos tecnológicos nos diferentes temas curriculares. Entre as atividades realizadas, destaca-se a preparação e dinamização de uma sessão de natureza prática, numa aula, por cada um dos grupos de FPs, assente na exploração de uma ferramenta digital. Essas sessões partiam da exploração de uma tarefa matemática proposta pelo grupo, a realizar com o suporte do recurso tecnológico escolhido, com o objetivo de permitir aos restantes FP desenvolver capacidades para utilização do recurso e compreender as potencialidades e limitações por ele apresentadas no que diz respeito ao nível de escolaridade escolhido (do 3º ciclo ou do ensino secundário). Dando continuidade a este trabalho, como componente da sua avaliação, os grupos elaboraram um plano de aula, curricularmente enquadrado, com base na tarefa e no recurso tecnológico selecionados para o ensino de um tópico específico do programa de Matemática, à sua escolha. Este documento integrou também uma parte introdutória de fundamentação das opções tomadas pelos FPs na elaboração do plano.

Os referidos planos de aula e respetivas fundamentações, solicitados aos FPs, criaram condições para mobilizarem o seu conhecimento nos domínios do conteúdo (matemático), pedagogia e tecnologia, resultante do trabalho que desenvolveram nas UCs, e as suas dificuldades na planificação de aulas com respeito à integração da tecnologia. No quadro seguinte, para cada UC, sintetizamos as propostas apresentadas pelos três grupos de FPs (cujos nomes são fictícios) nos seus planos, no que respeita aos tópicos matemáticos, às tarefas – classificadas segundo ^{Ponte (2005)} – e aos recursos tecnológicos selecionados.

Metodologia da pesquisa

A presente pesquisa foi realizada no contexto de duas UCs da área de Didática da Matemática (apresentadas na seção anterior), assumindo uma natureza interpretativa e qualitativa (^{BOGDAN; BIKLEN, 1994}). Os participantes do estudo são os oito FPs que frequentaram as referidas UCs e deram expresso consentimento quanto à sua participação na pesquisa. No entanto, o estudo propriamente dito foi realizado somente após o término das duas UCs.

A recolha de dados incidiu sobre os planos de aula elaborados pelos grupos de FPs nas duas UCs, incluindo os materiais que lhe estavam associados (nomeadamente as tarefas matemáticas e guiões elaborados para os alunos) e as reflexões escritas pelos grupos, nas quais eles exprimem e justificam as principais opções tomadas na elaboração do plano (nomeadamente a escolha da tarefa matemática e das ferramentas tecnológicas), assim como refletem sobre as aprendizagens realizadas e as dificuldades enfrentadas nessa atividade de planificação. Dado que neste estudo estávamos interessados em perceber o nível de desenvolvimento do TPACK dos FPs, particularmente quando planificam aulas numa perspectiva de ensino exploratório, não foi considerado o Grupo C, cuja abordagem escolhida para essa aula não se enquadra nessa perspectiva.

A análise de dados baseia-se nos níveis de integração de ^{Niess et al. (2009)}, relativamente ao desenvolvimento do TPACK, embora com algumas adaptações dos aspectos considerados pela autora, nomeadamente a redução do número de descritores dos diferentes níveis (ver Anexo A), uma vez que o presente estudo diz respeito apenas às intenções dos FPs expressas nos planos de aula e nas suas reflexões escritas, não apresentando elementos de prática efetiva de sala de aula. É de salientar que o nível 5 também não é considerado na análise dos dados, uma vez que não estava prevista a implementação destes planos em aula.

Em seguida, apresentamos os resultados da análise realizada, organizados de acordo com os três temas do modelo de análise (^{NIESS et al., 2009}) considerados para este estudo: currículo, aprendizagem e ensino. O tema Acesso não foi considerado, dado que os planos foram elaborados visando a uma hipotética sala de aula, que teria as condições materiais necessárias à sua concretização. Para cada um dos temas considerados, fazemos uma análise descritiva, apresentando extratos dos planos de aula e das respetivas fundamentações feitas pelos FPs, e indicamos o nível de integração da tecnologia evidenciado pelos grupos de FPs.

Resultados

Currículo

Os planos de aula elaborados pelos FPs na UC de DMII visavam, como requisito do trabalho proposto, à promoção da aprendizagem de Estatística com recurso à tecnologia. Na UC de MEM, tendo já oportunidade de diversificar as suas escolhas, os FPs optaram pelas seguintes áreas temáticas da aprendizagem da Matemática, identificando-as também como adequadas para serem abordadas com tecnologia: Álgebra, Geometria e Trigonometria.

Todos os tópicos específicos abordados nestes planos foram enquadrados curricularmente, de acordo com os programas de Matemática dos ensinos básico e secundário. Os planos de aula contemplaram objetivos de aprendizagem (mais ligados aos tópicos dos programas) e capacidades transversais (uma orientação curricular mais geral, que emerge de diferentes documentos analisados e discutidos nas UCs), tendo sido considerada a presença da tecnologia como recurso orientador das atividades dos alunos e para desenvolver capacidades associadas ao seu uso, evidenciando que os FPs reconhecem que exprimir ideias com tecnologia é útil para estes tópicos. Na Figura 2, apresentam-se alguns objetivos de aprendizagem e capacidades transversais propostas pelos FPs nos seus planos, nomeadamente aqueles que fazem referência ao uso da tecnologia.

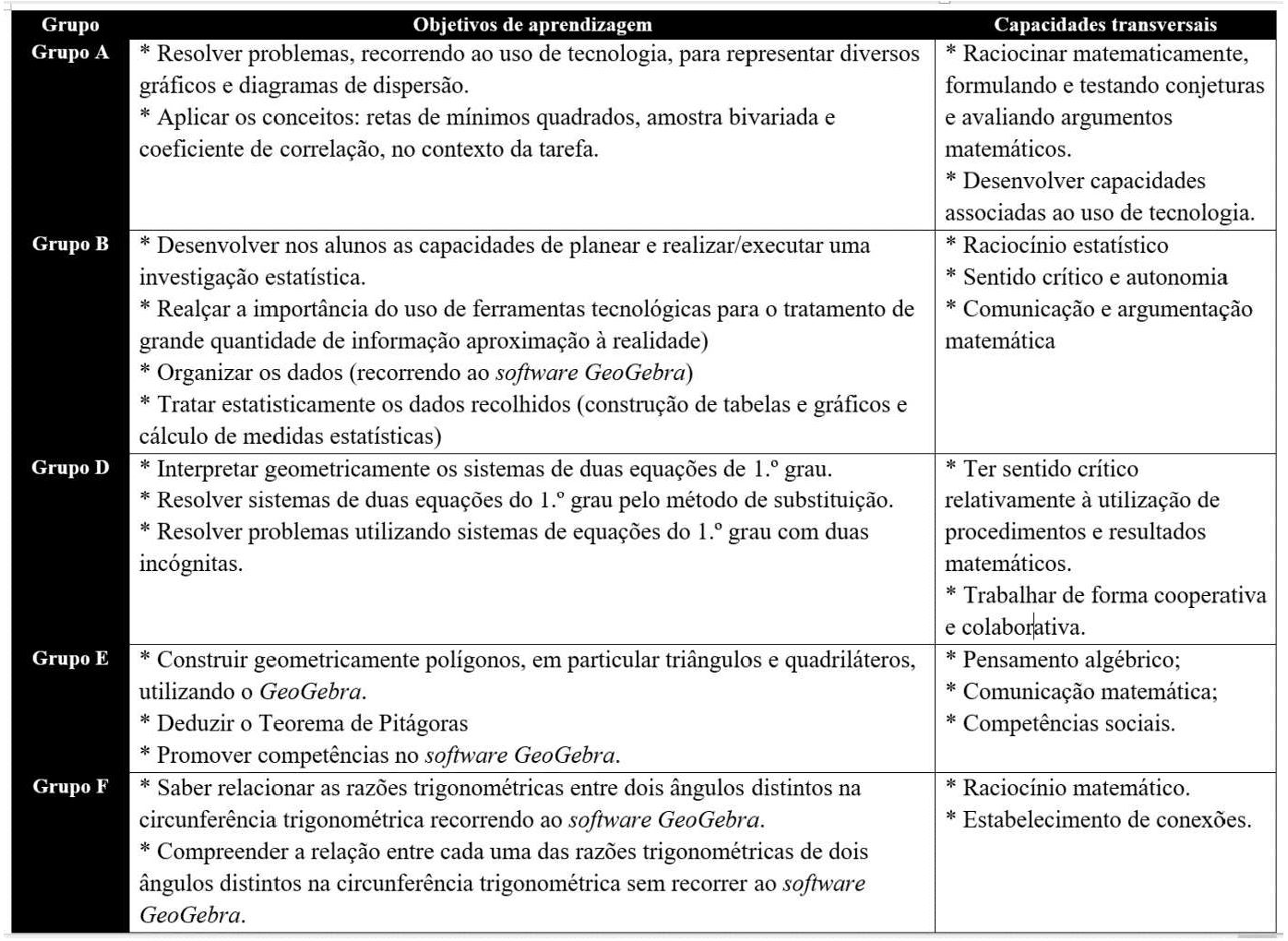
Fonte: Elaborado pelos autores.

Figura 2 – Objetivos de aprendizagem e capacidades transversais propostas pelos FPs nos planos de aula 

Os recursos tecnológicos selecionados para serem usados na sala de aula também constituem uma componente curricular importante para evidenciar o conhecimento dos FPs. Nestes cinco planos de aula, os FPs selecionaram o computador, mas salientaram nos planos, por exemplo, que “a sala de aula devia estar dotada de computadores” (Plano Grupo B), a fim de viabilizar o desenvolvimento das tarefas propostas. A escolha do software recaiu sobre o Excel (Grupo A) e o GeoGebra (demais grupos), ambos de licença livre, por reconhecerem que se trata de uma condição necessária à incorporação desta tecnologia na sala de aula, como mostra a justificação dada pelo Grupo B no seu trabalho: “O software GeoGebra foi a ferramenta tecnológica escolhida para trabalhar a tarefa em sala de aula. Trata-se dum software desenhado especificamente para o ensino, é dinâmico e gratuito podendo encontrar-se em www.geogebra.org”. A escolha destas tecnologias específicas foi fundamentada pelos FPs em razão do seu potencial e suas limitações para abordar os tópicos. Por exemplo, o Grupo A argumenta na sua reflexão que o Excel é apropriado para trabalhar a Estatística porque permite “realizar tarefas que envolvem grande quantidade de dados, permite que o aluno seja liberto de atividades rotineiras e repetitivas, dando-lhe a hipótese de explorar uma diversidade de conjeturas por ele formuladas”. Também o Grupo E, em relação ao uso do GeoGebra para trabalhar a Geometria, fundamenta sua escolha afirmando que “os programas de geometria dinâmica permitem o desenho, a manipulação e a construção de objetos geométricos, facilitando a exploração de conjeturas e a investigação de relações que precedem ao uso do raciocínio formal”. A referência, em ambas as citações, à possibilidade de os alunos explorarem conjeturas sugere que os FPs entendem o papel e os benefícios de utilizar tecnologia apropriada para desenvolver o raciocínio dos alunos ao adotar uma perspectiva exploratória de ensino e aprendizagem da Matemática.

Outro recurso curricular comum a todos os planos de aula é a elaboração de um manual ou guião de comandos do software respetivo, o qual não era solicitado aos FPs. Identificamos que os FPs elaboraram este documento com dois propósitos: para orientar a exploração e o uso do software e para promover o trabalho autônomo dos alunos durante a resolução da tarefa. Em todos os grupos, este guião está bem enquadrado com a tarefa proposta e é um recurso fundamental na sua planificação quando procuram promover a autonomia no trabalho dos alunos, a qual é essencial quando se pretende levar a cabo uma aula com abordagem exploratória.

Estes resultados sugerem, portanto, que os FPs conhecem tecnologias específicas para o ensino e aprendizagem da Matemática e identificam o seu possível alinhamento com os objetivos curriculares, sendo capazes de identificar tópicos que podem ser abordados com tecnologia e de reconhecer alguns benefícios da sua integração ao ensino e à aprendizagem, para reforçar as aprendizagens definidas nesses objetivos. Assim, no tema Currículo, os FPs demonstram ter alcançado o nível 3 (Adaptar, de integração da tecnologia).

Finalmente, uma das expectativas do nível 4 (Explorar, de integração da tecnologia) é que os FPs proponham ideias e estratégias de ensino para que a tecnologia (como recurso curricular) tenha um papel mais central na Matemática que os alunos devem aprender, o qual não se evidencia nos planos de aula. Alguns dos grupos, por exemplo, usam a tecnologia para explorar conhecimentos prévios (ver resultados do tema Aprendizagem) e outros utilizam-na para explorar inicialmente os conceitos, mas sentem a necessidade de consolidar a aprendizagem dos alunos sem o uso da tecnologia (ver os objetivos de aprendizagem do Grupo F na Figura 2). Em ambos os casos, embora sejam reconhecidos pelos FPs os benefícios dos recursos tecnológicos, a tecnologia não ocupa ainda um papel central no ensino e na aprendizagem, pelo que, globalmente, não atingiram este nível 4.

Aprendizagem

Nos planos de aula elaborados em DMII pelos grupos A e B, os FPs consideraram possíveis estratégias e dificuldades dos alunos na resolução das tarefas propostas. No que respeita às estratégias de resolução, os FPs fazem uma descrição muito geral do uso que os alunos podem fazer da tecnologia para responderem às questões da tarefa, que evidencia a sua utilização mais como ferramenta de ensino, para exprimir e verificar ideias matemáticas, do que de aprendizagem, para facilitar a compreensão de conceitos e desenvolver aspectos do pensamento matemático. Por isso, associam as possíveis dificuldades dos alunos mais a aspectos técnicos no uso das ferramentas do software específico e menos a aspectos conceituais ou da aprendizagem dos alunos quando envolvidos em atividades de alto nível (como as investigações estatísticas) com uso de tecnologia, como mostra o seguinte excerto de plano de aula do Grupo A (Figura 3).

Fonte: Plano de aula do Grupo A.

Figura 3 – Possível resolução e dificuldades associadas identificadas pelo Grupo A 

Para além disso, a análise da articulação entre os objetivos de aprendizagem propostos pelos FPs do Grupo A (ver Figura 2) e os conhecimentos prévios que eles consideram necessários para os alunos se envolverem de forma efetiva na aula (“Noção das definições dos seguintes conceitos: Média, Moda, Mediana, Quartil; Amostra Bivariada; Reta de Mínimos Quadrados; Coeficiente de Correlação”), particularmente na tarefa que lhe serve de base, também sugere uma utilização da tecnologia como uma ferramenta para exploração de conceitos previamente aprendidos, atribuindo à tecnologia um papel pouco relevante na promoção da aprendizagem de novos conceitos.

Nesta fase, os FPs também indicam outras estratégias que os alunos poderiam seguir na resolução das tarefas propostas sem fazer uso da tecnologia, evidenciando que concebem a tecnologia como um recurso opcional para atingir os objetivos curriculares, não sendo por isso uma ferramenta fundamental para facilitar a aprendizagem de tópicos específicos de Matemática. Este aspecto está bastante saliente na fundamentação que os FPs apresentam nos seus planos, a qual revela as suas concepções e pressupostos referentes ao uso da tecnologia para promover a aprendizagem dos alunos na sala de aula. Por exemplo, o Grupo A, na sua reflexão, considera que a tecnologia pode constituir um obstáculo à aprendizagem e exprime preocupação em relação ao foco da atenção dos alunos poder se desviar da aprendizagem dos tópicos matemáticos para a tecnologia:

A utilização da tecnologia nas aulas pode não ser sempre vantajosa para as aprendizagens dos alunos. Quando numa aula de caráter investigativo o professor reserva um tempo para o aluno trabalhar de forma autônoma, ainda que conduzido pela tarefa e pelo professor, este pode correr o risco de o aluno passar demasiado tempo a explorar o software utilizado, não se preocupando minimamente com a tarefa.

De modo semelhante, na fundamentação do seu plano de aula, os FPs do Grupo B evidenciam ter preocupações em relação ao tempo requerido para lecionar aulas com abordagem exploratória quando usam a tecnologia, aspecto que pode constituir um obstáculo à sua integração na sala de aula como ferramenta de aprendizagem da Matemática: “há ainda a dificuldade que se prende no tempo de aprendizagem necessário para uma eficiente utilização do software por parte dos alunos que, devido à extensão dos programas, inviabiliza que esta se faça em sala de aula”.

Atendendo a estas preocupações expressas pelos FPs e à sua tendência para conceberem a tecnologia mais como ferramenta de ensino do que de aprendizagem, consideramos que nesta fase da sua formação eles revelam conhecimentos de integração da tecnologia de nível 2 (Aceitar, de integração da tecnologia) no tema Aprendizagem, no que se refere à Estatística.

No entanto, os FPs revelaram ter progredido no seu conhecimento sobre a integração da tecnologia na aprendizagem da Matemática quando analisamos os planos de aula e reflexões elaborados por eles na UC de MEM. Por exemplo, os elementos do Grupo D expressam claramente que reconhecem a utilidade da tecnologia na aprendizagem da Matemática ao argumentarem no seu plano: “defendemos que o uso de novas tecnologias, como o computador, pode ser um suporte facilitador da aprendizagem dos alunos”. Este grupo também descreve possíveis dificuldades específicas dos alunos no uso da tecnologia para desenvolver aspectos do pensamento matemático e a compreensão de conceitos, como mostra a Figura 4, e explicita na fundamentação do seu plano de aula qual o foco da aprendizagem: “o foco serão as conclusões sobre a classificação dos sistemas de equações que os alunos poderão retirar da tarefa, através do GeoGebra, e não na manipulação do programa”. Nos pontos do excerto do plano presente na Figura 4, também fica evidenciado que o uso da tecnologia está ao serviço da aprendizagem da Matemática, incluindo ações de orientação do professor perante as dificuldades dos alunos, de modo a não permitir que, durante a resolução da tarefa, eles se dispersem na tecnologia, mas mantenham o foco na Matemática.

Fonte: Plano de aula do Grupo D.

Figura 4 – Possíveis dificuldades e atividade do professor identificadas pelo Grupo D 

No plano elaborado pelo Grupo E, os FPs também começaram a conceber que os alunos podem desenvolver o seu pensamento matemático quando a tecnologia é usada como uma ferramenta para a aprendizagem da Matemática, argumentando:

Achamos que um ambiente de aprendizagem integrado com a utilização da tecnologia permite a elaboração de uma maior quantidade de exemplos e contraexemplos num curto espaço de tempo, permitindo a disponibilidade dos alunos para processos cognitivos que se situam para além do cálculo e da compreensão de conceitos e relações matemáticas simples, deixando espaço para o desenvolvimento de processos reflexivos em torno das atividades propostas. (grifos nosso).

Esta posição do Grupo E viu-se refletida no plano de aula, principalmente na secção relativa ao momento de discussão final (Figura 5). Na planificação desta discussão, promovem-se processos cognitivos como argumentar, justificar e comunicar matematicamente as suas ideias, em torno da resolução da tarefa, e simultaneamente se promove o desenvolvimento de processos reflexivos, desafiando os alunos a refletirem sobre as estratégias e erros da sua resolução e das dos seus colegas.

Fonte: Plano de aula do Grupo E.

Figura 5 – Estratégias a adotar na discussão da tarefa indicadas pelo Grupo E 

Os FPs também preveem possíveis estratégias de resolução e dificuldades dos alunos associadas à compreensão dos conceitos, quando realizam tarefas com tecnologia, como mostra a Figura 6.

Fonte: Plano de aula do Grupo F.

Figura 6 – Possíveis estratégias de resolução e dificuldades identificadas pelo Grupo F 

Consideramos, por isso, que nesta fase da sua formação, os FPs dos grupos D, E e F atingem o nível 4 (Explorar, de integração da tecnologia) no tema da Aprendizagem, evidenciando capacidade para planear e refletir sobre o ensino e aprendizagem da Matemática, com a preocupação de orientar os alunos na compreensão através do uso da tecnologia, o que resulta num avanço significativo em relação aos planos de aula elaborados na UC de DM II, mostrando maturidade na planificação da aprendizagem dos alunos.

Ensino

Os FPs planificaram aulas de 90 ou 100 minutos centradas na exploração de uma tarefa e estruturadas em quatro momentos caraterísticos do ensino exploratório: (i) apresentação da tarefa; (ii), trabalho autônomo dos alunos na resolução da tarefa; (iii) discussão coletiva sobre as resoluções dos alunos; e (iv) sistematização das aprendizagens matemáticas. Esta estrutura já tinha sido abordada com os FPs nas UCs, mas não era requisito do trabalho que lhes foi proposto, pelo que esta sua opção evidencia que compreendem como se estruturam as aulas numa perspectiva de ensino exploratório e são capazes de adaptar e incorporar metodologias adequadas para satisfazer os objetivos curriculares e envolver os alunos em atividades que promovem pensamento de nível elevado, a discussão entre alunos e entre estes e o professor e a aprendizagem da Matemática com compreensão, usando a tecnologia. Na Figura 7, apresenta-se um exemplo dos momentos da aula propostos pelo Grupo F no seu plano.

Fonte: Plano de aula do Grupo F.

Figura 7 – Momentos da aula segundo o Grupo F 

Por seu lado, o Grupo B, diferentemente dos outros grupos, incluiu também no seu plano um momento inicial da aula, dedicado a uma breve revisão dos comandos do software GeoGebra, visando a sua utilização mais efetiva e autônoma por parte dos alunos na resolução da tarefa. Os FPs entendem que, deste modo, poderão assumir o papel de guias durante a exploração da tarefa, usando a tecnologia, ao invés de conduzi-la.

Dentro desta estrutura de aula, a tecnologia foi integrada como um recurso de apoio ao ensino, principalmente para orientar o trabalho autônomo dos alunos. Neste contexto, o professor teria um papel na monitorização das aprendizagens adquiridas pelos alunos durante a resolução da tarefa e do progresso dos alunos em relação ao uso do software:

Devido à tecnologia a ser utilizada requerer algum tempo de aprendizagem elaborámos um guião de ajuda ao aluno, de forma a criar competências no domínio da mesma e conferir autonomia à realização da tarefa por parte dos alunos. Desta forma, o Professor concentrar-se-á na dupla tarefa de verificar se os alunos apreenderam bem os conteúdos, neste caso, do Teorema de Pitágoras, e se se sentem progressivamente mais seguros e confiantes na sua capacidade de utilizar o GeoGebra. (Fundamentação do plano de aula – Grupo E).

Integrada nas estratégias de ensino, a seleção da tecnologia a usar em sala de aula foi bem fundamentada pelos FPs, que destacaram, principalmente, aspectos de natureza cognitiva e de gestão curricular. Por exemplo, tal como justificado pelo Grupo D no seu plano, o software selecionado permite motivar e envolver os alunos na exploração dos conteúdos matemáticos de forma dinâmica, em diferentes representações, poupando tempo na realização da tarefa:

O GeoGebra toma um papel importante na resolução desta tarefa, pois facilita a visualização e permite conjeturar, confirmar ou refutar hipóteses com velocidade e facilidade de construção gráfica. Desta forma, permite ao aluno uma melhor exploração da atividade matemática, pois funciona como um precioso instrumento de motivação.

Os FPs também referem que “a utilização da tecnologia como instrumento de apoio ao ensino-aprendizagem da matemática incentiva o trabalho colaborativo entre os alunos, aumentando as oportunidades de discussão e comunicação” (Fundamentação do plano de aula – Grupo E), o que evidencia que eles concebem a integração da tecnologia como determinante na gestão da sala de aula, nomeadamente na organização dos pequenos grupos de trabalho dos alunos. Por exemplo, a opção de que em cada grupo de trabalho existam alunos que saibam usar a tecnologia, para que possam apoiar o trabalho dos colegas, é considerada no plano do Grupo B, que indica, no campo relativo à atividade do professor, o seguinte: “O professor distribui o guião de trabalho da tarefa Hábitos Alimentares pelos alunos”; “Lê e explica os objetivos e a natureza da tarefa e anuncia as metodologias de trabalho nas diferentes fases”; “O professor assegura-se que em cada grupo existam alunos que têm facilidade em utilizar o software GeoGebra.”

Ainda em relação à gestão de sala de aula, são poucos os grupos que reconhecem os desafios que enfrentam os professores quando se utiliza a tecnologia na sala de aula. Por exemplo, na fundamentação do seu plano de aula, o Grupo E refere que a tecnologia cria “um ambiente de aula com mais movimento, mais ruído e mais sobressaltos para os professores”, mas não se identificam, no plano, estratégias específicas que ajudem a minimizar o impacto destes desafios.

No que diz respeito às intervenções do professor, identificamos nos planos algumas referências específicas ao seu papel em sala de aula quando o uso da tecnologia é considerado. Estas intervenções têm essencialmente duas naturezas: (i) levantamento de questões para guiar o trabalho dos alunos, apelando ao uso do software como facilitador dos procedimentos envolvidos, por exemplo, “Se vocês têm um software para trabalharem, por que é que calculam/fazem os gráficos à mão?” (Plano de aula – Grupo A); e (ii) dar informação e apoio técnico na manipulação do software e no uso do computador, por exemplo, “Nas questões relacionadas com o GeoGebra o professor pode dar uma ajuda mais direta e sempre que necessário falará para a turma (garantindo assim que todos os grupos concluam a construção [do triângulo retângulo])” (Plano de aula – Grupo E).

Estas intervenções evidenciam um ensino dedutivo, ou seja, o FP planifica a sua aula pensando nas formas de manter o controle daquilo que o aluno está a fazer, para garantir que os objetivos da aula sejam cumpridos dentro de um contexto sequenciado e organizado para tal fim. A Figura 8 mostra como o Grupo B também tem essa intenção de conduzir os alunos de forma direta e dedutiva na exploração do software durante a resolução da tarefa, neste caso, perante dificuldades que estes possam manifestar.

Fonte: Plano de aula do Grupo F.

Figura 8 – Apoio do professor perante possíveis dificuldades dos alunos, segundo o Grupo B 

Com base nestes resultados, podemos considerar que, de forma geral e no tema do Ensino, os FPs estão no nível 3 (Adaptar, de integração da tecnologia), pois, tal como foi evidenciado, a tecnologia é usada para reforçar os conceitos Matemáticos, os FPs adaptam as suas aulas para integrar a tecnologia de maneira efetiva, e as estratégias de ensino propostas são de natureza dedutiva, orientadas pelo professor, a fim de manter o controle do progresso das atividades da sala de aula. Também foi possível identificar nos planos elaborados um dos descritores de nível 4 (Explorar, de integração da tecnologia), referente ao envolvimento dos alunos na exploração dos conceitos matemáticos com tecnologia, em que o professor desempenha um papel de guia e orientador do trabalho dos alunos na sala de aula. Contudo, não se vislumbra nos planos que os alunos pudessem ser suficientemente envolvidos em atividades de pensamento de nível elevado, nem as estratégias de ensino indicadas pelos FPs são diversificadas ao ponto de incluir, para além das estratégias dedutivas, as estratégias de ensino indutivas, o que permitiria uma maior autonomia aos alunos na sua aprendizagem sobre o uso da tecnologia para resolver as tarefas propostas.

Conclusões

Os elementos que emergem da análise dos planos de aula e das reflexões escritas, incluindo os materiais que lhe estavam associados, oferecem indicações importantes sobre o conhecimento que os FPs de Matemática do 3º ciclo do ensino básico e ensino secundário estão a desenvolver relativamente à integração das tecnologias digitais na planificação de aulas de Matemática numa perspectiva de ensino exploratório.

Os FPs evidenciam um conhecimento de integração da tecnologia de nível 3 (Adaptação) (^{NIESS et al., 2009}) em relação aos temas Currículo e Ensino, na medida em que conhecem tecnologias específicas para o ensino e aprendizagem da Matemática e indicam o seu alinhamento com os objetivos curriculares, entendendo os benefícios de integrá-la no ensino para reforçar as aprendizagens definidas nesses objetivos, particularmente no que respeita ao raciocínio matemático dos alunos. Também é evidente que os FPs reconhecem o papel da tecnologia para reforçar e, em alguns casos, introduzir os conceitos matemáticos quando adotam uma perspectiva exploratória de ensino e aprendizagem da Matemática (^{CANAVARRO; OLIVEIRA; MENEZES, 2014}), adaptando as suas aulas para integrá-la de maneira efetiva. Contudo, propõem estratégias de ensino pouco diversificadas, de natureza essencialmente dedutiva e orientadas pelo professor, para manter o controle do progresso das atividades da sala de aula, sem envolver suficientemente os alunos em atividades de pensamento de nível elevado nem lhes dando muita autonomia na sua aprendizagem sobre o uso da tecnologia para resolver as tarefas propostas. De alguma forma, verifica-se neste estudo algo próximo do paradoxo da planificação referido por ^{Ainley, Pratt e Hansen (2006)}, no que diz respeito à atividade proposta com a tecnologia no quadro de objetivos de aprendizagem contidos num programa de Matemática construído sob a lógica de metas curriculares. Os FPs tendem a interpretar a solicitação que lhes foi feita para elaboração do seu plano de aula nesse quadro curricular estrito e, dessa forma, embora pretendam promover capacidades transversais como a resolução de problemas ou a comunicação, acabam por condicionar a atividade do aluno. Os FPs podem, por isso, requerer mais tempo e experiências significativas durante a sua formação, para aprender a usar a tecnologia e transformar o ensino, criando oportunidades de aprendizagem para os alunos.

No que respeita ao tema Aprendizagem, os FPs começaram por evidenciar conhecimento de integração da tecnologia de nível 2 (Aceitação), expressando diversas preocupações em relação ao uso da tecnologia na sala de aula como ferramenta de aprendizagem da Matemática numa abordagem exploratória. A descrição geral do uso que os alunos podem fazer da tecnologia na resolução das tarefas e as possíveis dificuldades que eles enfrentam, estas últimas associadas a aspectos técnicos no uso das ferramentas de software específico, também salientam que os FPs concebem a tecnologia mais como uma ferramenta de ensino e um recurso opcional para atingir os objetivos curriculares, não sendo por isso fundamental à aprendizagem de tópicos específicos de Matemática. O fato de os FPs terem uma reduzida experiência de lecionação e, consequentemente, dos alunos e seus processos de aprendizagem pode limitar bastante o desenvolvimento desta dimensão do seu conhecimento, pelo que serão as experiências significativas na formação inicial que poderão ajudá-los a ampliar e enriquecer o seu TPACK. Quanto a esse aspecto, salienta-se que, no decorrer do curso de formação, os FPs revelaram ter progredido no que tange à integração da tecnologia, elevando-a ao nível 4 (Exploração), mostrando maturidade na planificação da aprendizagem dos alunos. Na verdade, os planos finais dos FPs já evidenciam maior capacidade para planear e refletir sobre o ensino e aprendizagem da Matemática, com a preocupação de orientar os alunos para a aprendizagem com compreensão, um traço importante da abordagem exploratória, através do uso da tecnologia. Para tal podem ter contribuído as oportunidades de discussão e reflexão geradas na construção dos próprios planos e em trabalho colaborativo no seio de cada grupo (^{MUTTON; HAGGER; BURN, 2011}), assim como a sessão que dinamizaram com os colegas no âmbito da UC de MEM.

Com este estudo, evidencia-se a pertinência do modelo de análise adotado para avaliar o nível de TPACK dos FPs (^{NIESS et al., 2009}), embora assumindo desde o início a necessidade da sua adaptação, por ter sido originalmente pensado para descrever o conhecimento de professores em serviço. Este modelo poderá também constituir uma referência para a planificação de cenários de aprendizagem na formação inicial de professores, permitindo ao formador analisar o modo como os FPs estão a desenvolver o seu conhecimento e que aspectos necessitam aprofundar. Para além disso, destacou-se o potencial dos planos de aula para colocar em evidência o nível de TPACK dos FPs, tal como já observado no estudo de ^{Prescott, Bausch e Bruder (2013)} em relação ao conhecimento didático. Finalmente, os resultados deste estudo permitem-nos refletir sobre a formação desenvolvida no domínio da integração das tecnologias digitais no ensino da Matemática no curso. Reconhecendo que tal integração é complexa e que não existem soluções únicas e diretas, é importante que os FPs tenham mais oportunidades de entrar em contato com experiências concretas de uso da tecnologia com os alunos e, desejavelmente, de levarem os seus planos à prática, refletindo sobre a sua implementação em sala de aula, o que poderá vir a ocorrer no semestre final do curso.