INTRODUÇÃO E OBJETIVOS
As escolas da Rede Federal de Educação Profissional e Tecnológica (RFEPT) representam uma política pública importante na educação profissional, em especial para o nível do ensino técnico integrado ao ensino médio, logo, é natural que sejam avaliadas pelos seus resultados. Entretanto, medir a eficácia de instituições escolares, em geral, apresenta-se como um problema, já que essa ação se realiza por comparação e, frequentemente, discute-se a adequação ao comparar instituições com características e finalidades distintas por indicadores sintéticos.
Para medir a qualidade das escolas federais de educação profissional é preciso compreender melhor suas características, comparando-as às demais escolas de ensino médio do Brasil, inclusive pelos seus resultados. Todavia, também, há que considerar seu contexto e papel social. É plausível que esse objetivo possa ser buscado por diversos tipos de estudos qualitativos e quantitativos, entretanto dificilmente seria possível avaliar o contexto da escola de forma integral e plena em um único estudo. De fato, esse tipo de investigação é mais um processo contínuo e ininterrupto, que vai evoluindo ao longo do tempo, e o estudo aqui proposto é apenas um entre os muitos necessários.
As avaliações em larga escala no Brasil, particularmente as avaliações do Sistema de Avaliação da Educação Básica, o Saeb, têm permitido a realização de estudos extensivos. Tais estudos tratam das relações que podem ser estabelecidas entre o desempenho escolar dos alunos em testes de larga escala e os fatores individuais e contextuais - tanto internos quanto externos à escola - e que se associam ao aprendizado (Soares & Brooke, 2008).
Nesse contexto, o primeiro e mais importante objetivo deste artigo1 é realizar uma análise das correlações entre os desempenhos dos alunos das diferentes escolas de ensino médio, da rede pública e privada do Brasil no Saeb. O artigo analisa a edição de 2017 da avaliação e relaciona o resultado a características das escolas e de seu alunado. Em outros termos, o trabalho investiga e analisa os fatores intra e extraescolares que influenciam o desempenho dos estudantes de ensino médio, de forma diferencial pelo tipo de rede escolar, destacando-se os resultados das escolas federais de educação profissional, a partir dos conceitos de eficácia escolar e aplicação da metodologia de modelagem multinível multivariada aos dados do Saeb.
A aplicação da modelagem multinível multivariada na explicação simultânea dos desempenhos nas disciplinas de Língua Portuguesa e Matemática permite construir de forma mais sintética e precisa a análise dos fatores associados ao desempenho dos estudantes, quando comparada com estudos individualizados para cada disciplina. Um aspecto importante da presente análise é tentar medir o “efeito” do tipo de escola na proficiência condicionalmente a uma série de variáveis de controle, em particular a condição socioeconômica dos alunos e o critério de admissão na escola. Portanto, aqui, deve-se entender “efeito” como sendo a intensidade da correlação entre a variável e a proficiência, condicionada às variáveis explica- tivas do modelo.
Desse modo, no que concerne ao conceito de qualidade da educação e seus desdobramentos nos indicadores de avaliação e eficácia escolar, este, em um primeiro momento, pode ser um conceito subjetivo e polissêmico, e que tende a ser demasiadamente amplo. No entanto, conforme Soares (2009, p. 218):
A Unesco, em suas publicações mais recentes, postula que o aprendizado é um direito do aluno e, portanto, legitima a posição de que a educação deve ser também analisada pelos resultados dos alunos, caracterizados por seu aprendizado. Em outras palavras, se a educação escolar não produz o desempenho cognitivo dos alunos esta não é legítima.
Em conformidade com o exposto pelo autor, não se pode negligenciar a consideração do aprendizado na avaliação da qualidade. Da mesma forma, há outros aspectos que também precisam e podem ser considerados, como o da equidade e o da justiça social.
Logo, tendo em vista o conceito de qualidade da educação manifestado acima, um segundo objetivo do artigo é analisar os aspectos da qualidade das escolas federais de educação profissional por meio de outros indicadores de eficácia, particularmente o Índice de Desenvolvimento da Educação Básica, o Ideb, comparando-os com indicadores obtidos por meio dos modelos multiníveis. Pretende-se que essa análise contribua para uma exposição da limitação de se usar apenas alguns indicadores isolados na avaliação da qualidade da escola, sem levar em conta a potencialidade dos indivíduos e outros aspectos que o aluno traz consigo (background), além de outros fatores contextuais, internos e externos à escola, e sua influência para o aprendizado (Alves & Franco, 2008).
DESEMPENHO DAS ESCOLAS DE ENSINO MÉDIO NO SAEB 2017 E O IDEB
A partir da edição de 2017, as avaliações do Saeb passaram a ser censitárias e não mais amostral para as escolas públicas de ensino médio. Segundo o Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep), órgão responsável pelo Saeb e Ideb, isso permitiu calcular o índice por escola para esse nível de ensino. Para as escolas particulares, a aplicação da avaliação ocorreu de forma amostral, com a possibilidade de adesão voluntária (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira [Inep], 2018).
A Tabela 1 permite a análise da proficiência média por segmento das escolas (estadual, municipal, federal de educação profissional e particular) de 3º ano do ensino médio nas avaliações de Língua Portuguesa (LP) e Matemática (MT) que participaram da edição do Saeb de 2017. Essa proficiência foi calculada a partir da média aritmética das proficiências dos alunos em ambas as disciplinas avaliadas, agrupadas por segmento escolar. A medida do desempenho nas avaliações do Saeb é uma escala originalmente definida com média 250 e desvio padrão 50.
TABELA 1 Proficiência média nas avaliações de Língua Portuguesa e Matemática das escolas de 3º ano do ensino médio no Saeb 2017, segundo a rede escolar
| PROFICIÊNCIA MÉDIA | ||
|---|---|---|
| Língua Portuguesa | Matemática | |
| Federal | 330 | 357 |
| Estadual | 259 | 259 |
| Municipal | 272 | 275 |
| Particular | 315 | 329 |
Fonte: Elaboração dos autores com base em Inep (2018).
As escolas federais de educação profissional apresentaram proficiência média de 330 em LP e de 357 em MT superiores às médias das escolas das demais redes escolares e às médias nacionais, que foram de 268 em LP e 270 em MT (Inep, 2019a). As escolas particulares apresentaram as médias de 315 em LP e 329 em MT. As escolas estaduais, por sua vez, apresentaram médias de 259 em ambas as disciplinas avaliadas. As escolas municipais obtiveram médias de 272 e 275, em LP e MT, respectivamente, portanto, suas médias foram superiores às das escolas estaduais.
Entre as críticas que se pode fazer ao discorrer isoladamente sobre os resultados dos testes dos alunos presentes apenas ao final da etapa educacional em análise é que ela desconsidera os alunos que não participaram das avaliações, por exemplo, alunos infrequentes que possivelmente apresentam níveis de proficiências inferiores aos presentes. Por outro lado, e por razões óbvias, desconsideram-se os alunos que abandonaram ou foram reprovados na escola ao longo da etapa escolar. É também evidente que não se deseja um sistema educacional excludente ou que negue a educação a parte dos alunos. O Ideb, então, foi proposto como uma medida da qualidade de um sistema educacional que pondera não apenas os resultados dos testes, mas, também, as taxas de aprovação escolar na etapa considerada.
O Ideb foi instituído pelo decreto n. 6.094 de 24 de abril de 2007. Apesar de críticas que tem recebido (ver Soares & Xavier, 2013), ele é, ainda hoje, um dos principais indicadores de qualidade da educação básica no Brasil e acolhi- do por boa parte dos gestores e da sociedade. Assim sendo, é evidente, que mesmo sob críticas, o impacto que a divulgação do Ideb tem sobre a gestão escolar e as repercussões sociais que advêm dessa divulgação não podem simplesmente ser negligenciadas.
Assim como todo e qualquer indicador, ele apresenta virtudes e problemas. Sua composição sintética é, simultaneamente, uma virtude para sua assimilação pela sociedade, entretanto pode não evidenciar problemas em nichos educacionais mais específicos, conforme manifestado por Soares e Xavier (2013, p. 920):
Por outro lado, levam imediatamente ao uso de hierarquizações como forma de análise da realidade educacional. Grande parte da cobertura da imprensa se limita a isso. Analisar as escolas por uma hierarquização é uma opção metodológica muito pobre. Essa não é, entretanto, uma limitação do indicador. A solução é produzir e divulgar interpretações alternativas.
Em sua concepção o Ideb é definido como o produto de dois indicadores: o que mede o desempenho das escolas brasileiras a partir da média de proficiências nas disciplinas de LP e MT avaliadas no Saeb, padronizadas em uma escala de 0 a 10, e um indicador de rendimento escolar que se constitui pela média harmônica das taxas de aprovação da escola ao longo dos anos da etapa escolar considerada (Inep, 2019a). Desse modo, o Ideb da escola i na etapa j é dado pelo produto do indicador de desempenho pelo indicador de rendimento, isto é:
Portanto, um valor de Ideb baixo é explicado pelos resultados baixos na taxa de aprovação (menos alunos são aprovados) e/ou no desempenho nos resultados do Saeb (menos alunos alcançam boas notas). Entre escolas com mesmo desempenho no Saeb, terá maior Ideb aquela com maior taxa média de aprovação, e vice-versa.
O peso “igual” atribuído aos dois indicadores na formulação do índice não é suficientemente explicado no documento original do Ideb (Inep, 2018), porém parece ter sido escolhido propositalmente de tal forma a tornar o indicador sensível o bastante a alterações nas taxas de aprovação das escolas, evitando-se reprovações intencionais, por exemplo. Estudos mostram que não há uma linearidade na equivalência para trocas entre os pesos no indicador, e para níveis mais baixos de desempenho é mais fácil alcançar variações relevantes no índice a partir de variações nas taxas de aprovação (Soares & Xavier, 2013). De qualquer forma, parece que havia uma intencionalidade, segundo os autores, pelo menos em um primeiro momento, de forçar o aumento nas taxas de aprovação para níveis elevados antes de alcançar um aumento mais sensível nas taxas de desempenho.
O Ideb é, portanto, um indicador sintético e tem se mostrado eficaz como um indicador da qualidade da educação no Brasil, particularmente, da educação pública. Ele tem evidenciado dois problemas da qualidade da educação brasileira, exaustivamente apontados pela literatura desde os anos 1990: o baixo aprendizado dos alunos e as taxas de reprovação elevadas das escolas públicas. Assim, é natural em um primeiro momento que ele seja o principal parâmetro na percepção da qualidade da escola pela sociedade e, consequentemente, na elaboração das políticas públicas educacionais.
A Tabela 2 apresenta estatísticas do Ideb calculadas para os 4 segmentos escolares de ensino médio (federal, estadual, municipal e particular). O valor médio foi obtido pelo cálculo da média aritmética dos índices de cada escola, por tipo de rede escolar. Também, constam da Tabela 2 os valores de Ideb mínimo e máximo encontrados para cada segmento escolar.
TABELA 2 Ideb mínimo, médio e máximo das escolas de 3º ano do ensino médio no Saeb 2017, segundo a rede escolar
| ESTATÍSTICAS DO IDEB | |||
|---|---|---|---|
| Mínimo | Média | Máximo | |
| Federal | 1,9 | 5,2267 | 7,7 |
| Estadual | 1,0 | 3,8372 | 7,7 |
| Municipal | 1,9 | 4,0782 | 6,7 |
| Particular | 2,3 | 5,7756 | 8,4 |
Fonte: Elaboração dos autores com base em Inep (2018).
Para o ano de 2017, o Inep determinou como meta o valor de 4,4 para o Ideb das escolas públicas, e 6,7 para as escolas particulares. Na Tabela 2, o Ideb médio das escolas de educação profissional da rede federal (5,22) ultrapassa o da meta estipulada para as escolas públicas, enquanto a rede estadual (com Ideb médio de 3,83) e municipal (4,07) não atingiram a meta (Inep, 2018).
Conforme contextualizado na Tabela 1, as escolas federais de educação profissional obtiveram os maiores desempenhos médios na avaliação do Saeb, ligeiramente superiores aos das escolas particulares. No entanto, o Ideb médio deste segmento escolar (5,22) se mostra inferior ao das escolas particulares (5,77). De fato, como as escolas federais apresentaram desempenho superior nas avaliações do Saeb, consoante com os resultados apresentados na Tabela 1, e seu valor médio do Ideb é inferior ao das escolas particulares, isso, notadamente, se explica pelo menor índice de aprovação de seus alunos na etapa considerada.
A Tabela 3 apresenta a taxa de aprovação das escolas de ensino médio por tipo de rede escolar (federal, estadual, municipal e particular), a partir dos dados de indicadores de fluxo escolar disponibilizados pelo Inep dos anos de 2017 a 2019 (Inep, 2019b).
TABELA 3 Taxas de aprovação das escolas de ensino médio por tipo de rede escolar nos anos de 2017 a 2019
| TAXAS DE APROVAÇÃO | |||
|---|---|---|---|
| 2017 | 2018 | 2019 | |
| Federal | 85,8 | 87,72 | 89,10 |
| Estadual | 82,5 | 82,75 | 85,91 |
| Municipal | 84,9 | 84,41 | 87,33 |
| Particular | 95,5 | 95,87 | 96,26 |
Fonte: Elaboração dos autores com base em Inep (2019a).
Na Tabela 3, observa-se que as escolas de ensino médio da rede particular são aquelas que apresentaram as maiores taxas de aprovação, com médias acima de 95% nos três anos analisados. As menores taxas foram apresentadas pela rede estadual, com média aproximada de 83%. A média nos três anos analisados das escolas federais foi de aproximadamente 87%, e, tendo em vista que o índice do Ideb considera além das médias dos alunos da escola nas avaliações do Saeb as taxas de aprovação na etapa escolar, o fato de as posições das escolas federais no Ideb serem inferiores às das escolas particulares é reflexo das menores taxas de aprovação das instituições. Isso ocorre pois elas obtiveram médias nas avaliações do Saeb superiores às das outras redes de ensino, inclusive às da rede particular.
Os questionários contextuais aplicados no Saeb informam o Indicador de Nível Socioeconômico (Inse) das escolas que participaram da avaliação do Saeb na edição de 2017. Este indicador permite contextualizar as escolas por nível socioeconômico de seus alunos. As bases para a construção desse índice foram as respostas dos questionários contextuais dos alunos participantes do Saeb, e depois agregados por escola e apresentados na base de dados das respostas ao questionário das escolas em uma escala que varia de 1 a 7 (nível 1 corresponde à classificação do Inse “muito baixo” e 7 a “muito alto”), conforme classificação do Inep (Diretoria de Avalição da Educação Básica [Daeb], 2021).
A Tabela 4 apresenta a distribuição percentual das escolas pelo Inse e segmentada por rede escolar.
TABELA 4 Distribuição percentual das escolas pelo Indicador de Nível Socioeconômico no Saeb 2017, segundo a rede escolar
| NÍVEL SOCIOECONÔMICO | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Federais | 1,2 | 17,1 | 38,1 | 28,0 | 14,8 | 0,8 |
| Estaduais | 6,9 | 11,4 | 45,4 | 31,8 | 4,5 | 0,0 |
| Municipais | 4,5 | 16,2 | 20,1 | 39,0 | 18,2 | 1,9 |
| Particulares | 0,0 | 1,5 | 14,3 | 24,2 | 40,6 | 19,0 |
Fonte: Elaboração dos autores com base em Ministério da Educação (2019).
A partir da Tabela 4 conclui-se que cerca de 60% das escolas particulares são classificadas no nível socioeconômico 5 e 6 (médio alto e alto). Enquanto isso, a maioria das escolas dos segmentos federal, estadual e municipal estão classificadas nos níveis socioeconômicos 3 e 4 (médio baixo e médio).
Nesse sentido, apesar de as escolas federais de educação profissional atenderem a um público de nível socioeconômico inferior ao das escolas particulares e mais semelhante ao público atendido pelas escolas estaduais e municipais, o desempenho médio nas avaliações do Saeb foram superiores aos da rede particular, conforme apresentado na Tabela 1.
É fato conhecido que as escolas federais de educação profissional realizam seleção de seus alunos para ingresso nos cursos nas diferentes modalidades. A seleção, ou não, introduz uma complicação adicional na avaliação da eficácia da escola. Infelizmente, não é claro que ela possa ser simplesmente abolida dessas instituições, pois cumpre dois papeis sociais muito importantes. O primeiro, diz respeito à expressividade e prestígio social dessas escolas, principalmente para as camadas economicamente mais desfavorecidas e, ainda, para a classe média ascendente, tipicamente brasileira. Em tais conjuntos há muito menos vagas do que há potenciais candidatos. O segundo, diz respeito ao objetivo primordial desse modelo de escola que é a formação técnica profissional, no âmbito do ensino médio, que impõe naturalmente limites mínimos de proficiências cognitivas na formação geral necessárias para a adequada formação técnica do aluno. Esses dois papéis conjugados justificariam, a princípio, um processo seletivo dos alunos, necessário a essa modalidade de ensino. No entanto, como será visto nas análises, parte considerável das escolas federais de educação profissional seleciona seus alunos por algum tipo de sorteio. Infelizmente, carece na literatura nacional a ocorrência de estudos que avaliam esses dois tipos de ingresso no contexto das instituições federais.
A qualidade da formação técnica, em certa medida, também justifica maior rigor na formação propedêutica do que aparentemente é exigido nos demais tipos de escolas, particularmente as públicas, o que pode se refletir em taxas de reprovação um pouco mais elevadas do que em uma escola de ensino propedêutico tradicional. Assim, a escola federal de educação profissional atende a um conjunto muito particular de alunos, não uma elite social, tendo em vista que seus alunos são provenientes dos mesmos estratos sociais atendidos habitualmente pelas escolas públicas brasileiras, mas um grupo provavelmente com mais proficiência cognitiva do que a mediana dos alunos que pertencem aos mesmos estratos sociais. E ela parece cumprir a dupla finalidade de ascensão social de alunos provenientes de classes sociais menos elevadas e a formação técnica profissional, ambas muito necessárias ao desenvolvimento social e econômico do país.
Nesse contexto, uma questão imediata a ser discutida é: se o Ideb é um indicador satisfatório para aferir a qualidade e eficácia escolar das escolas federais de educação profissional, uma vez que não considera outras medidas contextuais que influenciam no aprendizado dos alunos, como, por exemplo, o Inse dos alunos. A questão considera como perspectiva atual a concepção do indicador, que pondera apenas os parâmetros de desempenho nas avaliações no Saeb e fluxo escolar, conforme apresentado na Equação 1. Certamente, isso não desconsidera o fato de que as taxas de aprovação não sejam as ideais, sendo que a preocupação com o abandono escolar e a reprovação deve ser uma constante no trabalho pedagógico e de gestão de todos os tipos de escola.
Infelizmente, os dados provenientes do Saeb, de natureza transversal, não permitem uma análise longitudinal da agregação das proficiências dos alunos ao longo dos anos escolares, inclusive a dos alunos não aprovados - incluindo aqueles que decidem mudar de escola por diferentes motivos, o que poderia redundar em análises mais precisas da eficácia das escolas de ensino médio. No entanto, por se tratar de uma avaliação muito abrangente, quase universal, e conter instrumentos contextuais bastante relevantes, permite de forma coerente realizar inferências sobre a eficácia das escolas (ver Soares, 2005a; Alves & Soares, 2008; Bonamino & Oliveira, 2013).
METODOLOGIA DO ESTUDO E AMOSTRA DE DADOS
Alguns fatores associados à aprendizagem dos alunos no Brasil, relevantes nas abordagens com dados educacionais, não são fornecidos diretamente na base de dados do Saeb, a exemplo do Indicador de Nível Socioeconômico individual dos alunos (e não o agregado por escola, este sim disponibilizado), sendo, portanto, necessário construí-los por meio das respostas aos itens abordados nos questionários contextuais. Aliás, um dos limitadores no campo de pesquisa em avaliação educacional e eficácia escolar no Brasil é que, em geral, é necessário utilizar dados secundários, como os do Saeb e, portanto, limitados à estrutura e concepção dos questionários contextuais das avaliações em larga escala, como estabelecidos. Por outro lado, essas bases são extensivas e contêm múltiplos instrumentos que permitem aos pesquisadores a elaboração própria de determinados indicadores educacionais e que são muito úteis nesse tipo de estudo (Franco & Bonamino, 2005; Soares, 2005b; Karino & Laros, 2017).
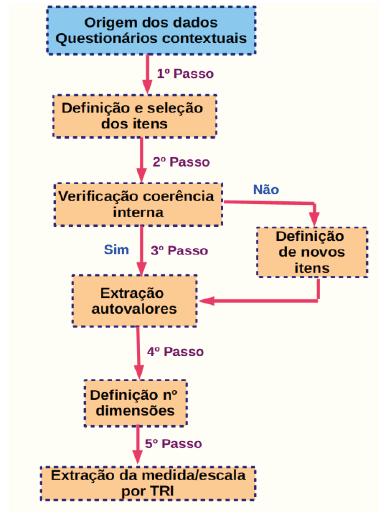
No âmbito do presente trabalho, a construção dos indicadores/medidas alinhados à investigação de interesse se dá inicialmente pela identificação e pelo agrupamento dos itens dos questionários conforme o constructo de interesse ao qual estão associados. Em seguida, emprega-se a metodologia da Teoria da Resposta ao Item (TRI) para a construção dos indicadores (Soares, 2005; Andrade et al., 2000).
Após o desenvolvimento dos indicadores educacionais definidos como sendo de interesse, analisa-se a complexidade daqueles associados à proficiência escolar por meio de metodologias de modelagem hierárquica/multinível multivariada de dados que envolvam níveis que englobem a estrutura escolar. Em seguida, amparados pelos estudos extensivos da análise contextual, propõe-se um modelo para medir a eficácia das escolas federais de educação profissional e comparam-se os resultados da investigação com os resultados do Ideb. Os detalhes dos procedimentos metodológicos são apresentados a seguir.
Procedimentos metodológicos para construção dos indicadores a partir da TRI
Para construção dos indicadores por meio da metodologia da TRI, a partir dos itens dos questionários aplicados no Saeb, utilizou-se o pacote “mirt” do software livre R (versão 1.2.1335). No referido pacote computacional, é possível ajustar o modelo adequado para o constructo latente de interesse, inclusive os modelos multidimensionais (R. Core Team, 2017; Chalmers, 2012).
Assim, quanto aos procedimentos metodológicos para construção dos indicadores: os itens para composição da medida em análise são escolhidos, respeitando os critérios de coerência interna e fidedignidade (Cronbach, 1951); em seguida, é feita a análise e a validação do número de dimensões/fatores mais apropriado para a medida a partir dos critérios de Kaiser e a análise paralela de Horn (Pasquali, 2003; Horn, 1965); por fim, são feitos o cálculo e a extração da medida, pela TRI.
O fluxograma da Figura 1 ilustra os procedimentos metodológicos elencados acima, em ordem de execução, para a produção dos indicadores adotados no pre- sente trabalho.
Metodologia para modelagem multinível multivariada dos dados
A modelagem multinível multivariada que foi empregada no presente trabalho considera em uma mesma equação mais de uma variável dependente (Y), sendo que seu equacionamento matemático segue o mesmo raciocínio de modelos multiníveis univariado (Leckie, 2018; Kiwanuka et al., 2016).
Assim, a abordagem multivariada permite a observação de associações diferenciais das covariáveis com as proficiências, e estimação das correlações residuais entre pares de resultados dentro e entre as classes ou escolas (Kiwanuka et al., 2016). Portanto, assim como na modelagem multinível univariada, a abordagem multivariada permite a análise dos fatores que afetam o desempenho nas avaliações, tanto em nível de aluno, quanto contextuais, em nível de escola. Entretanto, segundo Leckie (2018), a abordagem tradicional dos modelos univariados para cada resultado separadamente apresenta a desvantagem em relação à abordagem multivariada de produzir resultados tendenciosos, além de aumentarem as variâncias dos erros devido a não incorporação da correlação entre as variáveis resposta. Por outro lado, o interessante é que uma única análise é realizada em vez de duas análises univariadas.
As publicações de Masci et al. (2017), Leckie (2018) e Kiwanuka et al. (2016) demonstram algumas aplicações de modelos multinível multivariado em dados educacionais internacionais. Todavia, no âmbito nacional com dados de escolas brasileiras, a aplicação desses modelos ainda é incipiente, predominando majoritariamente a abordagem univariada (Pires, 2021).
Como ferramenta computacional para desenvolvimento dos modelos multivariados foi utilizado o software R (versão 1.2.1335), por meio do pacote MCMCglm, a partir dos métodos de MCMC (Markov Chain Monte Carlo, ou, em português, Monte Carlo via cadeia de Markov).
Seleção das amostras de escolas para as análises multiníveis
Na população dos alunos de ensino médio que realizaram o exame do Saeb na edição de 2017 predominam os da rede estadual de ensino (94% dos alunos avaliados estavam matriculados na rede estadual, enquanto 1,5% estavam na municipal, 0,6% na federal e 4,1% na particular).
No que concerne ao tamanho da população em termos do número de escolas que realizaram o exame do Saeb em 2017, de um total de 19706 escolas avaliadas (Tabela 5), apenas 390 (cerca de 2%) eram escolas federais de educação profissional. Por outro lado, nos questionários das escolas, professores e diretores, foi apurado que um número considerável de escolas não apresentou questionários integralmente respondidos ou questionários com um número robusto de questões não respondidas. Na análise foram excluídas do banco de dados aquelas escolas que não apresentaram pelo menos um dos questionários em nível de escola (escola, professores ou diretores) adequadamente respondido. Assim, a partir da exclusão dos dados faltantes pelo método de listewise (Zhang, 2003), em nível de escola, a amostra resultante teve redução no número de escolas e alunos em relação à população original abordada no presente trabalho, conforme Tabela 5. Ressalta-se, no entanto, que os resultados dos modelos desenvolvidos a partir da aplicação do método listewise foram bastante similares aos encontrados quando aplicados outros procedimentos relativos ao tratamento de dados ausentes, como o método pairwise, ou por meio de preenchimento de dados faltantes em nível de escola.
Por outro lado, observou-se a similaridade no que concerne à distribuição das principais variáveis, proficiências e nível socioeconômico médio, entre a amostra final ponderada e a população. Admite-se, portanto, neste trabalho, que o “missing data” ocorra de forma completamente aleatória. Assim, devido ao extenso volume de dados e limitações dos softwares utilizados, preferiu-se reportar os resultados após o emprego do método listewise e subsequente amostragem das escolas.
Desse modo, uma amostra de 1.205 escolas foi extraída de forma aleatória, após o tratamento de dados realizado por meio da exclusão de dados ausentes, em nível de escola, pelo método listewise.
No entanto, não foi possível aplicar a amostragem aleatória simples, tendo em vista que poucas escolas federais de educação profissional, nas quais este estudo tem foco, fariam parte da amostra final, em comparação com as escolas da rede estadual, cujo número é majoritário na população. Logo, para equilibrar a disparidade entre as redes de ensino, foram extraídas amostras aleatórias estratificadas por rede, de forma não proporcional, conforme a descrição na Tabela 1. Posteriormente, a amostra foi ponderada de tal forma que os dados refletissem os pesos amostrais originais da população. O objetivo foi garantir informação relevante em cada um dos estratos da amostra usada nas análises. No entanto, a interpretação dos resultados correlacionais considera os pesos originais da população do Saeb.
A Tabela 5 apresenta o número de escolas e de alunos por rede na base do Saeb original (sem tratamento de dados e exclusão), após o tratamento de dados com a exclusão de escolas com dados faltantes e, por fim, as respectivas porcentagens de seleção e os números da amostra utilizada nas análises dos modelos hierárquicos multivariados. Após a exclusão das escolas com dados ausentes, foram selecionadas de forma aleatória, para a rede particular e estadual, 15% das es- colas remanescentes de cada rede. Para a rede federal, a amostra foi de 100% das escolas remanescentes nessa rede, assim como para a rede municipal. Ressalta-se que o tamanho da população sem a retirada de um percentual amostral inviabilizaria o desenvolvimento da pesquisa pelas limitações de esforços computacionais devido aos softwares utilizados.
TABELA 5 População de escolas e de alunos antes e depois da exclusão por dados faltantes e amostra aleatória selecionada - Saeb, 2017
| POPULAÇÃO | AMOSTRA | |||||
|---|---|---|---|---|---|---|
| Exclusão de escolas com dados faltantes | Escolas | Alunos | % | Escolas | Alunos | |
| Federal | Antes | 390 | 22001 | |||
| Depois | 200 | 8951 | 100% | 200 | 8951 | |
| Estadual | Antes | 17890 | 1365873 | |||
| Depois | 4508 | 92740 | 15% | 675 | 13314 | |
| Municipal | Antes | 180 | 9409 | |||
| Depois | 158 | 6952 | 100% | 158 | 6952 | |
| Particular | Antes | 1246 | 59042 | |||
| Depois | 1230 | 56415 | 15% | 172 | 8642 | |
Fonte: Elaboração dos autores (2021).
Variáveis de estudo
Diante do objetivo do presente trabalho, sabe-se que os fatores associados ao aprendizado dos alunos são múltiplos, em especial quando se trata do campo da educação, cuja bibliografia sugere que o aprendizado do aluno é definido não somente por seu background, mas também pela característica de seu ambiente familiar, econômico e escolar (Alves & Franco, 2008).
Os fatores em nível de aluno basearam-se nas respostas ao questionário dos alunos, e são constructos desenvolvidos por meio da TRI, assim como de covariáveis retiradas diretamente do questionário, tais como sexo e raça do aluno. A escolha dos fatores desse nível teve como embasamento teórico as publicações de Soares e Mendonça (2003), Soares (2005a, 2005b), Franco e Bonamino (2005), Alves (2006), Alves e Franco (2008) e Alves e Soares (2009), e que incluem as variáveis de controle, as quais compulsoriamente devem constar nos modelos e caracterizar o background do aluno, e são as variáveis indicadoras do sexo, cor/raça, Inse, repetência e do atraso escolar (Alves & Franco, 2008).
Já os fatores caracterizadores do nível escola basearam-se nos questionários da escola, dos professores e do diretor. A sua elaboração fundamentou-se especialmente na publicação de Alves e Franco (2008), que classificaram os fatores que se associam ao aprendizado do estudante e eficácia escolar descritos na literatura brasileira em categorias principais, sendo elas: recursos escolares, organização e gestão da escola, clima acadêmico, formação e salário docente e ênfase pedagógica. Assim como abordado por Alves e Franco (2008), além desses fatores contextuais, devem ser levados em conta aqueles fatores relacionados à composição social da escola, que precisamente devem ser considerados como variáveis de controle, e foram a “média Inse da escola”, a “média da defasagem idade-série da escola” e o “tipo de rede escolar” (variável dummy que indica se a escola é da rede estadual, municipal, federal ou particular).
Os fatores em nível de aluno e escola desenvolvidos não foram apresentados no artigo devido às limitações de espaço, porém os autores disponibilizam os dados utilizados no desenvolvimento do trabalho e demais resultados dos modelos.
Limitações às interpretações do estudo
O trabalho permite verificar a associação entre as proficiências medidas ao final da etapa escolar e as covariáveis disponíveis de escola e aluno, condicionalmente. Assim, o fato de haver muitas variáveis de controle tanto em nível do aluno quanto em nível da escola e, entre elas, medidas das condições econômicas e variáveis dos processos escolares, traz consigo evidência de eficácia escolar quanto aos resultados finais devidamente embasada em teorias educacionais que apoiem as conclusões (Alves & Soares, 2013; Soares & Brooke, 2008).
Naturalmente, no que se refere ao aprendizado, a questão é muito mais complexa. Seria interessante medir o ganho de aprendizado dos alunos, com controle do abandono e reprovação ao longo do ensino médio, mas para isso seriam necessários dados longitudinais, especialmente estudos por coortes, que não são possíveis de serem realizados diretamente por meio dos dados fornecidos no âmbito do Saeb, cujas medidas são transversais.
A maioria dos autores tende a concordar que essa medida de evolução, valor agregado, é mais adequada para medir a eficácia da escola do que apenas uma medida de posição, standing (Bonamino & Oliveira, 2013). Mas isso não quer dizer que as medidas de posição não se correlacionem às medidas de evolução, ao contrário. De fato, o controle por covariáveis específicas dos alunos, como Inse e defasagem idade série, por exemplo, que são proxies do desempenho prévio, permite produzir o que se denomina de medida de posição contextualizada. Estudos mostram alta correlação dessa medida com medidas típicas de valor agregado (ver Soares et al., 2017). Além disso, por outros argumentos, certos autores afirmam que apenas o aprendizado não é suficiente, mas o nível alcançado também deve ser considerado (Alves & Franco, 2008; Soares & Brooke, 2008; Bonamino & Oliveira, 2013). Entretanto, essa é uma questão que não será tratada no presente estudo, tendo em vista que neste trabalho apenas medidas de posição podem ser consideradas.
A replicação dos estudos para outras edições do Saeb seria interessante e desejável. Infelizmente, dados mais abrangentes relativos às escolas federais de educação profissional só foram divulgados pelo Saeb a partir do ano de 2017, e, quando este estudo se iniciou, os dados de 2019 ainda não haviam sido publicados. Para estudos futuros a replicação pode ser conveniente para verificar a robustez e a estabilidade dos resultados de edições próximas.
Finalmente, um ponto que mereceu atenção diz respeito ao quesito da seletividade dos alunos pelas escolas federais de educação profissional. Embora, tradicionalmente, a seletividade fosse a regra, nos dados do Saeb de 2017 um percentual significativo das escolas federais declarou que realizam sorteio para a seleção dos alunos, e não vestibulares. Essa variável foi usada como controle no modelo. Evidentemente esse controle não resolve completamente a questão de uma possível contaminação endógena das medidas de eficácia - isto é, alunos potencialmente aptos ao aprendizado escolhem deliberadamente as escolas federais -, entretanto, com a inclusão dessa variável como controle no modelo, presume-se que se reduza parte do efeito do viés de seleção, tendo em vista que escolas que sorteiam os alunos tendem a atrair uma população mais abrangente.
RESULTADOS DOS MODELOS MULTIVARIADOS
Para a apresentação dos resultados, adotou-se a análise com a inclusão dos fatores de ambos os níveis, aluno e escola (modelo completo). Na Tabela 6 são apresentadas as estimativas do modelo multivariado completo para os dados em análise. Para evitar sobrecarregar a Tabela 6 com os resultados da modelagem, apresentaram-se os coeficientes somente dos fatores que apresentaram significância estatística no modelo em pelo menos uma das duas disciplinas avaliadas (p-value = < 0,05). Os demais fatores em nível de aluno e escola que não apresentaram significância estatística (p-value > 0,05) em ambas as disciplinas não tiveram seus coeficientes apresentados e foram retirados da modelagem. Portanto, o modelo completo é definido apenas com aqueles fatores de ambos os níveis que apresentaram significância estatística.
TABELA 6 Resultados do modelo multivariado completo - MT e LP - 3º ano Saeb 2017
| VARIÁVEL/ESCALA - NÍVEL DE ALUNO | COEF. EFEITO FIXO | P-VALUE |
|---|---|---|
| Intercepto LP | 247,87 | 0,00 |
| Intercepto MT | 214,06 | 0,00 |
| Sexo em LP | -5,61 | 0,00 |
| Sexo em MT | 9,56 | 0,00 |
| Cor em LP | 2,12 | 0,01 |
| Cor em MT | 4,92 | 0,01 |
| Defasagem idade-série em LP | -6,93 | 0,00 |
| Defasagem idade-série em MT | -6,37 | 0,00 |
| Inse em LP | 2,02 | 0,00 |
| Inse em MT | 3,51 | 0,00 |
| Reprovação escolar em LP | -7,83 | 0,00 |
| Reprovação escolar em MT | -7,98 | 0,00 |
| Trabalha fora em LP | -4,62 | 0,00 |
| Trabalha fora em MT | -3,71 | 0,00 |
| Utilização biblioteca em LP | 1,30 | 0,00 |
| Utilização biblioteca em MT | 1,80 | 0,00 |
| Gosta de estudar LP- Efeito em LP | 6,49 | 0,00 |
| Gosta de estudar LP-Efeito em MT | 1,01 | 0,08 |
| Gosta de estudar MT-Efeito em MT | 24,40 | 0,00 |
| Gosta de estudar MT-Efeito em LP | 0,98 | 0,08 |
| Incentivo dos pais em LP | 3,42 | 0,00 |
| Incentivo dos pais em MT | 3,13 | 0,00 |
| Hábito e frequência de leitura em LP | 4,33 | 0,00 |
| Hábito e frequência de leitura em MT | 0,09 | 0,09 |
| Engajamento dever de casa LP-Efeito em LP | 0,13 | 0,67 |
| Engajamento dever de casa LP-Efeito em MT | 0,10 | 0,15 |
| Engajamento dever de casa MT-Efeito em MT | 1,21 | 0,00 |
| Engajamento dever de casa MT-Efeito em LP | 0,50 | 0,08 |
| Média Inse em LP | 18,71 | 0,00 |
| Média Inse em MT | 21,80 | 0,00 |
| Rede Federal em LP | 35,00 | 0,00 |
| Rede Federal em MT | 42,00 | 0,00 |
| Rede Municipal em LP | 6,70 | 0,00 |
| Rede Municipal em MT | 6,14 | 0,00 |
| Rede Particular em LP | 28,70 | 0,00 |
| Rede Particular em MT | 37,60 | 0,00 |
| Critério de admissão dos alunos em LP | 10,47 | 0,00 |
| Critério de admissão dos alunos em MT | 15,86 | 0,00 |
| Conteúdo curricular previsto e desenvolvido em LP | 2,22 | 0,00 |
| Conteúdo curricular previsto e desenvolvido em MT | 2,58 | 0,00 |
| Percepção docente aos problemas de aprendizagem- nível aluno em LP | -3,90 | 0,00 |
| Percepção docente aos problemas de aprendizagem- nível aluno em MT | -5,29 | 0,00 |
| Titulação professor (mestrado/doutorado) em LP | 4,70 | 0,04 |
| Titulação professor (mestrado/doutorado) em MT | 8,55 | 0,00 |
| EFEITO ALEATÓRIO | VARIÂNCIA | |
| Entre escolas LP (µ0) | 265,01 | |
| Entre escolas MT (µ0) | 372,00 | |
| Entre escolas- covariância LP-MT (µ0) | 286,02 | |
| Entre alunos LP (rij) | 1660,03 | |
| Entre alunos MT (rij) | 1684,10 | |
| Entre alunos- covariância LP-MT (rij) | 796,00 | |
| Deviance | 768787 | |
| ICC da Disciplina de LP | 13,76% | |
| ICC da Disciplina de MT | 18,10% | |
Fonte: Elaboração dos autores.
A partir dos resultados do modelo completo mostrados na Tabela 6, observa-se que, para a disciplina de LP, as variáveis “Aluno gosta de estudar MT - efeito em LP”, “Engajamento no dever de casa LP - Efeito em LP”, “Engajamento no dever de casa MT - Efeito em LP” e “Titulação do professor (mestrado/doutorado)” foram estatisticamente não significativas no modelo. Para a disciplina de MT, os fatores que não apresentaram significância estatística foram: “Hábito e frequência de leitura”, “Aluno gosta de estudar LP - efeito em MT” e “Engajamento no dever de casa de LP - Efeito em MT”. Essas variáveis estão com seus coeficientes de p-value destacados em negrito na referida tabela.
Diferente da modelagem univariada, onde se inserem os fatores em nível de aluno e escola como covariáveis explicativas para análise de seus efeitos em determinada variável de saída (por exemplo, a proficiência na disciplina de LP ou MT), na análise multivariada inserem-se as covariáveis no modelo e os coeficientes de efeito fixo dessas covariáveis irão ser estimados para as n variáveis de saída definidas. Logo, por exemplo, ao inserir no modelo multivariado o fator “Engajamento no dever de casa de LP”, as estimativas dos efeitos desse fator serão realizadas tanto para a proficiência em LP como para a proficiência em MT (variáveis de saída do modelo multivariado em análise). Assim, alguns fatores incluídos podem apresentar significância estatística para uma determinada variável de saída (por exemplo, para a disciplina de LP) e podem não ser significantes para a outra variável de saída (disciplina de MT) do modelo.
A partir dos resultados mostrados na Tabela 6, as variáveis de controle que apresentaram os maiores efeitos positivos nas disciplinas analisadas foram a “Média Inse da escola” e as variáveis indicadoras do tipo de rede escolar, que são variáveis em nível de escola. Em MT, o aumento em uma unidade na média do Inse da escola impacta o aumento de aproximadamente 21 pontos o desempenho do aluno. Em LP, esse impacto é de aproximadamente 18 pontos.
Os alunos matriculados nas escolas municipais apresentaram, pelos resultados expostos, aproximadamente 6 pontos a mais em MT e LP que os alunos matriculados na rede estadual (a rede estadual é a variável base da variável dummy que indica o tipo de rede escolar). Enquanto isso, os alunos da rede particular apresentaram aproximadamente 37 pontos a mais em MT e 28 pontos em LP. Os alunos da rede federal apresentaram em média 42 pontos a mais em MT e 35 pontos a mais em LP.
Com efeito negativo, a variável de controle indicadora da “defasagem idade-série” do aluno apresentou o maior efeito em diminuir os escores nas disciplinas entre as variáveis de controle, sendo que a cada ano de atraso escolar diminui-se em média 6 pontos em ambas as disciplinas. O sexo do aluno também é um fator que impacta o desempenho, uma vez que os meninos apresentaram em média aproximadamente 9,5 pontos a mais que as meninas em MT, e, em contrapartida, obtiveram 5 pontos a menos que as meninas em LP.
Quanto às demais variáveis contextuais em nível de aluno, os resultados mostraram que, para ambas as disciplinas, o fator que apresentou maior efeito positivo na proficiência foi aquele que indica se o aluno gosta de estudar a disciplina, cujo efeito é capaz de elevar a proficiência em 24 pontos em MT e em 6 pontos em LP. Em contrapartida, negativamente o maior efeito foi apresentado pela variável indicadora de reprovação escolar: se o aluno já tiver sido reprovado em alguma série, suas proficiências diminuem em aproximadamente 7 pontos.
Ademais, pelos resultados apresentados observou-se que os fatores em nível de escola fazem diferença, em distintas magnitudes de efeito, seja pelo clima escolar ou recursos humanos da escola. Entretanto, os efeitos desses fatores, com exceção das variáveis de controle caracterizadoras do tipo de rede escolar e da média do Inse da escola, são inferiores aos efeitos apresentados pelas variáveis contextuais em nível de aluno.
O fator em nível de escola que apresentou maior efeito positivo na proficiência dos alunos em ambas as disciplinas foi a variável indicadora do tipo critério de admissão do aluno na escola (se foi por prova de seleção ou não). Pelos resultados a admissão do aluno ter sido através de prova de seleção tem efeito positivo na proficiência de MT de aproximadamente 15 pontos e em LP de 10 pontos em relação ao aluno que ingressou na instituição de ensino por outro critério de admissão. Desse modo, as escolas federais de educação profissional que realizam provas de seleção para ingresso dos alunos em suas instituições (91% do número total de escolas federais da amostra) se encontram em posição de vantagem em relação às demais instituições de ensino que não realizam esse critério de seleção para ingresso.
Em MT a segunda variável com maior efeito positivo na proficiência foi aquela que indica a “Titulação do professor (mestrado/doutorado)”, isto é, a variável indicadora da titulação do docente, se possui mestrado ou doutorado. Pelo resultado exposto, o professor da disciplina ter a titulação de mestrado ou doutorado tem o efeito de aumentar em média 8 pontos a proficiência do aluno. Em LP essa variável não apresentou significância estatística no modelo, assim como as demais variáveis indicadoras da titulação docente.
Na contramão desse efeito positivo, a variável contextual em nível de escola que apresentou maior impacto negativo nas proficiências é a indicadora da “Percepção docente aos problemas de aprendizagem - nível aluno”. Essa variável é um constructo/escala construída a partir de itens que relacionam a percepção do professor sobre os problemas de aprendizagem dos alunos, e que ocorrem devido à baixa autoestima dos mesmos, desinteresse e/ou falta de esforço nos estudos, indisciplina em sala de aula e alto índice de abstinência nas aulas. Pelo resultado, o aumento em uma unidade dessa medida diminui em 5 pontos a proficiência em MT e 4 pontos em LP.
A medida da heterogeneidade das escolas, representada pelo Índice de Correlação Intraclasse (ICC), no modelo completo foi de 13,76% para LP e 18,10% para MT, isto é, essa é a proporção da variância nas proficiências das disciplinas que pode ser atribuída às diferenças entre as instituições de ensino, suas práticas internas ou suas políticas pedagógicas adotadas.
A partir dos resultados apresentados pelo modelo multinível desenvolvido, e considerando os fatores em nível de aluno e escola, observa-se que as variáveis que mais impactam a proficiência são aquelas em nível de aluno, ainda que o efeito coletivo de algumas dessas variáveis apresentasse efeito ainda mais relevante na proficiência, em conformidade com estudo de Andrade e Soares (2008), que chamaram isso de “efeito dos pares”. Em relação às variáveis contextuais em nível de escola, observa-se pelos resultados que, apesar de apresentarem efeitos menos expressivos na proficiência das disciplinas quando comparadas com as variáveis contextuais em nível de aluno, elas têm associação na aprendizagem dos alunos e, portanto, devem ser consideradas nos modelos em análise.
No que tange à eficácia do tipo de escola no modelo completo desenvolvido, observa-se que o efeito das escolas federais de educação profissional é consideravelmente maior do que o dos demais tipos de escola (35 pontos a mais em LP e 42 pontos em MT, se comparado com a rede estadual de ensino). Contudo, é importante notar que nesse modelo é descontado parte do efeito proporcionado por características importantes e favoráveis às escolas federais, como a titulação docente e o critério para admissão de alunos. A maioria das escolas nessa rede realiza vestibular para ingresso de seus alunos e possui um número mais expressivo de professores com maior titulação (mestre e doutores) em seu quadro docente, conforme dados disponibilizados pelo Saeb.
Medição da eficácia escolar pelo coeficiente de resíduo em nível de escola do modelo multinível
Além dos coeficientes de efeito fixo do modelo completo, outra estatística analisada a partir da modelagem multinível refere-se aos coeficientes de resíduos em nível de escola (µ0j). A estimativa dos resíduos no âmbito dos modelos com os dados educacionais pode ser compreendida como o efeito individual da instituição de ensino na proficiência dos alunos, podendo assim ser interpretada como o resultado das práticas pedagógicas e de gestão de cada organização escolar no desempenho de seus alunos (Soares et al., 2017).
Nesse contexto, após a inclusão das variáveis de controle em nível de aluno, incluindo o Inse familiar do aluno, e alguns fatores caracterizadores em nível de escola (“Média Inse”, “Média defasagem idade-série da escola”, “Critério de admissão dos alunos” e “Titulação professor”), o resultado das estimativas dos resíduos indica se as instituições de ensino obtiveram pontuações acima ou abaixo do esperado, considerando/comparando escolas com características semelhantes. Conforme Soares et al. (2017), denomina-se esse tipo de medida de eficácia como medida de status contextualizado.
Para esse modelo, a análise da eficácia escolar pelo coeficiente de resíduo com a inclusão das variáveis acima citadas denominou-se Modelagem 1 (em azul nos gráficos das figuras 2 e 3). Novamente, em outra modelagem (Modelagem 2, em verde) optou-se por retirar do modelo o efeito da titulação docente e do critério de admissão dos alunos. Nesse segundo caso, o objetivo era analisar a eficácia escolar a partir do desconto ou não do efeito dessas covariáveis de escola, que são características importantes e favoráveis às escolas federais.
Os gráficos em boxplot das figuras 2 e 3 apresentam os coeficientes de resíduos dos modelos desenvolvidos (Modelagem 1 em azul e Modelagem 2 em verde) para as disciplinas de LP e MT, respectivamente, por tipo de rede escolar (sendo 1-Federal, 2-Estadual, 3-Municipal e 4-Particular). Considerando as quatro redes de ensino, aquela que apresentou os maiores efeitos positivos na proficiência em ambas as disciplinas e modelagem (efeito escola além do esperado) foi a rede federal, seguida pela rede particular. Entre as escolas que apresentaram baixo efeito nas proficiências, destacam-se as instituições da rede estadual.
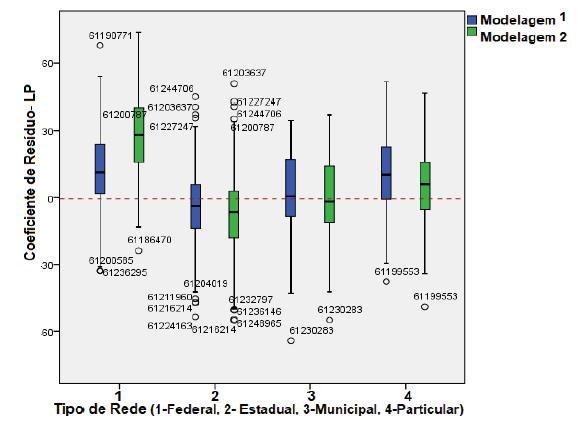
Fonte: Elaboração dos autores (2021).
FIGURA 2 Boxplot dos coeficientes de resíduos (Modelagem 1 e 2) das amostras das escolas por tipo de rede- LP
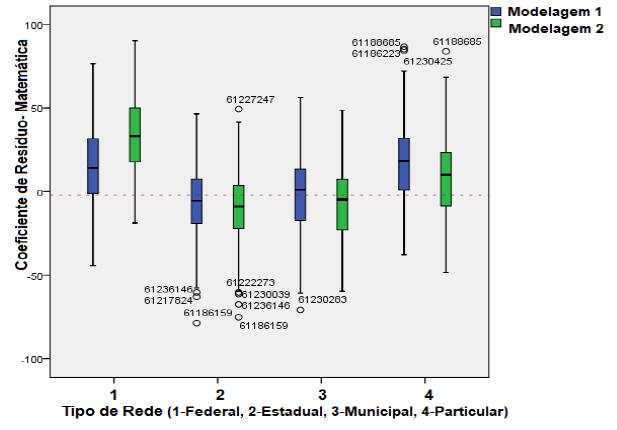
Fonte: Elaboração dos autores (2021).
FIGURA 3 Gráfico boxplot dos coeficientes de resíduos (Modelagem 1 e 2) das amostras das escolas por tipo de rede - MT
Portanto, a partir dos gráficos das figuras 2 e 3, é possível observar a eficácia escolar medida pelos coeficientes de resíduos das amostras de escolas das diferentes redes escolares para ambos os modelos, com destaque para a eficácia das escolas da rede federal, que é ligeiramente superior ao das escolas da rede particular e bem superior ao das demais redes escolares. Isso é evidente no caso da Modelagem 1, que desconta o efeito das variáveis caracterizadoras da titulação docente e do critério de admissão dos alunos, assim como é proporcionalmente superior a todas as demais redes de ensino no caso da Modelagem 2, que não desconta esse efeito.
Os resultados também apontaram uma forte correlação positiva entre as proficiências em MT e LP (ρ de Pearson de 0,76), em que o aumento na média de uma disciplina também se associa a um aumento na média da outra disciplina. Quanto aos resultados dos efeitos das escolas nas proficiências, observa-se também uma correlação positiva nos coeficientes de resíduos de ambas as disciplinas (ρ de Pearson de 0,83). Isto é, quando as instituições apresentam um efeito escola positivo acima da média em MT, há também uma forte tendência de que o efeito seja positivo em LP, contribuindo assim para a constituição de um ambiente propício ao aprendizado individual e coletivo dos alunos, justificando o uso da soma ou da média dos dois resíduos como uma possível medida única da eficácia escolar.
CONCLUSÕES E DISCUSSÃO
O modelo multinível multivariado completo desenvolvido, que considera tanto os fatores caracterizadores em nível de aluno e escola, aponta que as variáveis que mais impactam as proficiências em Matemática e Língua Portuguesa são aquelas caracterizadoras em nível de aluno, como a variável indicadora de reprovação escolar. Ele ratifica o efeito coletivo, ou efeito dos pares, de algumas das variáveis em nível de aluno na explicação das proficiências, a exemplo da média Inse dos alunos da escola. Por outro lado, os resultados encontrados para os efeitos das variáveis de controle, habitualmente apontadas na literatura, foram consistentes com as principais teorias de eficácia e outros estudos realizados no contexto brasileiro. Merece destaque, no entanto, a medição da magnitude dos efeitos do engajamento dos alunos em MT, o cumprimento curricular em ambas as disciplinas, o efeito do hábito de leitura nos resultados de LP, o incentivo dos pais e a percepção docente sobre os problemas de aprendizagem.
Os resultados também sinalizam para os efeitos da variável caracterizadora do tipo de escola na explicação das proficiências. Observa-se que o efeito das escolas federais de educação profissional é consideravelmente maior do que o dos demais tipos de escola. Evidentemente, considerando todas as limitações deste estudo, conforme apontado na seção “Limitações às interpretações do estudo”, os resultados dos modelos multiníveis apontam a eficácia das escolas federais relativamente superiores aos demais tipos de escolas analisadas.
Da mesma forma, a eficácia das escolas federais foi medida com base na análise dos coeficientes de resíduos de segundo nível dos modelos, tomados como medida da eficácia escolar, considerando duas diferentes modelagens, em ambas incluindo nos modelos as variáveis de controle habitualmente usadas, tais como as variáveis caracterizadoras do sexo do aluno, cor/raça, repetência, anos de defasagem idade-série e Inse - as duas últimas consideradas tanto em nível do aluno quanto da escola. Na Modelagem 1 foi admitido controle pelo tipo de admissão (se prova de seleção ou não) e pela titulação dos professores, enquanto na Modelagem 2 esses controles foram retirados. Entretanto, na Modelagem 2, que não desconta os efeitos mencionados, os coeficientes de efeito escola foram, como esperado, significativamente superiores aos da Modelagem 1.
Sendo o Ideb o índice de uso comum mais utilizado no país para medir a qualidade da escola, o que, em grande medida, pode ser traduzido também como uma medida da eficácia, não há como considerar comparativamente o resultado das medidas de eficácia obtidas pelos modelos multiníveis e essa medida em particular. No que concerne aos resultados do Ideb das escolas de ensino médio, públicas e privadas, no ciclo de avaliação do ano de 2017, observou-se que apenas as escolas da rede federal apresentaram um valor de Ideb médio acima da meta esperada pelo Inep. Porém, o índice médio sendo superior aos das escolas estaduais e municipais, foi inferior ao das escolas particulares, ainda que, comparativamente, as escolas federais apresentassem desempenho superior nas avaliações do Saeb em todos os tipos de escola. Logo, pela concepção do índice, isto é, devido à associação, para os pesos ponderados, dos indicadores de taxas de aprovação considerados em seu cálculo, e conforme mostrado na Tabela 3, as taxas de aprovação das escolas da rede federal foram inferiores às das escolas particulares, o que impactou em seu valor do Ideb.
Nesse contexto, deve-se notar que, sendo o Ideb um índice composto por dois indicadores, que, por sua vez, constituem-se de diferentes tipos de médias que consideram os resultados em testes de avaliação em larga escala e as taxas de aprovação dos alunos, torna-se evidente que a escolha subjetiva da importância, isto é, dos pesos desses dois indicadores, tem forte repercussão na medida. Nesse caso, diferentemente da eficácia medida pelos modelos multiníveis, calculados de forma objetiva, o Ideb introduz uma subjetividade na composição do índice que pode estar penalizando excessivamente determinadas escolas.
Note-se, por exemplo, que é sabido que o fluxo escolar se relaciona à condição socioeconômica do aluno, uma vez que alunos de condições econômicas inferiores apresentam maiores dificuldades de acompanhar as aulas e permanecer na escola em comparação com alunos de melhores condições.
Nesse sentido, o Ideb desconsidera, praticamente, o contexto socioeconômico do público atendido pelos diferentes tipos de escolas. É preciso observar que o esforço de uma instituição escolar que atende alunos com situação socioeconômica desfavorecida e com trajetória escolar irregular na promoção de aprendizado e, consequentemente no desempenho escolar, é nitidamente maior em comparação ao esforço daquelas instituições que atendem alunos em situações mais favoráveis. Assim, apesar de o Ideb ser um indicador da qualidade apropriado para escolas de características similares, talvez não seja adequado para comparar escolas de características consideravelmente distintas. Por exemplo, comparar as instituições federais de educação profissional com as escolas particulares, visto que em termos de perfil socioeconômico e de fluxo escolar as escolas federais se assemelham melhor com as demais escolas públicas do que com as instituições particulares.
Embora seja uma tarefa difícil comparar escolas que sejam muito distintas em seu contexto social, investimentos, gastos, insumos e em seus objetivos principais, uma proposta alternativa mais abrangente para uma medida da qualidade da educação seria um indicador calibrado a partir de abordagens que envolvam modelos multinível de status contextualizado e/ou de valor agregado a partir de dados longitudinais. Nesse caso, conforme abordado no presente trabalho, os modelos objetivamente ponderariam não somente o desempenho dos estudantes em avaliações em larga escala e as taxas de aprovação, como também o contexto socioeconômico dos alunos e as condições de oferta da escola.
Também ficam como sugestões para estudos futuros a repetição do presente estudo para bases mais recentes do Saeb, pós-pandemia, verificando-se a robustez dos resultados aqui apresentados ou a mudança do cenário observado. Um estudo futuro, de particular interesse, é a comparação do efeito da seleção ou do sorteio na eficácia das escolas federais de educação profissional. Além disso, estudos de “cross level” podem trazer informações interessantes sobre a equidade das escolas, que são pouco exploradas na literatura.