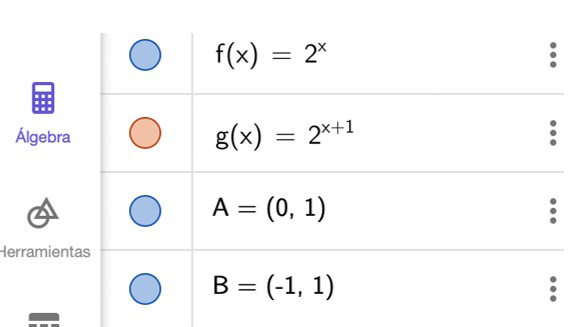Spanish (pdf)
Article in xml format
Automatic translation
Send this article by e-mail
Permalink
Introducción
La enseñanza y aprendizaje de las funciones exponenciales y logarítmicas ha sido un tema de interés para diversos investigadores en el área de Educación Matemática (Campo-Meneses et al ., 2021 ; Campo-Meneses; Cruz, 2020 ; Campo-Meneses; García-García, 2020 ; Ferrari-Escolá; Martínez-Sierra; Méndez-Guevara, 2016 ; Kuper; Carlson, 2020 ; Trejo; Ferrari, 2018 ; Weber, 2002 ). La razón es porque se considera que: a) se trata de la enseñanza-aprendizaje de conceptos base para la comprensión de conceptos más avanzados en el área de Matemáticas (Weber, 2002 ); b) tienen diversas aplicaciones en la vida real y en otras disciplinas; c) su estudio permite el desarrollo del razonamiento covariacional en estudiantes (Ferrari-Escolá; Martínez-Sierra; Méndez-Guevara, 2016 ; Trejo Martínez; Ferrari; Martínez-Sierra, 2021 ; Trejo; Ferrari, 2018 ), y d) son funciones útiles para modelar fenómenos físicos, económicos y biológicos, entre otros.
En lo que respecta al aprendizaje de las funciones exponencial y logarítmica, se identifican investigaciones cuyo foco ha sido analizar, o bien promover, el aprendizaje de estas funciones en los estudiantes, desde el nivel de secundaria hasta el nivel universitario. Estas investigaciones se han realizado poniendo el foco en los registros de representación semiótica (Castro et al ., 2017 ; Sureda; Otero, 2013 ); el razonamiento covariacional (Ellis et al. , 2016 ; Ferrari-Escolá; Martínez-Sierra; Méndez-Guevara, 2016 ; Kuper; Carlson, 2020 ; Trejo; Ferrari, 2018 ; Trejo; Ferrari; Martínez-Sierra, 2021 ); las conexiones matemáticas (Campo-Meneses et al ., 2021 ; Campo-Meneses; García-García, 2020 ); la teoría APOE (Acción, Proceso, Objeto y Esquema) (Weber, 2002 ); y, de manera general, han reportado que los estudiantes presentan dificultades en el momento de resolver tareas que involucran a estas funciones.
Algunas de estas dificultades son las siguientes: 1) dificultad para establecer relaciones entre las leyes exponenciales y logarítmicas (Weber, 2002 ); 2) dificultad para establecer la conexión matemática de reversibilidad entre estas funciones, lo cual es consecuencia del no establecimiento de las demás tipologías de conexiones matemáticas (Campo-Meneses; García-García, 2020 ); 3) dificultad para conseguir una comprensión no superficial de estas funciones (Campo-Meneses; García-García, 2021 ); 4) dificultad para alcanzar niveles altos de razonamiento covariacional (Ferrari-Escolá; Martínez-Sierra; Méndez-Guevara, 2016 ); y 5) dificultad para trabajar los diferentes registros de representación semiótica y resolver problemas no algorítmicos (Castro et al ., 2017 ; Sureda; Otero, 2013 ).
Este panorama en torno al aprendizaje de las funciones exponenciales y logarítmicas ha llevado a algunos investigadores a direccionar su mirada en la enseñanza de esas funciones. En este sentido, se encuentran trabajos enfocados en el diseño de lecciones (Frketic; Berk; Rossi, 2019 ; Lagos, 2020 ), el conocimiento del profesor (Escobar, 2014 ), la valoración de la propia práctica docente (Morales-López; Font, 2019 ) y otros direccionados a caracterizar la práctica del profesor (Campo-Meneses; Cruz, 2020 ). Cabe señalar que estas investigaciones han tomado como objeto de estudio la función exponencial o la logarítmica, pero no los dos tipos de funciones en conjunto, y reportan que es necesario continuar investigando al respecto con el fin de identificar qué ocurre en todo el proceso de enseñanza de estas funciones.
Por ello, se considera pertinente investigar acerca de la enseñanza de estas funciones en conjunto. Una vía para hacerlo es analizar clases de matemáticas en las cuales se aborden dichas funciones con el fin de inferir los criterios que los profesores usan para llevar a cabo sus clases y así concluir a qué criterio le dan más peso y, también, qué criterios deberían los profesores tener en cuenta para contribuir a un mejor aprendizaje de esas funciones por parte de los estudiantes.
El análisis de dichos criterios se puede hacer a la luz del constructo teórico, los criterios de idoneidad didáctica (CID), que propone el enfoque ontosemiótico (EOS) (explicados en la siguiente sección), ya que la literatura muestra diferentes trabajos que han buscado identificar o bien analizar qué criterios usa el profesor en la clase de matemáticas empleando como categoría a priori los CID (Breda et al. , 2021 ; Burgos et al. , 2020 ; Garcés-Córdova; Font-Moll, 2022 ; Hummes; Font; Breda, 2019 ), lo cual ha permitido, entre otros aspectos, analizar lo que ocurre en el aula y buscar mejoras mediante el proceso de reflexión de la práctica docente.
Aunque la mayoría de las investigaciones citadas (relacionadas con las funciones exponenciales y logarítmicas) no se han enfocado directamente en analizar criterios empleados en el diseño de tareas o en la enseñanza, se identifica que se ha dado importancia al aprendizaje de los estudiantes, al uso de diferentes representaciones, al establecimiento de conexiones intra y extramatemáticas, y a proponer tareas con alta demanda cognitiva, lo cual son indicadores inmersos en los siguientes criterios de idoneidad didáctica: cognitivo, epistémico y ecológico (estos se abordan en el marco teórico y los componentes específicos se observan en la Tabla 1 ). Particularmente, la investigación realizada por Morales-López y Font ( 2019 ) presenta la valoración de una profesora de su propia clase, en la que aborda la función logarítmica, en la cual los elementos valorados en mayor medida fueron los relacionados con los criterios epistémico e interaccional.
Así, en la línea de análisis de los criterios que orientan la práctica del profesor usando como categoría a priori los CID, esta investigación trata del estudio de caso de un profesor que imparte cálculo diferencial en un bachillerato general de la ciudad de Acapulco en México, del cual se han registrado 15 clases videograbadas sobre el tema de funciones exponencial y logarítmica. Se ha recopilado información de sus materiales académicos y de los documentos curriculares que debe seguir, además se le ha realizado una entrevista semiestructurada, de manera que la triangulación de estas fuentes nos ha permitido contestar la siguiente pregunta: ¿Cuáles son los criterios que orientan la práctica de un profesor en México al enseñar las funciones exponencial y logarítmica en bachillerato?
Marco teórico
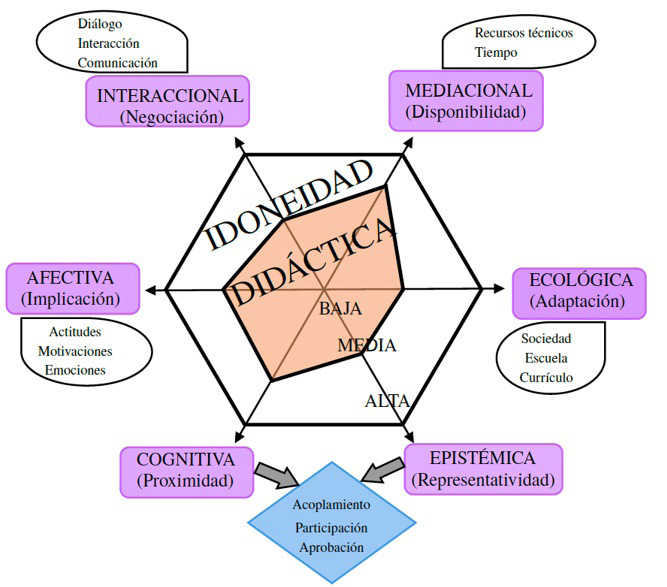
La idoneidad didáctica de un proceso de instrucción, de acuerdo con Breda, Pino-Fan y Font ( 2017 ), se define como el grado en que dicho proceso (o una parte de este) reúne ciertas características que permiten calificarlo como óptimo o adecuado para conseguir la adaptación entre lo que los estudiantes comprenden y lo que se pretende enseñar, teniendo en cuenta las circunstancias y recursos disponibles (entorno). La noción de idoneidad didáctica puede dividirse en seis categorías específicas, a la que denominaremos criterios de idoneidad ( Figura 1 ).
Los criterios de idoneidad funcionan a priori como principios que orientan cómo se deben realizar las cosas y, a posteriori , permiten la valoración del proceso de estudio implementado (Breda; Lima, 2016 ).
La valoración de la idoneidad didáctica es un tipo de análisis que hace parte de un modelo más amplio, llamado análisis didáctico de procesos de instrucción propuesto por el EOS. Este modelo está compuesto por cinco tipos de análisis: identificación de prácticas matemáticas; elaboración de configuraciones de objetos y procesos matemáticos; análisis de las trayectorias e interacciones didácticas; identificación del sistema de normas y meta-normas; y la valoración de la idoneidad didáctica del proceso de instrucción.
La noción de idoneidad didáctica es multidimensional y se desglosa en seis criterios de idoneidad específicos: 1) Idoneidad epistémica, que identifica si las matemáticas enseñadas son unas “buenas matemáticas”; 2) Idoneidad cognitiva, que permite valorar, antes del proceso de instrucción, qué tan razonable es la distancia entre lo que se pretende enseñar y lo que saben los estudiantes, y, después de la instrucción, si lo que aprendieron los estudiantes se acerca a lo que se pretendía enseñar; 3) Idoneidad interaccional, que posibilita valorar si la interacción ha resuelto dudas y dificultades presentadas en los estudiantes; 4) Idoneidad mediacional, para valorar la adecuación de recursos materiales y temporales empleados en el proceso de enseñanza; 5) Idoneidad afectiva, que permite valorar el interés o la motivación de los estudiantes en el proceso de enseñanza; y, finalmente, 6) Idoneidad ecológica, para valorar la adecuación del proceso de enseñanza al proyecto educativo de la institución, las directrices curriculares, las condiciones del entorno social y profesional, entre otros (Font; Planas; Godino, 2010 ).
Para la operatividad de los criterios de idoneidad didáctica se define un conjunto de componentes e indicadores observables que sirven de guía para el análisis y valoración de un proceso de instrucción en cualquier etapa educativa (Breda; Pino-Fan; Font, 2017 ). En la Tabla 1 se detallan los criterios y componentes de idoneidad didáctica.
Tabla 1 . Criterios y componentes de idoneidad didáctica
| Criterio | Componente |
|---|---|
| Epistémico | (IE1) Errores, (IE2) Ambigüedades, (IE3) Riqueza de procesos, (IE4) Representatividad de la complejidad de la noción a enseñar. |
| Cognitivo | (IC1) Conocimientos previos, (IC2) Adaptación curricular a las diferencias individuales, (IC3) Aprendizaje, (IC4) Demanda cognitiva. |
| Interaccional | (II1) Interacción docente-estudiante, (II2) Interacción entre estudiantes, (II3) Autonomía, (II4) Evaluación formativa. |
| Mediacional | (IM1) Recursos materiales, (IM2) Número de estudiantes, horario y condiciones del aula, (IM3) Tiempo. |
| Afectivo o emocional | (IA1) Intereses y necesidades, (IA2) Actitudes, (IA3) Emociones. |
| Ecológico | (IEC1) Adaptación al currículo, (IEC2) Conexiones intra e interdisciplinares, (IEC3) Utilidad sociolaboral, (IEC4) Innovación didáctica. |
Fuente: Morales-López y Font ( 2019 , p. 5).
Metodología
Esta investigación es de tipo cualitativa, específicamente un estudio de caso (Kothari, 2004 ), en el que se busca comprender y describir los criterios que orientan la práctica didáctico-matemática de un profesor en México al impartir clases sobre las funciones exponencial y logarítmica.
De manera general, este trabajo se llevó a cabo teniendo en cuenta la ruta metodológica planteada en Garcés ( 2021 ). Los detalles de cómo se desarrolló cada fase se muestran a continuación:
Fase 1. Búsqueda y selección del caso de estudio: Para seleccionar el caso de estudio, en un primer momento se contactaron a cinco profesores de matemáticas en México que trabajaban en bachillerato y que, específicamente, estuvieran enseñando la asignatura de Matemáticas IV. Después, se les preguntó si estaban dispuestos a grabar sus clases en las que estuvieran enseñando la función exponencial y logarítmica, a proporcionar información de su plan de clase y a ser entrevistados. Finalmente, como respuesta se obtuvo que solo uno de los cinco profesores estuvo de acuerdo con proporcionar la información solicitada. De esta manera, se seleccionó al profesor que se considera el caso estudio en esta investigación, y lo hemos denominado profesor “Paul”.
El profesor Paul tiene 28 años, es egresado de la licenciatura en Matemáticas y de la maestría en Matemáticas Aplicadas. Tiene tres años de experiencia como profesor de Matemáticas: dos años en Universidad y uno en bachillerato. Actualmente trabaja en una institución de carácter privado en Acapulco. En el momento de la recolección de datos el profesor Paul tenía a cargo las asignaturas de Matemática II (corresponde con geometría y trigonometría), Matemáticas IV (se enfoca en el estudio de relaciones y funciones) y Cálculo Integral.
Las clases del profesor Paul se llevaron a cabo mediante Google Meet, pues debido a las circunstancias del país por la pandemia del Covid-19, el tipo de enseñanza que se estaba llevando a cabo era la enseñanza remota de emergencia.
Fase 2. Recopilación de las videograbaciones de las clases impartidas por el profesor Paul: Se le solicitó al profesor Paul que grabara las sesiones dedicadas a las funciones exponencial y logarítmica impartidas en Matemáticas IV, para lo cual se obtuvo 15 clases videograbadas, que fueron proporcionadas mediante Google Drive.
Fase 3. Diseño y aplicación de la entrevista semiestructurada: Se elaboró el protocolo de la entrevista semiestructurada teniendo en cuenta los criterios de idoneidad didáctica y una vez el profesor proporcionara las videograbaciones de sus clases, se procedió a realizarle la entrevista, la cual tuvo una duración aproximadamente de media hora. En un primer momento se indagó acerca de la formación del profesor y después se le hicieron preguntas relacionadas con algunos de los criterios. Algunas preguntas fueron: ¿En la planeación tiene en cuenta usted los conocimientos previos de los estudiantes? ¿De qué manera evalúa a los estudiantes? ¿Relaciona las tareas y actividades en clase con otras asignaturas o con la vida real? ¿Considera que ha cometido errores matemáticos en la enseñanza de esas funciones? ¿Cuáles?
Fase 4. Transcripción de la entrevista y videos de clase: Una vez recopiladas las videograbaciones y la entrevista, se procedió a realizar la transcripción de cada clase y de la entrevista semiestructurada.
Fase 5. Recopilación de los documentos en los que se basa el profesor: Se le solicitó al profesor Paul los documentos que usó en las clases, el cual nos proporcionó el libro de Matemáticas IV de la institución (acorde al plan de estudios del bachillerato general mexicano), los PDF de las tareas que dejó en algunas sesiones y una presentación que utilizó para explicar las propiedades de los exponentes. El profesor Paul no proporcionó un plan de clase, ya que manifestó que él solo se guiaba con el libro.
Fase 6. Inferencia de los criterios a partir del análisis de la entrevista semiestructurada: Se analizaron las respuestas a la entrevista semiestructurada dadas por el profesor Paul mediante el análisis de contenido de manera similar a como se hace en Seckel et al. ( 2019 ) y en Garcés-Córdova y Font-Moll ( 2022 ). Para ello, se identificaron extractos en la transcripción de la entrevista que evidenciaran los criterios usados por él y, luego, se reinterpretaron en términos de los componentes e indicadores de los CID. En esta fase los criterios se infieren de lo que él dice.
Fase 7. Inferencia de los criterios a partir del análisis de las videograbaciones : Se realizó el análisis de las clases videograbadas teniendo en cuenta el análisis didáctico propuesto por el EOS, ya que los criterios de idoneidad, que corresponden con el quinto tipo de análisis, se sustentan en los primeros cuatro tipos de análisis. En el apartado de análisis se explica cómo esto se llevó a cabo. En esta fase los criterios se infieren de lo que él hace.
Fase 8. Triangulación de fuentes de información : Se compararon principalmente los resultados de la fase 6 y 7, es decir, la diferencia entre lo que dice y lo que hace.
Análisis
El análisis se llevó a cabo en dos momentos: Primero, se realizó el análisis de contenido de las respuestas a la entrevista semiestructurada, como se planteó en la fase 6 de la metodología. Para ello, se identificaron extractos en la entrevista en los cuales el profesor mencionaba cuestiones que se pueden reinterpretar en términos de los criterios de idoneidad didáctica. Por ejemplo, en el siguiente extracto se puede apreciar los componentes Interacción docente-estudiante e Interacción entre estudiantes del criterio interaccional, pues el profesor, si bien globalmente realiza una clase que se puede considerar de tipo magistral, se esfuerza por generar momentos de diálogo entre los estudiantes y entre él y los estudiantes.
Entrevistador : ¿O sea que el trabajo específico fue explicación suya del tema y después que ellos aplicaran lo que usted les había explicado?
Paul: Eso fue lo que hice y preguntas para que explicaran lo que habían hecho en el ejercicio frente a sus compañeros, lo proyectaban para ver los demás qué opinaban.
Entrevistador : ¿Qué tal le fue con esa estrategia?
Paul : Eso hacía que se motivaran más, porque les decía que participaran, que ayudaran a su compañero, que lo apoyaran y entonces algunos decían “no, profe, no es así”, o “no, maestro, no es así” o “yo lo hice así también” y ahí se veía un poco más la participación , porque si les decía sólo háganlo y mándenme la tarea, yo sé que muchos iban a desconectarse […].
En un segundo momento se analizaron las clases videograbadas a partir del análisis didáctico como se planteó en la fase 7. Este análisis está compuesto por cinco tipos: En el primero se identificaron las prácticas matemáticas realizadas en el proceso de instrucción acerca de la función exponencial y logarítmica; en el segundo, se identificaron qué objetos y procesos matemáticos intervinieron y emergieron en las prácticas; en el tercer tipo, se describieron los patrones de interacción, las configuraciones didácticas y su articulación secuencial en trayectorias didácticas; en el cuarto tipo, se estudió la trama de normas que regularon el proceso de instrucción; y en el quinto, basado en los tipos de análisis anteriores, se infirieron los criterios de idoneidad.
Los cuatro primeros tipos de análisis permiten descomponer una transcripción de una sesión de clase en una trayectoria de configuraciones didácticas y, para cada configuración, analizar diferentes aspectos, tal como se muestra en Breda et al . ( 2021 ) y en Garcés ( 2021 ). Así, teniendo en cuenta los primeros cuatro tipos, en la Tabla 2 se ilustran los aspectos estudiados en la configuración didáctica 1 (CD1) de la clase número 3. De manera metafórica podemos decir que la trayectoria de configuraciones didácticas es una radiografía del proceso de enseñanza realizado. Por ejemplo, en la CD1 una lectura en vertical nos informa de la dinámica de cómo evoluciona el proceso de enseñanza, mientras que la mirada horizontal nos informa de la complejidad de lo que está pasando en un momento determinado.
Tabla 2 . Configuración didáctica 1 de la clase número 3 del profesor Paul
| Prácticas | Objetos | FS | Procesos | Funciones del profesor | Funciones del estudiante | Tipo de configuración | Conflictos semióticos | Patrones de interacción |
|---|---|---|---|---|---|---|---|---|
| P1: Define el desplazamiento horizontal de una gráfica | D1: Desplazamiento horizontal de la función exponencial Pp1: La función original f ( x )=2 x se ha trasladado o desplazado una unidad de manera horizontal o respecto al eje x… en sentido contrario al signo del número que se ha adicionado. |
D1-Pro1 | Significación Y generalización |
Explicar | Escuchar y entender la explicación del profesor | Magistral | No se evidencia | El profesor pregunta si tienen dudas y el estudiante manifiesta que no |
| P2: Representa verbal y simbólicamente las funciones f ( x )=2 x +1 y f ( x )=2 x | R1: Representación verbal de la función exponencial R2: Representación simbólica de la función exponencial y f ( x )=2 x . R3: Representación simbólica de la función exponencial f ( x )=2 x +1 . 
|
R1-R2 | Representación y conversión | |||||
| P4: Ubica el punto característico y la asíntota de la función f ( x )=2 x | Pp2: Como la función es f ( x )=2
x +1 la función original se desplaza una unidad a la izquierda D2: Asíntota D3: Punto característico Pp3: El punto característico de la función f ( x )=2 x es (0,1) Pp4: La asíntota de la función es f ( x )=2 x y la asíntota y =0 Pr1: Procedimiento para graficar la función dado el punto característico. |
R2-Pro2 | Particularización | |||||
| P5: Representa gráficamente la función f ( x )=2 x | R4: Representación gráfica de la función exponencial f ( x )=2
x . 
|
R2-R4 Pr1-R4 |
Representación | |||||
| P6: Ubica el punto característico y la asíntota de la función f ( x )=2 x +1 | Pp5: El punto característico para la función f ( x )=2
x +1 es (-1,1). Pp6: La asíntota de la función f ( x )=2 x +1 es la misma de la original f ( x )=2 x . Pp7: La asíntota de la función f ( x )=2 x +1 es y =0. |
R3-Pp5 Pp6-pp7 y pp4 R3-pp7 |
Particularización | |||||
| P7: Representa gráficamente la función f ( x )=2 x +1 | R4: Representación gráfica de la función exponencial f ( x )=2
x +1 .  Pp8: La representación gráfica de la función exponencial f ( x )=2
x +1 es la de color naranja. |
R3-R4 R4-Pp8 |
Representación |
Fuente: Elaboración propia. La letra D se usa para definición; P para práctica; Pp para proposición; Pro para procedimiento; R para representación y FS para función semiótica.
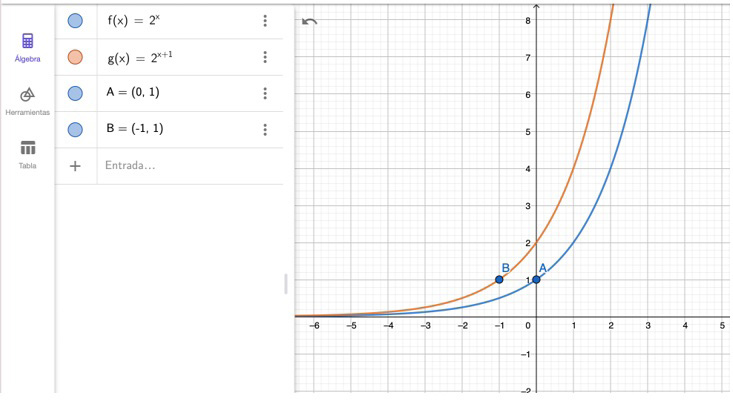
La clase número 3 estuvo enfocada en trabajar traslaciones de funciones exponenciales. Como se muestra en la Tabla 2 , la CD1 empieza después de que el profesor Paul ha saludado a los estudiantes y tomado la asistencia, corresponde a la configuración didáctica de la primera parte del desarrollo del tema, en el que el profesor define el desplazamiento horizontal de una función exponencial y lo ilustra mediante el caso de la función f ( x )=2 x +1 , y termina cuando el profesor finaliza dicho ejemplo.
Después de la transcripción de cada clase en una trayectoria de configuraciones didácticas, empleamos la herramienta de los CID para inferir los criterios que orientan la práctica del profesor Paul (corresponde con la fase 7), sin llegar a hacer una valoración de la idoneidad didáctica desde la perspectiva de un observador externo. Para el caso de la CD1 que se muestra en la Tabla 2 , se observa que el profesor Paul le da importancia al aprendizaje de los estudiantes, haciendo énfasis en tener en cuenta que las tareas sean representativas de aspectos de la complejidad de la función exponencial (solo tiene en cuenta el uso de diferentes representaciones) y en el desarrollo de algunos procesos, lo cual se relaciona con los criterios epistémico y cognitivo.
Finalmente se hace una triangulación de los resultados de la fase 6 (los criterios declarados e inferidos de lo manifestado por el profesor en la entrevista) y los resultados de la fase 7 (los criterios identificados en las clases del profesor Paul por los investigadores). Por ejemplo, lo evidenciado en la CD1 de la Tabla 2 es consistente con lo declarado por el profesor Paul en la entrevista, pues como se muestra en el siguiente extracto, el profesor Paul afirma, entre otras cosas, que se enfoca en el aprendizaje de los estudiantes respecto a las traslaciones de las funciones exponenciales, enfatizando la conexión entre la representación simbólica y la gráfica.
Paul : Según el libro solo vienen las traslaciones fundamentales, yo trato un poco de que ellos vean qué le ocurre a la función cuando cambiamos los parámetros, me suelo enfocar en que ellos vean y sepan trazar los gráficos de estas funciones cualesquiera, que puedan tomar los valores de los parámetros y en situaciones cuando es creciente o decreciente, que eso suele ocasionarles mucho problema. […].
Resultados
Los resultados se presentan a continuación en tres momentos: Primero, se muestran los criterios que orientan la práctica del profesor Paul que se infieren de la entrevista realizada; segundo, se presentan los criterios que orientan la práctica del profesor evidenciados en las videograbaciones; y, finalmente, se comparan los dos resultados para analizar cuáles son aquellos criterios que declara y realmente son desarrollados en el aula.
Criterios que orientan la práctica del profesor Paul según el análisis de la entrevista
En la entrevista se le preguntó al profesor directamente qué criterios empleaba para planear sus clases relacionadas con las funciones exponencial y logarítmica. El profesor Paul manifiesta basarse en las directrices curriculares de la institución, como lo es planear las clases a partir de lo planteado en el libro de matemáticas propuesto por el colegio; buscar situaciones diferentes a las del libro donde haya diferentes modelos; emplear recursos tecnológicos, como GeoGebra, y llevar al estudiante a que entienda el comportamiento de las funciones tanto gráfica como simbólicamente. Estos elementos que menciona el profesor hacen alusión a los criterios de idoneidad: cognitivo , principalmente a los componentes de aprendizaje y adaptación curricular; epistémico , en el componente representatividad de la complejidad de las nociones que se van a enseñar; y ecológico , respecto a los componentes conexiones extramatemáticas y adaptación al currículo.
Para poder indagar más acerca de los criterios que él empleaba para planear su clase, se realizaron otras preguntas que de alguna manera proporcionaron información un poco más detallada, la cual se muestra en la Tabla 3 mediante cada componente de los CID.
Tabla 3 - Análisis de las respuestas del profesor Paul a la entrevista
| CID | Componentes | Análisis |
|---|---|---|
| E | Errores | Afirma no cometer errores en sus clases sobre estas funciones. |
| Ambigüedades | Considera que sus explicaciones son claras y, por tanto, no generan confusión en los estudiantes. | |
| Riqueza de procesos |
Establece conexiones entre las representaciones simbólica, gráfica y lenguaje natural. Ejemplifica a la familia de estas funciones, las caracteriza y generaliza sus propiedades. |
|
| Representatividad de la complejidad de la noción a enseñar |
Propone ejemplos de estas funciones que son base para abordar otros ejemplos sobre estas. Hace énfasis en las representaciones gráfica, simbólica, tabular y lenguaje natural para representar las funciones. |
|
| C | Conocimientos previos | Tiene en cuenta los conocimientos previos de los estudiantes para planear la clase. Dedica un tiempo de las clases, previo al tema de función exponencial, para explicar los conocimientos previos más relevantes para estas funciones, como lo son las leyes de los exponentes, pues lo concerniente al tema de funciones lo ha trabajado en clases anteriores, según el plan de estudios. |
| Adaptación curricular a las diferencias individuales | Considera que la mayoría de los estudiantes pueden salvar la distancia entre sus conocimientos previos y lo que el profesor les está enseñando acerca de las funciones. | |
| Aprendizaje |
Tiene en cuenta las dificultades de cada estudiante y busca estrategias para minimizarlas. Propicia espacios para que los estudiantes hagan preguntas o expongan sus trabajos para contribuir a su aprendizaje. Focaliza las clases en que los estudiantes puedan aprender las propiedades de estas funciones, puedan hacer diferentes representaciones y caracterizar dichas funciones. Considera que la participación y preguntas en clase, y las evaluaciones sumativas, le permiten analizar si los estudiantes aprendieron o no. |
|
| Demanda cognitiva | Considera que abordar estas funciones tiene una alta demanda cognitiva, pues son funciones que se comportan muy diferente a las que se han trabajado previamente. | |
| I | Interacción docente-estudiante | Se esfuerza para que los estudiantes participen y le pregunten cuestiones que no hayan quedado claras, además trata de preguntarle a los estudiantes acerca de algún procedimiento a seguir para graficar la función propuesta. |
| Interacción entre estudiantes | Propicia espacios para que los estudiantes expongan sus ideas acerca de alguna tarea y puedan discutir con los demás compañeros. No promueve el trabajo en equipo para el caso de estas funciones por lo que en las funciones anteriores se ha trabajado en ese sentido. | |
| Autonomía | Considera que el trabajo individual permite más responsabilidad y autonomía a los estudiantes. | |
| Evaluación formativa | Le da importancia a la participación en clase, puesto que le permite analizar el progreso de cada estudiante. Dedica tiempo para aclarar ideas y responder dudas. | |
| M | Recursos materiales | Emplea el software GeoGebra para abordar las traslaciones de las funciones. Además, usa Classroom para subir las actividades y retroalimentar a los estudiantes. |
| Número de estudiantes, horario y condiciones del aula | Plantea que el número de estudiantes es crucial para llamar la atención de los estudiantes respecto al tema. Considera que en presencial 28 estudiantes es un número adecuado, pero para la virtualidad lo ideal es un grupo de 10 a 15 estudiantes. | |
| Tiempo | No es suficiente el tiempo (1 semana y media) que se propone en el plan de estudios para enseñar estas funciones, y considera que dos semanas para cada función es ideal. | |
| A | Intereses y necesidades | Propone actividades de la vida real, ya que son de interés para los estudiantes aprender conceptos que pueden usar en su cotidianidad. El uso de GeoGebra genera interés en los estudiantes, puesto que pueden visualizar las gráficas en movimiento. |
| Actitudes | Ha notado que a los estudiantes no les gusta participar, así que decide hacerles preguntas acerca del ejemplo que se está abordando y eso los lleva a tener una actitud participativa en clase. | |
| Emociones | Genera espacios para que los estudiantes se apoyen mutuamente y los que no entienden puedan motivarse a corregir en lugar de quedarse en el error. | |
| EC | Adaptación al currículo | Afirma que usa el libro de la institución para impartir sus clases. Este libro está creado acorde al plan de estudios de bachillerato. |
| Conexiones intra e interdisciplinares | Afirma que finaliza el tema de estas funciones con ejercicios de aplicación en otras áreas como la biología o la medicina y en la vida real. | |
| Utilidad sociolaboral | Considera que aprender estas funciones es importante para cursos de la universidad, además les permite resolver situaciones de la vida real. | |
| Innovación didáctica | Usa GeoGebra en sus clases y algunos estudiantes también empezaron a usar este software, sin embargo, la forma de llevar la clase y de evaluar a los estudiantes sigue siendo tradicional, pues se debe acoger a las directrices de la institución. |
Fuente: Elaboración propia.
Criterios que orientan la práctica del profesor Paul según el análisis de las clases
Los criterios empleados por el profesor Paul que se infieren de las videograbaciones de sus clases, en las que se dedica a enseñar las funciones exponencial y logarítmica, se presentan en la Tabla 4 .
Tabla 4 . Análisis de las videograbaciones de las clases del profesor Paul
| CID | Componentes | Análisis |
|---|---|---|
| E | Errores | Comete dos errores de los que al parecer no cae en cuenta: en la clase número 8 cuando al introducir la expresión g ( t )=20 *2 t afirma que la gráfica no es correcta, pero si lo era. Y en la clase 12 el profesor afirma que la función y =log 6 ( x -2)+3 no corta el eje de las x, esto lo afirma basándose en la parte de la derecha de la representación gráfica de la función. |
| Ambigüedades |
En la explicación acerca de las funciones exponencial y logarítmica se observan diferentes metáforas, pues el profesor Paul afirma que las funciones se mueven de un lado a otro (hacia arriba, abajo, a la izquierda a la derecha); cuando se refiere a la asíntota dice que la función se acerca, pero no la toca; personifica la función diciendo que la asíntota y el punto característico cambian. El uso excesivo de metáforas ocasionó que algunos estudiantes, en ocasiones, confundieran el punto característico con la asíntota o que dieran una respuesta incorrecta acerca de estos elementos. |
|
| Riqueza de procesos |
Establece conexiones entre las representaciones simbólica, gráfica y lenguaje natural. Ejemplifica y caracteriza a la familia de funciones exponenciales y logarítmica. Argumenta cómo se obtiene la representación gráfica de cada función usando las propiedades que ha explicado, además les pide a los estudiantes que argumenten los procedimientos realizados en clase. La mayoría de los ejemplos y tareas que propone son intramatemáticas y contribuyen a la memorización de pasos para graficar una función. Menciona que estas funciones tienen diversas aplicaciones en la vida real y otras ciencias, pero no propone tareas de modelización o aplicación fuera de la matemática. |
|
| Representatividad de la complejidad de la noción a enseñar |
Propone ejemplos de funciones exponencial y logarítmica que son base para abordar otros ejemplos de estas familias de funciones. Aborda principalmente las representaciones gráficas, simbólicas y lenguaje natural para representar las funciones, realizando tratamientos y conversiones. Aborda el significado de las funciones exponencial y logarítmica como número de forma intramatemática y como función, pero sin su aplicabilidad. |
|
| C | Conocimientos previos | En la primera clase, el profesor se dedica a recordar las leyes de los exponentes, lo cual es un conocimiento previo. Además, antes de abordar la función logarítmica, también dedica un espacio para explicar las leyes logarítmicas. |
| Adaptación curricular a las diferencias individuales |
El contenido abordado en las clases está en la zona de desarrollo próximo de los estudiantes. Se observa que la forma de abordar las funciones (priorizando que los estudiantes aprendan a graficar a partir de las unidades significantes) contribuye a que los estudiantes logren relacionar la representación simbólica de la función con su representación gráfica, además de permitir la visualización. El profesor propone tareas para realizar en casa y, cuando considera que el estudiante tiene confusiones frente a la explicación, procura explicárselo de nuevo, aunque de la misma manera. |
|
| Aprendizaje |
Involucra tecnología digital y propicia espacios para que los estudiantes hagan preguntas o expongan sus trabajos para contribuir al aprendizaje de estas funciones por parte de ellos. Focaliza las clases en que los estudiantes puedan aprender a graficar las funciones a partir de la representación simbólica, identificando las características de cada una, como el punto característico, asíntota, monotonía, etc. Considera la evaluación mediante la entrega de tareas, participación en clase y las evaluaciones, dándole más importancia a las evaluaciones sumativas. | |
|
| Demanda cognitiva | El abordar las funciones enfocándose solo en cómo representarlas gráficamente ocasiona que los estudiantes ejerciten el proceso de pasar del registro simbólico al gráfico, lo cual implica demanda cognitiva, pero deja de lado el uso de estas funciones en diferentes situaciones en las que se son útiles, lo cual hace que la demanda cognitiva esté en un nivel medio. | |
| I | Interacción docente-estudiante |
Se observa que hace un gran esfuerzo para que los estudiantes participen, aunque en ocasiones no resulte. Durante las explicaciones trata de preguntarles a los estudiantes acerca de algún procedimiento que sigue para graficar la función propuesta, resuelve dudas y corrige errores cometidos por los estudiantes. Sus clases se observan organizadas de manera lógica y, aunque trata de que las clases sean magistrales y dialógicas, no lo logra, pues los estudiantes cuando participan se limitan a responder las preguntas del profesor, y en ocasiones se logra que las clases sean magistral-interactivas. |
| Interacción entre estudiantes |
Propicia espacios para que los estudiantes expongan sus ideas acerca de alguna tarea y puedan discutir con los demás compañeros, pero no se logra una discusión, pues los estudiantes son muy callados y solo participan cuando el profesor les hace pregunta e insiste bastante. Promueve el trabajo individual, por lo cual no se logra que haya interacción entre los estudiantes. |
|
| Autonomía | El trabajo individual promueve que algunos de los estudiantes sean responsables en la entrega de sus tareas. | |
| Evaluación formativa | Se observa que al profesor le interesa que los estudiantes participen en clase, pues con ello se da cuenta si han entendido o no lo que se ha explicado. Dedica tiempo para aclarar ideas, responder dudas y socializar las tareas. | |
| M | Recursos materiales | Emplea GeoGebra para abordar las representaciones gráficas de las funciones a partir de las simbólicas. Además, usa Classroom para subir las actividades y retroalimentar a los estudiantes. |
| Número de estudiantes, horario y condiciones del aula | Dado que las clases se realizaron en línea, se observó que el número de estudiantes no es adecuado, ya que es más complejo tanto captar la atención de todos como saber qué están haciendo. | |
| Tiempo | Se observa que, dado las condiciones de la clase, el tiempo para abordar todo no es suficiente, pero el profesor dedica mucho tiempo en enseñar a graficar funciones exponenciales y logarítmicas, lo cual podría hacerse en menos tiempo y así abordar algunas aplicaciones. | |
| A | Intereses y necesidades | El profesor no propone situaciones extramatemáticas donde se aplican estas funciones. |
| Actitudes | El profesor trata de motivar a los estudiantes mediante el uso de GeoGebra y les menciona que estas funciones son importantes. Además, los estudiantes le hacen preguntas cuando él está explicando, buscando que ellos quieran aprender. | |
| Emociones | Se observa que el profesor es paciente y amable con los estudiantes. Además, procura hacerles preguntas a los estudiantes que casi no participan para que lo hagan. | |
| EC | Adaptación al currículo | El profesor aborda los contenidos del libro pero deja de lado las aplicaciones de las funciones, lo cual es importante en el plan de estudios. |
| Conexiones intra e interdisciplinares | Afirma y muestra en una clase que estas funciones son importantes, pues tienen diversas aplicaciones, pero solo les muestra un ejemplo que se aborda en el libro de texto. No promueve conexiones con otras áreas ni con la vida real. | |
| Utilidad sociolaboral | No se evidencia que el profesor busque la forma de desarrollar competencia matemática en los estudiantes a fin de que ellos logren usar las funciones en diferentes contextos. | |
| Innovación didáctica | Aunque el profesor usa GeoGebra para explicar el contenido, la forma de trabajar sigue siendo tradicional. |
Fuente: Elaboración propia.
Comparación de los criterios identificados al analizar la entrevista y las clases del profesor Paul
Al comparar los análisis realizados, se identificó que en cuanto al criterio epistémico, aunque el profesor declara en la entrevista no cometer errores ni evidenciar ambigüedades en sus explicaciones, las clases acerca de las funciones exponencial y logarítmica tuvieron algunos errores: uno referido al análisis de una representación gráfica de un caso particular de la función logaritmo y otro relacionado con la forma de la gráfica de un caso particular de la función exponencial. Además, en algunas de las explicaciones, el profesor al referirse a la asíntota afirmaba que era una recta (diciendo × o y igual a algo), pero en otros casos solo decía que la asíntota estaba en cierto número (ver el siguiente extracto), lo cual no era claro y ocasionó que, en clases posteriores, los estudiantes se confundieran entre el punto característico y la asíntota.
Paul: […] por ejemplo, si tenemos la función f ( x )=2 x -4, ¿qué le pasó a mi función? Y aquí mi función si va a cambiar su asíntota, si, por favor, aquí tengo mi función y = f ( x )=2 x -4, mi punto característico ya no está en (0,1), mi asíntota cambió, como tengo -4, ahora mi asíntota va a estar en -4 […] .
Los procesos que el profesor declara que promueve son los mismos que se observan en el aula, además de constatar otros. Aunque se evidencia que el profesor propone ejemplos matemáticamente representativos y aborda algunos significados de las funciones, deja de lado situaciones (en la vida real u otras ciencias) que son representativas de estas funciones.
Aunque el profesor afirma en la entrevista que en sus explicaciones no hay ambigüedades, en las clases analizadas se observa que hace un uso excesivo de metáforas y personifica la función y sus elementos, lo cual ocasionaba que las explicaciones en algunos momentos no fueran claras. Por ejemplo, en el extracto anterior se observa que el profesor declara que la función es de él, que le ocurren cosas y que tanto la asíntota como el punto característico cambian de una función a otra. Además, el profesor afirma que las funciones se desplazan por el plano, lo que lleva a interpretar que es la misma función que se va moviendo, como se evidencia en el siguiente extracto:
Paul: Ahora, vamos a hacer lo mismo, pero con la siguiente función f ( x )=2 x -5 . En este caso, la función original 2 x se va a desplazar en el eje cinco unidades ¿hacia la izquierda o hacia la derecha? ¿Qué creen ustedes chicos se desplaza hacia la izquierda o hacia la derecha según lo que les expliqué?
Estudiante 1: Hacia la derecha, profe, porque el 5 tiene signo negativo.
Como se muestra en el extracto, algunos estudiantes entendieron lo que el profesor estaba explicando; pero había otros que no participaron, lo cual podría ser porque no entendieron o porque no querían participar. El uso de este tipo de metáforas puede ocasionar que los estudiantes creen una idea errónea de la representación gráfica de la función, pensando que esta se va moviendo en el plano de un lado a otro como si fuera un objeto físico y, por ende, considerar que es la misma función. En este mismo sentido, en el siguiente extracto se observa que el profesor Paul usa una metáfora para tratar de explicarle a un estudiante qué es una asíntota para que, así, este mencione cuál es la asíntota de una función en particular.
Paul : Tengo f ( x )= log 2 ( x -5), ¿qué le pasó a mi asíntota? ¿Dónde ahora creen que está? ¿Se desplazó para la derecha o para la izquierda? […].
Estudiante 2 : Diez.
Paul: ¿Dónde un diez? Tenemos aquí logaritmo en base 2 de x menos 5, ¿dónde tú crees que sea la asíntota? ¿En qué recta, dime, qué recta tú crees?
Estudiante 2: No sé, profe, ¿cero?
Paul: Esta la azul [el profesor hace referencia a la gráfica de color azul que proyecta en GeoGebra] es la función logaritmo en base 2 de x , que es lo que estamos viendo que se trasladó ahí [El profesor señala la función de color morado que corresponde a la función de la cual está haciendo las preguntas]. Voy a quitar la azul para que no te confundas, ¿dónde tú crees que tendría la asíntota esta esta función? ¿Dónde tú crees? ¿ A qué recta tú crees que ella se acerca, pero no la toca ?
Estudiante 2: En cinco.
En lo que respecta al criterio cognitivo, lo que declara el profesor sobre los conocimientos previos y adaptación curricular coincide con lo evidenciado en las clases. No obstante, a pesar de que él afirma que las funciones trabajadas exigen alta demanda cognitiva, la forma en que las aborda hace que la demanda sea en un nivel medio. En el criterio interaccional, lo declarado por el profesor coincide con lo observado respecto al interés del profesor para que los estudiantes participen y haya diálogo entre ellos, aunque no lo logra. Promueve el trabajo individual, tal como lo declaró en la entrevista, mencionando que de esta forma propicia autonomía, y dedica tiempo para solucionar dudas y explicar nuevamente.
Del criterio mediacional, se destaca que lo declarado por el profesor de acuerdo con los recursos y el número de estudiantes coincide con lo evidenciado en la clase, si embargo, lo que declara respecto al tiempo no, pues el profesor no optimizó el tiempo destinado para abordar otras cuestiones de estas funciones, enfocándose solamente a pasar de la representación simbólica a la gráfica de estas funciones.
En cuanto al criterio afectivo o emocional, lo declarado por el profesor respecto al componente intereses no coincide con lo evidenciado, pues el profesor afirma proponer situaciones de la vida real para generar interés en los estudiantes y esto no se evidencia en las clases. Los componentes de actitudes y emociones sí aparecen de la misma manera como el profesor lo manifiesta en la entrevista y lo observado en sus clases.
Finalmente, del criterio ecológico, se puede decir que el profesor se basa en el libro propuesto por la institución donde labora y, aunque usa GeoGebra, su clase sigue siendo tradicional, tal como lo declaró en la entrevista. Afirma promover conexiones extramatemáticas, pero estas no se evidencian en la clase, lo mismo ocurre con el componente utilidad sociolaboral.
Discusión y conclusiones
En esta investigación se buscó responder la pregunta: ¿Cuáles son los criterios que orientan la práctica de un profesor en México al enseñar las funciones exponencial y logarítmica en bachillerato? Después del análisis realizado, se encontró que el profesor Paul afirma que los criterios que orientan su práctica referida a las funciones exponencial y logarítmica son: el criterio epistémico, cognitivo y ecológico. No obstante, al analizar sus clases se observa que además de estos criterios le da mucha importancia al criterio interaccional, pues él procura generar diálogo entre él y los estudiantes y entre los mismos estudiantes, a pesar de que no lo logra con éxito.
Después de indagar en todos los criterios de idoneidad didáctica, tanto en el análisis de la entrevista como en el análisis de las clases, el profesor declara cuestiones que tiene en cuenta, pero algunas de estas no se evidencian en sus clases, tal como se mostró en el apartado anterior.
A partir del análisis realizado, se afirma que, en las clases en general, el profesor logra caracterizar matemáticamente las funciones exponencial y logarítmica, así como aborda los significados de estas como número y como función (criterio epistémico). Sin embargo, el foco de las clases es que los estudiantes aprendan a hacer una gráfica partiendo de la expresión simbólica, lo cual hizo que se propiciara la mecanización del proceso de pasar de un registro simbólico al gráfico, dejando de lado cuestiones importantes como algunas aplicaciones de las funciones, que permitirían trabajar mejor el significado de estas funciones como función y que propiciaran diversos procesos matemáticos.
Esto se debe principalmente a que el profesor aborda tal cual lo que dice el libro propuesto por la institución, esto de manera similar es reportado en Molares-López y Font ( 2019 ) respecto a la función logarítmica. Cabe señalar que otro factor influyente es el hecho de que la enseñanza llevada a cabo fuera enseñanza remota de emergencia, pues le impedía al profesor tener un mejor acercamiento al trabajo de cada estudiante y, aunque existían diferentes recursos para ponerlos en función de la clase y sacarles el mayor provecho, el profesor quizá no los conocía o bien no contaba con estrategias para llevar a cabo exitosamente este tipo de enseñanza.
Lo anterior se justifica en el hecho de que la pandemia obligó a los profesores, de forma inesperada, a ingeniarse cómo dar sus clases en el contexto virtual en el que ellos no estaban familiarizados (Zañartu Canihuante; Guerra Zamora; González Ortiz, 2023 ). Por ejemplo, uno de los criterios de idoneidad que se vio afectado en gran medida con esta forma de enseñanza fue el interaccional, ya que no es lo mismo estar en un salón presencial donde constantemente puede haber interacción, que estar frente a una pantalla donde algunos estudiantes no prendían su cámara y algunos, además de eso, parecían que solo se conectaban a la clase y no atendían a las explicaciones del profesor.
El profesor usa en exceso las metáforas al hablar principalmente de desplazamientos de las funciones y de las asíntotas, como rectas a las cuales las funciones se acercan, pero no las tocan. También personifica las funciones, afirmando que son de él y que estas van cambiando de asíntota y punto característico. Esto puede ocasionar que los estudiantes presenten dificultades para comprender una representación gráfica de una función exponencial o logarítmica, pues podrían crear ideas relacionadas con que se trata de la misma función la cual se va moviendo en el plano como si fuera un objeto de la vida real. Si bien el uso de metáforas ayudó a algunos estudiantes a responder correctamente algunas preguntas, también generó confusión en otros estudiantes. Cabe señalar que algunas de las metáforas empleadas por el profesor son causadas por el libro, pues en este se hace énfasis en “el desplazamiento de funciones”, de manera similar como el profesor lo explica.
El profesor emplea GeoGebra en su clase para explicar, lo cual es parte del componente de recursos del criterio mediacional, pero les exige a los estudiantes que hagan sus gráficas a lápiz y papel, lo que hace que su clase siga siendo tradicional. Además, la forma en que abordó las funciones evidenció que se trabajan por separado, pues, aunque afirmó que eran inversas no usó esta relación, y esto es una de las causas de que los estudiantes tengan dificultades al trabajar tareas que involucran estas funciones (Campo-Meneses; García-García, 2021 ; Campo-Meneses et al ., 2021 ).
En su totalidad, las clases fueron de tipo magistral-interactivo, aunque los estudiantes solo participaban porque el profesor estaba evaluando o porque el profesor insistía en que lo hicieran. No todos los estudiantes participaron, casi siempre eran los mismos y en los momentos donde los estudiantes cometían errores, el profesor no usaba esto como base para generar discusión (criterio interaccional), sino que solo corregía al estudiante diciendo la respuesta correcta y en algunos casos explicando nuevamente, pero de la misma manera.
El uso de criterios de idoneidad didáctica para analizar la entrevista y las clases del profesor Paul permitió inferir los criterios que guían la práctica de este profesor (los criterios de más peso) y, a su vez, analizar qué y cómo usaba todos los criterios en sus clases, con el fin de analizar qué está ocurriendo en la enseñanza de las funciones exponencial y logarítmica. Esto aporta al panorama de cómo se estaba llevando a cabo la enseñanza de las funciones en estudio en la modalidad virtual, que quizá pueda suceder en otros contextos (aún en la presencialidad) y ser una causa de algunas dificultades reportadas en la literatura (Campo-Meneses; García-García, 2020 ; Sureda; Otero, 2013 ; Weber, 2002 ), ya que en las clases se promovió en gran medida la mecanización de procedimientos y no se le dio importancia a situaciones que llevaran al estudiante a analizar las funciones en diferentes contextos y, así, poder establecer la relación de inversas, lo cual impidió que hubiese alta demanda cognitiva.
Finalmente, lo reportado en esta investigación puede ser útil para contrastar lo que puede ocurrir en una clase presencial, además sería interesante que en futuras investigaciones se reporten análisis de clases presenciales en que se aborden estas funciones, con el fin de continuar ampliando el panorama al respecto y, así, poder aportar en la creación de diseños de tareas que contribuyan a la mejora de la práctica de los profesores y la comprensión en los estudiantes.
