INTRODUÇÃO
Inobserváveis e leis aproximativas - como partículas e o isocronismo - fazem parte da visão de mundo científica. Ao invés de serem “dados” a partir do domínio empírico, eles são produtos de abstrações e idealizações realizadas com uma intenção realista, ou seja, na tentativa de representar e explicar o mundo. Portanto, ser capaz de entender o conhecimento científico implica ter certa compreensão sobre a natureza dessas representações e explicações.
Que significado, por exemplo, esperamos que os alunos atribuam a massas pontuais, superfícies sem fricção, raios de luz, em relação ao mundo real ao seu redor? Como eles podem perceber a relação entre as teorias científicas e os objetos a que essas teorias supostamente se referem? Se as práticas de ensino não estão relacionadas com tais questões, é possível que os alunos concluam que não há nenhuma relação entre teorias e realidade. Acreditamos que desenvolver algum nível de compreensão sobre o caráter aproximado do conhecimento científico pode oferecer um contributo substancial nessa direção. O papel dos modelos e discussões de modelos pode ser introduzido em contextos de educação científica nesta perspectiva.
Apesar do amplo consenso da importância dos modelos, não há, na área da educação científica, uma definição única de modelo. Um dos motivos para isso talvez esteja na própria filosofia da ciência, campo no qual também esse conceito é entendido de diferentes formas. Ainda assim, existem evidências quantitativas e qualitativas de que práticas de ensino baseadas em modelos têm efeitos positivos na aprendizagem científica. Alguns exemplos podem ser encontrados nos trabalhos de Halloun e Hestenes (1987); Clement, (1989), Grosslight et al (1991); Harrison e Treagust, (2000); Angell et al (2008) e Gilbert e Justi (2016), entre muitos outros que poderiam ser citados.
Ainda no campo da filosofia da ciência, alguns autores têm defendido que a essência dos modelos na ciência seria justamente seu papel como elementos que permitem relacionar as teorias com a realidade a que elas se referem. Um autor que explora de forma bastante detalhada essas relações é o físico e filósofo Mario Bunge. Sendo um realista, Bunge situa os modelos científicos como entidades fundamentais na busca por compreender conceitualmente a realidade. Eles desempenhariam um papel de mediadores, à semelhança do que foi proposto mais tarde por Morgan e Morrison (1999), entre a realidade e a teorização que pretende versar sobre esta.
Acreditamos que os pontos de vista da Bunge em relação à modelização científica podem ser relevantes para contextos de ensino e aprendizagem de ciências porque destacam aspectos importantes do conhecimento científico. Em primeiro lugar, esta visão enfatiza o caráter aproximativo e parcial de conceitos, modelos e teorias na ciência: uma vez que todos eles assumem uma versão idealizada e conceitual da realidade como referência imediata, esses elementos também devem ser aproximativos e parciais. Consideramos que esse entendimento é relevante para a educação científica, pois pode ser difícil para um estudante perceber como a física da escola poderia se aplicar a um mundo onde não existem massas pontuais nem superfícies sem atrito. Nesse sentido, o conceito de objeto-modelo de Bunge pode ajudar a tornar explícita a relação não-identitária entre objetos reais e nossas ideias sobre esses objetos, que são empregados para desenvolver o conhecimento científico. Além disso, a perspectiva de Bunge incorpora as teorias gerais no processo de modelização, enfatizando seu papel como constituintes heurísticos e integradores na construção de modelos.
Mas como essa relação entre a realidade e o conhecimento teórico (no caso, aquele das ciências naturais) se estabelece no pensamento dos estudantes? Uma possibilidade para estudar a modelização do ponto de vista cognitivo individual é a busca por elementos, no pensamento dos estudantes, que possam desempenhar o papel daqueles da modelização na proposta bungeana (isto é, objetos-modelo, modelos teóricos e teorias gerais). Tal opção implica discutir sobre como ocorre a apropriação conceitual da realidade por parte dos sujeitos, em termos das representações que estes desenvolvem sobre os objetos em questão.
Nessa direção, um referencial teórico cognitivo que tem se mostrado frutífero para aprofundar o conhecimento sobre os processos de pensamento dos estudantes de ciências naturais e matemática é a Teoria dos Campos Conceituais (TCC), de G. Vergnaud. Em sua teorização, esse autor oferece um referencial que permite analisar a dinâmica dos conhecimentos-em-ação (conceitos tidos como relevantes e teoremas tidos como verdadeiros) mobilizados pelos sujeitos ao enfrentarem diferentes tipos de tarefas. Para analisar esses aspectos, Vergnaud atribui uma importância considerável às características dos próprios conhecimentos que são conceitualizados. É essa ênfase que nos conduz a buscar suportes teóricos na obra de Vergnaud, aliada à sua preocupação específica com a conceitualização dos conhecimentos escolares.
A busca por conhecimentos-em-ação (no sentido da TCC) no pensamento dos sujeitos os quais poderiam desempenhar o papel dos elementos do processo de modelização (objetos-modelo, modelos teóricos e teorias gerais) requer o desenvolvimento de uma articulação entre esses dois referenciais - epistemológico e cognitivo - que demonstre a viabilidade de se conceber os elementos da modelização como conhecimentos-em-ação. No presente estudo, visamos articular estes dois referenciais, discutindo aproximações e distanciamentos entre as visões de Bunge e Vergnaud sobre a apropriação do conhecimento.
1. A TEORIA DOS CAMPOS CONCEITUAIS DE G. VERGNAUD
Proposta pelo psicólogo e didata francês Gérard Vergnaud, a Teoria dos Campos Conceituais (TCC) é uma teoria cognitivista, de matriz neopiagetiana, mas também com reconhecidas contribuições de Vygotsky (VERGNAUD, 2007a). Tendo por objeto o processo de conceitualização do real, a TCC provê um referencial teórico que permite localizar e analisar continuidades e rupturas na formação de um conceito, do ponto de vista de seu conteúdo (VERGNAUD, 1990). Nesse sentido, possivelmente o avanço mais importante da proposta de Vergnaud em relação a outros teóricos seja a consideração das especifidades dos conhecimentos científicos como essenciais para compreender o processo de conceitualização desenvolvido pelos sujeitos.
O pressuposto do autor é que o conhecimento organiza-se em campos conceituais, a serem progressivamente dominados pelos sujeitos ao longo do tempo. A noção de campo conceitual desenvolvida por Vergnaud é, de certa forma, análoga ao conceito de domínio, embora não seja idêntica. À dimensão das representações, Vergnaud acrescenta a dimensão das situações. Um campo conceitual é formado por um conjunto de situações entrelaçado com um conjunto de conceitos (VERGNAUD, 2009). A ideia central da teoria é a de que o sentido de um conceito só pode ser formado a partir de uma multiplicidade de situações, ao passo que cada situação requer, também, mais de um conceito para ser analisada. Embora os exemplares apresentados pelo autor sejam concentrados nos campos conceituais das estruturas aditivas e multiplicativas, a TCC não se restringe à conceitualização na Matemática. No caso da Física, o próprio Vergnaud interessou-se pelo campo conceitual da Mecânica (WEIL-BARAIS; VERGNAUD, 1990) e da Eletricidade (VERGNAUD, 1993).
De um ponto de vista epistemológico, Vergnaud (2002) rejeita a noção na qual a essência da Ciência estaria no método. Para esse autor, o progresso da Ciência é, principalmente, o progresso da conceitualização: conceitos mais amplos, mais interligados e que possuem propriedades mais definidas vão substituindo, seja por etapas, seja por evoluções bruscas, aqueles conceitos mais primitivos e que possuem validade mais restrita. O conhecimento científico estaria assim fortemente relacionado com a produção de sistemas gerais envolvendo diversos conceitos e teoremas. Tais sistemas é que dariam à Ciência o seu caráter explicativo. Mas a produção desse tipo de sistemas exige uma criatividade por parte dos cientistas: é através dela que eles chegam a representar objetos e relações que não correspondem diretamente a nenhuma percepção, tais como a força, o átomo ou o gene (VERGNAUD, 2002).
O processo de conceitualização é modelizado na TCC principalmente através do conceito de esquema, que por sua vez é indissociável da noção de situação. Vergnaud atribui ao conceito de esquema uma interpretação mais detalhada do que aquela dada por Piaget, com uma ênfase mais forte na noção de situação. Para esse autor, o esquema pode ser descrito como a organização sequencial da ação do sujeito, a qual é invariante para uma certa classe de situações. É através do esquema que os recursos cognitivos podem se adaptar a situações de complexidade progressiva. Assim, a função dos esquemas na aprendizagem é dupla: por um lado, contém aqueles modos de proceder que foram formados nas situações já dominadas pelo sujeito; por outro, é necessário que ofereçam conceitos abertos, adaptáveis, assegurando que existam possibilidades de inferência quando o sujeito enfrenta situações novas.
Assim, a relevância do conceito de esquema reside no pressuposto básico de que a construção do conhecimento pode ser entendida como um processo adaptativo, no qual os esquemas adaptam-se às situações. Reciprocamente, as situações adaptam-se aos esquemas na medida em que as tarefas são percebidas de formas diferentes pelo sujeito à medida que vão sendo por ele dominadas. A relação entre esses dois construtos - esquemas e situações - é tão próxima que, segundo Vergnaud (2009), por vezes eles são confundidos, de modo que alguns pesquisadores utilizam a expressão esquema para se referir a situações. Por outro lado, essa proximidade entre os dois conceitos revela a amplitude da noção de esquema: os sujeitos utilizam esquemas cotidianamente em uma grande variedade de situações na sua realidade vivencial, tanto em tarefas simples quanto em tarefas complexas, seja o ato de falar, fixar um prego na parede, dirigir, analisar a validade de uma dada argumentação, resolver um problema, produzir uma explicação, e assim por diante.
É essencial destacar que o conceito de esquema não se refere somente à conduta observável, mas igualmente às atividades de pensamento subjacentes (VERGNAUD, 2011). Isso significa dizer que a representação também é parte integrante dos esquemas, e ela “... não é nem uma biblioteca, nem um dicionário: é uma instância eminentemente ativa” (VERGNAUD, 2011, p. 47, tradução nossa). É aplicando e adaptando seus esquemas que os sujeitos tentam dar sentido a uma situação nova. Vergnaud (2007b) atribui ao próprio Piaget o hábito de declarar: “os sentidos são os esquemas” (p.10, tradução nossa). Assim como ocorre com os esquemas, os sentidos atribuídos a um mesmo conceito podem ser diferentes conforme as distintas situações que ajudam a formá-lo. Nas páginas que se seguem, pormenorizamos a constituição dos esquemas e, em seguida, discutimos de modo mais detalhado a relação entre as situações e a construção de sentidos.
1.1 COMPONENTES DOS ESQUEMAS
Vergnaud (2007b) propõe quatro componentes básicos dos esquemas: o aspecto intencional, que se traduz como um ou mais objetivos, sub-objetivos e antecipações; o aspecto gerador, que envolve as regras do tipo “se... então...” e que dirigem a ação do sujeito-em-situação; o aspecto epistêmico, que se refere às invariantes operatórias (denominadas pelo autor como conceitos-em-ação e teoremas-em-ação) e o aspecto operacional, relativo às várias possibilidades de inferência dentro da atividade.
Os objetivos são essenciais para a organização da atividade, mesmo que muitas vezes não sejam totalmente conscientes. Eles revelam já alguma forma de decisão cognitiva, ao refletirem a escolha por um ou outro caminho, ao direcionarem a ação para uma ou para outra questão. Os objetivos podem derivar em sub-objetivos, organizados sequencialmente e hierarquicamente (VERGAUD, 2013). A própria seleção de determinados objetivos, e não de outros, já é, por si mesma, realizada tendo por base algum teorema-em-ação.
Os invariantes operatórios são aqueles elementos do esquema que tem por função reconhecer e identificar os objetos, suas propriedades, relações e transformações. São os responsáveis por possibilitar que o conhecimento do sujeito assuma sua função operatória (para além da função predicativa). Invariantes operatórios podem ser de dois tipos: conceitos-em-ação e teoremas-em-ação. Os conceitos-em-ação constituem-se como categorias de pensamento tidas como relevantes pelo sujeito e são os elementos a partir dos quais é possível construir os teoremas-em-ação. Um teorema-em-ação é uma proposição sobre a realidade que envolve mais de um conceito e que é tida como verdadeira na atividade. Ao contrário do que ocorre com um conceito-em-ação, um teorema-em-ação é suscetível de verdade ou falsidade.
As regras de ação, que envolvem a tomada e o controle das informações, podem ser entendidas como uma “tradução” dos teoremas-em-ação na prática. Considerando que as variáveis das situações podem ser diversas, o sujeito que domina o esquema deve ser capaz de adaptar a aplicação do teorema-em-ação às variáveis específicas daquela situação particular, e o elemento que se “adapta” nesse processo são as regras de ação. Ao dizer que essa componente é a que gera a ação do sujeito, Vergnaud (2007b) não se refere apenas à conduta observável, mas também à atividade não diretamente observável, inclusive a construção das inferências.
Um esquema não é um estereótipo e não pode ser interpretado como uma simples automatização dos modos de fazer, pois a ação do sujeito não é desencadeada diretamente pelo estímulo fornecido pela situação. É por esse motivo que a questão das várias possibilidades de inferências é incluída entre os componentes dos esquemas (VERGNAUD, 2013).
1.2 SITUAÇÕES E SUAS CLASSES
Para Vergnaud, o conhecimento se forma a partir de problemas a resolver ou, o que significa a mesma coisa, de situações a dominar: isso “... pode ser visto na história das ciências e das técnicas, igualmente no desenvolvimento dos instrumentos cognitivos da criança jovem, notavelmente na apropriação do espaço e na compreensão e categorização de objetos comuns” (VERGNAUD, 1986, p. 21, tradução nossa). Assim também deveria ser, continua Vergnaud, no ensino. Porém, não é isso que ocorre: os procedimentos e algoritmos de resolução de exercícios parecem ter centralidade, e não as situações. Um problema, ou uma situação, no sentido dado por Vergnaud, refere-se amplamente a toda situação na qual é preciso descobrir relações, explorar hipóteses e verificá-las para produzir resoluções. De forma simples, situações são tarefas a resolver.
Com base nas considerações feitas até este ponto, é possível elucidar melhor a afirmação central da TCC, que declara que a construção de um conceito requer uma diversidade de situações ao mesmo tempo em que cada situação põe em jogo uma multiplicidade de conceitos. Tomemos como exemplo um caso amplamente investigado e analisado por Vergnaud: o campo conceitual das estruturas aditivas. Quais são as propriedades da adição a serem conceitualizadas pela criança durante o desenvolvimento nesse campo conceitual?
Uma dessas propriedades é dada pela composição de medidas. Um exemplo de situação que envolve essa propriedade é a contagem do número total de pessoas presentes em uma sala, sendo conhecida uma parte e outra parte. Outra é a de uma transformação entre estados, na forma F = T(I), em que T é uma transformação e F e I são os estados final e inicial. É o caso de situações que solicitam, por exemplo, a altura de uma árvore dados a altura inicial e a taxa de seu crescimento; a quantidade de bolinhas de gude que pertencem a André, conhecendo a quantidade inicial e o número delas que ele ganhou em uma partida; e assim por diante. Uma terceira significação da adição é a de comparação entre medidas: se João tem cinco bolinhas e Pedro tem oito, quantas Pedro tem a mais do que João? Observe-se que neste último caso a operação efetuada consiste em uma subtração, na forma em que foi apresentada. O mesmo pode ocorrer com os exemplos anteriores, quando se invertem a variável solicitada com alguma das variáveis dadas ou ainda quando as variações são negativas. Cada uma dessas possibilidades dá origem a uma classe de situações: percebe-se, assim, que mesmo para o campo conceitual das estruturas aditivas, existem numerosas classes de situações (VERGNAUD, 2007b). Daí que a variedade é uma característica importante das situações que formam um campo conceitual.
Muito mais do que uma mera classificação, essa forma de categorizar as situações pertinentes a um campo conceitual permite evidenciar, no contexto do ensino, a importância de compreender a diferença entre um significante e seus possíveis significados. A relação entre significante e significado não é biunívoca (VERGNAUD, 1996). Basta pensar em quantos significados diferentes podem estar representados por símbolos aparentemente tão simples como (+) e (-)! O que poderíamos considerar, nesse contexto, sobre conceitos científicos de alto nível de abstração, como os conceitos de energia, potencial e entropia?
Uma análise detalhada do conjunto de classes de situações correspondentes a Campos Conceituais no domínio da Física - que, por si só, demandaria a implementação de projetos de pesquisa específicos para esse fim - está além do escopo desse artigo. Contudo, podemos vislumbrar a importância da variedade das situações, por exemplo, na conceitualização da energia. Ao longo do processo de apropriação desse conceito, os estudantes encontram situações que destacam diversas propriedades da energia: a energia pode representar uma grandeza que se transforma de um tipo em outro, como é o caso de problemas em que ocorre transformação da energia potencial gravitacional em energia cinética, ou vice-versa; pode constituir uma grandeza que se transfere de um corpo para outro, como nos problemas de trocas de calor; pode ser uma grandeza que se conserva ao longo do tempo, como no caso de problemas enfocando a conservação da energia; pode representar uma quantidade, associada a um corpo, cuja variação corresponde a uma variação da massa desse corpo.
Cada uma dessas propriedades associa-se a diferentes situações que poderiam ser propostas na ação didática. É nesse sentido que Vergnaud destaca a multiplicidade de situações necessárias na formação de certo conceito. Durante o processo de conceitualização, estudantes poderão ter êxito em tarefas que remetem a certa classe de situações, enquanto ainda não o têm em outras classes, assim como poderão mobilizar, para determinadas classes de situações, teoremas-em-ação, conceitos-em-ação e esquemas de natureza diferente daquela que mobilizariam para outras. Assim, Vergnaud enfatiza a importância do reconhecimento da diversidade de situações que dão sentido ao conceito como subsídio ao professor em sua tarefa de propor situações que favoreçam a aprendizagem conceitual.
2. MODELOS E MODELIZAÇÃO: A CONTRIBUIÇÃO DE M. BUNGE
Sendo um realista, Bunge situa os modelos científicos como entidades fundamentais na busca por compreender conceitualmente a realidade. Eles desempenhariam um papel de mediadores, à semelhança do que foi proposto mais tarde por Morgan e Morrison (1999), entre a realidade e a teorização que pretende versar sobre esta. Mas o que se entende por “realidade” nesse contexto?
O conceito de realidade a que se refere Bunge consiste na agregação de todas as coisas que mantém entre si relações espaço-temporais: “a realidade de um objeto consiste em ser ele parte do mundo” (BUNGE, 1977, p. 161, tradução nossa). Posto que nosso foco de estudo localiza-se no ensino de ciências naturais, ao usar esse termo nos referimos à realidade natural (ou a realidade física, quando a referência for a conhecimentos físicos). Não nos referimos, portanto, a outras realidades, pertencentes a outros níveis, tais como os pensamentos ou sentimentos. Dito de outra forma, uma “coisa real” no contexto do conhecimento físico seria o referente pretendido de uma teoria física (BUNGE, 1977).
Essa definição deixa de fora objetos conceituais, tais como os construtos da ciência. Esses não são dotados de realidade, embora existam conceitualmente. Além disso, notamos também que a realidade não é redutível à observação, já que postula a existência de entidades inobserváveis como ondas e forças, e ainda menos à experiência comum, pois aceita componentes que não poderiam ser dela extraídos, tais como o elétron e a inércia (BUNGE, 1973b). Por fim, a realidade é mutável, ou seja, existem reais possíveis, que podem ainda não estar atualizados. Assim, a realidade pode ser dividida em duas classes: atualidades e possibilidades reais (BUNGE, 1977).
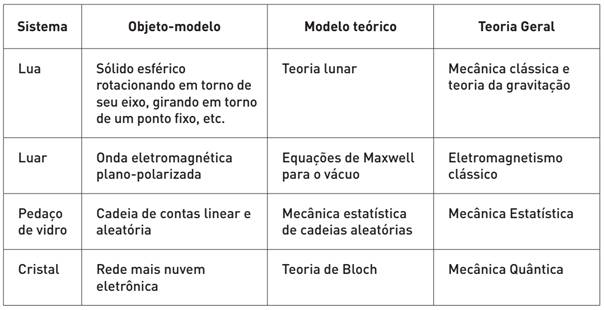
Bunge enfatiza o caráter parcial e aproximativo do conhecimento científico. Segundo o autor, a conquista conceitual da realidade se inicia a partir de idealizações e abstrações operadas pelo sujeito epistêmico sobre o objeto que este quer conhecer. Essas operações resultam em uma representação conceitual do objeto, chamada pelo autor de objeto-modelo (como massas pontuais, corpos rígidos, ondas eletromagnéticas, planas, espécies). A articulação entre o objeto-modelo e uma teoria geral (algumas teorias gerais podem ser a Mecânica Clássica, Teoria da Relatividade Restrita, Eletromagnetismo Clássico, Teoria da Evolução) resulta em um sistema hipotético-dedutivo denominado modelo teórico, que pode ser confrontado com a experiência - ao contrário do que ocorre com as teorias gerais - e que herda o caráter aproximativo e idealizado do objeto-modelo.
Teorias gerais, por si mesmas, não podem ser testadas. Um motivo para isso é o fato de que, justamente por serem gerais, não fazem nenhuma previsão específica sem que se lhes acrescente hipóteses adicionais. Portanto elas não geram, sozinhas, proposições contrastáveis com algum tipo de dado empírico. Outra forma de colocar essa característica é considerar que qualquer teoria geral poderia, a princípio, produzir um número infinito de previsões, de acordo com as hipóteses adicionais que lhe fossem acrescentadas. Inversamente, a refutação empírica de um modelo teórico não implica na refutação da teoria geral que tomou parte na sua elaboração. Em resumo, as teorias gerais podem ser apoiadas ou enfraquecidas pelos testes de seus modelos teóricos, mas não provadas ou refutadas conclusivamente (BUNGE, 1973b).
Objetos-modelo são representações esquemáticas de objetos reais. Contudo, o termo “esquemático” aqui não significa pictórico ou figurativo. Objetos-modelo precisam ser conceituais, já que eles são essencialmente ideias sobre seus referentes. Esse aspecto é o que permite que sejam encaixados em teorias gerais. Seu caráter esquemático vem do fato de que perdem algumas das características de seus referentes, já que são criados através de abstrações e idealizações (BUNGE, 1973a). Imaginar o cérebro como uma rede de neurônios, a Lua como uma massa pontual ou a matéria sólida como uma rede cristalina podem ser citados como exemplos do emprego de construtos para representar coisas - ou seja, de objetos-modelo. Esse conceito é importante porque mostra a relação de não-identidade entre os objetos da realidade e o conhecimento produzido sobre esses objetos.
Mas os objetos-modelo, sozinhos, não têm poder explanatório. Construir uma explicação requer a elaboração de modelos teóricos, que podem ser criados se incorporando um objeto-modelo em uma teoria geral. Por exemplo, para explicar o comportamento de um gás confinado em um recipiente, criamos uma ideia sobre o gás, isto é, um objeto-modelo. Podemos imaginar as moléculas desse gás como massas pontuais colidindo umas com as outras e com as paredes do recipiente. Abstraímos as variações de energia das moléculas, assim como as interações eletromagnéticas entre elas. Através dessas abstrações e idealizações, criamos um objeto-modelo que representa conceitualmente o gás: nesse caso, chamado de “gás ideal”. Mas isso, por si só, não configura um modelo teórico. Quando combinado com uma teoria geral tal como a mecânica clássica é que é possível desenvolver um modelo teórico (nesse caso, chamado de “teoria cinética do gás ideal”). Este modelo permite estabelecer relações entre as variáveis do sistema e fazer previsões sobre seu comportamento, construindo assim uma porção modesta, porém frutífera, de conhecimento científico. Outros exemplos sugeridos por Bunge são apresentados no Quadro 1.
O mesmo objeto real pode ser transformado, por operações de pensamento, em diferentes objetos-modelo, e encaixado em diferentes teorias gerais, resultando em uma dinâmica que oferece uma multiplicidade de caminhos possíveis para a construção de conhecimentos científicos novos. Cada um destes consiste em um diferente modelo teórico. Não se trata, portanto, de uma receita ou de um mero algoritmo. Além disso, os modelos teóricos disponíveis distribuem-se em um amplo espectro de profundidade em seu poder explicativo, desde as abordagens mais simples, que apenas relacionam variáveis de entrada com variáveis de saída (modelos do tipo caixa-preta), até abordagens mais fortemente interpretativas (as caixas “translúcidas”). As primeiras são vistas como estágios iniciais da pesquisa, tendo-se como objetivo fazê-las evoluir para as últimas, pois são estas que permitem a construção de uma interpretação da realidade, objetivo maior do empreendimento científico (BUNGE, 1974). Nessa perspectiva, o modelo teórico é a entidade que faz a mediação entre a teoria e a realidade; daí se depreende seu papel central na construção do conhecimento científico.
Os conceitos bungeanos enriquecem e dão maior clareza à proposta de que modelos são parcialmente independentes tanto da teoria quanto dos dados e que consistem em agentes relativamente autônomos, defendida por Morgan e Morrison (1999). Isso ocorre porque a construção de modelos teóricos para a mesma situação física é possível tanto se criando diferentes objetos-modelo quanto adotando diferentes teorias gerais. Ainda no exemplo dos modelos de gás, se tomarmos os volumes das moléculas e as forças intermoleculares em consideração teremos criado outro objeto-modelo para o gás: se este for engastado na mesma teoria geral de antes, teremos outro modelo teórico, o modelo de van der Waals. Inversamente, mantendo o mesmo objeto-modelo anterior e utilizando outra teoria geral, como a dinâmica relativística, seria obtido ainda outro modelo teórico. E não são só os modelos teóricos que possuem essa relativa autonomia, mas o mesmo também vale para os objetos-modelo: nenhum deles é propriedade exclusiva de um modelo, ao menos a priori. Assim, por exemplo, a ideia de massa pontual é compartilhada por um grande número de modelos teóricos, seja de um sistema massa-mola, o movimento de um pêndulo, a queda livre, os projéteis, entre muitos outros.
Qualquer modelo teórico herda o aspecto parcial e aproximativo do objeto-modelo. Isso significa que não devemos esperar que algum modelo possa espelhar a realidade. Ao contrário, modelos teóricos são provisórios por natureza. Podem concordar com a realidade de forma aproximada, na melhor das hipóteses. São muito mais ricos do que os objetos-modelo, por um lado, e muito mais abertos ao escrutínio do que as teorias gerais (que não podem ser testadas empiricamente, justamente por serem gerais), por outro. Mas eles podem possuir diferentes níveis de poder explanatório, de acordo com as diferentes abordagens que podem ser tomadas ao construí-los.
As abordagens do tipo “caixa-preta” (também chamadas pelo autor de abordagens fenomenológicas) são consideradas por Bunge (1973a) como as mais superficiais, e têm como objetivo descrever e prever o comportamento de sistemas, relacionando variáveis de entrada com variáveis de saída. Nessa abordagem, não há uma consideração de possíveis “mecanismos internos” da caixa. Consequentemente, esse tipo de abordagem fornece representações globais e simplistas do sistema sendo modelado. Alguns exemplos dessa abordagem são a cinemática, a óptica geométrica e a teoria behaviorista da aprendizagem. Frequentemente, uma abordagem do tipo caixa-preta é empregada nos estágios iniciais do desenvolvimento de certa área científica (BUNGE, 1998).
Por estarem relativamente mais próximas dos dados empíricos e por serem mais superficiais ao mesmo tempo, caixas-pretas tendem a ser mais difíceis de refutar. Por exemplo, a lei de Ohm relaciona a corrente que passa por um condutor com a diferença de potencial entre os terminais de um condutor. Esse modelo teórico foi desenvolvido inicialmente por Georg Ohm usando um termopar e um galvanômetro. Ele fornece uma relação entre as variáveis escolhidas, mas não explica por que a relação é conforme o estabelecido. Adicionalmente, por ser aproximativa por natureza, essa relação é válida apenas à temperatura constante, o que estritamente não é possível, principalmente por causa do aquecimento devido ao efeito Joule.
Em contraste, existem também as caixas translúcidas (ou abordagens representacionais), que procuram explicar o mecanismo interno de um sistema ou evento. Esse mecanismo é hipotético, e é inventado usando conceitos abstratos e inobserváveis. Entre caixas-pretas e translúcidas, existe um espectro de abordagens intermediárias, semitranslúcidas. A elaboração de modelos assim não requer um processo separado das caixas-pretas, mas pode ocorrer utilizando-as como um fundamento inicial.
Assim, para o propósito de construir caixas translúcidas ou semitranslúcidas, é necessário criar construtos inobserváveis através das abstrações e idealizações. Adicionalmente, esse processo envolve também a integração com as teorias gerais. Por exemplo, no caso da condução elétrica, a corrente passa a ser modelada como certa distribuição de elétrons se movendo através de um meio com centros espalhadores (íons da estrutura do condutor) e este objeto-modelo é conectado à mecânica clássica e à eletrodinâmica como teorias gerais, seguindo-se daí a proporcionalidade entre a densidade de corrente e o campo elétrico, o que é uma versão reformulada da lei de Ohm, o modelo teórico correspondente. Outros objetos-modelo podem (e foram) criados para representar a corrente em um condutor, e outras teorias gerais podem ser usadas para modelizar seu comportamento. Novamente, isso ilustra a relativa autonomia de um modelo teórico e seu papel em mediar entre a teoria e os objetos aos quais ela supostamente se refere.
Este exemplo permite iluminar alguns pontos sobre caixas translúcidas. Em primeiro lugar, os construtos necessários para desenvolver uma explicação acerca do mecanismo interno do sistema não são vistos ou medidos, mas antes imaginados e inventados: elétrons, estruturas cristalinas, campos, potenciais, são objetos-modelo de alto nível de abstração. Além disso, as teorias gerais são importantes não apenas como um meio de derivar um modelo, mas especialmente como formas de atribuir significados para as variáveis intervenientes, assim permitindo criar interpretações acerca da estrutura interna e estimulando o surgimento de explicações mais profundas. No caso do exemplo supracitado, a resistência pode ser agora interpretada como uma propriedade da estrutura do condutor, ao invés de simplesmente ser uma constante que relaciona entrada e saída. Uma última observação que pode ser feita sobre as caixas translúcidas é sua propriedade de permitir que um modelo seja integrado em uma estrutura teórica de amplo alcance, que são as teorias gerais: dessa forma, elas já não são mais algo à parte do resto da Ciência, como é o caso das caixas-pretas (BUNGE, 1973a).
Apesar de caixas-pretas serem consideradas por Bunge como necessárias, especialmente ao enfrentar um novo problema, ele também as considera insuficientes, pelas razões discutidas acima. Para ele, o objetivo de longo prazo da Ciência não é acumular dados, mas explicar a realidade. Portanto, construir caixas translúcidas é altamente desejável na atividade científica e deveria ser encorajado. Além disso, para produzir explicações sobre o mecanismo interno, juntar dados e mais dados pode não ser de nenhuma ajuda. Tal objetivo requer um esforço inventivo, usando a imaginação do sujeito.
Nesse ponto, é possível perceber mais claramente como a idealização e abstração auxiliam a construir a explicação científica. Ambos os processos são necessários para construir caixas menos opacas, cinzentas ou translúcidas, que por sua vez proporcionam modelos com mais alto poder explanatório (BUNGE, 1973a). Contudo, isso não significa dizer que a construção de caixas-pretas seja mais fácil ou que não necessite de imaginação e criatividade. Na verdade, mesmo para desenvolver esse tipo de modelos é preciso recorrer a abstrações e a idealizações.
3. ARTICULANDO OS REFERENCIAIS DE VERGNAUD E BUNGE: ELEMENTOS PARA COMPREENDER O CONHECIMENTO E SUA APROPRIAÇÃO
Evidentemente, as duas teorias são construídas em âmbitos diferentes - da epistemologia, em um caso, e da psicologia cognitiva, no outro. Também é verdade que, a rigor, são elaboradas tendo em vista objetivos distintos: enquanto Bunge elabora um modelo da relação entre o conhecimento científico e o seu referente, Vergnaud modeliza o progresso do conhecimento do sujeito ao longo do tempo, com interesse na sua aprendizagem e seu ensino. Por outro lado, ambas oferecem uma interpretação para a relação entre o pensamento e o mundo. Nessa direção, parece-nos que, se buscamos compreender o papel da modelização no processo de conceitualização dos sujeitos, um caminho poderá ser a procura de pontos de aproximações e afastamentos entre as ideias desses autores.
A concepção de modelos desenvolvida por Bunge consiste em uma teorização voltada essencialmente para a filosofia da ciência, sem uma preocupação a priori com questões relacionadas ao ensino e à conceitualização. Apesar disso, defendemos que ela permite o desenvolvimento de algumas considerações relevantes para essas áreas, uma vez que a visão que se tem de ciência influencia diretamente em seu ensino. Nos parágrafos que se seguem, pontuamos algumas destas considerações para, em seguida, analisar mais detidamente algumas aproximações entre as concepções de Bunge e Vergnaud sobre o processo de apropriação de conhecimento.
O primeiro aspecto a destacar com base na modelização bungeana é a relação de não-identidade entre os objetos da realidade e os conhecimentos produzidos sobre eles. A ausência do estabelecimento correto dessa relação é muito frequente na prática escolar de Física e conduz a um enfraquecimento do significado atribuído pelos estudantes aos conhecimentos físicos, levando-os à percepção de que a Física não se relaciona com a realidade. O enfrentamento desse problema requer uma compreensão sobre os processos de abstração e idealização que permitem a construção de um objeto-modelo. Permanece em aberto o problema de como a ação didática pode favorecer a aprendizagem relativa a esses processos.
Também notamos que grande parte dos problemas e exemplares utilizados nas aulas de Física retratam situações esquemáticas específicas que devem ser resolvidas mediante a aplicação de uma teoria geral e, nesse sentido, podem ser comparados a um processo possível (embora não o único: discutiremos o processo alternativo na sequência) de criação de modelos teóricos. Um exemplo clássico é o conjunto de problemas no estudo da Mecânica em que se apresenta uma determinada configuração de massas e solicita-se a obtenção da aceleração do sistema. O resultado esperado fornece uma expressão para a aceleração, em geral, em função das massas e da aceleração gravitacional. A resolução do problema/exercício/tarefa requer não apenas a constituição de um objeto-modelo, mas também novas abstrações e idealizações a serem feitas (ausência de atrito, fios inextensíveis e sem massa, entre outros), além do reconhecimento de vínculos do sistema (tais como cordas ligando duas massas) e outras operações de pensamento, que não estão contidas na enunciação da teoria geral. Portanto, não se trata de um procedimento automatizado, mas de um processo adaptativo, comparável ao desenvolvimento de um esquema.
Seguindo-se a epistemologia de Bunge, também é possível compreender a elaboração de modelos teóricos no caminho inverso, isto é, partindo-se do domínio empírico, procurar relacionar determinadas variáveis em uma situação física. Nesse caso, o modelo construído será do tipo caixa-preta e fará surgir uma variável interveniente, cuja interpretação completa dependerá da interlocução com a teoria. Para o contexto do ensino de Física, a consideração do domínio empírico se traduz, via de regra, no desenvolvimento de atividades experimentais. Uma vez que seja assumido o objetivo de estabelecer uma relação coerente entre o objeto real e o objeto-modelo, a presença do domínio empírico pode ser entendida como um requisito: “uma boa atividade modelizadora deveria necessariamente se preocupar na passagem dos dados brutos contidos numa observação, até uma representação conceitual de um fenômeno enfocado” (PIETROCOLA, 2002, p. 106).
Consistentemente com essa perspectiva, Vergnaud posiciona a conceitualização como uma questão estreitamente ligada ao problema da relação entre o real e a sua representação (VERGNAUD, 1994). Sobre esse problema, o autor destaca sua rejeição ao triângulo epistemológico clássico que representa em seus vértices o objeto, a representação e o símbolo. Para compreender a conceitualização, segundo o autor, é preciso complexificar o triângulo, admitindo uma leitura dupla do real: ao invés de ser formado apenas pelo polo do objeto, o real precisaria ser entendido como o conjunto de objetos somado ao conjunto de situações. Portanto, ao usar o termo “realidade”, Vergnaud refere-se ao mesmo tempo a um conjunto de situações - com diferentes níveis de complexidade - e a um conjunto de objetos - com diferentes níveis de abstração. A noção de situações empregada aqui é aquela usual do autor e já discutida anteriormente, consistindo nas tarefas e problemas que requerem enfrentamento. No conjunto de objetos, por sua vez, Vergnaud inclui no seu entendimento de realidade não apenas os objetos concretos (fisicamente reais), mas também os objetos conceituais, que Bunge denomina de construtos. Para Vergnaud, “... objetos podem existir em níveis de abstração muito diferentes: o espaço vetorial é um objeto para o matemático” (VERGNAUD, 1998, p. 237).
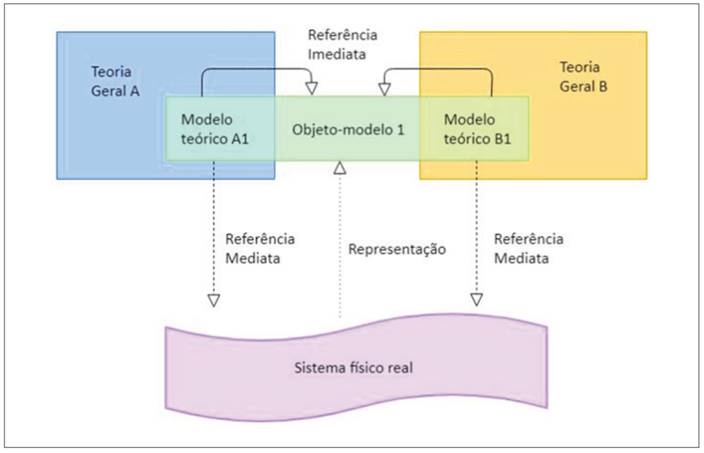
Nesse ponto, importa relembrar que Vergnaud focaliza a referência do conhecimento matemático ao desenvolver a TCC, muito embora a teoria não se restrinja exclusivamente à conceitualização em Matemática. E a Matemática, assim como a Lógica, não é uma ciência empírica, de modo que não causa grande surpresa a associação considerada por Vergnaud dos objetos conceituais na categoria da realidade. Ou, expressando nos termos utilizados por Bunge (1979, 1983), a Matemática uma ciência formal, não factual: ela cria seus próprios objetos, ao contrário de outras ciências como a Física, a Química ou a História, cujos objetos existem fora delas próprias. Embora na Física os referentes imediatos das teorias sejam objetos conceituais (modelos), estes são criados com a intenção de representar os referentes mediatos, que são os objetos reais, conforme representado na Figura 1. Isso, porém, não ocorre no caso da Matemática: os objetos conceituais são já os referentes dessa ciência. Portanto, é bastante coerente que Vergnaud, sendo matemático e trabalhando em uma teoria do desenvolvimento que nasce no contexto da aprendizagem matemática, tenha uma compreensão de realidade que inclua objetos abstratos, diferentemente do que ocorre com Bunge.
Com base nessas considerações, e levando em conta as diferenças de âmbito e de objetivos entre as propostas teóricas de Bunge e de Vergnaud, podemos interpretar que, embora ambos investiguem a relação entre o pensamento e o mundo, cada qual o faz do modo que melhor sirva às suas contingências: no caso da TCC de Vergnaud, no lugar de procurar essa relação na dupla realidade/teoria, esta é substituída pela dupla situações/esquemas. As situações e seus objetos fazem, assim, o papel de referente para os conhecimentos que sobre eles são produzidos, analogamente ao modo pelo qual a realidade constituiria o referente mediado dos modelos, no contexto da modelização bungeana. Essa interpretação também é reforçada pela esquematização proposta por Vergnaud para representar a representação, apresentada na Figura 2.
Ao discutir o homomorfismo entre o real e a representação, Vergnaud (1994) dá destaque ao que denominou de seleção como uma característica extremamente geral do pensamento. Essa característica estaria relacionada com a tomada de informação sobre o real, ou seja, a seleção do que é pertinente - em geral, uma parte pequena do real (VERGNAUD, 1994).
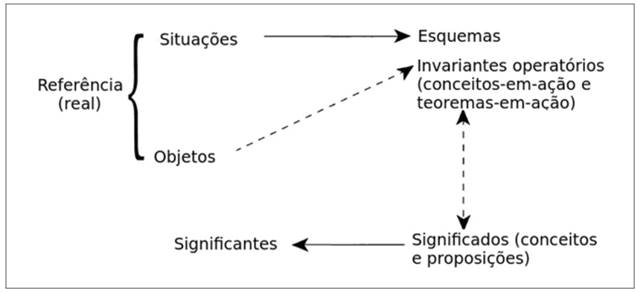
Fonte: Traduzido e adaptado de Vergnaud (1994), p. 34.
Figura 2 Uma análise alternativa da representação, segundo Vergnaud
É interessante notar que o autor apresenta essa característica justo em um trabalho que discute o homomorfismo entre o real e a representação, pois, como se depreende de sua conceituação, trata-se de uma categoria de pensamento que corresponderia, ao menos de forma aproximada, àquilo que chamamos de abstração. Já que a desenvolve no contexto de uma análise sobre a conceitualização, Vergnaud (1994) acrescenta ainda que são os invariantes operatórios - conceitos-em-ação e teoremas-em-ação - que servem para guiar essa seleção e distinguir o que é pertinente do que não é.
Assim como Bunge, Vergnaud destaca que os objetos de pensamento proporcionados pela Ciência são muitas vezes relacionados apenas de forma distante com os objetos reais conforme percebidos pelos sujeitos em seu ambiente e, portanto, são o resultado de uma construção (VERGNAUD, 2002). Ainda se referindo ao caso dos objetos com que lida a ciência, Vergnaud vai mais longe nessa direção ao afirmar que estes “contradizem a leitura comumente feita dos fenômenos” (2002, p. 34). Mesmo sem a utilização desse termo, é possível identificar a ideia bungeana de objeto-modelo no texto citado, particularmente ao observar a declaração de que, aos cientistas, a imaginação...
... seria necessária para representar objetos e relações que não correspondem diretamente a nenhuma percepção: Newton não poderia perceber diretamente o conceito de força, nem Lavoisier o de oxigênio, nem Darwin o de evolução, nem Freud o de inconsciente. E Newton era muito ousado para afirmar o princípio de que se um corpo em movimento não está sujeito a nenhuma força, seu movimento é retilíneo e uniforme. (VERGNAUD, 2002, p. 33, tradução nossa).
Para o autor, um conceito, seja ele científico ou um conceito-em-ação, é sempre redutor, no sentido de negligenciar parte das características dos objetos e situações ao qual se refere. Por causa disso, toda explicação é sempre parcial. E o mesmo pode ser afirmado acerca da conceitualização, que pode ser pensada como uma espécie de explicação de nível superior. Essa redução simplificadora não é, contudo, considerada negativa: ela dá à ação e à conceitualização características de viabilidade e de economia, evitando uma busca vã pela exaustividade. Além disso, seja na ciência, seja na ação, uma representação altamente esquemática pode sempre ser refinada, se for necessário (VERGNAUD, 2002). Nessas considerações é possível notar que um papel criativo é atribuído à redução e à simplificação do real, em uma perspectiva consistente com a proposta bungeana de objeto-modelo.
Esse caráter parcial atribuído ao conhecimento - seja científico ou individual - conduz a outro ponto de aproximação entre as propostas dos dois autores: Vergnaud parece, também, ser levado a uma posição crítica em relação ao problema da possibilidade do conhecimento. Ainda quando discute o homomorfismo entre o real e a representação, sustenta que “... é preciso integrar uma visão do real em termos de classes de situações. Mas as situações não se deixam classificar facilmente” (VERGNAUD, 1994, p. 34, tradução nossa). Essa interpretação é corroborada pela indicação de Vergnaud (2002) da “resistência indefinida do real” e do “caráter incontornável da decisão em situação de incerteza” (p. 40, traduções nossas) como duas características fundamentais da atividade científica. E estas são, também, características das situações com que os sujeitos se deparam no seu desenvolvimento, e que impõem a necessidade da tomada de decisões cognitivas. Ao manter aberta a possibilidade de um aperfeiçoamento das representações simplificadas de acordo com as contingências da situação, Vergnaud parece admitir, como Bunge, uma forma de conhecimento por aproximação.
Apesar de não focalizar especificamente o tema dos modelos em sua obra, Vergnaud admite a existência de uma diferença entre teorias e modelos. Ele atribui aos modelos um caráter de conhecimentos mais abertos ao escrutínio e à exploração e, principalmente, mais hipotéticos, enquanto no caso das teorias tratar-se-ia de algo mais do que apenas hipóteses, pois existiria um componente mais forte de crença por parte do sujeito cognoscente. Nas palavras do autor:
Pode-se supor que um pesquisador elabora um modelo para ver, como se diz, isto é, para explorar as possibilidades nas quais acredita moderadamente, mas um pesquisador não elabora uma teoria em que não acredita. Newton, Lavoisier, Darwin, Mendel e Freud acreditavam no que eles inventaram (VERGNAUD, 2002, p. 34).
Outro ponto importante tanto na TCC quanto na concepção epistemológica de Vergnaud é a importância atribuída à integração dos conhecimentos no sentido da formação de sistemas teóricos. Ao comparar os invariantes operatórios aos conhecimentos científicos, por exemplo, o autor destaca que os primeiros são, em geral, dotados de escopo de validade bastante local e limitado, enquanto os últimos não apenas apresentam uma abrangência mais ampla, mas se organizam em sistemas integrados: “a ciência é sistêmica ou não é ciência” (VERGNAUD, 1998, p. 231). A própria ideia de campo conceitual, em sua essência, é consistente com essa visão sistêmica do conhecimento, ao fundamentar-se justamente no pressuposto de que um conceito não pode ser compreendido apenas como uma definição. Ao sustentar que um conceito não pode ser entendido com base em uma única situação, nem uma situação pode ser tratada através de apenas um conceito, a TCC pressupõe exatamente uma integração entre os conhecimentos e aponta para a necessidade de estudar o desenvolvimento em termos de campos (VERGNAUD, 1989).
No caso do conhecimento científico, uma parte importante dessa integração que culmina com a emergência de sistemas é representada pelas teorias gerais no sentido bungeano, por fornecerem um quadro teórico de análise conjugável para uma grande diversidade de situações sob seu domínio. Pode-se pensar, por exemplo, no caso da Mecânica: enquanto Galileu e seus contemporâneos desenvolvem modelos individuais para cada problema abordado, seja a queda livre, o movimento do pêndulo, o movimento de projéteis, entre outros, cada um desses modelos funciona aproximadamente como uma caixa-preta, descrevendo o comportamento de cada sistema específico separadamente. Algumas das ideias desenvolvidas nesses modelos são transpostas de uma situação para outra (por exemplo, a ideia de composição de movimento, ou a noção de inércia galileana), mas não há princípios gerais propriamente ditos que efetivamente os integrem em um sistema de pensamento orgânico. Essa integração irá se desenvolver principalmente a partir do advento da mecânica de Newton, que estabelece justamente uma teoria geral para esse domínio do conhecimento.
CONCLUSÕES E IMPLICAÇÕES
Em síntese, destacamos que os conhecimentos científicos, que são objeto da análise epistemológica como a de Bunge, são também, ao mesmo tempo, conhecimentos-em-ação - no sentido de Vergnaud - para os cientistas. Similarmente, suas versões escolares são conhecimentos-em-ação (ou, pelo menos, podem ser) para outros sujeitos epistêmicos, os estudantes. A partir dessa consideração e da compatibilidade entre as compreensões desses autores sobre a natureza do conhecimento e sobre a relação entre o conhecimento e seu referente, que viemos discutindo até aqui, concluímos que esses dois referenciais teóricos podem ser articulados, e defendemos que essa articulação pode contribuir para avançar no entendimento de como os estudantes conceitualizam o processo de modelização.
Explicitamente, essa articulação se dá pelo reconhecimento de que aqueles elementos do conhecimento científico que constituem objetos-modelo, teorias gerais e modelos teóricos (por exemplo, as ideias de massa pontual, o modelo do sólido cristalino, a segunda lei da termodinâmica), podem constituir conceitos-em-ação e teoremas-em-ação nos esquemas mobilizados por estudantes de ciências. De forma mais precisa, são as versões escolares daqueles conhecimentos científicos que potencialmente são apropriadas pelos estudantes e mobilizados como conhecimentos-em-ação.
Um aspecto relevante derivado da articulação desenvolvida aqui é a busca pela caracterização de quais objetos-modelo que são mobilizados pelos estudantes na forma de conceitos-em-ação (e quais deixam de ser), e em quais classes de situações eles são mobilizados. Tal estudo poderia auxiliar na concepção e proposição de situações, na prática de ensino, capazes de ajudar os estudantes a identificar a relevância dos objetos-modelo da Física em uma maior diversidade de situações e, com isso, contribuir para o desenvolvimento de suas habilidades de modelização.
Outro aspecto importante para o desenvolvimento dessas habilidades é o reconhecimento das teorias gerais da Física como amplos e abrangentes sistemas de pensamento, capazes de integrar o conhecimento de todo um Campo Conceitual. Nessa direção, a articulação aqui desenvolvida oferece um caminho de pesquisa que parece ser profícuo para buscar compreender em que medida os estudantes reconhecem e mobilizam as teorias gerais enquanto teoremas-em-ação que possibilitam a elaboração de modelos teóricos, ao enfrentar diferentes situações durante a aprendizagem em Física.
Evidentemente, isso não significa igualar os conhecimentos-em-ação às versões escolares de conhecimentos científicos. Muitos desses conhecimentos não terão origem escolar, já que o pensamento dos estudantes é rico em concepções alternativas. Porém essas últimas também podem, ao menos em princípio, exercer os papéis de objetos-modelo, modelos teóricos e teorias gerais nos esquemas individuais de pensamento dos sujeitos, e certamente também podem ser tratados como conceitos-em-ação e teoremas-em-ação.
Por um lado, a determinação de quais objetos-modelo consistirão, de fato, em conceitos-em-ação, e quais teorias gerais e modelos teóricos consistirão em teoremas-em-ação, e em quais classes de situações, são questões que requerem estudos empíricos. Por outro lado, a articulação desses dois referenciais teóricos ajudou a explicitar que a referência direta dos teoremas-em-ação são construtos - e não os objetos reais em si mesmos -, além da compreensão de que as teorias gerais, muito mais do que serem apenas equações de ampla aplicabilidade, integram e dão organicidade aos modelos teóricos, já que estes possuem em comum o mesmo Campo Conceitual, que por sua vez encerra o conjunto de situações que dão sentido aos conhecimentos.