INTRODUCTION
One of the most important tasks that the Mathematics Education (ME), seen as a field for the production of knowledge related to the mathematics teaching and learning processes, should assume is the professional development of the mathematics educators. Therefore, it should impulse formative processes that empower such development. The education of the mathematics educators plays a fundamental role in the students’ math learning, and consequently in the probability that the citizens reach a high-quality education in mathematics (ADLER, 2008).
As it is stated by León, Beyer, Serres and Iglesias (2012) in their report presented in Costa Rica, the education of the mathematics educators in Venezuela exists in different types and levels: an initial education (undergraduate studies) and a continuous education (graduate studies). In addition to these two types of education, we have considered in this research a third type that we name Complementary Education. This kind of education corresponds to the studies of not formal matter and short time that are procured by the students who expect to become mathematics teachers (the ones in initial education), the mathematics teachers who carry out specialization, Master and Doctoral studies (who are in an advanced education), and the educators who teach mathematics in the different levels of the educational system. All of them are motivated by their necessities and opportunities to update and improve academically. This third type of education is found in academic events and congresses devoted to the teaching of mathematics in local, regional, national and international levels.
These aspects invite us to the following reflection: to have a high quality teacher education, all the education types mentioned above must be very interrelated, that is to say, that all of them must converge in common goals: Educate a professionally competent educator; to foster a coherent learning and to help the professional development of the educators who teach mathematics in the country. In this process the Complementary Education Spaces portray a great importance because they represent spaces of synergistic convergence (BELISARIO, 2015) for both teachers of initial education and the teachers in continuous education in the search of improvements for their professional performance through the different activities that take place in those spaces. Then, our interest is to offer an answer to the main question of this study: what are the characteristics of those Complementary Education Spaces?
The Evem is one of the education spaces that the Venezuelan mathematical educators count on and which constitutes a scenario for various of the aspects of the SBa (BELISARIO, 2015). This is an annual event that has taken place since 1997 until current days which is carried out in the Facultad de Ciencias Básicas of the Universidad de Los Andes in Merida State (Venezuela). Future and active mathematics educators from almost all of the states of the country participate in the courses, workshops and conferences of this event. Among those who participate repeatedly in the Evem there are some of the reference actors (TOULMIN, 1977) of the Venezuelan Mathematics Education. The courses are taught by guest professors who should produce a book that serves of support material for the development of the corresponding course.
The Evem is considered a useful case to characterize the Complementary Education Spaces of the Venezuelan Mathematics Educators (EFC-EMV in Spanish) due to its stability (an uninterrupted implementation since 1997), the kind of participants (future and active educators), the bibliographic production associated (books), and the repeated participation of reference actors. In order to confirm this conjecture, a study was carried out to see the details in depth, beginning, development and actual situation of the Venezuelan School of the Teaching of Mathematics (Evem). This article aims at reporting such study which purpose is the theoretical conceptualization of the Complementary Education Spaces of the Venezuelan Mathematics Educators. (EFC-EMV).
THEORETICAL PERSPECTIVES
For the theoretical support of this research, it was built a Repertory of Theoretical Coordinates and Conceptual References, (Repertorio de Coordenadas Teóricas y Conceptuales de Referencia, RCT-CR; GONZÁLEZ, 2017) made up by: the social conception of history (BERNAL, 1968), the hints of development of the historical science, (BARROS, 2011), the Thought´s Styles and Thought´s Collectives (FLECK, 1986), the notion of Scientific Field, (BOURDIEU, 1994), the conditioning factors of the development of disciplinary field (MALIZIA, 2013), the concept of Epistemic Synergy Of The Venezuelan Mathematics Education (SEEMV) (BELISARIO, 2015), and the Conceptual Evolutionism theory (TOULMIN, 1977).
The social character of the sciences proposed by Bernal (1968), in which he makes reference to the role sciences can exert in a society willing to serve itself of its capacity to produce social progresses; as well as Barros’s position of development as disciplinary field of history (2011). This author recognizes ten important dimensions to characterize a scientific discipline. The system of ten dimensions presented by this author shows a set of criteria applied to History, as field of knowledge, to certify it as scientific discipline which is adaptable to other alternative disciplines. Due to these disciplines are social facts represented by a history, these perspectives helped us to characterize the historic trajectory of the Evem as a Space of Complementary Education for the Venezuelan Mathematics educators.
It is important to point out that the approaches of historic and social nature used to explain the creation of disciplinary fields are different. Among them the vision of Fleck (1986) who through his ideas related to the Thought´s Styles and Thought´s Collectives explains how knowledge is produced. The importance of the work of this author lies on his ideas about a) the socialization of knowledge assuming that the collective aspects of the scientific work determine both the generation of new ideas as well as their development, which implies the development of a new community of subscribers of such ideas; b) the historic character of the generation of knowledge; and c) the reformulation of the concept of historic fact, associating it with a concrete Thought´s Collective (p. 97).
In other words, according with Fleck, science is a social process done by communities of researchers who constitute thought collectives that develop a specific thought style which links concepts, theories and methods developed by specific sectors and individuals of the thought collective.
From Bourdieu (1994), we assume the notion of scientific field that he defines as “[…] the place of a competitive struggle that has the scientific authority monopoly as specific challenge” (p. 12).
Bourdieu (op. cit.), attributes to history a big importance as a explanatory factor of the social phenomena. The social implies a double existence, suppressed in what is considered: the field as the objective (the social made a thing) and the habitus as the subjective (the social included in the body), and from the dialectic relationship between both areas the social practices begin. The objective structures cultivate the habitus which is “a set of established and long-lasting dispositions that determine our way of acting, feeling and thinking.” (BOURDIEU, 1994, p. 173). This allows the agents to handle dynamics inside the field established by a structure of relationships. The capital is made of everything that can be used in the field to obtain a benefit (BOURDIEU, 1994, p. 173); thus, the capital is a product of the field and it does not exist out of it. The different kinds of capital create different effects in other fields; the fields are defined by the power relationships that the capital exerts, and by the actions of the subjects to maintain and acquire more capital. The central elements of this theory are: the fields, the capital and the habitus.
It is worth noting that the habitus of Bourdieu’s field theory can be assimilated with the institutional forums and the groups of reference of Toulmin’s Conceptual Evolution Theory (1977) that was adopted here with the purpose of supporting the notion of Complementary Education Spaces which characterization and dynamics are the main objective presented in this article.
Toulmin (op. cit.) asserts that the purposes, concepts and theories that result from the solution of disciplinary problems, as well as the methods and the dominant philosophical approaches in the scientific thinking, are changeable characteristics in the disciplines. Meanwhile the concrete problems of the discipline are the starting point of such characteristics. Consequently, this author points out that the proto-specific elements: ideas and conceptual notions are progressively accepted thanks to what he denominates “groups of reference” and “forums of dissemination.”
The former are made of all those individual or collective actors that carry the ideas, concepts and general expressions of theoretical nature that constitute the ideational core of the disciplines in formative process. Meanwhile, the latter constitute spaces that promote social interactions between the future professionals of the new emergent scientific discipline (MALIZIA, 2013, p. 18).
Regarding the notion of Epistemic Synergy of the Venezuelan Mathematics Education (SEEMV) developed by Belisario (2015), it can be said that it constitutes an extension of Beyer’s systemic vision (2001a; 2001b) about the mathematics education in Venezuela. According to Beyer (op. cit.) the ME is a system constituted by the organizations, the graduate programs, the investigations, publications and the events (local, regional, national and international). According to this author, these elements considered systematically constitute what he calls the Venezuelan system of Mathematics Education, and they are sufficient to draw the teaching of mathematics in the country. Although, Belisario (2015) extended it, developing the Epistemic Synergy of the Venezuelan Mathematics Education that consists of
A relationship of bilateral mediation that is established between two or more individuals or entities, especially when they work or do something of interest in the context of this disciplinary field, such as contributing in the construction of its history and providing evidences for the certification of its scientific condition (BELISARIO, 2015, p. 123).
It is important to point out that we consider Mathematics Education as a scientific field that joins social and diversified activities related to the teaching and learning of mathematics through the events of the area. Moreover, these conditions have favored the permanent transformation that the ME has experienced as a scientific discipline and it will continue experiencing depending on the development of the ideas and concepts of mathematics itself and other sciences.
This is the reason why the examination of the components of the SEMV and of the SEEMV by Beyer and Belisario; besides the propitious conditions for the rise of the scientific disciplines taken from Stephen Toulmin’s perspective of the conceptual evolutionism to the Mathematics Education; in addition to the ideas of Pierre Bordieu, Ludwick Fleck, José D. Barros and John Bernal about the scientific field, allows us to define the activities that define the ME in Venezuela as a scientific discipline based on the contribution of the Venezuelan School of the Mathematics Education (Evem) in the process of education of the Math teachers.
METHOD
The considerations by González and Villegas (2009) were taken into account to construct a suitable strategy that worked as a base for the recollection of the necessary information to answer the research question of this study. These authors consider that each problem of investigation requires and demands a specific approach. They conceive this moment of the investigation “as a strategic disposition of resources (material, financial, conceptual, human, etc.) that serve to collect the necessary information to answer the interrogatives of the investigation” (p. 103). The construction of such strategy requires the adaptation to a research paradigm associated to a methodological perspective that supports the design of the investigation. It implies the definition of techniques and the adaptation or construction of instruments ad hoc. For the study here reported it was adopted a design of case study. The details are presented below.
Research paradigm
The approach of this investigation was qualitative. This makes possible approaching the phenomenon with the capacity to discover, to interpret and to understand it.
Methodological perspective
A historic perspective of descriptive-interpretative nature was assumed. Historic, since a timeline of the Evem was reconstructed to identify characters, dates and key situations that define its trajectory. Descriptive, since the characteristics of the school, their qualities and attributes, were identified, pointed out and explained. It is interpretative because besides the collection of information, the meaning of the event was added in the context of the disciplinary development of the Venezuelan Mathematics Education.
Research design
Regarding the design, the investigation constituted an instrumental, unique, critical accessible and analytical case study. It is instrumental because the Evem was assumed as an illustrative case which study gives enough and suitable elements to characterize theoretically the Complementary Education Spaces of the Venezuelan mathematics educators. Furthermore, it is unique since the Evem is the only case considered for the study. Moreover, it is critical because the study was not limited to a mere description of the characteristics of the Evem, but it was also accompanied of reflections that place it in a major framework with the disciplinary development of the Mathematics Education in Venezuela. Also, it is accessible due to the direct relationship that the researcher maintains with the Evem because, through the time, she has performed diverse roles in it since her first participation as assistant until becoming a guest speaker. Finally, it is analytical because the direct participation of the researcher in the Evem allowed her to access to the information obtained in primary sources. This factor facilitated the conformation of a corpus which content analysis provided high quality information that was used to answer to the interrogative of this investigation.
Corpus of study
Two types of sources were used to construct the Corpus of the present study: documental and testimonial. First, some efforts were made to obtain the biggest amount of documents that contained the direct information related with the Evem. Then, the testimonies of the people linked with the school were procured parallel and simultaneously. Therefore, non-structured interviews, face to face meetings and conversations were made with people who are associated with the Evem; this is the way the experiential information about the School was obtained. Information that could have been impossible to obtain through other ways. The following criteria was followed to the selection of the key informants: (1) they should have knowledge of the history of the Evem; (2) they should have participated in any of the editions of the school; (3) they should be available and willing to provide information about the Evem. Following this criteria, eight (8) key informants were selected, see table 1. The interviews were made following an initial script, which was extended and modified depending on the interview, elaborated according with the selection criteria and the kind of participation of the person interviewed.
Table 1 - Key informants of the research.
| N° | KEY INFORMANTS | DESCRIPTION | SELECTION CRITERIA |
|---|---|---|---|
| 1 | Arístides Arellán | Mathematics Educator. Associate Professor, retired from the ULA, with a Master in Analysis. | Coordinator of the Evem since its foundation. |
| 2 | Kuong Chang | Active Mathematics Professor in the Sciences Faculty of the ULA. | He was part of the protocol logistics of the Evem and has been a facilitator of courses and workshops. |
| 3 | Dubraska Salcedo | Professor in the ULA in the Trujillo Extension. Doctorate student in the ULA Mérida. | She has been part of the organizing and logistics support committee of the Evem. |
| 4 | Diana Silva | Student of the V semester of Petroleum engineering in Luz. | Participant in the Evem in courses and workshops. |
| 5 | Elías Velazco | Mathematics Professor in the IUTM Maracaibo and Unefa Zulia. | Continuous participant and facilitator of courses and workshops in the Evem. |
| 6 | Francisco Carrillo | Specialized Mathematics and Physics educator in the Instituto Pedagógico Experimental de Barquisimeto. | Continuous participant and facilitator of workshops. |
| 7 | Lisandro Alvarado | Mathematics professor and trainer for the Mathematics Olympics. | Continuous participant of the Evem since 2000 |
| 8 | Pedro Infante | Mathematics Professor in Luz. | Participant in courses and facilitator of courses and workshops since beginnings of the Evem. |
Source: study data.
Another testimonial information was provided by the researcher who, from her own memories, recovered her personal experiences associated with her participation in the Evem. She wrote a detailed, exhaustive and meticulous narration of the different roles and participations that she has had in the Evem. This allowed her to make explicit the pertinence of the investigation considering her “personal epistemological place” conceived by González (2003) as
the position from which knowledge is produced; which is associated with the life story, personal and professional formation, as well as the vital experiences as a human being (GONZÁLEZ, 2003, p. 140).
The narration based on the perspective by Lindón (1999) consisted in a written story in which the researcher provides her personal experiences in the Evem; it was done in freestyle from the retrospective recovery of memories which is a fundamental input for this work, the way of explaining how a study starts. The elaboration of this narrative allowed her to recover her personal experience as participant of the School while this constitutes a space where she has developed a large part of her life, both professional and personal. Professional because the attendance and participation in this event has been a great help in her trajectory as an educator. Personal because it has allowed her to create links with other members of the professional community, active or future mathematics educators from different regions of the country. This has made possible the creation of a network of professional mathematics educators with whom she shares curiosities and common interests.
Corpus content analysis
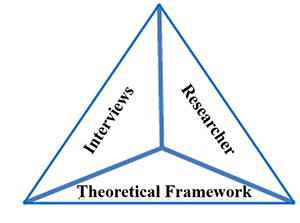
After organizing the constitutive information of the Corpus-build from the interviews, the narration of the researcher and the theoretical framework- the analysis of the content was carried out in two dimensions: quantitative and qualitative. This analysis was based in a source triangulation process as it is seen in the Figure 1.
The quantitative information is related to measurable aspects such as: amount of participants, courses, workshops, conferences, released books in the Evem (Table 2), taking into consideration the period 2000-2016 since there is no available information about the period 1997-1999.
Table 2 - Quantitative information of the Evem (2000-2016).
| ASPECTS | AMOUNT |
|---|---|
| Participants | 4819 |
| Courses | 115 |
| Workshops | 24 |
| Conferences | 16 |
| Books | 115 |
Source: research data.
The Evem has been a space for meeting between mathematics educators (professors and students of mathematics and other alike careers) from different regions of the country who look for the update and improvement of their insights and didactics; as well as their personal growth to develop general and specific competences of their educational labor through the academic activities promoted in the School.
Analysis of the qualitative information
The qualitative information is associated with the names of people, topics studied in the different editions of the Evem, theoretical and methodological approaches from the books used to support the courses, the content of the conferences and many others. The analysis was done in two phases.
PHASE I
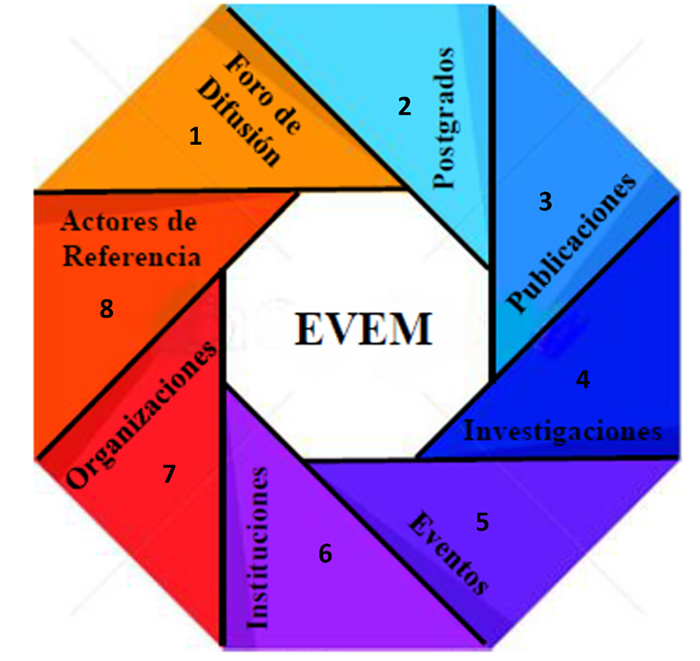
This phase consisted on the primary analysis of the Evem taking into account the categories that Belisario (2015) denominates Beyer System Extended (BSe). These categories are: graduate programs, publications, events, organizations and investigations, institutions and reference actors. Although it was relevant to include the Forums and dissemination scenarios category. This made possible by what we call the Octocategorial System of the Venezuelan Mathematics Education (SOEMV); which is related to the unveiling of conditioning factors of the development of the ME as a scientific field that can help the reconstruction of the Venezuelan ME and its certification as a scientific discipline in the national territory (MALIZIA, 2013).
Next, it was done an analysis of the dynamic interrelation between the emergent categories of the Evem, considering the notion of Epistemic Categorical Dynamic Synergy conceived by Belisario (2015). This is how the category Graduate Programs, that is to say the education programs of superior level such as the specialization, masters and doctorates are interrelated with the Institutions, which are the spaces where these studies are developed. Similarly they are related to the Reference Actors who represent the people that contribute with the education focused on the production of knowledge through Investigations, which are turned in as undergraduate conclusion works, Master’s degree works and Doctoral thesis published through scientific articles in specialized magazines. In short, the graduate category is related with institutions, reference actors, investigations and publications.
It was done a similar analysis, to the previous paragraph, with each of the eight categories identified in the Evem. This made possible the construction of a dynamic figure that is shown in the Figure 2 and that we have called Categorical Dynamics of the Venezuelan Mathematics Education (DCEMV). The figure makes reference to the existent interrelationships between the constitutive categories of the SOEMV, assuming that each of them exerts forces that motivate actions to each other, contributing with the base of the disciplinary field.
PHASE II
The key informant interviews were analyzed during the second phase using the software Atlas-ti. This analysis permitted the unveiling of the categories and subcategories that show the underlying structure of the information that worked as a base to the global and conceptual characterization of the Complementary Education Spaces of the Venezuelan Mathematics Educators. See table 3.
Table 3 - Information underlying categories system.
| CATEGORIES | SUBCATEGORIES |
|---|---|
| Values of the teacher education | - Institutionalism |
| - Diversity | |
| - Continuity | |
| - Accessibility | |
| - Integration of insights | |
| - Rationality | |
| - Flexibility | |
| - Social commitment | |
| - Participation and promotion of knowledge | |
| - Excellence | |
| Education strategies | - Courses |
| - Conferences | |
| - Workshops | |
| - Didactic material | |
| Strategic plan | - Preparation |
| - Planning | |
| - Production | |
| - Objectives | |
| - Achievements | |
| - Motivation | |
| - Assessment | |
| - Permanence |
Source: research data.
COMPLEMENTARY EDUCATION SPACES OF THE VENEZUELAN MATHEMATICS EDUCATORS (EFC-EMV): A CONCEPTUAL CHARACTERIZATION PROPOSAL
From the analysis of the collected information about the Evem it was contextualized the EFC-EMV in the following way:
Efc-emv characteristics
It offers diverse modalities, places, update moments and practical improvement to the participants.
It privileges the reflection about the professional performance of the educators who participate in the space.
It extends both the theoretical and practical insights of the active and future mathematics educators.
It promotes the exchange and dissemination of the experiences between the educators with minor experiences and those who have a larger career in the educational discipline.
It develops procedures that allow the feedback from the participants about their actions and results in order to improve the performance of new editions.
It develops actions to promote the support for the academic activities from institutions, organizations and other financing agents in order to guarantee the accurate execution of all the expected activities.
It counts on the frequent participation of reference actors of the mathematics education of local, regional, national and even international contexts.
It promotes the production of didactic material that supports the academic activities carried out such as books, brochures, bulletins, and some others.
It deals with the academic necessities of the participants promptly and flexibly during the event.
Basic principles of the efc-emv
The Decalogue of the EFC-EMV is shown below. It summarizes the basic principles that should lead to the conception, implementation and assessment of a Complementary Education Space of the Venezuelan Mathematics Educators.
Forming in the diversity: the complementary education of the Mathematics educators should give an answer to the variety of moments and situations that the professional development of the future and active educator passes. This means that an EFC-EMV should deal with the education needs of the diverse participants: the educator in initial and continuous education and the experienced professionals who have varied development needs. This diversity also implies the attention to the community that needs it. Therefore, it must be so varied and multiple that allows both individual and collective education options. In other words, the complementary education should comprise diverse moments, places and modalities.
Having social pertinence: it relates with the degree of correspondence that should exist between the social and individual needs that want to be satisfied with the creation of the EFC-EMV and the goals that can be really reached. The complementary education should be based on the reflection about the practice, with the purpose of creating consciousness about the complex work of the educator and answering to the needs of the professionals that promote the mathematics teaching and learning processes.
Complementing the initial and continuous education: it implies the academic update and improvement through the organization of courses, workshops and conferences that contribute with the reinforcement of the professional and educational knowledge of the participants. The teacher education should be approached as a process throughout the professional career with the purpose of generating continuous and nutritive meetings between the educators in initial and continuous education as well as the experts in the educational world.
Generating and spreading knowledge: in this principle the complementary education of the mathematics educators can be carried out in a planned way through research and development activities and the use of problem solution techniques. Also, through the contact with people who share their wisdom, passion and interests about some of the topics of the discipline, and who interact to acquire, spread and share their insights.
Self-regulating its own development: it constitutes a formative assessment process that generates information that allows the constant revision of a high quality education and social pertinence. This is how the EFC-EMV displays a knowledge production dynamics that permits the self-regulation of the educator. It allows the educator to revise and prepare himself for the innovations that occur in his environment. It becomes a professional self-improvement process.
Counting on social support: every EFC-EMV should count on a group of human and material resources provided by the institutes, organization and persons related with the mathematics education, all of this with the intention of generating a harmonic climate between the people who seek for the improvement of their pedagogical tasks.
Promoting the social interaction: in an EFC-EMV the exchange between the assistants and other reference actors must be promoted in order to achieve the expected goals.
Producing support material: it is indispensable to design, publish and apply didactic resources that can be used as support material that prevail to the disposition of the mathematics educator’s community.
Being flexible: this principle favors the individual education of the future or active educator since it allows them to promote their own learning according to their own rhythm or with the flexibility to elaborate academic strategies that fits with their needs. Consequently, the education is customized and planned according to the individual availability.
Using varied education activities: the EFC-EMV should count on methodological strategies that foster the enhancement of the practice. Moreover, it should dispose of diverse activities (courses, workshops, conferences) that motivate the professional development through the combination of theory and practice. These activities should be based on the needs and interests of the participants. Furthermore, they should be adapted to the individual and collective context and based on the reflection of the education process.
AN APPROXIMATION TO THE CONCEPTUAL DEFINITION OF COMPLEMENTARY EDUCATION SPACE OF THE VENEZUELAN MATHEMATICS EDUCATORS (EFC-EMV)
Three types of arguments were used to construct the definition of EFC-EMV: theoretical, historical and social.
From the theoretical viewpoint, we assumed the notion of scientific field developed by Pierre Bourdieu (2005), and the notion of conceptual evolutionism of Stephen Toulmin (1977), specifically his notion of “Dissemination space.” On this base, an EFC-EMV is conceived as a place where a dynamic of interrelationships that reflect the reference actors corresponding to the Mathematics education thought as a disciplinary field in a Bourdieu’s sense.
In the Toulminian perspective, an EFC-EMV constitutes a dissemination scenario, that is to say, an area where different individual and collective actors of the Venezuelan mathematics education converge. These actors are represented by the professors who write the books and facilitate the courses based on such writings; also, there are included the guest speakers who present the main conferences, and the responsible groups of the specific activities inside the space. (for example, the group Sumatoria founded by the professor Lisandro Alvarado for the Evem). This is how, through courses, conferences, workshops and books, an EFC-EMV works as a channel for the circulation of epistemological, ideological and cultural viewpoints related with teaching and learning methodologies of the mathematics education.
In a historic perspective, it could be affirmed that the EFC-EMV testimonies a trajectory that began around the 60’s decade of the last century. It should be remembered that it was in December 1961 when the I Ciaem took place in Bogotá. A Venezuelan delegation of mathematics professors attended to that event. After their return, they developed a huge education labor associated with the modern mathematics ideas through workshops, short courses and seminaries. In 1973, the Cenamec was created and in 1974, the first Master Program in the Teaching of Mathematics in Latin America was founded at the Instituto Pedagógico de Caracas. It could be considered that those are the historic beginning of these EFC-EMV that received a notorious impulse with the creation of the Asovemat in 1972. The founders of the Venezuelan School for the Teaching of Mathematics (Evem) were the receivers of this tradition. A tradition that this study has assumed as an illustrative case that worked as a base for the theoretical conception of the EFC-EMV.
From a social viewpoint, an EFC-EMV should count on the responsible commitment of a human team that is able to accomplish the support of the reference actors of the Venezuelan Mathematics Education. Similarly, they should inspire enough trust to summon the assistance and participation of the rest of the active and future educators so that the expectations of update and improvement of their professional life can be satisfied accurately in order to enhance a higher quality of the mathematics education of the citizens of the country.
Taking all that into consideration, the following definition of Complementary Education Space of the Venezuelan Mathematics Educators (EFC-EMV) is proposed:
A EFC-EMV is a scenario of sociocultural dissemination of knowledge (TOULMIN, 1977) associated with the teaching and learning processes of the Mathematics which are generated and institutionalized by the diverse reference actors of the Venezuelan Mathematics Education (op. cit.) who assume the responsibility of promoting the diverse academic activities programmed as a space for the natural dynamics of a disciplinary field (BOURDIEU, 1994). Such dynamics are illustrated through the divulgation of that the reference actors make about their knowledge about the pedagogical labor in general and the particular teaching and learning processes of the mathematics.
FINAL THOUGHTS
The Mathematics Education in Venezuelan has reached its progressive consolidation as a scientific discipline thanks to the people who have shown their interest in the academic education of the mathematics educators. In this process, the Venezuelan School for the Teaching of Mathematics has had a relevant role since 1997, propitiating the conformation of a national collective consciousness about the necessity and importance of the continuous improvement of the teaching of mathematics in the country.
This is how the Evem constitutes an illustrative case of a conceptual notion denominated Complementary Education Space of the Venezuelan Mathematics Education (EFC-EMV). A space where the future and active professors and graduate students converge synergically who due to their large trajectory are recognized as reference actors of the Venezuelan Mathematics Education.










 text in
text in