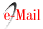Servicios Personalizados
Revista
Articulo
Compartir
Educação em Revista
versión impresa ISSN 0102-4698versión On-line ISSN 1982-6621
Educ. rev. vol.39 Belo Horizonte 2023 Epub 15-Mayo-2023
https://doi.org/10.1590/0102-469836486
ARTICLE
ASSOCIATIONS BETWEEN NEUROPSYCHOLOGICAL PERFORMANCE AND ARITHMETIC PERFORMANCE: A STUDY WITH ELEMENTARY STUDENTS
1Universidade Federal do Rio Grande do Sul (UFRGS). Porto Alegre, RS, Brazil.
This article aimed at examining the cognitive functions associated with difficulties in arithmetic, with a special focus on a) analyzing the relationship between neuropsychological performance and arithmetic performance in the total sample of each school year; and b) investigating students’ performance in neuropsychological functions, divided according to their performance in arithmetic, for each school year. The participants of this study were 167 students from the 4th and 6th grades of elementary school between the ages of 9 and 12. For the analysis, the main tools used were the scores of the Arithmetic Subtest of the School Performance Test (TDE) and the neuropsychological assessment battery NEUPSILIN-Inf. Pearson correlations were made between the total sample of each school year and the t-test, in order to find differences between the groups of each school year, formed according to the performance of the TDE. The results suggest that the better the arithmetic performance in the TDE, the higher the scores in memory, calculations, and verbal fluency on NEUPSILIN-Inf. Students in the group with arithmetic difficulties had lower scores on the tests, which especially evaluated executive functions and memory. Investments should be made in the future for educational practices that encourage the development of such cognitive functions, in order to prevent arithmetic difficulties.
Keywords: neuropsychological performance; arithmetic performance; executive functions
Este artigo teve como objetivo principal examinar as funções cognitivas associadas às dificuldades em aritmética, focando com foco em: a) analisar a relação entre o desempenho neuropsicológico e o desempenho em aritmética da amostra total de cada ano escolar; e b) investigar o desempenho dos alunos nas funções neuropsicológicas, divididos de acordo com o desempenho em aritmética, para cada ano escolar. Participaram do estudo 167 alunos do 4.º e do 6.º anos do Ensino Fundamental, com idades entre 9 e 12 anos. As principais análises realizadas envolveram os escores do Subteste de Aritmética do Teste de Desempenho Escolar (TDE) e da bateria de avaliação neuropsicológica NEUPSILIN-Inf. Foram feitas correlações de Pearson entre a amostra total de cada ano escolar e o Teste t para averiguar diferenças entre os grupos, de cada ano escolar, formados com base no desempenho do TDE. Os resultados sugerem que, quanto melhor o desempenho aritmético no TDE, mais altos os escores em memória, cálculos e fluência verbal no NEUPSILIN-Inf. Os alunos do grupo com dificuldades aritméticas apresentaram escores inferiores nos testes que avaliaram, especialmente, funções executivas e memória. Sugere-se um investimento em práticas educacionais que estimulem o desenvolvimento de tais funções cognitivas com o intuito de prevenir as dificuldades aritméticas.
Palavras-chave: desempenho neuropsicológico; desempenho aritmético; funções executivas
Este artículo tuvo como objetivo examinar las funciones cognitivas asociadas a las dificultades en aritmética, centrándose en: a) analizar la relación entre rendimiento neuropsicológico y rendimiento aritmético en la muestra total de cada año escolar; y b) investigar el rendimiento de los estudiantes en funciones neuropsicológicas, divididos según su desempeño en aritmética, para cada año escolar. Participaron del estudio 167 alumnos del 4.º y 6.º año de la escuela primaria, con edades comprendidas entre los 9 y los 12 años. Los principales análisis realizados consistieron en las puntuaciones de la subprueba de aritmética del Examen de Rendimiento Escolar (TDE) y la batería de evaluación neuropsicológica NEUPSILIN-Inf. Se realizaron correlaciones de Pearson entre la muestra total de cada año escolar y la prueba t para encontrar diferencias entre los grupos, de cada año escolar, formados según el rendimiento del TDE. Los resultados sugieren que mientras mejor sea el rendimiento aritmético en el TDE, mayores serán las puntuaciones en memoria, cálculos y fluidez verbal en NEUPSILIN-Inf. Los estudiantes del grupo con dificultades aritméticas obtuvieron puntuaciones más bajas en las pruebas que evaluaron especialmente las funciones ejecutivas y la memoria. Se sugiere una inversión en prácticas educativas que fomenten el desarrollo de dichas funciones cognitivas, con el fin de prevenir dificultades aritméticas.
Palabras clave: rendimiento neuropsicológico; rendimiento aritmético; funciones ejecutivas
INTRODUCTION
Mathematics is a complex learning area that depends on several external and internal factors for the person to perform successfully. Among the external aspects, there are family and social issues and school practices, which should prioritize hierarchical teaching of specific domain skills (CORSO; ASSIS, 2017). Among the internal issues, there is the biological functioning of the individual. In this article, one of these internal possibilities is investigated, neuropsychological functioning (which is based on the individual's cognitive functioning) and its relationship with arithmetic performance (which enables to follow the evolution of arithmetic learning).
Thus, dealing with mathematics offers challenges to a greater or lesser extent, for all learners. However, for a large portion of students, mathematics causes many difficulties and compromises school performance, so lags in this area contribute to the alarming rates of school failure faced by the Brazilian educational system (BRASIL, 2018). Naturally, the impact of such a situation has adverse consequences for the student and society (PICCOLO et al., 2016). Studies that combine contributions from neuropsychology and education, with a focus on stimulating cognitive skills (CRAGG; GILMORE, 2014; CRAGG et al., 2017), show gains in the processes of learning mathematics and have shown promise in coping with such a scenario (DIAMOND, 2013).
The propensity for mathematical reasoning in human beings can be identified since babies when they are already able to distinguish small quantities (DEHAENE, 1997; GEARY, 1995; STARKEY; COOPER, 1980). It is an innate ability related to numerical skills (linked to number knowledge, numerical relations, and numerical operations), originating from a biological apparatus, which enables the subject to pay attention to numerosity (DEHAENE, 2001). Furthermore, social experiences play a fundamental role in the construction of numerical knowledge (SPINILLO, 2014; SILVA et al., 2015). In the cerebral scope, neuroimaging studies reveal areas of the brain predisposed to develop mathematical skills to make comparisons, estimates, and mental calculations (BASTOS, 2016), which indicates that there is not a specific center to deal with numbers, but different brain regions involved with this function (CONSENZA; GUERRA, 2011). Therefore, the evolution of mathematical learning is influenced by brain development and interactions with the environment (DIAMOND, 2013).
ARITHMETIC PERFORMANCE AND NEUROPSYCHOLOGICAL FUNCTIONS
Mathematics is a science that encompasses various domains such as geometry, estimation, measurement systems, and interpretation of graphs and tables, among others (DOWKER, 2005). Arithmetic is one of those mathematical domains dedicated to the study of numbers and the possible operations between them. It is not a unitary skill but can be divided into different processes and each of them has numerous subcomponents: a) basic arithmetic facts, which correspond to different types of operations and mathematical calculations; b) procedural skills, which comprise the procedures applicable to each operation; c) conceptual understanding, which involves understanding mathematical problems, as well as the principles and relationships between mathematical concepts (DOWKER, 2005).
Efficient mathematical performance depends on several underlying skills, and when some previous skills are not well developed, such as counting principles, notions of magnitude, and other aspects of number sense, arithmetic skills are impaired (CORSO; DORNELES, 2015; SILVA et al., 2015; GOLBERT; SALLES, 2010). Mathematical mastery, according to Geary's model (2004), is composed of basic conceptual and procedural skills that, if not properly constituted, will potentially lead to inefficient school performance, that is, below the minimum levels expected for each school year. The author suggests that the influence of executive functions on mathematical performance is measured in specific domain competencies.
Based on research carried out by them with participants aged 8 to 25 years, Cragg et al. (2017) concluded that executive function skills, in particular working memory (WM), support processes in the specific domain of mathematics, which support overall math performance. It is possible to observe in Figure 1 the importance of knowing the student's neuropsychological profile since these functions have a direct interference with their arithmetic performance.
Source: Cragg et al., 2017
Figure 1 - Direct and indirect influences of executive functioning on mathematical performance.
Neuropsychology is an interdisciplinary area (BOLLER, 1999), belonging to neuroscience, which seeks to understand the relationships between the brain and behavior (HAASE, 2016), more specifically between the brain and cognitive functions (LURIA, 1981). The cognitive model, studied by cognitive neuropsychology and which theoretically supports this work, aims to understand “how people perceive, learn, remember and think about information” (STERNBERG, 2008, p. 22). Among the neuropsychological functions evaluated in this study are orientation, attention, perception, arithmetic skills, language, visuoconstructive skills, memory, and executive functions (FONSECA; SALLES; PARENTE, 2009; SALLES et al., 2016).
The literature points out that one of the neuropsychological functions most involved with arithmetic processes is working memory (or operational memory). It refers to the ability to temporarily store and manipulate information to perform complex cognitive tasks (BADDELEY; HITCH, 1974). Theoretically, it is divided into its central executive, phonological and visuospatial components (CHEN et al., 2017; CORSO, 2018; CORSO; DORNELES, 2015; HAASE et al., 2012; TOLL et al., 2011). The last two components mentioned (phonological and visuospatial) are essential for good performance in arithmetic (BULL; LEE, 2014; DORNELES; HAASE, 2018; GEARY, 2011; GONÇALVES et al., 2017; HAASE et al., 2012; PENG et al., 2012). Such components are always recruited during the execution of a mathematical calculation. The individual must know how to organize spatially to successfully carry out transports during arithmetic procedures and correctly frame commas, units, tens, and hundreds. Phonological memory, on the other hand, is used when information must be “held”, vocally or subvocally, until it is written to perform mental calculations and for simple processes, such as counting.
Peng et al. (2012) found that Chinese students, in the 5th grade of Elementary School, with mathematical difficulties showed a deficit only in the numerical span task, which evaluated the phonological component, with adequate performance in the word span. In the study with 302 Brazilian students, from the 1st to the 9th grade of Elementary School and Middle School (GONÇALVES et al., 2017), phonological memory was a predictor of arithmetic performance, regardless of the age group and the mathematical content that the children were learning. The finding corroborates the studies by Viapiana et al. (2016) who investigated the validity of the arithmetic subtest of the School Performance Test (TDE-II) with 111 students from the same teaching stages of the previous research. Phonological working memory proved to be relevant for automating basic facts, understanding concepts, procedures, and numerical transcoding.
Regarding executive functioning, inhibition, updating, and switching∕shifting are signaled as basic functions for good mathematical performance (BULL; LEE, 2014; BULL; SCERIF, 2001; CHEN et al., 2017; CRAGG; GILMORE, 2014; CRAGG et al., 2017; PENG et al., 2012; VAN DER SLUIS; DE JONG; VAN DER, 2004). The ability to update is the ability to replace old information from memory with more recent and relevant ones and, for Bull and Lee (2014), it was the most influential finding in the sphere of arithmetic learning. Inhibition is important insofar as it gives the individual the ability to control their behaviors, emotions, and thoughts to do what is appropriate for the situation, such as choosing a more appropriate arithmetic fact (DIAMOND, 2013; CRAGG; GILMORE, 2014). From this perspective, inhibition is a great predictor of arithmetic performance, especially from the 1st to the 5th year of elementary school (GONÇALVES et al., 2017), when this function is still in the process of maturing. In mathematics, it assists in maintaining attention, ignoring external stimuli, keeping relevant information in mind, and suppressing irrelevant information that may occupy space in working memory (BULL; LEE, 2014; TOLL et al., 2011).
Switching is characterized by the disengagement of a set of irrelevant tasks or strategies and the subsequent activation of a more adequate strategy (VAN DER SLUIS; DE JONG; VAN DER, 2004). Regarding mathematical performance, it gives the person the opportunity to change strategies between different stages of arithmetic resolutions (TOLL et al., 2011). As in the first years of Elementary School, the tasks are not so complex, studies indicate that, with increasing school levels, students need to recruit more inhibition and switching skills (GONÇALVES et al., 2017; TOLL et al., 2011; VIAPIANA et al., 2016).
Exploring the associations between neuropsychology and education can help promote arithmetic learning, prevent difficulties in this field, and make it possible to better understand the cognitive processes potentially necessary for arithmetic development. Most of the time, studies focus only on some neuropsychological functions, if not on a single function such as language, leaving aside the discussion of other important cognitive functions that are also fundamental for the development of arithmetic.
In this context, the main objective of this article was to examine the cognitive functions associated with arithmetic difficulties, focusing on a) analyzing the relationship between neuropsychological performance and arithmetic performance of the total sample of each school year; and b) investigating student performance in neuropsychological functions, divided according to performance in arithmetic, for each school year. The hypotheses raised are that performance in neuropsychological functions such as executive functions and memory will be associated with performance in arithmetic for this sample. It is believed that students with difficulties in arithmetic will perform worse in neuropsychological functions, especially in executive functions and working memory, than students without difficulties in arithmetic.
PARTICIPANTS
The participants of this research are 167 students from the 4th and 6th grades of Elementary School and Middle School, ranging from 9 to 12 years old (see Table 1). These school years were chosen considering that the students were already fully literate (reducing the chances of language deficits as they were in the literacy process) and a difference in age/school year to verify the differences between performances in arithmetic and in neuropsychological functions (leading to consider the age limit of the instrument in question). The sample consisted of 91 students from the 4th year (39 girls - 43%) and 76 students from the 6th year (49 girls - 64%), from three state schools in the city of Porto Alegre, RS, located in the same region, which showed similarities in teaching methodology and socioeconomic and cultural characteristics, according to the Inep School Census (2019) indices.
Table 1: Descriptive information on the age of participants by school year and total sample
| School year | Mean | SD | Minimum | Maximum | Median |
|---|---|---|---|---|---|
| 4th | 10.25 | 0.67 | 9.03 | 12.28 | 10.01 |
| 6th | 12.00 | 0.38 | 11.44 | 12.97 | 11.91 |
| Total | 11.04 | 1.03 | 9.03 | 12.97 | 11.43 |
Source: The authors
To compose one of the analyzes of the study, the participants were divided into two groups. In the first, there are students with arithmetic difficulties (N = 20 from the 4th grade; N = 24 from the 6th grade), who presented scores lower than those expected for their respective school years in the TDE arithmetic subtest. The second group is made up of students without difficulties (N = 71 in the 4th grade; N = 52 in the 6th grade), formed by those who obtained a good performance in the arithmetic subtest.
The research was approved by the Research Ethics Committee of the Federal University of Rio Grande do Sul, under number 44047215.3.0000.5347. The student’s parents were presented with an Informed Consent Form (ICF) explaining all the research objectives. Inclusion criteria for participation in the study were as follows: being a speaker of Brazilian Portuguese, not presenting neurological or psychiatric diseases, presenting scores above the 25th percentile in Raven's Colored Progressive Matrices test (ANGELINI et al., 1999), and being younger than to 12 years old, age limit for application of the battery of neuropsychological tests used.
INSTRUMENTS
Socioeconomic and health questionnaire (CORSO; SPERB; SALLES, 2013): Completed by the child's parents or guardians to exclude from the sample students with serious diagnoses, such as neurological diseases (traumatic brain injuries, or neurodevelopmental problems, such as autism and others) and psychiatric illnesses (for example severe depression and others), as well as knowing the participants' family and social contexts. Data such as age, school level, history of the student's illnesses, and use of medication were collected.
Raven's Colored Progressive Matrices (ANGELINI et al., 1999): Instrument used to assess the non-verbal intelligence quotient (IQ). Participants were considered to have to perform above the 25th percentile to be included in the sample (intellectually average or higher rating).
Arithmetic subtest of the School Performance Test (STEIN, 1994): Instrument standardized for the southern region of Brazil and considered sensitive to identify individuals with arithmetic difficulties (GONÇALVES et al., 2017; VIAPIANA et al., 2016). It consists of 38 questions, which include arithmetic calculations with an increasing degree of difficulty. Students who had lower performance, equivalent to the 25th percentile or less, for this study, were considered students with difficulties in arithmetic. Students with average or higher performance, equivalent to the 50th percentile or higher, were considered students with no difficulties in arithmetic.
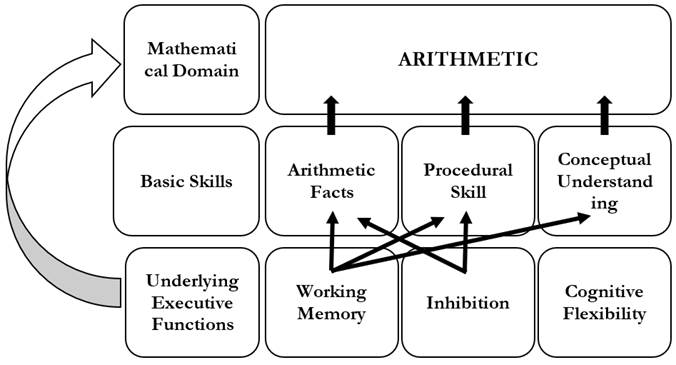
Brief Child Neuropsychological Assessment Instrument - NEUPSILIN-Inf (SALLES et al. 2016): It verifies the student's neuropsychological performance in the following neuropsychological functions: orientation, attention, perception, memory, language, visuoconstructive skills, arithmetic skills, and executive functions. The instrument comprises 26 subtests (Box 1). The instrument has standardization for public and private schools in Porto Alegre.
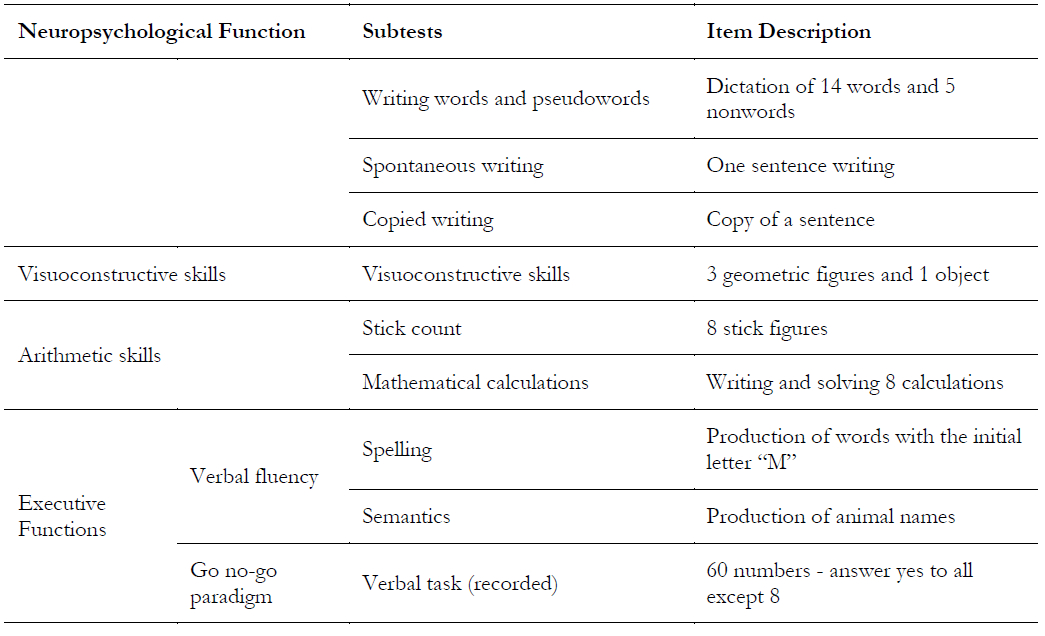
Source: Salles et al., 2011
Box 1: List and description of the 26 subtests of the NEUPSILIN-Inf instrument
PROCEDURES
The first stage of data collection involved the collective application of Raven's Colored Progressive Matrices test (maximum of eight participants per group), performed by a psychologist, lasting approximately 20 minutes per group. Then, the TDE arithmetic subtest was applied by the study researcher to each class, collectively. Finally, there was the individual application of the NEUPSILIN-Inf, carried out by psychology undergraduates (after training with the psychologist in charge), lasting about 40 minutes per student. The individual tasks were carried out in a space provided by the schools and the presentation order was the same for all subjects.
DESIGN AND DATA ANALYSIS
This study followed a cross-sectional, group-comparison, and correlational design with convenience sampling. Descriptive statistics were performed to characterize the sample and the variables of interest. To examine the relationship between the neuropsychological performances and the arithmetic performances of the total sample for each school year, a Pearson correlation was performed between the z scores of the neuropsychological functions assessed by NEUPSILIN-inf and the z scores achieved in the TDE. Also, the t-Test was used to observe the differences between groups, created according to the performance in arithmetic in the TDE (groups with and without difficulties) concerning the performance in the neuropsychological functions, investigated by NEUPSILIN-Inf, and concerning the quotient of non-verbal intelligence. Cohen's d statistic was performed to study the effect size of this difference between groups, separated by grade.
RESULTS
Table 2 shows sample characterization data in terms of attendance divided by school year. A large part of the total sample is made up of girls; however, 4th grade is mostly boys. Regarding grade repetition, 21% of the sample from the 4th and 6th grades had already failed a school year, and, according to parents' reports, 23% of the students in these two school years had already had previous reading and writing problems.
Table 2: Frequency of the sample's descriptive variables according to the school year
| Variables | 4th grade (N=91) | 6th grade (N=76) | |||
|---|---|---|---|---|---|
| N | % | N | % | ||
| Gender | Female | 39 | 43 | 49 | 64 |
| Male | 52 | 57 | 27 | 36 | |
| School year repetition | No | 67 | 75 | 61 | 84 |
| Yes | 22 | 25 | 12 | 16 | |
| Visual impairment | No | 76 | 84 | 58 | 80 |
| Yes | 14 | 16 | 15 | 20 | |
| Wearing glasses | No | 77 | 86 | 63 | 85 |
| Yes | 13 | 14 | 11 | 15 | |
| Previous reading and writing problems | No | 62 | 70 | 61 | 85 |
| Yes | 26 | 30 | 11 | 15 | |
Source: The authors
Table 3 shows data, with statistical significance, from the Pearson correlation performed to verify the relationship between performance on the TDE and performance on the NEUPSILIN-Inf subtests. For the 4th grade, the positive and moderate correlations between the TDE z scores and the z scores of the Semantic Memory subtests (r=0.4; p=0.001) and Calculations (r=0.5; p<0.001) of NEUPSILIN-Inf. Therefore, the better the performance in arithmetic, the better the performance of these students in evoking knowledge based on concepts and in performing simple mathematical calculations.
For the 6th grade, there are positive and moderate correlations between the z scores of the TDE and the z scores of the Digit Span subtests (r=0.4; p=0.002), Calculations (r=0.5; p<0.001) and total Verbal Fluency (r=0.4; p=0.001) from NEUPSILIN-Inf. Therefore, the better the arithmetic performance of students in that school year, the better their performance in retaining and manipulating numerical information for a short period, performing simple mathematical calculations, and organizing the strategies used to evoke words from the lexicon. The other correlations were positive and weak for both school years.
Table 3: Pearson correlations between the TDE z scores and the z scores of the NEUPSILIN-Inf subtests for the 4th and 6th grades of elementary school
| Variables | 4th grade | 6th grade | ||
|---|---|---|---|---|
| r | p | R | p | |
| Guidance | Without statistical sig. | 0.2 | 0.04 | |
| Episodic-Semantic Memory (Immediate Verbal) | Without statistical sig. | 0.3 | 0.01 | |
| WM Digit Span | 0.2 | 0.04 | 0.4 | 0.002 |
| Visuospatial WM | 0.3 | 0.01 | 0.3 | 0.01 |
| Semantic Memory | 0.4 | 0.001 | Without statistical sig. | |
| Phonemic Subtraction | 0.3 | 0.001 | Without statistical sig. | |
| Phonological Awareness | 0.2 | 0.03 | Without statistical sig. | |
| Inferential Process | 0.3 | 0.01 | Without statistical sig. | |
| Syllable Reading | 0.2 | 0.04 | Without statistical sig. | |
| Word Writing | 0.3 | 0.004 | 0.3 | 0.01 |
| Visual Constructive Skills | 0.3 | 0.01 | Without statistical sig. | |
| Calculations | 0.5 | <0.001 | 0.5 | <.0001 |
| VF Orthographic | Without statistical sig. | 0.3 | 0.002 | |
| Semantic VF | Without statistical sig. | 0.3 | 0.02 | |
| Total Verbal Fluency | Without statistical sig. | 0.4 | 0.001 | |
| Go/no-go paradigm | Without statistical sig. | 0.3 | 0.01 | |
Notes: WM = Working memory; VF = verbal fluency; r = Pearson's correlation coefficient; p = statistical significance; without statistical sig. = without statistical significance.
Source: The authors
Regarding the comparison of the neuropsychological performance (calculated by the z score) of the groups with and without difficulty in arithmetic, for the 4th-grade students, significant differences were found in three NEUPSILIN-Inf tasks presented in Table 4. Students without arithmetic difficulty performed significantly better than those with difficulty in arithmetic skill scores, calculations, and visuoconstructive skills.
Table 4: Descriptive statistics and differences in neuropsychological performance between groups with and without arithmetic difficulties for the 4th grade of elementary school
| No arithmetic difficulty | With arithmetic difficulty | Statistical test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables (Z score) | N | M | SD | Median | N | M | SD | Median | t | Sig. | Effect size | Magnitude |
| Arithmetic Skill | 71 | -0.38 | 1.29 | 0.01 | 20 | -3.14 | 2.43 | -2.7 | 4.88 | 0.001 | -1.23 | High |
| Calculations | 71 | -0.38 | 1.29 | 0.00 | 20 | -2.78 | 2.86 | -2.63 | 3.65 | 0.001 | -0.92 | High |
| Visuoconstructive Skill | 71 | -1.02 | 1.80 | -0.67 | 20 | -2.07 | 1.91 | -2.17 | 2.21 | 0.04 | -0.56 | Average |
Notes: N = the number of participants; M = mean; SD = standard deviation; t = Test t; sig. = significance
Source: The authors
Regarding 6th-grade students, significant differences were found in eight NEUPSILIN-Inf tasks, shown in Table 5. Students without arithmetic difficulty performed significantly better than those with difficulty in calculation scores, arithmetic ability, spelling fluency, total verbal fluency, visuospatial working memory, total working memory, episodic-semantic memory, and total memory.
Table 5: Descriptive statistics and differences in neuropsychological performance between groups with and without arithmetic difficulties for the 6th grade of Elementary School
| No arithmetic difficulty | With arithmetic difficulty | Statistical test | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables (Z Score) | N | M | DP | Mediana | N | M | SD | Median | t | Sig. | Effect size | Magnitude |
| Calculations | 52 | -0.39 | 1.51 | 0.45 | 24 | -2.82 | 3.71 | -1.09 | 3.10 | 0.001 | 1.01 | High |
| Arithmetic Skill | 52 | -0.12 | 1.59 | 0.45 | 24 | -2.76 | 3.68 | -1.03 | 3.37 | 0.001 | 1.08 | High |
| Spelling fluency | 52 | -0.14 | 0.88 | -0.25 | 24 | -0.62 | 0.81 | -0.52 | 2.33 | 0.02 | 0.56 | Average |
| Total Verbal Fluency | 52 | -0.28 | 0.72 | -0.27 | 24 | -0.77 | 0.78 | -0.88 | 2.62 | 0.01 | 0.67 | Average |
| Visuospatial WM | 52 | -0.14 | 1.43 | 0.15 | 24 | -1.29 | 2.00 | -0.80 | 2.53 | 0.02 | 0.71 | Average |
| Total WM | 52 | -0.42 | 1.67 | -0.24 | 24 | -1.23 | 1.37 | -1.07 | 2.25 | 0.03 | 0.52 | Average |
| Episodic-Semantic Memory | 52 | -0.65 | 1.06 | -0.72 | 24 | -1.30 | 1.12 | -1.04 | 2.41 | 0.02 | 0.61 | Average |
| Total Memory | 52 | -0.56 | 1.24 | -0.22 | 24 | -1.41 | 1.66 | -1.36 | 2.24 | 0.03 | 0.61 | Average |
Notes: N = the number of participants; M = mean; SD = standard deviation; t = Test t; sig. = significance; WM = Working memory
Source: The authors
The tasks of Calculations (4th year: t=3.65, d=-0.92; 6th year: t=3.10, d=1.01; p=0.001) and Arithmetic Skills (4. st year: t=4.88, d=-1.23; 6th year: t=3.37, d=1.08; p=0.001) of NEUPSILIN-Inf were the ones that presented the greatest magnitude (size of effect) in both grades when comparing groups with and without difficulties in arithmetic. Such data is significant due to the important weight that the groups formed from the TDE (with and without difficulty) gain, as another test confirms similar performance, providing validity to the subtests involved.
An important result still to be considered is observed in the Raven's Colored Progressive Matrices Test, which did not show a significant difference between the groups with and without arithmetic difficulties in the 4th grade but showed such a difference in the 6th-grade groups (see Table 6). This result suggests that the non-verbal intelligence (IQ) factor is not associated with arithmetic performance in the 4th grade, but, for the 6th grade, it plays a general domain skill.
Table 6: Descriptive statistics and performance differences in the Raven Test between the groups with and without arithmetic difficulty for the 6th and 4th grades of Elementary School
| 4th grade | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No arithmetic difficulty | With arithmetic difficulty | Statistical tests | ||||||||||
| Raven Variables | N | M | SD | Median | N | M | SD | Median | t | Sig. | Effect size | Magnitude |
| Raw Score | 71 | 28.35 | 4.22 | 28 | 20 | 27.80 | 4.94 | 28 | 0.46 | 0.65 | -0.12 | negligible |
| Percentile | 69 | 75.87 | 19.45 | 80 | 20 | 73.95 | 21.19 | 80 | 0.36 | 0.72 | -0.09 | negligible |
| 6th grade | ||||||||||||
| Raw Score | 51 | 31.43 | 3.29 | 32 | 24 | 29.04 | 2.68 | 29 | 3.34 | 0.001 | 0.77 | average |
| Percentile | 51 | 77.45 | 20.04 | 80 | 24 | 62.71 | 16.68 | 60 | 3.34 | 0.001 | 0.77 | average |
Notes. N = the number of participants; M = mean; SD = standard deviation; t = Student's t-test; sig. = significance
Source: The authors
DISCUSSION
Among the objectives proposed for this study, we initially sought to: a) analyze the relationship between neuropsychological performance and arithmetic performance of the total sample of each school year; and b) investigate student performance in neuropsychological functions, divided according to performance in arithmetic, for each school year.
Regarding the first objective, we found that, for the 4th grade, the neuropsychological functions concerning arithmetic performance are the following: working memory, semantic memory, oral and written language subtasks, calculations, and visuoconstructive skills. In the 6th grade, the relationships appeared significantly in the following variables: orientation, episodic-semantic memory, working memory, writing words, calculations, and executive functions. The results go in the same direction as those presented by Zelazo and Carlson (2020), Viapiana et al. (2016), and Gonçalves et al. (2017), which demonstrate that the higher the educational level, the more executive functions, as the required curriculum content is more complex. Thus, the findings of this study corroborate the hypothesis listed that arithmetic performance is associated with executive and memory functions, especially in the 6th grade sample. As for the NEUPSILIN-Inf calculation task, which correlated with the TDE for the two years, we observed that these variables converge to what they measure and may provide evidence of validity to the instruments and tasks involved. It is important to remember that one of the eight neuropsychological functions examined by NEUPSILIN-Inf is the arithmetic ability, assessed through counting and arithmetic calculation tasks. We found in this study that such NEUPSILIN-Inf tasks were sensitive to identifying arithmetic difficulties, which were measured based on the Arithmetic Subtest of the School Performance Test (TDE).
For the 4th grade, semantic memory was the “memory variable” that stood out the most. It is possible that this semantic component, with oral language and visuoconstructive skills, proves to be important for the arithmetic performance of the 4th grade, considering that initial mathematics is guided by teaching based on orality and the use of concrete materials (CARBONNEAU; MARLEY; SELIG, 2013).
Research with children from preschool age reveals that performance in language tasks is a predictor of later arithmetic performance (FAZIO, 1994; LEFEVRE et al., 2010). The learning of numbers is linked to vocabulary and oral language because the early learning of mathematics is related to hearing and speech (ZHANG, 2015), and language is an expression of thought. Cirino (2011) presents studies (LEFEVRE et al., 2010; KOPONEN et al., 2007; KRAJEWSKI; SCHNEIDER, 2009) with preschool children who have subtests like those of the NEUPSILIN-Inf such as naming, phonological awareness, and comprehension, which are directly associated with mathematical competence.
A recent study with a sample of 23,220 Chinese and American 4th-grade children revealed that language is a very influential general domain skill in arithmetic performance (MCCLUNG; ARYA, 2018) since language makes it possible to manipulate mathematical information, like counting and expressing the name of numbers. Thus, in less transparent languages, such as Portuguese, the relationship between language and mathematics becomes even more evident. This language opacity is even seen in the decimal numbering system when two-digit numbers have irregular names (ZHANG; OKAMOTO, 2017). It is relevant, therefore, that the names of the numbers and their magnitudes are well-worked, to avoid an accumulation of later mathematical difficulties (MCCLUNG; ARYA, 2018).
As for the second objective of the study, we found that, for the 4th grade, the neuropsychological skills that differentiate students with and without difficulties are arithmetic, calculations, and visuoconstructive skills. Regarding the 6th grade, eight neuropsychological functions distinguish students with and without difficulties. For a clear classification, the division proposed by the NEUPSILIN-Inf instrument will be used: the subtests of spelling fluency, semantic fluency, and total verbal fluency are configured as executive functions; episodic-semantic memory, visuospatial working memory, total working memory, and total memory are configured as the memory function; and oral language, such as language (see Table 2).
In the 4th grade, concerning arithmetic skills and calculations, as expected, the group with arithmetic difficulties had a much lower performance when compared to the average and high-performance group (considered, in this study, a group without difficulties). As for visuoconstructive skills, research points to the importance of this general domain skill for good numerical competence (CIRINO, 2011; ZHANG, 2015). It is known that early mathematics education is governed by visual skills (CARBONNEAU; MARLEY; SELIG, 2013) as well as oral language skills. This is because, especially in teaching arithmetic, teachers use many oral and concrete resources to guide their teaching: counting aloud, making use of fingers, records with drawings and many concrete means to develop numerical concepts. Considering Dehaene's (1992) “triple code” model, in which numerical processing involves oral language (verbal representation of the number), writing (representation of the Arabic numeral), and non-verbal representation (magnitude/quantity), it would be possible to understand why language and visual skills may be impaired in children with arithmetic difficulties. According to this model, language (through verbal and written representation) and visual skills (through the representation of magnitudes) support numerical processing and, therefore, lags in these skills end up compromising arithmetic performance.
Research brings WM, with an emphasis on the visuospatial component, as one of the predictors of mathematical performance (BULL; JOHNSTON; ROY, 1999; SIMMONS; WILLIS; ADAMS, 2012; CHEN et al., 2017), but few present results on visuoconstructive skills. This may occur because visuoconstructive skills and visuospatial WM are intertwined (ZHANG, 2015). Considering that this study used evaluation measures for both functions, we can distinguish them, highlighting the most statistically significant finding.
Visuospatial skills are perceived in babies and continue to develop throughout early childhood (SPELKE, 2000). Siegler and Booth (2004) point out that such skills play a crucial role in the initial learning of numbers, corroborating the findings of Zhang et al. (2014) who claim that spatial visualization contributes to numerical understanding. Studies with children of preschool age (ASSEL et al., 2003; BARNES et al., 2011; GUNDERSON et al., 2012; VERDINE et al., 2014; ZHANG; LING, 2015) indicate that visuospatial skills predict children's arithmetic performance years later, because, when learning to count, they depend on concrete objects and, even when they automate this process, they make mental representations of numbers (ASSEL et al., 2003). These results also reinforce Geary's model (2004; 2013) regarding the potential causes of difficulties in mathematics regarding counting and operative procedures, which would be subsidized by the linguistic/phonological system and the visuospatial system.
Contrary to what was hypothesized, the students in this sample of the 4th grade with arithmetic difficulties did not demonstrate executive functions, with emphasis on working memory, which was less preserved. It is known that many studies show positive relationships between these variables (CIRINO, 2011; ZHANG, 2015). One aspect to consider in explaining such a result may be the methodological choice of the different investigations, considering, for example, the variation in the ages of the participants, and the different tasks to measure executive functions and arithmetic performance (MEYER et al., 2010). These points reinforce the importance of future research in this field paying attention to the search for greater uniformity in the instruments that assess those domains, to generate research data that can be compared and validated (CORSO, 2018).
As previously pointed out, language and executive functions are skills underlying mathematics learning and very often differentiate students with and without learning difficulties (GEARY, 2013; ZHANG, 2015; CIRINO, 2011). For the results of the 6th grade, it is again possible to use the most current models of Geary (2013) and Zhang (2015) as theoretical support, which consider that language and executive functions are skills underlying the learning of mathematics.
The episodic-semantic memory, evaluated as declarative or even explicit memory, is configured as a long-term memory. The deficit of this in students with arithmetic difficulties can be explained by the fact that they have difficulty accessing information quickly and accurately. This hinders, for example, the possibility of easily recovering the basic facts (HOPKINS; LAWSON, 2006; CORSO; DORNELES, 2015). A low processing speed, combined with counting errors and an inefficient WM, would explain the low development of this memory (CORSO; ASSIS, 2020).
Executive functions are already punctuated, in previous studies, as being very related to arithmetic performance (BULL; LEE, 2014; BULL; SCERIF, 2001; CHEN et al., 2017; CRAGG; GILMORE, 2014; CRAGG et al., 2017; PENG et al., 2012; VAN DER SLUIS; DE JONG; VAN DER, 2004). Inhibition and cognitive flexibility, assessed using the verbal fluency subtests, showed a strong association with arithmetic performance. Inhibition assists in maintaining attention, choosing the arithmetic calculation, and suppressing irrelevant information so as not to occupy space in the TM (BULL; LEE, 2014; CRAGG; GILMORE, 2014; TOLL et al., 2011). Cognitive flexibility, in turn, allows the subject to face a problem from a distinct perspective and seek alternative or innovative solutions, without sticking to pre-established patterns of behavior (DIAMOND, 2013). When solving complex mathematical problems, flexibility allows the individual to alternate different procedures (addition and subtraction, for example), adapting to the demands of the task.
WT, even more than other executive functions, appears as a leading function in studies that relate neuropsychological functioning and arithmetic performance, since all its components engage in mathematical procedures (CHEN et al., 2017; CORSO, 2018; CORSO; DORNELES, 2015; HAASE et al., 2012; TOLL et al., 2011). However, unlike some studies that revealed that WM is a more substantial predictor of arithmetic performance than IQ (ALLOWAY; ALLOWAY, 2008; BULL; LEE, 2014; KYLLONEN; CHRISTAL, 1990), the present study, regarding the 6th grade, showed that the intelligence measured by the Raven test showed great statistical significance when the groups with and without difficulties were compared, a significance that was greater than that of the memory tests.
Although the Total WM had a high association with arithmetic performance, when the subtests are analyzed separately, it is possible to observe that the visuospatial WM was more relevant than the phonological WM. This finding corroborates the studies by Simmons, Willis, and Adams (2012) who state that this memory plays a more evident role as school progresses, for activities of writing numbers and judgment of magnitudes.
An increase in the percentage of students with difficulties in arithmetic was observed between school years (21.9% for the 4th year and 31.5% for the 6th year, that is, an increase of almost 10%), which can be attributed to demands for more abstract content. Mathematics has a hierarchical structure that must be respected: counting principles, understanding the decimal number system, basic facts, retrieving facts, understanding place value, multi-digit calculations, and problems (ANDERSSON, 2008; CASAS; GARCÍA CASTELAR, 2004; CORSO; ASSIS, 2017; GEARY; HAMSON; HOARD, 2000). When teaching disregards this hierarchy and disregards content that has not yet been consolidated, difficulties arise, and learning is not effective.
The increase in lags from the 4th to the 6th graders also appears in neuropsychological performance, since the group with difficulties in the 4th grade presented some language subtests and deficits in visuoconstructive skills; the 6th grade revealed several subtests of impaired executive functions, memory, and language. This result demonstrates that there is a growing effect for the 6th grade, which is due to the greater number of neuropsychological functions in delay when compared to the 4th grade. In this sense, such data reinforce studies that show that, with the increase in school level and the complexity of content, students need to recruit more of their neuropsychological functions (GONÇALVES et al., 2017; TOLL et al., 2011; VIAPIANA et al., 2016).
FINAL CONSIDERATIONS
The data obtained in this study contributed to the literature in education and neuropsychology focused on the school environment since there are few Brazilian studies that relate neuropsychological performance and arithmetic performance. It is even more significant by the fact that it covers eight different neuropsychological functions, from twenty-six subtests, making it possible to verify the neuropsychological functions related to arithmetic performance. In this perspective, it is worth remembering that the tasks that assessed the arithmetic and calculation abilities of the NEUPSILIN-Inf were sensitive to identifying arithmetic difficulties. This finding is pioneering, considering that this is the first study that establishes a relationship between this neuropsychological battery in its entirety and arithmetic performance.
It is important to emphasize the educational implications of this research. Initially, we believed it to be essential that scientific evidence reach teachers so they can know, reflect, and give more meaning to their teaching work since teaching needs to be based on scientific evidence, and not on teacher intuition (DORNELES; HAASE, 2018). The investigation of the different neuropsychological functions relating them to the arithmetic performance of groups of students with and without difficulties in this area allows the design of specific interventions for the functions that are impaired. Also, it provides the basis for educational practices that can prevent difficulties in arithmetic. Investigations of this type also help with subsidies for the development of consistent assessments, capable of highlighting students at risk of developing difficulties in arithmetic. Therefore, advances in this area of research are fundamental and promising. Knowing these aspects will provide the classroom teacher with a fresh look at their student, in addition to more support and authority to request a multidisciplinary evaluation and intervention.
It is worth remembering the limitations of the study. The sample size and the homogeneity of the groups of students can also be a factor that hinders the generalizability of the data. We suggest that future research may consider larger samples and between schools with other sociodemographic characteristics.
The importance of further studies that investigate the relationships between arithmetic performance and neuropsychological functions is highlighted in such a way that knowledge about the alterations and impacts of these associations in different academic areas is expanded. It is also necessary to invest more in assessment and intervention instruments in neuropsychological functions, as well as in training teachers who can stimulate these functions in the school environment.
REFERENCES
ALLOWAY, Tracy. P.; ALLOWAY, Ross. Working memory: is it the new IQ? Nature Precedings, v. 3, p. 1-17, 2008. [ Links ]
ANDERSSON, Ulf. Working memory as a predictor written arithmetical skills in children: the importance of central executive functions. Br. J. Educ. Psychol., v. 78, p. 181-203, 2008. [ Links ]
ANGELINI, Arrigo. L. et al. Manual: matrizes progressivas coloridas de Raven. São Paulo: Centro Editor de Testes e Pesquisas em Psicologia, 1999. [ Links ]
ASSEL, Mike. A. et al. Precursors to Mathematical skills: examining the roles of visual-spatial skills, executive processes, and parenting factors. Applied Developmental Science, v. 7, n. 1, p. 27-38, 2003. [ Links ]
BADDELEY, Alan. D.; HITCH, G. Working memory. In: BOWER, G. H. (ed.). The psychology of learning and motivation: advances in research and theory. New York: Academic Press, 1974. v. 8, p. 47-89. [ Links ]
BARNES, Marcia. A. et al. Mathematical skills in 3- and 5-year-olds with spina bifida and their typically developing peers: a longitudinal approach. Journal of the International Neuropsychological Society, v. 17, n. 3, p. 431-444, 2011. [ Links ]
BASTOS, José. A. Matemática: distúrbios específicos e dificuldades. In: ROTTA, N. T. et al. Transtornos da aprendizagem: abordagem neurobiológica e multidisciplinar. 2. ed. Porto Alegre: Artmed, 2016. p. 176-189. [ Links ]
BOLLER, François. History of the International Neuropsychological Symposium: a refletion of the evolution of a discipline. Neuropsychologia, v. 37, p. 17-26, 1999. [ Links ]
BRASIL. MEC/INEP. Relatório do Sistema Nacional de Avaliação da Educação Básica (SAEB). Brasília, 2019. [ Links ]
BULL, Rebecca.; JOHNSTO, R. S.; ROY, J. A. Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: views from cognition and developmental neuropsychology.Developmental Neuropsychology, v. 15, p. 421-442, 1999. [ Links ]
BULL, Rebecca.; LEE, K. Executive functioning and mathematics achievement. Child Dev. Perspect, v. 8, p. 36-41, 2014. [ Links ]
BULL, Rebecca.; SCERIF, G. Executive functioning as a predictor of children’s mathematics ability: Inhibition, switching, and working memory. Developmental Neuropsychology, v. 19, p. 273-293, 2001. [ Links ]
CARBONNEAU, Kira. J.; MARLEY, S. C.; SELIG, J. P. A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. Journal of Educational Psychology, v. 105, n. 2, p. 380-400, 2013. [ Links ]
CASAS, Ana. M.; GARCÍA CASTELLAR, R. Mathematics education and learning disabilities in Spain. Journal of Learning Disabilities, v. 37, n. 1, p. 62-73, 2004. [ Links ]
CHEN, Xiaoying. et al. Effect of working memory updating training on retrieving symptoms of children with learning disabilities. Journal of Learning Disabilities, v. 51, n. 5, p. 507-519, 9 jun. 2017. [ Links ]
CIRINO, Paul. T. The interrelationships of mathematical precursors in kindergarten. Journal of Experimental Child Psychology, v. 108, p. 713-733, 2011. [ Links ]
CONSENZA, Ramon. M.; GUERRA, L. B. Neurociência e educação: como o cérebro aprende. Porto Alegre: Artmed, 2011. [ Links ]
CORSO, Luciana. V. Memória de trabalho, senso numérico e desempenho em aritmética. Revista Psicologia: Teoria e Prática, v. 20, n. 1, p. 141-154, 2018. [ Links ]
CORSO, Luciana. V.; ASSIS, É. F. Reflexões acerca da aprendizagem inicial da matemática: contribuições de aspectos externos ao aluno. In: PICCOLI, L.; CORSO, L. V.; ANDRADE, S. S.; SPERRHAKE, R. (org.). Pacto Nacional pela Alfabetização na Idade Certa - PNAIC UFRGS: práticas de alfabetização, aprendizagem da matemática e políticas públicas. São Leopoldo: Oikos, 2017. p. 114-138. [ Links ]
CORSO, Luciana. V.; ASSIS, É. F. Interface entre a velocidade de processamento cognitivo e o desempenho aritmético e leitor de alunos do 5.º e 7.º anos do Ensino Fundamental. Bolema: Boletim de Educação Matemática, v. 34, n. 66, p. 225-245, 2020. Disponível em:https://doi.org/10.1590/1980-4415v34n66a11. Acesso em: 20 set. 2021. [ Links ]
CORSO, Luciana. V.; DORNELES, B. V. Perfil cognitivo dos alunos com dificuldades de aprendizagem na leitura e matemática. Revista Psicologia: Teoria e Prática, v. 17, n. 2, p. 185-198, 2015. [ Links ]
CORSO, Luciana. V.; SPERB, T. M.; SALLES, J. F. Comparação entre maus compreendedores e bons leitores em tarefas neuropsicológicas [Comparison between poor comprehenders and typical readers in neuropsychological tasks]. Psicologia em Pesquisa, v. 7, p. 37-49, 2013. [ Links ]
CRAGG, Lucy. et al. Direct and indirect influences of executive functions on Mathematics achievement. Cognition, v. 162, p. 12-26, 2017. [ Links ]
CRAGG, Lucy.; GILMORE, C. Skills underlying Mathematics: the role of executive function in the development of Mathematics proficiency. Trends NeurosciEduc., v. 3, p. 63-68, 2014. [ Links ]
DEHAENE, Stanislas. Précis of the number sense. Mind & Language, v. 16, p. 16-36, 2001. [ Links ]
DEHAENE, Stanislas. Varieties of numerical abilities. Cognition, v. 44, n. 1-2, p. 1-42, 1992. [ Links ]
DEHAENE, Stanislas. Babies who count. In: DEHAENE, S. The number sense: how the mind creates Mathematics. New York: Oxford University Press, 1997. [ Links ]
DIAMOND, Adele. Executive functions. Annual Review of Psychology, v. 64, p. 135-168, 2013. [ Links ]
DORNELES, Beatriz. V.; HAASE, V. G. Aprendizagem numérica em diálogo: neurociências e educação. In: LENT, R.; BUCHWEITZ, A.; MOTA, M. B. (org.). Ciência para educação: uma ponte entre dois mundos. São Paulo: Atheneu, 2018. v. 1, p. 133-160. [ Links ]
DOWKER, Ann. Individual differences in arithmetic: implications for psychology, neuroscience, and education. New York: Psychology Press, 2005. [ Links ]
FAZIO, Barbara. The counting abilities of children with specific language impairment: a comparison of oral and gestural tasks. Journal of Speech, Language, and Hearing Research, v. 37, p. 358-368, 1994. [ Links ]
FONSECA, Rochele. P.; SALLES, J. F.; PARENTE, M. A. M. P. Instrumento de avaliação neuropsicológica breve NEUPSILIN. São Paulo: Vetor, 2009. [ Links ]
GEARY, David. C. Reflections of evolution and culture in children’s cognition: implications for mathematical development and instruction. American Psychologist, v. 50, n. 1, p. 24-37, 1995. [ Links ]
GEARY, David. C. Mathematics and learning disabilities. Journal of Learning Disabilities, v. 37, p. 4-15, 2004. [ Links ]
GEARY, David. C. Cognitive predictors of achievement growth in Mathematics: a 5-year longitudinal study. Developmental Psychology, v. 47, n. 6, p. 1539-1552, 2011. [ Links ]
GEARY, David. C. Early foundations for Mathematics learning and their relations to learning disabilities. Current Directions in Psychological Science, v. 22, p. 23-27, 2013. [ Links ]
GEARY, David. C.; HAMSON, C. O.; HOARD, M. K. Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability. Journal of Experimental Child Psychology, v. 77, p. 236-263, 2000. [ Links ]
GOLBERT, Clarissa.; SALLES, J. F. Desempenho em leitura/escrita e em cálculos aritméticos em crianças de 2.ª série. Psicologia Escolar e Educacional, v. 14, p. 203-210, 2010. [ Links ]
GONÇALVES, Hosana. A. et al. Funções executivas predizem o processamento de habilidades básicas de leitura, escrita e matemática? Revista Neuropsicologia Latinoamericana, v. 9, n. 3, p. 42-54, 2017. [ Links ]
GUNDERSON, Elizabeth. A.; RAMIREZ, G.; BEILOCK, S. L.; LEVINE, S. C. The relation between spatial skill and early number knowledge: the role of the linear number line. Developmental Psychology, v. 48, p. 1229-1241, 2012. [ Links ]
HAASE, Vitor. G. et al. Heterogeneidade cognitiva nas dificuldades de aprendizagem da matemática: uma revisão bibliográfica. Psicologia em Pesquisa, v. 6, n. 2, p. 139-150, 2012. [ Links ]
HAASE, Vitor. G. Introdução. In: SALLES, J. F. et al. NEUPSILIN-Inf. São Paulo: Vetor, 2016. p. 15-19. [ Links ]
HOPKINS, Sarah. L.; LAWSON, M. J. The effect counting speed has on developing a reliance on retrieval in basic addition. Contemporary Educational Psychology, v. 31, p. 208-227, 2006. [ Links ]
KOPONEN, Tuire.; AUNOLA, K.; AHONEN, T.; NURMI, J. Cognitive predictors of single-digit and procedural calculation skills and their covariation with reading skills. Journal of Experimental Child Psychology, v. 97, p. 220-241, 2007. [ Links ]
KRAJEWSKI, Kristin.; SCHNEIDER, W. Exploring the impact of phonological awareness, visuo-spatial working memory, and preschool quantity-number competencies on Mathematics achievement in elementary school: findings from a 3-year longitudinal study. Journal of Experimental Child Psychology, v. 103, p. 516-531, 2009. [ Links ]
KYLLONEN, Patrick. C.; CHRISTAL, R. E. Reasoning ability is (little more than) working-memory capacity. Intelligence, v. 14, p. 389-433, 1990. [ Links ]
LEFEVRE, Jo. A. et al. Pathways to mathematics: longitudinal predictors of performance. Child Development, v. 81, p. 1753-1767, 2010. [ Links ]
LURIA, Aleksandr. R. Fundamentos de neuropsicologia. São Paulo: EDUSP, 1981. [ Links ]
MCCLUNG, Nicola. A.; ARYA, D. J. Individual differences in fourth-grade Math achievement in Chinese and English. Frontiers in Education, v. 3, 2018. [ Links ]
MEYER, Meghan. L. et al. Differential contribution of specific working memory components to Mathematics achievement in 2nd and 3rd graders . Learning and Individual Differences, v. 20, p. 101-109, 2010. [ Links ]
PENG, Peng. et al. Phonological storage and executive function deficits in children with Mathematics difficulties. Journal of Experimental Child Psychology, v. 112, p. 452-466, 2012. [ Links ]
PIAGET, Jean. Os seis estudos de psicologia. 24. ed.Rio de Janeiro: Forense Universitária, 1999. [ Links ]
PICCOLO, Luciane. R.; GIACOMONI, C. H.; JULIO-COSTA, A.; OLIVEIRA, S.; ZBORNIK, J.; HAASE, V. G.; SALLES, J. F. Reading anxiety in L1: reviewing the concept. Early Childhood Education Journal, v. 45, n. 4, p. 537-543, 2017. [ Links ]
SALLES, Jerusa. F. et al. Desenvolvimento do instrumento de avaliação neuropsicológica breve infantil NEUPSILINInf-. Psico-USF, v. 16, p. 297-305, 2011. [ Links ]
SALLES, Jerusa. F.; PARENTE, M. A. M.; FONSECA, R. P. Instrumento de avaliação neuropsicológica breve NEUPSILIN-Inf. São Paulo: Vetor, 2016. [ Links ]
SIEGLER, Robert. S.; BOOTH, J. L. Development of numerical estimation in young children. Child Development, v. 75, p. 428-444, 2004. [ Links ]
SILVA, Júlia. B. L.; MOURA, R. J.; WOOD, G.; HAASE, V. G. Processamento fonológico e desempenho em aritmética: uma revisão da relevância para as dificuldades de aprendizagem. Temas em Psicologia, v. 23, n. 1, p. 157-173, 2015. [ Links ]
SIMMONS, Fiona. R.; WILLIS, C.; ADAMS, A. Different components of working memory have different relationships with different mathematical skills. J Exp Child Psychol, v. 111, n. 2, p. 139-155, 2012. [ Links ]
SPELKE, Elizabeth. S. Core knowledge. American Psychologist, v. 55, n. 11, p. 1233-1243, 2000. [ Links ]
SPINILLO, Alina. G. Usos e funções do número em situações do cotidiano. In: BRASIL. Pacto Nacional pela Alfabetização na Idade Certa: quantificações, registros e agrupamentos. Brasília: MEC, SEB, 2014. p. 20-29. [ Links ]
STARKEY, Prentice.; COOPER, R. G. Perception of number by human infant. Science, v. 210, p. 1033-1035, 1980. [ Links ]
STEIN, Lilian. M. Teste de desempenho escolar: manual para aplicação e interpretação. São Paulo: Casa do Psicólogo, 1994. [ Links ]
STERNBERG, Robert. J. Psicologia cognitiva. 4. ed. Porto Alegre: Artmed, 2008. [ Links ]
TOLL, Sylke. W. et al. Executive functions as predictors of math learning disabilities. Journal of Learning Disabilities, v. 44, p. 521-532, 2011. [ Links ]
VAN DER SLUIS, Sophie.; DE JONG, P. F.; VAN DER LEIJ, A. Inhibition and shifting in children with learning deficits in arithmetic and reading. Journal of Experimental Child Psychology, v. 87, p. 239-266, 2004. [ Links ]
VERDINE, Brian. N.; IRWIN, C. M.; GOLINKOFF, R. M.; HIRSH-PASEK, K. Contributions of executive function and spatial skills to preschool mathematics achievement. Journal of Experimental Child Psychology, v. 126, p. 37-51, 2014. [ Links ]
VIAPIANA, Vanisa. F. et al. Evidências de validade do subteste aritmética do TDE-II : da psicometria moderna à neuropsicologia cognitiva. Revista Neuropsicologia Latinoamericana, v. 8, n. 2, p. 16-26, 2016. [ Links ]
ZELAZO, Philip. D.; CARLSON, S. M. The neurodevelopment of executive function skills: implications for academic achievement gaps. Psychology & Neuroscience, v. 13, n. 3, p. 273-298, 2020. [ Links ]
ZHANG, Xiao. Linking language,visual spatial,and executive function skills to number competence in very young Chinese children. Early Child, 2015. [ Links ]
ZHANG, X.iao; LIN, D. Pathways to arithmetic: the role of visual-spatial and language skills in written arithmetic, arithmetic word problems, and nonsymbolic arithmetic. Contemporary Educational Psychology, v. 41, p. 188-197, 2015. [ Links ]
ZHANG, Dake.; XIN, Y.; HARRIS, K.; DING, Y. Improving multiplication strategic development in children with Math difficulties. Learning Disability Quarterly, v. 37, p. 15-30, 2014. [ Links ]
ZHANG, Yu.; OKAMOTO, Y. Encoding “10ness” improves first-graders’ estimation of numerical magnitudes. PsychArchieves, p. 190-201, 2017. [ Links ]
Received: September 29, 2021; Accepted: June 14, 2022











 texto en
texto en