INTRODUÇÃO
Na última década, houve um crescente interesse das pesquisas da área da cognição numérica em identificar habilidades cognitivas que são subjacentes ao desempenho matemático (NOGUES; DORNELES, 2021). Conhecer quais são as habilidades envolvidas no desenvolvimento da compreensão matemática é um meio fundamental para pensar em intervenções adequadas e direcionadas para auxiliar a aprendizagem nessa área. Da mesma forma, esse entendimento pode dar suporte aos profissionais da educação na identificação de crianças que estão em risco de desenvolverem dificuldades de aprendizagem matemática.
Muitos fatores têm sido identificados como importantes para o desempenho matemático, os quais incluem tanto habilidades de domínio geral, que se referem às capacidades cognitivas de ordem superior e que estão relacionadas a diversas competências acadêmicas, como leitura, escrita e matemática, quanto de domínio específico, que são consideradas como capacidades que contribuem com o desempenho em uma competência escolar específica (ARAGÓN et al., 2019; PASSOLUNGHI; LANFRANCHI, 2012; XENIDOU-DERVOU et al., 2018). Além disso, também se faz importante conhecer a causalidade do desempenho matemático dos estudantes, isto é, quais habilidades cognitivas são explicativas desse desempenho e podem exercer influência para determinar um baixo ou alto desempenho nessa área.
Nesse sentido, algumas pesquisas já sugerem quais habilidades cognitivas podem ser explicativas do desempenho matemático posterior (GEARY, 2011; GILMORE et al., 2018; HABERMANN et al., 2020; NUNES et al., 2007). Dentre as habilidades de domínio geral, as evidências destacam memória de trabalho (ARAGÓN et al., 2019; GEARY, 2011; PASSOLUNGHI; LANFRANCHI, 2012), habilidades espaciais (CARR et al., 2020; HAWES et al., 2019), velocidade de processamento (ARAGÓN et al., 2019; GEARY, 2011; PASSOLUNGHI; LANFRANCHI, 2012) e consciência fonológica, que inclui a consciência fonêmica (HECHT et al., 2001; SIMMONS; SINGLETON; HORNE, 2008), como preditores do desempenho matemático. Em relação às habilidades de domínio específico, muitos estudos indicam como preditoras habilidades numéricas básicas como a contagem (CHING; NUNES, 2017; DESOETE et al., 2009; GEARY, 2011), o reconhecimento de números, também denominado de transcodificação numérica (HABERMANN et al., 2020; KISS; NELSON; CHRIST, 2019; MALONE; BURGOYNE; HULME, 2019), e a estimativa numérica (ARAGÓN et al., 2019; GILMORE et al., 2018; SASANGUIE; VAN DEN BUSSCHE; REYNVOET, 2012), assim como a habilidade em cálculos de adição e subtração, a recuperação de fatos aritméticos e o raciocínio quantitativo (CASEY et al., 2017; KISS; NELSON; CHRIST, 2019; MALONE; BURGOYNE; HULME, 2019; NUNES et al., 2012).
Entretanto, algumas habilidades ainda carecem de evidências sobre sua relação com a aritmética, citam-se aqui, como exemplo, as habilidades de leitura de palavras e compreensão leitora. Estudos sugerem que a leitura de palavras isoladas é preditora do desempenho aritmético (FUCHS et al., 2006; WONG; HO, 2017), indicando que a decodificação e o reconhecimento de palavras estão diretamente relacionados à capacidade de resolver cálculos aritméticos. Da mesma forma, a compreensão leitora parece exercer influência também na resolução de cálculos aritméticos e na recuperação de fatos aritméticos (ANDERSSON, 2008). Ainda assim, as evidências sobre essa influência são poucas e, por isso, mais estudos são necessários para elucidar a relação entre a leitura e compreensão leitora e a aritmética.
Na tentativa de investigar quais habilidades exercem influência no desempenho matemático posterior, pesquisas concentram esforços na avaliação de tais habilidades no início da vida escolar dos estudantes para analisar suas influências no desempenho matemático um ou dois anos depois (HABERMANN et al., 2020; MALONE; BURGOYNE; HULME, 2019; PASSOLUNGHI; LANFRANCHI, 2012; XENIDOU-DERVOU et al., 2018). Entretanto, se faz importante verificar, também, como acontecem essas relações em crianças já inseridas há mais tempo no contexto escolar, inclusive em estudantes já alfabetizados, o que permitirá identificar habilidades mais complexas do desempenho matemático.
Portanto, o presente estudo tem como proposta identifcar habilidades de domínio geral e específico como preditoras do desempenho aritmético de estudantes de 3º e 4º anos do ensino fundamental. Para isso, algumas habilidades cognitivas foram selecionadas com base nas evidências de pesquisas que indicam valores de influência significativos dessas habilidades no desempenho aritmético. Ademais, essa escolha foi feita levando-se em consideração habilidades tanto de domínio geral quanto específico e que tivessem tarefas de rápida aplicação para a condução das avaliações dentro do contexto escolar. Assim, uma bateria de testes relativa às habilidades de memória de trabalho, consciência fonêmica, compreensão leitora, transcodificação numérica, estimativa numérica e raciocínio quantitativo foi utilizada para avaliar a capacidade dos alunos nessas medidas. Em seguida, foram investigadas as relações entre os desempenhos nessas tarefas e em uma tarefa de aritmética. Destaca-se, também, que os desempenhos matemáticos considerados como variável desfecho na literatura abrangem desde somente cálculos simples de aritmética até medidas combinadas de aritmética, resolução de problemas e geometria, por exemplo, para definir uma medida de desempenho matemático geral. No estudo que se apresenta aqui, o enfoque será dado ao desempenho aritmético, isto é, à habilidade de resolver cálculos com as quatro operações fundamentais: adição, subtração, multiplicação e divisão. Tal enfoque está de acordo com o que é mais comumente abordado na disciplina matemática oferecida nas escolas brasileiras, além de ser o foco principal do currículo escolar brasileiro, referente a essa área do conhecimento, nessa etapa dos anos iniciais da escolarização (BRASIL, 2018).
Nas seções seguintes, apresenta-se o embasamento teórico para este estudo, fornecendo uma visão geral das evidências sobre o papel das habilidades cognitivas selecionadas em relação à aprendizagem matemática nos anos iniciais da escolarização.
Preditores de domínio geral
Muitos estudos focaram na análise dos preditores do desempenho matemático com o objetivo de elucidar quais habilidades cognitivas são subjacentes a esse desempenho e, assim, também ser possível identificar estudantes em risco de desenvolverem dificuldades de aprendizagem matemática (ARAGÓN et al., 2019; GEARY, 2011; PASSOLUNGHI; LANFRANCHI, 2012). Essa identificação pode facilitar a implementação de medidas de remediação e prevenção das dificuldades matemáticas com benefícios, inclusive a longo prazo.
Assim, uma habilidade bastante avaliada nesses estudos é a memória de trabalho, que se refere a um sistema, isto é, a um “espaço de trabalho” da memória que armazena e processa informações de forma imediata ou por um curto período ao realizar tarefas cognitivas (BADDELEY, 2011; PASSOLUNGHI; VERCELLONI; SCHADEE, 2007; XENIDOU-DERVOU et al., 2018). O modelo teórico adotado neste estudo é o de Baddeley e Hitch (1974), o qual apresenta a memória de trabalho como um sistema composto por três componentes: o fonológico, que armazena temporariamente informações verbais e auditivas, o visuoespacial para o armazenamento temporário de informações visuais e espaciais, e o executivo central, responsável por coordenar e processar as informações retidas pelos outros dois componentes. Mesmo já havendo uma atualização mais recente desse modelo (BADDELEY, 2000), que considera um quarto componente, o buffer episódico, optou-se pelo modelo anterior pela consistência teórica e disponibilidade de tarefas para avaliação (CANÁRIO; NUNES, 2012; GATHERCOLE, 2008; NOBRE et al., 2013).
Boa parte das pesquisas mostraram que a memória de trabalho está relacionada a várias habilidades matemáticas, desde a contagem até cálculos aritméticos (ARAGÓN et al., 2019; GEARY, 2011; PASSOLUNGHI; VERCELLONI; SCHADEE, 2007). Além disso, estudos indicam a memória de trabalho como uma habilidade precursora da aprendizagem matemática, principalmente nos primeiros anos de escolarização (ARAGÓN et al., 2019; PASSOLUNGHI; VERCELLONI; SCHADEE, 2007; XENIDOU-DERVOU et al., 2018), reduzindo a sua influência conforme o amadurecimento do conhecimento pelo aluno (CHU; VANMARLE; GEARY, 2016; GEARY, 2011).
Resolver tarefas matemáticas requer o processamento de informações verbais e visuoespaciais, pois exigem procedimentos de solução com vários passos. Portanto, não é surpreendente que a memória de trabalho exerça um papel fundamental tanto na aritmética quanto no desempenho matemático geral (XENIDOU-DERVOU et al., 2018), visto que também é uma habilidade conveniente para reter informações relevantes durante um cálculo ou enquanto se interpreta o enunciado de um problema para acessar informações de longo prazo, lembrar fatos aritméticos e para representar o problema (ARAGÓN et al., 2019).
A relação entre o desempenho em memória de trabalho e em testes que avaliam a competência numérica e matemática já está reportada e estabelecida na literatura (GEARY, 2011; GEARY; HOARD; HAMSON, 1999). Mesmo sendo avaliada simultaneamente ou anos depois, as evidências indicam que quanto maior a capacidade da memória de trabalho, melhor o desempenho em tarefas de matemática (BULL; ESPY; WIEBE, 2008; PASSOLUNGHI; VERCELLONI; SCHADEE, 2007). Entretanto, alguns estudos mostram que os efeitos da memória de trabalho também podem aparecer indiretamente relacionados ao desempenho matemático quando competências numéricas são conjuntamente avaliadas. Assim, o efeito de predição prevalece para essas habilidades numéricas iniciais, mas sua relação é mediada por elas no desempenho matemático posterior (FUHS; HORNBURG; MCNEIL, 2016; PASSOLUNGHI; LANFRANCHI, 2012).
Quanto à habilidade de consciência fonológica, define-se como a habilidade de segmentar as palavras em unidades menores, isto é, focalizando e separando as palavras nos sons que as constituem. A consciência fonológica pode ser separada em três níveis principais: consciência da sílaba, consciência de rimas (intrassilábica) e consciência do fonema (consciência fonêmica) (GILLON, 2017; SOARES, 2019). Esta última é considerada o nível mais avançado da consciência fonológica, pois é o entendimento de que as palavras são compostas por sons individuais (GILLON, 2017), sendo alcançada por meio da associação entre grafema (letra) e seu respectivo fonema (som) (SOARES, 2019). Nesse sentido, pelo fato da consciência fonêmica ser o mais alto nível de consciência fonológica, optou-se por avaliá-la neste estudo como uma medida representante da consciência fonológica. Não existe consenso entre os estudos que consideraram tal habilidade como preditora do desempenho matemático. Alguns estudos que avaliaram a consciência fonológica, e mais especificamente a consciência fonêmica, encontraram relação direta com o desempenho matemático (HECHT et al., 2001; LOPES-SILVA et al., 2014; 2016), enquanto outros não encontraram relação alguma (PASSOLUNGHI; LANFRANCHI, 2012; PASSOLUNGHI; VERCELLONI; SCHADEE, 2007). A codificação fonêmica dos numerais verbais é o primeiro passo nos procedimentos de transcodificação numérica, antes mesmo do uso das regras de algoritmos e da recuperação de fatos da memória de longo prazo (LOPES-SILVA et al., 2014). Portanto, limitações na capacidade de processamento fonológico podem restringir a capacidade de transcodificação numérica, particularmente no caso de números de magnitudes maiores (LOPES-SILVA et al., 2014).
As evidências que indicam a associação da consciência fonológica no desempenho matemático incluem também uma relação causal, isto é, de que a consciência fonológica exerce um papel de influência especificamente na resolução de cálculos aritméticos. Para exemplificar, ao resolver um cálculo, o estudante pode primeiro converter os termos do problema, os valores e a operação em um código baseado na fala. A utilização da tradução arábica para verbal é bastante comum em criança ao resolverem tarefas aritméticas, pois elas necessitarão processar essa informação fonológica para realizar sua estratégia. Por exemplo, no cálculo “5x2” a criança irá buscar uma resposta baseada em um código fonológico da memória de longo prazo (GEARY; HOARD; HAMSON, 1999). Da mesma forma, quando recorre a uma estratégia baseada na contagem, o sistema fonológico será ativado quando os nomes dos números (códigos numéricos fonológicos) são usados para contar (HECHT et al., 2001).
Em um estudo estado-unidense, 201 crianças foram acompanhadas do 2º ao 5º ano do ensino fundamental e avaliadas quanto à sua capacidade de processamento fonológico, o qual abrangeu as três áreas: velocidade de nomeação, memória fonológica e consciência fonológica. A partir disso, os autores verificaram a influência dessa habilidade no desempenho aritmético dos estudantes ao longo desses anos escolares. Foi possível verificar que o processamento fonológico foi um importante preditor no aumento do desempenho aritmético das crianças em todos os anos escolares avaliados, porém especificamente a consciência fonológica teve o maior valor de predição dentre as demais áreas do processamento fonológico. Além disso, a consciência fonológica apresentou contribuição preditiva única no desempenho do 3º para o 4º ano e do 4º para o 5º ano (HECHT et al., 2001).
A capacidade de compreender e lidar com as informações é um fator relevante para todas as habilidades descritas, bem como para o desempenho matemático. Nesse sentido, a compreensão leitora pode ser uma habilidade importante para identificar a capacidade das crianças em lidar com a informação. Outro estudo estado-unidense que avaliou preditores específicos para a resolução de problemas nos anos iniciais da escola indicou a compreensão leitora como uma habilidade significativa e capaz de predizer a capacidade de resolução de problemas (DECKER; ROBERTS, 2015). Em relação ao desempenho aritmético, algumas evidências apontam para a habilidade de leitura de palavras estar relacionada com o desempenho em resolver cálculos (GILLIGAN; FLOURI; FARRAN, 2017; WONG; HO, 2017). Vale destacar que um estudo sueco, preocupado em investigar especificamente a relação de predição da memória de trabalho no desempenho em aritmética, considerou também uma medida de compreensão da leitura dentre as variáveis avaliadas. Nesse estudo, foram avaliados 141 estudantes de 3º e 4º anos e os resultados indicaram que a compreensão de leitura apareceu como uma das habilidades preditoras do desempenho em cálculos aritméticos, sendo a mais importante para a recuperação de fatos aritméticos (ANDERSSON, 2008).
Percebe-se, com isso, a associação de habilidades cognitivas de domínio geral com o desempenho matemático, sendo sua estimulação precoce muito importante para o desenvolvimento da aprendizagem numérica e para a prevenção de dificuldades nessa área. Por isso, este estudo se propôs a investigar a influência das habilidades descritas anteriormente no desempenho aritmético de estudantes brasileiros.
Preditores de domínio específico
Conhecer as habilidades cognitivas que formam a base do desenvolvimento matemático das crianças é fundamental tanto para a comunidade científica quanto para a prática educacional. Existem evidências consideráveis de algumas habilidades de domínio específico envolvidas no conhecimento matemático. Especialmente, a literatura indica que habilidades numéricas iniciais, mesmo quando avaliadas em uma idade precoce, são preditores importantes para o desempenho matemático posterior, tanto de níveis iniciais quanto finais da escolarização (CHING; NUNES, 2017; HABERMANN et al., 2020; KISS; NELSON; CHRIST, 2019; KRAJEWSKI; SCHNEIDER, 2009). Portanto, destaca-se que fornecer uma base consistente da competência matemática é importante para o sucesso escolar (CHING; NUNES, 2017), podendo beneficiar o desempenho dos estudantes em vários níveis da escolarização e favorecer aprendizagens de conteúdos mais avançados da matemática.
Dentre as habilidades numéricas iniciais, destacam-se, neste estudo, a transcodificação numérica e a estimativa numérica como importantes preditores para o desempenho aritmético, especificamente. A transcodificação numérica é considerada como a capacidade de notação dos símbolos numéricos a partir da conversão entre as linguagens verbal e escrita (MOURA et al., 2015). As evidências sobre a relação entre a transcodificação numérica e o desempenho aritmético ainda são escassas, mas, mesmo assim, alguns estudos encontraram associação significativa entre a leitura e escrita de números e o desempenho matemático (GEARY; HAMSON; HOARD, 2000; GEARY; HOARD; HAMSON, 1999). Inclusive, existem evidências de que, quando comparado à capacidade de memória de trabalho e a representações numéricas não simbólicas, o conhecimento da forma de escrita do valor posicional dos números, em crianças no final do primeiro ano escolar, é o melhor preditor do desempenho matemático dois anos depois (MOELLER et al., 2011).
Um estudo australiano que avaliou 519 estudantes na educação infantil e, logo depois, no 1º ano, preocupado em investigar as habilidades preditoras do desempenho aritmético, indicou que o conhecimento dos números em formato arábico no início da escolarização foi importante para o desenvolvimento de habilidades aritméticas posteriores (MALONE; BURGOYNE; HULME, 2019). Esses achados são corroborados por um estudo britânico que também acompanhou seus 71 participantes da educação infantil até o 1º ano, o qual investigou especificamente a relação entre o conhecimento numérico arábico e o desempenho aritmético. Em tal estudo, verificou-se que o conhecimento numérico aos 4 anos de idade, avaliado pela habilidade de transcodificação numérica, é um preditor único da habilidade aritmética aos 6 anos de idade (HABERMANN et al., 2020).
Outra habilidade cognitiva envolvida no conhecimento numérico inicial e indicada como importante para o desempenho matemático é a estimativa numérica. Para avaliar essa habilidade, comumente é utilizada uma tarefa em que os participantes devem indicar a posição de um número em uma reta numérica, que está apenas com as marcações do número inicial e final. Alguns estudos sugerem que quanto melhor a capacidade em realizar estimativas, melhor o desempenho em testes padronizados de matemática (BOOTH; SIEGLER, 2006), e que o desempenho em estimativa melhora progressivamente conforme o aumento da idade e do ano escolar (LINK; NUERK; MOELLER, 2014; SASANGUIE; VAN DEN BUSSCHE; REYNVOET, 2012). Além disso, já existem resultados indicando que quanto mais precisas as crianças são em localizar números na reta numérica, melhor será seu desempenho matemático anos depois (ARAGÓN et al., 2019; GILMORE et al., 2018; SASANGUIE; VAN DEN BUSSCHE; REYNVOET, 2012).
As principais evidências são de que o desempenho em estimativa numérica está relacionado com habilidades numéricas básicas, como a categorização e comparação de magnitudes numéricas, e com habilidades complexas da aritmética, como os cálculos com as quatro operações fundamentais (BOOTH; SIEGLER, 2006; 2008; LASKI; SIEGLER, 2007; LINK; NUERK; MOELLER, 2014; SIEGLER; BOOTH, 2004). Além disso, a estimativa numérica é um recurso importante para a representação e compreensão numérica inicial, pois exige uma integração entre o conhecimento numérico conceitual, como a familiaridade com os números, o valor posicional e a compreensão numérica, e o conhecimento numérico de procedimento, como as estratégias utilizadas e o julgamento proporcional (DACKERMANN et al., 2015; GILMORE et al., 2018; LASKI; SIEGLER, 2007; SIEGLER; THOMPSON; OPFER, 2009).
Partindo do conhecimento numérico inicial, que envolve a compreensão do sistema numérico, passa-se para o entendimento das quatro operações fundamentais (adição, subtração, multiplicação e divisão). Nesse sentido, a compreensão das operações matemáticas ultrapassa simplesmente o fato de o aluno ser apto a resolver um algoritmo. Compreender as operações matemáticas envolve, primeiramente, conhecer as relações entre elas e, principalmente, perceber as relações entre as quantidades envolvidas para, depois disso, ser possível operar com os números envolvidos no cálculo, com a possibilidade de seguir outras estratégias de resolução além dos algoritmos preestabelecido (NUNES; BRYANT, 2015). Essa compreensão das relações entre as quantidades, se estão aumentando ou diminuindo, sendo agrupadas ou repartidas, por exemplo, é o que se define como raciocínio quantitativo (NUNES et al., 2016). Entender as relações entre as quantidades irá auxiliar na compreensão da matemática inicial e até mesmo dos cálculos aritméticos.
O raciocínio quantitativo pode ser classificado em raciocínio aditivo e multiplicativo, de acordo com as relações estabelecidas entre as quantidades (NUNES et al., 2016). Ambos são essenciais para a compreensão das quatro operações fundamentais da matemática e suas relações. A partir do momento em que a criança coordena os esquemas necessários para a solução dos problemas matemáticos, ela irá desenvolver o raciocínio operatório e obterá um melhor desempenho nas tarefas de matemática (NUNES et al., 2009). Ainda existem poucas evidências de estudos longitudinais que investigaram o raciocínio quantitativo como habilidade capaz de predizer o sucesso matemático em anos posteriores. Destaca-se a pesquisa de Nunes e colaboradores (2007), em que foi investigado se o raciocínio quantitativo, medido ao iniciar a vida escolar, era um preditor significativo do desempenho matemático, avaliado 16 meses depois por um teste padronizado. Para isso, foram acompanhadas 53 crianças britânicas com média de idade variando de 6 a 7,3 anos, de acordo com o momento em que foi feita a avaliação. Os resultados indicaram o raciocínio quantitativo como preditor significativo e específico do desempenho matemático, mesmo após controlar o nível de inteligência e a capacidade de memória de trabalho desses participantes (NUNES et al., 2007). De maneira similar, um estudo também longitudinal investigou se as habilidades de raciocínio quantitativo e aritmética de 1680 estudantes britânicos eram preditoras de seu desempenho matemático posterior, avaliado aos 11 e aos 14 anos de idade (NUNES et al., 2012). Seus achados mostraram que o raciocínio quantitativo tem uma contribuição única na predição do desempenho matemático em ambos os momentos avaliados para além dos efeitos de memória de trabalho, inteligência e habilidades aritméticas.
Mais recentemente, um estudo realizado com 115 crianças chinesas avaliadas no 1º ano e, em seguida, no 2º ano, também com o objetivo de investigar as contribuições do raciocínio quantitativo, especificamente o aditivo, para o desempenho matemático posterior, o indicou como medida substancialmente explicativa do desempenho matemático, tanto para habilidades de cálculo quanto para a resolução de problemas (CHING; NUNES, 2017). Destaca-se, a partir dessas evidências, a importância do raciocínio quantitativo para a aprendizagem matemática e o quanto a compreensão das relações entre as quantidades é fundamental para o entendimento dos algoritmos formais utilizados na resolução de cálculos aritméticos, bem como para o melhor desempenho matemático em geral.
Assim, ressalta-se a influência de habilidades cognitivas de domínio específico no desenvolvimento da aprendizagem matemática. Além do mais, destaca-se que habilidades numéricas iniciais bem estabelecidas proporcionam uma compreensão matemática mais consistente e, consequentemente, o sucesso escolar nessa área.
O presente estudo
Neste artigo, é apresentada uma pesquisa que buscou identificar as habilidades, dentre as propostas, que predizem o desempenho aritmético de crianças de 3º e 4º anos do ensino fundamental. Em outras palavras, o objetivo é verificar a influência de preditores de domínio geral e específico na performance aritmética de um mesmo grupo de estudantes avaliados no início e no final do ano letivo. Para isso, foram selecionadas seis habilidades importantes para o desempenho aritmético, são elas: memória de trabalho, consciência fonêmica, compreensão leitora, transcodificação numérica, estimativa numérica e raciocínio quantitativo. Como hipótese, esperava-se encontrar influência tanto de habilidades de domínio geral quanto de domínio específico para o desempenho aritmético, isto é, que pelo menos algumas das variáveis avaliadas contribuíssem de forma independente para a variável desfecho, especialmente a memória de trabalho, que é bastante reportada na literatura como preditora, e o raciocínio quantitativo, vista a proximidade de procedimentos com a aritmética.
Cabe dizer que a maioria das pesquisas até o momento focou na investigação das habilidades cognitivas de alunos da educação infantil e do 1° ano. Assim, este estudo propõe a avaliação das habilidades cognitivas de estudantes com mais tempo de escolarização, além de verificar a relação de medidas como a compreensão leitora e o raciocínio quantitativo, as quais, além de requererem um ensino formal escolar, são pouco exploradas como possíveis preditoras do desempenho aritmético. Desse modo, este estudo permite a identificação de habilidades precursoras do desempenho aritmético de estudantes brasileiros já inseridos há mais tempo no contexto escolar.
Assim, o desempenho dos alunos foi avaliado nas habilidades cognitivas selecionadas para identificar a contribuição única de cada uma para o desempenho aritmético posterior. Cabe mencionar que este estudo está inserido em um projeto de pesquisa cadastrado na Plataforma Brasil e aprovado pelo Comitê de Ética em Pesquisa da universidade de origem dos pesquisadores, sob o número 82570618.9.0000.5347. A seguir, são descritas a composição da amostra, os procedimentos e as tarefas selecionadas para avaliar as habilidades propostas.
MÉTODO
Este estudo foi realizado de forma quantitativa, reunindo dados longitundinais sobre o desempenho dos estudantes, o qual foi avaliado em dois momentos ao longo do mesmo ano letivo. Para as análises dos dados, foram considerados testes estatísticos adequados para responder os objetivos propostos neste estudo. Na sequência, são descritos os procedimentos da coleta de dados, bem como a seleção dos participantes e os instrumentos de avaliação utilizados.
Participantes
A quantidade mínima de participantes para conduzir o estudo foi determinada a partir de um cálculo amostral, utilizando o software Winpepi (v11.48), para uma análise de regressão, considerando seis preditores, com coeficiente de determinação R² = 0,90, com poder de 80%, nível de significância de 5% e considerando uma perda de 30% dos participantes. Isso resultou na quantidade mínima necessária de 98 crianças, quantidade mínima suficiente para realizar os testes estatísticos pretendidos.
Quanto à participação da pesquisa, foi solicitada à Secretaria Municipal de Educação uma autorização para realização da pesquisa nas escolas. Também foi requerido um termo de autorização de cada escola participante, bem como a assinatura de um termo de participação à professora responsável por cada turma. Aos responsáveis dos alunos interessados em participar, exigiu-se a assinatura de um Termo de Consentimento Livre e Esclarecido e, aos alunos participantes, um Termo de Assentimento Livre e Esclarecido.
Esta pesquisa contou com 127 crianças de 3º e 4º anos do ensino fundamental de duas escolas municipais da cidade de Porto Alegre (RS). Inicialmente, a amostra contava com 163 alunos, os quais realizaram todas as atividades de avaliação das habilidades cognitivas descritas anteriormente (transcodificação numérica, estimativa numérica, raciocínio quantitativo, memória de trabalho, consciência fonêmica e compreensão leitora) e a avaliação do nível intelectual. Foram considerados dois critérios para inclusão dos participantes na amostra: o nível intelectual e a alfabetização. O nível intelectual foi medido a partir da avaliação do raciocínio não verbal, feita por meio do instrumento Matrizes Progressivas Coloridas de Raven - Escala Especial (ANGELINI et al., 1999). A aplicação dessa medida tem como intenção homogeneizar a amostra, isto é, desconsiderar as crianças com possibilidade de apresentarem deficiência intelectual. Com base no teste, foi considerado o ponto de corte no percentil 25, que indica o participante como sendo intelectualmente médio. Abaixo desse percentil, o sujeito é classificado como abaixo da média intelectual ou com alguma deficiência intelectual (ANGELINI et al., 1999). A alfabetização foi identificada a partir da habilidade de leitura, considerando como alfabetizados apenas os participantes que conseguiram completar as tarefas de consciência fonêmica e de compreensão leitora. Assim, tem-se o resultado de um grupo amostral de 127 alunos.
Coleta de dados
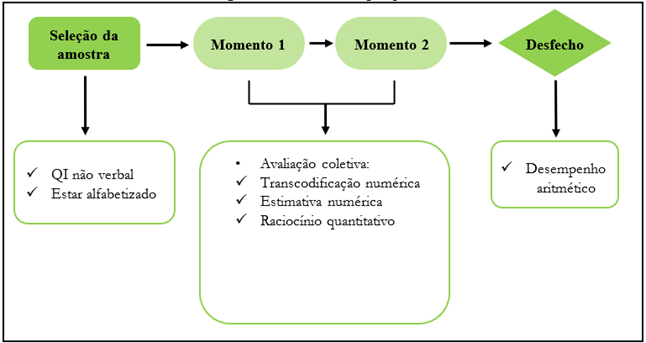
O processo de coleta de dados ocorreu no ano de 2018, tendo de iniciar e terminar ao longo do mesmo ano letivo para minimizar perdas de sujeitos da amostra. Optou-se por realizar dois momentos de avaliação, medindo-se as mesmas habilidades em ambos, com a intenção de verificar uma possível influência da escolarização no desenvolvimento dessas habilidades, bem como de caracterizar um estudo longitudinal de predição. O primeiro momento de avaliação foi realizado durante os meses de abril e maio (início do ano letivo) e, o segundo momento, em outubro e novembro (final do ano letivo), seguido imediatamente pela avaliação do desempenho aritmético (variável desfecho). O fluxograma abaixo (Figura 1) resume as etapas seguidas para a coleta de dados deste estudo.
A coleta de dados consistiu na aplicação de seis tarefas, uma para cada habilidade, mais a avaliação do nível intelectual dos estudantes e do desempenho aritmético. Durante a avaliação nos momentos 1 e 2, os alunos participaram de três sessões em cada momento, sendo duas sessões coletivas, em que participaram todos os alunos ao mesmo tempo, e uma individual, na qual foi avaliado um aluno de cada vez. Na primeira sessão coletiva do momento 1, foi avaliado o raciocínio não verbal dos estudantes e, na segunda sessão coletiva, foram avaliadas as habilidades de transcodificação numérica, estimativa numérica e raciocínio quantitativo, as quais foram aplicadas em sequência e nessa ordem. Todas as tarefas foram aplicadas em sala de aula, durante o turno escolar, com duração aproximada de uma hora para a primeira sessão e de duas horas para finalizar todas as tarefas na segunda sessão. Na terceira sessão do momento 1, que foi feita de forma individual, foram avaliadas a memória de trabalho, a consciência fonêmica e a compreensão leitora, também durante o turno escolar, porém em sala separada e com duração média de 30 minutos por participante.
No momento 2, as sessões configuraram-se da seguinte maneira: primeira sessão coletiva, em que se avaliou a transcodificação numérica, o raciocínio quantitativo e a estimativa numérica, seguindo essa ordem de aplicação; segunda sessão individual, em que foram avaliadas a memória de trabalho, a consciência fonêmica e a compreensão leitora; e a terceira sessão coletiva, para avaliar o desempenho aritmético. A seguir, constam as descrições dos instrumentos utilizados, seguindo a mesma ordem de aplicação.
Tarefa de avaliação da transcodificação numérica
Nesta tarefa, os participantes são solicitados a escrever em algarismos os números ditados a eles. A tarefa avalia a capacidade de transcodificação numérica, sendo composta por 28 números de um até quatro dígitos, que devem ser escritos com seus algarismos correspondentes (LOPES-SILVA et al., 2014; 2016; MOURA et al., 2013). Um ponto é atribuído para cada resposta correta, totalizando 28 pontos como escore máximo, e não contém critérios de interrupção1.
Tarefa de avaliação da capacidade de estimativa numérica
A tarefa de estimativa numérica utilizada foi a versão número-posição (SIEGLER; OPFER, 2003), que consiste em solicitar ao participante que marque a posição de um número em uma reta delimitada pelos números 0 (à esquerda) e 100 (à direita). Os 22 números a serem estimados, retirados de Laski e Siegler (2007), foram apresentados de forma aleatória e as crianças tiveram que marcar suas estimativas em um caderno contendo uma reta numérica e um número a ser estimado em cada página. Essa tarefa não apresenta critérios de interrupção. O desempenho foi determinado pelo cálculo da precisão com que os alunos estimam cada número solicitado, ou seja, pelo cálculo da porcentagem do erro absoluto (PEA) de cada criança. Esse cálculo é adaptado de Siegler e Booth (2004) e é feito dividindo-se a diferença, em valor absoluto, entre a estimativa feita pela criança e o número a ser estimado, pela escala da reta. Melhor explicando: se uma criança é solicitada a estimar o número 40, mas realiza uma marcação correspondente ao número 30, a porcentagem do erro absoluto será de 10%. Esse valor corresponde ao resultado de|(30-40)/100|. Para fins de análise, a variável estimativa numérica foi considerada como “1 - PEA”, ou seja, no exemplo acima, a precisão considerada seria de 90% (1 - 0,10 = 0,90). O escore máximo nesta tarefa corresponde a 1 (100%), portanto quanto mais próximo desse valor, mais precisa é a resposta dada pela criança.
Tarefa de avaliação do raciocínio quantitativo
A tarefa de raciocínio quantitativo, baseada em Nunes (2009), foi aplicada com o objetivo de avaliar a habilidade de resolver problemas aritméticos simples, isto é, que envolvem apenas uma operação matemática e números até 20. As relações quantitativas envolvidas são o raciocínio aditivo, o qual inclui situações de composição de quantidades, de transformação e de comparação, e raciocínio multiplicativo, que contém situações de relação direta e inversa entre quantidades e de combinação. A tarefa compreendeu 18 problemas, 9 de raciocínio aditivo e 9 de raciocínio multiplicativo. Cada participante recebeu um caderno contendo apenas as ilustrações dos problemas, com um problema por página, e sem informações por escrito. As instruções foram dadas oralmente pela avaliadora, pois, assim, não exige a habilidade de leitura dos alunos para o entendimento do enunciado. A tarefa não apresenta critérios de interrupção. Para a correção, foi levado em consideração o número de acertos sobre o total de questões, podendo chegar a 18 pontos como escore máximo.
Tarefa de avaliação da memória de trabalho
A avaliação da capacidade da memória de trabalho foi realizada por meio da Bateria de Testes de Memória de Trabalho para Crianças (PICKERING; GATHERCOLE, 2001). Desse material, foram utilizadas as tarefas Memória de Blocos, para avaliar o componente visuoespacial, e Memória de Dígitos em ordem direta e inversa, para avaliar os componentes fonológico e executivo central, respectivamente. As tarefas são separadas em níveis, que vão aumentando progressivamente a quantidade de informações a serem lembradas em cada sequência. O teste é interrompido caso a criança cometa três erros em um mesmo nível. O desempenho nesta tarefa é medido de acordo com o número de sequências repetidas corretamente (PICKERING; GATHERCOLE, 2001), com um escore máximo de 54 pontos para as tarefas de Memória de Dígitos em ordem direta e Memória de Blocos e de 36 pontos para a tarefa de Memória de dígitos na ordem inversa.
Tarefa de avaliação da consciência fonêmica
Esta tarefa avalia a consciência fonêmica da criança por meio da supressão de fonemas, isto é, a criança ouve uma palavra e deve dizer qual é a nova palavra formada quando excluído um fonema especificado, por exemplo: “gavião” sem /g/ é “avião”. A tarefa é composta por 28 palavras, que variam de 2 a 3 sílabas e os fonemas a serem suprimidos estão em diferentes posições nas palavras. Essa tarefa é aceita em pesquisas, tendo sido aplicada anteriormente também em amostras brasileiras (LOPES-SILVA et al., 2014; 2016). Sua correção é determinada pelo total de respostas dadas corretamente, podendo chegar ao escore máximo de 28 pontos, e não possui critérios de interrupção.
Tarefa de avaliação da compreensão leitora
A tarefa utilizada neste estudo é a de avaliação da compreensão leitora de textos expositivos, proposta por Saraiva, Moojen e Munarski (2017), que estão de acordo com as possibilidades cognitivas dos alunos em relação a conceitos e conhecimentos sobre o assunto lido. Para cada ano escolar, foi apresentado um texto diferente, respeitando as capacidades cognitivas esperadas de cada nível escolar. Foi solicitada a leitura silenciosa e oral do texto, para, em seguida, realizar seis perguntas referentes ao texto: cinco com respostas encontradas no próprio texto e uma com resposta inferencial. A pontuação foi determinada pelo número de respostas dadas corretamente, com o máximo de 12 pontos, e não apresenta critérios de interrupção.
Tarefa de avaliação do desempenho aritmético
O desempenho aritmético foi avaliado pelo Subteste de Aritmética do Teste de Desempenho Escolar (TDE) (STEIN, 1994). O TDE é um teste padronizado para a realidade brasileira e amplamente utilizado em pesquisas no Brasil para verificar o aproveitamento escolar das crianças do ensino fundamental. Esse teste compreende três subtestes: aritmética, leitura e escrita. Para esta pesquisa, foi utlizado apenas o subteste de aritmética, o qual é composto de três problemas simples apresentados oralmente e 35 cálculos aritméticos apresentados de forma escrita, com nível crescente de complexidade. As crianças são solicitadas a realizar o maior número de questões que puderem, sem limite de tempo e sem critérios de interrupção. Sua pontuação é determinada pelo total de questões realizadas corretamente, que podem chegar ao escore máximo de 38 pontos.
Análise dos dados2
Foi realizada uma análise quantitativa, utilizando-se o software R v.3.6.3, com o intuito de verificar, dentre as habilidades avaliadas, quais são precursoras do desempenho aritmético. Para isso, primeiramente foram realizadas as análises descritivas dos desempenhos dos participantes nas tarefas, considerando os dois momentos de avaliação: no início e no fim do ano letivo. Em seguida, foi conduzido teste de comparação de Wilcoxon para verificar a existência de diferença significativa entre os desempenhos nesses dois momentos de avaliação. Também foi calculado o coeficiente alfa (α) de Conbrach para medir a consistência interna dos instrumentos utilizados, levando-se em consideração o total de questões de cada tarefa e as respostas dos estudantes para cada item.
Logo depois, foi realizada uma análise de correlação linear de Pearson entre os desempenhos dos estudantes em cada habilidade avaliada. Após, foi feita uma análise de regressão linear múltipla para verificar o valor preditivo de cada uma das medidas no desempenho aritmético. Cabe dizer que, para tais análises, utilizou-se os desempenhos no primeiro momento de avaliação, no qual considera-se que os estudantes receberam menos influência do ensino escolar. Por fim, foi conduzida análise de mediação, na intenção de investigar efeitos diretos e indiretos das variáveis preditoras no desempenho aritmético.
RESULTADOS
O presente estudo teve como objetivo identificar habilidades cognitivas como preditoras do desempenho aritmético de alunos de 3º e 4º anos do ensino fundamental. Para isso, foram analisados os desempenhos de 127 estudantes. A descrição da amostra, indicando a quantidade de crianças por gênero, por ano escolar e a média das idades, pode ser verificada na Tabela 1.
Tabela 1 Categorização da amostra
| Total (%) | Média (DP) | Mínimo | Máximo | ||
|---|---|---|---|---|---|
| Ano escolar | 3º | 55 (43,31) | |||
| 4º | 72 (56,69) | ||||
| Gênero | F | 79 (62,20) | |||
| M | 48 (37,80) | ||||
| Idade | 9,3 (0,7) | 8,2 | 11,3 |
Fonte: dados da pesquisa.
As análises descritivas, indicadas na Tabela 2, mostram o desempenho dos estudantes nas tarefas em ambos os momentos de avaliação, no início (momento 1) e no final (momento 2) do ano letivo. Além disso, verifica-se a confiabilidade das tarefas medida pelo alfa (α) de Cronbach, o qual indica que quanto maior o valor de α, mais confiáveis são as tarefas, ou seja, mais coerentes as tarefas são com aquilo que se propõem a medir. Assim, percebe-se que as tarefas tiveram valores aceitáveis e com boa confiabilidade, permitindo uma interpretação mais consistente dos resultados. Também foi realizado o teste de comparação de Wilcoxon para verificar se houve uma melhora significativa nos desempenhos dos estudantes entre os dois momentos de avaliação. Os resultados dessa comparação estão indicados na tabela pelo p-valor, que indica a probabilidade de significância do resultado do teste estatístico realizado, portanto, quando esse valor é menor do que 5% (0,05), temos que o resultado do teste é significativo. Assim, a partir do p-valor, confere-se que o desempenho das crianças melhorou em todas as tarefas ao final do ano letivo, confirmando a hipótese de uma possível influência do ensino escolar no desenvolvimento dessas habilidades.
Tabela 2 Análises descritivas das tarefas avaliadas nos momentos 1 e 2
| Momento 1 | Momento 2 | |||||
|---|---|---|---|---|---|---|
| α* | Média (DP) | Mín. - Máx. | Média (DP) | Mín. - Máx. | p-valor | |
| MT - Fonológico | 0,89 | 25,81 (4,97) | 16 - 42 | 26,56 (5,29) | 16 - 48 | < 0,01 |
| MT - Visuoespacial | 0,79 | 21,40 (3,98) | 13 - 29 | 22,32 (4,09) | 8 - 31 | < 0,05 |
| MT - Executivo Central | 0,84 | 9,26 (3,48) | 1 - 21 | 10,22 (3,57) | 5 - 22 | < 0,01 |
| Compreensão Leitora1 | 0,73 0,69 | 6,90 (2,63) | 0 - 12 | 7,61 (2,58) | 2 - 12 | < 0,05 |
| Consciência Fonêmica | 0,90 | 19,53 (6,53) | 1 - 28 | 21,27 (5,47) | 5 - 28 | < 0,001 |
| Transcodificação Numérica | 0,92 | 21,31 (5,73) | 7 - 28 | 24,48 (4,33) | 13 - 28 | < 0,001 |
| Estimativa Numérica | 0,90 | 0,89 (0,05) | 0,69 - 0,97 | 0,91 (0,04) | 0,77 - 0,97 | < 0,05 |
| Raciocínio Quantitativo | 0,72 | 8,24 (3,08) | 0 - 16 | 10,28 (4,16) | 0 - 18 | < 0,001 |
| Desempenho Aritmético | -- | -- | -- | 13,17 (4,02) | 2 - 23 | -- |
*Coeficiente alfa (α) de Cronbach: calculado com base no total de questões em cada tarefa, mede a confiabilidade das tarefas e a consistência interna das questões com base nas respostas dos participantes. Sendo valores entre 0,6 e 0,7, um nível questionável, entre 0,7 e 0,8, aceitável, entre 0,8 e 0,9, um nível bom, e maiores do que 0,9, excelente.
1Nota: Na tarefa de Compreensão Leitora, o coeficiente de confiabilidade foi separado por ano escolar, visto que o texto e as questões são diferentes para cada ano. Porém, as demais inferências são feitas com base na amostra total.
Fonte: dados da pesquisa.
Em seguida, para a compreensão das relações entre as variáveis cognitivas e o desempenho aritmético, foi realizada uma análise de correlação linear de Pearson entre os desempenhos dos alunos nessas medidas, considerando apenas o primeiro momento de avaliação (Tabela 3). Esse momento foi escolhido para conduzir as demais análises por dois motivos: primeiro, pela precedência no tempo de avaliação em relação à variável desfecho, o que caracteriza o estudo longitudinal; segundo, por ter sido coletado no início do ano letivo, apresentando, portanto, menor interferência escolar do que no segundo momento de avaliação, em que as crianças obtiveram melhores desempenhos nas tarefas avaliadas, visto que receberam o ensino escolar ao longo do ano letivo.
A partir dessa análise, observa-se que o desempenho em aritmética apresentou correlação significativa com todas as habilidades avaliadas, sendo a mais fraca delas com a capacidade do componente executivo central da memória de trabalho (r=0,21, p<0,05) e a mais forte com a transcodificação numérica (r=0,61, p<0,001). A tabela de correlações também auxilia na interpretação dos resultados da análise de regressão que será relatada posteriormente, pois, assim, é possível entender as variáveis que não foram consideradas no processo de modelagem como aquelas com baixo índice de correlação.
Tabela 3 Correlações entre as tarefas avaliadas no momento 1 e o desempenho aritmético
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 1. MT - CF | - | |||||||
| 2. MT - VE | -0,01 | - | ||||||
| 3. MT - EC | 0,29*** | 0,26** | - | |||||
| 4. CF | 0,26** | 0,21* | 0,39*** | - | ||||
| 5. CL | 0,12 | -0,03 | 0,27** | 0,37*** | - | |||
| 6. TN | 0,35*** | 0,24** | 0,28** | 0,34*** | 0,24** | - | ||
| 7. EM | 0,12 | 0,28** | 0,28** | 0,31*** | 0,26** | 0,43*** | - | |
| 8. RQ | 0,17 | 0,28** | 0,33*** | 0,34*** | 0,40*** | 0,52*** | 0,36*** | - |
| 9. DA | 0,23** | 0,30*** | 0,21* | 0,38*** | 0,23** | 0,61*** | 0,32*** | 0,50*** |
*p<0,05; **p<0,01; ***p<0,001
Legenda: 1. MT - CF: Componente Fonológico da Memória de Trabalho; 2. MT - VE: Componente Visuoespacial da Memória de Trabalho; 3. MT - EC: Componente Executivo Central da Memória de Trabalho; 4. CF: Consciência Fonêmica; 5. CL: Compreensão Leitora; 6. TN: Transcodificação Numérica; 7. EN: Estimativa Numérica; 8. RQ: Raciocínio Quantitativo; 9. DA: Desempenho Aritmético.
Fonte: dados da pesquisa.
Logo após, uma análise de regressão linear múltipla foi conduzida. Primeiramente, foram colocadas todas as variáveis ao mesmo tempo no modelo, considerando o desempenho aritmético como variável desfecho. Os resultados podem ser conferidos na Tabela 4. As variáveis ano escolar e idade não foram inseridas no modelo por não serem variáveis de interesse, visto que o objetivo está na identificação especificamente de habilidades cognitivas como preditoras. Também cabe dizer que foi gerada a variável Memória de Trabalho, calculada a partir da média da pontuação total (número de tentativas corretas) em cada um dos três componentes da memória de trabalho. Essa decisão foi tomada a partir dos índices de correlação de cada um desses componentes com o desempenho aritmético, os quais indicam uma correlação significativa, mas fraca, entre as variáveis (componente fonológico: r=0,23, p<0,01; componente visuoespacial: r=0,30, p<0,001; componente executivo central: r=0,21, p<0,001). Sabe-se que a memória de trabalho costuma ser uma medida importante para o desempenho matemático, por isso foi verificado se a variável composta pelos três componentes apresenta um maior índice de correlação com o desempenho aritmético. Então, a partir disso, observou-se que o índice de correlação aumentou para uma correlação moderada (r=0,37, p<0,001), o que poderia favorecer a inclusão dessa variável no modelo de regressão.
A partir desse primeiro modelo de regressão, o qual explicou 40,9% do desempenho aritmético (F(7,119)=13,46, p<0,001), as variáveis transcodificação numérica (β=0,31, p<0,001) e raciocínio quantitativo (β=0,28, p<0,05) foram as únicas indicadas como preditoras da variável desfecho.
Tabela 4 Modelo 1 de Regressão Linear Múltipla
| Desempenho Aritmético | |||
|---|---|---|---|
| Variáveis Preditoras | Β | IC | p-valor |
| Raven | -0,00 | -0,15 - 0,15 | 0,761 |
| Memória de Trabalho | 0,05 | -0,18 - 0,29 | 0,996 |
| Consciência Fonêmica | 0,09 | -0,00 - 0,19 | 0,062 |
| Compreensão Leitora | -0,04 | -0,27 - 0,20 | 0,762 |
| Estimativa Numérica | 0,18 | -12,18 - 12,55 | 0,977 |
| Transcodificação Numérica | 0,31 | 0,19 - 0,43 | <0,001 |
| Raciocínio Quantitativo | 0,28 | 0,04 - 0,51 | 0,021 |
R² ajustado = 0,409, F(7,119) = 13,46, p<0,001
Fonte: dados da pesquisa.
Em busca de um modelo mais adequado, foi realizado o método stepwise forward de seleção de variáveis, no qual cada variável é adicionada ao modelo separadamente, uma após a outra, considerando a ordem decrescente de influência. O próprio programa de análise estatística identifica as variáveis a serem adicionadas ao modelo final conforme sua influência e interrompe a modelagem quando nenhuma outra variável acrescentada apresenta um valor significativo. Portanto, foram consideradas seis variáveis como possíveis preditores: memória de trabalho, consciência fonêmica, compreensão leitora, transcodificação numérica, estimativa numérica e raciocínio quantitativo. Dessa forma, seguindo os passos do método de regressão escolhido, no modelo resultante, foram indicados três preditores para o desempenho aritmético. Primeiramente, foi adicionada a variável transcodificação numérica, em seguida, a variável raciocínio quantitativo e, por último, a variável consciência fonêmica, conforme é possível verificar na Tabela 5. Esse modelo explica 42,7% da variância do desempenho em aritmética (F(3,123)=32,27, p<0,001), as demais medidas não apresentaram efeito significativo para serem inseridas no modelo e auxiliar na explicação do desempenho aritmético.
Tabela 5 Modelo 2 e final da Regressão Linear Múltipla
| Desempenho Aritmético | |||||
|---|---|---|---|---|---|
| Variáveis Preditoras | R² parcial | ΔR² | Β | IC | p-valor |
| Transcodificação Numérica | 0,371 | 0,371 | 0,32 | 0,21 - 0,43 | <0,001 |
| Raciocínio Quantitativo | 0,410 | 0,039 | 0,27 | 0,06 - 0,48 | 0,003 |
| Consciência Fonêmica | 0,427 | 0,017 | 0,10 | 0,01 - 0,19 | 0,034 |
Modelo final: R² ajustado = 0,427, F(3,123)=32,27, p<0,001
Fonte: dados da pesquisa.
A partir desses resultados, verificamos que somente três variáveis apareceram como preditoras do desempenho aritmético e aquela com maior valor de influência foi a transcodificação numérica (β=0,32, p<0,001). Também é possível observar, de acordo com o modelo resultante, que essa mesma variável explica sozinha 37,1% da variância no desempenho aritmético, enquanto o raciocínio quantitativo contribui para um adicional de 3,9% e a consciência fonêmica acrescenta 1,7% na explicação da performance aritmética dos estudantes.
Para se ter uma ideia mais completa de como essas variáveis influenciam o desempenho aritmético, foi conduzida uma análise de mediação. Esse tipo de análise nos auxilia a identificar se uma variável intermediária também está envolvida na relação entre uma das variáveis preditoras e a variável resposta. Então, para isso, foi considerada como variável mediadora aquela com o maior valor de influência (coeficiente de regressão, β) no modelo indicado na Tabela 5, que corresponde à medida de transcodificação numérica (β=0,32, p<0,001). Acrescenta-se a isso o fato de que a influência das medidas de raciocínio quantitativo e de consciência fonêmica aumenta quando é controlado o efeito da transcodificação numérica, conforme pode ser verificado na Tabela 6.
Tabela 6 Modelo de Regressão sem a influência da variável transcodificação numérica no desfecho
| Desempenho Aritmético | |||
|---|---|---|---|
| Variáveis Preditoras | Β | IC | p-valor |
| Raciocínio Quantitativo | 0,54 | 0,05 - 0,25 | <0,001 |
| Consciência Fonêmica | 0,15 | 0,33 - 0,75 | 0,003 |
Modelo final: R² ajustado = 0,285, F(2,124) = 26,13, p<0,001 Fonte: dados da pesquisa.
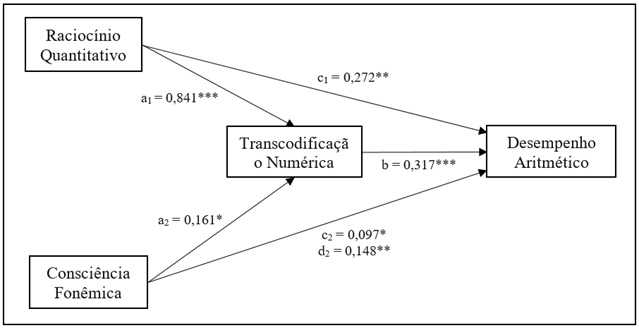
Na sequência, conduziu-se o modelo de análise de mediação, com o qual foram estimados os efeitos diretos (c1 e c2) e indiretos (a1b e a2b) para as variáveis preditoras raciocínio quantitativo e consciência fonêmica, respectivamente, por meio da transcodificação numérica, que foi considerada como variável intermediária. Vale dizer que os efeitos direto e indireto, respectivos de cada medida, quando somados, equivalem ao efeito total de cada uma das variáveis independentes, raciocínio quantitativo e consciência fonêmica, na variável desfecho, desempenho aritmético.
Como pode ser observado na Figura 2, ao analisar, primeiramente, a relação de mediação entre raciocínio quantitativo e desempenho aritmético por meio da transcodificação numérica, verifica-se que foram encontrados efeitos significativos direto (c1=0,272, SE=0,103, p<0,001) e indireto (a1b=0,267, SE=0,066, p<0,001) entre raciocínio quantitativo e aritmética. Isto indica que a transcodificação numérica é uma mediadora parcial da relação entre as outras duas medidas, já que uma parte do efeito total (d1=0,539, SE=0,103, p<0,01) também é explicada pelo efeito direto entre raciocínio quantitativo e aritmética. Para melhor explicar, embora um desempenho maior em raciocínio quantitativo esteja relacionado a um escore mais alto em aritmética, o efeito dessa relação é reduzido praticamente pela metade (49,5%) quando a habilidade de transcodificação numérica também é considerada.
Em seguida, também foi verificado o efeito de mediação inserindo-se a variável consciência fonêmica e mantendo-se a transcodificação numérica como variável mediadora. Os resultados sugerem efeitos direto (c2=0,097, SE=0,044, p<0,05) e indireto (a2b=0,051, SE=0,024, p<0,05) significativos. Portanto, a transcodificação numérica também explicou uma parte do efeito total (d2=0,148, SE=0,049, p<0,01) entre a relação da consciência fonêmica com a aritmética. Também cabe destacar que o efeito indireto da consciência fonêmica no desempenho aritmético é maior do que o efeito direto, ou seja, seu efeito na aritmética é mais relevante quando mediado pela transcodificação numérica.
Com isso, os resultados indicam que as variáveis raciocínio quantitativo e consciência fonêmica são explicativas do desempenho aritmético e apresentam efeitos mediados pela transcodificação numérica. Especialmente, os resultados sugerem um possível caminho para tentar elucidar a importância da consciência fonêmica para o desempenho aritmético. Assim, a análise deste estudo pode ser sintetizada em um modelo final de equações estruturais, a partir do qual pode-se concluir que os três preditores para o desempenho aritmético tiveram efeitos indiretos e diretos significativos, o que sustenta sua relevância para o desenvolvimento do raciocínio aritmético.
CONSIDERAÇÕES FINAIS
Neste artigo, apresenta-se uma pesquisa realizada com estudantes de 3º e 4º anos do ensino fundamental que objetivou identificar habilidades cognitivas como preditoras do desempenho aritmético, isto é, verificar a existência de uma relação causal entre algumas habilidades cognitivas, de domínio geral e específico, e a aritmética. A partir da literatura, algumas habilidades foram selecionadas para testar a hipótese de serem preditoras do desempenho aritmético em estudantes já alfabetizados. Das diferentes habilidades indicadas, este estudo focou nas habilidades de memória de trabalho, consciência fonêmica, compreensão leitora, transcodificação numérica, estimativa numérica e raciocínio quantitativo. Para atingir o objetivo, os estudantes foram avaliados em dois momentos ao longo do ano letivo, no início e no fim, porém, apenas o momento avaliado no início do ano letivo foi considerado para evitar o efeito da aprendizagem escolar durante esse período.
Os resultados principais deste estudo mostram que os preditores significativos do desempenho em aritmética foram a consciência fonêmica como habilidade de domínio geral e a transcodificação numérica e o raciocínio quantitativo, dentre as habilidades de domínio específico. Isso está de acordo com evidências anteriores que indicam a importância da identificação de números, incluindo a leitura e a escrita dos algarismos, para a aprendizagem aritmética. Além disso, a consciência fonêmica, que faz parte do processamento fonológico, também é destacada como uma preditora do desempenho matemático geral, especialmente em cálculos aritméticos (HECHT et al., 2001; SIMMONS; SINGLETON; HORNE, 2008). O modelo de regressão também confirma a hipótese de que o raciocínio quantitativo contribui significativamente para a habilidade aritmética. De fato, pode-se pensar que compreender a relação entre as quantidades e entre as operações é necessário para decidir qual procedimento seguir e aplicá-lo corretamente. Portanto, o raciocínio quantitativo é de importância anterior à aprendizagem dos algoritmos para resolver as operações matemáticas. Mais especificamente, a aritmética não é apenas sobre memorizar fatos básicos, mas também sobre entender as relações entre os números para resolver as tarefas matemáticas, o que supõe a compreensão do sistema numérico e das características específicas que o compõem (CHING; NUNES, 2017). Nesse sentido, é a partir da compreensão do número e do sistema numérico que o raciocínio quantitativo irá contribuir para o conhecimento aritmético. Com base nisso, também será possível o desenvolvimento de estratégias de solução mais eficazes, uma vez que o processo de cálculo requer uma compreensão mais detalhada do número e das relações entre as operações. Desse modo, a compreensão dessas relações irá formar a base para o desenvolvimento de estratégias de cálculo mais avançadas que, por sua vez, irão auxiliar as crianças a tornar problemas complexos em maneiras mais simples de resolver (CHING; NUNES, 2017).
A partir dos achados, também é válido destacar que a memória de trabalho não apareceu como preditora do desempenho aritmético de estudantes de 3° e 4° anos. Tal resultado diverge de pesquisas prévias que indicam essa habilidade como explicativa do desempenho matemático ao longo dos anos iniciais do ensino fundamental. Primeiramente, é pertinente levar em consideração a diversidade de tarefas existentes para avaliar a capacidade de memória de trabalho, o que pode ocasionar em resultados divergentes entre as pesquisas devido à escolha da tarefa utilizada. No entanto, ao tentar elucidar esse resultado não significativo da influência da memória de trabalho no desempenho aritmético, algumas razões são levantadas. Uma explicação possível é de que uma maior demanda da memória de trabalho está vinculada à complexidade da tarefa matemática avaliada. Nesse sentido, o teste utilizado neste estudo para avaliar o desempenho aritmético dos estudantes solicitava apenas a resolução de cálculos com operações, as quais vários alunos já estavam habituados a resolver em sala de aula, por isso, a tarefa pode não ter demandado tanto a memória de trabalho dos estudantes. Também é importante salientar que os alunos deixaram em branco cálculos com operações ainda não aprendidas na escola. Esse fato pode ser devido à forma como a matemática é ensinada nas escolas, a qual prioriza o entendimento de uma sequência de passos a ser seguida para resolver determinado algoritmo e, muitas vezes, apenas uma forma de se chegar ao resultado. Então, quando o aluno se depara com um algoritmo cujo procedimento de resolução desconhece, acaba desistindo de pensar em uma estratégia para resolvê-lo, não incluindo, assim, maior demanda da memória de trabalho para organizar as informações e elaborar uma estratégia de solução. Outra explicação possível é a de que conforme o amadurecimento cognitivo do aluno, isto é, o desenvolvimento do conhecimento, e o avanço nos anos escolares, menos demanda da memória de trabalho é exigida para procedimentos já aprendidos.
Coloca-se como possibilidade, também, que o fato das demais variáveis não aparecerem como preditoras do desempenho aritmético se deve à tarefa considerada para avaliação do desfecho, a qual exigiu pouca leitura e elaboração de estratégias de resolução. Apesar disso, as habilidades de compreensão leitora e estimativa numérica apresentaram correlação, mesmo que em um nível fraco, com o desempenho aritmético, indicando que são habilidades importantes para essa aprendizagem, embora não exerçam influência de explicação para tal desempenho. No entanto, a proposta deste estudo foi avaliar a predição a partir de um teste padronizado, o qual mede somente a habilidade em cálculos aritméticos. Assim, outras tarefas que avaliem conhecimentos matemáticos mais abrangentes podem ser necessárias para identificar a predição dessas habilidades em alunos já alfabetizados no contexto brasileiro.
Ao analisar com mais detalhes os achados deste estudo, um ponto que merece atenção é o fato de a transcodificação numérica ter sido a medida com mais alto valor de explicação do desempenho aritmético. Percebe-se, pelas análises, que, quando ela é retirada do modelo, o valor de predição das demais variáveis aumenta. Assim, observa-se que a transcodificação numérica possa estar compartilhando esse efeito explicativo. Por isso, uma análise de mediação foi conduzida, confirmando que ela é uma medida intermediária do efeito do raciocínio quantitativo e da consciência fonêmica para o desempenho em aritmética.
Esse fato também elucida o motivo de a consciência fonêmica, ou, mais abrangentemente, a consciência fonológica, estar envolvida na aritmética. Estudos indicam essa habilidade cognitiva como importante para o desempenho em matemática (HECHT et al., 2001; SIMMONS; SINGLETON; HORNE, 2008; LOPES-SILVA et al., 2014; 2016), mas pouco ainda é discutido sobre porque essa habilidade estabelece uma relação causal com a aritmética. Portanto, os achados deste estudo auxiliam nesse esclarecimento ao mostrar que a relação entre consciência fonêmica e aritmética é mais explicativa quando mediada pela transcodificação numérica. Isso pode ser explicado pelo fato de a consciência fonêmica envolver diferentes recursos cognitivos, mais do que apenas ser responsável pela qualidade da codificação fonológica (SIMMONS; SINGLETON; HORNE, 2008). Essa habilidade também envolve a retenção da informação fonológica na memória de curto prazo, ao mesmo tempo em que essa informação é processada por meio de recursos do executivo central (HECHT et al., 2001; SIMMONS; SINGLETON; HORNE, 2008). Isso, em parte, também é necessário no momento de representar números, pois a identificação de símbolos multidígitos explicitamente requer a transcodificação do número falado, na forma verbal, para o formato escrito em algarismos (HABERMANN et al., 2020). Nesse sentido, as evidências aqui reportadas convergem com as de estudos anteriores que também indicam a transcodificação numérica e a consciência fonêmica como preditoras do desempenho aritmético. Ademais, os resultados descritos vão além de estudos prévios, indicando a transcodificação numérica como mediadora da relação causal entre consciência fonêmica e aritmética.
Algumas limitações devem ser levadas em consideração. Os dados foram coletados em um mesmo ano letivo, o que impediu investigar se essas habilidades estão relacionadas também a mudanças individuais na aprendizagem aritmética dos estudantes ao longo do tempo e se essas habilidades permanecem preditoras em anos escolares posteriores. Todavia, este foi um estudo exploratório e, portanto, esses resultados podem ser confirmados por meio de pesquisas futuras, preferencialmente longitudinais, que possam acompanhar o desempenho aritmético dos estudantes ao longo dos anos escolares e verificar as habilidades cognitivas que permanecem com influência nessa aprendizagem. Além disso, é importante levar em consideração o desempenho matemático de forma mais abrangente, avaliando o conhecimento dos estudantes em outros domínios como resolução de problemas, geometria, álgebra etc., visto que a tarefa avaliada interfere nas habilidades cognitivas que serão demandadas para sua resolução.
Assim, conclui-se que habilidades básicas de identificação de números e sua representação por meio de algarismos são fatores determinantes para a melhor aprendizagem aritmética, visto que saber escrever um número requer o conhecimento do sistema numérico. Outrossim, é importante compreender a relação entre as quantidades e entre as operações para entender o procedimento a seguir em um algoritmo. Apostar no desenvolvimento dessas habilidades, desde o início da escolarização, possibilita ganhos significativos no desempenho aritmético em anos posteriores. Neste estudo, habilidades básicas como essas mostraram-se importantes também na fase final dos anos iniciais do ensino fundamental, o que possibilita inferir que desenvolver tais habilidades desde o primeiro ano escolar permite, também, a prevenção de dificuldades matemáticas que eventualmente possam surgir.
Quando se pensa sobre o ensino e a aprendizagem da matemática na escola, uma ideia comum entre os professores e profissionais da educação é de que primeiro os alunos precisam ser ensinados sobre como resolver formalmente cálculos aritméticos para depois lidarem com vários tipos de problemas matemáticos. Por isso, os alunos são ensinados a raciocinar sobre as relações após aprenderem a resolver algoritmos. Porém, os resultados mostraram que o raciocínio quantitativo, ou seja, a compreensão das relações entre as quantidades, é causa de um melhor desempenho em aritmética. Assim, a sugestão é evitar a predominância da aprendizagem por procedimentos, as quais muitas vezes são apresentadas sem conexão com situações do cotidiano, e encorajar as crianças a discutirem os problemas propostos e as relações envolvidas entre as quantidades. Somado a isso, propor tarefas que desenvolvam a compreensão do sistema numérico e o reconhecimento dos números nos seus formatos arábico e verbal.
Em resumo, as evidências aqui relatadas apontam para a importância de habilidades numéricas no desenvolvimento da compreensão aritmética dos estudantes brasileiros. Além disso, este estudo contribui para uma compreensão mais ampla dos processos cognitivos envolvidos na aprendizagem aritmética. Destaca-se, a partir disso, que a compreensão do sistema numérico, bem como a compreensão conceitual da aritmética são fundamentais para o desenvolvimento da aritmética procedimental.










 texto en
texto en