1 Introdução
O Índice de Desenvolvimento da Educação Básica (Ideb) é hoje o único indicador nacional de qualidade escolar desenhado como tal, tendo em vista que o “Enem por escola” (a média da escola no Exame Nacional do Ensino Médio) apresenta diversas limitações metodológicas (TRAVITZKI, 2013). O Ideb leva em conta o Trade Off1 entre proficiência e taxa de aprovação no contexto das políticas de prestação de contas (accountability) (FERNANDES, 2007). Ou seja, o Ideb inclui tanto provas quanto taxa de aprovação porque a ideia é evitar que as escolas promovam exclusão de certos alunos para garantir boas notas nas provas. A criação do Ideb foi possível devido a avanços anteriores na coleta de dados educacionais no Brasil, com a consolidação do Sistema de Avaliação da Educação Básica (Saeb) e do Censo Escolar2.
O criador da metodologia do Ideb, Reynaldo Fernandes, considera que o indicador contribui para a construção de um modelo brasileiro de Educação Básica ancorado em três princípios: 1) descentralização na oferta dos serviços educacionais; 2) critérios de financiamento definidos pela Federação; 3) avaliação centralizada (FERNANDES, 2016). Para Francisco Soares e Flávia Xavier, “o Ideb, sem questionar a necessidade de novos recursos e expansões, coloca o aprendizado e a regularidade na trajetória escolar dos alunos como elementos essenciais de um sistema educacional” (SOARES; XAVIER, 2013, p. 904).
Iniciativas inspiradas no Saeb e no Ideb foram desenvolvidas em muitos estados, contribuindo para o desenvolvimento das avaliações externas e seus efeitos nas formas de gestão e na cultura escolar (BROOKE; CUNHA; FALEIROS, 2011). Segundo Bernardete Gatti, as avaliações externas de escolas e redes de ensino foram inicialmente muito criticadas no Brasil, mas têm sido progressivamente consolidadas dentro de uma cultura fundada na ideia de accountability. Para a autora, as avaliações deveriam ser vistas como uma oportunidade para mudanças e aprimoramentos, não como formas de punição (GATTI, 2009).
Para Luana Almeida e colegas (ALMEIDA; DALBEN; FREITAS, 2013), a avaliação externa é importante para ajudar na tomada de decisões, e é necessário
[...] repensar seu escopo e aliá-la a uma autoavaliação institucional e ao diagnóstico das fragilidades […] Para além da divulgação dos dados, da responsabilização e da criação de um ethos competitivo entre as escolas, a avaliação externa precisa integrar medidas de operacionalização, ou seja, ações políticas de intervenção no funcionamento das escolas e na gestão do sistema (ALMEIDA; DALBEN; FREITAS, 2013, p. 479).
Além disso, há outro aspecto importante relacionado às avaliações externas que raramente é trazido à tona: a incerteza associada a cada indicador. Este aspecto é importante porque delimita as possibilidades de interpretação das informações produzidas pela avaliação externa. Por exemplo: para saber se uma escola melhorou seu Ideb de um ano para outro, basta conferir se houve um aumento no indicador? Ou existe uma “margem de erro” (intervalo de confiança) para o Ideb? Esta questão técnica aparentemente pequena tem consequências importantes para a interpretação e, portanto, para o uso do Ideb. Se uma escola piorou, porém dentro da “margem de erro”, significa, na verdade, que não há evidências confiáveis de que ela piorou.
Na Inglaterra, país com grande tradição na avaliação de escolas, o governo utiliza modelos de valor adicionados com dados contextuais para estimar a eficácia escolar (LECKIE; GOLDSTEIN, 2011). Em tais modelos, busca-se avaliar o quanto cada aluno melhorou, comparando resultados de provas do mesmo aluno em diferentes séries, incluindo também informações contextuais, como nível socioeconômico. A vantagem de tais modelos é que representam melhor o trabalho realizado pela escola do que as médias simples, dado que estas são predominantemente influenciadas pelos insumos (GORARD, 2010). Tal limitação é conhecida no Brasil. As médias do Enem por escola, por exemplo, podem ser predominantemente explicadas (em torno de 80% da variância) por fatores que não dependem do trabalho realizado pelos professores e gestores, mas sim de condições externas à escola (TRAVITZKI; CALERO; BOTO, 2014).
Os rankings escolares na Inglaterra são divulgados publicamente com diversos indicadores, em plataforma amigável e prática3. Além disso, há um intervalo de confiança para cada escore4 (LECKIE; GOLDSTEIN, 2011). Uma das preocupações por lá, ao menos para George Leckie e Harvey Goldstein, é tornar essa incerteza do indicador mais compreensível para os cidadãos. Outra preocupação dos autores, investigada em estudo anterior (LECKIE; GOLDSTEIN, 2009), é que cada série é diferente da outra, mas os pais só podem escolher a escola dos filhos com base em informações de outras séries. Pode parecer um detalhe técnico, mas os autores verificaram esse aspecto nos dados das escolas inglesas e concluíram que, levando em conta a incerteza dos modelos e a variação entre as séries, os rankings escolares são pouco úteis para os pais escolherem a escola dos filhos, salvo em um punhado de casos.
Para Gorard (2010), as incertezas e efeitos indesejáveis dos rankings escolares (mesmo com modelo de valor adicionado) levam à necessidade de repensar o que queremos dizer com eficácia escolar e como queremos avaliá-la. Alguns questionamentos são importantes nesse caminho: “precisamos decidir se estamos felizes com um efeito escola de soma zero5, se uma escola é realmente uma unidade de análise adequada e como vamos estimar a propagação máxima de erros” (GORARD, 2010, p. 760, tradução nossa).
Neste artigo, em consonância com tais questionamentos, propomos um método para o cálculo do intervalo de confiança do Ideb, com base nas leis de propagação da incerteza (FARRANCE; FRENKEL, 2012). Inicialmente há uma breve revisão da bibliografia pertinente ao Ideb e à sua incerteza. Discute-se então as possibilidades de estimação da incerteza do Ideb. A seguir, há uma descrição do método aqui proposto, em uma linguagem mais detalhada e especializada em Matemática e estatística. Ao final, aplicamos o método aos dados disponibilizados publicamente pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) e analisamos algumas decorrências da incerteza, comparando o Ideb de vários anos em dois níveis de análise (escola e estado).
O Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) não divulga um intervalo de confiança ou outro indicador de incerteza associado ao Ideb das escolas, estados e municípios. Ao que parece, o Inep não possui um método para calcular esta incerteza, pois quando foi solicitado via Lei de Acesso à Informação (LAI), o Instituto só forneceu a média e o erro padrão das provas de Matemática e de Português por escola6. O único método encontrado na literatura para esta finalidade provém de uma tese da Universidade de São Paulo (MELO, 2017). Neste artigo, buscamos superar algumas limitações do método proposto por Melo, com o objetivo de contribuir para o aprimoramento da avaliação escolar no Brasil, especialmente no que se refere ao uso dos indicadores disponíveis.
2 O Ideb e seus objetivos
O Ideb foi criado em 2007, juntamente com a Prova Brasil, com o objetivo de contribuir para o estabelecimento de um padrão de qualidade educacional no país, integrando indicadores de desempenho e indicadores de fluxo. O pressuposto é que existe um Trade Off entre os dois tipos de indicador, e que ambos os aspectos são importantes para a qualidade da Educação. Não é desejável, por exemplo, que as escolas melhorem o desempenho das séries finais de cada etapa, aumentando as taxas de reprovação e evasão.
O indicador proposto possui a vantagem de ser de fácil compreensão, simples de calcular, aplicável às escolas e explícito em relação à “taxa de troca” entre probabilidade de aprovação e proficiência dos estudantes. Ou seja, o indicador torna claro o quanto se está disposto a perder na pontuação média do teste padronizado para se obter determinado aumento na taxa média de aprovação (FERNANDES, 2007, p. 16).
O cálculo do Ideb pode ser descrito como o produto do indicador de desempenho com o indicador de fluxo, seja no nível da escola, do município ou do estado. O indicador de desempenho é a média das provas de Matemática e de Português, padronizada por um número de 0 a 10. O indicador de fluxo é a média das taxas de aprovação (de 0 a 1), levando em conta todas as séries da etapa de ensino:
Para Francisco Soares e Flávia Xavier, “a criação do Ideb significou uma grande e positiva mudança no debate educacional brasileiro” (SOARES; XAVIER, 2013, p. 915). O que não significa o fim do debate. Pelo contrário, os autores consideram que talvez o mais importante seja “transformar o Ideb em um primeiro passo para o processo de reflexão interna nas escolas, na busca de melhores e mais efetivas práticas pedagógicas” (SOARES; XAVIER, 2013, p. 921). Os avanços do Ideb se referem tanto à inclusão de indicadores de resultado (não apenas de indicadores de processo) quanto à preocupação em se contrapor à chamada “pedagogia da repetência”, tão característica e proeminente no Brasil.
3 Limitações e críticas ao Ideb
Por outro lado, ainda segundo Soares e Xavier (2013), há algumas questões relacionadas ao cálculo do Ideb e sua interpretação. Em relação à interpretação, por exemplo, há certa dificuldade de entendimento do significado do número do Ideb. Isto porque o indicador é entendido em uma escala de 0 a 10, em que as notas abaixo de 5 são normalmente interpretadas como ruins7. No entanto, o Ideb médio é 4,5. Além disso, as notas das escolas se concentram no meio dessa escala e, portanto, há uma grande diferença entre um Ideb de 4,5 e outro de 6,0. Um segundo ponto destacado pelos autores é que, embora a Prova Brasil seja supostamente censitária8, na prática isso não se verifica. Os alunos incluídos são aqueles que estão presentes no dia de prova, sendo que o limite mínimo para divulgação do Ideb é 50% dos alunos registrados no Censo Escolar. Em 2011, exemplificam, 22% dos testes do 9o ano voltaram sem respostas. Um terceiro ponto seria a forma de padronizar as proficiências, o que acaba dando uma importância maior para Matemática do que Português, podendo levar à maior valorização de uma em detrimento da outra. Um quarto ponto destacado é a conhecida influência do nível socioeconômico nas médias de provas. Uma quinta crítica relevante seria que, como o Ideb é uma média, implicitamente ele aceita que “o bom desempenho de um aluno compensa o mau desempenho de outro” (SOARES; XAVIER, 2013, p. 916), abrindo a possibilidade de exclusão educacional. Por fim, uma limitação apontada por estes e diversos outros autores se refere ao número restrito de matérias escolares avaliadas no Ideb: apenas duas (Matemática e Português).
Outros pontos críticos do Ideb e, de um modo geral, do uso das avaliações padronizadas em larga escala, são apontados em estudo recente (FIGUEIREDO et al., 2018). Os autores encontraram, ainda, certas incoerências internas nos resultados do Ideb 2015, como a baixa correlação, em alguns estados, entre o Ideb das diferentes etapas da Educação Básica, e também entre o Ideb e o Enem. Outra incoerência interna encontrada foi a ausência de correlação significativa, no nível dos estados, entre a nota padronizada do Ideb e o índice de rendimento.
Em virtude de suas limitações, o Ideb pode ser visto como um, mas não o único indicador para avaliação do trabalho desenvolvido pelas escolas (ALMEIDA; DALBEN; FREITAS, 2013). Os autores destacam ainda que, embora as avaliações externas tenham incontestável importância, a forma pela qual o Ideb é calculado e divulgado pode ter como consequência, por exemplo, “a desresponsabilização, de forma branda, do sistema educativo e social mais amplo sobre tais resultados” (ALMEIDA; DALBEN; FREITAS, 2013, p. 1169).
Há também limitações inerentes à avaliação externa de modo geral. Para Chirinéa e Brandão (2015), a avaliação externa é importante por fornecer informações para a tomada de decisão, porém
é preciso repensar seu escopo e aliá-la a uma autoavaliação institucional e ao diagnóstico das fragilidades, com a perspectiva de articulação entre as esferas macro, meso e micro do processo de avaliação […] É preciso integrar os resultados do desempenho escolar com os contextos ou dinâmicas intra e extraescolares, na medida em que esta integração dará condições para a gestão escolar traçar suas próprias metas e estratégias (CHIRINÉA; BRANDÃO, 2015, p. 479)
Por fim, há um tipo de crítica que não costuma ser feito com frequência: em que medida o número de cada Ideb é preciso e confiável? Como saber se este número não tem uma variação aleatória relevante? Em outras palavras, qual é a incerteza associada a este indicador?
O único estudo encontrado sobre o tema, além da tese de Melo (2017), é de Pontes e Soares (2017). É analisada a volatilidade do Ideb, que pode ser gerada por uma infinidade de fatores aleatórios, como um barulho intenso no dia de prova ou uma relação extremamente cordial entre professor e alunos. Levando em conta a volatilidade estimada a partir de dados longitudinais, os autores aconselham que, para a tomada de decisões, sejam analisados os resultados de uma escola ao longo de certo tempo. Foi constatada uma grande flutuação nas notas médias das escolas, com considerável impacto sobre o cumprimento das metas estabelecidas para cada uma.
4 Transparência e incerteza
Um dos pressupostos para a implementação eficaz das políticas de accountability, entre as quais se inclui o Ideb, é a transparência do sistema educacional. Indicadores bem construídos e válidos para todo o sistema certamente contribuem para a transparência, permitindo a comparabilidade, a visão geral, a identificação de particularidades. A existência de um único indicador deste tipo, por outro lado, é preocupante no campo da Educação, além de torná-lo ainda mais suscetível à chamada Lei de Campbell9 e à sobrevalorização.
Em que sentido o Ideb pode ser sobrevalorizado? Suponhamos uma escola que tenha melhorado seu Ideb em 0,3 pontos comparando 2013 e 2015. Será que ela tem de fato algo a comemorar? Se fosse o inverso, teria o que lamentar? Tal questionamento não tem como objetivo a desresponsabilização ou desmobilização dos educadores e gestores, mas sim a busca pelo uso adequado de cada instrumento de medida. O mapeamento da incerteza associada a cada indicador torna o sistema ainda mais transparente e eficaz.
Neste artigo, buscou-se realizar tal mapeamento no Ideb. Cabe notar que o termo “erro” é aqui utilizado como sinônimo de “incerteza”, sendo relacionado à confiabilidade de cada informação disponível. Em termos operacionais, o erro pode referir-se a uma média10, informando o quanto podemos confiar nela, ou seja, o quanto a variável em questão está dispersa e, portanto, longe da média. De forma geral, o erro é a diferença entre o valor previsto e o valor observado.
A incerteza de uma medida se refere ao “intervalo do valor medido dentro do qual é provável que se encontre, no nível declarado de confiança, o valor verdadeiro ou o valor verdadeiro convencional da quantidade medida” (GUPTA, 2012, p. 20, tradução nossa). Em tal definição, a incerteza assume a forma de um intervalo de confiança, embora possa ser representada também pelo erro padrão ou desvio padrão, dependendo do estudo.
Quando é possível realizar várias medidas da mesma quantidade, a incerteza da média vai diminuindo, conforme o número de medidas vai aumentado. Em distribuições normais, isso significa dividir a variância pelo número de observações e, depois, calcular a raiz quadrada. Obtém-se, com isso, o erro padrão da média, que tende a ser menor em amostras maiores.
No entanto, quando há duas ou mais quantidades diferentes em uma fórmula, gerando um único indicador, a incerteza de cada quantidade se propaga para o indicador. Em outras palavras, dada uma certa função, a incerteza associada a cada input (entrada) se propagará, segundo princípios específicos, para o output (saída) (FARRANCE; FRENKEL, 2012). Esses princípios são as leis de propagação da incerteza.
Em termos conceituais e operacionais, no caso do Ideb pode-se conceber ao menos dois tipos de incerteza: 1) relacionada à agregação das notas individuais em médias por escola; 2) relacionada à imprecisão do instrumento de medida, no caso, as provas.
5 Por que estimar a incerteza do Ideb?
Uma crítica que poderia ser feita ao objetivo central deste trabalho é que o Ideb das escolas, por ser censitário, não apresentaria um erro associado à agregação na média. De fato, quando conhecemos toda a população (os alunos da escola), não é necessário calcular o erro padrão para saber se duas médias são diferentes. No entanto, há dois pontos a serem considerados.
Em primeiro lugar, embora a Prova Brasil seja planejada como censitária, na prática isso não se realiza completamente. A edição de 2015, por exemplo, apresentou 23% de dados ausentes, ou seja, alunos que estavam no Censo Escolar, mas não fizeram as provas. Em 2011 não foi diferente. Há, portanto, alguma incerteza derivada dessa falta de informação.
Em segundo lugar, é necessário levar em conta os diferentes usos do Ideb para que se possa definir com clareza qual é a população e se, de fato, a conhecemos por completo. Por exemplo, se o objetivo for comparar os alunos do 9o ano das diferentes escolas em 2015, poderíamos dizer que os dados são de fato censitários – ignorando os 23% de dados faltantes. Isso porque conheceríamos toda a população e não apenas uma amostra dela. Nesse caso, não faria muito sentido calcular o erro padrão da média. Por outro lado, nossas conclusões estariam restritas a esta população: alunos do 9o ano de 2015. No entanto, se o objetivo for verificar se uma escola melhorou ou piorou desde 2013, nossa população já não se refere mais aos alunos do 9o ano de 2015. Da mesma forma, se o objetivo for usar o Ideb como indicador de qualidade de toda a etapa de ensino (não apenas do 9o ano), novamente a população total extrapola os dados coletados.
Em suma, quando se pretende interpretar o Ideb como um indicador de qualidade da escola em certa etapa de ensino – e não apenas dos alunos da última série de cada etapa em um certo ano – é necessário considerar a incerteza associada a esse indicador. Vale destacar que o documento de referência na criação do Ideb já apontava a importância de não se restringir às médias por escola: “vários aprimoramentos são possíveis, como, por exemplo, incluir a dispersão das notas, ao invés de se considerar apenas o desempenho médio” (FERNANDES, 2007, p. 16). Tal dispersão das notas, supomos, pode referir-se ao desvio padrão, ao erro padrão ou mesmo à separação por quantis ou níveis de proficiência.
6 Como estimar a incerteza do Ideb?
Em primeiro lugar, é preciso definir as possíveis fontes de incerteza. Dentre elas, destacam-se:
erro de medida na Prova Brasil (o quanto a nota do aluno reflete sua proficiência?);
erro de medida no Censo Escolar (o quanto os dados coletados correspondem à realidade?);
erro da média das notas por escola (o quanto a média por escola representa seus alunos?);
erro da média das taxas de aprovação (o quanto a taxa média de aprovação na etapa de ensino representa as taxas nas diferentes séries?);
alunos ausentes (quanto se pode deduzir deles a partir dos alunos presentes?).
O método aqui proposto inclui duas fontes de incerteza: (a) e (c).
O único método existente até o momento (MELO, 2017) inclui apenas a fonte (a), embora não se trate, na prática, das mesmas informações utilizadas aqui. O método de Melo se fundamenta na Teoria da Resposta ao Item e utiliza os parâmetros dos itens (dados não disponíveis publicamente) e os resultados por aluno (públicos) na Prova Brasil. Essencialmente, os erros de medida são calculados a partir da nota do aluno e da função de informação do teste11. Embora engenhoso, o método parte de uma população genérica de alunos, deixando de levar em conta as particularidades de cada um, expressas em seu padrão de respostas. Em outras palavras, no método de Melo dois alunos com a mesma nota sempre recebem o mesmo erro de medida. Além disso, os microdados já fornecem erros de medida para as notas de cada aluno, que se supõe mais precisos do que os estimados de forma genérica. Outra limitação do método é não levar em conta os princípios de propagação da incerteza.
Com efeito, buscando superar algumas limitações do método anterior, o método aqui proposto apresenta as seguintes características:
7 Métodos
Foram calculados dois tipos de erro, ou incerteza, para o Ideb. Em primeiro lugar, calculamos o Erro Padrão da média (EP1), que se baseia em informações sobre dispersão, ou seja, na diferença entre as notas dos alunos de uma escola. Quanto mais diferenças ocorrerem nas notas dos alunos de uma escola, maior é o intervalo de confiança da média por escola. Em segundo lugar, calculamos o erro de medida (EP2) subjacente a essa média, com base no erro de medida individual, disponível nos microdados. Para tanto, foram utilizadas técnicas estatísticas básicas (como o cálculo do erro padrão e intervalo de confiança) e também leis de propagação da incerteza (como o cálculo do erro propagado de duas médias de diferentes grandezas) (FARRANCE; FRENKEL, 2012; GUPTA, 2012).
A Figura 1 proporciona uma visão geral do método aqui proposto. As fontes de informação são os microdados do Saeb (nota e erro padrão da nota, de cada aluno em cada prova – Matemática e Português) e o Ideb de escolas e estados publicado bianualmente (Inep, 2018), de onde coletamos o Índice de Rendimento e a série histórica do Ideb.
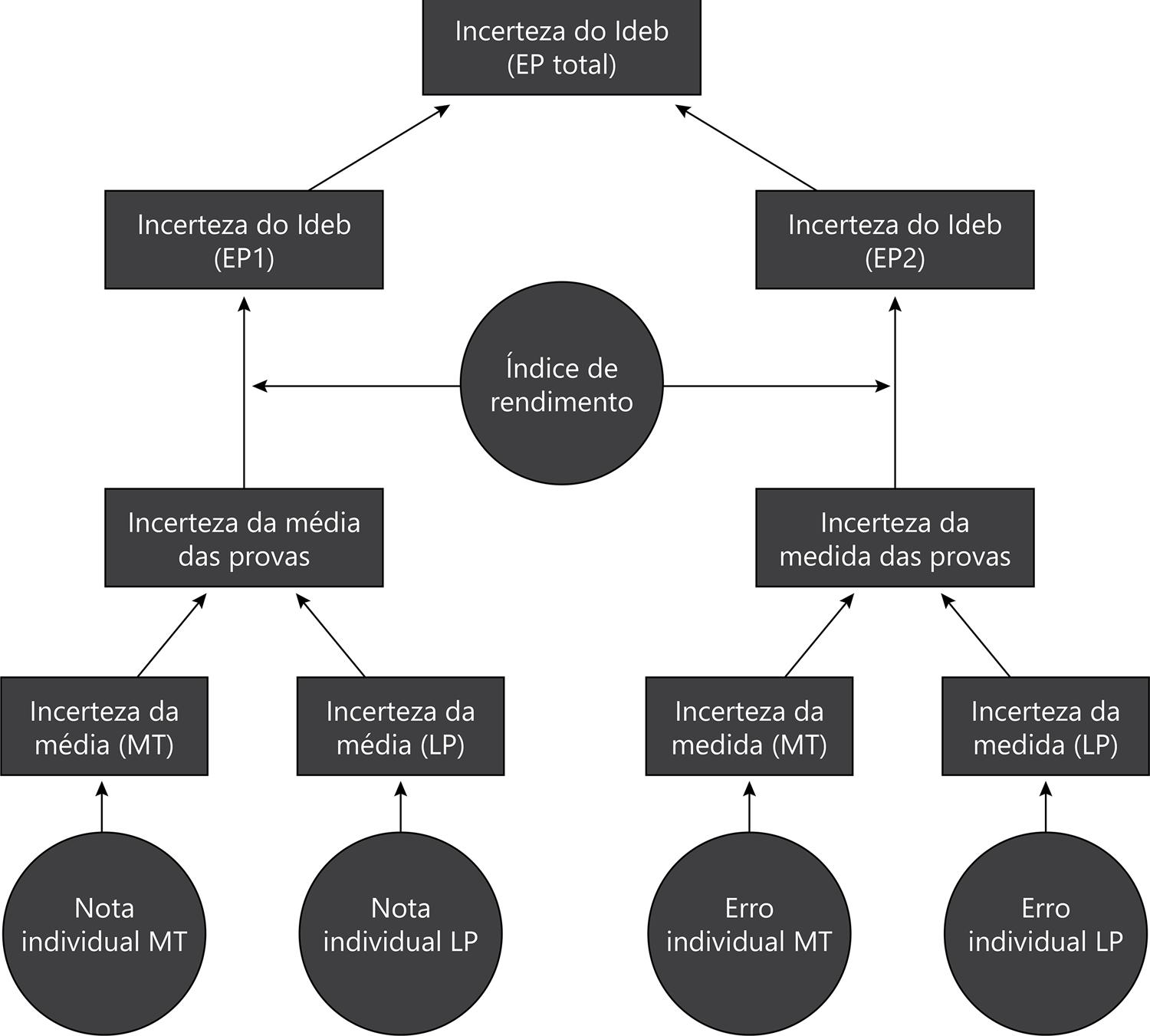
Os círculos representam dados públicos provenientes do Inep, enquanto os retângulos representam valores calculados neste trabalho.
Fonte: Elaboração própria (2019)
Figura 1 – Visão geral do método proposto
A seguir descrevemos detalhadamente cada etapa.
7.1 Cálculo do erro da média (EP1)
As incertezas se comportam de forma diferente da que ocorre com as médias. Por esse motivo, quando se calcula uma média de dois números que representam médias (como no Ideb, quando se calcula a média das médias em Português e Matemática), é necessária uma função específica para estimar a incerteza da média resultante. Esta função, no caso de distribuições normais, é conhecida como lei geral de propagação da incerteza (FARRANCE; FRENKEL, 2012, p. 60). A equação 1 é uma simplificação desta lei, adaptada à metodologia do Ideb.
σT: desvio padrão da média das duas médias
σM, σP: desvio padrão das notas de Matemática e Português
covMP: covariância entre as notas de Matemática e Português
Em seguida, é necessário padronizar a escala das provas de acordo com a metodologia do Ideb. Para isso, inicialmente foi calculado o Coeficiente de Padronização (CP) a partir das notas máxima e mínima das escolas (equação 2).
CP: coeficiente de padronização
notamax, notamin: notas máxima e mínima na prova, segundo documentação do Ideb
No caso do 9o ano, a nota máxima foi 400, e a mínima, 100 para as duas provas (FERNANDES, 2007), resultando em CP = 30. Este número foi então substituído na equação 3, juntamente com o resultado da equação 1, para adequar a incerteza calculada na escala do Ideb.
σTP: desvio padrão das duas médias padronizadas
Por fim, foi utilizada a equação (4), que ignora a incerteza do IR, mas o inclui no cálculo da incerteza do Ideb. Na prática, a inclusão do IR diminui um pouco a incerteza do Ideb, dado que o IR é sempre menor do que 1. Além disso, a equação (4) transforma o desvio padrão das provas em erro padrão, permitindo o cálculo do intervalo de confiança do Ideb.
EP1: erro padrão da média do Ideb por escola
n: número de alunos da escola que fizeram as provas
IR: Índice de Rendimento da etapa de ensino
7.2 Cálculo do erro de medida (EP2) e erro total
O método neste segundo caso se assemelha bastante ao anterior. A principal diferença está no início, ou seja, na definição do tipo de incerteza proveniente das provas. Neste caso, trata-se da incerteza associada à nota recebida por cada aluno12. A equação 5 descreve a agregação deste erro de medida individual (σi) no nível da escola.
σM, σP: médias dos erros de medida das provas (de Matemática ou Português) no nível da escola
σi: erro de medida13 das provas (de Matemática ou Português) para o aluno i
n: número de alunos na escola
Para calcular o erro de medida do Ideb, primeiro utilizamos a equação (5) para calcular o desvio padrão de cada escola em cada uma das provas. Os resultados foram, então, incluídos na equação (1), mas não foi incluída a covariância nesse caso. Em seguida, utilizamos novamente as equações (3) e (4) para calcular o erro padrão do Ideb levando em conta a incerteza do instrumento de medida (EP2).
O erro total do Ideb da escola, por sua vez, consiste na soma dos dois tipos de erro (equação 6). Uma limitação deste método é desconsiderar possíveis interações entre os dois tipos de erro.
7.3 Descrição dos dados e erros estimados
O método foi aplicado ao Ideb 2015, utilizando os microdados da Prova Brasil e Censo Escolar – séries finais do Ensino Fundamental. Foram analisados 2.381.722 alunos de 29.313 escolas de todos os estados. Os dois tipos de incerteza estimados (na forma de erro padrão) são descritos na Tabela 1, juntamente com o Ideb e seus componentes desagregados. Nota-se que o erro da média (EP1) foi maior do que o erro de medida (EP2). Nota-se também que o IR médio das escolas (relativo às taxas de aprovação) é de 85%.
Tabela 1 – Descrição do Ideb 2015 e dos erros estimados
| Indicador | Média | Desvio Padrão | Mínimo | Máximo | Número de escolas |
|---|---|---|---|---|---|
| IR | 0,85 | 0,11 | 0,18 | 1,00 | 29.304 |
| Provas | 4,89 | 0,64 | 2,45 | 8,57 | 29.313 |
| Ideb | 4,16 | 0,87 | 0,90 | 8,50 | 29.304 |
| EP1 | 0,15 | 0,05 | 0,03 | 0,48 | 29.304 |
| EP2 | 0,07 | 0,02 | 0,01 | 0,16 | 29.304 |
| EPtotal | 0,22 | 0,07 | 0,04 | 0,61 | 29.304 |
Fonte: Elaboração própria (2019) a partir de dados do Inep (anos finais do Ensino Fundamental de 2015)
7.4 Incerteza do Ideb em 2015
Quando duas escolas têm Ideb diferente, ele é, de fato, diferente, levando em conta as incertezas? Para responder a esta pergunta, usamos o erro total estimado (EPtotal) para criar uma “margem de erro” (intervalo de confiança, 95%) para cada escola. A Figura 2 sintetiza os resultados, mostrando as médias (em preto) e intervalos de confiança destas médias (em cinza).
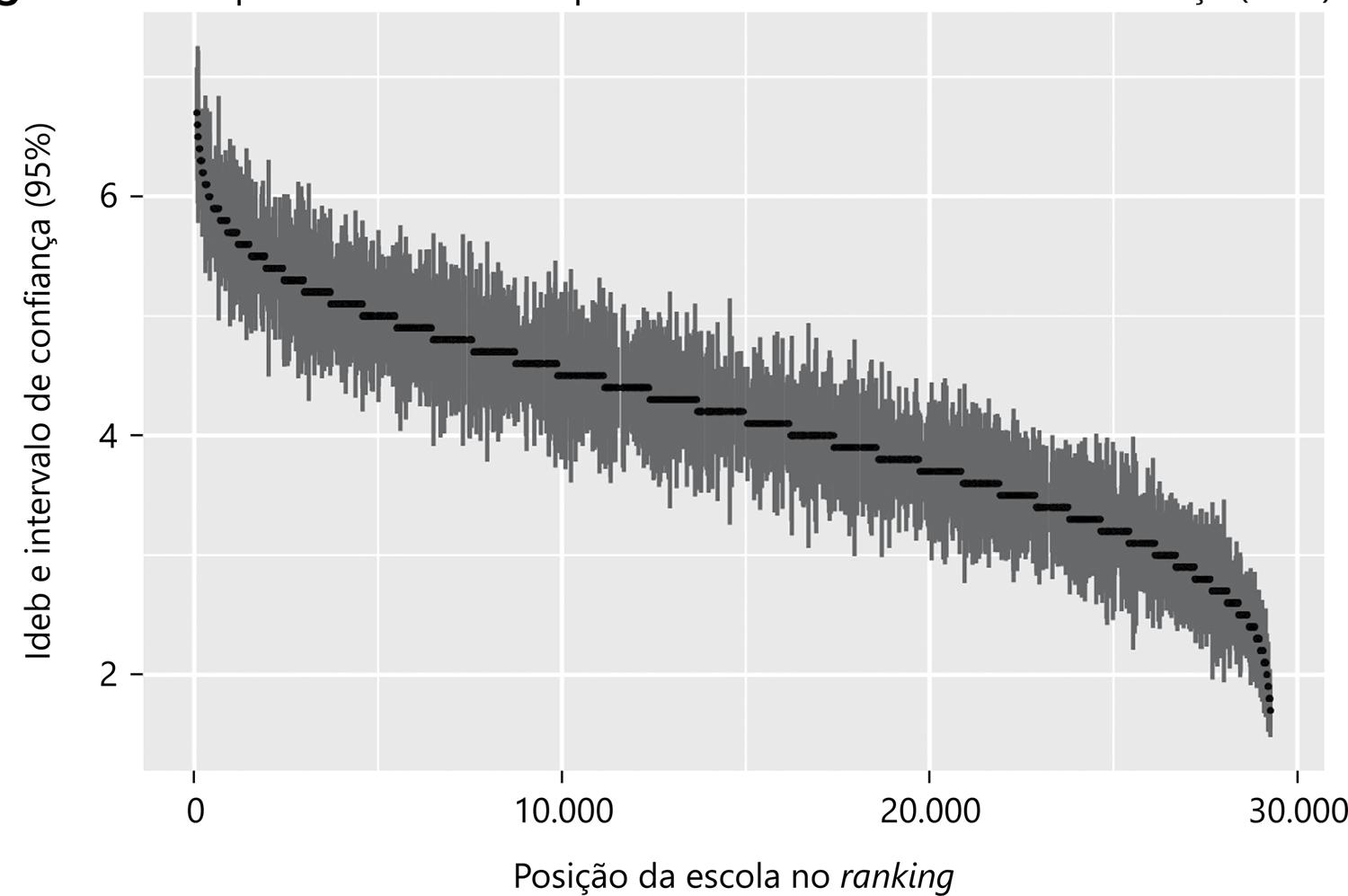
As cores representam o Ideb da escola (preto) e seu intervalo de confiança (cinza). Intervalo de confiança calculado a partir do erro total (Eptotal).
Fonte: Elaboração própria (2019) a partir dos dados do Inep (anos finais do Ensino Fundamental de 2015)
Figura 2 – Ranqueamento do Ideb por escola com intervalo de confiança (95%)
Nota-se que há uma grande sobreposição dos intervalos de confiança no Ideb por escola. Considerando o ranqueamento, uma escola na posição 10 mil pode ter um Ideb semelhante (levando em conta as incertezas) ao de uma escola na posição 20 mil. O que não é pouco.
Para fins de comparação, a Figura 3 mostra o mesmo tipo de dado, porém no nível dos estados (foram adicionadas linhas horizontais nas extremidades dos intervalos, para facilitar a visualização). Nota-se que, diferente do que ocorre nas escolas, nos estados não há sobreposição de intervalos de confiança14. Basta utilizar o Ideb por estado com uma casa decimal (um número depois da vírgula) que o intervalo de confiança não seria necessário, pois a diferença entre Idebs é sempre significativa. Isso ocorre porque o número de observações no estado é muito maior do que na escola, e, portanto, a incerteza diminui.
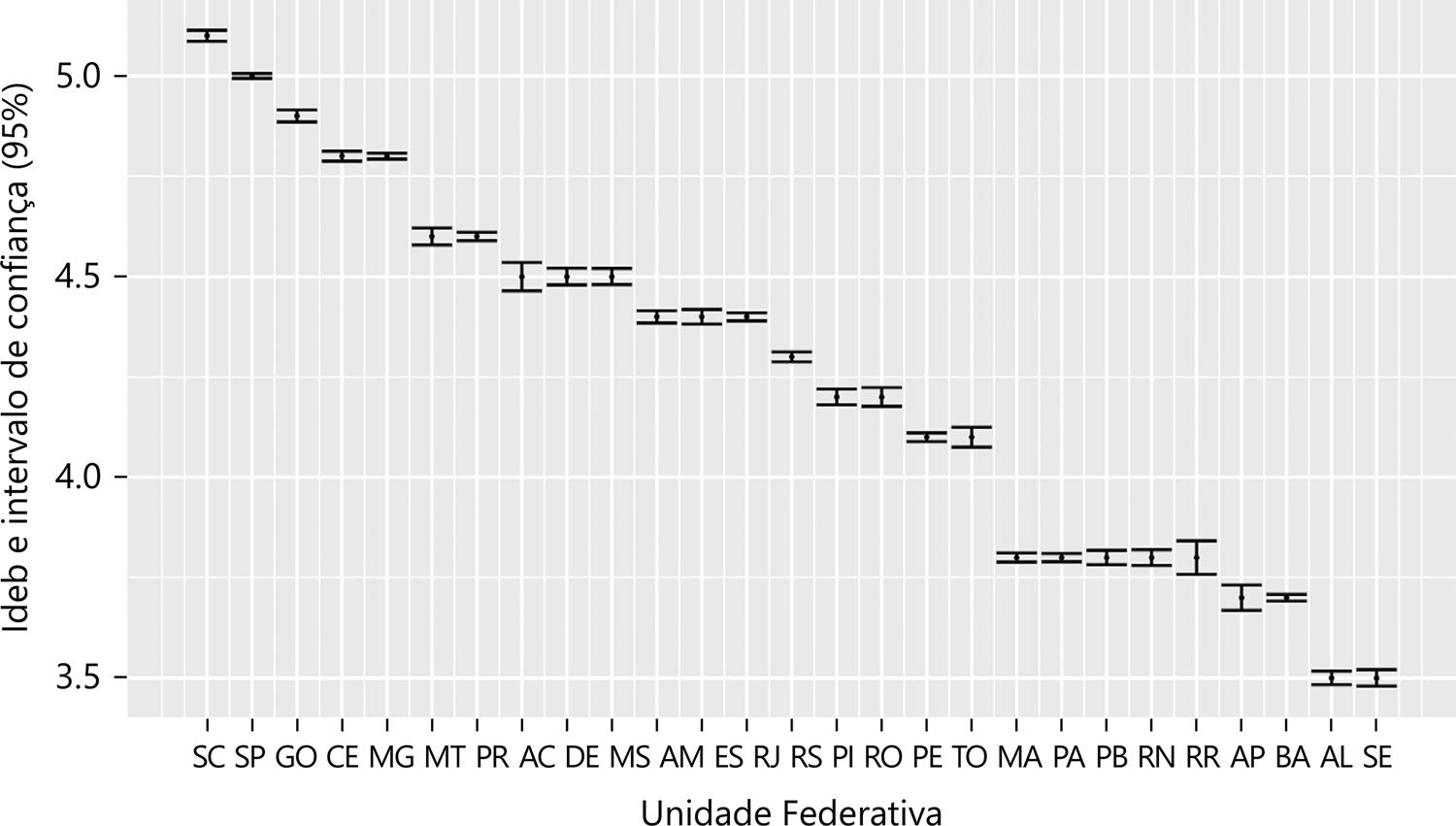
Intervalo de confiança calculado a partir do erro total (Eptotal).
Fonte: Elaboração própria (2019) a partir dos dados do Inep (anos finais do Ensino Fundamental de 2015)
Figura 3 – Ranqueamento do Ideb por Unidade Federativa com intervalo de confiança (95%),
Em suma, respondendo à pergunta inicial com os dados de 2015: quando duas escolas têm Ideb diferentes, ele muitas vezes não será diferente, levando-se em conta as incertezas. Isso porque há uma intensa sobreposição de intervalos de confiança no Ideb por escola. Com efeito, tal constatação aponta a necessidade de divulgação de uma “margem de erro” para o Ideb por escola, seja com o método aqui proposto, seja com outro.
Por outro lado, se a mesma pergunta se aplicar aos estados, ao invés de escolas, a resposta será outra. Bastaria divulgar o Ideb por estado com uma casa decimal que já não haveria sobreposição dos intervalos de confiança. Em outras palavras: quando dois estados têm Ideb diferentes, eles devem ser, de fato, diferentes, levando-se em conta as incertezas.
7.5 Incerteza do Ideb ao longo do tempo
Ao comparar o Ideb de 2015 com a série histórica, as conclusões apontam na mesma direção da seção anterior: o Ideb dos estados apresenta discriminação suficiente para comparações na maioria dos casos, mas ocorre o inverso com o Ideb das escolas.
A Tabela 2, por exemplo, mostra que a curto prazo (2 anos), 81% das escolas não apresentou mudança significativa de 2013 para 2015, ocorrendo praticamente o mesmo (83%) de 2015 para 2017. A médio prazo (6 anos), ainda há 68% de escolas que não mudaram seu Ideb, levando em conta as incertezas. Seriam necessários 10 anos de diferença para que a maioria das escolas (55%) apresentasse uma mudança significativa no Ideb. Em relação ao planejamento de longo prazo (de 2007 às metas de 2022), apenas 4% das escolas permaneceriam com Ideb semelhante em 2021 caso todas alcancem suas metas, uma proporção ignorável para este tipo de política pública.
Tabela 2 – Comparação do Ideb/2015 das escolas com a série histórica, pela sobreposição de Intervalos de Confiança (95%)
| Ano | Número de escolas | Sem sobreposição de IC | Com sobreposição de IC | Ideb semelhante |
|---|---|---|---|---|
| 2005 | 14.746 | 8.112 | 6.634 | 45% |
| 2007 | 21.153 | 9.219 | 11.934 | 56% |
| 2009 | 24.774 | 7.877 | 16.897 | 68% |
| 2011 | 25.114 | 6.118 | 18.996 | 76% |
| 2013 | 26.193 | 4.915 | 21.278 | 81% |
| 2017 | 19.147 | 3.307 | 15.840 | 83% |
| Metas * | 21.153 | 20.392 | 761 | 4% |
Foi utilizado o erro total (EPtotal) de 2015 para quase* todas as comparações.
IC = Intervalo de Confiança.
* Esta linha é diferente: compara o Ideb/2007 com a projeção de 2021 segundo as metas estabelecidas.
Fonte: Elaboração própria (2019) a partir dos dados do Inep (anos finais do Ensino Fundamental)
No nível dos estados, os resultados se invertem (Tabela 3). No curto prazo, poucos estados (um ou três) permaneceram com o mesmo Ideb, o que pode, de fato, representar uma estabilidade. Do médio prazo adiante, já não há estados com Ideb semelhantes, levando em conta as incertezas.
Tabela 3 – Comparação 1do Ideb/2015 das Unidades Federativas com a série histórica, pela sobreposição de Intervalos de Confiança (95%)
| Ano | Número de UF | Sem sobreposição de IC | Com sobreposição de IC | Ideb semelhante |
|---|---|---|---|---|
| 2005 | 27 | 27 | 0 | 0% |
| 2007 | 27 | 27 | 0 | 0% |
| 2009 | 27 | 27 | 0 | 0% |
| 2011 | 27 | 25 | 2 | 7% |
| 2013 | 27 | 26 | 1 | 4% |
| 2017 | 27 | 24 | 3 | 11% |
| Metas * | 27 | 27 | 0 | 0% |
Foi utilizado o erro total (EPtotal) de 2015 para quase* todas as comparações.
UF= Unidade Federativa; IC = Intervalo de Confiança.
* Esta linha é diferente: compara o Ideb/2007 com a projeção de 2021 segundo as metas estabelecidas.
Fonte: Elaboração própria (2019) a partir dos dados do Inep (anos finais do Ensino Fundamental)
8 Conclusão
A produção de bons indicadores pode tornar a rede de ensino mais transparente como um todo. Quando os limites e incertezas de cada indicador estão claros e explícitos, a transparência é ainda maior, promovendo o uso adequado de cada informação e potencializando o funcionamento da rede. Para contribuir nesse sentido, foi desenvolvido um método que estima o intervalo de confiança do Ideb com base em dois tipos de incerteza: o erro da média e o erro de medida. O erro total de cada escola/estado foi calculado somando-se esses dois erros.
Em relação ao uso do Ideb para acompanhar a evolução de uma escola, conclui-se que: a curto e médio prazo (1 e 6 anos, respectivamente) a maioria das escolas (em torno de 80% e 70%, respectivamente) não apresentou alteração significativa de Ideb, o que só começa a ocorrer depois de 10 anos. Por outro lado, quando analisamos a evolução dos estados, a conclusão é diferente: no curto prazo, há poucos estados (de 4% a 11%) sem mudança significativa no Ideb, e no médio prazo todos os estados já sofreram mudança no indicador.
Em relação ao uso do Ideb para o estabelecimento de metas de longo prazo, tanto as escolas quanto os estados terão apresentado mudança significativa caso alcancem suas metas. Tais metas foram criadas em 2007 tendo como horizonte final o ano de 2022.
Para as políticas públicas baseadas em evidências, tais resultados sugerem que, levando em conta a incerteza estatística, o Ideb apresenta consistência suficiente nas metas de 2022 e para acompanhar a evolução dos estados, mesmo no curto prazo. Porém, o Ideb não se mostrou consistente para acompanhar a evolução das escolas em curto e médio prazo.
Com base nesses resultados, sugere-se que o Inep divulgue um intervalo de confiança associado a cada Ideb por escola (por estado não seria tão importante), seja com base no método aqui proposto, seja outro. É importante destacar que a divulgação das incertezas associadas aos indicadores não tem como objetivo desmobilizar professores e gestores, mas, sim, proporcionar um uso adequado das informações disponíveis, que é um dos pilares das políticas baseadas em evidências.
Algumas limitações deste estudo precisam ser destacadas. No método proposto não foi considerada a interação entre os dois tipos de erro no cálculo do erro total. Além disso, só foram incluídas algumas fontes de incerteza – as únicas com dados públicos, disponibilizados pelo Inep – o que significa que os erros aqui calculados podem estar subestimados. Em relação à comparação do Ideb de diferentes anos, há outra limitação, que é o intervalo de confiança fixo para cada escola/estado nos diferentes anos.