Introdução

O desenvolvimento do sentido de número, que inclui o número racional, é parte integrante das orientações curriculares para o ensino básico (ensino fundamental). Porém, o tema dos números racionais, em particular das frações, é considerado difícil de aprender e de ensinar. O domínio das frações é fundamental para a aprendizagem de conceitos matemáticos mais avançados (POST et al., 1991; ^{RIBEIRO, 2011} ; ^{SIEGLER; LORTIE-FORGUES, 2015} ). Dada a relevância do conceito de fração, espera-se que as crianças em Portugal, e à semelhança daquilo que acontece em muitos outros países, aprendam frações a partir do 2º. ano de escolaridade (7-8 anos de idade) (DGE, 2013).

Os alunos manifestam dificuldades em compreender o conceito de fração e suas operações ( ^{SIEGLER; LORTIE-FORGUES, 2015} ), mas também os professores e os futuros professores manifestam dificuldade com esse conceito matemático (MAMEDE; RIBEIRO; PINTO, 2021; OLANOFF; LO; TOBIAS, 2014). A análise e compreensão do conhecimento matemático dos professores torna-se, assim, essencial, já que esse tem impacto na qualidade do ensino (BALL; THAMES; PHELPS, 2008; ^{COPUR-GENCTURK, 2021} ; ^{SHULMAN, 1986} ). E, tratando-se de um conceito tão complexo como o de número racional, as dificuldades na abordagem desses números na aula podem agravar-se ( ^{MAMEDE; PINTO, 2017} ; PINTO; RIBEIRO, 2013; POST et al., 1991; TIROSH et al., 1998), pelo que deve dedicar-se especial atenção às dificuldades, antecipáveis, resultantes do conhecimento de conteúdo e de ensino do professor.

Tradicionalmente, a abordagem das frações em sala de aula exclui contextos relevantes para a construção do conceito pelos alunos, criando facilmente neles uma visão limitada de fração. Para combater esse efeito, o professor do Ensino Fundamental deveria mobilizar conhecimentos matemáticos e didáticos que vão além dos usualmente utilizados (CARDOSO, 2017; CARDOSO; MAMEDE, 2021; ^{MAMEDE; PINTO 2017} ; MAMEDE; RIBEIRO; PINTO, 2021), dominando a representação, a ordenação e a equivalência de frações, em contextos diversos.

Apesar de conhecidas as dificuldades dos professores com o conceito de fração, a investigação em torno das suas concepções e práticas continua um assunto atual (BEHR et al., 1992; BALL; LUBIENSKI; MEWBORN, 2001; CARDOSO; MAMEDE, 2021; MAMEDE; RIBEIRO; PINTO, 2021; OLANOFF; LO; TOBIAS, 2014; POST et al., 1991).

O currículo português para a matemática, tal como sucede noutros países, antecipa um contato com as frações para os primeiros anos de escolaridade. Uma análise das concepções e ideias sobre as práticas dos professores portugueses do 1º. ciclo do ensino básico (anos iniciais do ensino fundamental), relativamente ao conceito de fração, é tão mais essencial se tivermos presente que tais concepções e práticas poderão ser comuns às de professores de outros países.

O conhecimento do professor para ensinar

A ideia de que existe um conjunto de conhecimentos que são específicos para o ensino é reconhecida (BALL; THAMES; PHELPS, 2008; BORN; PRADO; FELIPPE, 2019; ^{SHULMAN, 1986} ). ^{Shulman (1986)} sugere a classificação do conhecimento necessário para ensinar em três categorias: a) conhecimento de conteúdo — conhecimento de teorias, princípios e conceitos de uma disciplina; b) conhecimento pedagógico de conteúdo — vai para além do conhecimento de conteúdo, na medida em que trata do conhecimento necessário para ensinar, incluindo o conhecimento de estratégias que tornem o conteúdo compreensível para os alunos; c) conhecimento curricular — conhecimento do currículo, envolvendo a capacidade de relacionar conteúdos que os alunos estão a aprender simultaneamente noutras disciplinas (articulação horizontal), bem como o conhecimento daquilo que os alunos aprenderam em anos anteriores e do que aprenderão em anos posteriores, na disciplina (articulação vertical).

Mais recentemente, Ball, Thames e Phelps (2008) apresentaram um quadro teórico do conhecimento do professor para o ensino específico da Matemática. Com base no modelo universal de ^{Shulman (1986)} , os autores sugerem que o conhecimento de conteúdo proposto por este pode ser subdividido em conhecimento de conteúdo comum e conhecimento de conteúdo especializado, incluindo, ainda, nesse domínio, o conhecimento do horizonte matemático. Sugerem, ainda, a subdivisão do conhecimento pedagógico de conteúdo de Shulman em conhecimento de conteúdo e alunos, conhecimento de conteúdo e ensino, e conhecimento curricular.

O conhecimento de conteúdo comum é o conhecimento matemático utilizado noutros contextos para além do ensino, podendo incluir a capacidade de reconhecimento de erros, de uma correta realização de cálculos e de uma correta utilização de termos técnicos. Trata-se de conhecimento exigido para ensinar, muito embora não sendo exclusivo desse contexto. Por sua vez, o conhecimento de conteúdo especializado é o conhecimento matemático utilizado para o ensino, sendo, então, exclusivo do contexto didático. Esse conhecimento inclui a capacidade de interpretar os erros dos alunos e a capacidade de reconhecer a natureza dos mesmos. O conhecimento de conteúdo e alunos combina o conhecimento matemático com o conhecimento dos alunos, e inclui a capacidade de antecipar ideias e concepções erradas dos alunos, isto é, a familiaridade com o pensamento matemático dos alunos. O conhecimento de conteúdo e ensino combina o conhecimento de conteúdos matemáticos com conhecimentos sobre o ensino desses conteúdos. Essa categoria inclui: a) o conhecimento de metodologias para o ensino concreto de determinado conteúdo; b) a capacidade de avaliar potencialidades de diferentes representações de conceitos; c) a capacidade de seleção de exemplos promotores de compreensão. Finalmente, o conhecimento do horizonte matemático traduz-se na consciência da relação entre os tópicos matemáticos a ensinar e a variedade de tópicos incluídos no currículo (BALL; THAMES; PHELPS, 2008). A Figura 1 ilustra o quadro teórico apresentado por Ball, Thames e Phelps (2008).

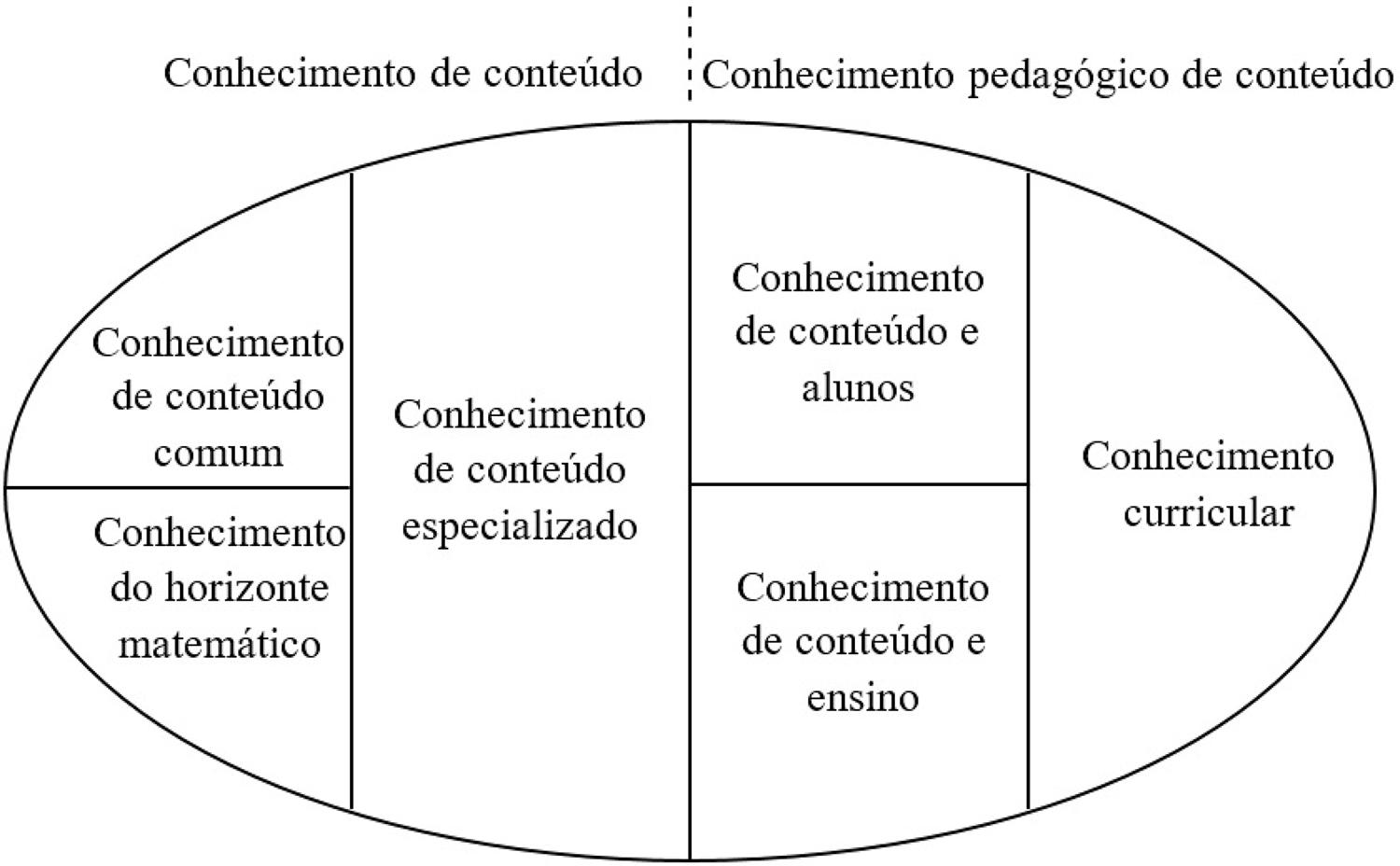
Fonte: Ball; Thames; Phelps (2008).

Figura 1 – Domínios do conhecimento para o ensino da matemática (mathematical knowledge for teaching – MKT) 

Reconhecendo a relevância de todas as dimensões do conhecimento matemático para ensinar, importa analisar o conhecimento do professor no caso particular das frações, dado tratar-se de um assunto altamente pertinente, mas manifestamente difícil.

Conhecimento dos professores sobre frações

O pleno domínio do conceito de fração pressupõe o domínio da representação e da operação com frações em diferentes contextos (BEHR et al., 1983; KIEREN, 1976; NUNES et al., 2004). É possível encontrar na literatura diferentes classificações de significados ou interpretações de fração. Umas assentam na noção de “subconstruto” apresentado por Kieren (1976) (BEHR et al., 1992; KIEREN, 1976, 1993), outras baseiam-se na noção de “situação” da teoria de Vergnaud (1997) para a construção de um conceito matemático (NUNES et al., 2004).

O currículo atual para o 1º ciclo do ensino básico aborda os significados: quociente, parte-todo, operador e medida. Sendo a e b números inteiros ( b ≠0), no significado quociente, a/b representam a relação entre a itens repartidos por b recipientes (por exemplo, 2/3 representa 2 barras de chocolate repartidas por 3 crianças), mas a/b também representa a quantidade que cabe a cada recipiente (por exemplo, 2/3 representa a quantidade de chocolate que cada criança recebe). No significado parte-todo, a/b representa a relação entre b , o número de partes iguais em que o todo é dividido, e a o número dessas partes que são retiradas (por exemplo, 2/3 de uma barra de chocolate significa que a barra foi dividida em 3 partes iguais e 2 dessas partes foram consideradas). No significado operador, que envolve um conjunto de quantidades discretas como um todo, na fração a/b, b indica o número de grupos iguais em que o conjunto inicial é dividido e a é o número de grupos que lhe são retirados (por exemplo, 2/3 de 12 contas significa que foram formados 3 grupos iguais de contas e retirados 2 desses grupos) (NUNES; BRYANT, 2008). Por último, no significado medida, a fração a/b indica que é medida uma distância usando como unidade 1/b repetida a vezes (por exemplo, 2/3 indicam que a medida 1/3 foi usada 2 vezes).

A diversidade de contextos para abordar frações em sala de aula e o modo como promovem a resolução de problemas, o raciocínio e a comunicação matemática assumem-se como fundamentais para a literacia matemática do indivíduo. A resolução de problemas permite articular conhecimentos e potencializa a capacidade de desenvolver estratégias apropriadas e obter soluções válidas em diversos contextos; o raciocínio matemático promove a compreensão de relações matemáticas e o estabelecimento de argumentos válidos e análise crítica de raciocínios produzidos por outros; a comunicação matemática estimula a discussão de ideias matemáticas, a organização e consolidação prévia das ideias e processos matemáticos, promovendo a compreensão das ideias matemáticas (DGE, 2018; NCTM, 2017).

Estudos centrados no conhecimento do professor sugerem que este é consideravelmente menos confiante e menos bem sucedido no domínio dos números racionais do que no domínio dos números inteiros (BALL; HILL; BASS, 2005). No âmbito do Rational Number Project (RNP), Post et al. (1991) conduziram um estudo para traçar o perfil de 218 professores (níveis 4-6), relativamente ao seu conhecimento sobre os números racionais. Identificaram-se, nomeadamente, dificuldades com os significados de fração e com a ordenação e a equivalência de frações. Os autores sublinharam dificuldades dos professores em justificar pedagogicamente cálculos por eles efetuados com números racionais.

Tirosh et al. (1998) avaliaram o conhecimento de 147 futuros professores do ensino básico, relativamente aos números racionais. Os autores sublinham o conhecimento segmentado e rígido desses futuros professores, reduzindo a matemática a uma coleção de técnicas de cálculo desprovidas de justificação formal. Concluíram, ainda, que os futuros professores tendem a aplicar, inapropriadamente, propriedades dos números inteiros aos números racionais.

Mais recentemente, em Portugal, Pinto e Ribeiro (2013) aplicaram um questionário a 27 futuros professores do 1º. ciclo do ensino básico, e referem que estes possuem um conhecimento limitado de número racional. Designadamente, identificaram dificuldades com os significados de fração (quociente, parte-todo e operador), com a compreensão do papel da unidade de referência, e com a equivalência, ordenação e densidade do conjunto dos números racionais.

^{Mamede e Pinto (2017)} aplicaram um questionário a 86 futuros professores do 1º. ciclo, para analisar o seu conhecimento sobre frações. Os resultados sugerem: dificuldades na compreensão do papel da unidade de referência; fraco domínio dos significados de fração, mormente no âmbito de problemas envolvendo o significado quociente e no âmbito da representação de números na reta numérica, quando números diferentes de 1 são usados como referência na reta e quando é necessária uma redefinição da escala; fraco domínio da propriedade de densidade do conjunto dos números racionais; e dificuldades com a ordenação e equivalência de frações.

Li, Zhang e Song (2021) inquiriram 180 professores do ensino básico (anos iniciais do ensino fundamental), sobre a confiança e os conhecimentos matemáticos e didáticos dos docentes para ensinar a divisão de frações. Concluíram que os professores são fortes no conhecimento matemático processual, mas menos fortes na vertente conceitual, afetando a confiança no seu desempenho pedagógico. Alertam, ainda, para a necessidade de mais formação matemática e pedagógica, incrementando a confiança dos professores na sua capacidade de ensinar.

A literatura elenca já algumas das dificuldades do professor com o conceito de fração ( ^{MAMEDE; PINTO 2017} ; MAMEDE; RIBEIRO; PINTO, 2021; PINTO; RIBEIRO, 2013; POST et al., 1991; TIROSH et al., 1998), mas a investigação em torno das concepções e práticas de professores merece ainda atenção (BALL; LUBIENSKI; MEWBORN, 2001; CARDOSO; MAMEDE, 2021; MAMEDE; RIBEIRO; PINTO, 2021; OLANOFF; LO; TOBIAS, 2014; PINTO; RIBEIRO, 2013). O contributo da pesquisa aqui apresentada reside na procura de uma resposta a essa carência investigativa justificada no currículo português para o ensino da matemática. O estudo foca-se nas concepções e práticas sobre frações, dos professores do 1º. ciclo do ensino básico (anos iniciais do ensino fundamental), em Portugal. Procurando saber: 1) Que ideias possuem os professores sobre as frações? 2) Como entendem que deve ser o seu ensino?

Metodologia

O presente estudo procura perceber quais conhecimentos matemáticos e didáticos possui o professor dos anos iniciais do ensino fundamental, relativamente ao conceito de fração. A pesquisa desenvolvida enquadra-se no paradigma interpretativo, conferindo especial relevância ao significado que os indivíduos atribuem aos fenômenos (ERICKSON, 1986). Nesse âmbito, optou-se pela modalidade de estudo de caso qualitativo. De acordo com Merriam (2009), é um design ideal para compreender e interpretar fenômenos do contexto educativo, sendo particularmente adequado quando se procura resposta a “como?” e “por que?” e se pretende uma profunda compreensão dos acontecimentos (MERRIAM, 2009; YIN, 2014).

Participaram deste estudo 31 professores, sendo 25 do gênero feminino (80,6%) e 6 do gênero masculino (19,4%), distribuídos por nove escolas públicas do 1º. ciclo do distrito de Braga, Portugal.

Os participantes tinham idades entre os 30 e 57 anos (média de 42 anos; desvio padrão de 10). O tempo de serviço variava de 3 a 34 anos (média de 16 anos; desvio padrão de 9). Dez professores tinham pouca experiência de ensino (≤10 anos de serviço); 11 experientes (11-20 anos); e 10 muito experientes (≥ 20 anos de serviço).

Vinte e um professores gostavam de lecionar matemática, 7 reconheceram não gostar de lecionar matemática, e 3 preferiam lecionar língua portuguesa.

Entrevistas individuais semiestruturadas foram aplicadas aos participantes. As entrevistas constituem uma técnica fundamental de recolha de dados no âmbito da investigação qualitativa, particularmente quando se pretende um estudo individualizado da atividade e das formas de pensar de elementos de um mesmo grupo (GUBA; LINCOLN, 1994; YIN, 2014).

A entrevista semiestruturada baseia-se num conjunto de questões previamente definidas, podendo eliminar-se algumas das questões ou incluir novas, promovendo-se, ainda, respostas livres por parte dos entrevistados. Sendo híbrida, tem a vantagem de possibilitar a obtenção de dados de forma paralela e comparável entre diversos sujeitos (BOGDAN; BIKLEN, 2010; GUBA; LINCOLN, 1994; YIN, 2014). A entrevista integrava 16 questões, 9 centradas no conceito de fração e suas propriedades, e 7 na resolução de problemas envolvendo frações, adaptadas de Lamon (2006), Nunes et al. (2004) e ^{Streefland (1991)} , versando aspectos essenciais da compreensão do conceito de fração (BEHR et al., 1983; NUNES et al., 2004; ^{STREEFLAND, 1991} ).

No decurso da entrevista, a apresentação das questões seguiu uma ordem aleatória, mas igual para todos os entrevistados. As questões da entrevista contemplavam as representações simbólica, pictórica e verbal, em diferentes significados de fração.

Procurou-se, assim, aferir as ideias dos professores sobre o conceito de fração e suas propriedades, e analisaram-se, ainda, as ideias dos professores sobre os conhecimentos matemáticos e didáticos envolvidos na resolução de alguns problemas, adequados aos alunos do ensino fundamental. Na entrevista, todas as frações representavam números racionais menores ou iguais a 1, por estas serem as frações mais simples (HART, 1981; MAMEDE, 2007).

Cada entrevista individual teve a duração média de 35 minutos. A cada entrevistado foi disponibilizada uma folha de papel em branco para utilizar, se necessário. A recolha de dados foi feita com recurso de gravação do áudio integral de cada entrevista, com a autorização dos participantes, e com recurso às notas de campo da investigadora (uma das autoras deste artigo).

O caráter semiestruturado da entrevista permitiu uma comparação sistemática dos argumentos apresentados por cada indivíduo, com vista à sua categorização.

Resultados

Atribuiu-se 1 ponto a cada resposta correta e 0 a respostas erradas ou incompletas. Nas questões sobre o conceito de fração e suas propriedades, a porcentagem média de acertos é de 63,4 (desvio padrão 21,9), na resolução de problemas envolvendo frações é de 54,3 (desvio padrão 19,3). Apesar de positivos, esses resultados são pouco expressivos, pois os problemas da entrevista são adequados aos alunos do 1º. ciclo do ensino básico. A Tabela 1 resume a porcentagem de acertos dos professores às perguntas sobre o conceito de fração e suas propriedades.

Tabela 1 – Porcentagem de respostas corretas sobre o conceito de fração (N=31) 

Questão	Respostas corretas (%)
Como definiria o conceito de fração?	100
A figura pode representar 3/4 ?	100
Assinale as opções que representam dois terços: a) 2x3; b) 3/2 ; c) 2÷3; d) 2/3; e) 3÷2; f) Outra: _____	77,4
Que significados de fração conhece?	0
A figura pode representar 3/4?	16,1
A figura pode representar 3/4?	29,00
Verdadeiro ou Falso – Todo o número decimal pode ser escrito como uma fração	61,3
A figura pode representar 3/4?	100
A figura pode representar 3/4?	87,1

Fonte: Elaboração nossa.

Todos os professores tiveram sucesso na definição do conceito de fração, tendo surgido ideias tais como: “Uma fração traduz uma divisão de dois números inteiros. Tem o numerador e o denominador… o denominador não pode ser zero”, ou “Uma fração é uma parte de um todo”, “Representa a parte de um todo”, “A parte de algo é uma fração. Por exemplo, se dividirmos a maçã em duas partes…. metade da maçã é 1/2”).

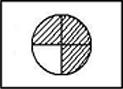
Todos os professores reconheceram que um círculo ou um retângulo dividido em 4 partes iguais, das quais 3 se encontravam sombreadas, podia representar 3/4. Nesses modelos, os professores argumentaram corretamente que o denominador da fração indicava o número total de partes em que o círculo se encontrava dividido (4 partes) e que o denominador indicava o número de partes sombreadas (3 partes) , ou no caso do semelhante do retângulo dividido em 4 partes iguais . Os professores revelaram, assim, um conhecimento matemático sólido na representação pictórica de frações, no significado parte-todo.

Quando questionados sobre quais significados de fração conheciam, 74,2% dos professores apresentaram respostas que sugerem desconhecimento dos diferentes significados, sendo que 22,6% referiu somente que a fração representa uma parte de um todo e 1 professor não respondeu à questão.

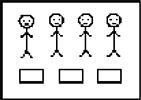
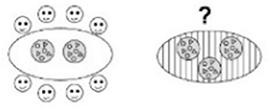
Em contraste com os resultados obtidos no reconhecimento de 3/4 de um círculo/retângulo sombreado, os professores não foram tão bem sucedidos ao identificar uma imagem de 4 crianças e 3 barras de chocolate 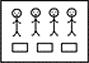como sendo uma representação de 3/4. Apenas 16,1% disseram que esta seria uma representação pictórica de 3/4, argumentando que “O que está aqui é uma partilha de 3 barras de chocolate por 4 meninos. Cada um vai comer 3/4 de uma barra de chocolate. São 3 a dividir por 4”. Os professores restantes (83,9%) manifestaram dificuldades em reconhecer a fração como uma relação entre duas variáveis de natureza diferente (meninos e barras de chocolate). Para esses professores, a representação de uma fração envolve sempre itens da mesma natureza, como acontece, por exemplo, nos significados parte-todo ou operador, chegando mesmo a argumentar que “Têm bonecos e retângulos. Não é igual!”; “Não é tudo o mesmo conjunto”; “Têm bonecos e retângulos. Não sei qual é a unidade”; “Não encontro nenhuma relação”; “Não está nada assinalado. Não há divisão”; “Tem 7 elementos e teria de ter 4. Se tivéssemos 3 barras de chocolate pintadas já era 3/4”.

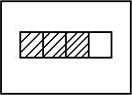
Face a uma representação pictórica de 3/4 envolvendo quantidades discretas, os resultados foram francamente positivos (87,1%) quando se apresentavam 4 círculos dos quais 3 estavam pintados 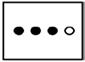. No entanto, quando os grupos indicados pelo denominador da fração têm mais de um elemento, por exemplo 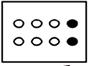, apenas 29% dos professores reconheceram que esta poderia ser uma representação de 3/4. Erradamente, em 19,4% das argumentações só teríamos 3/4 se fossem 4 elementos e não 8; em 51,6 % dos casos, como se tratava de 8 círculos sendo 6 não pintados e 2 pintados, houve professores que reconheceram 1/4 nesta representação, mas não reconheceram 3/4 (por exemplo, “É uma parte das quatro”; “Para ser 3/4 teria de ter seis [elementos] pintados”; “A parte que está pintada é 1/4”).

Quando inquiridos sobre se todo o número decimal pode ser escrito como uma fração, 61,3% dos professores consideraram que sim, justificando que “o número decimal resulta de uma divisão”; “O número decimal resulta de uma divisão. Duas décimas correspondem à unidade dividida em 10 partes e tiram-se 2. Portanto, 2 sobre 10”; “Porque um número decimal é uma porção da unidade”; “Representa uma parte da unidade”; “Porque a fração e o número decimal indicam uma divisão”. Essa argumentação sugere o domínio da tradução do número racional nas representações fracionária e decimal. Contudo, 38,7% dos professores referiram não saber responder à questão. Essa dificuldade é muito importante tratando-se de professores do ensino fundamental, já que os programas curriculares em vigor para a matemática desses níveis de escolaridade abrangem a articulação dos diferentes modos de representação dos números racionais.

Os resultados sugerem dificuldades nas concepções do professor sobre a diversidade de significados de fração a trabalhar em sala de aula e a tradução de números racionais, na forma de dízima e fracionária. Contudo, ambos os aspectos integram os programas oficiais de matemática para o 1º. ciclo do ensino básico, devendo, portanto, ser conteúdos dominados pelo professor.

Procurando saber mais sobre as práticas dos professores, analisaram-se as suas respostas a problemas com frações que pudessem ser levados para a sala de aula, procurando perceber-se como os abordariam com os seus alunos.

A análise às resoluções dos problemas propostos evidencia algumas discrepâncias entre as concepções e as práticas dos professores. A Tabela 2 resume a porcentagem de respostas corretas dos professores nos problemas propostos.

Tabela 2 – Porcentagem de resoluções corretas nos problemas (N=31) 

Questão	Resoluções corretas (%)
Uns amigos foram a uma pizzaria e distribuíram-se por 2 mesas. Todos os amigos comeram a mesma quantidade de pizza. Quantos amigos comeram na mesa da toalha de riscas?	90,3
Dois chocolates foram divididos igualmente por 5 crianças. Quanto recebeu cada uma?	90,3
O João perdeu 6 das 16 bolas de gude que tinha. Que fração de bolas de gude perdeu?	58,1
Observe a figura: Sabendo que cada taça tem o mesmo número de contas, que parte das contas tem cada taça?	19,4
A Ana tem uma caixa com 50 lápis de cor. O Rui tem dessa quantidade de lápis. Quantos lápis tem ele?	96,8
Considere a seguinte figura: Como preencheria os seguintes espaços em branco	22,6

Fonte: Elaboração nossa.

Os professores reconhecem alguns significados de fração (ver Tabela 2 ), contudo quando inquiridos sobre esses significados revelaram desconhecimento (ver Tabela 1 ). Isso sugere algum desconhecimento curricular, no que toca à diversidade de significados de fração a abordar na aula. Num dos problemas apresentados aos professores, que envolvia a comparação das frações 2/8 e 3/12, partindo da sua representação pictórica no significado quociente, 90,3% das respostas foram corretas. O recurso ao estabelecimento de correspondências entre o número de itens e o número de recipientes foi espontâneo (por exemplo, “Dá uma pizza para 4 meninos. Se aqui temos 3 pizzas então comeram 12 meninos nessa mesa”; “São 2 pizzas para 8 meninos o que dá 1 pizza para 4 meninos, precisa-se mais quatro para outra… são 12 meninos”). Sobre a forma como abordariam esse problema com os alunos, os professores referiram que o fariam com base no mesmo raciocínio: ou destacando, desde logo, o fato de existir uma 1 pizza para 4 meninos; ou dividindo cada pizza em 4, e fazendo uma correspondência de 1 pedaço de pizza para cada menino. Contudo, quando anteriormente questionados sobre os significados de fração, ninguém referiu o significado quociente.

Ainda no significado quociente, procurou saber-se que quantidade de chocolate cabe a cada criança, numa divisão em partes iguais de 2 barras de chocolate por 5 crianças, agora apresentado sem suporte pictórico. Cerca de 29% dos professores apresentou a resolução correta do problema, assente na interpretação dos valores do numerador e do denominador, no significado quociente. Argumentam, ainda, ser essa a melhor abordagem em sala de aula, por ser uma situação do quotidiano dos alunos, que envolve a partilha equitativa (por exemplo, “Cada menino come 2/5 […] são 2 barras de chocolate e 5 meninos. Os alunos estão habituados com essas situações de repartir igualmente”; “Eles já conhecem esses problemas. Começava com esses problemas! Para eles é natural pensar em dividir um chocolate. Aqui daria 2/5 para cada menino”). O conhecimento matemático e o conhecimento didático (BALL; THAMES; PHELPS, 2008) desses professores, a respeito das frações e seu ensino, parecem estar bem articulados, permitindo aos alunos explorar o raciocínio proporcional, assente na correspondência de um-para-muitos, estimulando, assim, a compreensão do conceito de fração.

Contudo, ainda no problema sobre a partilha de 2 itens por 5 crianças, em 61,3% das resoluções apresentadas, os professores efetuaram a divisão para responder ao problema, em vez de se basearem na articulação entre numerador (número de barras de chocolate) e denominador (número de crianças) para representar a quantidade que caberia a cada criança, 2/5. Essa opção levou os professores a justificar que, uma questão envolvendo a divisão de 2 itens por 5 recipientes, colocaria muitas dificuldades aos alunos, já que da aplicação do algoritmo da divisão resultaria um número decimal. Na realidade, o conhecimento matemático desses professores compromete o seu conhecimento didático, privando os seus alunos da oportunidade de construir um conceito de fração mais completo.

Num outro problema, procurava-se a fração do total de bolas de gude que perdeu o João, sabendo-se que perdeu 6 das 16 bolas de gude que possuía, sem suporte visual. Constatou-se que 58,1% dos professores responderam corretamente, estabelecendo uma correspondência entre o valor do numerador e o número de bolas de gude perdidas, e entre o valor do denominador e o número total de bolas de gude, dizendo que procederiam do mesmo modo em sala de aula (por exemplo, “Perdeu 6/16. O total é embaixo e o que se perde em cima”; “A unidade é 16/16 por isso perdeu 6/16”; “Perdeu 6/16 ou perdeu 3/8. Tenho 16 partes. Perdi 6. São 6 das 16 partes: 6/16. Decompondo chego a 3/8”; “Ao todo tinha 16. Perdeu 6. Seis a dividir por 16 chego à fração 6/16”; “O número que tinha é no denominador e o número que perdeu no numerador. Perdeu 6/16”; “Perdeu 6/16. São 6 de 16. Dezasseis é o todo e 6 é a parte”). Perto de 39% dos professores não responderam a essa questão; e apenas 1 professor aplicou o algoritmo da divisão. Cerca de 40% dos professores revelaram dificuldades no conhecimento matemático quando estão envolvidas frações com quantidades discretas.

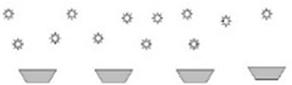
Em outro exemplo de problema temos que, sabendo-se que o total de elementos (contas) a distribuir é 12, solicitou-se a fração de elementos que caberia a cada uma de 4 taças dadas. A porcentagem de respostas corretas foi de apenas 19,4%. As respostas basearam-se na correspondência entre o valor do denominador e o número de grupos iguais em que o total de elementos foi dividido, e entre o valor do numerador e o número de grupos iguais de elementos que são retirados/considerados (por exemplo, “Três doze avos. Primeiro contei as estrelas. Tenho de dividir em 4 grupos. As taças vão ter uma parte do total. Vão ter 3. Se no total são 12, cada [taça] vai ter 3/12”; “É a quarta parte. Dividi as contas pelas 4 taças”; “Quarta parte de 12 estrelas”). Em contraste, 80,6% das respostas revelaram uma interpretação incompleta do problema: os professores indicaram o número de elementos que caberia a cada taça, não referindo, porém, a fração a que corresponde essa quantidade (por exemplo, “São 3 para cada taça. Contei as flores e dividi por 4 taças”; “Ficam 3 em cada taça. Doze a dividir por 4 dá 3”; “Cada taça terá 3 flores. É 12 a dividir por 4”). Mencionaram, ainda, que essa seria a abordagem ao problema na aula. Note-se que esse problema e o anterior envolvem quantidades discretas, pelo que o trabalho com frações exige maior cuidado na abordagem didática, articulando três quantidades: a dimensão dos grupos iguais, o numerador (número de grupos iguais considerados) e o denominador (número total de grupos iguais) das frações. As concepções desses professores podem comprometer a qualidade das suas práticas.

Novamente, em um outro problema, ainda envolvendo quantidades discretas, era conhecido o conjunto inicial e a fração que operava sobre esse conjunto, e solicitava-se a indicação do número de elementos correspondente a essa fração, sem suporte visual. Os professores tinham de encontrar 2/5 de um total de 50 elementos, não tendo manifestado dificuldades no processo. Cerca de 19,4% realizaram o cálculo mentalmente (por exemplo, “Primeiro vi quanto era 1/5 de 50. São 10. Multipliquei por 2 o que dá 20”; “Muito simples! Divido 50 por 5 e tenho 1/5 e multiplico por 2. Tenho 20 lápis!”). Sobre a abordagem dessa tarefa em sala de aula, as respostas assentaram na formação de grupos de 10 elementos e posterior destaque de 2 desses grupos, com recurso a representações pictóricas (por exemplo, “Vemos que a unidade está dividida em 5 grupos. Pedia aos alunos para fazerem 5 grupos iguais com os 50 lápis. Ficavam com 5 grupos de 10 lápis. Ora 2/5 são 2 partes desses 5 o que daria 20 lápis”; “Com 50 lápis podem fazer grupos de 10 e ver quanto é 1/5 e depois 2/5. Faziam um desenho!”). Face à mesma situação, 77,4% dos professores multiplicaram o valor do numerador da fração pelo número total de elementos, dividindo o valor assim obtido pelo valor do denominador. Esses professores referiram que abordariam o problema na aula aplicando o mesmo tipo de procedimento algébrico. No entanto, não acompanharam a sua opinião de eventuais explicações a apresentar aos alunos (por exemplo, “Sim, utilizava esse problema para trabalhar frações com os alunos. Aqui eles tinham de fazer cálculos, aplicavam a regra de multiplicar e dividir”; “Fazia isto com os alunos, sim... Operar com frações é difícil. Lá para o 3º. ou 4º. ano… Depois de aprenderem é fácil. É só multiplicar e dividir… É fazer isto sempre…”; “É só multiplicar e dividir. Multiplica-se 50 por 2 e divide-se por 5. Dá 20 lápis”). Apenas 1 professor disse não saber responder. Repare-se que, nesse problema, procura-se encontrar uma quantidade, conhecida a fração que opera no conjunto inicial. Os elevados níveis de sucesso refletem a facilidade dos professores nessa abordagem, em sala de aula. Em contraste, no problema anterior, onde se procurava a fração que operava sobre o conjunto, é notória a dificuldade dos professores no conhecimento didático, aliado a um conhecimento de conteúdo débil.

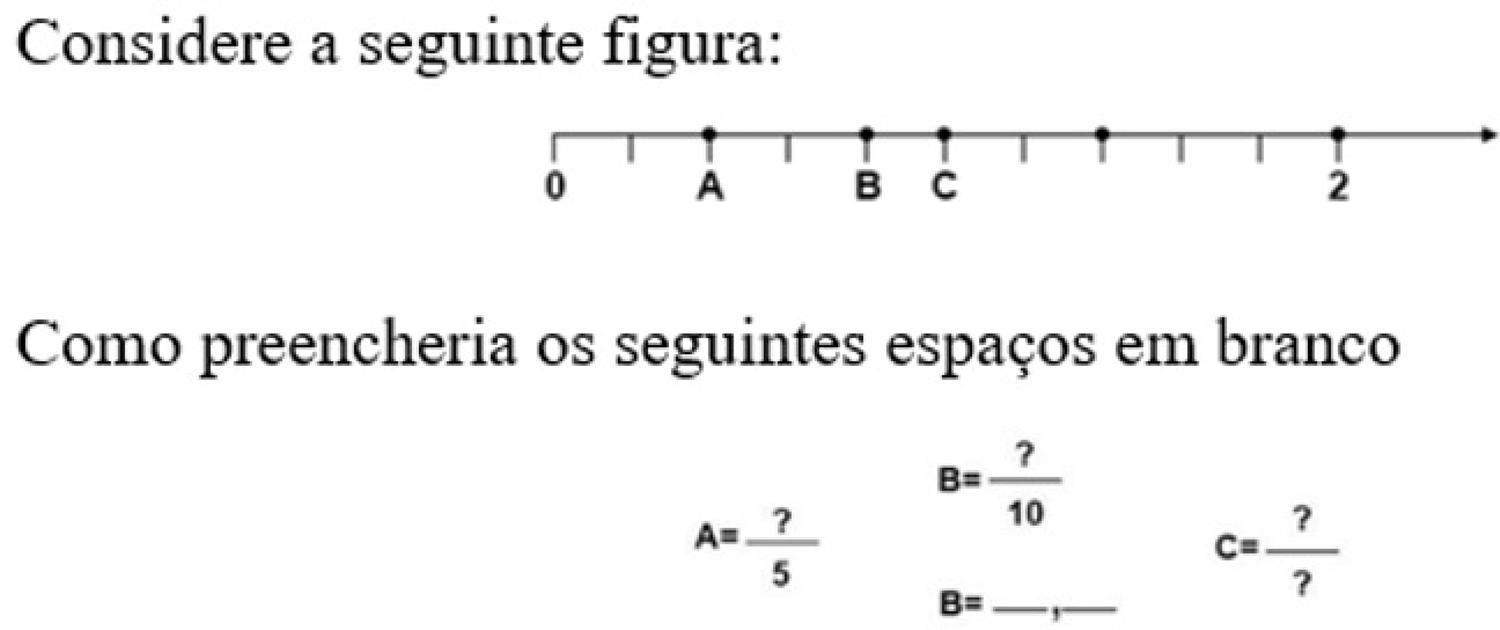
Igualmente relevante no currículo para a Educação Básica (ensino fundamental) é a tradução da representação decimal para a representação fracionária e vice-versa. Solicitou-se aos professores que identificassem as frações 2/5 e 8/10 representadas por pontos, A e B, numa dada reta numérica, na qual o intervalo 0 e 2 estava dividido em 10 partes iguais. Tinham, ainda, de identificar o ponto C que correspondia a 1 (ver Figura 2 ).

Fonte: Elaboração nossa.

Figura 2 – Questão sobre representação de números racionais na reta 

Nessa questão, 22,6% dos professores identificaram corretamente a unidade e mediram a distância ao ponto A, iterando sucessivamente 1/5 da unidade. Referiram, ainda, que utilizariam o mesmo procedimento para apresentação do problema aos alunos (por exemplo, “Dividia ao meio e tinha C=1. Como de 0 a 1 estava dividido em 5 partes iguais então cada uma seria 1/5. Como até A são 2 partes então A é 2/5”; “Primeiro vi quanto valia cada espaço. Como a unidade está dividida em 5 partes iguais então cada é 1/5 . O A será 2/5”; “Encontrava primeiro o C que era 1. Via que estava a fazer uma contagem de 1/5 em 1/5 e com essa contagem encontrava todos os outros valores”. Enquadráveis nesse argumento, houve respostas igualmente consideradas corretas para a identificação de B e sua tradução da representação fracionária para decimal, por exemplo, de 1/8 para 0,8. Surpreendentemente, na mesma questão, 48,3% das respostas foram consideradas incorretas. Frequentemente os professores consideram erradamente como unidade o intervalo de 0 a 2, posicionando nele os pontos solicitados. A indevida consideração desse segmento como a unidade de comprimento conduziu a uma identificação incorreta das frações representadas: ao ponto A, correspondente à fração 2/5, os professores associaram incorretamente a fração 1/5; ao ponto B associaram a fração 4/10, quando deveria ser 8/10; ao ponto C associaram 1/2 (ou fração equivalente) em vez de 5/5 (ou fração equivalente). Para uma hipotética abordagem ao problema na aula, as explicações apresentadas refletiram a mesma incorreção. As respostas mais representativas relativamente à identificação do ponto A foram: “Duas divisões dessas têm de ser 1/5, para chegarmos ao fim e termos a unidade”; “Metade é 50%. Um quarto é 25%. Podemos dividir a reta em 5 partes. Repetimos 1/5 e temos a unidade”; “Primeiro tinha que ver que estava dividido em 10 espaços. Se estava dividido em 10 para chegar ao A tinha de pintar 2 espaços…. era metade… via que, assim, estava dividido em 5 partes e o A era 1/5”; “Dividimos a unidade em 10 partes mas para o ter o A contamos 5. O A é 1/5”; “São 10 casos. Para o A temos de agrupá-los. São 5 e o A é o primeiro, é 1/5”. Em 29% dos casos, os professores disseram não saber responder. O resultado obtido nesse problema sugere haver alguma dificuldade dos professores na exploração de uma reta numérica, em que não esteja explícita a unidade. Mas não será a marcação de pontos na reta numérica um conteúdo essencial, ao desenvolvimento do sentido de número, nos anos iniciais de escolaridade? Parece também aqui, no que respeita à representação de números racionais, existirem fragilidades no conhecimento dos professores, quer matemático quer didático.

Considerações finais

O ensino de frações é considerado difícil (LAMON, 2007; ^{SIEGLER; LORTIE-FORGUES, 2015} ) pelo motivo de pressupor o domínio do conceito, das suas diversas representações e da aplicação do conceito na resolução de problemas envolvendo diversos significados. Contudo, práticas de ensino frutíferas requerem conhecimentos matemáticos e didáticos adequados por parte do professor (BALL; THAMES; PHELPS, 2008; BORN; PRADO; FELIPPE, 2019; ^{SHULMAN, 1986} ).

Tal fato encontra eco nos resultados do presente estudo, quando sugerem que os professores do 1º. ciclo do ensino básico (anos iniciais do ensino fundamental) tendem a possuir conhecimentos pouco consistentes no que diz respeito ao conceito de fração e ao seu ensino. Por um lado, os professores não conhecem em profundidade os significados de fração, chegando mesmo a não saber indicar qualquer significado quando tal lhes é pedido. Identifica-se, assim, um incompleto conhecimento do currículo, já que em Portugal o tópico das frações integra as orientações curriculares para a Educação Básica (ensino fundamental). O conhecimento do currículo é uma das dimensões essenciais do conhecimento que o professor deve possuir para ensinar (BALL; THAMES; PHELPS, 2008; ^{SHULMAN, 1986} ). É expectável que os professores detenham um conhecimento apurado sobre os documentos curriculares, incluindo não só a capacidade de relacionar os conteúdos de ensino que lecionam com conteúdos que os alunos estejam aprendendo simultaneamente noutros domínios de saber – articulação horizontal, mas também o conhecimento daquilo que os alunos aprenderam em anos anteriores e que aprenderão em anos posteriores – articulação vertical (BALL; THAMES; PHELPS, 2008; CARDOSO, 2017; ^{SHULMAN, 1986} ).

No que toca à resolução de problemas envolvendo frações, com diversos significados (quociente, parte-todo, operador e medida), evidencia-se um forte conhecimento matemático. Tal contraste entre a falta de reconhecimento dos significados de fração e a capacidade de aplicação dos mesmos, na resolução de problemas, levanta questões sobre a relevância e a sistematicidade com que os professores abordam a diversidade de significados de fração, na aula de matemática. Esse aspecto merece a maior atenção, pois a construção do conceito de fração só está completa quando os alunos dominam os diferentes significados de fração e os traduzem em diferentes modos de representação (BEHR et al., 1983; CARDOSO; MAMEDE, 2009; NUNES et al., 2004). Um conhecimento matemático forte sobre a diversidade de significados de fração facultará aos alunos uma construção do conceito mais consistente. Aqui assume-se como particularmente importante o raciocínio, a comunicação e as representações matemáticas, inerentes à abordagem dessa diversidade de significados na sala de aula.

Ainda no caso da resolução de problemas, os conhecimentos matemáticos e didáticos dos professores revelaram-se não tão fortes quando se tratava de quantidades discretas e da representação de números na reta numérica. Na marcação de frações na reta numérica, os professores revelaram algumas dificuldades quando a unidade não se encontrava expressamente indicada. ^{Mamede e Pinto (2017)} identificaram essa mesma dificuldade entre alunos da formação inicial de professores. Esse aspecto pode constituir-se como condicionante à promoção de práticas que estimulam o raciocínio e a comunicação matemática, nos diferentes modos de representação dos números racionais.

Outro dos aspectos evidenciados neste estudo, e que merece reflexão, é a pouca consistência do conhecimento dos professores para traduzir e articular eficazmente as representações fracionárias e decimais. Contudo, esse é um ponto crucial no ensino de frações. O domínio dos diferentes modos de representação do número racional requer o domínio dessa articulação (BEHR et al., 1992; CARDOSO; MAMEDE, 2021; LAMON, 2007).

O conhecimento matemático dos professores influencia a aprendizagem dos alunos, pelo que é desejável a robustez desse conhecimento. Subscrevendo Li, Zhang e Song (2021), tal necessidade justifica-se pelo fato de proporcionar aos professores mais qualidade e confiança nas suas práticas de ensino. No ensino de frações, o professor necessita de um sólido conhecimento matemático e didático, que contemple uma diversidade de situações e representações, já que esta tem o potencial de promover um desenvolvimento apropriado do sentido de número racional dos alunos (CARDOSO; MAMEDE, 2021; MAMEDE; RIBEIRO; PINTO, 2021; ^{RIBEIRO, 2011} ).

Os resultados deste estudo, dizendo respeito à realidade portuguesa, podem encontrar afinidades noutras realidades. A formação inicial e a formação contínua de professores assumem aqui um papel crucial na promoção de práticas de ensino mais eficazes.