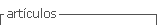Introdução
O tema ‘visualização’ tem sido objeto de investigação no cenário internacional, como na Conference of the International Group of Mathematics Education. Nessa direção, são apontados aspectos levantados em referências a trabalhos oriundos do Psychology of Mathematics Education (PME). Nos anais da 29a edição dessa conferência aparecem sugestões de investigações que podem proporcionar aos estudantes construções de fórmulas algébricas, por exemplo, com a inclusão de visualização e a manipulação de figuras nas quais os procedimentos de generalização são baseados (Gutièrrez; Boero, 2006).
Além disso, as representações estão presentes em processos investigativos sugeridos, como a transição entre o raciocínio visual e o analítico, com base em diferentes representações. Também é apontado que as representações constituem elemento importante que não deve ser confundido durante a visualização de gráficos, por exemplo, sem flexibilizá-la.
O Livro Didático (LD), no entender do autor deste artigo, desempenha, incontestavelmente, um papel significativo na tarefa do professor em sua ação pedagógica. Portanto, cabe investigar e analisar o que está sendo apresentado nessas referências, tanto do ponto de vista pedagógico quanto intelectual, muito embora o material disponibilizado pelo governo passe por um crivo de especialistas da área.
A experiência do autor do artigo com a formação de professores indica que esses geralmente se apoiam no livro didático que lhes é fornecido pelo governo, especialmente porque esses livros vêm acompanhados de um manual do professor que, de certa forma, reduz a tarefa de elaborar atividades diferenciadas, já que a carga em sala de aula, particularmente na escola pública, é bastante elevada, sendo acrescida da burocracia associada – mais ainda após a pandemia de COVID-19.
Ainda, a respeito do uso do LD pelo professor de Matemática, a pesquisa de Figueiredo e Sales (2009) buscou averiguar o nível de conhecimento de professores a respeito dos objetivos que fazem com que um determinado livro seja adotado e se ele se torna um instrumento de trabalho desses professores. Figueiredo e Sales (2009, p. 242) verificaram que “[...] há quem segue à risca a sequência e a metodologia proposta pelo livro”. Dessa forma, é importante que se discuta e se analise o LD, especialmente no que diz respeito à conceituação geométrica apresentada e à respectiva coerência.
Portanto, justifica-se a presente comunicação científica, que buscou investigar como duas coleções apresentam o conteúdo sobre polígono em níveis de ensino distintos, analisando inconsistências apresentadas, especialmente as teóricas e dos registros realizados.
Procedimentos Metodológicos
O presente artigo aborda uma pesquisa em educação em ciências, a qual, segundo Moreira (2011, p. 73), é compreendida como “[...] a produção de conhecimentos resultante da busca de respostas a perguntas sobre ensino, aprendizagem, currículo e contexto educativo em ciências [...]”, portanto, com foco qualitativo. A pesquisa qualitativa buscou responder ao seguinte problema: existe coerência conceitual em duas coleções de livros didáticos aprovados pelo Programa Nacional do Livro Didático (PNLD) a respeito do uso do conceito de polígono? A fim de buscar resposta, delineou-se o seguinte questionamento: livros didáticos do Ensino Fundamental apresentam de modo coerente o conceito de polígono? Esse objetivo pode ser focado nos seguintes objetivos específicos: (a) analisar como uma coleção de LD destinada ao primeiro segmento do Ensino Fundamental apresenta o tema polígono; (b) analisar como uma coleção de LD destinada ao segundo segmento do Ensino Fundamental aborda o tema polígono, e (c) verificar a coerência conceitual abordada nos registros em língua natural e figural do conceito polígono.
Ao analisar como o conceito de polígono é apresentado em livros de primeiros anos do Ensino Fundamental e, posteriormente, dos quatro anos finais desse mesmo segmento, de duas coleções avaliadas pelo PNLD, pode-se interpretar essas colocações à luz dos conceitos matemáticos formais.
Para Severino (2016, p. 131), em relação à natureza da pesquisa, a bibliográfica “[...] é aquela que se realiza a partir do registro disponível, decorrente de pesquisas anteriores em documentos impressos, como livros, artigos, teses etc.” Sendo o LD um documento impresso, disponibilizado aos professores inclusive com manuais específicos e com sugestões de respostas, entende-se ser esse um precioso material de pesquisa como a que se propõe neste artigo – a saber, como livros didáticos abordam o conceito de polígono e a coerência entre o conceito matemático formal e o respectivo figural.
É importante destacar o que os Parâmetros Curriculares Nacionais (PCN) recomendam a respeito da temática. Em Brasil (1997), tem-se o bloco ‘Espaço e Forma’ para os Anos Iniciais, em que é sugerida: a identificação de figuras poligonais; identificação de semelhanças e diferenças entre polígonos; identificação de que qualquer polígono pode ser compostos a partir de figuras triangulares, dentre outros. Cabe destacar, como detalhar-se-á mais a frente, polígonos são figuras constituídas de linhas (segmentos de reta).
Por sua vez, o mesmo documento apresenta o conteúdo ‘Grandezas e Medidas’, que destaca a escolha de uma unidade de medida da mesma espécie do atributo (Brasil, 1997) – por exemplo, comprimento e área, aqui destacados em virtude da pretensão do artigo de argumentar sobre uma distinção fundamental entre os conceitos de polígono e região poligonal que nem sempre é bem feita no LD, como será ilustrado nas análises. De imediato pode-se já indicar que as linhas correspondem à medida ‘comprimento’ e as regiões, à medida ‘área’.
Foram analisados dois livros, aqui nomeados como L11 e L12 para evitar que sejam identificados. O L11 é voltado ao 1º ano e o L12, ao 2º ano do Ensino Fundamental – Anos Iniciais. Além disso, foram analisados os livros L21, L22, L23 e L24, direcionados a turmas do 5º ao 9º ano. O primeiro índice indica a coleção e o segundo, o volume.
Ambas as coleções foram analisadas a partir do manual do professor a fim de que fosse possível constatar se as respostas/resoluções dadas pelos autores e/ou as sugestões eram condizentes com os conceitos matemáticos envolvidos na temática. Assim, partiu-se do que é apresentado aos estudantes ao começar sua formação inicial do conceito de modo a verificar como ocorre a visualização e a representação desses polígonos para, posteriormente, verificar se o conceito chega a ser trabalhado de forma rigorosa (conceitual) ao final desse nível de escolaridade. Além disso, intenciona-se comprovar que, em algumas situações, são feitas confusões e que o registro em língua natural (conceito) não corresponde ao registro figural (figura).
Na sequência, são apresentados alguns pressupostos teóricos sobre as habilidades de visualização e representação encontradas na literatura, bem como sobre os registros de representação semiótica.
Pressupostos Teóricos
O tema ‘visualização’ é abordado por Leivas (2009, p. 111) como “[...] um processo de formar imagens mentais, com a finalidade de construir e comunicar determinado conceito matemático, com vistas a auxiliar na resolução de problemas analíticos ou geométricos”. Esse é o tema de pesquisa de vários autores internacionais, como Arcavi (1999), Presmeg (1986), entre outros.
Além disso, faz-se necessário investigar tipos de raciocínio que no que diz respeito ao ensino e na aprendizagem, nos quais a imaginação visual é empregada na formação de conceitos matemáticos e esquemas mentais – o que é reiterado nas pesquisas de Duval (2004), particularmente na conversão entre registros. Isso, por sua vez, vai ao encontro do que Skemp (1993) denomina compreensão relacional, em contrapartida à instrumental. Para ele, um símbolo visual tem um vínculo mais estreito com o conceito do que o verbal, com o que se julga pertinente associar aos pressupostos por Duval (2004).
Ao abordar os aspectos cognitivos de aprendizagem e ensino do conteúdo com base na teoria de Duval (2004), Hitt e González-Martín (2004, p. 38) afirmam:
[...] as representações matemáticas dos objetos são fundamentais, uma vez que elas permitem a apreensão de conceitos matemáticos. O processo de conversão entre diferentes representações, portanto, desempenha um papel essencial na construção de conceitos matemáticos, articulação entre registros de representação, tornando-se uma parte essencial do processo de aprendizagem.
Segundo os autores supracitados, é importante explorar as representações no ensino de polígonos, particularmente no Ensino Fundamental, em que a formação do pensamento matemático/geométrico se estabelece.
Para Piaget e Inhelder (1993), a análise psicogenética do espaço apresenta uma grande dificuldade tendo em vista que a construção das formas ocorre de modo contínuo em relação às espaciais. Para os autores, essa construção ocorre “[...] em dois planos bem distintos: o plano perceptivo ou sensório-motor e o plano representativo ou intelectual” (p. 17). Isso significa que é necessário, já no início da escolaridade, que seja proporcionado à criança se colocar ante atividades que venham desenvolver a primeira das duas habilidades e, somente nos anos subsequentes, parta para as representações, quando ela já teria construtos mentais do objeto matemático internalizado. Evidentemente isso também requer outras habilidades como a intuição, a criatividade e a imaginação, que, conjuntamente, propiciam o desenvolvimento do pensamento geométrico.
Em relação ao espaço perceptivo, os autores indicam que sua construção ocorre em três grandes linhas no desenvolvimento da criança, desde o nascimento até chegar à fase da representação. São elas: período dos puros reflexos e aquisição dos primeiros hábitos; período das reações circulares secundárias – isto é, quando se inicia a manipulação dos objetos – e, período das reações circulares terciárias, no qual tem início a experimentação (Piaget; Inhelder, 1993).
Portanto, é fundamental que o LD dos Anos Iniciais conduza a atividades que visem ao desenvolvimento desses estágios iniciais da formação das crianças. Por essa razão, a presente pesquisa começou analisando como o LD elaborado para os dois primeiros anos do Ensino Fundamental focava a temática ‘polígono’ dentro de um contexto como o indicado por Piaget e Inhelder (1993).
Ao abordar a transição de imagens mentais (visualização no sentido apontado pelo autor deste artigo) embasado nas representações semióticas e na visualização (no sentido apontado por Duval (2004)), Hitt e González-Martín (2004, p. 38), embora focando no tema ‘funções e cálculo’, tratado no PME, indicam que os processos de conversão entre os diferentes registros de representação são partes essenciais da aprendizagem, e as pesquisam mostram que “[...] O objetivo principal é compreender as dificuldades que os alunos experimentam ao fazer um tratamento no mesmo registo de representações [...]”. Na realidade, isso é o que geralmente ocorre quando são abordados esses dois temas por meio da aplicação direta de regras de derivação e integração, por exemplo, ou da identificação de funções pelas suas leis algébricas (compreensão instrumental, segundo Skemp (1993)).
Concluindo os pressupostos teóricos, busca-se, na literatura especializada, os conceitos de polígono e de região poligonal. No clássico livro de Downs (1971, p. 271), o autor diz que “Uma região poligonal é uma figura plana formada pela justaposição de um número finito de regiões triangulares, de um plano, de tal modo que, se duas se interceptam, a intersecção é um ponto ou um segmento”. A partir disso, discorre sobre implicações relacionadas a esse conceito, como os postulados de área, de congruência, de adição de áreas etc.
No livro 2 de sua obra, Downs (1971, p. 474) diz que “Um polígono é uma figura formada pela junção de segmentos, extremidade a extremidade” e ilustra com várias representações figurais para, então, definir formalmente:
Seja P1, P2, ..., Pn uma sequência de n pontos distintos num plano com n>3. Suponha que os n segmentos P1 P2, P2 P3 ,..., Pn-1 Pn ,, Pn P1 têm as seguintes propriedades:
1. Nenhum par de segmentos se intercepta a não ser nas suas extremidades.
2. Nenhum par de segmentos com extremidade comum é colinear.
Então, a reunião dos n segmentos é chamada de polígono. P1, P2 , ..., Pn são chamados seus vértices e P1 P2, P2 P3 ,..., Pn-1 Pn ,, Pn P1 são os seus lados
(Downs, 1971, p. 474).
Em outra obra específica, Barbosa (2005) aborda a temática a partir do conceito de poligonal; ou seja, de uma linha e não de triângulos, como é feito pelo autor anterior. Para o autor, “Uma poligonal é uma figura formada por uma sequência de pontos A1, A2, ..., An e pelos segmentos A1A2, A2A3, ..., An-1An” (Barbosa, 2005, p. 38). Percebe-se aqui que o autor se utiliza de outra representação para segmentos, não colocando uma barra acima das letras que definem os extremos, porém esses são precedidos da palavra ‘segmento’. Nota-se, também, o uso do termo ‘linha’ (não fechada). O autor utiliza, além disso, atividades propostas para envolver os conceitos. Na atividade seguinte, diz que “Um polígono é uma poligonal em que as seguintes 3 condições são satisfeitas: (a) An=A1, (b) os lados da poligonal se interceptam somente em suas extremidades, (c) cada vértice é extremidade de dois lados e (d) dois lados com mesma extremidade não pertencem a uma mesma reta” (Barbosa, 2005, p. 38). Após cada uma das definições, o autor traz uma tarefa para o leitor resolver, inclusive com registros geométricos.
A escolha das duas referências deve-se às datas em que foram publicadas, uma vez que coincidem com o período da reforma do ensino brasileiro e do surgimento de uma diversidade de livros didáticos.
Análise dos livros
A primeira obra analisada foi a L11, direcionada ao 1º ano do Ensino Fundamental, cuja avaliação se deu através do manual do professor. Busca-se, na literatura especializada consagrada, os conceitos de polígono e região poligonal. A obra é constituída por unidades que se conectam a temas do dia a dia da criança, sem ater-se a definições. Na apresentação, os autores explicitam: “Você já deve ter observado que em quase todas as situações do nosso dia a dia utilizamos conhecimentos diversos inclusive conhecimentos matemáticos” (L11)2.
Nota-se, pois, a intencionalidade de colocar a criança face a face com situações reais, como em pequenas histórias envolvendo curiosidades, aventuras, animais, álbuns etc. Ao explorar embalagens, a ilustração mostra uma senhora que contorna as faces de uma caixa com diferentes formatos geométricos coloridos (um paralelepípedo retângulo, um cubo e um cilindro, na linguagem matemática) em folhas de papel. Em seguida, o LD apresenta a Figura 1 e questiona qual desenho poderia representar as faces contornadas por ela.
As figuras são enumeradas de 1 a 3, com um número embaixo de cada uma, e questiona-se qual é o formato de caixa desenhado. Nota-se aqui a importância, já nesse início de escolaridade, do que seja uma linha (poligonal ou circular) e não de uma região, como é encontrado em muitos livros didáticos o que se observará mais adiante. Isso vai na direção das definições supracitadas. Outro fato importante é o uso de cores e materiais concretos para introduzir noções geométricas, o que ocorre nas páginas subsequentes ao passar para outras imagens de figuras planas, desvinculando do material concreto – o que vai ao encontro da visualização como construto mental (Leivas, 2009). Em seguida, o autor do LD passa a usar a fita métrica e a régua para explorar medidas. Portanto, evoca-se aqui o preconizado nos PCN e BNCC a respeito dos quesitos: ‘Geometria e Formas’ e ‘Grandezas e Medidas’. No final do livro há moldes que o professor pode trabalhar com seus alunos e, com isso, sanar dificuldades, como indicado por Piaget e Inhelder (1993) a respeito da construção das formas, pois explora-se, nesse tipo de atividade, os planos ‘perceptivo’ ou ‘sensório-motor’ e o ‘representativo’ ou ‘intelectual’, uma vez que podem ser introduzidos os registros figurais.
Passando à análise do volume seguinte da mesma coleção – isto é, o L12 –, verifica-se o mesmo tipo de abordagem do primeiro volume, ou seja, a associação de formas geométricas com o mundo real da criança. Por exemplo, certa atividade do LD indica que uma menina (nome retirado para evitar identificação) percebe que a laranja tem formato de esfera e, ao parti-la ao meio, faz uma descoberta. O registro figural da laranja e suas duas metades é apresentado e, em seguida, indica que o formato do corte na figura lembra um círculo – o que é apropriado, pois o volume anterior abordou linhas e, no caso, a imagem fornecida estaria associada a uma região.
Cabe salientar que as bordas das duas metades são bem destacadas pela casca, o que permitiria uma diferenciação inicial, pela criança, de circunferência e círculo – o que nem sempre é explorado, uma vez que, para Euclides, usar o registro ‘círculo’ correspondia à ‘circunferência’ e vice-versa. No entanto, com Descartes, a Geometria passa a abordar, também, os objetos através de registros algébricos. Enquanto para o círculo tem-se uma desigualdade, para a circunferência tem-se uma igualdade, nas respectivas leis. Como afirma Duval (2004), só há aprendizagem quando ocorre a conversão de dois tipos de registros, ao menos. Portanto, é importante que a nomenclatura correta surja naturalmente já no início da aprendizagem.
Na sequência, o LD apresenta novas atividades envolvendo caixas, oferecendo moldes para as crianças montarem e verificarem se alguma das formas resultantes tinha o formato da esfera. Muito embora também se deva fazer distinção entre uma esfera e um sólido de superfície esférica pelos motivos já citados, aqui houve a preocupação de diferenciar as figuras geométricas espaciais que rolam das que não rolam. Dessa maneira, explorando o visual, o LD buscou diferenciar os paralelepípedos (objetos com faces) dos objetos que rolam (sem faces, cilindros, cones etc). Na sequência são abordadas as pirâmides.
O L12 volta a tratar das embalagens, contornando as faces em representações figurais para generalizar o conceito de polígono com número de lados maior do que os apresentados tanto nesse exemplar quanto no L11.
Conclui-se da análise realizada nesses dois primeiros exemplares que os aspectos cognitivos a respeito de polígonos foram coerentes com o indicado pelos dois autores que abordam a matemática formal, Downs e Barbosa, num processo de ensino que poderá proporcionar uma boa formação de pensamento geométrico por desenvolver (habilidade visuais, a criatividade e a imaginação dos alunos. Isso também vai ao encontro do que Hitt e González-Martín (2004) afirmam a respeito da importância da teoria de Duval (2004) no que diz respeito à apreensão dos conceitos matemáticos, em particular o aqui analisado – polígono –, explorando a conversão de pelo menos dois registros. Os dois volumes exploram a imaginação quando a criança vivencia uma pequena situação hipotética, associa com o material oferecido pelo professor e abstrai para as representações figurais.
A fim de não delongar na análise preliminar realizada, a qual mostra uma boa forma de iniciar o processo de ensino do tema em apreço, passa-se à análise dos livros da segunda coleção – ou seja, os livros L21, L22, L23 e L24, respectivamente de 6º, 7º, 8º e 9º ano – feita a partir dos exemplares destinados ao professor.
No primeiro deles, o livro trata das figuras geométricas espaciais. Ao discorrer sobre a nomenclatura de prisma e pirâmide, os autores propõem atividades para o aluno responder. A partir da ilustração de uma pirâmide de base hexagonal, entre outros itens, as seguintes perguntas são feitas aos alunos: Qual a forma de suas faces laterais? E de sua base? As respostas, grifadas em vermelho no exemplar do professor, são: triângulos; hexágonos. Como a figura não é apresentada apenas pelas arestas, e, sim, colorida, percebe-se aqui um conflito cognitivo, uma vez que a face não é um polígono e sim uma região plana. Portanto, a resposta sugerida pelos autores deveria ser uma forma triangular ou região triangular e uma forma hexagonal ou região hexagonal. Isso, no entender do autor deste artigo, confunde o conceito de ‘Geometria e Formas’ e pode gerar uma falsa associação com ‘Grandezas e Medidas’, uma vez que o polígono apresenta a medida do comprimento, enquanto a região apresenta a medida da área.
No mesmo volume, mais adiante, os autores oferecem um capítulo sobre polígonos, que tem início com cinco representações de linhas diversas, abertas e fechadas, caracterizando-as como linhas planas. Em seguida, solicitam, entre outras coisas, que os alunos desenhem, em uma folha de papel, várias linhas planas fechadas e pintem a região do plano limitada por elas. As regiões coloridas são apresentadas em dois grupos, um na qual constam regiões convexas e outro com regiões não convexas delimitadas por um quadrado, um triângulo e um hexágono, portanto, regiões poligonais. Os autores orientam o professor que a atividade visa proporcionar aos alunos o aprendizado sobre o conceito de polígono, e ampliam a orientação recomendando ao professor que divida os alunos em duplas para elaborarem uma descrição de polígonos convexos e não convexos, muito embora a atividade explorasse uma região poligonal, já que o interior das linhas estava todo colorido.
Dando sequência, o assunto trabalhado foi a identificação de polígonos, sendo sugeridas quatro figuras com o interior totalmente preenchido: a primeira no formato oval, a segunda limitada por um paralelogramo, a terceira limitada por um triângulo e a quarta, por uma circunferência. O LD destaca que, entre elas, as que estão limitadas por linhas fechadas simples, formadas unicamente por um segmento de retas, são chamadas de “polígonos”. Em seguida, esclarece que “Polígono é a reunião de uma linha fechada simples, formada apenas por segmento de reta, com a sua região interior” (L24, grifo próprio). Na sequência são trabalhados polígonos específicos: triângulos, quadriláteros etc., sempre usando o conceito de polígono, porém com o interior da figura colorido – ou seja, identificando a região e não o polígono. Inclusive, ao desenvolver o conceito de ‘comprimento’, os autores utilizam figuras com a região interior colorida.
Retomando os conceitos de Downs (1971) e Barbosa (2005), conclui-se que há um equívoco na definição apresentada no conjunto da obra (registro em língua natural), bem como nos registros figurais. Portanto, a conversão preconizada por Duval (2004) e possivelmente desejada pelos autores do L21, não fornece aprendizagem. Além disso, não ocorre uma aprendizagem por compreensão relacional (que leva à conceituação), nem por compreensão instrumental (uso de regras), como indicado por Skemp (1993).
Ao analisar o manual do professor do livro L22, constata-se que seus autores elaboraram um capítulo destinado a transformações geométricas e simetrias. Ao introduzi-lo com considerações sobre artes e envolvimento de figuras, solicitam que seja identificado, entre quatro delas, se há o reconhecimento de figuras geométricas que possuem a mesma forma e o mesmo tamanho. Entre essas figuras, as quatro primeiras, de fato, envolvem polígonos (quadrados, triângulos etc.), e na quarta imagem já são vistas algumas formas preenchidas.
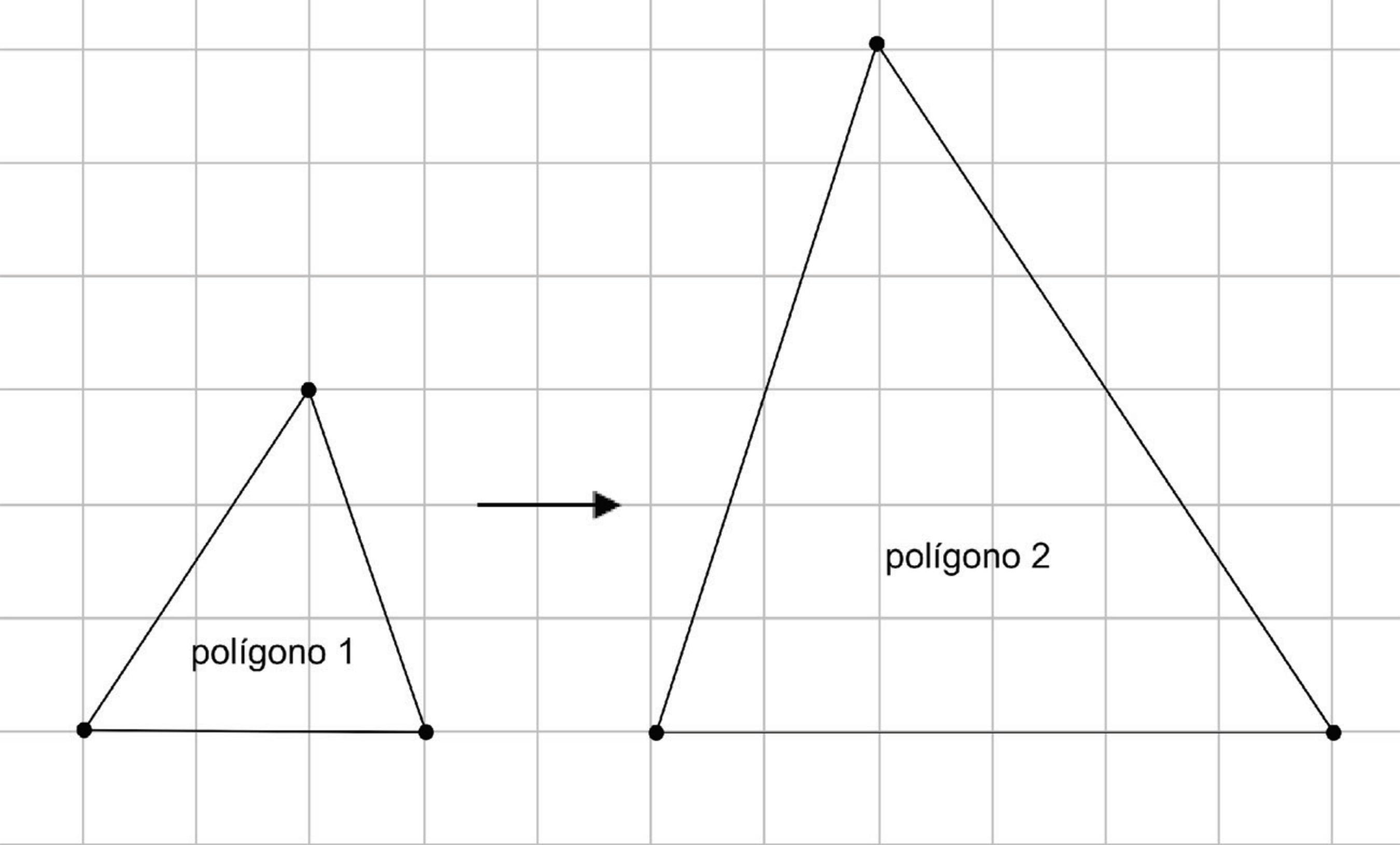
Na sequência, praticamente todas as atividades são representações de regiões poligonais, inclusive quando se indica a reflexão de uma figura em uma grade quadriculada em torno de um ponto e ilustra-se uma figura similar à do tipo a seguir (Figura 2).
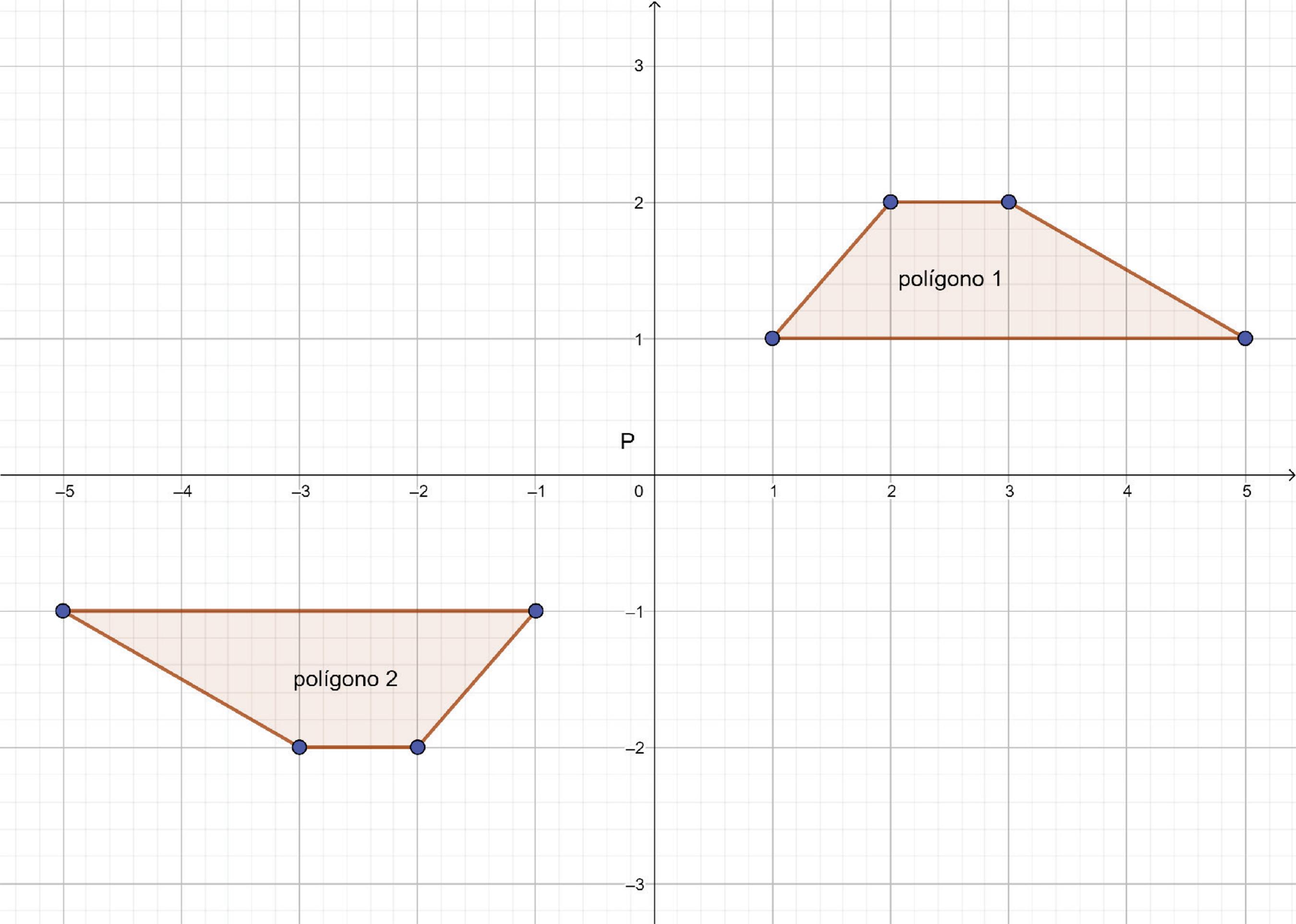
Fonte: Adaptado de L22 pelo autor no Geogebra.
Figura 2 Representações de polígonos/regiões segundo os autores.
Percebeu-se que, tanto no texto inicial quanto no explicativo ao lado, é dito que o polígono 2 tem a mesma forma e tamanho que o original (grifo do autor do artigo para destacar a linguagem utilizada pelos autores do LD).
Na página seguinte é utilizada uma imagem para ilustrar a ampliação (ou a redução) de figuras geométricas, e, para os autores, a figura representa polígonos (Figura 3).
Fonte: Adaptado de L22 pelo autor no Geogebra.
Figura 3 Representações de polígonos/regiões segundo os autores.
Nessa atividade, os autores pretendiam explorar a ampliação e/ou a redução, segundo eles, de um “polígono”. Na orientação didática, na mesma página, os autores afirmam ser essa uma forma diferente de usar uma malha quadriculada para fazer ampliação e redução de “polígono”. Em páginas subsequentes, novamente são feitas alusões a polígonos quando são indicadas as representações figurais em conexão com a simbólica em língua natural.
A visualização é tratada por Leivas (2009) como um processo de formação de construtos mentais e, nesse sentido, ter duas representações distintas para um mesmo conceito certamente não leva à sua construção. Considera-se, novamente, o indicado por Duval (2004), que diz que a aprendizagem se consolida na medida em que o estudante consegue realizar uma conversão de um registro para outro e vice-versa. Assim, ao apresentar dois registros figurais associados ao registro em língua natural de um polígono, possivelmente se estabelecerá um conflito cognitivo para o estudante.
No livro L23 da mesma coleção, voltado ao 8º ano, é feito um estudo sobre ângulos e triângulos. Aqui, os autores começam a construção de triângulos por meio de palitos, inclusive de um triângulo e de um quadrado. Em seguida já é retomado o termo ‘triângulo’ e a representação figural correspondente tem a região interior colorida, até que, ao estudar alturas, uma das representações, dá somente por linhas, mas volta-se a colorir a região interior ao envolver medianas, bissetrizes e mediatrizes. Isso ocorre nas atividades que seguem. Ao desenvolver polinômios e expressões algébricas é utilizado, já de início, o retângulo como anteriormente apresentado – ou seja, uma região retangular. Já mais para o final da obra, volta-se a trabalhar com polígonos para explorar seus elementos, e não há conversão de um registro para outro, uma vez que o figural não corresponde ao simbólico em língua natural. Retoma-se aqui o dito por Arcavi (1999, p. 217) quando o autor destaca a visualização como “[...] o processo e o produto de criação, uso e comentário sobre figuras, imagens, diagramas etc”, o que conduz, no entender do autor do artigo, a uma falta de caracterização de polígono, confundindo o conceito com o de região poligonal, uma vez que os dois registros não são coesos.
Por fim, para concluir a análise dos quatro exemplares da obra, destacam-se algumas colocações sobre a temática do presente artigo no que diz respeito ao L24, destinado ao 9º ano. De forma similar ao que foi apresentado nos três volumes anteriores, nesse também raramente o polígono tem sua representação visual feita corretamente pelos segmentos que o formam. Em quase todas as vezes que aparece, o termo polígono é associado à figura de uma poligonal com seu interior totalmente colorido – ou seja, representando a região poligonal. Isso ocorre, inclusive, quando são abordados produtos notáveis e o Teorema de Pitágoras.
Os autores apresentam o que denominam de triângulo retângulo (Figura 4a) indicando em registro natural o que são catetos e o que é hipotenusa, e, em seguida, trazem o registro figural do Teorema de Pitágoras (Figura 4b).
Reforça-se a intencionalidade dos autores em manter as figuras geométricas de polígonos pintando o interior delas. Julga-se importante destacar, no processo de ensino do Teorema de Pitágoras, o estabelecimento da diferença conceitual envolvendo a palavra ‘quadrado’. Como não há distinção entre o registro em língua natural do termo e o figural, os estudantes ficam com a concepção errônea de que o teorema é válido somente para esse quadrilátero, o que não corresponde à realidade matemática. O Teorema de Pitágoras é válido quando se usam triângulos, retângulos, lunas etc. sobre catetos e hipotenusa. Portanto, o uso de outros registros figurais permite que não se faça confusão com o termo ‘quadrado’, que corresponde à operação de elevar ao quadrado e não à figura. Um trabalho que aborda a Teoria de Van Hiele e tais representações podem ser encontradas em Leivas (2017).
Para finalizar esta análise, reporta-se que, no final do L24, os autores tratam das relações métricas na circunferência e, nesse capítulo, de fato, o conceito empregado é o de uma linha. Ao abordar a área do círculo, a representação figural de fato surge com interior colorido. Porém, no que diz respeito à inscrição de polígonos, esses têm seu interior preenchido.
Considerações Finais
Este artigo teve como objetivo analisar como alguns livros didáticos abordam o conceito de polígono, considerando que os registros de representação dos objetos geométricos proporcionam aprendizagem na medida em que são oferecidas atividades que indiquem conversões entre eles (figural, língua natural, simbólico), como indicam autores supra citados.
Dessa forma, proporcionar aos estudantes, especialmente aos do Ensino Fundamental, atividades condizentes com os conceitos podem oportunizar processos de ensino e de aprendizagem que os conduzam ao desenvolvimento do pensamento geométrico, inclusive à chegada ao formal e às relações entre os elementos, no caso de polígonos – tema abordado ao longo deste segmento educativo.
Entende-se que o processo e o produto de criação bem como o de representação como citados por autores referenciados neste artigo, precisam ser desenvolvidos desde o início da formação da criança, o que leva à importância de que os livros didáticos sejam coerentes tanto no que diz respeito à formalização correta de nomenclaturas, quanto ao nível de aprofundamento conceitual.
Por essas razões, tomou-se para análise dois volumes destinados aos dois primeiros anos do Ensino Fundamental e, posteriormente, quatro outros volumes, destinados aos quatro anos finais do mesmo ciclo, de duas coleções distintas, por meio de exemplares do manual do professor aos quais se teve acesso.
Foi constatado que os livros analisados destinados aos primeiros anos da Educação Infantil exploram, por meio de histórias hipotéticas ou de elementos encontrados ao redor dos indivíduos, o conceito de polígono estabelecendo, geralmente, conversões possíveis entre o conceito (ainda não formal) – porém na linguagem correta e na figural, com os polígonos determinados por linhas fechadas.
Portanto, a coordenação visual-motora é empregada, e, ao que tudo indica, a visualização vai se estabelecendo como um construto mental.
Já na segunda coleção analisada, era esperado que o formalismo conceitual se estabelecesse em seus quatro volumes. No entanto, reiteradamente os livros trazem o registro da palavra polígono, porém o representam a partir de uma região poligonal, uma vez que deixam o interior da figura colorido. Logo, o construto mental do que seja um polígono confunde-se com o de região poligonal, e isso tem consequência imediata no que diz respeito aos conceitos de Geometria e Forma e de Grandeza e Medida.
Percebe-se, portanto, que ao solicitar que o estudante observe uma figura e identifique o que é polígono e o que não é, entre outras colocações, é possível que não ocorra uma conversão entre os dois tipos de registros, e, com isso, o conceito de polígono como definido anteriormente não é consolidado.
Entende-se, portanto, que os livros da primeira coleção propiciam um início de ensino e de aprendizagem coerentes com o indica como compreensão relacional, o que, por sua vez, não acontece com os livros da segunda coleção.