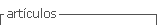Introdução
O campo de pesquisa dedicado ao estudo da matemática e dos aspectos envolvidos em sua aprendizagem é amplo e repleto de investigações com diferentes enfoques. Para melhor compreender como os pesquisadores abordam a matemática e os fatores envolvidos no seu aprendizado e, consequentemente, as dificuldades de aprendizagem, serão discutidos elementos essenciais para a aquisição da matemática, como o senso numérico e um de seus aspectos: os princípios de contagem. Além disso, serão apresentados estudos preditivos do desempenho matemático, pesquisas que investigam as características das crianças que apresentam dificuldades de aprendizagem nessa área, assim como estudos de intervenção.
Senso numérico e princípios de contagem
O senso numérico é um constructo geral, o qual engloba um conjunto amplo de conceitos que o aluno aprende gradualmente, partindo de suas interações com o meio social; é uma forma de interagir com os números, seus usos e suas interpretações, de modo a possibilitar que os sujeitos lidem com situações diárias que envolvam quantificações e que desenvolvam estratégias eficientes para lidar com problemas numéricos (Corso; Dorneles, 2010). Sua origem é tanto inata quanto construída, uma vez que, conforme afirma Spinillo (2014), há comprovação da existência de um aparato biológico que permite prestar atenção às numerosidades (Antell; Keating, 1983; Dehaene, 1997; Starkey; Cooper, 1980; Strauss; Curtis, 1981), mas, ainda assim, é necessário ter experiências sociais para construir aprendizagens matemáticas.
Esse constructo é composto de diversos aspectos e habilidades, constituindo-se como uma forma de pensar que deve permear todas as situações de ensino, em todos os campos da matemática, desde a educação infantil até o final da escolarização (Spinillo, 2014). Sua aprendizagem começa com experiências informais do cotidiano, como utilizar o controle remoto da televisão, formar conjuntos de brinquedos e até mesmo contar.
A contagem, por sua vez, possui papel muito importante na aprendizagem matemática, conforme discute Dorneles (2004) ao referir que é uma ferramenta cognitiva relevante para o desenvolvimento de habilidades matemáticas e para a compreensão de conteúdos posteriores. Na área de estudos do ato de contar, Gelman e Gallistel (1978) foram alguns dos primeiros pesquisadores a se dedicarem à análise da contagem das crianças. Os autores evidenciaram a existência de cinco princípios de contagem que regem o processo:
1) correspondência termo a termo: cada item contado em uma matriz é marcado uma vez, distintamente;
2) ordem constante: os nomes usados para contar os itens em uma matriz serão sempre ditos da mesma forma em uma ordem repetível;
3) cardinalidade: o último nome dito ao final da contagem de itens em uma matriz corresponde ao total de itens;
4) abstração: qualquer conjunto pode ser contado;
5) irrelevância da ordem: o mesmo número cardinal será encontrado, independentemente da ordem em que os itens na matriz forem contados, desde que os princípios anteriores sejam respeitados.
Em relação à contagem, é possível, ainda, analisar as estratégias e os procedimentos utilizados pelas crianças. Entre as estratégias, Geary (2004) identifica a contagem verbal, a contagem nos dedos, a decomposição e a recuperação imediata. No que se refere aos procedimentos, o autor identifica o “contar todos” e o “contar a partir de”, considerando que o primeiro envolve contar as duas parcelas e depois realizar o cálculo, por exemplo, 3+8 = 1, 2, 3 + 1, 2, 3, 4, 5, 6, 7, 8 = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, enquanto o segundo consiste em iniciar a contagem pela parcela maior e seguir contando a outra parcela: 8+3 = 8 + 6,7,8 = 11 (Geary, 2004).
Os estudos preditivos apresentados no Quadro 1 foram realizados visando identificar quais são os fatores preditores do desempenho matemático posterior. Diferentes estudos identificam a presença do senso numérico e dos princípios de contagem como fatores com forte valor preditivo do desempenho matemático.
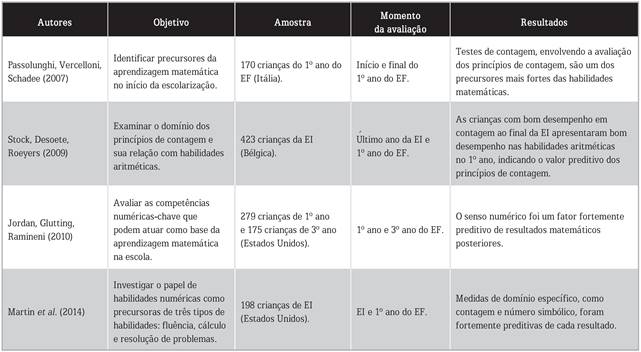
Fonte: Elaborado pelas autoras.
Legendas: EI: educação infantil.
EF: ensino fundamental.
Quadro 1 Estudos preditivos
Considerando o senso numérico e os princípios de contagem como importantes preditores do desempenho matemático, de acordo com os resultados apresentados anteriormente, outros estudos foram desenvolvidos visando investigar as características dos alunos com e sem dificuldades de aprendizagem em matemática. Os achados foram organizados no Quadro 2.
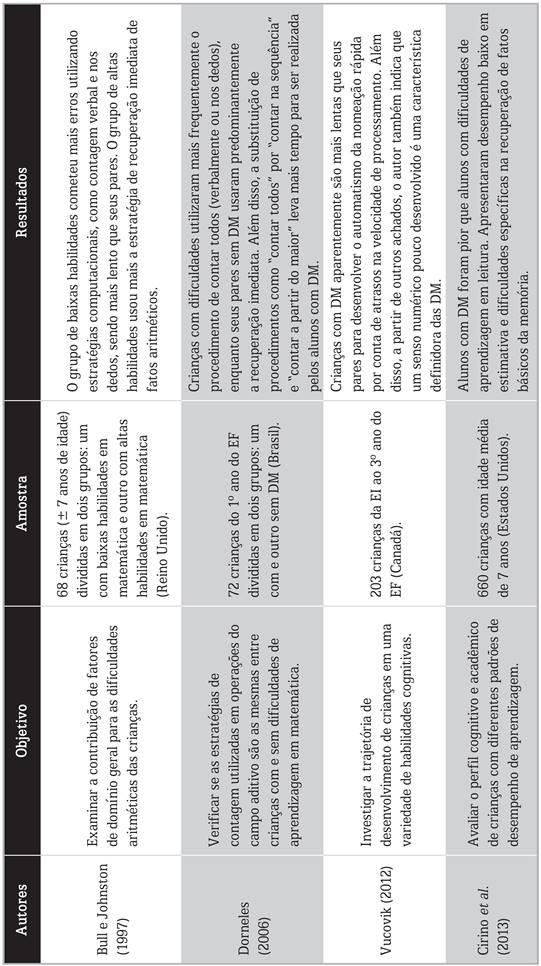
Fonte: Elaborado pelas autoras.
Legendas: EI: educação infantil.
EF: ensino fundamental.
DM: Dificuldades em matemática.
Quadro 2 Estudos sobre as características de alunos com e sem dificuldades de aprendizagem
Entre os resultados expostos, pode-se identificar que alunos com dificuldades de aprendizagem em matemática utilizam estratégias de contagem imaturas por mais tempo (contar nos dedos, por exemplo) e têm problemas para recuperar fatos básicos da memória. Como mencionado anteriormente, a contagem é um fator imprescindível para a aprendizagem matemática, e a falta de domínio nesse âmbito pode resultar em sérios problemas. Além disso, o senso numérico pouco desenvolvido também foi apontado como característica definidora das DM e, consequentemente, acabou sendo alvo do desenvolvimento de intervenções para auxiliar as crianças a consolidá-lo. Algumas pesquisas desse tipo são descritas no Quadro 3.
Essas pesquisas de intervenção foram realizadas com foco no senso numérico, como se pode observar na descrição dos componentes enfatizados em cada estudo. De fato, os pesquisadores reconhecem a importância do constructo para a aprendizagem matemática e, nesse sentido, buscam auxiliar as crianças a consolidá-lo, mas há escassez de pesquisas de intervenção especificamente em princípios de contagem, alertando para a necessidade do desenvolvimento de estudos nesse âmbito. A relevância da realização de um trabalho desse tipo é justificada, uma vez que a contagem é imprescindível para construir conhecimentos matemáticos posteriores (Dorneles, 2004), sendo evidenciada como um aspecto problemático no grupo de alunos que apresenta DM (Bull; Johnston, 1997; Cirino et al., 2013; Dorneles, 2006).
No intuito de contribuir com essa discussão, desenvolveu-se um estudo experimental de intervenção em princípios de contagem com alunos de 1º ano do ensino fundamental. Realizar uma intervenção nessa área logo no início da escolarização formal é uma forma de prevenir e/ou minimizar possíveis dificuldades de aprendizagem em matemática, uma vez que a consolidação de tais princípios, conforme mencionado anteriormente, é fundamental para o desenvolvimento de conhecimentos matemáticos posteriores. Os objetivos destacados são: a) verificar a ocorrência de avanços nos princípios de contagem, em crianças do 1º ano, do pré-teste, para o pós-teste; b) avaliar a efetividade de uma intervenção de curta duração, específica sobre os princípios de contagem, comparando o desempenho entre grupo controle e grupo experimental. Tem-se como hipótese que todas as crianças apresentem avanços do pré-teste para o pós-teste, uma vez que estarão frequentando as aulas regulares e, consequentemente, aprendendo conteúdos relacionados à matemática. No entanto, espera-se que os avanços das crianças do grupo experimental sejam maiores que os avanços daquelas do grupo controle, de modo a evidenciar a melhora no desempenho por conta do programa de intervenção, o que possibilitará verificar a efetividade deste.
Método
Amostra
Inicialmente, 150 crianças foram autorizadas por seus responsáveis, mediante o Termo de Consentimento Livre e Esclarecido, a participar da pesquisa. Dessa amostra, uma menina trocou de escola; 2 meninos não concordaram em realizar as avaliações; 7 crianças estavam ausentes nos dias em que o pré-teste foi realizado; 4 alunos não conseguiram responder às tarefas avaliativas por conta de algum tipo de deficiência. Considerando a exclusão desses 14 sujeitos, a amostra total do estudo experimental contou com 136 crianças: 6 alunos não tiveram a idade identificada por insuficiência de informações reportadas pelos pais, enquanto a maioria da amostra possuía idades entre 6 e 7 anos (média: 6,65 anos), cursando o 1º ano do ensino fundamental. Do total, 63 (46,32%) eram meninas e 73 meninos (53,67%). As crianças são alunos de três escolas públicas de Porto Alegre, sendo uma estadual e duas municipais, as quais aceitaram participar da pesquisa por meio do Termo de Autorização para Escolas. Foram, no total, 10 turmas, e as professoras responsáveis concordaram em tomar parte também do estudo, assinando o Termo de Participação. O estudo foi aprovado pelo Comitê de Ética em Pesquisa da Universidade Federal do Rio Grande do Sul.
Procedimentos
O estudo ocorreu entre os meses de setembro e dezembro de 2017, em três etapas. Na primeira, pré-teste, os alunos foram avaliados na tarefa de construção dos princípios de contagem (Dorneles, 2004; 2006). Na segunda, foram divididos em grupo controle e grupo experimental, em que este recebeu a intervenção e aquele apenas o ensino regular ministrado pelas professoras na sala de aula. Na terceira etapa, pós-teste, toda a amostra foi reavaliada na mesma tarefa aplicada no pré-teste.
Instrumentos
Avaliação dos Princípios de Contagem
O instrumento utilizado para avaliar a construção dos princípios de contagem pelas crianças foi o mesmo utilizado por Dorneles (2004; 2006). Para cada princípio, os sujeitos são classificados em três grupos: princípio construído (S - sim); demonstram dúvidas e respostas pouco consistentes (EC - em construção); não mostram nenhuma compreensão do princípio (N - não).
1) Ordem constante/ordem estável - Pergunta-se à criança: “Até quanto sabes contar?”, e pede-se que ela conte.
2) Correspondência um a um/correspondência termo a termo - Mostra-se à criança dez fichas enfileiradas, perguntando: “Quantas fichas têm?”. Depois, dez fichas não mais enfileiradas, pergunta-se: “Quantas fichas têm?” Então, repete-se esse procedimento com 15, 25, 35 e 45 fichas (neste estudo, esta questão foi realizada com 10 e 15 fichas).
3) Cardinalidade - Ao final da contagem de um grupo de 15 elementos, pergunta-se: “Quantos têm ao todo? Podes me dar 10 fichas?”
4) Abstração - Pergunta-se à criança: “Se tu estivesses contando 15 balas, tu contarias da mesma forma que tu contaste as fichas?”
5) Irrelevância da ordem - Pede-se que a criança conte o mesmo número de 15 fichas, apresentadas linearmente, em outra ordem, isto é, começando por outra ficha. Depois, solicita-se que ela diga quantas fichas ficariam ao desmanchar a linearidade do conjunto. Em seguida, pede-se que ela conte, primeiro, 8 fichas do mesmo conjunto, separando-as, e depois 7 fichas, perguntando quantas ficam ao todo.
Durante a realização da avaliação, foram estabelecidos alguns critérios para classificar a resposta das crianças, uma vez que algumas perguntas têm mais de uma solicitação. Sendo assim, nesses casos, com as questões 2, 3 e 5, foi estabelecido que a resposta seria classificada como “sim”, se o aluno respondesse corretamente a todos os questionamentos de cada questão; “em construção”, se não cumprisse com alguma das solicitações; “não”, se não atendesse corretamente a nenhuma parte da pergunta.
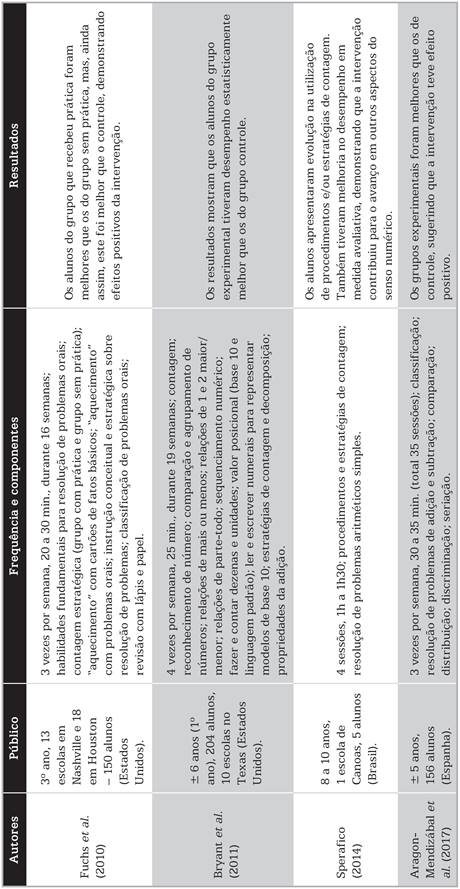
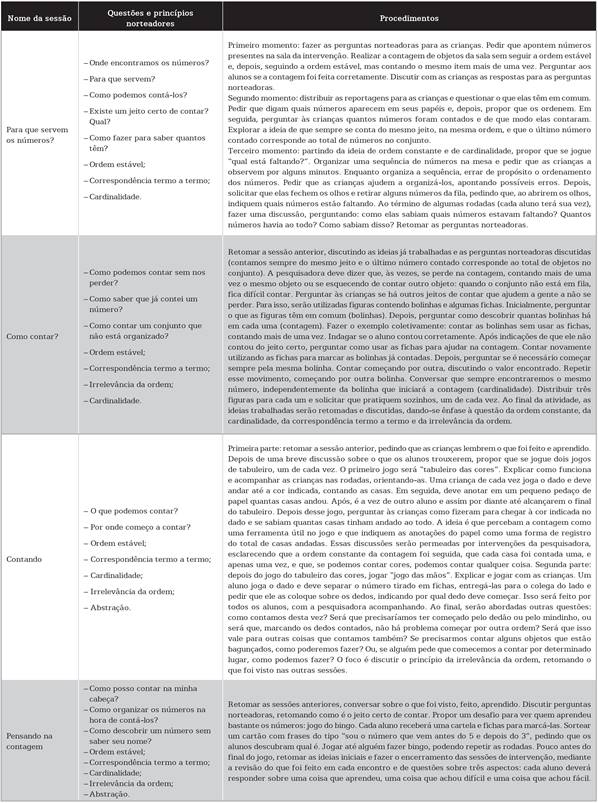
Intervenção
As sessões de intervenção foram realizadas duas vezes por semana, durante duas semanas, com duração de 20 a 35 minutos, incluindo o tempo de deslocamento das crianças. Os encontros ocorreram com pequenos grupos (no máximo cinco crianças), em laboratórios de aprendizagem e/ou salas de aula desocupadas, disponibilizadas pelas escolas. O programa de intervenção foi aplicado pela pesquisadora em todas as sessões.
No que se refere ao programa, no mês anterior (agosto) ao início da coleta de dados para o estudo experimental, foi realizado um estudo piloto para avaliar sua aplicabilidade. A versão utilizada neste trabalho, portanto, foi organizada com base em resultados anteriores, que visaram contribuir para a melhoria da dinâmica, e em atividades pensadas para cada sessão. A seguir, a organização do programa de intervenção e sua descrição.
É importante ressaltar que as 60 crianças do grupo experimental receberam todas as sessões de intervenção. Mesmo quando o aluno, por algum motivo, perdia a sessão, a pesquisadora a realizava em outro momento, objetivando completar os quatro encontros previstos.
Análise de dados
A análise dos dados foi realizada por meio do teste Z de comparação de proporções entre os grupos. Isto é, para cada princípio de contagem, foi comparado se a proporção de progressos do grupo experimental foi maior que a proporção de progressos do grupo controle.
Resultados
Na Tabela 2, estão reportados os resultados da intervenção. A denominação “atividade A” corresponde ao princípio da correspondência termo a termo; “atividade B” à cardinalidade; “atividade C” à abstração; e “atividade D” ao princípio da irrelevância da ordem. A ordem constante não foi considerada na tabela porque todas as crianças sabiam contar corretamente até determinado número.
Tabela 2 Progresso na construção dos princípios de contagem
| Atividade | Grupo | N | Progresso | (%) | p-valor |
|---|---|---|---|---|---|
| A | Controle | 82 | 29 | 35,37 | 0,016 |
| Experimental | 66 | 39 | 59,09 | ||
| B | Controle | 77 | 9 | 11,69 | 0,0138 |
| Experimental | 65 | 17 | 26,15 | ||
| C | Controle | 82 | 14 | 17,07 | 0,1093 |
| Experimental | 67 | 17 | 25,37 | ||
| D | Controle | 88 | 38 | 43,18 | 0,0001 |
| Experimental | 74 | 53 | 71,62 |
Fonte: Elaborada pela autora.
Legendas: atividade A - correspondência termo a termo; atividade B - cardinalidade; atividade C - abstração; atividade D - irrelevância da ordem; N - número de avanços; % - porcentagem de avanços; p- valor < 0,05.
A Tabela 2 mostra o progresso de construção dos princípios (N, EC e S), de modo comparativo entre os grupos controle e experimental, com os p-valores relativos ao Teste Z de comparação de proporções entre os grupos. Isto é, para cada atividade, foi comparado se a proporção de progressos do grupo experimental foi maior que a proporção de progressos do grupo controle. Cada teste teve hipóteses teóricas e hipóteses estatísticas.
Analisando os resultados expostos na Tabela 2, é possível observar que, na atividade A (correspondência termo a termo), a taxa de avanço na construção dos princípios pelos alunos do grupo experimental foi de 59,09%, sendo estatisticamente superior (p-valor < 0,05) à do grupo controle (35,37%). Na atividade B (cardinalidade), novamente o grupo experimental demonstrou taxa de avanço (26,15%) maior que a do grupo controle (11,69%), obtendo significância estatística (p-valor < 0,05). Na atividade C (abstração), os alunos do grupo experimental também obtiveram taxa de avanço superior (25,37%) à dos alunos do grupo controle (17,07%), mas não evidenciaram superioridade estatística (p-valor > 0,05). Na atividade D (irrelevância da ordem), o grupo experimental novamente evidenciou taxa de avanço maior (71,62%) em relação ao grupo controle (43,18%), obtendo significância estatística (p-valor < 0,05).
Discussão
Inicialmente, o estudo objetivou promover avanços no desempenho matemático em princípios de contagem das crianças de 1º ano, do pré para o pós-teste. A análise dos dados demonstrou que, de fato, os alunos da amostra tiveram avanços do pré para o pós-teste: tanto os sujeitos do grupo experimental quanto os do grupo controle apresentaram taxas de avanço consideráveis, conforme exposto na Tabela 2. Tal melhora, no entanto, poderia ser atribuída não apenas à intervenção, como também às aulas regulares que as crianças seguiram frequentando.
Em razão disso, o segundo objetivo estabelecido neste estudo, a avaliação da efetividade de uma intervenção de curta duração, e específica sobre princípios de contagem, partiu da hipótese de que os avanços dos estudantes do grupo experimental foram maiores que os avanços apresentados pelos sujeitos do grupo controle, evidenciando que a melhora no desempenho se deu devido ao programa de intervenção em questão. Novamente, a expectativa se confirmou: os resultados demonstraram que, além das taxas de avanços do grupo experimental terem sido superiores às taxas de avanço do grupo controle, em três princípios de contagem (correspondência termo a termo, cardinalidade e irrelevância da ordem), essa melhora obteve superioridade estatística. Isso aponta para a efetividade do programa de intervenção, de curta duração (duas vezes por semana, em duas semanas) e com foco nos princípios mencionados.
Esses resultados vão ao encontro de outros estudos de intervenção que também realizaram uma comparação entre grupos controle e experimental. Fuchs et al. (2010), ao apresentarem os achados do estudo interventivo sobre prática em contagem, evidenciaram que os três grupos de crianças participantes (experimental com prática, experimental sem prática e controle) obtiveram melhoras no desempenho, com os sujeitos que receberam algum tipo de intervenção, demonstrando avanços maiores que os indivíduos do grupo controle.
Da mesma forma, Dyson, Jordan e Glutting (2011) mostram que os alunos de baixa renda participantes da condição de intervenção em senso numérico apresentaram crescimento maior que os sujeitos do grupo controle no pós-teste. As autoras Praet e Desoete (2014) também mostram achados semelhantes: os dois grupos experimentais de seu estudo (um com foco em comparação numérica e outro em contagem) demonstraram melhor desempenho que o grupo controle depois de receberem intervenção. Mononen e Aunio (2016), em pesquisa de intervenção sobre habilidades de contagem para crianças com baixo desempenho, destacaram que os estudantes do grupo experimental melhoraram significativamente suas habilidades em comparação com os indivíduos do grupo controle, depois do término da intervenção. Esses e outros autores evidenciam que intervenções específicas, para crianças pequenas, envolvendo um ou mais aspectos do senso numérico, são efetivas e promovem avanços no desempenho matemático (Aragon-Mendizábal et al., 2017; Bryant et al., 2011; Dowker; Sigley, 2010; Dyson, Jordan, Glutting, 2011; Fuchs et al., 2010; Mononen; Aunio, 2016; Praet; Desoete, 2013; Sperafico, 2014).
Limitações
O estudo apresenta como limitação a não inclusão de avaliação do QI dos indivíduos participantes da pesquisa. Sem dúvida, poder utilizar esse dado na seleção da amostra e na análise dos resultados seria de grande importância, uma vez que informaria acerca do potencial intelectual das crianças, auxiliando na compreensão do desempenho de cada uma. Do mesmo modo, outros instrumentos de avaliação poderiam ter sido utilizados no estudo, como investigação do senso numérico, da atenção, da memória de trabalho e outros aspectos de domínio geral e de domínio específico. Dessa forma, teria sido possível analisar a relação dos princípios de contagem com tais instrumentos, bem como desenvolver outros tipos de análise nos resultados.
Por fim, é válido chamar a atenção para o fato de que os indivíduos participantes da amostra obtiveram os resultados aqui expostos por conta dos contextos e das escolhas empregados na pesquisa, sendo necessário interpretar os dados e resultados apresentados com precaução, considerando os aspectos deste estudo específico. Ainda assim, nesse sentido, é importante ressaltar que os achados do trabalho podem e devem atuar como bons indicativos para a prática pedagógica, uma vez que o desenvolvimento e a aplicação da intervenção em alunos do 1º ano se mostraram recursos efetivos para a aprendizagem deles. Tanto pesquisadores quanto professores podem se basear nos resultados aqui apresentados para pensar e problematizar futuros estudos e ações pedagógicas, buscando favorecer o aprendizado dos estudantes.
Direções futuras
Os resultados deste estudo apontam para a necessidade da continuação do trabalho com princípios de contagem, demonstrando a importância da valorização de seu desenvolvimento pelas crianças pequenas, no início da escolarização formal. Atingir esse objetivo requer problematizar algumas questões, principalmente as que se referem à relação entre o que é produzido pelos pesquisadores da área da matemática e o que é praticado pelos professores da educação básica.
Os estudiosos dessa área produzem conhecimento relevante para a compreensão desse grupo de alunos, conforme evidenciado ao longo do artigo, por meio da discussão de estudos preditivos, de perfil e interventivos. Cada uma das pesquisas contribui para o entendimento das características dos alunos que têm dificuldades, no que estas consistem, quais são os fatores imprescindíveis para alcançar um bom desempenho em matemática, como ajudar aqueles que estão começando a apresentar problemas e muitos outros aspectos. Os resultados podem contribuir muito para a prática pedagógica, mas estabelecer relação entre o universo acadêmico e o universo escolar é uma tarefa complexa.
Nesse sentido, a formação dos professores pode ser aprimorada, envolvendo elementos relevantes à aprendizagem matemática, abordando com mais frequência os estudos desenvolvidos no campo e partindo das evidências encontradas para pensar em ações pedagógicas. Da mesma forma, os pesquisadores também podem buscar maior envolvimento dos docentes nos estudos: ouvi-los mais, procurando entender suas percepções acerca dos estudantes; investigar a relação deles com a matemática, visando compreender como foi a formação recebida e de que maneira planejam as aulas; preocupar-se não apenas com as necessidades de aprendizagem dos alunos, por exemplo, mas também com as necessidades dos professores ao ensinar em uma turma heterogênea, precisando seguir o currículo estabelecido na escola, dividindo o tempo com aulas especializadas e várias outras questões enfrentadas na rotina escolar.
Considerando esses aspectos, pode-se afirmar que o estudo aqui apresentado foi ao encontro de determinadas necessidades docentes. A intervenção desenvolvida se baseou em princípios norteadores que necessitam ser incorporados às aulas regulares e, além disso, foi realizada em curto espaço de tempo, o qual também necessita ser incluído no planejamento matemático dos professores. Os materiais utilizados foram produzidos pela pesquisadora e entregues às dez professoras participantes do estudo, possibilitando seu uso posterior e sem custo em outras aulas. Os resultados, por sua vez, demonstraram que mesmo o investimento de curta duração em princípios de contagem provocou melhoras no desempenho das crianças, evidenciando que é possível promover aprendizagens significativas por meio de intervenções concisas e de qualidade, dedicadas a determinado conteúdo, no planejamento pedagógico.