Serviços Personalizados
Journal
Artigo
Compartilhar
Educação e Realidade
versão impressa ISSN 0100-3143versão On-line ISSN 2175-6236
Educ. Real. vol.46 no.2 Porto Alegre 2021 Epub 04-Ago-2021
https://doi.org/10.1590/2175-6236112151
THEMATIC SECTION: MATHEMATICS EDUCATION
Machines and Numbers: translations of Nicole Picard’s texts in Porto Alegre during the 1970s
IUniversidade Federal do Rio Grande do Sul (UFRGS), Porto Alegre/RS – Brazil
The article focuses on readings, translations, and quotations of Nicole Picard’s texts by teachers at the Instituto de Educação General Flores da Cunha, in Porto Alegre, in the 1960s and 1970s. The translations are interpreted as evidence of an encounter, through texts, between teachers who sought to renew the teaching of mathematics in elementary school, in France, and in Brazil. Among the themes addressed, the study of machines as representations of operators, aiming at the understanding of numerical operations, stands out. In the context of the modern mathematics movement, the meeting was favored by the shared valorization of active methods, Piagetian psychology, and the classroom as an object and scope of research on learning.
Keywords: History of Education; Mathematics Teaching; Primary Education; Teacher Education; Modern Mathematics
O artigo tem como foco leituras, traduções e citações de textos de Nicole Picard realizadas por professoras do Instituto de Educação General Flores da Cunha, em Porto Alegre, nos anos 1960 e 1970. As traduções são interpretadas como evidências de um encontro, por meio de textos, entre professoras que buscavam a renovação do ensino de matemática na escola primária, na França e no Brasil. Dentre os temas abordados, destaca-se o estudo de máquinas como representações de operadores, visando a compreensão das operações numéricas. No contexto do movimento da matemática moderna, o encontro foi favorecido pela valorização partilhada dos métodos ativos, da psicologia piagetiana e da sala de aula como objeto e âmbito de investigação sobre aprendizagem.
Palavras-chave: História da Educação; Ensino de Matemática; Ensino Primário; Formação de Professores; Matemática Moderna
In the 1960s and 1970s, the General Flores da Cunha Educational Institute – a teacher training institution in Porto Alegre – was a center for the discussion and propagation of ideas to modernize mathematics teaching in the early school years. Teachers at the Institute read, studied, experimented, and disseminated proposals for curricular innovation through courses, lectures, and articles published in educational journals. In the elaboration of these proposals, they took as reference authors from other parts of the country and the world who were engaged in the great wave of reforms known as “modern mathematics.” In line with the reforms in secondary education, these authors advocated changes in the teaching of elementary notions, such as number and numerical operations; their study should be anchored in the understanding of set ideas and basic mathematical structures (Bonfada; 2017; Búrigo, 1989; Silva, 2019).
Articles, books, and teaching materials by Nicole Picard, a researcher at the Institut Pédagogique Nacional (IPN) and coordinator of an experiment carried out in France, circulated in the Institute of Education (IE) and, more precisely, in its Mathematics Laboratory – an aggregating center for teachers interested in teaching renewal. Translations of extracts from these texts, found in the collection of the laboratory, are evidence of mobilization to learn and disseminate the French author’s proposals. This finding is interesting, considering that Nicole Picard is rarely mentioned in previous studies on modern mathematics in Brazil. Moreover, this is not an author who traveled throughout Brazil, articulating exchanges, as Georges Papy, Lucienne Félix, or Zoltan Dienes (Oliveira; Leme da Silva; Valente, 2011; D’Ambrosio, 2017). Nor is this an author whose name has circulated widely throughout the country via textbooks, articles, or the media.
How did Nicole Picard’s writings get into IE? What are the translations of her texts about? How did IE teachers mobilize to study and disseminate her writings? These questions guide the investigation and discussion of this study.
From the perspective of connected history, we seek to understand the circulation and translation of Nicole Picard’s texts as an articulation between the processes of modernization in both countries and, in particular, as a connection between teachers engaged in these processes in France and Brazil; we do not look at it as an unfolding of the developments at IE in the 1960s, nor as a consequence of the dissemination of her books and materials, which were aimed at the French public. We emphasize the protagonism of women teachers when the most known and most cited authors of the modernizing movement, internationally, were men.
Bertrand (2007, p. 70) describes connected history as “the history of real connections, that is, of ‘contact situations’ between groups of actors belonging to geographically distant societies.” Understanding these “contact situations” involves considering the views and logic of these groups. In line with this perspective, we initially present what we consider evidence of connections between Nicole Picard and the IE 2 teachers – the translations found in the Mathematics Laboratory. Next, we briefly present the modernizing movements that preceded the reception of her books at IE and the context of the production of Picard’s books in France. In a third moment, we deal with the reception, reading, and dissemination of texts in Porto Alegre, looking closely at the themes and excerpts that were the object of translation and presenting some conjectures about the choices that led to the selection of these extracts.
With the narrative of this meeting between an author and her translators – which took place above all (but not only) through books and teaching materials – we intend to untie one more of the knots in the plot that constituted the movement of modern mathematics, which had as one of its notable features the intense exchange between educators who worked at different stages of schooling and in different parts of the world.
Translations of Nicole Picard in the IE Mathematics Laboratory collection
The Mathematics Laboratory of the Institute of Education was created in 1951 to gather teaching materials produced by students of the Didactics of Mathematics discipline of the School Administration course. At the end of the decade, a Study Group was created to discuss texts and organize courses for teachers (Instituto..., 1961).
Activities were intensified in the 1960s and renewed in the 1970s and 1980s. The Laboratory was deactivated at some point, around the year 2000. The room that housed the Laboratory also became storage for textbooks. The documents, books, and teaching materials gathered over 50 years were kept in cardboard boxes or filing cabinets. In 2014, they were found covered in dust by a team of students who participated in the Institutional Scholarship Program for Teaching Initiation (PIBID). Their interest in teaching materials motivated the team to reorganize the room, and the Laboratory was revitalized (Dalcin, 2016). In 2016, when the Institute was closed for restoration, all materials were taken to a room at the Institute of Mathematics and Statistics of the Federal University of Rio Grande do Sul1. In 2017, the constitution project of the collection began with the cleaning, inventory, packaging, and digitization of documents2.
During the inventory process, it was possible to notice that the documents, produced at different times, had been regrouped and reordered in the 1980s and 1990s, as they were initialed during this period. But it is also likely that they were later removed or rearranged, without clear criteria: copies of the same document were found in different boxes, some with misplaced pages. Many translations were noticed in an initial classification of the documents; at the end of the cleaning and inventory process, 309 sets of handwritten, typed, or mimeographed translations were listed.
The activities of translating texts about teaching mathematics, didactics, or psychology are also mentioned in the Laboratory team reports, indicating that these were regular, planned, and valued practices. Many of the translations feature texts by authors linked to the modern mathematics movement, such as Caleb Gattegno, Frédérique Papy, and the aforementioned Lucienne Félix and Zoltán Dienes. Seventeen texts are translations of extracts from the works of Nicole Picard3.
Chart 1 shows translations of Nicole Picard’s texts found in the collection. It identifies the title given to each translation; the inventory or registration number of the item; the title of the work from which the translated excerpt was extracted; the teacher responsible for the translation; the year in which the translation was performed, according to the Laboratory reports; the nature of the extract; the type of graphic record (handwritten or typewritten, possibly reprographed);4 and the number of sheets or pages of the item. So far, it has not been possible to establish the copy from which each translation was made.
Source: Prepared by the authors from the digital collection Práticas e saberes matemáticos nas Escolas Normais do Rio Grande do Sul.
Chart 1 Translations of Nicole Picard’s texts found in the IE Mathematics Laboratory
Chart 1 shows that excerpts from two articles by Nicole Picard were translated. They were published in the pedagogical journal Le Courrier de la Recherche Pédagogique, a publication of the French National Pedagogical Institute (IPN). The extracts concern the themes of numbering and “machines,” which correspond to the mathematical idea of an operator, as we will comment further on.
The other translations correspond to textbooks5 or guides for teachers on the use of the cards. Most are extracts from the Commentaires pour le maître, a teachers’ guide for the Journal de Mathématique ICE 2, a set of activity cards for students of Cours élémentaire 2, or CE 2 – the third year of elementary education in France, which brings together students of 8 and 9 years old. In the Journal, the cards are grouped by themes: Space Organization, Schemas, Machines, and Numbering, in that order. The study of numerical operations is prepared by the study of the preceding themes and, in particular, the study of machines: “thanks to working with numerical machine chains, children will be led to develop the aptitude for mental calculation” (Picard, 1971, p. 37). The translations of extracts from the guide Commentaires pour le maître, therefore, provide teachers with guidelines for working with each group of cards.
To understand the reception of the books and the mobilization for the translation of her texts, we will deal with events that preceded them in the IE Mathematics Laboratory and the experimentation directed by Nicole Picard in France.
Movements for the modernization of mathematics teaching in Porto Alegre
The movements that preceded the reception of Nicole Picard’s books at the Institute combine two trends: the construction of an environment to discuss the teaching of mathematics – in particular, the Didactics of Mathematics – since the beginning of the 1950s, that occurred at the IE Mathematics Laboratory; and the emergence of an international movement of curriculum innovation, which mobilized mathematicians, teachers, and government agencies, and had strong resonances in Brazil.
In the constitution of this environment, Odila Barros Xavier played a leading role: professor of Didactics of Mathematics, she took the initiative to create the Laboratory and was its main driving force for many years (Dalcin; Bonfada; Rheinheimer, 2018). In a retrospective text, Odila Xavier mentions reading Piaget’s work since the 1940s. The publication of the collection L’enseignement des mathématique by Jean Piaget, Caleb Gattegno, and mathematicians who participated in the Commission Internationale pour l’Étude et l’Amélioration de l’Enseignement des Mathématiques (CIEAEM), in 1955, soon received Odila and the Laboratory teachers’ attention. According to Professor Odila, the chapter Les structures mathématiques et les structures opératoires de l’intelligence by Piaget (1955), opened “new perspectives for questions and searches” (Xavier, 1963, p. 6). From the chapter by Gattegno – La pédagogie des mathématiques – a study of George Cuisenaire’s teaching material began.
These readings would have been decisive for the new look at the teaching of mathematics and motivated an effort to “update and improve primary teachers in mathematics” (Xavier, 1963, p. 8). For this update, the collaboration with Joana de Oliveira Bender was decisive, “[...] the first mathematics teacher who valued, in Porto Alegre, our enormous, painful, and almost dramatic efforts to improve the teaching of mathematics in primary school” (Xavier, 1963, p. 9). Joana Bender, graduated in Mathematics and professor at the Mathematics Department at the Federal University of Rio Grande do Sul (UFRGS), had worked for many years in primary education – as a teacher, school group principal, and collaborator at the Center for Research and Educational Guidance (CPOE). From 1953 on, at the invitation of the IE professors, she taught courses on Set Theory. The II National Congress of Mathematics Teaching, held in Porto Alegre in 1957, was also an important space for the dialogue between primary and secondary teachers (Xavier, 1963; Búrigo, in press).
In 1961, the IE Mathematics Laboratory already had a small library with Mathematics books (such as Sets and Functions by Leopoldo Nachbin and The Modern Algebra, by M. Queysanne and A. Delachet) and various works in the field of Didactics of Mathematics, including books by authors linked to the modernizing movement such as Caleb Gattegno and Lucienne Félix, two leaders of CIEAEM. In that same year (1961), Professor Antonio Ribeiro from UFRGS, at the invitation of the Study Group, taught yet another course in Set Theory to a wide audience of CPOE professors, students, and technicians (Instituto..., 1961).
These movements at the Institute of Education preceded the creation of the Study Group on Mathematics Teaching (GEEM) in São Paulo – considered a milestone for the movement of modern mathematics in Brazil. A great renewal wave would be promoted from 1962, when the GEEM presented a new program proposal for mathematics teaching in secondary school, at the IV Brazilian Congress of Mathematics Teaching, in Belém do Pará. The GEEM proposals were received by the IE teachers “with emotion,” in the words of Odila herself; in particular, she mentions Omar Catunda’s text, concerned with communicating the ideas of set and structure in a simple language, “which are also basic concepts for the primary teacher’s work when directing the learning of mathematics” (Xavier, 1963, p. 14).
Keeping up with the national movements with a profusion of lectures, teacher training courses, and the dissemination of news in the media, the IE teachers continued their endeavor to study modern mathematics in the early 1960s. In 1965, a new course in Mathematics was taught by Professor Joana Bender with 144 participants, mainly teacher trainers and teachers from the primary school attached to the IE (Instituto..., 1965).
All these initiatives indicate a great interest in following the modernizing movement in different ways: studying new teaching materials; getting to know books in circulation; studying “modern mathematics,” with new notions and uses of language, which was not only different from the mathematics taught in the IE Regular Course, but also from the mathematics advocated by the current primary education programs and, especially, from the mathematics learned by teachers throughout their school and university life.
A new character joined the group of IE teachers in 1966. Esther Pillar Grossi was hired in 1965 as a math teacher in an experimental high school class at Colégio Estadual Pio XII in Porto Alegre. In oral testimony, she reports that she first met the ideas of modern mathematics through a course in Logic, taught in 1964 by Osvaldo Sangiorgi, president of GEEM, and through Papy and Dienes’ books, which were already circulating in Porto Alegre. She states that she was encouraged to teach modern mathematics by Lucienne Félix during her visit to Porto Alegre in August 1965. In January 1966, Esther presented an account of her experience at the V Brazilian Congress of Mathematics Teaching in São José dos Campos; there, she had contact with IE professors, who invited her to work at that institution (Grossi, 1988; 2007a).
Still in 1966, a specialization course in Didactics of Modern Mathematics for Primary School was offered (with a duration of one and a half years), aimed at primary and preschool teachers of the Institute. The teachers of Didactics of Mathematics at IE, as required by law, were graduates in Pedagogy. Esther Grossi, with a degree in Mathematics, was entrusted with the discipline of Mathematical Foundation, with 93 weekly meetings (Instituto..., 1967a).
Nicole Picard’s first books arrived at the Laboratory in 1967, as the course progressed into its second year: Des ensembles à la découverte du nombre; À la conquête du nombre, and Blocs logiques, aimed at students and teachers of early childhood education and the first year of elementary school. According to the 1967 Activity Report, a total of 56 books were acquired that year for the Mathematics Laboratory, 24 of which were authored by Nicole Picard (Instituto..., 1967b).
In 1967, experimental classes began in some private schools of Porto Alegre in the first year of primary school, guided by the specialization course and inspired by Nicole Picard’s books; in 1968, the experience began in the primary school of the Institute of Education (GEEMPA, 1975; Instituto..., 1970).
Textbooks created from classroom experimentations
Nicole Picard’s books that were found in the Mathematics Laboratory are different from other materials in their format and intent. The books – aimed at students – consist of card collections, numbered in the recommended order for their use. These cards suggest activities for children: coloring objects, completing graphic schemes, writing numbers; the teachers’ books present the rationale for the proposed activities, the logic involved in the outlined sequence, and detailed guidelines for each activity. The use of cards is not typical of a book, as they can be rearranged or viewed at the same time, which book pages do not allow. Figure 1 shows one of the books found in the collection.
Each book is primarily intended for a series of elementary education; but the author warns about the importance of “following each child’s own pace and, in particular, of suppressing failures that only in exceptional circumstances are profitable,” some children might not complete a sequence of studies and activities in a given grade, continuing to “the following year without, however, being poor students” (Picard 1971, p. 9).

Source: Collection of the Mathematics Laboratory of the Instituto de Educação General Flores da Cunha.
Figure 1 Images from the Journal de Mathématique I CE 2 et exercices card collection
To understand the format and intent of the books, it is important to consider the context of their production: Nicole Picard, graduated in Mathematics, coordinated systematic experimentation in the renewal of mathematics teaching in primary school, undertaken by the Department of Pedagogical Research of the IPN, from the school year 19641965 until 1970. She also participated in the Commission d’étude pour l’enseignement des mathématiques (CEEM), established in 1966 by the Ministry of Education to plan an education reform (Picard, 1973).
The proposals for change in primary education in France were strongly inspired by debates about the modernization of mathematics teaching in universities and secondary schools. Since the 1940s, during the post-war period, the group of mathematicians under the pseudonym Bourbaki proposed a reorganization of university courses around mathematical structures, emphasizing the study of more general objects and properties based on rigorous axiomatics. Secondary teachers and university professors gathered in different forums and defended the use of this approach, with adaptations, for secondary education, as an alternative to a fragmented education based on the reproduction of poorly understood techniques. The structuralist approach defended active methods: students had to discover or construct the properties. At the end of the 1950s, the new approach was already proposed to elementary and preschool education: it was about involving students, from an early age, in activities that would promote the development of mathematical thinking (D’Enfert, 2011).
Mathematics secondary teachers mobilized towards the renewal of elementary education, with the intention of forming and guiding experiences that primary teachers would develop. In 1960, Lucienne Félix published the book Mathématiques modernes: enseignement élémentaire, aimed at primary and lower secondary school teachers. At the invitation of Roger Gal, who coordinated the Department of Pedagogical Research at the French IPN, Lucienne Félix produced, from 1961 to 1963, a newsletter addressed to primary school teachers entitled Education et mathématiques (Gal, 1966). In 1965, Guy Brousseau – then an elementary school teacher – published Les Mathématiques du cours préparatoire, a book with activities dedicated to first-year children (6 years old).
Nicole Picard mentions the productions of Lucienne Félix and Guy Brousseau in her articles. However, to justify broader experimentation, such as preparation for reform, she highlights projects developed in other countries, especially in different parts of the United States, directed by university teams. From Picard’s perspective, all supported the idea that children could build their own “mathematical universe” (Picard, 1966, p. 22) if they had the opportunity to perform a variety of activities, establish relationships, and build their own representations. The main reference for the experimentation, however, were the writings of Zoltan Paul Dienes, who had started a project in Leicester, England, and was a visiting professor at the University of Adelaide in Australia, from 1961 to 1965. (Picard, 1966). Dienes supervised internships at the IPN in 1965 and, according to Louis Legrand (Roger Gal’s successor), Dienes would have been one of the great promoters of the investigation coordinated by Picard (Legrand, 1967).
Inspired by Jean Piaget’s studies on the isomorphism between mathematical structures and intelligence structures and on the different stages of development of logical-mathematical thinking, Dienes defended a learning process entirely based on the construction of concepts and structures by children. Therefore, she proposed intense activity with manipulable materials, preceding writing, and interaction between children through games and discussions.
The IPN project began with first-year elementary school classes (cours préparatoire, 6 to 7 years old) in three schools in Paris: the École Alsacienne – secular private school and a place of various innovations since the nineteenth century – and two public schools: one for boys and one for girls. In the following year, the experience was expanded to second-year classes (cours élémentaire 1) and to first- and second-year experimental classes in different regions of France. So, it continued reaching one more grade of primary education each year (Picard, 1966; 1967).
In order to guide the work of teachers, a script of topics was created, quite different from the current program, although it preserved its main topics. For example, activities of classification, of establishing and studying relationships between elements of a set or between sets, and operations with sets should precede the study of numbers. The study of operators should precede numerical operations, as we will see later (Picard, 1966; 1967).
As coordinator of the grand trial, Nicole Picard played multiple roles at the same time. She animated meetings at the IPN every two weeks to discuss modern mathematics and experimentation with professors and researchers; she prepared scripts, activities, and materials; she coordinated, registered, and evaluated the experimentation in some schools, notably in the École Alsacienne. Regarding the meetings at the IPN, she reports that they, at first, brought together around 15 researchers, reaching 120 in the last year (Picard, 1973).
The general guidelines of the process were probably dealt with in this broad debate. However, the detailing and, above all, the validation of the experimentation was built during classroom monitoring:
For all [teachers], I provided types of exercises during the year accompanied, as far as possible, by pedagogical sheets with the purpose of explaining to the teachers the reason of things. I also went to classrooms but, to tell you the truth (I do not know the teachers’ opinions about this), I do not believe that my presence was indispensable to the teachers, unless there was a particular difficulty that we tried to solve together, right there in the classroom. On the other hand, for me, that was extremely precious. The organization of the experience was such that I did not have a ‘laboratory’ in which to rehearse and test mathematical and pedagogical ideas that seemed valid, so I gathered groups of 4 to 8 students that I worked within a corner of the room, I wrote down their reactions as carefully as possible, and I tested exercises with them before showing them to the teacher (Picard, 1966, p. 22).
The experiment was conducted in an artisanal way, but there was, from the beginning, an ambition to generalize it to all French primary schools. In 1966, Nicole Picard began publishing a detailed account of the ongoing experience in the magazine Courrier de la Recherche Pédagogique. In the same year, she began publishing her collection, with the book Des ensembles à la découverte du nombre, aimed at preschool and first-year elementary school teachers and À la conquête du nombre, a set of cards for first-year students. Modernizing ideas were also disseminated in films, which were broadcasted by Radio Télévision Scolaire from 1964 to 1971.
From October 1968 and throughout 1969, Esther Pillar Grossi resided in Paris; she was invited to an internship at the IPN, under Nicole Picard’s guidance, and to a master’s course at the University of Paris, under Pierre Gréco’s guidance, a researcher in cognitive developmental psychology and former collaborator of Piaget. During this period, she followed the classes at the École Alsacienne, observing children’s activities and discussions, taking notes, and participating in the planning and evaluation meetings of the ongoing experimentation (Grossi, 2007b).
Back in Porto Alegre, in 1970, Esther Grossi developed intense activities in the Mathematics Laboratory of the Institute. She resumed the course of Didactics of Modern Mathematics in Primary School, teaching 96 hours of classes; delivered a weekly cycle of lectures on Modern Mathematics in Kindergartens and Primary Schools; coordinated weekly study meetings; provided weekly orientation to teachers involved in the Mathematics Teaching Renewal Experience at the IE Primary School – which began in 1968 and was coordinated by Maria Celeste Koch (Instituto..., 1970).
In 1968, she had already published the article Introduction to the topology of the plan in the Revista do Ensino, a journal directed at primary school teachers of Rio Grande do Sul, reproducing activities contained in the Topologie chapter of the book À la conquête du nombre. In 1971, she published a series of three articles entitled so-called modern Mathematics in the first year of primary school, presenting reports of experiments in Porto Alegre and activities inspired by Dienes and Picard’s books.
Classes, lectures, study meetings, articles in the Revista do Ensino were spaces that disseminated Nicole Picard’s ideas and materials. However, in 1971, we did not find references to Esther Grossi in the reports of the Mathematics Laboratory. We can assume that Esther left the Laboratory to dedicate herself to the recently founded Study Group on Mathematics Teaching of Porto Alegre (GEEMPA), of which she was the main coordinator and president. Having been the first and bestknown publisher of Nicole Picard in Porto Alegre, Esther, however, was not responsible for the translations of her texts that were found in the IE Laboratory.
Machines: Study and Practice of Nicole Picard’s Ideas
The presence of Nicole Picard’s books in the collection of the Mathematics Laboratory does not reveal much about the interest of the Institute teachers in her work. However, the translations indicate some of their study objectives. Course activities and teachers’ and students’ productions exemplify how and when the French author’s ideas were put into practice.
In her books, Picard writes about her research experiences, articulating theory and practice. An article published in 1967 reports an experience developed with groups from cours élementaire 2 on working with machines. The excerpt of the article was translated by Ely Machado Campos, professor of Didactics of Mathematics, as shown in Chart 1. The 1971 report indicates that the translation was done in that year and that Machines was one of the most requested subjects in the consultations of teachers and students who visited the Laboratory (Instituto..., 1971).
The proposed study of machines is inspired by Dienes’ writings about operators. After exploring different types of relationships in different sets (for example, the relationship between “being a sibling to” or “being older than”), the work focuses on functional relationships (each element of the starting set corresponds to one element of the arrival set, as in the relation “being the son of,” in a group of men). Among the functional relationships, the ones that stand out are “those that transform an initial state into a final state; we will designate them under the name of operator” (Picard, 1967, p. 12, our translation). In arguing that the notion that a transformed machine is a familiar notion for children of the 20th century, activities with machines are proposed as a way to acquire the concepts of operator and function. Always privileging the most generic notions, Picard proposes starting with the exploration of non-numeric machines, for example, machines that transform manipulable objects, such as logic blocks (Picard, 1967). Figure 2 shows a box of logic blocks produced by the publisher Office central de librairie (OCDL), acquired by the Mathematics Laboratory, with reference to the mathematician and psychologist Zoltan Dienes6.

Source: Collection of the Mathematics Laboratory of the Instituto de Educação General Flores da Cunha.
Figure 2 Set of logic blocks
The text translated by Ely Campos contains records from Nicole Picard’s field diary: a situation in which she interacted directly with a group of children in the classroom. She reports that children from an experimentation class were invited to simulate machines that change color, machines that change shape, and machines that change both the color and shape of objects. Then, they dramatized the operation of a factory, making machines work in a chain; a child represented each machine. A child chose an object to be transformed, and the others should discover the product of the transformation of each machine. From the dramatization, several questions were proposed to the children: is it possible to replace the entire factory with just one machine? From this study of the composition of transformations, several properties were investigated: the existence of machines that do nothing (neutral element), the commutativity and associativity of the composition, and the existence of the machine that undoes what another does (inverse element).
The numerical operators were introduced from the observation of the input and output situations represented in Figure 3, in which the children identified with a machine that joins two objects, to which Nicole matches the writing +2 on a blackboard.
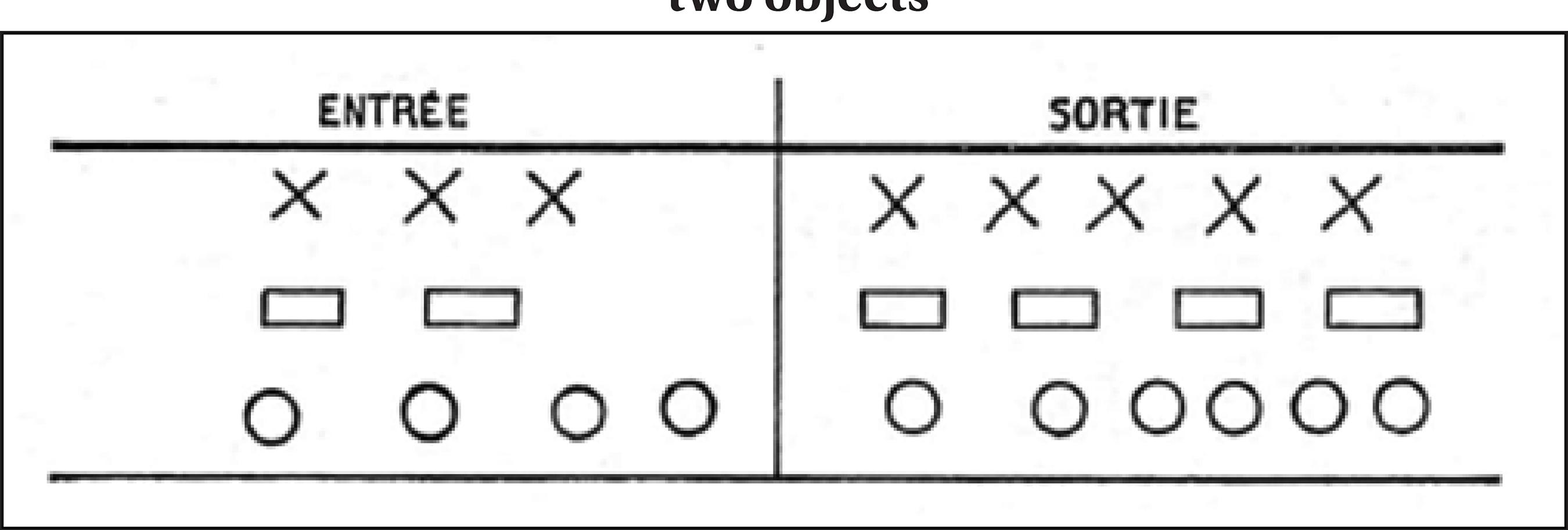
Source: Picard (1967, p. 18).
Figure 3 Nicole Picard’s representation of a machine that joins two objects
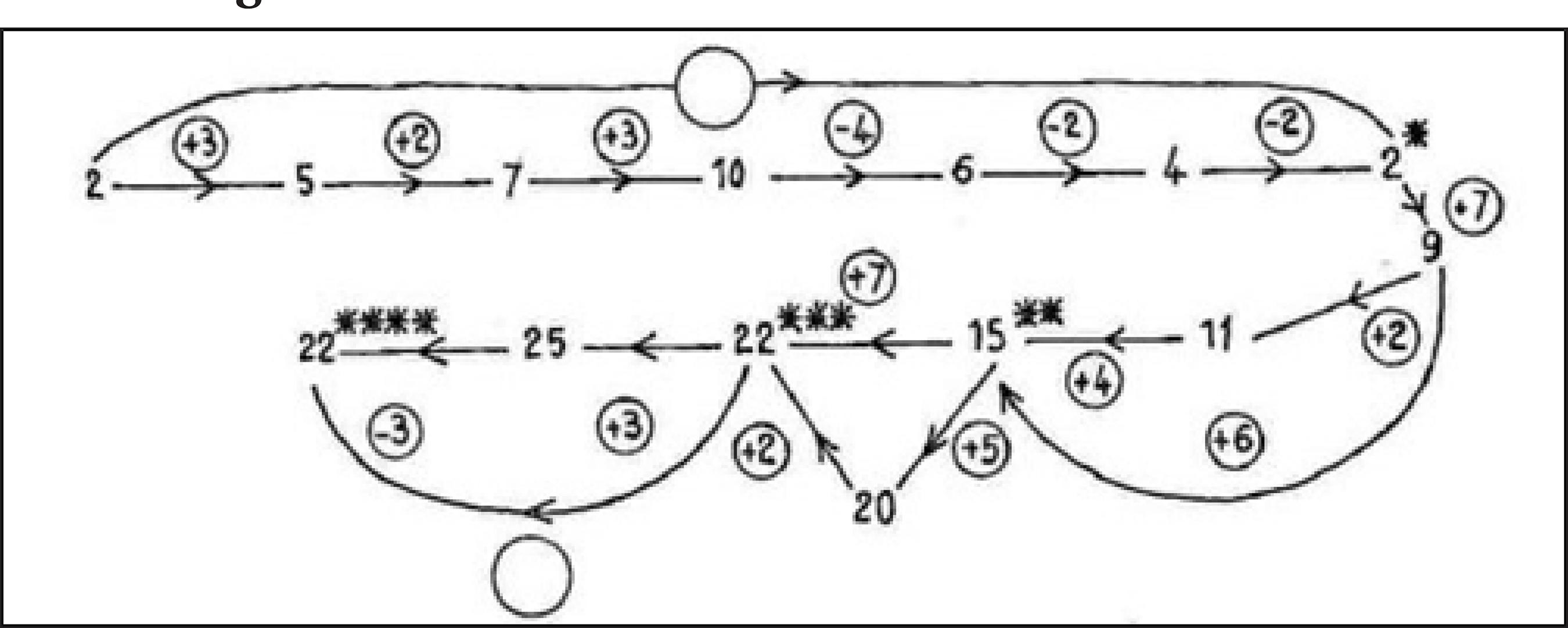
Next, a factory was built on small blackboards (commonly used by children at the time); the numerical operators were written: +2, +3,−2, +5, +1, and so on, representing the join and remove actions of objects in a collection. Each child holding a blackboard represented a machine. One child would say a number to the first machine, and another child would say the result, which fed the next machine, and so on. Figure 4 illustrates the role-play activity narrated by Picard (1967). She discussed with the children which machine could replace a certain sequence, whether one machine could be replaced by two or more, and so on.
All work with machines should prepare the study of numerical operations. Thus, Nicole Picard presents two different approaches to arithmetic operations: the operations between sets (union, difference, separation) and the notion of functions. Figure 5 illustrates the representation of the two points of view for operation 3 x 4 = 12.

Source: Picard (1967, p. 18).
Figure 5 Representation of operation 3 x 4 = 12 from the set and functional point of view
We believe that the methodology proposed by the author was a reason for curiosity and study by the teachers at the Institute, encouraging the translation of parts of her works.
The introduction of the concepts of operation or function using machines appears in materials and activities proposed in training courses involving contents of the movement of modern mathematics. The material “Algumas sugestões para introduzir o conceito de operação7,” used in the Update Course on Mathematics Teaching, sometime during the 1970s or 1980s, reproduces a sequence of approaches in which machines are the central theme. During an informal conversation, the teacher should ask if the students knew the term operation. After the students’ manifestations and few interventions from the teacher, the conversation about machines would begin, using students’ life experience as a guiding thread for the conversation. Considering Nicole Picard’s idea that the concept of machines is familiar to children, the text proposes an introduction to the concepts of operation and function.
In materials from the Mathematics Didactics Course, written by Nelcy Borella at some point in the 1970s or 1980s, the books A la conquête du nombre II and Journal de mathématique I appear as references. Figure 6 shows a section of the material “Sugestões de atividades sobre estados e operadores,” in which we see a clear reference to machines and logic blocks. This material was also used in the studies and activities of the Mathematics Laboratory.

>Source: Available at http://hdl.handle.net/20.500.11959/10000001146.
Figure 6 Activity suggestions about states and operators
Traces of Nicole Picard’s ideas appear in several other scattered documents, such as Esther Pillar Grossi’s Sugestões de Esther Pillar Grossi à Experiência de Introdução da Matemática Moderna no 1º ano Primário no Grupo Escolar Monteiro Lobato sob a orientação da professora Yeda Simões Pires (tome 846)8; a planning material for the Update Course on Teaching Mathematics – Kindergarten9, 1978; Suggestions of graphic cards, used in the Update Course on Teaching 1st to 4th grade Mathematics, 198310 (tome 1746).
Therefore, we can see that Nicole Picard’s ideas were referred to in materials produced and used in courses for teachers throughout the 1970s and 1980s. So, they circulated beyond the Institute of Education through the hands of teachers who attended refresh courses or sought guidance from the Mathematics Laboratory. Her ideas were experimented with at the Application School of the Federal University of Rio Grande do Sul (UFRGS) in 1973, when Mathematics teaching was supervised by professors Gelsa Knijnik and Léa Fagundes, who also participated in the Mathematics Laboratory of the Institute.
Machines in the curriculum planning of the new primary education
Marks of Nicole Picard’s ideas were also found in documents that propose a curricular orientation for primary education, constituted after the fusion of elementary school and gymnasium by Law n. 5692/71.
The curriculum guidelines proposed by the State Department of Education of Rio Grande do Sul (1972) present some ideas of the modern mathematics movement. But the idea of focusing on roles in the early years of primary education was not embraced. We found no evidence of the concepts addressed by Nicole Picard in the official text. However, they are present in other texts of the same period.
The document “Linhas metodológicas para o ensino-aprendizagem dos conteúdos matemáticos no 1º grau,” elaborated in 1974, presents a methodological proposal for primary education. In the reformulation of the teaching-learning of mathematics, referencing the works of Dienes and Picard, five guiding principles of the methodologies for classroom use are listed: constructivism principle; mathematical variability principle; perceptual variability principle; contrast principle; and the principle of using representations (Instituto..., 1974).
The document Selection of Mathematics Contents – Primary School Teaching, from 1976, presents an “attempt to establish a sequential line of mathematical contents for the General Flores da Cunha Educational Institute.” For the second grade, the topics Function–machine–operator are indicated to prepare students for the study of numbering systems and “basic facts of addition and subtraction.” In the third grade, the swelling machine and the withering machine should precede the study of multiplication and division (Instituto..., 1976).
In 1972, GEEMPA, chaired by Esther Pillar Grossi, started experimentation with eight pilot classes under Dienes’ guidance, which should last for eight years – corresponding to the primary education level. The curriculum proposal for the first grade was inspired by the IPN experiment in France: “The organization of this sequence of contents was carried out in parallel with experimentation in schools by GEEMPA teachers, and it was inspired by Nicole Picard’s research for the first grades in Paris” (GEEMPA, 1975, p. 26). The idea of machines is present in the first-grade curriculum as a construction component of the cardinal number concept; it also appears in the second and third-grade curricula, while the concepts of operator and function are mentioned in all grades.
We see that Nicole Picard’s proposals left marks in different curricular proposals developed in the mid-1970s in Porto Alegre, indicating that her ideas were studied, disseminated, and put into practice in primary school classrooms, both at the Institute of Education and other schools.
It is interesting to note that most translations of Nicole Picard’s texts in the collection date from 1975 and 1976 – the same period during which these curricular proposals were developed. The translations were attribution of Professor Maria Feijó Monteiro and revised by Professor Ely Machado Campos, coordinator of the Mathematics Laboratory. Professor Ely Campos was, therefore, one of the main drivers of the dissemination of Nicole Picard’s ideas in Porto Alegre.
Marks of a dialogue between modern teachers
The dynamics of change in mathematics teaching were different in France and Brazil. In France, discussions about a new mathematics program for primary education began in 1969. According to d’Enfert (2011), two proposals were under debate at CEEM: one of the IPN team, which intended a broad review to be applied gradually, grade by grade, and a more moderate one, defended by the general inspectors of education. The second alternative was adopted. On January 2, 1970, a ministerial decree introduced the changes to the primary education program, which had been in force since 1945. In the Circular that accompanies the decree, the idea of the operator appears in the fourth and fifth grades, but not in the way it was experimented at the IPN – as preparation for the construction of the idea of the number and numerical operations.
About this program, Nicole Picard (1973, p. 9) commented:
As it was expected, the second point of view was adopted by the Commission: some of its members were unfavorable to pedagogical freedom, and others, although they found the first project better, considered it premature and unacceptable to the administration. Such self-censorship is, in my opinion, a bad strategy for moving forward. [...] In fact, despite everything, the performed research had a certain influence on the wording of the program and the comments. A good part of the writers actually thought of this program in terms of children’s possibilities of abstraction. The introduction (not explicit) to the linear function in the fourth and fifth grades is the result of serious experiments. [...] But, always with the goal of not traumatizing teachers, from essay to essay, official comments made the new introductions less and less explicit. The comments provide examples – which are new and good – but the reason for the changes is not clear. Nor does it clear that the experiment showed that abstraction can only be made by substituting dogmatic methods, rule learning, and vocabulary for methods that mobilize the activity and participation of children.
Discussions coordinated by the IPN were also suspended in 1970. The Institut de recherche sur l’enseignement des mathématiques (IREMs) – created due to the demands of secondary school mathematics teachers – took over the research and debates about the change in mathematics teaching. The CEEM, which was in charge of planning the reform continuity, ended its work in 1973. At the end of the decade, new programs were published, which sought to reconcile the changes of 1970 with the emphasis on calculus skills, including the memorization of addition and multiplication tables (D’Enfert, 2017). Although Nicole Picard’s books and many other proposals continued to circulate, we can consider that the modernizing movement slowed down a lot in France.
In Brazil, debates on the modernization of education followed different rhythms and trends in each region. In Porto Alegre, the initiatives of teachers from the Institute of Education and GEEMPA promoted a broad debate on proposals for the renewal of primary education, supported by a constructivist perspective. Zoltan Dienes, in collaboration with GEEMPA, came to Porto Alegre several times to give courses, lectures and monitor the ongoing experimentation. Her books were published in Portuguese, and her name circulated much more in the media than Nicole Picard’s.
The traces found in the Mathematics Laboratory, however, show us that Nicole Picard’s texts were also relevant references for the efforts to renovate teaching in the Institute of Education, which ranged from the continuing education of teachers to the development of new curricula. And this reference was not limited to when Nicole Picard was directing the reform preparation in France; it lasted until the 1980s when many authors and professors considered that modern mathematics was a matter of the past.
The important role played by Picard in the IPN and CEEM contributed to the attention that teachers of the Institute paid to her writings. However, to understand how they mobilized to study, translate, and disseminate her texts, it is necessary to consider how Picard’s proposals dialogued with the renovation efforts undertaken at the Institute.
Nicole Picard aligned herself with the constructivism advocated by Dienes and supported by Piaget’s research. Consistent with the constructivist perspective, her didactic proposals were debated in wideranging meetings, discussed with teachers, and evaluated and corrected based on classroom experiments, detailed in her articles. The conduction of experiments – which Esther Grossi witnessed and experienced during her internship at the IPN – is an interesting example of dialogue between teachers with a degree in Mathematics and primary education teachers and trainers, as was also done at the Institute of Education.
Nicole Picard’s books were intended for classroom use; they contained activities that could be immediately replicated and detailed guidance to teachers on how to conduct them. Many cards addressed to students did not even require translation, as they only contained pictures. This format – built to dialogue with primary school teachers and students in France – certainly also favored the dialogue of Institute teachers with her texts.
Final considerations
At the beginning of this text, we mentioned an encounter between an author and her translators. Esther Pillar Grossi lived and learned with Nicole Picard during her internship at the IPN, in Paris. This interaction marked her trajectory as an educator and researcher, which she remembered many years later. But the meeting we are referring to took place, above all, through the texts that circulated at the Institute in their original or translated version. It was through these texts that many other teachers who attended the Laboratory met Nicole Picard and learned about her proposals and the experiments she was conducting.
When dealing with the meeting between Nicole Picard and teachers from the Institute of Education, we noticed a connection that was the result of female educators’ initiative. The mobilization of the Institute teachers is witnessed by the translations and reports. But we can think that the meeting was also the result of Nicole Picard’s effort to dialogue with teachers and actors from primary schools, suggesting a sequence and a repertoire of activities, encouraging their autonomy and initiative, recommending the flexibility of programs and assessment procedures.
Governments did not stimulate this connection, much less imposed it. As other works have already shown, it is not possible to understand modern mathematics without considering the engagement of teachers who had the desire to innovate. On the other hand, we can think that the huge international mobilization around the modernization of education favored the dissemination of texts such as Nicole Picard’s and the very idea that it was possible to learn from the experiments of others, as Picard herself sought to learn from the North American and English projects, and with French authors who were interested in primary education.
Nicole Picard proposed a whole reorganization of learning in primary school. The translations found in the Mathematics Laboratory deal with some of the topics covered in her texts and articles. In this text, we emphasize the study of numerical operations articulated with the idea of function since the initial grades, an approach that seems daring until today. How were these ideas tried and evaluated in primary school classrooms in Porto Alegre? This is a topic for further investigation.
Perhaps the most important and lasting effects of the readings of authors of modern mathematics can be seen in the constitution of mathematics teaching as a field of research in Porto Alegre. Nicole Picard’s writings were important, above all, to point out the possibility and the fecundity of the classroom as space and focus of investigation. The research field advanced in the following decades: Léa Fagundes, Gelsa Knijnik, and Nelcy Borella are some of the figures who participated in the Laboratory in the 1970s and became a reference in the field of mathematics education or cognitive psychology, in the country and in the world.
Can a look at the past help us to think about the present? We think so in different ways. One of the reflections raised by the findings of these documents concerns how teachers can become protagonists of their own training when they have the possibility of dialoguing and thinking about the programs, instead of being watched to execute them. And the variety of resonances that this mobilization can provoke.
1Through a Term of Guard signed by the direction of the Institute of Education and by the responsible researchers.
2The constitution of the collection of the IE Mathematics Laboratory was one of the main activities and goals of the project “Studying to teach: mathematical practices and knowledge of the Normal Schools of Rio Grande do Sul,” financed by CNPq Chamada Universal 2016 (Búrigo et al., 2016).
3These items were digitized and are part of the sub-collection Documentos do Laboratório de Matemática do Instituto de Educação General Flores da Cunha (1961-1979) of the digital collection Práticas e saberes matemáticos nas escolas normais do Rio Grande do Sul, hosted on the Documentation and Digital Collection of Research (CEDAP) of the Federal University of Rio Grande do Sul.
4For the regraphed texts, several copies were found; the item number that appears in the Table is that of the digital collection. In some cases, two or more copies were digitized, as they contained notes and other relevant marks.
5Here, we adopted the classification of the Bibliothèque Nationale de France, noting that the format is unusual for a bound book.
6In Brazil, this material was disseminated and known as the logic blocks of Dienes. Picard refers to the material as Hull-Dienes blocks. Dienes (1967) considers that the material was created by Vigotsky and adapted by William Hull.
7Available at: <http://hdl.handle.net/20.500.11959/10000001721>. Access on: March 12, 2021.
8Item 846 from the collection of the Mathematics Laboratory of the Institute of Education, not digitized.
9Available at: <http://hdl.handle.net/20.500.11959/10000001721>. Access on: March 12, 2021.
10Available at: <http://hdl.handle.net/20.500.11959/10000001721>. Access on: March 12, 2021.
REFERENCES
BERTRAND, Romain. Rencontres impériales. L’histoire connectée et les relations euro-asiatiques. Revue d’histoire moderne & contemporaine, Paris, Société d’Histoire Moderne & Contemporaine, v. 54, n. 4, p. 69-89, 2007. [ Links ]
BONFADA, Elisete Maria. A matemática na formação das professoras normalistas: o Instituto de Educação General Flores da Cunha em tempos de matemática moderna. 2018. 206 f. Dissertação (Mestrado em Ensino de Matemática) – Programa de Pós-Graduação em Ensino de Matemática, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2018. [ Links ]
BÚRIGO, Elisabete Zardo. Movimento da matemática moderna no Brasil: estudo da ação e do pensamento de educadores matemáticos nos anos 60. 1989. 293 f. Dissertação (Mestrado em Educação) – Programa de Pós-Graduação em Educação, Universidade Federal do Rio Grande do Sul, Porto Alegre, 1989. [ Links ]
BÚRIGO, Elisabete Zardo. Joana Bender, educadora matemática. In: GUTIERREZ, Ana Lérida Pacheco; BÚRIGO, Elisabete Zardo (Org.). Personagens do Instituto de Matemática e Estatística. Porto Alegre: no prelo 2001. [ Links ]
BÚRIGO, Elisabete Zardo; DALCIN, Andreia; DYNNIKOV, Circe Mary Silva da Silva; FISCHER, Maria Cecília Bueno; RIOS, Diogo Franco. Estudar para ensinar: práticas e saberes matemáticos nas escolas normais do Rio Grande do Sul (1889-1970). Projeto de pesquisa submetido à Chamada Universal 2016 do CNPq. Não publicado. [ Links ]
DALCIN, Andreia. Entre documentos, memórias e pó: processo de revitalização de um laboratório de matemática. In: COSTELLA, Roselane Zordan; HOFSTAETTER, Andrea; STURM, Ingrid Nancy; UBERTI, Luciane (Org.). Percursos da prática de sala de aula. São Leopoldo: Oikos, 2016. P. 44-55. [ Links ]
DALCIN, Andreia; BONFADA, Elisete Maria; RHEINHEIMER, Juliana Merceds. Odila Barros Xavier e o ensino de matemática: percursos de uma professora formadora. Educação Matemática em Revista-RS, Brasília, Sociedade Brasileira de Educação Matemática, v. 2, n. 19, p. 9-20, 2018. [ Links ]
D’AMBROSIO, Beatriz Silva. Dinâmica e as consequências do movimento da matemática moderna na educação matemática no Brasil. Campinas: Mercado de Letras, 2017. [ Links ]
D’ENFERT, Renaud. Une réforme ambigüe: l’introduction des ‘mathématiques modernes’ à l’école élémentaire (1960-1970). In: D’ENFERT, Renaud; KAHN, Pierre (Ed.). Le temps des réformes. Disciplines scolaires et politiques éducatives sous la Cinquième République: les années 1960. Grenoble: Presses Universitaires de Grenoble, 2011. P. 53-73. [ Links ]
D’ENFERT, Renaud. Quelles mathématiques pour l’école élémentaire? Une perspective historique (1945-début XXIe siècle). Education & Formations, Paris, Ministère de l’Éducation nationale, n. 94, p. 7-22, 2017. [ Links ]
GAL, Roger. Présentation. Le courrier de la recherche pédagogique, Paris, Institut National Pédagogique, n. 27, p. 3, 1966. [ Links ]
GEEMPA. Grupo de Estudos em Ensino de Matemática de Porto Alegre. Reformulação Metodológica do Ensino da Matemática no 1º Grau. Porto Alegre: 1975. Disponível em: <https://repositorio.ufsc.br/handle/123456789/201230>. Acesso em: 12 mar. 2021. [ Links ]
GROSSI, Esther Pillar. Entrevista concedida a Elisabete Zardo Búrigo. Porto Alegre: 1988. Não publicada. [ Links ]
GROSSI, Esther Pillar. Entrevista concedida a Elisabete Zardo Búrigo, Luiz Henrique F. Pereira, Maria Cecilia Bueno Fischer, Monica Bertoni Santos. Porto Alegre: setembro de 2007a. Não publicada. [ Links ]
GROSSI, Esther Pillar. La contribution des idées de Gérard Vergnaud à la démocratisation des apprentissages au Brésil. In: MERRI, Maryvonne (Ed.). Activité humaine et conceptualisation. Toulouse: Presses universitaires du Midi, 2007b. P. 307-319. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Laboratório de Matemática. Relatório de atividades de 1961. Porto Alegre: 1961. Disponível em: <http://hdl.handle.net/20.500.11959/10000001564>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Laboratório de Matemática. Relatório das atividades realizadas no decorrer do 1º semestre 1965. Porto Alegre: 1965. Disponível em: <http://hdl.handle.net/20.500.11959/10000001565>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Curso de Didática da Matemática Moderna para Escolas Primárias. Relatório do 1º ano de atividades do curso. Porto Alegre: 1967a. Disponível em: <http://hdl.handle.net/20.500.11959/10000001316>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Laboratório de Matemática. Relatório de 1967. Porto Alegre: 1967b. Disponível em: <http://hdl.handle.net/20.500.11959/10000001667>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Laboratório de Matemática. Relatório de 1970. Porto Alegre: 1970. Disponível em: <http://hdl.handle.net/20.500.11959/10000001666>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Laboratório de Matemática. Relatório de 1971. Porto Alegre: 1971. Disponível em: <http://hdl.handle.net/20.500.11959/10000001672>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Linhas Metodológicas para o Ensino-Aprendizagem dos Conteúdos Matemáticos no 1º grau. Porto Alegre: 1974. 13 f. Disponível em: <http://hdl.handle.net/20.500.11959/10000001701>. Acesso em: 12 mar. 2021. [ Links ]
INSTITUTO de Educação General Flores da Cunha. Seleção de conteúdos de matemática – Ensino de Primeiro Grau. Porto Alegre: 1976. 89 f. Disponível em: <http://hdl.handle.net/20.500.11959/10000001702>. Acesso em: 12 mar. 2021. [ Links ]
LEGRAND, Louis. Présentation. Les mathématiques en marche. Le courrier de la recherche pédagogique, Paris, Institut National Pédagogique, n. 31, p. 3-4, 1967. [ Links ]
OLIVEIRA, Maria Cristina Araújo de; LEME DA SILVA, Maria Célia; VALENTE, Wagner Rodrigues. O movimento da matemática moderna: história de uma revolução curricular. Juiz de Fora: UFJF, 2011. [ Links ]
PIAGET, Jean. Les structures mathématiques et les structures opératoires de l’intelligence. In: Piaget, Jean; Beth, Evert Willem; Dieudonné, Jean; Lichnerowicz, André; Choquet, Gustave; Gattegno, Caleb. L’enseignement des mathématiques. Neuchâtel: Delachaux & Niestlé, 1955. p. 11-34. [ Links ]
PICARD, Nicole. Une expérience d’enseignement de la mathématique au cours élémentaire. Le courrier de la recherche pédagogique, Paris, Institut National Pédagogique, n. 27, p. 12-76, 1966. [ Links ]
PICARD, Nicole. Recherches sur l’initiation aux mathématiques au cycle élémentaire. Le courrier de la recherche pédagogique, Paris, Institut National Pédagogique, n. 31, p. 5-41, 1967. [ Links ]
PICARD, Nicole. Journal de Mathématique I. C. E. 2. Commentaires pour le maître. Paris: OCDL, 1971. [ Links ]
PICARD, Nicole. Recherche dans le premier degré. Cahiers pédagogiques, Biarritz, Cercle de Recherche et d’Action Pédagogiques, n. 110, p. 8-12, 1973. [ Links ]
RIO GRANDE DO SUL. Ensino de 1º Grau no Rio Grande do Sul: currículos das 1ª, 2ª e 3ª séries. Porto Alegre: 1972. [ Links ]
SILVA, Sara Regina da. A formação de professores no Instituto de Educação General Flores da Cunha: o curso de didática da matemática moderna na escola primária (1966 - 1972). 2019. 164 f. Dissertação (Mestrado em Ensino de Matemática) – Programa de Pós-Graduação em Ensino de Matemática, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2019. [ Links ]
XAVIER, Odila Barros. Um problema em marcha. Porto Alegre: 1963. Disponível em: <http://hdl.handle.net/20.500.11959/10000001852>. Acesso em: 12 mar. 2021. [ Links ]
Received: March 15, 2021; Accepted: May 19, 2021










 texto em
texto em