1 Introducción
La lengua de signos española - en adelante, LSE - históricamente, ha estado reservada a espacios sociales concretos. Durante años, en ámbito educativo, el uso de esta lengua estuvo prohibido, o en ocasiones bajo presiones de uso minorizados, y se impuso el oralismo con el objetivo principal de enseñar el habla (Oviedo, 2006). Posteriormente, se crearon colegios específicos y en la actualidad el alumnado Sordo6 se encuentra escolarizado en los centros educativos ordinarios (colegios e institutos) y se aboga por el bilingüismo intermodal e intercultural.
La aprobación de la Ley 27/2007 de octubre, por la que se reconocen las lenguas de signos españolas y se regulan los medios de apoyo a la comunicación oral de las personas sordas, con discapacidad auditiva y sordociegas ha favorecido la inclusión educativa y social de las personas Sordas y, también, el acceso profesional de los Intérpretes de LSE -en adelante, ILSE- a un número cada vez mayor de contextos profesionales y, por ende, de ámbitos especializados del saber. Este hecho implica una necesidad de términos en LSE vinculados a materias a las que las personas Sordas no habían accedido con anterioridad o, al menos, con la importancia debida. Por ello, es habitual que los ILSEs encuentren carencias -por omisión o incorrección- en los materiales lexicográficos de la LSE. De esta necesidad surge nuestra investigación y el proyecto Mis Manos Hablan®, una plataforma online para compartir los resultados del estudio a través de glosarios de temáticas específicas que recogen propuestas de nuevos Signos7 para referentes que o no estaban presentes en los materiales de la LSE o, si lo estaban, no presentaban una relación referente-significado adecuada desde el análisis realizado.
En este estudio hemos centrado la atención en el ámbito matemático y en concreto las unidades léxicas vinculadas a la clasificación de los números donde hemos encontrado una excesiva influencia de la lengua oral sobre la LSE, abuso de las paráfrasis e, incluso, errores en la definición en español de alguno de los vocablos.
Debemos, en este punto, recoger las conclusiones que a este respecto formulan Santos y Takeco (2014, p. 457), cuando afirman que
[…] el intérprete no dominaba los conceptos físicos y, al intentar explicar estos conceptos, contribuía a reforzar las concepciones espontáneas, muy común en las Ciencias, o podía generar concepciones erróneas con respecto a los conceptos o contenido, ya que el intérprete no poseía formación en las disciplinas que él interpreta.
Extrapolando estas afirmaciones al ámbito de las matemáticas, se puede vislumbrar que la escasez de términos o la escasa calidad de las entradas de los materiales lexicográficos de la LSE darán lugar a interpretaciones complejas, más aún, si los ILSEs no poseen - por su formación personal - unos conocimientos profundos del vocabulario matemático; por lo que, en sus esfuerzos de ofrecer interpretaciones de calidad, al recurrir a la paráfrasis, se puede caer en errores vinculados al significado de los conceptos y/o los contenidos curriculares.
Además, es importante tener en cuenta, tal y como afirman Rodríguez y Mora (2007), que existe un bajo dominio de la LSE en el alumnado sordo que cursa la educación secundaria, situación que tiene su origen, por un lado en que un 95% aproximadamente tiene progenitores oyentes que no dominan la LSE y, por otro, que en los centros educativos de educación primaria este alumnado está expuesto de forma predominante a la lengua oral. Además, en esta línea es significativo recordar que los ILSEs son una pieza fundamental en el proceso de aprendizaje del alumnado Sordo (Uría & Camino, 2017).
En relación a la competencia matemática de las personas con déficit auditivo, son numerosas las investigaciones desarrolladas con niños sordos y oyentes (Allen, 1995, como citado en Pagliaro, 1998; Leybaert & Van Cutsen, 2002; Nunes & Moreno, 1998a; Traxler, 2000, como citado en Pagliaro & Ansell, 2002; Wolman, 1965, como citado en Nunes & Moreno, 2002; Wood, Wood, & Howarth, 1983) que concluyen que a igual edad, los primeros presentan resultados inferiores en las pruebas matemáticas; presentándose un desfase de al menos dos años (Wollman, 1965; como citado en Nunes & Moreno, 2002; Wood, Wood, Kingsmill, French, & Howarth, 1984).
Han sido varios los autores que han descartado la relación directa entre la sordera y el menor logro matemático (Nunes & Moreno, 1998a; Wood, Wood, & Howarth, 1983; Wood et al., 1984). En este sentido, a lo largo de las últimas décadas, los investigadores han analizado diferentes factores relacionados con la menor destreza matemática del alumnado Sordo y han propuesto procesos de intervención basados en el diseño de estrategias y herramientas que suplan las demandas de la población sorda y la resolución de problemas (Nunes & Moreno, 1998a, 1998b, 2002).
En relación directa con nuestro estudio, centrado en personas con la LSE como primera lengua o L-1 -caracterizados por presentar graves problemas de lectoescritura que les limitan el acceso a la información a través de la lectura y/o la lectura labial-, Kidd et al. (1993, como citado en Fuentes, 2005) señalan como un agente perjudicial el uso de palabras/Signos polisémicos cuyo significado difiere fuera y dentro del aula.
Por otro lado, el signo lingüístico es un fenómeno por el cual una señal o expresión perceptible ya sea visual, acústica, táctil... se asocia automáticamente a un significado o contenido (Herrero, 2000). De este modo las palabras y los Signos -unidades léxicas de las lenguas signadas- son signos lingüísticos.
Para De Sausurre (1945, p. 91), el signo lingüístico es una entidad de dos caras -el significante y el significado- que “no une una cosa y un nombre, sino un concepto y una imagen acústica” siendo la imagen acústica la representación del objeto o acción que nos dan nuestros sentidos -es lo que pensamos al oír una palabra o ver un Signo- y, en consecuencia, es una imagen sensorial. Por su parte, Pierce (Magariños, 2003 como citado en Vázquez, 2010, p. 13) indica que
Un signo esta por algo para la idea que produce o modifica. O es un vehículo que transporta adentro de la mente algo desde afuera. Aquello por lo que esta se llama su objeto; aquello que transporta, su significado; y la idea a la que da lugar su interpretante.
Independientemente de la visión del signo lingüístico, para que sea válido debe dar lugar a una imagen acústica o fundamento-idea. Dicho de otra forma, un signo lingüístico, sea una palabra o un Signo, debe evocar en la persona receptora una imagen en su cerebro, si esto no se produce el signo está vacío de significado y no dará lugar a procesos comunicativos. Por este motivo la dactilología, la lectura labial, el empleo de Signos de uso común para términos específicos y, en definitiva, los recursos basados en la lengua oral van a generar un perjuicio destacable en el alumnado signante objeto de nuestro estudio -personas sordas usuarias de una lengua de signos y monolingües en lengua oral; es decir, con un conocimiento escaso de la lengua de modalidad oral-auditiva- durante el proceso de adquisición de nuevos conceptos y su acceso a la información.
En este contexto, ante personas con problemas para desarrollar la competencia matemática al mismo nivel que sus compañeros oyentes, la calidad de los diccionarios y glosarios de la LSE cobran una especial relevancia.
2 Método
Mediante el análisis de los materiales lexicográficos de la LSE así como la puesta en marcha de un proceso de búsqueda, comparación, discusión y creación de neologismos pertenecientes a ámbitos especializados; el objetivo principal de nuestra investigación ha sido contribuir a que la LSE se adecue a las necesidades y funciones académicas, favoreciendo la labor del ILSE en las aulas y al mismo tiempo, el acceso al currículum por parte de los alumnos Sordos. Por otra parte, los objetivos específicos son: (a) identificar la posible existencia de errores o carencias léxicas en los materiales de la LSE vinculados al ámbito matemático; y, (b) proponer y/o recomendar neologismos, en caso de ser necesarios. Para lograr los objetivos indicados se desarrollan varias etapas que quedan recogidas en la Figura 1:
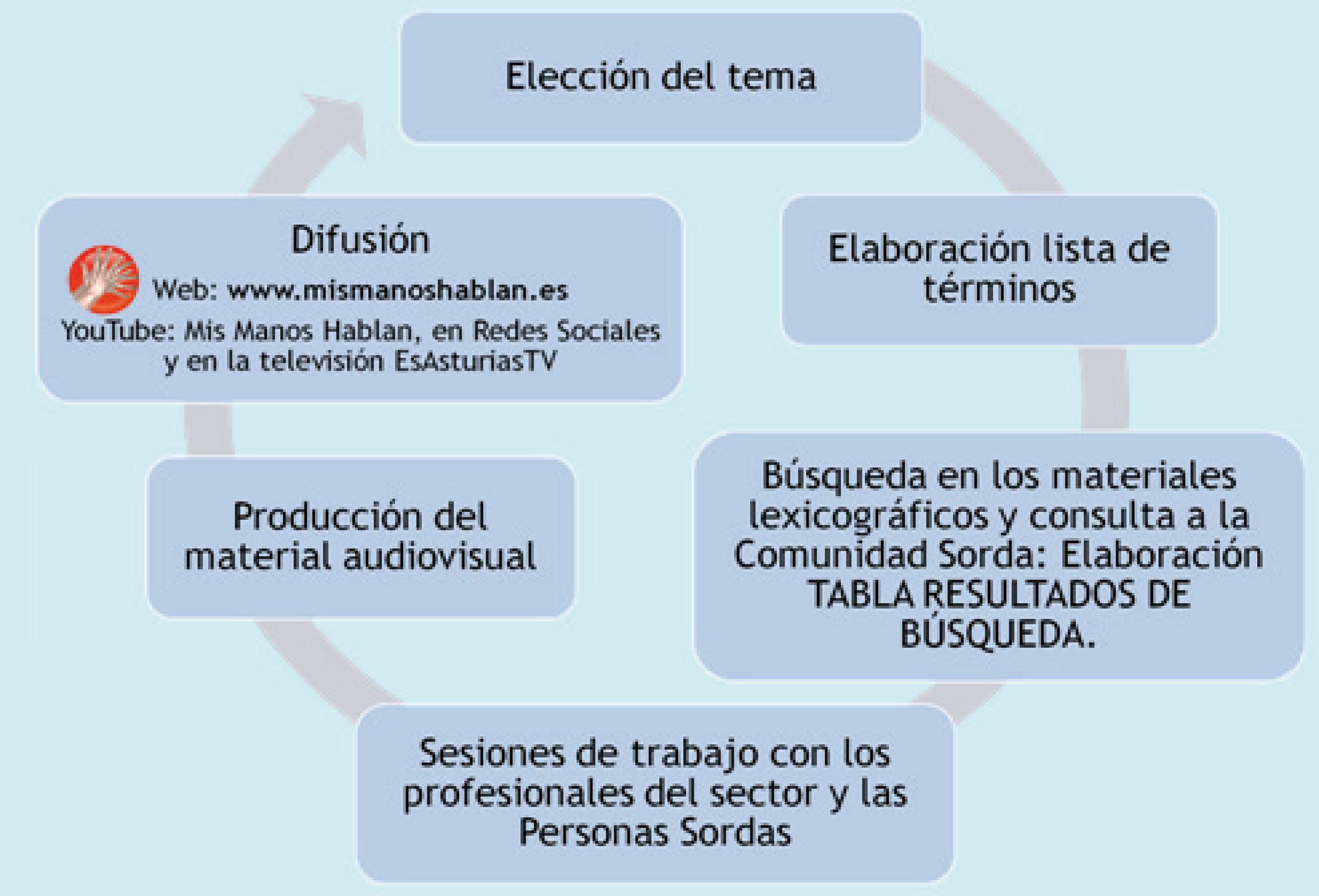
Fuente: Valdés-González, Álvarez-Arregui y Rodríguez-Martín (2017)
Figura 1 Resumen del método de trabajo
Elección del tema, en este caso, la clasificación de los números.
Elaboración de una lista de términos.
Reuniones con profesionales del sector o ámbito tratado.
Búsqueda en los materiales lexicográficos de la LSE -diccionarios y glosarios en papel u online- y consulta a miembros de la Comunidad Sorda.
Sesiones de trabajo, en las que cada uno de los términos se presenta a varias personas Sordas. El proceso seguido depende de la complejidad del vocablo en cuestión y varía desde la simple visualización de una fotografía del objeto o acción hasta la explicación reiterada a lo largo de los días con fases de comprobación y aplicación del término.
Tras asegurar que el concepto se ha entendido, comprobamos si hemos encontrado un Signo correcto y, de no serlo o ante vocablos sin Signo, procedemos a su creación.
Fase de producción del contenido audiovisual.
Difusión. A través de www.mismanoshablan.es, varias redes sociales y la cadena de televisión, EsAsturias Televisión®.
Esta etapa permitió conocer los materiales lexicográficos de la LSE; detectar carencias y errores en dichas fuentes; profundizar y aplicar los procedimientos de creación léxica que la LSE pone a nuestro alcance; y, principalmente, diseñar un método de trabajo que, a continuación en una segunda etapa, hemos aplicado al estudio lingüístico comparado de los Signos publicados -en diccionarios y glosarios- para varias materias del ámbito científico-técnico. En este ensayo se recogen parte de los resultados obtenidos, en relación a la clasificación de los números dentro del campo de las matemáticas.
Antes de comenzar la exposición de resultados queremos resaltar que: “Lo importante no es la seña, sino el concepto” (Sánchez, 2014, p. 13). Es decir, la seña acuñada para un determinado concepto no será mejor ni peor en base a su forma sino a la vinculación Signo-referente. Por otro lado, “O uso da datilologia leva o falante da língua de sinais a uma situação de desvantagem no acesso à informação, uma vez que condiciona sua compreensão ao conhecimento da língua oral. Caso o público da tradução não tenha conhecimentos nas duas línguas, provavelmente não terá a compreensão total do enunciado.” (Tavares, Ferreira, & Lima, 2010; p. 3). Extrapolando esta afirmación al resto de influencias de la lengua oral -calco, gesto prestado o vocalización, polisemia, etc. - para favorecer el acceso a la información de las personas signantes se deberá evitar promover la influencia del castellano sobre la LSE. En este sentido, a la hora de enseñar conceptos matemáticos abstractos y cuyas denominaciones en lengua oral presentan unidades de uso común (natural, entero, primo, etc.) a individuos usuarios de una lengua de signos -y, especialmente con los semilingües en lengua oral- es de suma importancia aprovechar la iconicidad, herramienta que permite entrever propiedades de los conceptos intangibles en la lengua oral (Becerra, 2015). Además la iconicidad, tal y como señalan Bosworth y Emmorey (2010), favorece el acceso al léxico como consecuencia de que los Signos con mayor grado de iconicidad se reconocen más rápido y con mayor precisión que los que no presentan esta característica.
3 Resultados, discusión y propuesta de neologismos
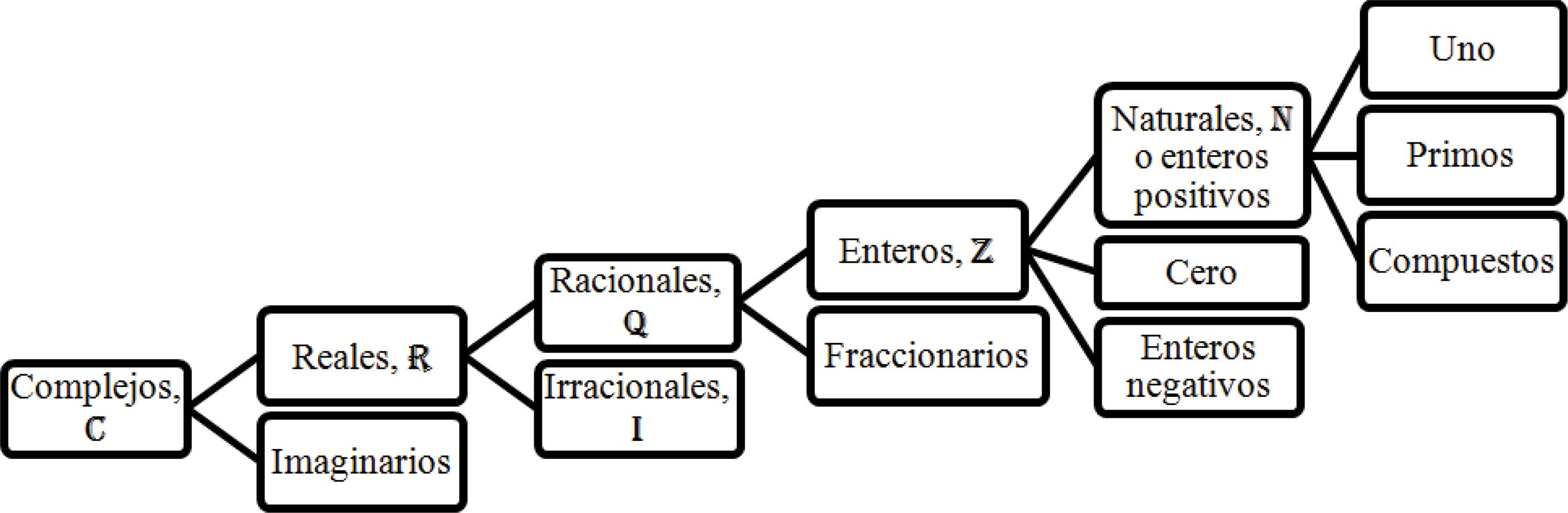
Antes de proceder al análisis y discusión de los resultados -unidades léxicas relativas a los distintos tipos de números- vamos a presentar dos esquemas en los que se muestra dicha clasificación.
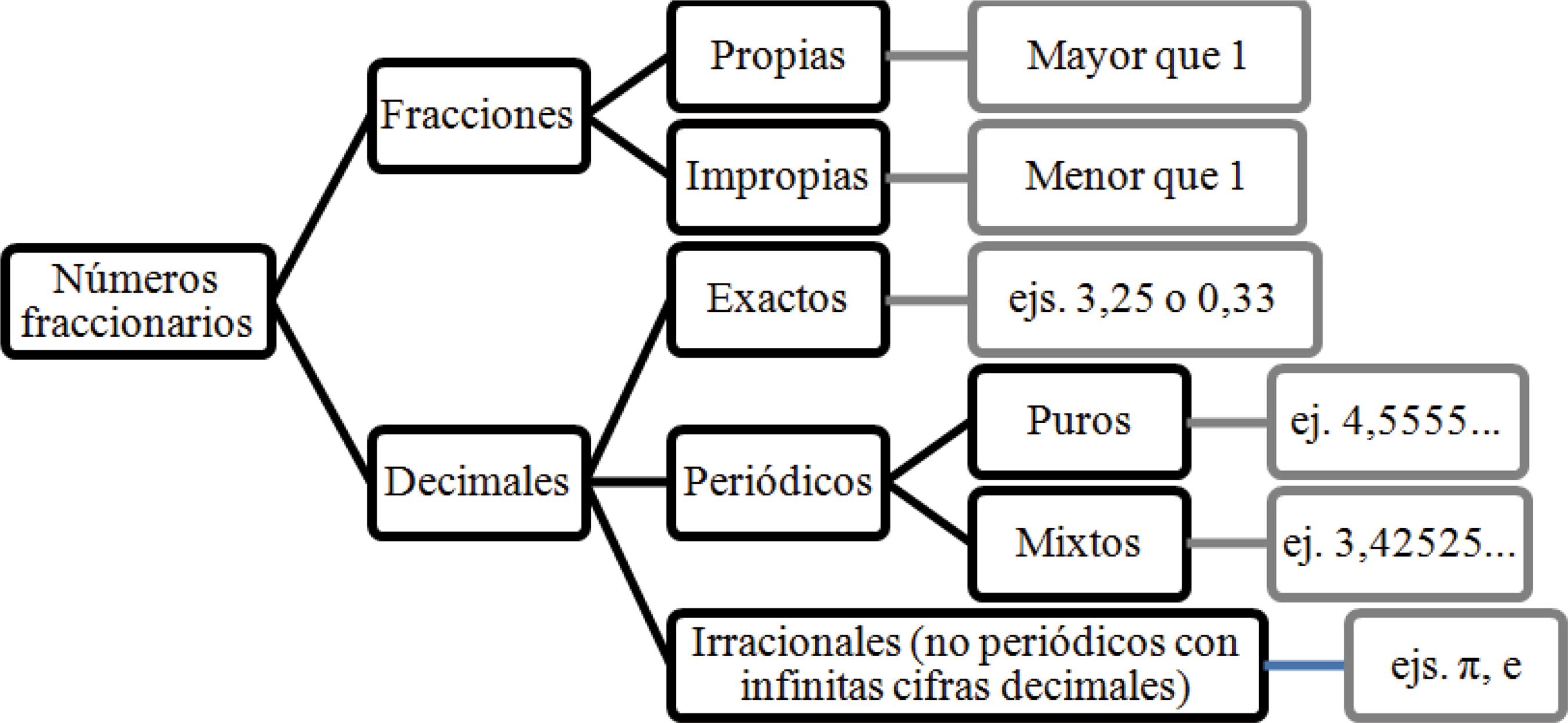
Los números fraccionarios (Figura 3) se pueden agrupar en: 1) fracciones propias -aquellas que representan números menores que la unidad-; e, impropias, representación de números mayores que la unidad y, 2) números decimales que pueden ser exactos, con un número finito de cifras decimales; periódicos con infinitos decimales; e, irracionales.
La unidad NÚMERO8 (Figura 4) aparece en todas las combinaciones de tipo secuencial localizadas para cada uno de los tipos de números. Por ello, y para disminuir el número de fotografías, hemos recogido solamente las unidades léxicas que siguen a NÚMERO.
El glosario de la Universidad de Sevilla9 -en adelante US- y las webs de Spread The Sign10 -en adelante, STS- y Sématos11 al publicarse en vídeo no suprimen el Signo NÚMERO. La Fundación CNSE, en su glosario (Aroca et al., 2002), lo omite indicando en la parte superior izquierda de cada imagen un logo en el que aparecen los números 1, 2, 3 y 4 describiendo un cuadrado (Figura 5) que significa que nos encontramos ante una entrada en la que NÚMERO debe signarse antes del Signo que se muestra.
A continuación se procede a recoger y analizar las entradas que nos brindan los distintos materiales lexicográficos de la LSE para las diferentes clases de números.
3.1 Números complejos
Son números que presentan: «una parte real y una parte imaginaria: z = a + ib. En el número complejo z, a es la parte real y b su parte imaginaria.» (Soto, 2011, p. 104). Por ejemplo, en z = -3 + 2i, el (-3) es la parte real y (+2i) su parte imaginaria.
En las unidades léxicas que nos proporcionan los materiales lexicográficos -para número complejo y para otros tipos de números, como iremos viendo- se detecta un error frecuente: el uso del calco que es la traducción literal de una estructura de la lengua oral a otra signada. Así, Aroca et al. (2002, p. 69) y Sématos recogen para el concepto número complejo el calco: NÚMERO+DIFÍCIL (Figura 5 y Figura 6). Por su parte la US nos propone una alternativa basada en una combinación secuencial con inserción dactilológica. De este modo, nos encontramos para número complejo con la combinación: NÚMERO+C.
Nuestra propuesta de neologismo para número complejo se basa en su definición: es un número formado por una parte real y otra imaginaria, a + ib. Así, para complejo, la primera unidad (Figura 7) representa las dos partes del número complejo -la real a y la imaginaria ib - mientras que la segunda, resalta la unidad imaginaria que define a un número de este tipo.
Finalmente, indicar que la propuesta de la US y la nuestra no son excluyentes, por considerarse ambas sin incorrecciones lingüísticas. Se usará, una u otra en función del contexto. Por ejemplo, en ejercicios de clasificación de números no se usará nuestra opción ya que su uso le estaría dando la respuesta al alumno al presentar la parte característica de los números complejos: la imaginaria. Pero, en preguntas en las que el alumnado deba relacionar cada tipo de número con la letra que los representa -en el caso de los complejos la C- el uso de nuestra variante sería la adecuada. En esta línea se sitúa una de las conclusiones de Tovar (2010, p. 304) que nos indica “la ventaja que traería para la LSC [lengua de signos colombiana] el contar con diferentes modos de denotar una misma entidad o actividad, […]” de forma que se usaría una u otra opción en función del contexto, el grado de tecnicismo o su formalidad.
Por otra parte, el neologismo que la US (única fuente que lo recoge) presenta para número imaginario respalda nuestra propuesta para número complejo. Dicho Signo (Figura 8) no presenta, bajo nuestro criterio, ningún problema lingüístico. Hemos de indicar, no obstante, que la definición de número imaginario de la US hace referencia al concepto unidad imaginaria. Como sabemos, un número imaginario es aquel que es:

Fuente: US (https://goo.gl/91XaGQ)
Figura 8 Signo para NÚMERO IMAGINARIONota: En realidad el Signo se correspondería con unidad imaginaria
[…] múltiplo de la unidad imaginaria. Por ejemplo, el número 2i es un número imaginario. La unidad imaginaria, que se denota con la literal i, es el número que tiene la propiedad de que cuando se multiplica por sí mismo obtenemos -1 como resultado. Es decir, i2 = -1. Los números complejos se llaman números imaginarios puros cuando su parte real es cero. (Soto, 2011, p. 105).
En base a este autor, los números complejos cumplen la forma z = a + i b - serán denominados números imaginarios puros cuando su parte real a es nula. Por tanto, todos los números imaginarios son complejos; pero, no todos los complejos son imaginarios.
Tomando como referencia las definiciones de número imaginario y unidad imaginaria se concluye, lo que ya avanzábamos previamente, que el Signo que la US propone para número imaginario en realidad hace referencia a unidad imaginaria -de la cual aportan la definición y Signo, bajo una entrada incorrecta-. A pesar de ello, un nuevo neologismo para unidad imaginaria que no esté basado en la inserción dactilología sería más visual (Figura 9) pero, nuevamente, se emplearía el presentado por la US o nuestra propuesta en función de las necesidades lingüísticas del contexto no considerándose ninguno de los dos incorrecto. Así, para el término número imaginario se empleará la combinación secuencial de dos Signos: NÚMERO+IMAGINARIO.
El siguiente grupo de números, tal y como recoge el esquema presentado con anterioridad, lo forman los números reales que se clasifican en: números racionales y números irracionales.
3.2 Números reales
Se definen los números reales como un: “Conjunto de números que se obtiene como la unión de los conjuntos de los números racionales y de los números irracionales […]” (Soto, 2011, p. 107), siendo los números racionales aquellos que “se pueden expresar como el cociente de dos números enteros, donde el denominador es distinto de cero” (Soto, 2011, p. 107) y los irracionales aquellos que: “no se pueden expresar como el cociente de dos números enteros, donde el denominador es distinto de cero. […] Ningún número racional es irracional y ningún número irracional es racional. Algunos números irracionales muy conocidos son π […] y e […]” (Soto, 2011, p. 105).
En otras palabras, los números reales son el conjunto de los números que se pueden expresar a través de una fracción con denominador distinto de cero -los números racionales que pueden representar un cociente entero (números enteros, Z) o decimal de tipo exacto o periódico (números fraccionarios)- y, aquellos números que no se pueden expresar en forma de fracción -los irracionales, no son periódicos ni exactos; como el número π-.
Es importante señalar que todos los números reales (R) son números complejos -que tienen b = 0 y por tanto, z = a + ib → z = a - pero, no todos los complejos son números R -tal y como se puede comprobar en la clasificación de la Figura 2- pues los números imaginarios son complejos pero no reales.
En las unidades léxicas recogidas en la Figura 10 se detectan los siguientes errores:
En la combinación secuencial NÚMERO+REAL proporcionada por Aroca et al. (2002, p. 72) y la web Sématos se detecta calco al emplear el Signo REAL.
-
Para número racional, en el glosario de la Fundación CNSE (Ibídem) y Sématos caen en la simplificación de considerar todos los números reales como fraccionarios cuando no lo son, obviando quizás que los números irracionales no son fraccionarios. Así, la unidad que presentan es, de acuerdo a nuestro análisis, incorrecta para el referente número racional -pero, sería adecuada para número fraccionario tal y como recogemos en la Figura 11-.
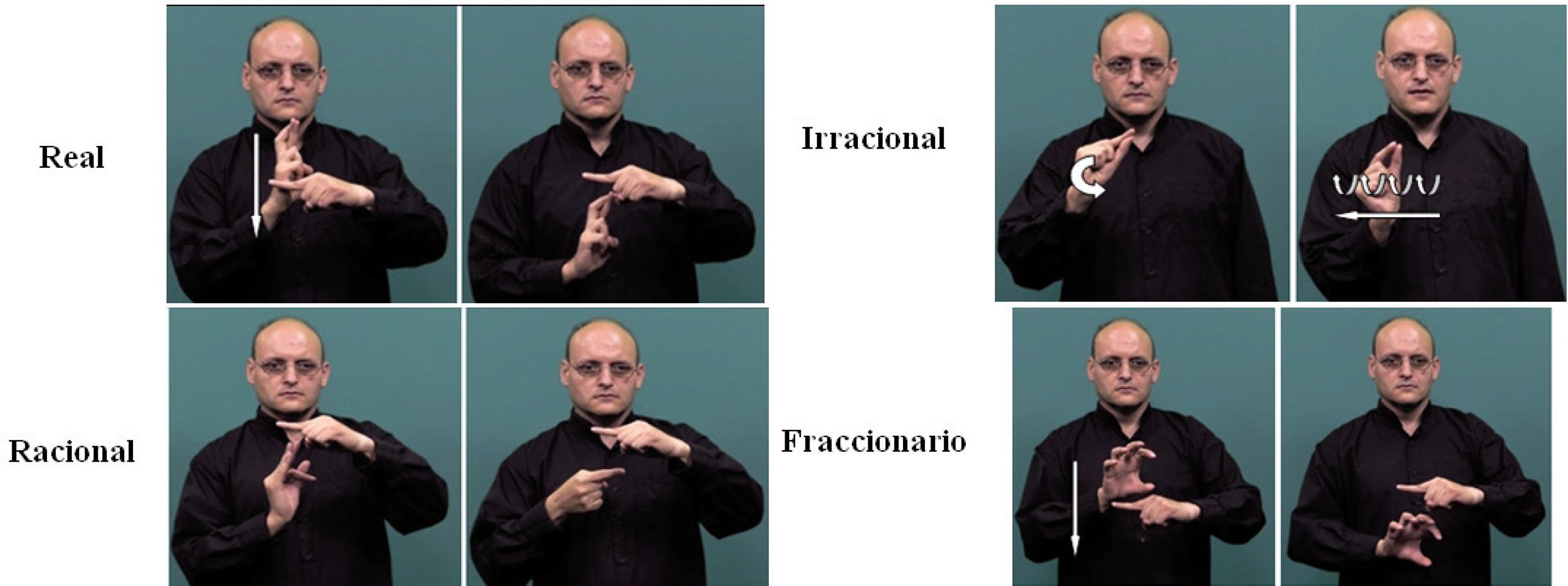
Por su parte, la US nuevamente presenta una alternativa válida para los conceptos: números reales y números racionales, basadas en la dactilología. Del mismo modo que para número complejo dicha opción de Signo se empleará en función del contexto y, como alternativa no excluyente a ellas presentamos dos neologismos en la Figura 11 -en la que también presentamos un neologismo para los vocablos entero y fraccionario, que no hemos encontrado en ningún material.
Los números racionales Q, a su vez, se clasifican en números fraccionarios y números enteros. “El conjunto de los números enteros se define como los números naturales, el cero, y los naturales dotados del signo negativo: Z = {…, -3, -2, -1, 0, 1, 2, 3,…}. […] Todos los números naturales son también números enteros.” (Soto, 2011, p. 104). De forma más sencilla, los números enteros son: los positivos o naturales, los números negativos y el cero.
Los neologismos de la figura superior -que se pueden usar en combinación con las propuestas de la US en función de las necesidades del contexto- precedidas de NÚMERO darían lugar a las expresiones: número real, número racional, número irracional y número fraccionario. Estas propuestas de neologismos se fundamentan en que:
Los números reales son todos aquellos que se pueden expresar a través de una fracción de denominador distinto de cero. Por ello, por inserción dactilológica -de la letra R- en el Signo FRACCIÓN se obtiene y propone el Signo de la imagen para REAL.
Los racionales son aquellos números reales que representan números decimales exactos o periódicos. Mientras que los irracionales, son números reales vinculados con un número decimal ni exacto ni periódico -es decir, números con infinitas cifras decimales sin relación de periodicidad-. Por ello, para RACIONAL se propone un neologismo que modifica al Signo FRACCIÓN y para IRRACIONAL se signa: COMA+CL«infinitos decimales».
Finalmente, para número fraccionario se emplea el Signo FRACCIÓN. Como ya indicábamos anteriormente este Signo se vincula de forma errónea en las fuentes a los números racionales: cuando no todos los números racionales son fraccionarios.
3.3 Números enteros
A continuación se muestran las unidades léxicas que hemos encontrado en las fuentes para: números enteros, naturales y números enteros negativos. Las incorrecciones detectadas en la Figura 12, son las siguientes:

Fuente: Aroca et al. (2002, p. 70 y 71), US, Spread Th e Sign, y Sématos.
Figura 12 ENTEROS, ENTEROS.POSITIVOS y ENTEROS. NEGATIVOS
-
Nuevamente, Aroca et al. (2002, p. 70) propone un Signo que reproduce Sématos, basado en el calco o interpretación literal de la expresión número entero, del siguiente modo: NÚMERO+ENTERO. En la Figura 13 se reproduce el Signo de la LSE para ENTERO.
La US presenta alternativas basadas en la dactilología para número entero y número natural. Además, para natural, los Signos recogidos por Aroca et al. (2002, p. 70 y 71) y Sématos y el presentado por la US podrían emplearse indistintamente y en función del contexto.
En cuanto a las unidades que presenta STS, para: entero, natural y negativo (Figura 12) parece que pretenden seguir una misma estructura, pero no la mantienen. Suponemos que la intención era indicar el signo -positivo o negativo- en el caso de los números positivos o enteros y los números negativos con la mano dominante mientras que la pasiva realiza un clasificador con función de boya que señala el valor absoluto del número. De forma que, en el caso de número entero, la mano dominante sería la que marcaría el valor en cuestión sin marcar ningún signo por ser los enteros la agrupación de: los positivos, los negativos y el cero.
-
Además de la entrada números positivos, STS recoge otra para números naturales -recordemos que ambos conceptos representan a los mismos números- en la que nos muestra una paráfrasis (Figura 14) innecesaria en la que además se observa un calco: al usar el Signo NATURAL en la definición de número natural.
La paráfrasis NÚMEROS.NATURALES (Figura 14) se glosaría de la siguiente forma: NÚMERO+NATURAL+NOMBRE+DAR y se interpretaría como un número al que se le da el nombre de natural. Por tanto, sería una paráfrasis poco apropiada que, además, emplea el calco NATURAL (Figura 15) unidad léxica a la que la Fundación CNSE (2011, s/p.) otorga los significados siguientes: “1. adj. Perteneciente o relativo a la naturaleza o conforme a la cualidad o propiedad de las cosas. 2. adj. Hecho con verdad, sin artificio, mezcla ni composición alguna.”. Aunque los números naturales son los más habituales y los que los alumnos trabajan con más naturalidad la combinación NÚMERO+NATURAL es un calco injustificado -en este caso, existen alternativas válidas- que da lugar a problemas de comprensión. En definitiva, a excepción del Signo NÚMERO.NATURAL que recoge Aroca et al. (2002) y Sématos; y, las propuestas de la US para número entero y número natural: NÚMERO+Z y NÚMERO+N, el resto presentan incongruencias y/o incorrecciones lingüísticas.
En esta ocasión, proponemos dos opciones de neologismos para cada uno de los términos. Una más visual, la opción A y, una segunda forma, con un carácter visual menos marcado -opción B- y más adecuada cuando se traducen/interpretan textos o ejercicios como el siguiente: -(-3)+(-7)-(-5) = 3-7+5 = +1, en los que: para evitar confusiones o traducciones/interpretaciones poco claras o erróneas se deberían diferenciar los signos de las operaciones de los correspondientes a los números enteros -ya sean, positivos o negativos-.
En la opción A la mano dominante marca el signo positivo o negativo del número con los Signos MÁS y/o MENOS y la mano pasiva hace referencia, mediante una boya, al valor absoluto del número. A pesar de ser una opción válida, consideramos más adecuada la opción B donde los Signos MÁS y MENOS se realizan sobre la palma de la mano, siendo estas unidades las que emplearemos en operaciones matemáticas con números enteros para diferenciar el Signo MÁS del SIGNO.MÁS (Figura 19).
Como se puede apreciar en las fotografías de la Figura 17 13 el Signo MÁS -signo matemático “más” o SIGNO.MÁS- se asocia también a SUMA/ADICIÓN. Por otra parte, ADICIÓN y SUMA presentan el mismo Signo y a ambas se les otorga el significado sumar.
En definitiva, tras búsqueda anterior y su análisis se concluye que: SUMA , SUMAR, MÁS, ADICIÓN y POSITIVO/SIGNO-MÁS son unidades polisémicas; hecho, que en la práctica de la enseñanza de las matemáticas da lugar a errores de comprensión. El mismo fenómeno, se observa en RESTA, RESTAR y NEGATIVO/SIGNO.MENOS (Figura 18).
Se pone de manifiesto que los materiales lexicográficos no emplean los recursos que nos proporciona la LSE por su condición de lengua de modalidad viso-gestual para diferenciar los tríos de términos SUMAR-SUMA-SIGNO.MÁS o RESTAR-RESTA-SIGNO.MENOS dando lugar a la confusión.
En definitiva, se observa la necesidad de nuevos Signos que representen las acciones RESTAR y SUMAR, las operaciones matemáticas RESTA y SUMA y los signos de los números enteros positivos o naturales, SIGNO.MÁS/POSITIVO; y, los enteros negativos, SIGNO.MENOS/NEGATIVO. Los neologismos que se presentan en la Figura 19 nos permiten diferenciar: las acciones SUMAR y RESTAR; las operaciones SUMA y RESTA; y, los signos matemáticos POSITIVO y NEGATIVO.
Es importante resaltar que, aun no siendo necesario disponer de un Signo por cada una de las palabras que forman el léxico del castellano, si la LSE nos permite diferenciarlos, siempre es mejor disponer de Signos diferentes que abusar de la polisemia y el gesto prestado. En este caso, los mecanismos de diferenciación empleados son muy básicos. Para las acciones SUMAR y RESTAR se usa el Signo MÁS y MENOS con un movimiento horizontal o vertical que indica la dirección de la acción y que estamos ante un verbo;14 para SUMA y RESTA se utilizan las combinaciones MATEMÁTICAS+MÁS y MATEMÁTICAS +MENOS que nos indican que estamos ante operaciones matemáticas; y, en SIGNO.MÁS y SIGNO.MENOS planteamos para diferenciarlos de SUMA y RESTA, por ser el signo de los números enteros “estático” frente a la acción de sumar y restar, el uso de una boya lingüística -mano pasiva en configuración dactilológica B- que indica que estamos ante un signo (positivo o negativo) escrito sobre un papel -superficie a la que hace referencia la boya.
3.4 Números primos y compuestos
Continuando con nuestro estudio, los números naturales se clasifican en números primos, números compuestos y el uno.
En esta ocasión el calco NÚMERO+PRIMO hace acto de presencia en las tres fuentes que recogen el concepto número primo. Por otra parte, número compuesto solo aparece en STS que lo ejecuta como: NÚMERO+AÑADIR -el verbo AÑADIR se ha modificado, pasando a ser bimanual-. En relación a esta estructura, no consideramos correcta la idea de adición o composición que se le otorga al concepto número compuesto.

Fuente: Aroca et al. (2002, p. 72), Universidad de Sevilla, Spread The Sign, y Sématos
Figura 20 NÚMERO.PRIMO y NÚMERO.COMPUESTO
Un número primo es aquel que solamente es divisible por sí mismo y la unidad; por ello, una cantidad n prima solamente se podrá agrupar/repartir como máximo de dos formas, todas juntas en una sola agrupación o, de una en una en n grupos. Así por ejemplo, trece bolígrafos se pueden aglomerar en un grupo que los contenga a los trece o en trece grupos de un único bolígrafo. Por ello, y tras analizar los conceptos en un grupo de personas Sordas y oyentes, se propone el neologismo, NÚMERO.PRIMO creado por combinación secuencial (Figura 21) y que se glosaría como: NÚMERO+GRUPO+BOYA.CL:“Grupo”-UNO++.
Por su parte, un número compuesto es aquel que es divisible por uno o más números, además de por sí mismo y la unidad. Una cantidad compuesta de objetos se podrán agrupar como mínimo de tres formas diferentes. Así, por ejemplo, cuatro vasos, se podrán agrupar de tres formas diferentes: 1) en un solo grupo con los cuatro vasos; 2) los vasos de uno en uno en cuatro “agrupaciones”; y, 3) en dos grupos de dos vasos cada uno. De acuerdo a esto, el neologismo presentado es: NÚMERO+GRUPO+CL:“grupo más pequeño”++.
3.5 Números decimales
Para finalizar el estudio abordaremos la clasificación de los números decimales exactos y periódicos - que se pueden expresar como una fracción- y los decimales de tipo irracional - que son números con infinitas cifras decimales no periódicos.
La Figura 22 recoge el resultado de la búsqueda realizada para el concepto número decimal. Además, Aroca et al. (2002, p. 69) acompaña el Signo con la siguiente definición de número decimal “Número que consta de una parte entera y una parte fraccionaria, que resulta de la división de la unidad por 10 o sus potencias”. Por su parte la US indica que: “Es el número que se expresa con los dígitos del 0 al 9. Tiene una parte entera y una parte decimal, separadas por una coma”.

Fuente: Aroca et al. (2002, p. 69), Universidad de Sevilla, Spread The Sign, y Sématos.
Figura 22 NÚMERO.DECIMAL
El Signo compuesto NÚMERO+COMA -en STS el orden es COMA+NÚMERO y aparece bajo la entrada: decimal- es totalmente congruente con su referente número decimal. Sin embargo, las definiciones no son válidas por las razones que se enumeran a continuación:
Aroca et al. (2002, p. 69) indica que los números decimales están formados por una parte entera y una fraccionaria -lo correcto es una parte entera y una decimal-. Un número constituido por una parte entera y una fraccionaria se conoce con el nombre de número mixto.
Además, la definición indica que son números que resultan “de la división de la unidad por 10 o sus potencias”. De este modo, se vincula, el término genérico número decimal con los decimales exactos: reduciendo así, el significado del referente.
Por su parte la US, proporciona una definición correcta de número decimal: “[…] una parte entera y una parte decimal, separadas por una coma”. Pero aporta una información innecesaria y confusa al indicar que un número decimal es “el número que se expresa con los dígitos del 0 al 9” cuando todos los números del sistema numérico decimal están constituidos por dichos dígitos -independientemente del tipo de número-.
-
Por último, en relación a los diferentes tipos de números decimales, solamente se ha encontrado un Signo para número decimal periódico (Figura 23) en Sématos. En la entrada aparece sólo la unidad léxica de la imagen, en la que se observa inserción dactilológica de LETRA.ERRE. Por tanto, haría referencia a un número periódico, entendiendo por ello un número decimal de tipo periódico, sin determinar si es puro o mixto. El resto de números decimales no cuentan con una entrada en los materiales lexicográficos de la LSE, por lo que se procede a su creación (Figura 24).
Finalmente, y en relación con los números decimales en STS se localizaron los conceptos, parte entera y parte decimal -que solamente hemos encontrado en dicha fuente-.
A diferencia de los neologismos que presentamos para parte entera y parte decimal en la Figura 26 -en la que también se recoge anteperiodo- las propuestas de STS no se pueden considerar unidades léxicas o Signos al ser explicaciones en LSE de ambos conceptos.

Fuente: Elaboración propia.
Figura 26 Neologismos PARTE.ENTERA.Y.DECIMAL, PARTE.ENTERA, PARTE. DECIMAL y ANTEPERIODO
A continuación, se justifican los neologismos de la Figura 24 y Figura 26:
Un número decimal exacto es aquel que tiene un número concreto de cifras decimales. Por ello, de forma bimanual se indica que tanto la parte entera como la parte decimal tienen un número concreto de dígitos.
Los decimales periódicos son aquellos que tienen infinitas cifras decimales. Se cumple que una -en caso de los periódicos puros- o más cifras -en los periódicos mixtos- se repiten hasta el infinito. Mediante inserción dactilológica R y uno o dos movimientos de izquierda a derecha nos referimos a decimales puros o mixtos.
En cuanto a los términos parte decimal y parte entera la creación de sus neologismos se basa en marcar si se encuentra a la izquierda o derecha de la coma.
Finalmente, el anteperiodo es una o varias cifras decimales de un número periódico que no pertenecen al periodo. Así, por ejemplo en 3,45555… el anteperiodo es la cifra decimal 4. El neologismo ANTEPERIODO recogido en la imagen es la combinación: COMA-PERIODO-CL“antes del periodo”.
En definitiva, los neologismos propuestos se basan en la forma de cada uno de los tipos de números decimales.
4 Conclusiones
Esta investigación muestra el resultado del proceso de búsqueda y análisis comparativo de unidades léxicas recogidas en los materiales lexicográficos de la LSE vinculadas a las diferentes tipologías de números. Además, se han analizado más de noventa locuciones matemáticas a partir de los vocablos: álgebra, ángulo, área, arista, base, cateto, coeficiente, constante, coordenadas, corchete, cuadrado, denominador, derivada; y, cientos de términos relativos a otros ámbitos específicos del saber. Este proceso, nos permite concluir que los errores más repetidos en los materiales lexicográficos de la LSE son (Valdés-González, 2017):
El vocablo del español y el Signo de la LSE no están vinculados al mismo referente, debido al exceso o falta de información.
Falta de diferenciación, abusándose de la polisemia y de la homonimia variando, únicamente, el gesto prestado -o, componente oral de la unidad léxica-.
Uso erróneo de los clasificadores y/o del espacio.
Influencia excesiva de la lengua oral sobre la LSE.
Errores en la definición del vocablo del español.
No se encuentran entradas en los materiales lexicográficos de la LSE, por no existir Signo o no estar recogido.
Asimismo, se ha observado un empleo excesivo de Signos de uso común para locuciones específicas del ámbito matemático; hecho que hace caso omiso a las recomendaciones de Kidd et al. (1993, como citado en Fuentes, 2005) que señalan como un agente perjudicial usar palabras/Signos polisémicos cuyo significado difiere fuera y dentro del aula.
Las evidencias mencionadas nos permiten concluir que los materiales lexicográficos de la LSE referentes a la temática tratada no son adecuados de forma completa, al presentar una calidad lingüística mejorable y, en consecuencia, se han presentado neologismos para cada uno de los términos sin un Signo adecuado. Asimismo, siguiendo a Tovar (2010) quien señala la importancia de tener varias unidades para denotar el mismo concepto en ocasiones se han propuesto neologismos para vocablos que ya presentaban un Signo, de modo que los profesionales cuenten con varios recursos en función de las necesidades interpretativas.
Por todo ello, entendemos que se han cumplido los objetivos planteados, al identificar de manera pormenorizada la existencia de errores o carencias léxicas en los materiales de la LSE en lo relativo a los nombres de los diferentes tipos de números; y, también, al proponer y recomendar neologismos en caso de ser necesarios. En definitiva, se contribuye a que la LSE se adecue a las necesidades y funciones académicas, facilitando la labor del intérprete en las aulas y al mismo tiempo se favorece el acceso al currículum del alumnado Sordo en igualdad de condiciones que sus compañeros oyentes (Domínguez, Rodríguez, & Alonso, 2011).
El hecho de que los profesionales de la interpretación se encuentren con carencias y lagunas terminológicas cuando se enfrentan a interpretaciones o traducciones vinculadas a conocimientos específicos y deban afrontar la creación y/o pacto de Signos provisionales con sus usuarios Sordos -unidades que, de forma general, se pierden- nos lleva a una situación en la que, en el mejor de los casos, los ILSEs son los protagonistas del proceso de enriquecimiento de la LSE. En este sentido debemos recordar que “[…] el papel de un ILSE no puede constituirse en modelo de lengua. Cualquier proceso de normalización exitoso no puede descargar el peso principal en la figura del intérprete. […]” (Nogueira, Villameriel, Costello, Barberà, & Mosella, 2012, p. 409). En esta misma línea, Bao y González (2013, p. 293) demandan “[…] avanzar en la investigación sobre la interpretación de LSE, al igual que la conveniencia de delimitar los parámetros de calidad en la interpretación de esta lengua a través de la evaluación de satisfacción en usuarios y profesionales.”
Además, consideramos que no solo es necesario evaluar la calidad de las interpretaciones y la satisfacción de los usuarios e intérpretes. Sería relevante someter a un estudio lingüístico riguroso a los Signos difundidos en los materiales lexicográficos de la LSE ya que es incuestionable que sin buenos materiales de trabajo y consulta, las interpretaciones español-LSE, o viceversa, no van a presentar la calidad que un intérprete nos puede proporcionar. Tal y como hemos puesto de relieve, en nuestra investigación, la labor del ILSE no está facilitada por los materiales de la LSE. Ello exige un diseño de los materiales que en su concepción y desarrollo tenga en cuenta la dificultad añadida que supone interpretar vocablos específicos y las necesidades de las personas usuarias de la LSE como L-1.
Por otro lado, la formación de los profesionales de la interpretación debe reforzarse con cursos de reciclaje vinculados a las materias del ámbito científico-técnico. El conocimiento profundo de los términos matemáticos favorecerá el análisis crítico y el uso correcto de las unidades léxicas que los ILSEs tienen a su disposición y, además, promoverá la elección del Signo más adecuado a cada situación lingüística. En este sentido, la publicación de los neologismos propuestos es necesaria pero es suficiente y deberá acompañarse de información adicional que permita la asimilación de los conceptos matemáticos por parte de los ILSEs y, de este modo, se evite una transmisión errónea de estos a sus usuarios Sordos. En este sentido, la implementación de un curso de reciclaje es inherente a la difusión de nuestros neologismos, tarea que afrontaremos a corto-medio plazo.
Los neologismos que presentamos se crean tras un cuidadoso trabajo de análisis lingüístico de las unidades léxicas previamente publicadas, respetando las características de las lenguas de modalidad viso-gestual y evitando las influencias de la lengua oral sobre la LSE. Son unidades léxicas no difundidas, de forma previa al presente artículo, por lo que tras su publicación se procederá a su divulgación en formato audiovisual para que sea la propia Comunidad Sorda quien se encargue de seguir valorándolos, usarlos y transmitirlos si lo estima oportuno y, en caso de ser necesario modificarlos ya que, tal y como indicamos al inicio en base a Sánchez (2014) lo importante no es el Signo sino el concepto. Además, coincidimos con Barreto (2015) en que serán los usuarios quienes en la vida cotidiana y/o académica den vida a estos neologismos.