1 O Projeto Logos II na década de 1970
A questão do professor não titulado, também conhecido como ‘professor leigo’, era um problema nacional na década de 1970. Para tentar resolver tal situação, foram criados diversos programas de habilitação de professores (EVANGELISTA; GROMANN DE GOUVEIA, 2014) e entre eles, o Projeto Logos II1. Esse Projeto surgiu como um mecanismo legitimador do Estado, na busca de respaldo da população, cujo “interesse era atingir significativos contingentes da sociedade, de preferência as camadas menos prestigiadas economicamente e mais carentes socialmente. Para isto, a educação era o ‘lugar ideal’ para tal ação, e o professor ‘leigo’, um ótimo motivo” (RAMALHO apud ANDRADE, 1995, p. 25).
O Projeto Logos II foi um programa de Educação a Distância (EAD) criado em 1975 e implantado em 1976 pelo Governo Federal por meio do Ministério da Educação e da Cultura (MEC) (BRASIL, 1975; CETEB, 1984). Tinha como intuito formar os professores leigos em regime emergencial, com habilitação em 2º Grau para exercício do Magistério. Inicialmente, o programa foi desenvolvido nos Estados do Piauí, Paraíba e Território Federal de Rondônia, Paraná e Rio Grande do Norte (BRASIL, 1975), em uma fase experimental, que valeria para um ano. Devido ao êxito do Projeto, antes de terminar o período-teste de um ano, houve a sua procura por outros Estados da Federação, abrangendo no total, dezenove deles (GROMANN DE GOUVEIA, 2016).
Os professores que se matriculavam no Logos II tinham níveis de escolaridade variados. Exigia-se, como escolaridade mínima para participar do projeto, a 4ª série do 1º grau e idade de 19 anos, sendo necessário ter 21 anos completos para a conclusão do curso. Era necessário, também, que o professor não titulado estivesse atuando nas quatro primeiras séries do primeiro grau, uma vez que esse local era seu “laboratório de aprendizagem e campo de observação e aplicação” (BRASIL, 1975, p.137).
A grade curricular do Logos II apresentada pelo projeto-piloto (BRASIL, 1975) era composta por 28 disciplinas (3.480 h) sendo dividida em duas categorias (Educação Geral e Formação Especial) e mais 2.000 horas de estágio. A parte de Educação Geral era direcionada para formação de 5ª a 8ª série do 1º Grau e o 2º Grau, enquanto a Formação Especial tinha como foco o ensino profissionalizante, nesse caso, o Magistério. No projeto-piloto constava que, no total, foram elaborados 208 módulos para atender a grade curricular do Logos II (BRASIL, 1975) “além de uma série introdutória denominada ‘preparação do cursista’, da qual constam as informações básicas do Projeto, sua operacionalização e as responsabilidades do aluno participante” (CETEB, 1984, p. 16).
Entre as disciplinas da parte de formação Específica tinha as de Didática da Matemática (DM) e de Técnica de Preparação de Material Didático (TPMD), sendo que a primeira, orientava os procedimentos didáticos para os professores-cursistas ensinarem Matemática no nível de 1ª a 4ª série do 1º Grau, e a segunda era destinada à confecção de material didático. Os módulos da disciplina de DM, diversas vezes fazem referência aos da disciplina de TPMD. Tais menções estão relacionados com a construção de materiais didáticos para o ensino de Matemática para as quatro primeiras séries do 1º Grau, estando entre eles o QVL que foi um instrumento pedagógico muito utilizado para o ensino do sistema posicional de base dez nos anos iniciais do 1º Grau, principalmente, nas décadas de 70 e 80 do século XX. Mediante ao que foi exposto, este artigo tem as seguintes questões norteadoras: quais foram as propostas dos módulos de Didática da Matemática e da TPMD do Logos II para a construção e utilização do QVL no ensino da Matemática? Quais as possíveis influências receberam esses materiais para a construção dessas propostas?
Ademais, este estudo abordará também uma experiência realizada com professores e futuros professores que participaram de uma oficina pedagógica intitulada Encontro de Pós-Graduação em Educação: Avaliação e Perspectivas (INTEGRAP 2017), realizado no Instituto de Biociências da UNESP de Rio Claro, em novembro de 2017. Nesse sentido, tentaremos responder: que considerações os participantes e os ministrantes de uma oficina pedagógica têm sobre a utilização do QVL em sala de aula?
Portanto, o trabalho em tela visa tecer uma elaboração histórica sobre as atividades propostas nos módulos de TPMD e suas ligações com o ensino da Matemática daquela época, tendo como objetivo analisar como que o QVL integrou a disciplina de DM dos módulos do Projeto Logos II, estabelecendo relações com os relatos dos ministrantes sobre a experiência com os participantes da oficina.
2 Referencial teórico-metodológico
As sociedades do passado nos deixaram rastros na forma de documentos e o ofício do historiador consiste no trabalho com eles, objetivando a construção de uma história. Para Certeau (1982), “Em história, tudo começa com o gesto de separar, de reunir, de transformar em ‘documentos’ certos objetos distribuídos de outra maneira. Essa nova distribuição cultural é o primeiro trabalho” (CERTEAU, 1982, p. 80). Nem todo documento constitui uma fonte histórica. Somente aqueles que respondem às perguntas do historiador tornam-se fontes históricas (LE GOFF, 2003). Dessa forma, para responder o nosso problema de pesquisa, serão utilizadas como fontes os oito módulos de DM e os dois de TPMD (Figura 1) e as literaturas da época relacionadas com a construção de material Didático.

Fonte: CETEB (1981, série 21, módulo 1); CETEB (1984, série 26, módulo 1).
Figura 1 Capa do módulo 01 de Didática da Matemática e da capa do módulo 01 de Técnica de Preparação de Material Didático
Para análise, utilizou-se do Método Indiciário (GINZBURG, 1989). Segundo Ginzburg, por milênios o homem foi um caçador, e durante muito tempo, aprendeu a antever o movimento e a prender suas presas, observando as pegadas nas lamas, ramos quebrados, bolotas de estercos, etc. O método proposto por Ginzburg, consiste na interpretação das pistas a partir de dados negligenciáveis.
Além disso, estamos também considerando que nenhuma fonte é inocente, é consequência não só de uma composição da história de uma época e de uma sociedade que a produziu, como também decorrente dos períodos que se sucederam. Por mais que determinadas fontes aparentam ter sido esquecidas em determinado período histórico, elas continuam sendo manipuladas, às vezes pelo silêncio (LE GOFF, 2003) e por esse motivo elas estão sujeitas a críticas (BLOCH, 2001).
De posse de todo esse aparato teórico-metodológico, a análise dos módulos de DM e de TPMD partiu de uma leitura abrangente dessas fontes, considerando os elementos presentes nos textos, tais como os conteúdos e as bibliografias sugeridas nesses materiais. A ideia é colocar em evidência os pormenores, e a partir daí, construir uma interpretação histórica que aponte quais eram as atividades propostas nos módulos de TPMD e DM que estavam relacionadas ao ensino da Matemática e como que eles estavam dialogando com os ideais daquela época.
A partir das atividades propostas nos módulos de DM e do TPMD, principalmente, aquelas envolvendo o QVL, em novembro de 2017, os autores elaboraram uma oficina pedagógica intitulada “Didática da Matemática: uma perspectiva histórica” para o INTEGRAP 2017. A oficina teve duração de 4 horas e na oportunidade participaram alguns alunos da Graduação e Pós-Graduação do IB – Unesp Rio Claro, bem como professores da rede pública do estado de São Paulo, sendo eles: 1 licenciada em Pedagogia, mestranda do programa de educação que lecionava na escola pública; 1 licenciada em Matemática, doutoranda do programa de educação que também ensinava na escola pública. As outras duas participantes eram estudantes do curso de Pedagogia do IB. A oficina tratava da confecção de alguns materiais pedagógicos a partir do que era ensinado nos módulos de DM e TPMD do Projeto Logos II. Tanto os conteúdos da oficina como a experiência dos autores com os participantes serão expostos no tópico quatro.
3 O Quadro Valor de Lugar nos Módulos do Projeto Logos II: relações entre a formação de professores, Matemática e materiais pedagógicos
De acordo com Valente (2008), o Movimento da Matemática Moderna (MMM) é uma expressão utilizada nos estudos sobre o ensino da Matemática, que caracteriza um período em que foram elaboradas novas referências para a disciplina de Matemática escolar. Após a Segunda Guerra Mundial, os Estados Unidos lançaram o Plano Marshall, de ajuda aos países europeus. Nesse plano, inseriu-se uma proposta de mudança da Matemática escolar, que foi traduzida numa proposta de internacionalizar essa disciplina, tornando-a mais “científica”, ou seja, mais próxima da Matemática dos cursos superiores (VALENTE 2008). Diversos professores brasileiros foram aos Estados Unidos para ter contato com essas novas referências. Na oficina que realizamos no INTEGRAP 2017, foi abordado um pouco sobre a vida do professor Osvaldo Sangiorgi, um dos principais expoentes do MMM no Brasil (VALENTE, 2008). Sangiorgi (1921-2017) foi professor de Matemática no Estado de São Paulo e autor de diversos livros de Matemática que abordavam em sua estrutura os ideais do MMM.
A partir de 1960, a proposta do MMM ganhou espaço nos currículos do ensino de Matemática de muitos países e, da mesma forma, no Brasil muitos estados absorveram esses ideários do MMM. O movimento defendia uma estrutura comum para o ensino de Matemática, a qual podia ser abordada em todas as séries iniciais. De acordo com Wielewski (2008), a teoria dos conjuntos constituía um exemplo de estrutura que poderia ser empregado universalmente no ensino da disciplina. Assim, a teoria dos conjuntos entraria como um elo entre os diversos campos da Matemática, quais sejam, as estruturas lógicas, algébricas e topológicas. Tais pressupostos eram difundidos, principalmente, por um grupo de matemáticos denominado Bourbaki2.
Em sua tese de doutorado, Costa (2013) analisou os módulos das disciplinas de DM do Projeto Logos II, e concluiu que na elaboração desses materiais foram utilizadas as concepções defendidas pelo MMM:
O vestígio marcante do ideário da modernização do ensino da Matemática, a Teoria de Conjuntos, foi o início da fundamentação pedagógica presente no material. As orientações indicavam, ainda, a utilização de material concreto, reforçando a necessidade da manipulação pela criança como forma de estimular a observação, a representação e a verbalização. A ideia de conjunto foi tratada como a noção de uma coleção de objetos organizada a partir de um critério. Nessa perspectiva, segundo o material didático, todas as experiências deveriam ser registradas inclusive na 1ª série, utilizando o recorte e a colagem. Dessa forma, outros conceitos deveriam ser inseridos no trabalho do professor, como a pertinência, a não pertinência, subconjuntos, contém, não contém, está contido, não está contido
(COSTA, 2013, p.178).
Gromann de Gouveia (2014, 2014a, 2016) ao olhar para esse mesmo material, concordou com a afirmação de Costa (2013). A teoria dos conjuntos era um conteúdo elementar no currículo defendido pelo MMM e foi utilizado em toda a construção dos módulos de DM do Logos II, sendo o primeiro conteúdo direcionado para o ensino da Matemática, sugerido aos professores-cursistas para ensinarem a seus alunos de 1ª a 4ª série (GROMANN DE GOUVEIA, 2014, 2014a, 2016; CETEB, 1981, série 21, módulo1). Portanto, os professores-cursistas que lecionavam nas primeiras séries do 1º Grau alfabetizariam matematicamente os seus alunos por meio da teoria dos conjuntos.
Segundo os elaboradores dos módulos de DM, a teoria dos conjuntos foi inserida nos programas direcionados para o 1º grau porque esse conteúdo dava continuidade e unidade a eles. Outro fator argumentado foi que a teoria dos conjuntos possibilitava que os alunos desenvolvessem atividades concretas que posteriormente levariam as crianças a abstração e a generalização (CETEB, 1981, série 21, módulo1).
Ademais, com a teoria dos Conjuntos, utilizada para a unificação dos conteúdos, os “modernistas” também defendiam uma abordagem axiomática e dedutiva para o ensino da Matemática. Nesse mesmo período, Piaget sustentava que havia uma relação entre o desenvolvimento das estruturas psicológicas da criança e o modo de ensinar os conteúdos matemáticos, sugerido pelos defensores do MMM. Portanto, a teoria cognitivista de Piaget e as concepções do grupo Bourbaki, nas quais as estruturas matemáticas eram a discussão central, deram argumentos e sustentação teórica para convencer sobre a eficácia das propostas do MMM, pois, tanto os estudos de Piaget como as pesquisas desenvolvidas pelos membros do Bourbaki foram bastantes usadas pelos defensores do MMM para justificar, legitimar e incentivar a utilização de metodologias experimentais (VALENTE, 2008).
Seguindo o fluxo da época, os módulos de DM traziam diversas concepções das teorias de Piaget, tais como a teoria do desenvolvimento cognitivo da criança que passa por quatro estágios, sendo: 1º período – sensório-motor, 2º período – pré-operatório, 3º período – operações concretas, 4º período – operações formais (FURTADO, 1999). O desenvolvimento desses estágios passa pelo uso de materiais concretos pela criança. Assim, com os conceitos da teoria dos conjuntos estava presente nos módulos as concepções que defendiam a utilização de material concreto em sala de aula, vejamos um exemplo: “O estudo de conjuntos deve partir de situações concretas, reais e ao nível das experiências das crianças. Utilize material variado como: bolinhas, carrinhos […]” (CETEB, 1981, série 21, p. 12).
Inicialmente, quando se pensa em material didático, a primeira problemática que se coloca é em relação a sua definição e no ambiente escolar, o livro constitui o primeiro na lista de materiais didáticos especialmente nas aulas de Matemática. Contudo, existem outros materiais que acompanham o professor nas suas atividades em sala de aula, como, por exemplo, as réguas, esquadros, o próprio quadro de giz e outros. Mas o que são materiais didáticos? Do ponto de vista histórico, é importante considerar as definições da época que se está estudando. Assim, nos módulos de TPMD do Logos II, o material didático era definido como:
[…] para tornar suas mensagens mais objetivas, facilitando assim a compreensão dos conteúdos e a efetivação da aprendizagem, você pode usar uma série de recursos ou meios que despertem o interesse e orientem a atenção dos alunos. Esses meios ou recursos são os materiais didáticos. Qualquer material de você use com a finalidade de promover a aprendizagem é material didático. Estão incluídas aí as coisas da natureza, o livro, o quadro-de-giz (também chamado lousa ou quadro-negro), o cartaz, o mapa, o globo, o flanelógrafo, o álbum seriado, etc.
(CETEB, 1984, série 26, módulo 1, p. 4).
O incentivo ao uso do material didático estava em consonância com a literatura da área pedagógica no período do Logos II. Desse modo, o ensino de Matemática por meio de material concreto estava em sintonia com as teorias de Piaget (1999). Para esse psicólogo, a criança sempre recorre a acontecimentos ou utiliza objetos que estão presentes no seu momento atual. De maneira gradativa o sistema operacional-concreto da criança a encaminha em direção ao abstrato. Entretanto, para antecipar o abstrato ela precisa partir do concreto (PIAGET, 1999). Os elaboradores dos módulos de DM orientavam os professores-cursistas nesse mesmo sentido: “depois de manipular o material concreto é que os alunos estarão capacitados para trabalhar mais abstratamente, usando somente lápis e papel” (CETEB, 1984, série 21, módulo 2, p. 12).
Ainda de acordo com os elaboradores dos módulos de DM, ao manipular o material concreto as crianças poderiam simular uma experiência, o que estimularia a observação do aluno perante essas situações concretas. Tal concepção estava em consonância com uma das teorias de John Dewey, que defendia que a experiência poderia ser vista como um processo investigativo com problemas reais, ou com a simulação de situações por meio de material concreto, nessa direção, os elaboradores da série 21 incentivam que os professores-cursistas trabalhassem com “situações de vivência das crianças” como nos sistemas de medidas e no sistema monetário (CETEB, 1981, série 21, módulo 2, p. 20).
Outra defensora da utilização dos materiais concretos para o ensino de Matemática em destaque na década de 1970, era a educadora e médica Maria Montessori (1870-1952). Para essa educadora, só depois que fosse despertado o interesse da criança é que poderia ser iniciado o processo de ensino-aprendizagem, desde que houvesse o estímulo a manipulação do material concreto. Para Montessori “Nada deve ser dado à criança, no campo da Matemática, sem primeiro apresentar a ela uma situação concreta que a leve a agir, a pensar, a experimentar, a descobrir, e daí, a mergulhar na abstração” (FIORENTINI & MIORIM, 1990, p.6). Semelhante às concepções de Montessori, os professores-cursistas eram aconselhados pelos módulos de DM a começarem do concreto para então partirem para o abstrato:
Através de situações concretas, os alunos serão levados a compreender as ações que as operações de adição e de subtração executam. […] O objetivo final é a abstração. Assim, esses exercícios serão realizados até que as crianças consigam responder prontamente: 2+5=7, sem terem de usar o material concreto
(CETEB, 1984, série 21, módulo 2, p. 5).
Um dos principais materiais concretos de Montessori e muito utilizado nas nossas escolas, é o Material Dourado. De acordo com Daltoé e Strelow (2010), o nome “Material Dourado” vem do nome “Material de Contas Dourada” e foi construído com o intuito de auxiliar nas atividades que envolviam o sistema de numeração decimal posicional. No material dourado, o cubinho representa as unidades, a barra as dezenas (10 cubinhos), a placa as centenas (100 cubinhos ou 10 barras) e o cubo maior, os milhares (1000 cubinhos, 100 barras ou 10 placas). Dessa forma, como será tratado no próximo tópico, assim como o Material dourado, com o QVL também poderia ser trabalhado com o sistema decimal posicional.
De uma forma geral, esclarecemos que os módulos de TPMD não eram para auxiliar exclusivamente a disciplina de DM, mas sim todas as disciplinas referentes à parte de Formação Especial. Deste modo, os módulos de DM direcionavam os professores-cursistas para os de TPMD em três momentos: para construir o flanelógrafo, o quadro de pregas e QVL. Analisaremos essas recomendações com a experiência dos autores com os participantes da oficina no tópico abaixo.
4 O Quadro Valor de Lugar na formação continuada de professores: uma experiência histórica
Nesta parte do artigo será apresentado e discutido as possibilidades do uso do QVL na formação continuada de professores. A experiência com a formação dos professores foi realizada por meio de uma oficina pedagógica, como já foi relatado. Essa oficina foi iniciada com uma apresentação de slides (Figura 2) sobre o contexto histórico dos materiais do Projeto Logos II, explicando aos participantes, assim como foi exposto no artigo em tela, quais foram os fatores que fundamentaram a utilização dos materiais pedagógicos nas aulas de Matemática para as primeiras séries do 1º grau, destacando o QLV.
Nessa apresentação, os autores exibiram um pouco sobre a biografia de Osvaldo Sangiorgi, o Grupo Bourbaki e as suas relações com o MMM, bem como expuseram as concepções do Movimento da Matemática Moderna (MMM). A maioria dos participantes da oficina afirmaram que nunca tinham ouvido falar sobre essas teorias, com exceção da participante formada em Matemática. Também, foram apresentadas as teorias cognitivista e estruturalista de Piaget relacionando-as tanto com o MMM como com a utilização do material em concreto em sala de aula. Referente às teorias de ensinar partindo do concreto em direção ao abstrato, além de Piaget, expomos as concepções de John Dewey, Maria Montessori, e citamos, rapidamente, outros pensadores, tais como Jerome Bruner, Ana Maria Poppovic e Édouard Claparède (Figura 3).

Fonte: Arquivo pessoal dos autores
Figura 3 Flanelógrafo, flanegravuras e quadro-de-pregas/QVL construídos pelos autores seguindo as instruções do módulo 02 de TPMD do Logos II
Assim, após a exposição desses pontos durante a oficina, explicamos sobre como os módulos de DM direcionavam os professores-cursistas para os de TPMD. A primeira indicação dos módulos de DM para que os professores-cursistas recorressem aos de TPMD, foi para a confecção de um flanelógrafo (Figura 3)3. Os módulos de DM também direcionavam os professores-cursistas para os de TPMD para instruírem como que se construía um quadro-de-pregas: “No módulo 2 de Técnica de Preparação de Material Didático – Série 26 ensinamos-lhe como confeccionar um quadro-de-pregas” (CETEB, 1981, série 21, módulo 1, p. 21). O quadro de pregas, também é construído em uma superfície plana, formado por pregas horizontais. Nessas pregas são inseridos cartões, palitos de picolé, canudos, cartões ilustrados, fichas palavras, frases, números, etc. “É um material que se presta muito ao ensino de matemática e também a alfabetização” (CETEB, 1986, série 26, módulo 2, p.04) (Figura 3).
Por fim, era sugerido aos professores-cursistas pelos elaboradores dos módulos de DM que trabalhassem as mesmas atividades sugeridas com o quadro-de-pregas no QVL, mas somente quando envolvessem as casas das centenas e milhares (CETEB, 1984, série 21, módulo 2). Os módulos de TPMD ensinavam a construir o QVL a partir do quadro-de-pregas. Pegava-se o quadro-de-pregas e dividia-o em quantas partes fossem necessárias para representar as classes e ordem dos números (Figura 3).
Nesse ponto, explicamos aos participantes da oficina que o QLV era um recurso didático exclusivo para o ensino/aprendizagem de Matemática, e normalmente era utilizado nos anos inicias do ensino fundamental, auxiliando no processo de contagem e formação dos números, na introdução dos conteúdos de ordem e valor posicional (unidade, dezenas, centenas, etc.) e nas operações matemáticas. Posteriormente, entregamos a cada participante um flanelógrafo/QVL, flanegravuras (Figura 3) e canudos de diversas cores e tamanhos para a execução das atividades.
Já os ministrantes da oficina utilizaram o mesmo material, mas de tamanho ampliado para orientação e exemplificação das atividades. Os ministrantes da oficina optaram por levar esse material pedagógico pronto, uma vez que, devido à carga horária, não seria possível a confecção dos materiais e o manuseamento dos mesmos. Todos os participantes relataram que não conheciam esses materiais concretos e nem a sua utilização para o ensino da matemática.
Depois de trabalharmos essas atividades com o flanelógrafo, partimos para a exercitação no QVL. Como já relatamos, a orientação dos módulos de DM era que, inicialmente, para melhor compreensão e fixação dos alunos, os professores-cursistas utilizassem o quadro-de-pregas dividido em duas partes para depois utilizar o QVL. Posteriormente, todas as atividades realizadas no quadro de pregas poderiam ser efetuadas no QVL. Como estávamos trabalhando com um grupo de adultos, optamos por praticar todas as atividades somente no QVL, que contemplava a casa da dezena, centena e milhar. Explicamos esses fatores aos participantes da oficina, e iniciamos a primeira atividade.
De acordo com os módulos de DM, o QVL permitiria ao professor-cursista ‘concretizar’ os numerais. A primeira atividade com o QVL sugerida por esse material era sobre o estudo de numeração decimal. O conceito de dezena ou conjunto de dez, só poderia ser iniciado depois que a criança soubesse agrupar até nove elementos. “Uma coleção com mais do que nove elementos, será chamado dezena” (CETEB, 1984, série 21, módulo 2, p.21) (Figura 4).
Fonte: (CETEB, 1984, série 21, módulo 2, p. 21).
Figura 4 Atividade com o QVL no módulo 2 de Didática da Matemática
Para trabalharmos o sistema de numeração decimal no QVL, entregamos aos participantes da oficina, canudos de diversas cores e tamanhos. Depois solicitamos que colocassem nove canudos de uma mesma cor no QVL, na parte correspondente às unidades. Logo em seguida, pedimos que acrescentassem um canudo, e assim ter-se-ia uma dezena. Nesse ponto, aconselhamos os participantes, que eles orientassem as crianças para que observassem que conjunto de 10 unidades (dezena), tem um lugar especial, o das dezenas (Figura 4), e então amarrassem os canudos e colocassem no das dezenas. A medida que as crianças fossem entendendo o conceito, poder-se-ia trocar o maço com 10 canudos, por um canudo maior e de outra cor. As crianças também deveriam observar que o lugar das unidades ficou vazio (zero unidade).
Inspirados pelos módulos de DM, alertamos aos participantes da oficina que tomassem cuidado quando fossem trabalhar com o conceito do zero no quadro-de-pregas ou no QVL:
Fazer com que as crianças observem que o lugar das unidades ficou vazio. Isso significa: não tem mais unidades ou tem zero unidades. A criança deverá compreender que o zero tem uma dupla função: indica a ausência das unidades e guarda o lugar delas. Também deverá compreender que podermos ter, no máximo, nove unidades em casa ordem
(CETEB, 1984, série 21, módulo 4, p. 22).
Os participantes da oficina relataram que trabalhar o conceito de zero no QVL facilitaria muito a explicação Matemática desse numeral.
Os professores-cursistas do Logos II também eram instruídos pelos módulos de DM a trabalhar a noção de valor posicional utilizando a decomposição dos números em suas ordens e classes, e o QVL: “Deve ser chamada a sua atenção [da criança], para o fato de que o valor de cada ficha está relacionado ao lugar em que ela ocupa no quadro. É o valor posicional do algarismo” CETEB, 1984, série 21, módulo 4, p. 22). Dessa forma, pedimos que os participantes da oficina colocassem onze canudos nos campos da unidade e da dezena, depois orientamos que eles conduzissem as crianças a observarem que o novo conjunto tem uma dezena e que ainda sobrou uma unidade de canudo.
Posteriormente, essas atividades deveriam ser trabalhadas com os outros campos do QVL, portanto, praticamos os seguintes exercícios com participantes da oficina: “a) Coloque no QVL – 11 elementos (canudos); B) proceder até o 19; c) represente o numeral 20 (duas dezenas) no QVL; d) coloque nove dezenas no QVL; e) coloque nove dezenas e nove unidades; f) agora, coloque mais um elemento (10 dezenas – 1 centena); g) representem os números 579; 853 e outros no QVL. Reforçamos ainda que tais atividades deveriam ser repetidas com alunos, até que as crianças tenham fixado a ideia de dezena e compreendam o significado do numeral 10.
As demais atividades, sugeridas pelos módulos de DM utilizando o QVL, estavam relacionadas com as quatro operações (adição, subtração, multiplicação e divisão). Efetuava-se elas utilizando a decomposição dos numerais (CETEB, 1984, série 21, módulo 2).
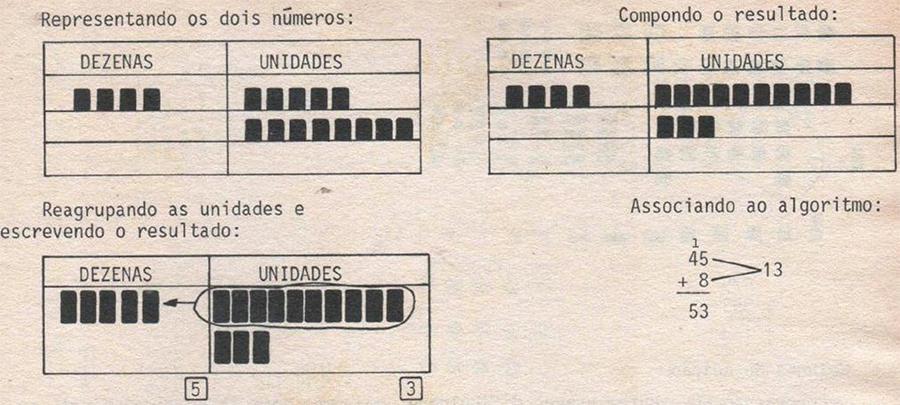
Nas adições os números são representados por um e dois algoritmos e depois reagrupados. É necessário representar as parcelas, colocando a unidade embaixo de unidade, dezenas embaixo de dezenas e assim sucessivamente (CETEB, 1984, série 21, módulo 2). Na oficina, demos alguns exemplos de como realizar a adição no QVL, e depois solicitamos que os participantes efetuassem algumas operações. Todos os participantes afirmaram que utilizando o QVL para ensinar a adição ficaria mais fácil de explicar e os alunos entenderem o sentido do “vai um” (Figura 5).
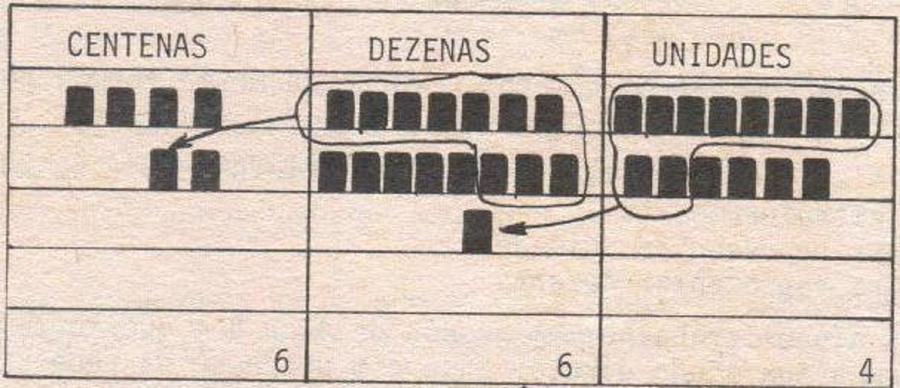
Na subtração primeiro deve-se se apresentar o problema, por exemplo: tenho 245 figurinhas; se eu der 197 delas a meu irmão, com quantas ficarei? Posteriormente, pede-se para o aluno representar o minuendo no QVL e depois retira-se o subtraendo. Contudo, como tirar 5 de 7 unidades? Para efetuar essa operação, temos que utilizar uma dezena e reagrupá-las com as unidades já existentes (Figura 6) (CETEB, 1984, série 21, módulo 3). Assim, como nas atividades de adição, demos exemplos de algumas subtrações para os participantes da oficina e depois pedimos que eles praticassem diversos exercícios de subtração no QVL. Os participantes foram unânimes em dizer que utilizando o QVL ficaria muito mais fácil explicar para as crianças o conceito de “empresta 1” e esse um se “transformar” em 10.
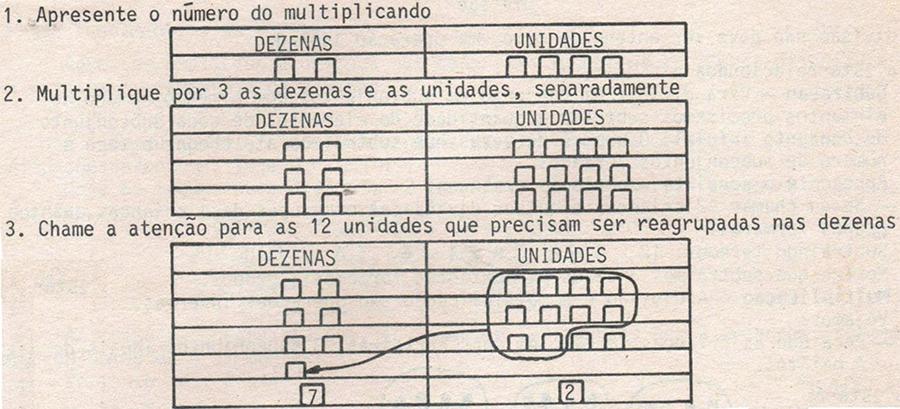
Na multiplicação explica-se para o aluno que esta operação é soma de parcelas iguais. Então é necessário representar com canudos no QVL o multiplicando na quantidade de vezes do multiplicador. Como na adição, as unidades devem estar embaixo das unidades, etc., depois realiza-se o reagrupamento (CETEB, 1984, série 21, módulo 4). (Figura 7).
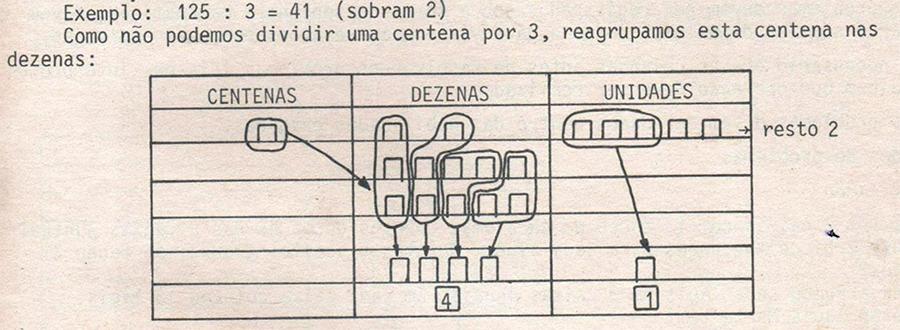
Já na divisão, assim como na subtração, deve-se ser iniciada por uma situação-problema. Por exemplo: hoje eu trouxe para escola 125 laranjas. Quero reparti-las com 3 amiguinhos. Quantas laranjas ganhará cada amigo? Para resolver essa atividade no QVL é necessário representar com canudos o dividendo e depois separar as unidades, dezenas e centenas em parcelas iguais na quantidade de vezes do divisor (CETEB, 1984, série 21, módulo 4). (Figura 8).
No caso do nosso exemplo, não teríamos como dividir duas dezenas para 3 amigos, por isso, pegou-se emprestado da centena. Ademais, sobraram laranjas, ou seja, a divisão foi inexata, então teve-se resto.
Tanto na multiplicação como na divisão, na oficina demos exemplos de como proceder na efetuação dessas operações no QVL e depois pedimos que os participantes realizassem diversas atividades envolvendo-as. Os participantes tiveram um pouco de dificuldades para executarem os exercícios, e relataram que no caso da multiplicação e da divisão, o QLV poderia dificultar no ensino e talvez, só tornaria mais complexo o entendimento das crianças em vez de facilitar. Para ensinar essas duas últimas operações, eles não considerariam utilizar em suas salas de aula.
A recomendação do QVL, pelos elaboradores dos módulos do Logos II, como recurso didático em sala de aula era que esse material possibilitava a concretização de ideias, já que com a comunicação somente verbal alguns alunos poderiam sofrer bloqueios de aprendizagem. Com esses recursos, somada a palavra oral e escrita, facilitaria que os professores-cursistas concretizassem ideias e conceitos. E por fim, o QVL permitia apresentar o assunto em etapas, porque os elementos vão sendo “colocados, retirados, deslocados da posição, à proporção que o desenvolvimento do assunto, no tempo e no espaço [que] assim o exige, e, por isso, introduzindo dinamismo na transmissão de uma idéia [sic]” (CETEB, 1986, série 26, módulo 2, p. 4).
5 Considerações finais
Olhar para esse passado, reconstruir a sua história, quiçá, um dia, poderá nos ajudar a entender um pouco sobre o papel do material didático na formação do professor, além de compreender as suas potencialidades e os seus limites, mas principalmente, construir uma narrativa que dê conta de contar histórias do material didático, em especial, o QVL que era destinado ao ensino de Matemática. Nesse trabalho foi mostrado uma conexão entre os conceitos de material didático ligado às concepções de Piaget, Montessori, Dewey e aos ideais do MMM.
A construção do QVL e outros materiais didáticos adquiriram um papel muito importante no Projeto Logos II, já que havia uma disciplina específica que ensinava o professor, no caso, a TPMD. Contudo, no artigo não foram tratadas de todas as relações entre o que era ensinado na disciplina de TPMD e de DM, o que constitui uma limitação do trabalho. Dessa forma, além de possibilidades de estudos que analisem mais a fundo essas relações, há necessidade de trabalhos que tratem sobre a presença ou não da disciplina de TPMD em outros cursos de magistério.
A opinião dos participantes da oficina, vai de encontro com o que era exposto nos módulos de DM e de TPMD, pois, de acordo com os elaboradores desses fascículos, o QVL e os outros materiais concretos deveriam facilitar a aprendizagem, e ser utilizados para motivar e manter o interesse, pois, permitiam “a apresentação de um assunto de maneira instantânea, visual, colorida e interessante, tornando o ensino mais atraente e dinâmico” (CETEB, 1986, série 26, módulo 2, p.4). Portanto, se não servisse a esse propósito não deveria ser utilizado.