INTRODUÇÃO
Este artigo refere-se a uma releitura de parte das informações coletadas em uma investigação1, que teve por objetivo idenjpgicar as possibilidades didático-pedagógicas de um trabalho sistematizado com cálculo mental, de forma dialógica, em Libras, com alunos surdos fluentes nesta língua.
Dentre as jusjpgicativas para a realização dessa investigação está o fato de que, mesmo com a adoção da abordagem bilíngue, a questão linguística constitui-se um entrave para crianças surdas nos anos iniciais de sua escolarização, particularmente na tarefa de construir o vocabulário matemático, seja em Libras, seja na Língua Portuguesa na modalidade escrita. Várias são as razões para isso, dentre as quais podemos apontar o fato de que mais de 90% das crianças surdas possuem pais ouvintes (GOMES, 2010) e, assim, elas, além de não serem expostas às diferentes situações socioculturais que permitem aos ouvintes perceber que as palavras que falam podem ser escritas, também não chegam à escola com a Libras já adquirida, pois não estão imersas em um ambiente linguístico favorável à essa aquisição. Dessa forma, o trabalho pedagógico com a alfabetização matemática de crianças surdas envolve três linguagens distintas: a matemática, com o traçado dos algarismos; a Língua Portuguesa na modalidade escrita; e a representação em Libras dos algarismos.
Estudos realizados acerca do ensino de Matemática para surdos apontam “[...] a necessidade de estratégias metodológicas diferenciadas, particularmente para suprir as lacunas no conhecimento prévio de crianças surdas ocasionadas pela interação prejudicada com o meio” (NOGUEIRA, BORGES, FRIZZARINI, 2013, p. 173). Os mesmos autores complementam que as crianças surdas também apresentam dificuldades na constituição de conhecimentos envolvendo operações aritméticas elementares, uma vez que estes são construídos de maneira informal e sustentados na interação com o meio.
Diante desses resultados e da constatação de uma das autoras, professora de Matemática da Escola Bilíngue para Surdos, de lacunas referentes aos conceitos matemáticos essenciais às operações aritméticas elementares como, em alunos de uma turma do 6º ano, conjecturou-se trabalhar com o cálculo mental na busca de minimizar tais lacunas e de proporcionar a interiorização dos conceitos e procedimentos matemáticos envolvidos. O trabalho foi realizado mediante a aplicação de um conjunto de atividades composto por dois blocos, o primeiro com as que se referem ao sistema de numeração decimal, das quais nove eram atividades especificas e seis complementares e o segundo bloco continha dezessete atividades de estruturas aditivas. A releitura aqui realizada refere-se ao desempenho de um dos participantes da investigação, denominado ficticiamente de João em uma das atividades complementares do primeiro bloco que envolveu a contagem de objetos.
A motivação para realizá-la emergiu de uma reunião de estudos do GEPeDiMa: Grupo de Estudos e Pesquisas em Didática da Matemática (UNESPAR), liderado pelas duas primeiras autoras desse artigo, ao ser discutida a afirmação de Vergnaud (1990) de que o conhecimento é constituído à medida que os “esquemas se adaptam às situações”. Em função do conhecimento profundo que as duas primeiras autoras possuíam da pesquisa realizada pela terceira2, durante essa discussão, para exemplificar, ambas utilizaram o desempenho de João, em algumas das situações propostas na investigação anteriormente desenvolvida. Como as análises realizadas naquele momento não tinham como propósito destacar a evolução do esquema de contagem desse educando, decidiram realizar a releitura aqui apresentada. Aliados a esse interesse, temos o fato de João apresentar como coocorrência da surdez, o Transtorno do Déficit de Atenção e Hiperatividade - TDAH com predominância do Déficit de Atenção, decorrendo daí destacada insegurança que o impedia de estabelecer um diálogo prolongado.
Em face do exposto, esta releitura das informações obtidas na investigação inicial acerca do desempenho do João objetiva aprofundar as análises de seu desempenho em relação a dois aspectos: o socioemocional e o que se refere ao conhecimento matemático, sempre à luz da teoria dos Campos Conceituais - TCC (VERGNAUD, 1990), considerando para o primeiro aspecto a mudança de conduta a partir da segurança que João foi adquirindo com a adoção da perspectiva dialógica que possibilitou o estabelecimento simultâneo da forma operatória (saber fazer) e da predicativa do conhecimento (saber explicitar), que, segundo Vergnaud (1996), é condição necessária para a construção do conhecimento. No que se refere ao aspecto do conhecimento matemático, esta releitura objetivou analisar a evolução do esquema de contagem de João, em face da diversidade de situações vivenciadas durante o desenvolvimento da investigação.
O APORTE TEÓRICO DA PESQUISA
A teoria de sustentação das análises é a teoria dos Campos Conceituais de Gérard Vergnaud que, dentre outros aspectos, atribui importância ao gesto na constituição da contagem (VERGNAUD, 1996), uma vez que a Libras, a língua veicular na escola cenário da investigação, é na modalidade visuo-motora e, portanto, de forte característica gestual.
De acordo com o autor, existem várias categorias gestuais, como a apontação do objeto e o direcionamento do olhar ao mesmo tempo em que é pronunciada a palavra-número. Esse conjunto de ações explicitam a ideia matemática de correspondência biunívoca entre os objetos contados, “[...] Se não há uma correspondência biunívoca entre esses conjuntos, a criança não pode contar” (VERGNAUD, 1996, p.11). Uma das dificuldades enfrentadas por João, sujeito desta pesquisa, residiu nessa correspondência, uma vez que a própria palavra-número é literalmente um gesto, ou melhor, um sinal em Libras.
Para Vergnaud (1998), as questões sociais não modificam a natureza do conhecimento matemático em si, mas têm influência como modo que esse conhecimento chega à sala de aula, pois cada professor tem sua visão sobre o ensino da Matemática e sobre a própria Matemática, que chegam aos alunos. No que se refere ao ensino de Matemática para alunos surdos, a influência do meio para as primeiras noções matemáticas pode ser prejudicada, em função do comprometimento da comunicação oral que ocorre desde seus primeiros anos de vida, como por exemplo, a memorização da sequência das palavras-número que é favorecida, no caso de crianças ouvintes por situações corriqueiras, como aquela em que a mãe sobe a escada de mãos dadas com seu filho pequeno e realiza a contagem dos degraus - um, dois, três degraus.
No contexto escolar, Vergnaud (2009b) considera a atividade da criança sobre a realidade decisiva, e defende que seus conhecimentos devem ser construídos por meio de situações que proporcionam “[...] relação direta com as operações que ela é capaz de fazer sobre a realidade, com as relações que é capaz de discernir, de compor e de transformar, com os conceitos que ela progressivamente constrói” (VERGNAUD, 2009b, p.15).
No que se refere ao papel do professor, Vergnaud (2009b) menciona que ele deve incentivar e explorar tais situações e, para isso, é preciso ter o conhecimento claro das noções a ensinar. Nesse sentido, importa que os resultados de pesquisas cheguem até as salas de aula, pois somente compreendendo as formas como aluno aprende é possível ensinar, ou seja, ao compreender as dificuldades enfrentadas pelas crianças e as etapas de seu desenvolvimento, o professor poderá propor boas situações que propiciam a aprendizagem dos alunos (VERGNAUD, 2009b; 1990).
Para Vergnaud (1990), são as situações que dão sentido a um conceito, ou seja, é a partir das diferentes situações vivenciadas no decorrer do processo escolar que o conceito é elaborado pelos sujeitos. Além disso, cada situação demanda um conjunto de representações simbólicas e de categorias de pensamento manifestadas na ação dos sujeitos. Nesse sentido, do ponto de vista psicológico, o pesquisador estabelece uma definição para um conceito a partir de três conjuntos, representado por C = (S, I, s), sendo:
S o conjunto das situações que dão sentido ao conceito;
I o conjunto dos invariantes operatórios3: operações de pensamentos, não necessariamente explícitas, que possibilitam modelizar ações dos estudantes face a determinada situação, relativas a propriedades, relações ou aplicação de um teorema;
s o conjunto das formas de linguagem: permite representar simbolicamente o conceito, suas propriedades, as situações, os processos de resolução.
Para Vergnaud (1990), a linguagem desempenha um papel relevante na conceitualização e na ação dos sujeitos; ela “[...] ajuda à designação, e, portanto, à idenjpgicação dos invariantes: objetos, propriedades, relações, teoremas; ajuda ao raciocínio e à inferência; ajuda à antecipação dos efeitos e dos objetivos, à planificação e ao controle da ação” (VERGNAUD, 1990, p.180). Dito de outra forma, além da função da comunicação e representação, a linguagem auxilia no saber fazer (forma operatória do conhecimento), ou seja, na organização e na reflexão sobre a ação, e no saber explicitar os procedimentos de resolução e os conceitos (forma predicativa do conhecimento).
No ensino para alunos surdos, a linguagem e as formas de representações são mais diversificadas do que para alunos ouvintes, pois mais uma língua - a Libras - está presente. Esta língua, além de ter como principal canal emissor as mãos, atribui significado gramatical às expressões faciais e corporais, e tem a visão como única via de recepção das informações. Assim, além da linguagem matemática, da Língua Portuguesa na modalidade escrita, do apoio de gestos como elementos paralinguísticos, as representações dos conceitos matemáticos são também realizadas e apreendidas em Libras.
É preciso considerar que a representação escrita de um número não pode ser confundida com o próprio objeto
matemático, e que existem diversas representações para um mesmo número. Tomando o número seis (6) como exemplo,
temos: 6 em escrita indo-arábica; VI em escrita romana; seis em escrita língua natural (língua natural dos ouvintes);
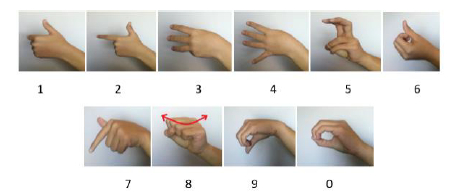
a indo-arábica para registrar uma quantidade ||||||; ******;  em Libras. Pode-se ter o mesmo número com todas as suas propriedades (cardinal de conjuntos de seis elementos, número par, múltiplo de três, sucessor de 5, antecessor de 7 etc.) em cada uma das diferentes representações, pois um número pode ser representado em vários sistemas de escritas e o Sistema de Numeração Decimal - SND, representação posicional de base dez, é um desses sistemas (VERGNAUD, 2009b). Em Libras, os algarismos são representados ou falados da seguinte forma:
em Libras. Pode-se ter o mesmo número com todas as suas propriedades (cardinal de conjuntos de seis elementos, número par, múltiplo de três, sucessor de 5, antecessor de 7 etc.) em cada uma das diferentes representações, pois um número pode ser representado em vários sistemas de escritas e o Sistema de Numeração Decimal - SND, representação posicional de base dez, é um desses sistemas (VERGNAUD, 2009b). Em Libras, os algarismos são representados ou falados da seguinte forma:
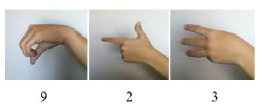
A partir do dez e até mil, os números são representados simplesmente fazendo a justaposição dos algarismos, como, por exemplo, no número 923:
Desta forma, pela maneira como são representados os números de ordem inferiores ao milhar, no que se refere ao contexto escolar do aluno surdo, Silva (2010) defende que para esses alunos:
[...] todos os números são transparentes, no sentido de que “se escreve como se fala”, ou dito de outra forma, os sinais referentes aos algarismos são expressos na mesma ordem em que são escritos. Esta transparência numérica se consubstancia em um fator que possibilita e desencadeia o pensamento e a construção dos elementos conceituais subsidiados por ela, fato que pode favorecer os surdos em detrimento dos ouvintes, pois estes últimos recebem a interferência da linguagem numérica oral não-posicional e devem realizar uma transcodificação para a escrita numérica posicional (SILVA, 2010, p. 222).
Esse argumento, entretanto, se aplica quando se considera a representação, em Libras, de cada algarismo que compõe o numeral, que coincide com a representação em Libras dos números inferiores a uma unidade de milhar ou mesmo da classe posterior que não compreenda o zero intercalado. Na representação dos números em Libras com zero intercalado este sofre alterações, como, por exemplo, a representação do número 1.000.050 em Libras.
Significa “um milhão e cinquenta” e não está sendo digitalizado como “um, ponto, zero, zero, zero, ponto, zero, cinco, zero”, correspondente à representação escrita do numeral em questão, conforme ilustrado nas fotos da Figura 4.

Fonte: GEPSEM e Projeto de Extensão Apoio à Difusão da Libras.
Figura 4 Digitalização de algarismo por algarismo de 1.000.005 em Libras
Para Vergnaud (2009a), a atividade gestual contém diversas operações de pensamento. É evidente que existem diferenças entre os gestos do bebê que aprende a pegar pequenos objetos e os gestos de um atleta adulto, ou de um pedreiro, por exemplo. Entretanto, a organização dos gestos, seja de um bebê, de uma criança ou de um sujeito adulto, contém os mesmos componentes: um objetivo, o sequenciamento e coordenação dos movimentos das diferentes partes do corpo, a idenjpgicação dos objetos materiais e de suas propriedades (volume, peso, características geométricas, distância, temperatura etc), cálculo das ações a serem efetuadas, das informações a serem obtidas, dos controles a serem realizados (VERGNAUD, 2009a).
Segundo Vergnaud (2009a), esses fatores conduzem à definição de esquema como sendo uma organização invariante da conduta para uma classe de situações. Uma outra definição de esquema é apresentada pelo pesquisador levando em consideração quatro categorias de elementos: i) objetivos, intenções e antecipações; ii) regras de ação; iii) invariantes operatórios; iv) possibilidades de inferência em situação (VERGNAUD, 1990).
O pesquisador chama atenção para a existência de duas classes de situações, nas quais o conceito de esquema não funciona do mesmo modo: a classe de situações que o sujeito dispõe das competências necessárias ao tratamento relativamente imediato da situação; e “[...] a classe de situações em que o sujeito não dispõe de todas as competências necessárias, o que o obriga a um tempo de reflexão e exploração, a hesitações, a tentativas frustradas, levando-o eventualmente ao sucesso ou ao fracasso” (VERGNAUD, 1990, p. 136).
Para Vergnaud (2003), o conhecimento se adapta e se desenvolve com o tempo, em função das situações vivenciadas, sendo reelaborado a cada nova situação enfrentada. Ao se deparar com situações novas, os sujeitos mobilizam seus conhecimentos prévios, os reformulam e tentam adaptá-los à nova situação. Conhecer novas situações conduz à organização de novos esquemas e à ampliação dos conhecimentos relativos a dado campo conceitual.
O esquema de contagem, por exemplo, envolve três elementos em jogo: a cardinalização, a capacidade de recitar nesta ordem as palavras-número e a capacidade de estabelecer correspondência entre a recitação e os objetos, sendo que o estabelecimento dessa correspondência é facilitado pela simultaneidade entre o manuseio ou apontação do objeto a ser contado e a verbalização da quantidade (VERGNAUD, 1993). Ainda, segundo o pesquisador, “[...] o gesto e o pensamento estão intimamente ligados” (VERGNAUD, 1996, p.12). No caso de adultos, essa apontação pode ser feita simplesmente pelo meneio da cabeça ou direcionamento do olhar, mas em crianças essa apontação é explícita, quase sempre com o auxílio do dedo indicador. Já com sujeitos surdos, existem outros aspectos particulares e necessários de serem considerados no interior de uma sala de aula, conforme análises a seguir.
A RELEITURA E ANÁLISE DOS DADOS
De acordo com os exames audiológicos, João apresenta diagnóstico de perda auditiva neurossensorial bilateral profunda, comunica-se somente por Libras, apresenta o TDAH com predominância do TDA e não mantém diálogo prolongado.
O TDAH, de acordo com a ABDA (Associação Brasileira de Déficit de Atenção), caracteriza-se por sintomas de desatenção, inquietude e impulsividade. Quanto às causas do TDAH, temos duas visões principais: a organicista e a visão histórica cultural. Para a primeira, a terapia medicamentosa é a forma determinante de enfrentamento do problema, enquanto a segunda considera ser a ação pedagógica mais eficaz do que os remédios. Segundo informações fornecidas pela equipe pedagógica da escola, João fazia uso de medicamentos, mas, por compartilharmos da visão histórico-cultural para o atendimento do TDAH, decidimos considerar, a partir do desempenho de João, se o trabalho sistematizado com o cálculo mental se constituiria em uma possibilidade de ação docente para esses alunos.
Embora esse não fosse o objetivo da primeira investigação, a presença de João e de mais uma participante da pesquisa com TDAH fizeram com que decisões fossem tomadas para a implementação da sequência de situações didáticas, como fixar em 15 minutos, tempo de duração da atenção útil desses educandos, a duração de cada encontro realizado. Também a organização do ambiente da investigação realizada anteriormente4 foi pensado de maneira que todos pudessem se comunicar visualmente entre si.
A sequência didática foi pensada para ser aplicada a alunos que cursavam no início da pesquisa o 6º ano do Ensino Fundamental (embora tenha sido implementada somente no ano seguinte) e, assim, foi assumido por hipótese que os estudantes sabiam contar objetos. Contudo, durante a resolução da sexta situação da sequência didática, relativa a um jogo que demandava a contagem de cartas, foi detectado que João não conseguiu contar as cartas, o que foi surpreendente, uma vez que o aluno já se encontrava no 2º bimestre do 7º ano do Ensino Fundamental, momento do processo escolar em que se espera que os estudantes tenham esquemas acomodados sobre a contagem de objetos.
Ao ser revisitada a filmagem da aula anterior, foi possível idenjpgicar as dificuldades de João ao manusear as cartas simultaneamente e representar as quantidades em Libras. Afinal, o aluno surdo utiliza uma das mãos para representar os sinais e fica praticamente impossível manusear as cartas com uma única mão, tornando muito complexo para a criança surda o desenvolvimento de um esquema, ou seja, uma organização invariante para atividade de contagem, análogo ao da criança ouvinte, que manuseia o objeto ao mesmo tempo em que verbaliza a quantidade. Esse fato revela que o esquema de contagem de objetos manipuláveis não se constrói da mesma forma para crianças ouvintes, que apontam, olham e verbalizam simultaneamente, e para as surdas, que não conseguem apontar e sinalizar ao mesmo tempo.
Para Vergnaud (2009b), o papel do professor deve ser o de incentivar a criança a realizar atividades que promovam o desenvolvimento de esquemas e, para isso, ele precisa ter um conhecimento claro das noções a ensinar, pois só assim poderá compreender as dificuldades deparadas pela criança e as etapas pelas quais esta passa. Ainda, a forma como cada sujeito age diante de cada situação depende dos esquemas que ele possui, cabendo ao professor observar o desempenho de cada um dos seus educandos.
Uma flagrante complexidade didática deriva do fato que os alunos não se desenvolvem todos da mesma maneira. Há alunos que compreendem bem umas coisas e outras não, o que implica uma individualização da ajuda por parte do professor. Provavelmente, esse é hoje o desafio mais importante ao magistério em todos os países do mundo (VERGNAUD, 2003, p. 50).
Considerando, ainda, que nos anos iniciais a noção de número é vista como a mais importante, pois é a base de tudo o que segue e, reconhecendo a complexidade do conceito de número, optou-se pela elaboração de situações complementares para serem aplicadas.
Tomando como base o pressuposto de Vergnaud (1990) de que as diferentes situações vivenciadas pelos sujeitos ocasionam a organização de novos esquemas e, portanto, proporcionam aprendizagens para os sujeitos, foram elaboradas seis situações complementares à sequência didática proposta inicialmente, das quais três são objeto dessa releitura, a saber: Situação 1 - Contagem de cartas; Situação 2 - Contagem de brinquedos (peças grandes, para facilitar o manuseio); Situação 3 - Contagem de cartas com sobrecontagem.
Situação 1: contagem de cartas
Ao realizar a tarefa proposta que demandava a contagem de cartas, João segurava todas as cartas com uma mão; e com a outra ele retirava cada carta e sinalizava cada uma delas. Após a décima carta João retomou toda a contagem; em outra tentativa de contagem, parou por um instante, como se estivesse tentando recordar o último número que havia contado e continuou a contagem, mas logo se perdeu e parou de contar as cartas. João não conseguia coordenar as cartas do baralho e realizar a contagem em Libras.
Analisando a conduta de João durante a contagem das cartas, foi possível constatar que o esquema utilizado por ele não era eficaz para a situação, pois o ato de segurar as cartas ocasionou dificuldades para que ele pudesse coordenar ao mesmo tempo as cartas nas mãos, os gestos de contagem para indicar cada carta e a contagem em Libras, que também depende das mãos e expressões faciais e corporais para a sinalização da quantidade. Essa situação revela que, enquanto para uma criança ouvinte a contagem demanda uma combinação de diversos elementos: gesto e apontamento da mão para o objeto, o olhar, a boca, a fala (VERGNAUD, 1993), para a criança surda, além destas, existem outras especificidades para a contagem que são relativas ao estabelecimento da correspondência entre os “sinais-número”, aqui denominados os sinais correspondentes às palavras-número e o objeto a ser contado.
Diante das dificuldades para a contagem das cartas, considerando a perspectiva dialógica de implementação da sequência, foi indagado a João se ele gostaria de ajuda e imediatamente João entregou todas as cartas para a professora, aceitando prontamente o apoio oferecido. Para auxiliar na organização de um novo esquema, a professora colocou todas as cartas empilhadas (uma sobre a outra) no chão, e com essa nova disposição das cartas João foi retirando cada carta da pilha, formando outra pilha ao lado, contando e sinalizando carta por carta. Foram realizadas diversas tarefas semelhantes, que João recorreu ao mesmo esquema: organizar os objetos a serem contados seguindo uma configuração e realizava a contagem sem segurar os objetos, mas mudando-os de posição, sempre reproduzindo a configuração anterior.
Considerando, então, a importância atribuída por Vergnaud (1996), à correspondência biunívoca entre os quatro conjuntos, a saber, dos objetos a serem contados, do gesto da mão, do olhar e da palavra, foi elaborada a Situação 2 buscando promover essa correspondência.
Situação 2: contagem de brinquedos (peças grandes, para facilitar o manuseio)
Essa situação foi pensada com o objetivo de promover a apontação explícita. A tarefa consistia em contar objetos “grandes”, que não eram passíveis de serem segurados em uma das mãos e, também, se inverteu o questionamento: ao invés de se indagar quantos objetos havia em determinado agrupamento, solicitou-se uma quantidade pré-determinada, caracterizando como uma situação diferente da Situação 1. A aplicação ocorreu no espaço da sala da brinquedoteca da Escola. Foram disponibilizados a João diversos brinquedos, e solicitado que ele escolhesse 15 brinquedos e os colocasse sobre uma mesa.
Ante a situação, João hesitou, refletiu e na sequência começou a colocar os objetos um a um sobre a mesa. Ao pôr o quinto brinquedo na mesa, João direcionou o seu olhar para a professora e sinalizou o número cinco, sendo por ela indagado: “5; falta quanto para 15?” João continuou colocando os objetos sobre a mesa, sem sinalizar. Quando estavam 12 objetos sobre a mesa, ele pegou mais dois e colocou sobre a mesa, como se tivesse finalizado a tarefa. João observou e realizou a contagem novamente, indicando apenas com o dedo cada objeto, sem sinalizar e pegou mais um brinquedo e sinalizou “15”. Essa nova situação de organizar brinquedos (peças grandes) em cima de uma mesa de modo “linear”, possibilitou a João estabelecer a correspondência biunívoca entre os quatro conjuntos mencionados por Vergnaud (1996): os brinquedos, a apontação, o olhar e o sinal-número correspondente, o que permitiu a João organizar as ações necessárias para a contagem e, assim, adaptar seu esquema de contagem de objetos a essa nova situação.
Considerando que João apresentou uma evolução em seu esquema de contagem, o que foi constatado em diferentes outras situações, havia necessidade, então, de avançar de maneira a idenjpgicar se João mobilizaria a sobrecontagem, em uma atividade envolvendo contagem progressiva e, assim, foi proposta a Situação 3.
Situação 3: contagem de cartas com sobrecontagem
Para realização dessa situação, foi disponibilizada uma pilha de cartas sobre a mesa e solicitado que fosse realizada a contagem. João realizou a contagem corretamente, do seguinte modo: com as cartas sobre a mesa com a mão esquerda pegava uma carta do monte e colocava em outro monte e com a mão direita sinalizava os números, carta a carta. Ele contou e sinalizou corretamente: “17”. Com a intenção de que fosse mobilizada a sobrecontagem, foi entregue mais uma quantidade de cartas e, seguindo o mesmo esquema anterior, com as cartas empilhadas sobre a mesa e pegando cada carta e colocando em outro monte, João realizou corretamente uma sobrecontagem a partir de 17, e finalizou sinalizando: “28”. Embora João tenha mobilizado de modo adequado o esquema de contagem para essa situação, com a intenção de perceber se ele estava realmente indicando a acomodação deste esquema envolvendo a sobrecontagem, foi entregue a ele mais uma quantidade de cartas. Ele as contou, utilizando sobrecontagem, e mesmo demonstrando um pouco de insegurança, sinalizou corretamente “34”. Nessa ação, João indicou ter adaptado seu esquema de contagem e de sobrecontagem, mobilizando o seguinte teorema em ação verdadeiro: Card(A∪B)=Card(A)+Card(B), desde que A∩B =∅.
A constatação de que João mobilizou a sobrecontagem é um resultado relevante para a pesquisa, pois esse esquema de contagem é essencial para a construção do sistema das dezenas, fundamental para a construção do SND (NOGUEIRA, BELLINI, PAVANELLO, 2013). Além disso, é preciso considerar o avanço na organização do esquema de sobrecontagem de João, pois, no início da implementação das atividades, João se sentia inseguro em relação à contagem e, em vários momentos anteriores, não mobilizava a sobrecontagem, juntando todos os objetos a serem contados e começava a contar desde o início.
Nessa mesma direção, relativa aos esquemas de contagem previstos para crianças acima de sete anos, Vergnaud (1996) menciona que, ao serem dadas inicialmente cinco cartas para uma criança, e depois mais seis e solicitar o total de cartas, uma criança de cinco anos iniciará a contagem desde o começo e contará uma a uma. Já uma criança de sete não retomará o todo; ela irá resumir a primeira informação cinco, que é número cardinal do primeiro conjunto e fará uma sobrecontagem a partir desse cardinal para indicar a quantidade total, onze cartas.
Vergnaud (1996) denomina esse procedimento de teorema de equivalência, ao considerar que para uma criança é equivalente fazer a soma das duas partes ou recontar o todo. Ao recorrer à sobrecontagem, “[...] a criança não é capaz de explicitar esse conhecimento. Mas não se pode compreender essa competência nova se na sua cabeça não existe esse conhecimento. Um dos problemas da psicologia cognitiva é o de reconstituir os conhecimentos implícitos na ação” (VERGNAUD, 1996, p.13). Diante disso, considerando que João realiza a sobrecontagem, podemos inferir que ele mobilizou implicitamente o teorema de equivalência, ou seja, ele percebeu que fazer a soma das partes ou recontar o todo conduz ao mesmo resultado: e assim, demonstrou ter desenvolvido um esquema organizado e eficaz para a Situação 3, relativo a uma tarefa de contar cartas.
Entretanto, em qualquer uma das tarefas solicitando a contagem de objetos, João indicou a manifestação de um esquema em que coordenava sua mão direita, que sinalizava os números com sua mão esquerda que mudava a carta para um monte, o que foi uma tarefa complexa de coordenação motora, pois houve dificuldades na combinação da cardinalização com a sinalização dos “sinais-número” da ordem das cartas e com a capacidade de estabelecer a correspondência entre a sinalização e os objetos, ou seja, entre a recitação da ordem das cartas e a correspondência entre a recitação e os objetos, conforme estabelecido por Vergnaud (1993).
Segundo Vergnaud (1993), para uma criança ouvinte “[...] chegar a contar, existe a combinação de diversos elementos, como o gesto da mão, o olhar, a boca, a fala” (p.79). O mesmo acontece com a criança surda que necessita combinar ações e regras como a indicação e o gesto da mão para apontar o objeto, o olhar e novamente utilizar a mão para sinalizar os números; olhando para o sinal o que acaba por dificultar a contagem de objetos se estes estiverem em uma de suas mãos, o que inviabiliza o apontamento.
Observar várias situações em que João esteve envolvido com a contagem oportunizou constatar que seus esquemas e conhecimentos implícitos em suas ações eram diferentes em cada nova situação enfrentada, promovendo a evolução dos esquemas quando se adaptavam às novas situações propostas.
Mas, a constatação que mais surpreendeu às veteranas professoras de surdos foi a de que como a Libras pode dificultar a contagem. Apenas com os estudos da TCC, com a consciência da importância da apontação para a contagem é que foi possível se pensar em ofertar situações complementares para João que considerassem a “correspondência biunívoca”, essencial no processo de contagem, conforme destacado por Vergnaud e, assim, adaptaram situações canônicas de contagem de objetos às especificidades da Libras.
Quando a contagem ainda não está interiorizada, isto é, quando ainda há necessidade da explicitação de cada palavra-número ou sinal-número ou quando a apontação (que os ouvintes realizam manualmente) não pode ser realizada mediante apenas o meneio de cabeça ou o direcionamento do olhar, os alunos surdos precisam recorrer a outros tipos de esquemas, pois eles necessitam das mãos para sinalizar cada quantidade intermediária até a totalização, o que é feito oralmente pelos alunos ouvintes ou apenas mentalizado, por ouvintes e surdos, quando a contagem já está interiorizada. Um esquema intermediário, nesse caso, pode ser a arrumação dos objetos a serem contados, de maneira linear em alguma superfície de maneira a facilitar o estabelecimento de correspondência apontando com a cabeça enquanto as totalizações parciais são sinalizadas uma a uma. Ou seja, o esquema de “arrumar os objetos” de maneira a permitir a apontação explícita ou o meneio dos olhos, integra o esquema de contagem da criança surda.
As discussões acima evidenciam que o conhecimento matemático de João, no que se refere à contagem e à estratégia de sobrecontagem, essencial ao desenvolvimento do SND, foi alcançado, o que pôde ser depreendido da evolução de seu esquema de contagem, sempre se reorganizando para se adaptar às novas situações propostas. Para que o esquema de contagem de crianças, surdas e ouvintes se interiorize, de se proporcionar diferentes situações de contagem em sala de aula, especialmente aos sujeitos surdos.
Quanto ao aspecto socioemocional, a metodologia dialógica, buscando sempre desenvolver, de forma simultânea as formas operatória e predicativa do conhecimento, promoveu significativas mudanças em João. No início da investigação João apresentava insegurança em suas respostas, baixa autoestima, falava impulsivamente, atitudes presentes em pré-adolescentes TDAH, e ao final da aplicação da sequência didática se mostrava mais seguro e autônomo. João melhorou seu rendimento escolar (notas) e “pensava” antes de falar. Isto ficou evidente durante a realização de uma tarefa, quando João inverteu os papéis, assumindo a condução da atividade, nos mesmos moldes da professora, inclusive indagando a mesma sobre “Como você pensou?”, pergunta recorrente na realização de todas as tarefas proposta pela professora.
De maneira geral, constatou-se mudança significativa de atenção quando, espontaneamente, explicitava suas estratégias para o grupo; aumento de interesse pelas tarefas, como quando relatou que em casa estudou a tabela da adição (sem que tivesse sido solicitado); de concentração em sala de aula; quando começou a responder “rapidamente” às questões formuladas pela professora; quando expôs uma dúvida quanto à contagem regressiva abordada em uma tarefa. O aumento de atenção ficou evidente quando João analisava a situação para responder considerando a estratégia do amigo ou propondo outra; e quando mantinha um diálogo prolongado em muitas situações.
Consideramos que a prática regular do cálculo mental em sala de aula de forma dialógica favoreceu o desenvolvimento da autonomia e da autoconfiança de João o que, para um aluno diagnosticado TDAH como ele foi muito importante, pois normalmente são sujeitos com características de baixa autoestima, conforme apontado por Almeida e Carvalho (2011), perfil também constatado em João no início desta investigação, que se modificou ao longo da mesma.
CONSIDERAÇÕES FINAIS
O ensino de Matemática para surdos é um campo cuja fecundidade heurística está longe de ser totalmente explorada. Entretanto, os resultados encontrados com a intervenção realizada permitiram destacar um novo viés: que a estratégia metodológica do cálculo mental na forma dialógica propiciou avanços tanto nos conhecimentos matemáticos de João quanto em sua interação social.
Vergnaud (1998) descreve que a natureza do conhecimento matemático em si não pode ser modificada pelas questões sociais, no entanto a maneira como esse conhecimento chega à escola e a cada sala de aula é influenciada pelo meio social e cultural. Isto pode ser evidenciado com o fato de que alunos surdos, muitas vezes, deixam de ampliar seus conhecimentos por não terem acesso, de maneira natural, a determinadas palavras-número ou ficarem expostos a situações cotidianas de contagem, o que ocorre cotidianamente com as crianças ouvintes.
Segundo Vergnaud (1990), a compreensão de um conceito ocorre por meio de diversas situações vivenciadas pelos alunos ao longo do processo escolar. Este fato se evidenciou com João, pois mesmo estando cronologicamente na faixa em que já deveria estar com o SND consolidado, cursando o início do sétimo ano, não possuía esquemas que lhe permitissem contar adequadamente objetos, particularmente em decorrência das especificidades da Libras, sua língua natural. Somente com a elaboração de tarefas convencionais de contagem de forma a serem realizadas em Libras, é que João pode, mediante sucessivas adaptações a novas situações, consolidar seu esquema de contagem.
Outro aspecto relevante e que condiz com a afirmação de Vergnaud (1990), de que um conceito demanda tempo e experiência para ser constituído, no caso de João, mesmo ele já tendo noção de cardinalidade, da representação na linguagem matemática, em Libras e na Língua Portuguesa escrita dos números, foram necessários aproximadamente oito meses para que ele manifestasse conhecimentos e um esquema mais organizado para a realização da contagem, que proporcionaram a conceitualização do número, essencial para a elaboração dos conhecimentos seguintes, como a realização de problemas de estruturas aditivas, etapa seguinte da implementação da sequência didática e na qual o desempenho de João foi acima da média.
A adoção da perspectiva dialógica, proporcionando trocas simbólicas, mostrou-se eficaz no caso de João, pois, de uma maneira geral, o tratamento de uma situação nova é acompanhado por uma atividade linguística e simbólica. Esta atividade é tanto mais importante e manifesta quanto mais nova é a situação e menos automatizado está o tratamento; a resolução de problemas muito novos é impossível sem a linguagem, nomeadamente quando apela a conceitualizações novas e à transformação de determinados elementos em objetos bem idenjpgicados de pensamento.
Desta forma, para que efetivamente a mediação escolar do conhecimento matemático promova o desenvolvimento de competências conceituais e o desenvolvimento psicológico do educando surdo, a escola não deve se limitar apenas a “traduzir” para a língua de sinais, metodologias, estratégias e procedimentos da escola comum, pensados para os ouvintes e executados pelo professor de sala de aula, na língua dos ouvintes, mas efetivar a Libras como língua veicular do conhecimento, com exploração plena de suas potencialidades, de maneira a permitir trocas simbólicas e, consequentemente, o avanço qualitativo do pensamento do surdo.