1 INTRODUÇÃO
A crise mundial de saúde, referente a pandemia da Covid-19, está sendo responsável por uma adaptação no sistema educacional, que gerou a necessidade de uma transformação, mesmo que provisória, na continuidade das aulas, que eram de ensino presencial para o ensino remoto emergencial (MORAES et al., 2020). Nessa nova realidade, as aulas remotas de matemática foram consideradas como uma possibilidade para propor um estudo sobre a interpretação gráfica de sequências com suporte do GeoGebra. Para essa proposta foram considerados Problemas Olímpicos (POs) como estratégias provocativas, competitiva e estimuladoras no processo de aprendizagem, pois para Alves (2021) os estudantes precisam conhecer e manifestar interesse pelo estilo competitivo com o viés matemático e usar as tecnologias digitais como apoio na visualização e construção do conhecimento.
Em conformidade com esse pensamento, Alves (2021) relata que o ensino de matemática num contexto direcionado para as competições em ciências se esforça para divulgar a informação de que o cidadão precisa criar a cultura de que a matemática é fundamental. Nesse contexto, denominado Olímpico, os elementos matemáticos são mobilizados pelos Problemas Olímpicos (POs) e são elaborados especificamente para competição/olimpíadas. Nele se destaca o ensino de sequências numéricas do tipo Progressão Aritmética e Geométrica, por ser um assunto recorrente na Olimpíada Brasileira de Matemática das Escolas Públicas – OBMEP e que podem ser trabalhados com o uso do GeoGebra.
As Progressões Aritméticas e Geométricas representam um importante conhecimento, porém Lima, Azevedo e Alves (2020) relatam que em relação ao ensino de sequências, “o professor fica restrito a métodos repetitivos” e quase sempre se limita à mera apresentação de fórmulas. A partir do exposto, foi gerada a seguinte pergunta: Como o GeoGebra pode contribuir na interpretação gráfica das Progressões Aritméticas e Geométricas na resolução de Problemas Olímpicos?
Assim, objetiva-se neste artigo apresentar o software GeoGebra como um recurso pedagógico para a interpretação gráfica das progressões aritméticas e geométricas. Nesse ínterim, Azevedo e Alves (2019, p. 103), corroboram que a utilização de softwares é uma tendência nos processos de ensino e aprendizagem “pelo fato de possibilitar, a partir dos softwares educativos, uma transposição didática e conhecimento prático, envolvendo manipulação pelo próprio estudante”. Já para Abar (2020), o GeoGebra dá suporte às estratégias metodológicas do professor, modernizando o saber escolar e transformando este saber em exercícios e problemas capazes de tornar os conceitos mais compreensíveis.
O GeoGebra oferece mais recursos para o ensino e aprendizagem de Matemática, para o aluno compreender, explorar e resolver o problema. Lima, Azevedo e Alves (2020, p. 344), acrescentam, ainda, que “[...] este software pode tornar o ensino e aprendizagem mais prazeroso e instigante, além de melhorar a visualização e dinamismo de certos conteúdos de matemática”. Mas para isso, os recursos computacionais devem ser explorados no âmbito escolar de forma prática e com maior frequência de uso nas aulas de Matemática. Partindo disso, Abar (2020, p 33) enfatiza que “o desenvolvimento das tecnologias da informação e comunicação, bem como sua introdução nas escolas e nos ambientes de formação, é acompanhado de fenômenos da mesma ordem que os da transposição didática”. Ou seja, esse software tem fornecido subsídios para que a transposição didática ocorra de forma significativa.
Realizou-se nesse estudo a resolução de uma questão olímpica com os estudantes de duas turmas de ensino médio de uma escola profissionalizante e o GeoGebra contribuiu na transposição didática, onde se projetou a construção dos gráficos a fim de fazer uma análise do seu comportamento. Para Chevallard (2013, p. 9), “A transição do conhecimento considerado como uma ferramenta a ser posto em prática, para o conhecimento como algo a ser ensinado e aprendido, é precisamente [...] transposição didática do conhecimento.”
Este artigo em sua estrutura, foi dividido em seções. Na primeira seção, apresentou- se uma exposição teórica dos assuntos relacionados ao tema, para um melhor entendimento sobre as definições trabalhadas na Situação Didática (SD). Na segunda seção apresentou-se a metodologia utilizada durante a SD, elencando-se as fases da Engenharia Didática (ED). Para a última seção apresentaram-se as considerações finais deste estudo a partir dos resultados obtidos com a prática realizada.
2 FUNDAMENTAÇÃO TEÓRICA
Os estudos apresentados nesta seção baseiam-se em autores como Lima, Azevedo e Alves (2020), Azevedo, Cidrão e Alves (2018), Sousa (2020), Oliveira (2016), Oliveira (2019) que abordam a utilização do GeoGebra no contexto de resolução de problemas olímpicos, Brousseau (1998) em relação a Teoria das Situações Didáticas (TSD), Artigue et al (1995) com a metodologia Engenharia Didática e Chevallard (2013) sobre a Transposição Didática.
2.1 Progressões Aritméticas (PA) e Progressões Geométricas (PG) no Ensino Médio e na OBMEP
Sobre o uso de definições, Lima (2010, p. 4) afirma que “uma definição matemática é uma convenção que consiste em usar um nome, ou uma sentença breve, para designar um objeto ou uma propriedade, cuja descrição normalmente exigiria o emprego de uma sentença mais longa.” o que corrobora o pensamento de Azerêdo e Rêgo (2016) sobre a linguagem matemática e as suas representações, por ser uma linguagem concisa exige uma caracterização universal para não acarretar dificuldades em seu entendimento. Portanto, é imprescindível observar-se a necessidade de se apresentar estas definições no intuito de contribuir para um melhor entendimento da matemática, que já é “possuidora de regras diferentes que precisam ser compreendidas e apropriadas pelos estudantes” (AZERÊDO; RÊGO, 2016, p. 160).
Em relação à definição de PA Lima et al. (2006), sugere uma abordagem simples e clara quando propõe a ideia de que segundo o exposto, uma progressão aritmética é: “uma sequência na qual a diferença entre cada termo e o termo anterior é constante.” definindo assim que essa diferença constante seja denominada de “razão da progressão” e sendo representada pela letra “”. O autor ainda destaca os casos especiais, nos quais os valores dessa razão r são caracterizados pelo seu valor numérico estar associado ao sinal positivo ou negativo, tornando a PA Crescente ou Decrescente respectivamente e no caso em que a razão é igual a zero ela será constante ou estacionária Lima et al. (2006).
Destaca-se ainda neste trabalho a relação de representação do termo geral de uma PA em que cada termo será obtido a partir do primeiro termo e da razão conforme exposto em Lima et al. (2006) que em uma progressão aritmética (𝑎| |1, 𝑎2, 𝑎3, 𝑎4, … , 𝑎𝑛 … ) para avançar um termo, partindo-se do primeiro termo, basta somar r ao primeiro termo; para avançar dois termos basta somar 2r ao primeiro termo e para avançar três termos, basta somar 3r ao primeiro termo, e consequentemente, seguindo o raciocínio proposto pelos autores na definição, podemos deduzir o termo geral conforme exposto a seguir:
𝑎1 = 𝑎1 + 0𝑟 ⇒ o primeiro termo da sequência conforme definição anterior
𝑎2 = 𝑎1 + 1𝑟 ⇒ segundo termo
𝑎3 = 𝑎1 + 2𝑟 ⇒ terceiro termo, assim é natural perceber que seguindo o raciocínio tem-se que à medida que avançam os termos a equação para o termo geral será dada por
𝑎𝑛 = 𝑎1 + (𝑛 − 1)𝑟 ⇒ termo geral da PA
É imprescindível para este estudo que sejam realizadas as devidas transposições didáticas conforme a definição do termo em Chevallard (1998) de que um conteúdo de conhecimento que foi designado como saber a ser ensinado, sofre a partir de um conjunto de transformações que vão torná-lo apto para ocupar um lugar entre os objetos de ensino. Chevallard (1998). O que reforça nossa ação em fazê-lo. Assim pode-se definir segundo LIMA et al. (2006) uma série de fórmulas para o estudo das progressões, mas que nem sempre essas fórmulas servem para ajudar o aluno e que algumas delas podem até confundir. No entanto, muitos livros apresentam a fórmula para o termo geral da PA conforme mostrado acima e para o termo geral da PG conforme material disponível em LIMA et al. (2006), em que
Ainda é conveniente mostrarmos o caso particular em que a sequência apresenta um pequeno número de termos, no caso, três, quatro ou cinco. Para esses casos podemos considerar o primeiro termo como um valor x e daí segue-se por definição que para uma PA de quatro termos teremos (x, x +r, x+2r, x+3r) com r sendo a razão e para a PG de três termos com razão q, o primeiro termo sendo um valor x, teremos a sequência (x, x.q, x.𝑞2). Apresenta-se também uma propriedade do estudo da sequência PG que será fundamental para a realização deste estudo sem, contudo implicar a necessidade de aprofundarmos o assunto, pois poderá ser encontrado em LIMA et al (2006) e observa-se que embora não tenha validade para todos os casos, serve para este, cujo exposto é que “Em uma progressão geométrica, o produto de dois termos equidistantes dos extremos é igual ao produto dos extremos.” ou “Em uma progressão geométrica com um número ímpar de termos, o termo central é a média geométrica dos extremos” (LIMA et al., 2006, p. 40). Em termos matemáticos referente à PG de três termos mostrada acima significa que:
[𝑥. (𝑥. 𝑞2] (𝑥. 𝑞)2. O que pode ser entendido mais facilmente quando colocamos os termos da seguinte forma 𝑎1. 𝑎3 = (𝑎| |2)2. Vale ressaltar que esta propriedade será válida sempre que tivermos uma razão tal que, q > 0 ou 0 < q < 1. Logo, no Problema Olímpico que será apresentado o motivo pelo qual o estudo realizado em uma questão de sequência extraída da OBMEP, será válido.
Em relação ao assunto de Sequências numéricas presentes na prova da OBMEP, Oliveira (2016) realiza uma análise sobre os trabalhos acadêmicos que envolvem o estudo de matemática com esse viés e apresenta uma série de investigações feitas em relação às olimpíadas de matemática e relata que “Há ainda trabalhos acadêmicos que priorizaram acrescentar informações que não faz parte dos currículos das escolas, porém que é exigido em Olimpíadas de Matemática, tais como sequências e séries diferenciadas” (OLIVEIRA, 2016, p. 29). Justificando o interesse do tema em debate aqui apresentado.
2.3 A Teoria das Situações Didáticas (TSD)
A Teoria das Situações didáticas (TSD), tem como objetivo caracterizar uma situação em um processo de aprendizagem que ocorre em sala de aula envolvendo o aluno, o professor e o saber. Brousseau (1998) defende que o trabalho intelectual do aluno deve ser de caráter investigativo científico, considerando que o aluno deve ser capaz de formular, provar, construir modelos, linguagem e trocar essas informações com outros alunos. Deve-se ressaltar que o importante não é a memorização de regras, teoremas e simplesmente fazer a sua aplicação quando for necessário. O mais importante é propor situações-problema que valorizem o raciocínio, a criatividade e dê condições de desenvolver estratégias e incentivos na construção do conhecimento do aluno. As relações envolvendo o saber, o professor e o aluno em sala de aula, devem propiciar condições para a consolidação da aprendizagem através das situações-problema que ocorrem no momento em que são desenvolvidas atividades de sala de aula. De acordo com Brousseau (1998), a TSD permite a intervenção, tanto do aluno como do professor.
Na TSD, a aprendizagem matemática acontece, efetivamente, sempre que o conhecimento que se aprende tem sentido e significado para o estudante, e aquele conhecimento aprendido é aplicado em outros contextos (LIMA; AZEVEDO; ALVES, 2020). Desta forma, a maneira com que os conteúdos matemáticos são apresentados aos estudantes são de grande importância na significação do saber escolar.
A TSD apresenta duas situações que pode gerar aprendizagem, sendo conhecidas: situação didática e situação adidática. A situação didática surge, no momento em que o professor tem a intenção de ensinar um saber com a finalidade de o aluno aprender de forma significativa. E as situações adidáticas têm como característica colocar o aluno diante de uma situação para que ele possa produzir o seu próprio conhecimento, o professor tendo o papel de mediador e orientador. Com isto, é importante que o professor, na condução da atividade, crie previamente um ambiente favorável para a aprendizagem do aluno.
Com a finalidade de facilitar o processo de aprendizagem, a teoria das situações didáticas observa e decompõe esse processo em quatro fases, a saber: situação da Ação, situação da Formulação, situação da Validação e a Institucionalização. Já a Situação Didática Olímpica (SDO), surge como uma nova proposta metodológica de ensino alicerçada na TSD e constitui uma nova roupagem para a resolução de problemas olímpicos (PO). Segundo Alves (2021), do ponto de vista notacional, pode-se estabelecer a seguinte equação característica:
Não obstante, para aplicação da SDO contará com o suporte do software GeoGebra, pois este terá um papel crucial tanto no apoio tecnológico como pedagógico. Na seção seguinte apresenta-se a metodologia de pesquisa.
3 METODOLOGIA
A metodologia utilizada neste trabalho foi a Engenharia Didática, desenvolvida por Artigue et al (1995). Esta metodologia tem natureza qualitativa e busca conciliar as obrigações de ensino com a reprodução e o estudo de fenômenos didáticos. De acordo com Almouloud e Coutinho (2008, p. 66), “caracteriza-se, em primeiro lugar, por um esquema experimental baseado em ‘realizações didáticas’” em sala de aula, isto é, na concepção, realização, observação e análise de sessões de ensino”. Esta metodologia pode ser organizada em quatro etapas: Análises Preliminares, Análise a priori, Experimentação e Análises a Posteriori e validação. Usamos como coleta de dados a observação participante, as gravações das aulas, os registros dos alunos e de um questionário de avaliação (enviado via WhatsApp).
A experimentação foi realizada, em dois encontros, simultaneamente, em duas turmas de 2º ano de uma escola profissionalizante de nível médio, situada na cidade de Fortaleza – CE. Os encontros aconteceram de forma online devido o isolamento social provocado pela Pandemia da Covid-19. Teve-se, em média, 60 alunos participando em cada encontro. A ferramenta utilizada para a aula remota foi a plataforma de videoconferência Google Meet, pois havia uma parceria da empresa Google com a Secretaria da Educação do Estado do Ceará (SEDUC – CE) que disponibilizou um pacote de ferramentas educacionais como o G suíte que oferece diversos recursos como Google Sala de Aula, Drive, Gmail entre outras para auxiliar o trabalho remoto dos professores.
Os encontros foram organizados da seguinte maneira: o primeiro encontro teve como objetivo apresentar o GeoGebra e as principais ferramentas utilizadas na resolução de PA e PG aos alunos. No decorrer do encontro o professor explorou algumas construções de funções Afins e exponenciais. No encerramento do encontro foi solicitado aos alunos que realizassem a instalação do software em seus equipamentos eletrônicos (Computadores, Tablets ou Smartphones) utilizados para as aulas remotas, com o intuito de preparar estes para a sua utilização no próximo encontro. No segundo encontro deu-se início ao estudo das sequências. O objetivo desse encontro foi estimular a exploração e interpretação gráfica da PA e PG pelos alunos. Inicialmente foi proposto uma situação-problema que envolvia os conceitos dessas sequências a serem trabalhadas no ambiente do GeoGebra. Foi solicitado aos alunos que realizassem a manipulação das ferramentas e desenvolvessem a solução da situação proposta.
Para ambientar os alunos dentro do programa, foram apresentados alguns exemplos de utilização de suas ferramentas, dando ênfase àquelas que eram mais necessárias para a resolução do problema olímpico a ser trabalhado. Após a vivência na experimentação, com o intuito de conhecer melhor os sujeitos, foi elaborado um questionário (Quadro 1) em que eram solicitadas informações sobre os aspectos de utilização do GeoGebra.
Quadro 1 Perguntas do questionário de avaliação
| 01 | Antes de hoje, você já tinha utilizado o GeoGebra na resolução de alguma atividade? |
| 02 | Você utilizou o computador ou o celular para participar da aula? |
| 03 | O uso do GeoGebra facilitou o entendimento da questão proposta? |
| 04 | Quais as vantagens de usar o GeoGebra ao invés do caderno para resolver o problema proposto? |
| 05 | Faça um breve comentário sobre o seu aprendizado com esta aula, elencando o que você aprendeu. Escreva sobre, em que o software facilitou no seu entendimento do assunto da aula! |
Fonte: Elaborado pelo autor.
A análise dos dados coletados nesta pesquisa segue na seção seguinte que de acordo com Almouloud e Silva (2012), esta fase consiste em analisar os dados que são colhidos na fase de experimentação e de tudo que é produzido pelos alunos e todos os registros feitos pelos observadores.
4 DESCRIÇÃO DA PRÁTICA SEGUNDO A ED
4.1 Análise preliminar
Na análise preliminar, contemplamos a epistemologia das progressões aritméticas e geométricas, em um momento síncrono, assim também como a análise das principais dificuldades encontradas pelos estudantes em relação a esse conteúdo, para que fosse possível depois apresentar o GeoGebra. Assim discorremos de forma mais detalhada esse momento síncrono. No decorrer do primeiro encontro foi mostrado vários exemplos do conceito de sequência e em que a Progressão Aritmética se difere da Progressão Geométrica. Ainda na primeira aula foi realizado uma breve apresentação do Software GeoGebra e demonstrado algumas de suas funcionalidades como ferramentas, Janelas de Visualização 2D e 3D, Janela de Álgebra entre outras informações necessárias para um melhor entendimento e utilização pelos alunos. Então, apresentamos as ferramentas “caixa de entrada” e o “bloco de notas” para que possam compreender a construção do gráfico da função e que possam explorá-la no decorrer da aula.
Como se espera que o aluno seja capaz de compreender a dinâmica do programa e consequentemente a resolução do problema é preciso que o professor valorize essa exploração a fim de fomentar o interesse em sua utilização, conforme ressalta Alves ( 2020), “Com tal ponto de vista, o professor poderá valorizar o papel da visualização, mediante a exploração do software GeoGebra, tendo em vista a aquisição de uma cultura matemática e o delineamento de hábitos intelectuais aplicáveis em outras situações”(ALVES, 2020, p. 340).
4.2 Análise a priori
Na análise a priori, fez-se o planejamento das atividades identificando possíveis dificuldades que os alunos poderiam encontrar ao se depararem com o problema olímpico e o uso do GeoGebra para interpretar a sua solução. Aqui, limitamos nosso olhar para as variáveis didáticas, com ênfase nas micro didáticas, pois “as variáveis micro didáticas ou locais, são relativas à organização local da sequência, isto é, a organização de uma sessão ou de uma fase da experimentação” (ALMOULOUD, 2016, p. 123).
Neste trabalho as fases da TSD serão vivenciadas pelos alunos com o objetivo de que eles possam construir o conhecimento na prática com o GeoGebra na resolução do PO e perpassem pelas situações: de Ação, Formulação, Validação e Institucionalização, que ocorrerão à medida que os estudantes avancem na resolução do problema. Assim, espera-se que durante esta fase, os estudantes possam compreender, por exemplo, que no PO a ser resolvido existem infinitas soluções e, além disso, espera-se que eles percebam que os pontos da PA estão dispostos em uma reta, enquanto os pontos da PG estão dispostos em uma curva de uma função exponencial. Espera-se ainda que com o uso do recurso do GeoGebra os estudantes compreendam que embora os termos das sequências mudem os seus valores, ainda assim elas mantêm as suas propriedades quanto ao comportamento nos gráficos.
4.3 Experimentação
A Situação Didática (SD) se iniciou com a formalização do contrato didático5 para estabelecer algumas regras de participação e comportamento dos estudantes e realizou uma revisão do conteúdo expondo os alunos aos conceitos de Progressão Aritmética e Progressão Geométrica, resolvendo algumas situações de cada assunto. Conforme Chevallard (2013, p. 7), “de forma decisiva o contrato determina e controla o comportamento de ambos os protagonistas”. Assim, estabeleceu-se, como parte do contrato, que os alunos deveriam tirar o print das construções e enviar para o grupo de mensagens instantâneas da turma a fim de gerar os registros necessários para a análise dos dados a posteriori.
A SD seguiu com a apresentação do problema olímpico aos alunos com a utilização do GeoGebra. Para isso, escolhemos uma questão da OBMEP, que trata da parte de sequências PA e PG em nível de ensino médio. Esses tipos de problemas, segundo Alves (2020), são denominados de Problemas Olímpicos (POs) e são extraídos diretamente de certames com essa natureza, como é o caso da OBMEP (ALVES, 2020).
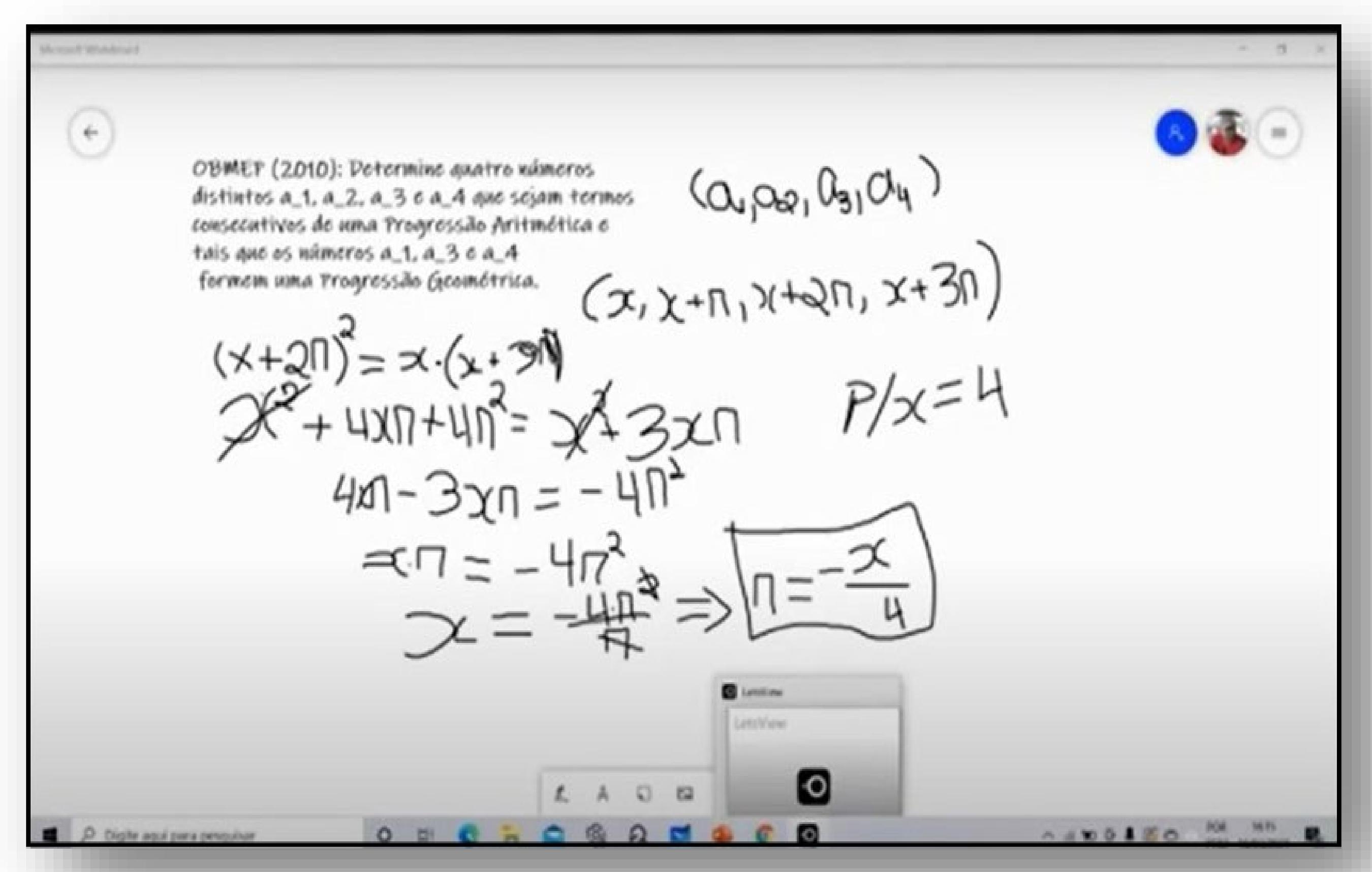
A questão escolhida foi uma do nível 3, extraída do banco de questões da OBMEP de 2010. No trabalho com esse tipo de questão, intencionamos proporcionar ao aluno o desenvolvimento da capacidade interpretativa dos problemas, o que será possível devido à transposição didática que busca agregar uma nova perspectiva para os Problemas Olímpicos (ALVES, 2020). O enunciado da questão tem a seguinte descrição: Determine quatro números distintos a1, a2, a3 e a4 que sejam termos consecutivos de uma Progressão Aritmética e tais que os números a1, a3 e a4 formem uma Progressão Geométrica.
Foi disponibilizado um tempo de cinco minutos para que os alunos tentassem resolver o PO apresentado, após esse tempo e observando as dificuldades apresentadas, foi preciso realizar algumas intervenções, em forma de perguntas para instigar os mesmos. Perguntamos, como é a razão da PA? Nesse momento observamos que os estudantes se encontravam na situação de Ação da TSD. Ao que houve respostas assertivas, porém não em uma linguagem matemática adequada, sobre a forma de se determinar a razão como sendo “o termo da frente menos o de trás”. O professor os instigou mais uma vez perguntando qual é o valor da razão da PA? Apesar da dificuldade inicial, alguns alunos responderam como sendo
Após esse momento, com a ajuda do professor, utilizando o recurso do White board para a resolução da razão, observou-se que houve uma melhor interação e participação das turmas através de perguntas e respostas para se chegar a um resultado. Mais uma vez o professor interveio com a seguinte pergunta: “De acordo com essa razão, quantas soluções são possíveis para esse problema?” Após algumas falas concluiu-se que havia infinitas soluções, bastando para isso determinar o valor de x na equação da razão. Foi nesse momento que o professor interveio novamente e pediu aos alunos que realizassem no caderno a construção da PA e da PG com os seguintes questionamentos: quais são os termos da PA? E quais são os termos da PG? Eles têm relação com os termos da PA? Aqui identificamos a vivência da situação de Formulação.
Para uma melhor compreensão foi sugerido que os alunos considerassem o valor de x=4 e a partir daí iniciassem as sequências. Alguns alunos sentiram dificuldade, ao que mais uma vez o professor interveio com as perguntas: quanto é o primeiro termo da PA? E os demais termos da PA? À medida que a primeira pergunta foi respondida, fez-se recorrente a próxima e assim os alunos iam construindo a sequência conforme o esperado. As perguntas instigadoras foram realizadas no decorrer da resolução e tiveram o propósito de orientar o raciocínio dos estudantes para a compreensão do resultado obtido da razão encontrada durante a aula, enquanto eram resolvidos os cálculos da razão e posteriormente ao determinar os termos da PA. Foi solicitado aos estudantes que realizassem a operação no caderno e comparassem com a resolução feita ‘online’ através do recurso digital, logo em seguida fez-se a orientação para que eles manipulassem o software de modo a construírem os gráficos referentes às sequências trabalhadas e verificassem o tipo de cada um. A seguir apresenta-se na figura 2 a evolução de um dos alunos no desenvolvimento do problema no software.
O professor lembrou aos estudantes os conceitos estudados na aula anterior sobre a construção de gráficos no plano cartesiano e de como são formados os pares ordenados referentes a cada termo da progressão, fazendo a devida transposição didática pelo GeoGebra, fortalecendo o pensamento exposto em Abar (2020, p 62) no qual acredita que “Tornar um conceito mais compreensível vem ao encontro do apoio das tecnologias digitais que, com o dinamismo inerente a algumas delas, permite a transformação de um objeto matemático facilitando seu aprendizado”. Após esse momento, outras perguntas estimuladoras foram levantadas sobre as dificuldades encontradas em relação à construção dos gráficos no sentido de instigar a participação.
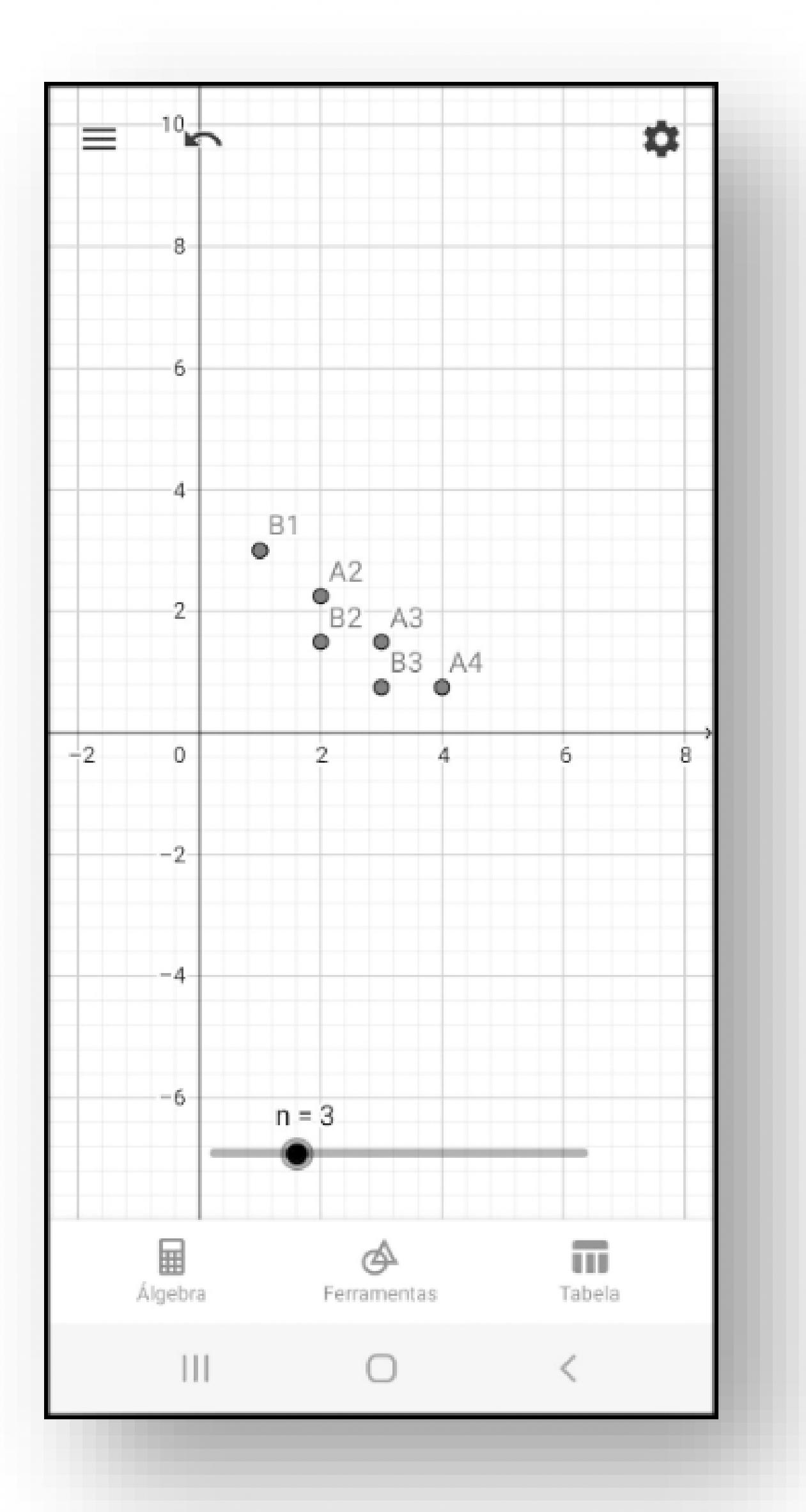
As perguntas iam sendo feitas à medida que os alunos demonstravam compreensão dos conceitos e avançavam na resolução do problema e eram basicamente as seguintes: no gráfico representado pelos pontos da PA, como os pontos estão dispostos? Como será o gráfico que passa pelos pontos referentes aos termos da PG? Os dois gráficos se encontram em quantos pontos? Foi fácil para os alunos perceberem que a PA determinava uma reta e que a PG uma curva. Houve participação efetiva dos estudantes durante a aula e na execução da atividade proposta, como responder à questão no caderno conforme se verifica nas Figuras 3 e 4 respectivamente a seguir. Escolhemos dentre os sujeitos da pesquisa, dois alunos, aos quais chamaremos aluno A e aluno B de modo a preservarmos suas identidades e para exemplificar as atividades por meio das imagens fornecidas por eles.
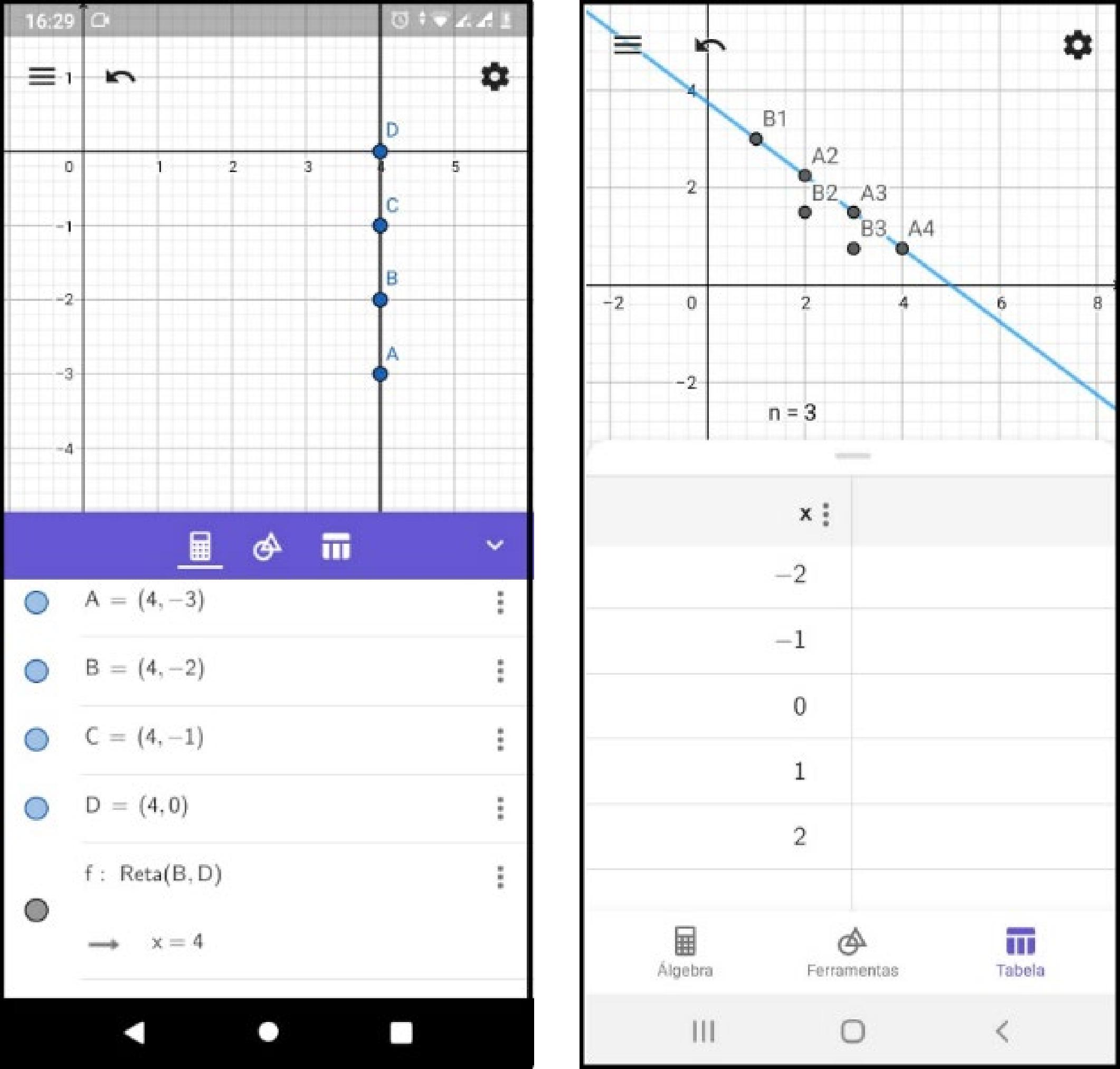
As imagens foram alteradas somente para preservação das identidades dos estudantes participantes da pesquisa. Após esse momento de resolução no caderno, os alunos foram incentivados a construir os gráficos no GeoGebra, utilizando os seus próprios telefones, em sua maioria, e comparar o resultado obtido com a utilização do software ao realizado anteriormente em seus cadernos. Observa-se nessa seção que os estudantes perpassam pela situação de Validação ao se depararem inicialmente com o problema e assim buscam interagir com o software a partir dos conhecimentos prévios para encontrarem a solução esperada. A seguir nota-se essa tentativa no print dos estudantes nas figuras 5 e 6 respectivamente.
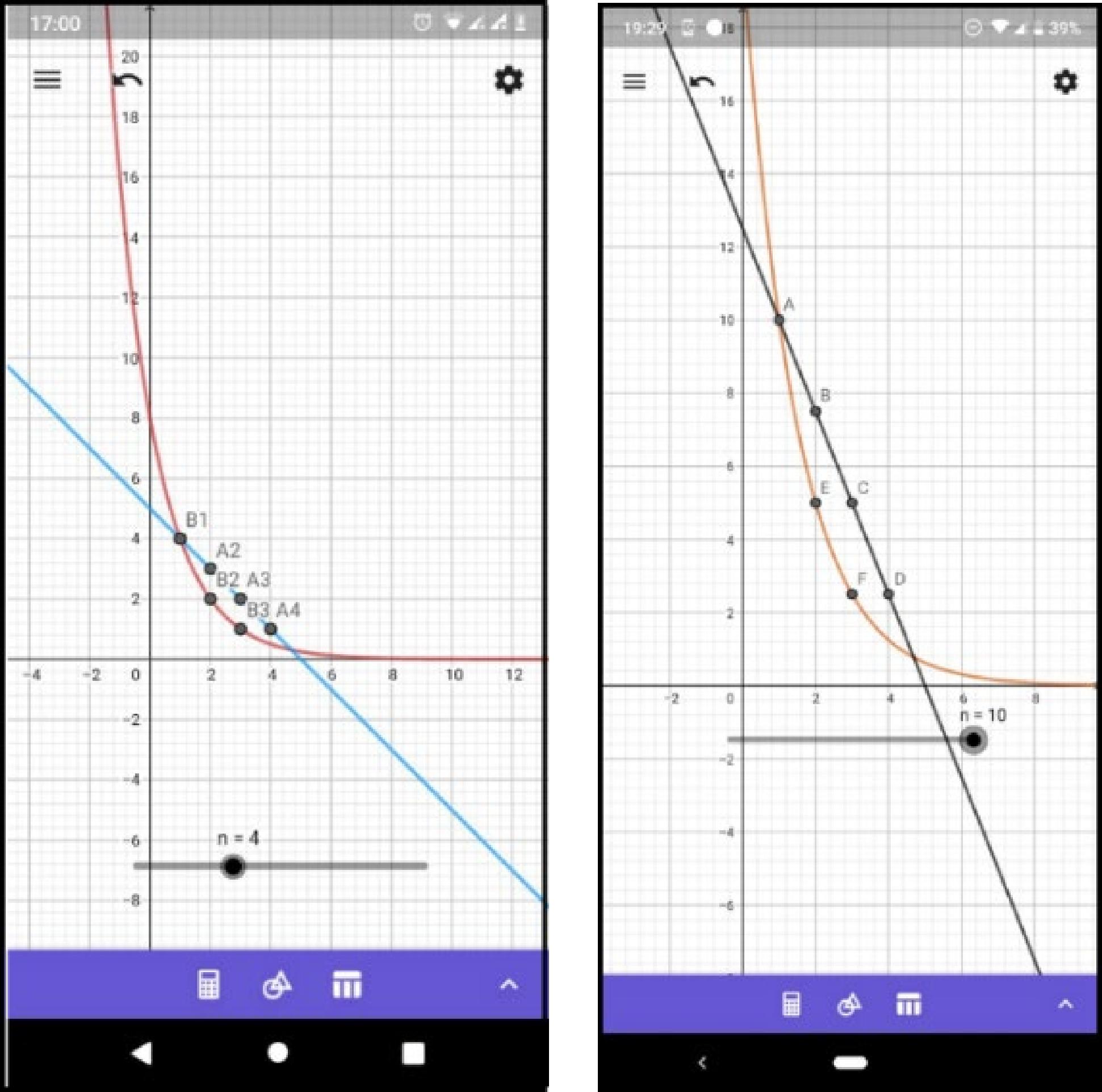
Justifica-se que o retorno de imagens da utilização do Software nesta situação, tenha sido apenas de prints de tela de celular conforme se verifica nas Figuras 7 e 8 respectivamente a seguir com as tentativas dos alunos em realizar a atividade pelo uso dos mesmos, aqui houve uma interação entre os estudantes sobre a melhor forma de representação dos gráficos e em comparação com os modelos encontrados no caderno, configurando a situação de Validação.
O uso dos recursos digitais que envolvem a geometria dinâmica, como o GeoGebra, por exemplo, podem ser uma excelente ferramenta para essa transposição didática realizada pelo professor, pois de acordo com Fioreze et al. (2013, p. 268), “O uso dos recursos digitais para a aprendizagem dos conceitos de Matemática abre um leque de possibilidades para o planejamento das atividades do professor.” O que é corroborado pela fala de Azevedo, Cidrão e Alves (2019) quando dizem que os softwares educacionais têm como proposta dar suporte ao processo de ensino aprendizagem, ou seja, suporte ao professor e ao aluno. Nesse momento o professor retomou o controle da aula e trabalhou os conceitos formais de PA e PG apresentando suas fórmulas generalizadas e comparando com o PO apresentado na aula e identificando cada termo no gráfico encontrado pelos estudantes no ambiente do GeoGebra e na lousa digital utilizada (White board). Assim verifica-se a Institucionalização dos conceitos.
4.4 Análise a Posteriori e Validação
Embora durante as aulas tenham ocorrido problemas de conexão com a ‘internet’, ainda assim foi possível realizar o experimento de forma satisfatória. A análise dos dados registrados no diário de campo e na gravação, mostraram que durante a aula, a maior parte dos estudantes permaneceu em silêncio e que apenas dois ou três de cada turma participaram ativamente das discussões e efetivamente da resolução do PO. Observou-se ainda que havia uma dificuldade em compreender os conceitos básicos das sequências e das operações relativas aos cálculos matemáticos.
Notou-se que a mediação do professor pesquisador teve papel fundamental para o desenvolvimento da resolução do PO, o que de fato está corroborado na fala de Lima, Azevedo e Alves (2020, p. 354) “Caso o aluno não tenha ideia de como resolver o problema, o professor deverá instigá-los, fazendo questionamentos, incentivando-os a analisarem as construções no GeoGebra”, tirando os alunos da zona de conforto e instigando-os ao raciocínio e efetivamente a utilização do software. Segundo Azevedo e Alves (2019, p. 105), “A escolha do software depende dos objetivos que o professor deseja alcançar com o conteúdo, necessitando de um planejamento que busque e almeje sempre a aprendizagem do aluno.” As fotos das atividades realizadas no caderno comparado com as atividades desenvolvidas no software mostraram que os alunos compreenderam bem que os pontos da PA estavam dispostos em uma reta e os pontos da PG em uma curva. Embora não tenha sido enviado imagens dos cadernos sobre o gráfico da PG, na gravação foi possível perceber que houve compreensão pelos alunos.
Nas fotos referentes aos gráficos construídos no software, percebeu-se que o aluno A considerou o valor de x contido na razão igual a 4 conforme sugerido, enquanto o aluno B não se limitou apenas a esse valor e realizou a construção dos gráficos considerando o valor de x igual a 10. Compreendendo que existem outras possibilidades de solução para o problema, o aluno B demonstrou melhor compreensão do uso do software ao utilizar um valor diferente do sugerido, conforme se percebe na fala do estudante a seguir que será denominado apenas de “E” para a preservação de sua identidade.
E - Eu aprendi que tem várias formas de resolução do (x), e que ao mudar o valor do
(x) muda a representação no gráfico.
Ao analisarmos o questionário de avaliação, percebeu-se que houve uma participação significativa, ao todo foram 61 estudantes, sendo 35 da turma de contabilidade 2 e 26 da turma de finanças 2. Elencou-se para análise do conteúdo das respostas do questionário, cinco categorias (quadro 2), que de acordo com Bardin (2016), funciona por operações de desmembramento do texto em unidades, em categorias segundo reagrupamentos analógicos.
Quadro 2 Categorias elencadas para análise das respostas do questionário
| Categorias | |
|---|---|
| 1 | Quantidade de estudantes que já haviam utilizado o GeoGebra antes da atividade proposta |
| 2 | Tipo de recurso tecnológico que o estudante utilizou para acompanhar a atividade |
| 3 | A utilidade do GeoGebra para o aprendizado dos conteúdos propostos |
| 4 | As vantagens da resolução de problemas com o uso do GeoGebra em relação ao uso do caderno |
| 5 | Análise subjetiva dos estudantes em relação à atividade aplicada utilizando o GeoGebra. |
Fonte: Elaboração nossa.
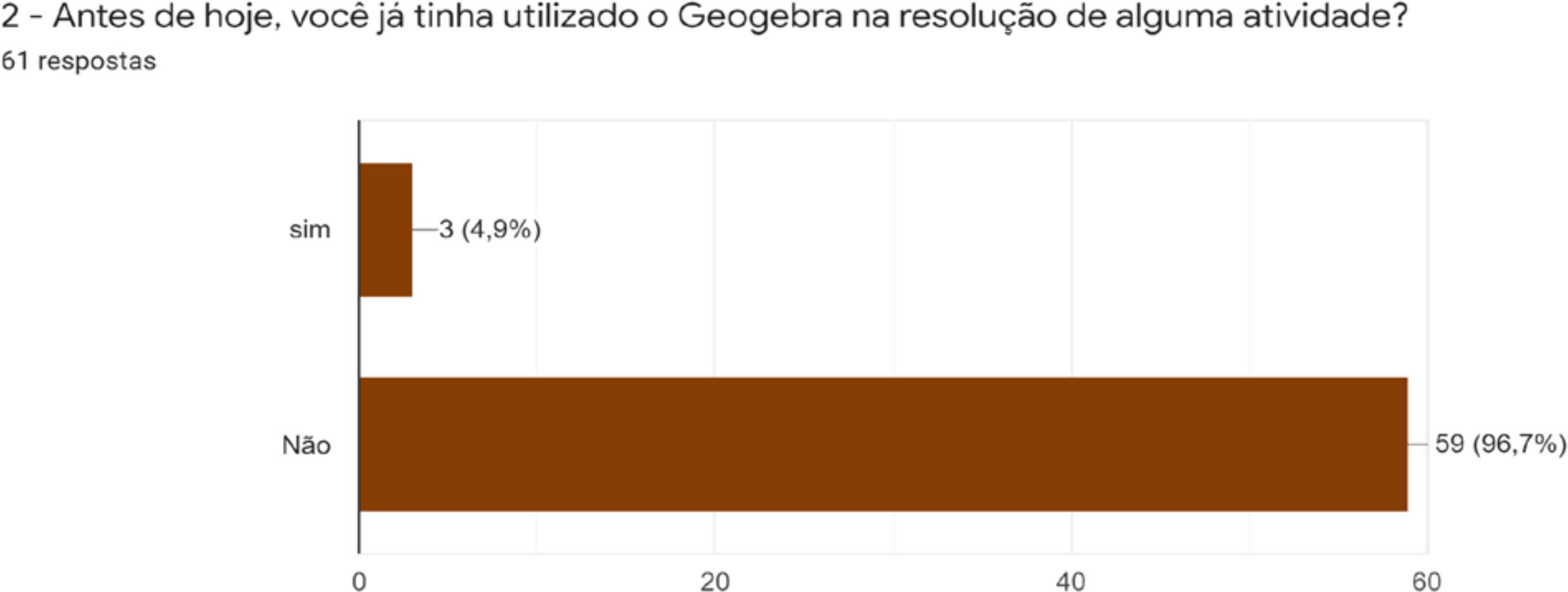
A primeira categoria evidenciou que apenas 4,97% dos estudantes já haviam utilizado o software para resolver algum tipo de problema, enquanto a grande maioria 96,7% não haviam utilizado o programa ainda. O que deixa claro que existe uma margem muito grande de possibilidade para a inserção de um novo conhecimento, como é o caso do GeoGebra aqui mencionado conforme a Gráfico 1 a seguir.
Fonte: Pesquisa
Gráfico 1 Representação quem já havia utilizado o GeoGebra ou não em alguma atividade
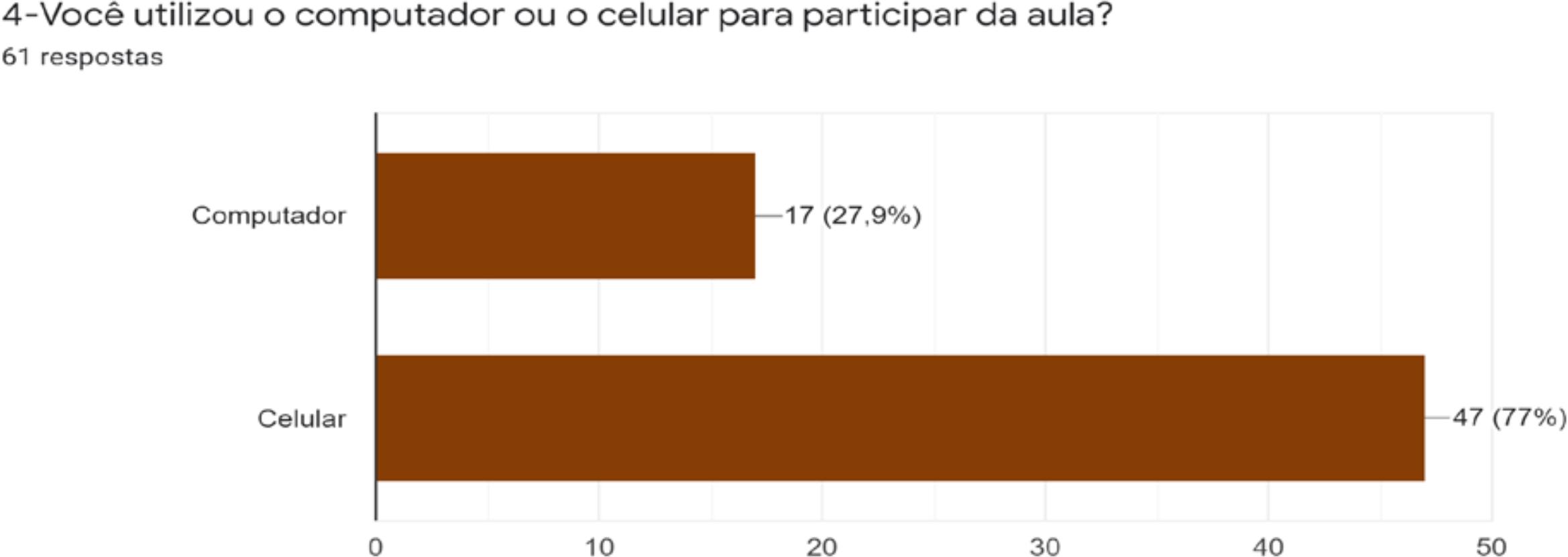
A segunda categoria mostrou que 77% dos estudantes utilizaram os seus smartphones tanto para assistir às aulas quanto para realizar as atividades online, conforme demonstrado no Gráfico 2
Fonte: Pesquisa
Gráfico 2 Representação percentual de alunos que utilizam ou computador ou telefone para assistir às aulas
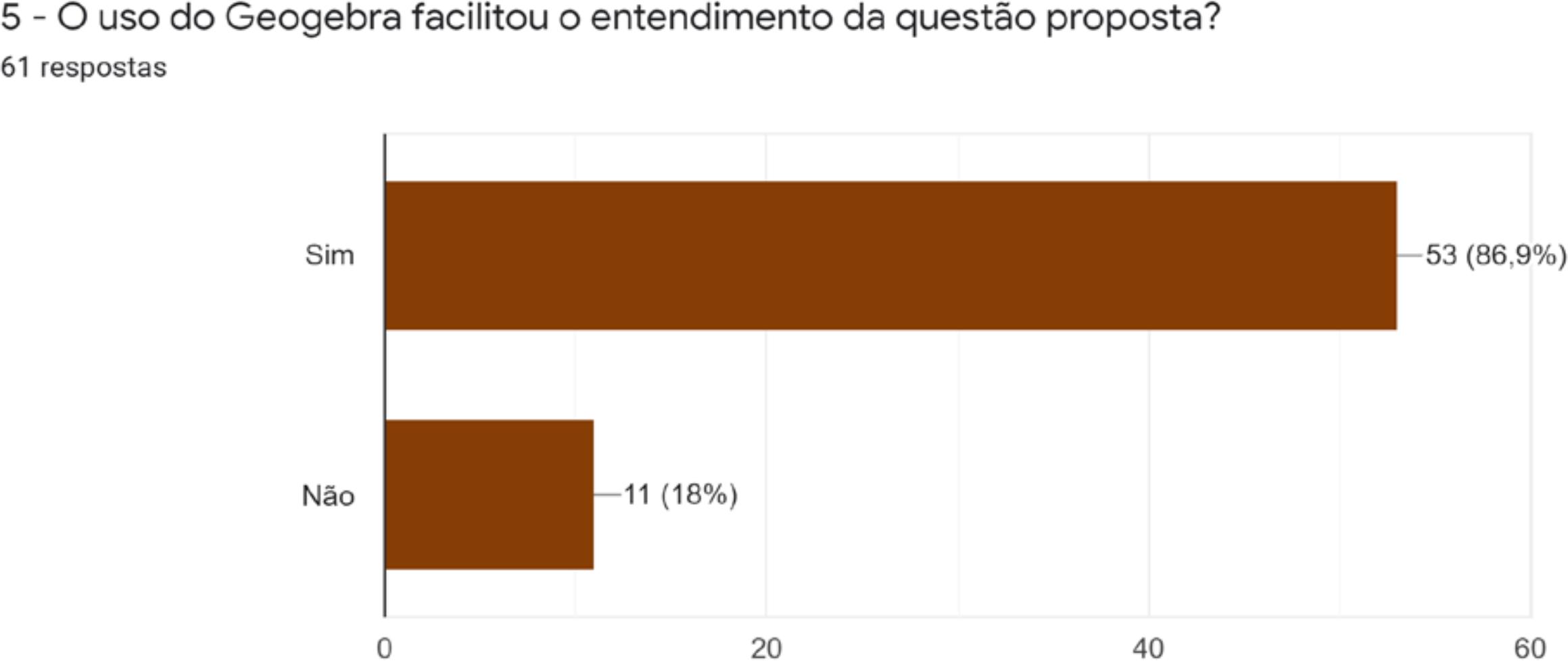
Ao serem questionados se o uso do GeoGebra facilitou ou não o entendimento da questão, 86,9% disseram que sim, demonstrando que a utilização do recurso foi importante para um melhor entendimento do problema e justificando a sua necessidade no contexto da Situação Didática Olímpica escolhida, de acordo com a terceira categoria elencada, conforme Gráfico 3 apresentada.
Na quarta categoria, notou-se que dentre os argumentos relatados como positivos pelos estudantes, o uso do software torna a solução e principalmente a construção do gráfico, um processo mais rápido e mais organizado. Elegeu-se a fala de três estudantes, denominados E1 a E3, a fim de preservar suas identidades e para representar esses aspectos observados,
E1 – Primeiro, não teremos que gastar folhas para cálculos. Segundo, com o geogebra já temos tudo em um lugar só, sendo assim, facilitando a hora que vamos fazer os cálculos.
E2 – Uma precisão maior nas figuras geométricas e um cálculo mais rápido.
E3 – “fica mais fácil e não gasta tanto temp
o no Geogebra como fazendo no caderno, apesar de que não poderia usar ele em alguma prova.
O aluno E1 referiu-se aos recursos apresentados dentro do software como as janelas de álgebra, janelas de visualização, e o GeoGebra notas, que foi apresentado na primeira aula. Nas impressões dos alunos E2 e E3, percebeu-se o alinhamento com as análises feitas por todos os estudantes nas respostas, apesar delas, na sua maioria, serem mais curtas e objetivas, o ponto central abordado é quase sempre o fator tempo e a facilidade de visualização e compreensão dos gráficos. Confirmando o que diz Lima, Azevedo e Alves (2020, p. 344), “assim, percebemos que este software pode tornar o ensino e aprendizagem mais prazeroso e instigante, além de melhorar a visualização e dinamismo de certos conteúdos de matemática”.
Na quinta categoria os estudantes fizeram uma análise subjetiva em relação à atividade aplicada, utilizando o GeoGebra. Foi solicitado que eles fizessem um breve comentário sobre o seu aprendizado, elencando o que aprenderam, com a utilização do software e suas vantagens. Nesse contexto notou-se que os estudantes foram mais categóricos em analisar a utilização do recurso e devolveram respostas interessantes e críticas em relação ao uso do software. Elegeram-se as falas de três estudantes, que denominamos E4 a E6 e expressam, em síntese, as opiniões de treze (13) estudantes.
E4 – “O app é muito bom para FAZER os gráficos. Porém, acho que fazer os cálculos na mão, como a senhora faz, é melhor.”
E5 – “Consegui tirar várias dúvidas na aula de hoje, porém não entendi muito bem as ferramentas do Geogebra. Como utiliza e taus.”
E6 – “O GeoGebra me confundiu sobre como usar esse software, mas eu entendi muito sobre PG.”
Apesar das falas destacadas parecerem contrárias às da categoria anterior, refletem um cuidado dos estudantes em não desaprovar o uso do GeoGebra por uma análise superficial nesse primeiro contato, no entanto houve uma preocupação dos estudantes em avaliar o uso das ferramentas do software. Notou-se que 48 estudantes gostaram de utilizar o recurso e que o seu uso facilitou o entendimento do conteúdo, conforme verifica-se nas falas a seguir de três estudantes, que chamaremos E7 a E9.
E7 - “facilitou a resolução da questão, colocando meus conhecimentos em prática”.
E8 - “gostei bastante da aula, principalmente por ter conhecido o GeoGebra, ficou muito melhor para resolver as questões”.
E9 - “Facilitou bastante o meu aprendizado, nunca tinha ouvido falar nesse aplicativo geogebra. Gostei muito!”
Verifica-se nas falas evidenciadas que houve interação entre o uso do GeoGebra e o conteúdo de forma salutar para o entendimento do assunto. Outros estudos sobre a utilização do GeoGebra para a construção de gráficos podem ser encontrados em trabalhos como o de Andrade e Brandão (2018, p. 766), quando apontam que “Vários estudos já apontam a eficiência do uso pedagógico do GeoGebra em diversas áreas do conhecimento, principalmente na matemática”. Dentre as conclusões levantadas com este estudo foi evidenciado que com a construção gráfica, as propriedades das funções são mais bem compreendidas, pois são percebidas pelos próprios alunos por experimentação. A seguir apresenta-se as considerações finais deste trabalho.
5 CONSIDERAÇÕES FINAIS
Este estudo teve como objetivo apresentar as contribuições do software GeoGebra como ferramenta de suporte pedagógico para a facilitação da aprendizagem na interpretação gráfica das Progressões Aritméticas e Geométricas. Conforme previsto, os estudantes vivenciaram cada situação na busca de compreender que, no PO resolvido existem infinitas soluções e, além disso, foi observado que eles perceberam que os pontos da PA estão dispostos em uma reta, enquanto os pontos da PG estão dispostos em uma curva de uma função exponencial.
Resgatando a pergunta geratriz deste trabalho “Como o GeoGebra pode contribuir na interpretação gráfica das Progressões Aritméticas e Geométricas na resolução de Problemas Olímpicos?”. Identificamos que a utilização do software surtiu o efeito esperado e foi fundamental para o entendimento e para a resolução do Problema Olímpico apresentado, conforme se verificou na coleta de dados referentes aos 48 estudantes que atestaram ter entendido o conteúdo e que o uso do GeoGebra foi necessário para esse entendimento.
Depreendeu-se que, quanto ao objetivo proposto, este estudo atingiu plenamente sua meta, conforme se verifica nas falas dos estudantes na avaliação final e nos dados apresentados. Ainda que tenham ocorridos problemas de conexão durante a aula e isso tenha atrapalhado o andamento normal da atividade, foi possível concluir a aula com a finalização da atividade. Esse foi o motivo de alguns estudantes terem levantado em suas falas, o fator tempo como uma possível causa para a falta de entendimento em alguns aspectos, ora referentes à utilização do software, ora para o conteúdo de progressões. Com o uso do recurso do GeoGebra os estudantes compreenderam que embora os termos das sequências mudem os seus valores, ainda assim elas mantêm as suas propriedades quanto ao comportamento nos gráficos.
Para finalizar, colocamos uma reflexão acerca dos processos de ensino e de aprendizagem com o uso de tecnologias educacionais como meio de subsidiá-los de forma a acompanhar o seu desenvolvimento e as transformações ocorridas nessa nova constituição de sociedade. No contexto de aulas ‘online’ e que se desenha para o futuro da educação no formato híbrido, entendemos que essa realidade requer uma nova abordagem e é baseado nisso que se propõe o uso do GeoGebra para o ensino de matemática e nesse caso o ensino de progressões conforme objeto deste estudo aqui apresentado.