Introdução
O movimento da Matemática Moderna, transcorrido no Brasil entre os anos 1960 e 1970, tem sido objeto de múltiplas investigações, que iluminam facetas variadas dos processos de produção e circulação de propostas de inovação do ensino de matemática na escola primária e secundária, naqueles tempos1. Menos abundantes são os estudos que tomam por objeto os impactos do movimento sobre a matemática ensinada nas escolas e as marcas dessa experiência nos currículos atualmente praticados2. Nesse contexto, as avaliações de um “fracasso” da Matemática Moderna, que circularam nos anos 1970 e 1980 pelas vozes de autores renomados como Kline (1976), tendem a se amalgamar com reminiscências de professores daquele tempo em uma representação ainda bastante disseminada de que as propostas do movimento teriam sido esquecidas ou abandonadas, após o seu refluxo.
O uso de cadernos escolares como fontes pode dar uma contribuição importante para as investigações sobre os efeitos de movimentos e reformas sobre os currículos escolares, uma vez que são ricos em registros das práticas de sala de aula (VIÑAO, 2008; LEME DA SILVA; VALENTE, 2009). Este artigo trata de uma investigação provocada por um registro de atividade de estudante, que encontramos em um caderno escolar do ano de 1968, muito assemelhado a um material utilizado em atividades de formação de professores para a Matemática Moderna. O caderno pertenceu a uma estudante do segundo ano do curso primário do Instituto de Educação General Flores da Cunha (GROSS, 1968) e o curso de formação ocorreu na mesma instituição.
A partir desses vestígios, buscamos outras fontes, com o intuito de identificar conexões entre as aulas de matemática daquela turma do segundo ano primário e as movimentações de renovação do ensino de matemática em curso, naquela época, no Rio Grande do Sul, na cidade de Porto Alegre e, mais precisamente, no Instituto de Educação.
O cruzamento do caderno com vários outros documentos permite identificar, naquela página do caderno, marcas do movimento da Matemática Moderna. O exercício tratava de combinar saias e blusas, um traje comum nos anos 1960 e, especialmente, um traje de uso das normalistas. A presença de saias e blusas em livros didáticos e em documentos curriculares recentes, como evocação do pensamento combinatório, nos permite, ademais, perceber aí uma marca permanente do movimento modernizador.
No texto que segue, apresentamos o percurso da pesquisa, acompanhado de algumas reflexões sobre os processos pelos quais são constituídos e modificados os currículos escolares.
Aprendendo a multiplicar com saias e blusas
Desde 2016, estamos engajados em uma campanha de coleta e digitalização de cadernos escolares com aulas de Matemática, para a constituição de uma coleção digital no âmbito do Repositório Institucional da Universidade Federal de Santa Catarina (UFSC)3. Dentre os cadernos coletados no Rio Grande do Sul, está o “Diário de aulas” produzido por Cristiane Gross, quando frequentava o segundo ano do curso primário no Instituto de Educação General Flores da Cunha, em 1968.
Durante a digitalização do caderno, deparamo-nos com um registro intitulado “Trabalho de Matemática”, datado de 8 de agosto. O primeiro exercício, exibido na Figura 1, tem como enunciado a pergunta “Tenho 8 blusas e 2 saias. Quantos trajes poderei formar?”
Entre a pergunta e a resposta – “Deram 16 trajes” – temos a imagem de um gráfico em que cada uma de duas saias (uma laranja e uma preta) está ligada a cada uma de 8 blusas (duas lilases, quatro amarelas e duas marrons) por uma flecha.
Viñao (2008, p. 25) nos adverte de que, pelos cadernos, não podemos saber tudo o que se passou em uma sala de aula:
Nem tudo está nos cadernos. Eles silenciam, não dizem nada sobre as intervenções orais ou gestuais do professor e dos alunos, sobre seu peso e o modo como ocorrem e se manifestam, sobre o ambiente ou clima da sala de aula, sobre as atividades que não deixam pistas escritas ou de outro tipo, como os exercícios de leitura (a leitura em voz alta, por exemplo) e todo o mundo do oral.
No caso em tela, não sabemos se a estudante, autora dos registros inscritos naquele caderno, escolheu as cores e os modelos das saias e blusas que desenhou, ou se seguiu alguma instrução da professora. Mas, daquilo que sabemos sobre a organização do ensino primário e o uso de cadernos, no Brasil, na segunda metade do século XX, e considerando o padrão dos registros ali contidos, incluídas as anotações de correção, podemos inferir que copiar e resolver o exercício era uma atividade atribuída a toda a turma. Tratava-se de um modo de aprender e exercitar a multiplicação. Mais ainda: considerando-se que aprender a resolver problemas aritméticos segundo padrões ensinados – incluindo a organização gráfica dos elementos da solução – era um elemento importante da cultura da escola primária dos anos 1960, podemos supor que o caminho adotado na resolução – desenhar saias em uma coluna e blusas em outra, ligar saias e blusas por flechas com a mesma cor das saias – seguiu um padrão indicado pela professora.
O que nos surpreendeu nesse registro de um exercício?
O uso de imagens para o ensino da multiplicação, na escola primária, não é uma novidade do final dos anos 1960.
Na segunda metade do século XIX, os livros de Antonio Trajano, inspirados no método intuitivo, já apresentavam imagens com representações de operações aritméticas. Como explica Oliveira (2017, p. 136), as ilustrações nos livros de Trajano “têm a função de induzir o aluno na construção do saber”. A Figura 2 apresenta uma imagem extraída da 68ª edição da Arithmetica Elementar Illustrada, com data de publicação estimada entre 1900 e 1910. A imagem cumpre a dupla função de ilustrar o problema – uma situação em que objetos aparecem agrupados em quantidades iguais – e possibilitar a obtenção da solução, pela contagem desses mesmos objetos.

Fonte: Trajano ([190-?], p. 27).
Figura 2 Problema sobre cerejas, cachos e galhos, introdutório à multiplicação
A circulação das ideias da Escola Nova, que enfatizam a ação dos alunos, em oposição à memorização e como alternativa aos métodos considerados tradicionais (LEME DA SILVA; VALENTE, 2013), suscita novos usos das imagens, como o de inspirar a redação de problemas pelos estudantes. A Figura 3 mostra uma sugestão apresentada aos professores por Irene de Albuquerque (1951), com o objetivo de substituir o estudo da tabuada.
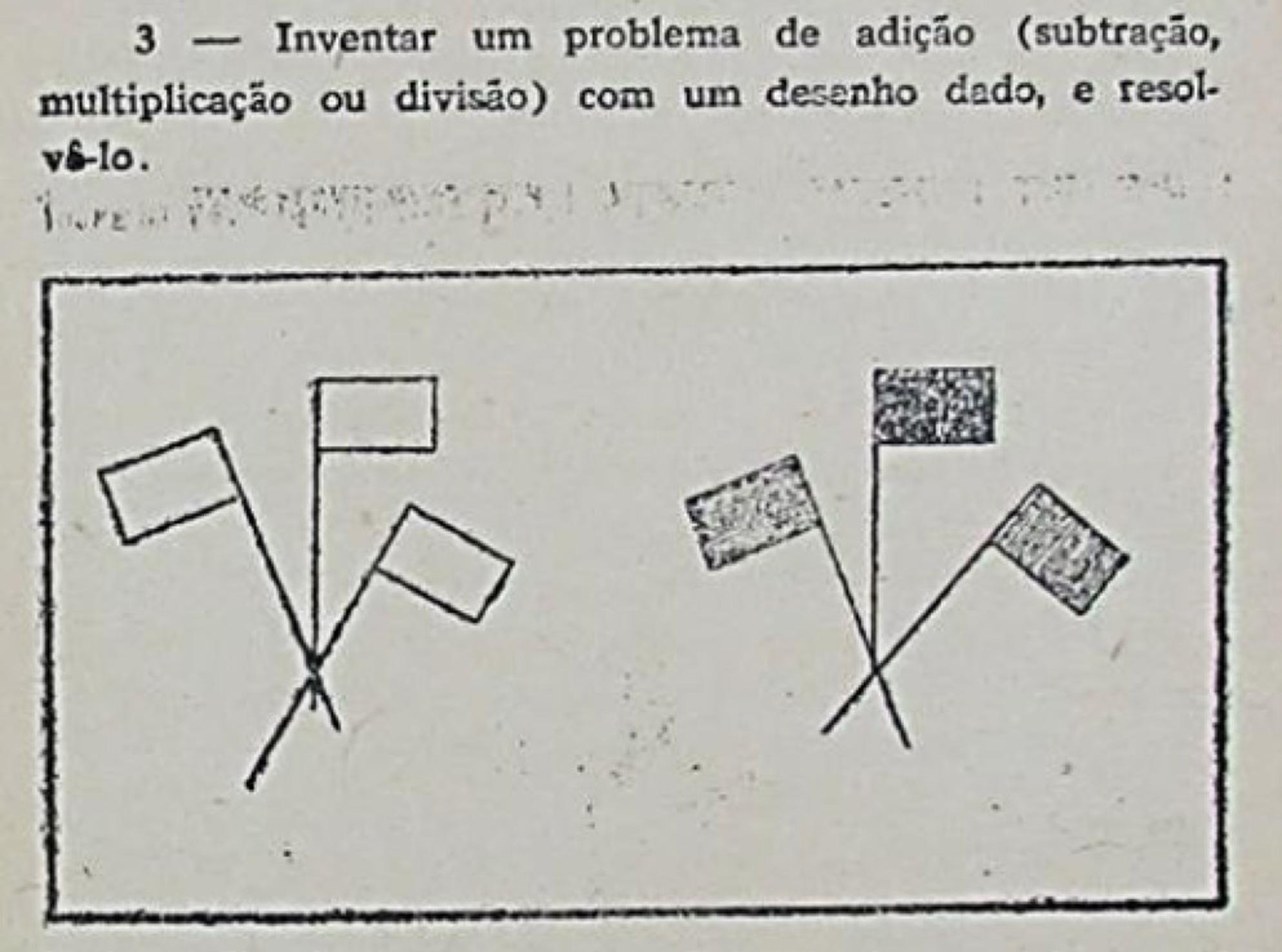
Fonte: Albuquerque (1951, p. 95).
Figura 3 Item das “Sugestões práticas” apresentadas aos professores
Sabemos, também, pelo depoimento de ex-alunas do Instituto de Educação, que nos anos 1950 e 1960 as normalistas aprendiam a ensinar as operações com o apoio de ilustrações e de objetos manipuláveis, como feijões e tampinhas de garrafas (BÚRIGO; PEIXOTO, 2018).
Considerando o uso já costumeiro de imagens para ilustrar e, inclusive, auxiliar no entendimento da multiplicação, é possível, contudo, identificar traços de inovação na abordagem da multiplicação registrada no caderno de Cristiane Gross (1968). Em primeiro lugar, a ideia de reunir agrupamentos com o mesmo número de objetos, do mesmo tipo, reiterada nos programas, manuais e artigos pedagógicos, é substituída pela ideia de combinar elementos de conjuntos diferentes. Em linguagem contemporânea, teríamos aí uma abordagem do pensamento combinatório, ou do princípio multiplicativo. A solução para o problema não é obtida como uma soma de parcelas iguais. A segunda novidade é o uso de flechas para representar graficamente as combinações. Diferente da solução sugerida por imagens como a da Figura 3, a resposta ao problema não é dada pela contagem dos objetos (saias e/ou blusas), mas pela contagem das flechas – um elemento gráfico acrescentado à representação da situação – que representam as combinações possíveis.
A mesma ideia reaparece no segundo exercício do “Trabalho de Matemática” do caderno: “Com 4 automóveis e 4 latas de tintas de cores diferentes, quantas combinações faremos?” (GROSS, 1968). Como o exercício anterior, esse é resolvido com um desenho: cada um de 4 automóveis é ligado a cada uma de 4 latas de tintas, por flechas coloridas. Ao final, consta a resposta “16 combinações”.
Em ambos os casos, há uma evocação da ideia de produto cartesiano entre dois conjuntos. Pensar em todas as combinações possíveis de saias e blusas equivale a tomar todos os pares ordenados distintos que podem ser formados tendo como primeiro elemento uma saia e como segundo elemento uma blusa. O mesmo vale para automóveis e latas de tinta. O número de pares ordenados – isto é, o cardinal do produto cartesiano – é o produto do cardinal do primeiro conjunto (saias ou automóveis) pelo cardinal do segundo (blusas ou latas de tinta).
No caderno, a expressão “produto cartesiano” não é mencionada. Mas o uso de flechas para representar as combinações sugere que, de algum modo, a ideia de “relação” – um tema valorizado pela Matemática Moderna – estava implicada na intenção da professora ou do autor ou autora daquela atividade. Mas qual ou quais teriam sido as fontes inspiradoras da atividade ou dessa intenção pedagógica?
A abordagem das operações aritméticas a partir das operações entre conjuntos é um traço reconhecido do movimento modernizador, ou das vertentes da Matemática Moderna que foram mais amplamente divulgadas no Brasil. Mas a ideia da multiplicação como produto cartesiano não está presente em algumas produções do movimento que tiveram ampla circulação. Por exemplo, não está presente nas primeiras edições da coleção Matemática – Curso Moderno para cursos ginasiais, de Sangiorgi (1964), que circulou em todo o País, ou nas coleções de Thofehrn e Cunha (1968), que circularam no Rio Grande do Sul.
Aprendendo a multiplicar com a Matemática Moderna
Saias e blusas, curiosamente, foram também encontradas em um repositório de documentos e materiais didáticos, em cuja organização estávamos – e estamos – também engajados: o acervo do Laboratório de Matemática do mesmo Instituto de Educação General Flores da Cunha (LM/IE)4. Em um envelope contendo fichas de atividades, havia figuras desenhadas em papel acartonado colorido e recortadas, de modo que pudessem ser dispostas e combinadas de modos variados, como no exemplo da Figura 4.

Fonte: Item 1031 do acervo LM/IE. Uma das fichas do envelope trazia inscrito o enunciado: “Uma menina tem duas saias, uma lisa e outra pregueada. Tem também duas blusas, uma lisa e outra com bolinhas. Quantos trajes diferentes ela pode formar?”. Pode-se supor, então, que as figuras foram produzidas para a experimentação de possibilidades de composição de trajes, como caminho para a resposta à pergunta.
Figura 4 Peças recortadas para composição de trajes
O cruzamento entre o caderno e o material didático nos fez atentar às prováveis conexões entre o ensino de matemática ministrado naquela turma do segundo ano primário e as atividades desenvolvidas no Laboratório de Matemática. O modo como o material foi cuidadosamente protegido e guardado sugere que a ficha e as figuras teriam sido usadas em planejamento de estágio ou em alguma disciplina ou curso de formação de professores oferecido pelo Instituto de Educação. Pois, de acordo com o Regulamento do Ensino Normal vigente, as classes do ensino primário deveriam se constituir em “campo de prática, orientação e experimentação pedagógica” (RIO GRANDE DO SUL, 1955, p. 93). Em entrevista, Cristiane Gross (2018) confirmou que, nas aulas do curso primário, era comum a presença de uma observadora na sala de aula.
Sabemos, de trabalhos anteriores, que propostas de modernização do ensino de matemática relacionadas à Teoria dos Conjuntos e às estruturas algébricas circularam no Instituto de Educação desde os anos 1950, por meio de palestras e cursos ministrados por professores da instituição e da Universidade Federal do Rio Grande do Sul (UFRGS), dentre os quais se destaca o nome de Joana de Oliveira Bender5 (BÚRIGO, 2010).
Bonfada (2018), a partir de relatórios encontrados no acervo do LM/IE, registra que, já em 1961, o Laboratório de Matemática contava com livros de autores engajados no movimento modernizador. A autora também apresenta registros da oferta do Curso de Didática da Matemática Moderna na Escola Primária, pelo Instituto de Educação, a partir de 1966, tendo como alunas professoras do curso primário e do Jardim de Infância do próprio Instituto. Conjecturamos, então, que calcular números de combinações de saias e blusas teria sido uma atividade planejada por participantes do Curso, aplicada ou replicada naquela turma do segundo ano do curso primário. Buscamos outros documentos, no acervo do Laboratório de Matemática e em outros repositórios, que pudessem auxiliar no refinamento dessa hipótese.
Encontramos uma discussão sobre a Matemática Moderna em uma ata de reunião de estudos das professoras de Didática, realizada em 16 de março de 1967:
Em que consiste a Matemática Moderna? Matemática Moderna não é apenas apresentação de novas técnicas de ensino. Aceitamos plenamente a opinião da professora Joana Bender para quem a Matemática Moderna é a reformulação e o enriquecimento de conteúdos (Teoria de Conjuntos e Teoria das Relações) e consequente apresentação que exige o aparecimento de novas Técnica, Terminologia e Simbolismo (Item 1316 do Acervo do LM/IE, p. 1).
Anexo à ata está o “Relatório do 1º ano de atividades do curso” do Grupo 711, que incluiu 93 aulas da “Parte referente à fundamentação matemática”, ministrada pela professora Esther Pillar Grossi6, duas aulas de Psicologia, ministradas pela professora Italia Faraco, e cinco aulas de Didática, ministradas pela professora Odila Barros Xavier7. O Relatório menciona também que foram lidas as obras Os conjuntos e as operações com conjuntos e A Matemática Moderna no ensino primário, de Zoltan Paul Dienes8, o livro Os números para contar, de Irving Adler9, e o primeiro capítulo do livro Mathématique Moderne que, pelos detalhes mencionados, pode-se concluir ser a obra Mathématique moderne, mathématique vivante do matemático francês André Revuz10 (1963).
Anexo ao relatório, por sua vez, está o texto “Fundamentação matemática”, que detalha os conteúdos abordados nessa parte do curso, agrupados como: Noção de Conjunto – primeiros conceitos; Introdução à Lógica Matemática; Propriedades das Relações; Conceito de Função; Cardinal; Relações no Conjunto dos Naturais. Esse último capítulo inclui o item “Operação multiplicação no Conjunto dos Naturais”.
No texto, a multiplicação é, inicialmente, associada à união de conjuntos de mesmo cardinal. Em seguida, é associada à ideia de produto cartesiano, “onde um dos fatores é representado pelo cardinal do número de classes e o outro é representado pelo cardinal do número de elementos de cada classe e, o produto é igual ao cardinal do número de duplas” (Item 1316 do Acervo do LM/IE, p. 10).
Na Figura 5, vemos os dois textos e os gráficos a eles associados, representando as duas abordagens da multiplicação. Ainda, após a apresentação desse item, constam “Considerações sobre conjunto universo”: “O conjunto universo das relações é o produto cartesiano de todos os elementos do conjunto de partida com todos os elementos do conjunto de chegada (Conjunto de todas as possibilidades de duplas)” (Item 1316 do Acervo do LM/IE, p. 11).
O relatório do Curso indica, portanto, que a ideia de produto cartesiano era abordada nas aulas de Fundamentação Matemática; mais ainda, que a ideia de multiplicação poderia ser explicada como produto cartesiano e, ainda, que esse produto cartesiano poderia ser representado graficamente por um conjunto de flechas ligando cada um dos elementos de um conjunto de partida A a cada um dos elementos de um conjunto de chegada B, sendo esses elementos representados por pontos associados a letras.
Quais teriam sido as referências para a abordagem da multiplicação como produto cartesiano, no Curso de Didática da Matemática Moderna?
Como comentado anteriormente, essa não era uma ideia disseminada de modo generalizado, nos textos de difusão da Matemática Moderna, nos anos 1960. Essa perspectiva não é explicitada, por exemplo, no livro Um programa moderno de matemática para o ensino secundário, elaborado em 1961 por um grupo de especialistas, a convite da Organização para a Cooperação e Desenvolvimento Econômico (OCDE), traduzido e publicado em 1965, no Brasil, pelo Grupo de Estudos do Ensino da Matematica (GEEM). Também não é mencionada na primeira publicação do GEEM, a coletânea Matemática moderna para o ensino secundário (GEEM, 1962).
Em escritos posteriores, Esther Grossi (2005, p. 12) afirma que os primeiros contatos com a Matemática Moderna foram “por meio de Lucienne Félix e, depois, com os blocos lógicos e as publicações de Zoltan Dienes, da mesma maneira que através dos livros de George Papy”. Mas a ideia de multiplicação como produto cartesiano não está presente na obra Mathématiques modernes ∩ enseignement élémentaire, de Lucienne Félix11 (1960), que integra o acervo do Laboratório de Matemática do IE. Ali, a multiplicação é diretamente enunciada como operação que pode ser definida para os números naturais e que caracteriza a estrutura de ℕ. Na publicação A Matemática Moderna no ensino primário, indicada como leitura para os alunos do curso, Dienes (1967, p. 53) aborda a multiplicação considerando conjuntos de conjuntos: “Enquanto se efetua uma multiplicação muda-se de universo: […]. Num produto um dos fatores pertence à família dos conjuntos, o outro à dos conjuntos de conjuntos”.
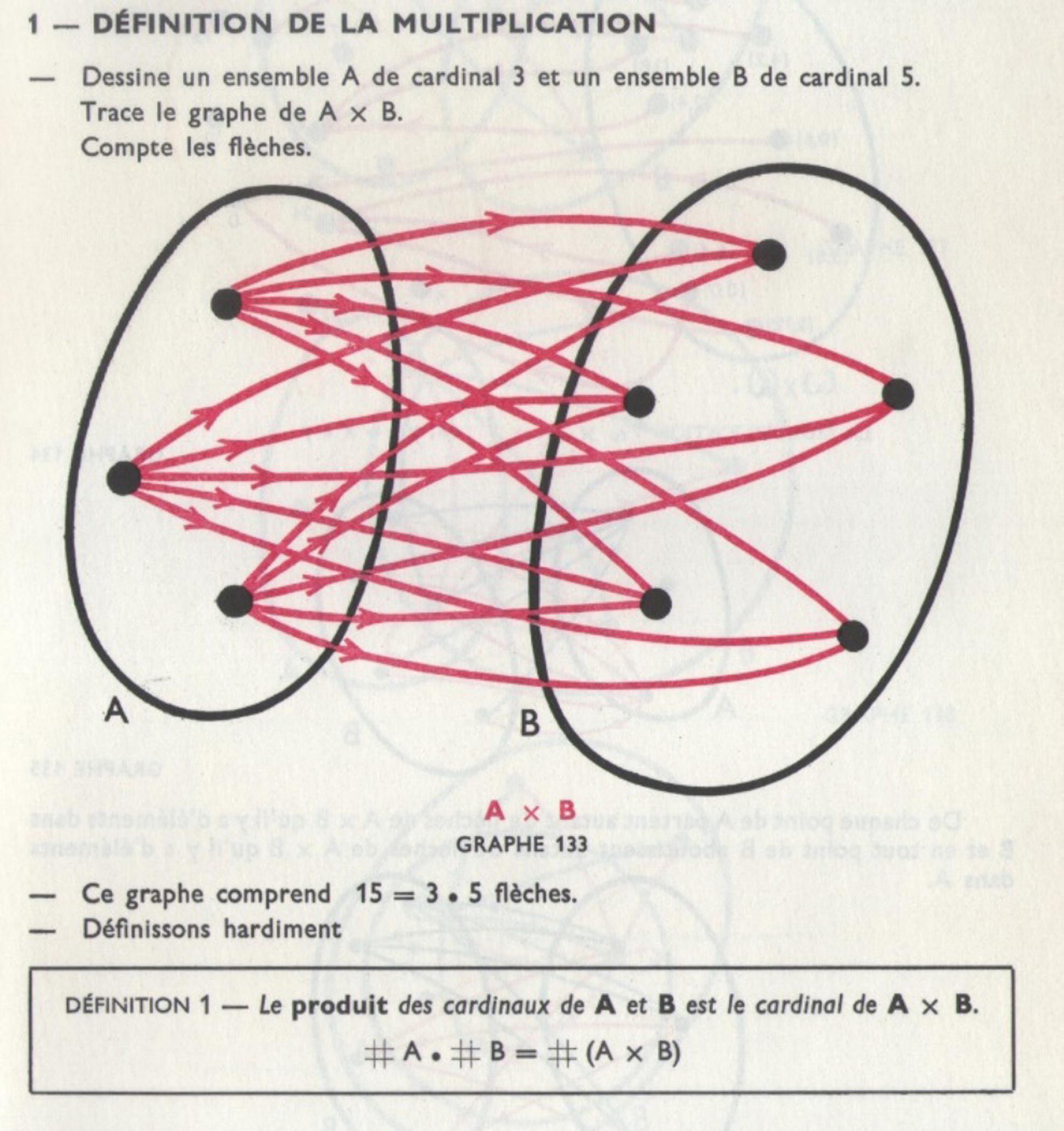
Finalmente, na coleção Mathématique moderne de Georges e Frédérique Papy12 (1965), encontramos uma provável referência para a abordagem da multiplicação apresentada na apostila da disciplina “Fundamentação matemática”. No primeiro volume da coleção, a multiplicação de números naturais é apresentada como um produto cartesiano. A Figura 6 mostra a definição apresentada no livro, que pode ser assim traduzida:
Desenhe um conjunto A de cardinal 3 e um conjunto B de cardinal 5. Trace o gráfico de A × B. Conte as flechas. Esse gráfico contém 15 = 3 5 flechas. Definamos ousadamente: […] o produto dos cardinais de A e B é o cardinal de A × B (PAPY; PAPY, 1965, p. 271, tradução e grifos nossos).
A partir de uma breve comparação entre as abordagens de diferentes autores, vemos que a apresentação da multiplicação como produto cartesiano, nas aulas de “Fundamentação Matemática”, corresponde a uma escolha por parte de Esther Grossi, responsável pela disciplina. Um possível motivo para essa escolha é o grau de detalhamento e de rigor com que a matemática elementar é apresentada na coleção Papy, tomada como suporte para um empreendimento inovador. A participação de Georges Papy no 5º Congresso Brasileiro de Ensino de Matemática, em 1966, em São José dos Campos, é indicativa do seu prestígio no Brasil e do interesse dos educadores brasileiros no intercâmbio com o diretor do Centre Belge de Pédagogie de la Mathématique. Joana Bender que, conforme mencionado acima, era uma referência para as discussões e experiências de formação desenvolvidas no Instituto de Educação, foi uma das professoras brasileiras que estagiou no Centre após esse Congresso (MOTA, 2008). Uma outra explicação que pode ser aventada é que, ao estudar a abordagem de Papy e Papy (1965), Esther e outras professoras, alunas do Curso, poderiam ter entrevisto, ali, uma possibilidade interessante de didatização, ou de construção de uma situação didática, dando um novo sentido à multiplicação de números naturais.
Ensinando a multiplicar com saias e blusas
A partir das considerações expostas acima, podemos pensar em saias e blusas como uma didatização da concepção de multiplicação como produto cartesiano. Ainda, é verossímil pensar que na atividade registrada no caderno de Cristiane Gross (1968) como continuidade (ou, talvez, como adaptação para uma sala de aula regular) da atividade de contagem dos trajes pela manipulação das figuras recortadas de saias e blusas com diferentes estampas.
Mas, não se trata de uma mera adaptação, concretização ou simplificação da ideia genérica de multiplicação como conjunto de pares ordenados, presente na coleção de Papy e Papy (1965) e na apostila do Curso de Didática da Matemática Moderna na Escola Primária. Há elementos próprios da matemática escolar na concepção dessa atividade de ensino que reúne elementos do universo infantil – roupas e cores –, introduz simbolismos modernos, como as flechas, e dá sentido à ideia de par ordenado – no caso, um possível traje.
Novamente, nos perguntamos sobre as inspirações para a criação da atividade, tomando como pressuposto que a ideia de produto cartesiano era objeto de estudo das professoras do curso primário do Instituto de Educação que frequentavam o Curso de Didática da Matemática Moderna na Escola Primária. Em conversa com Esther Grossi, durante a escrita deste texto – isto é, passados cinquenta anos da realização do Curso –, mostramos a fotografia que aparece na Figura 4. Ela, de imediato, mencionou que aquelas figuras faziam parte de um conjunto bem maior, e que as figuras eram usadas para que as crianças pudessem experimentar permutações. Lembrou, também, que Zoltan Dienes explorava, em diferentes atividades, o tema das permutações. Perguntamos se o material reproduzia produções já existentes ou era uma invenção da equipe envolvida no Curso e no Laboratório de Matemática do Instituto de Educação. Esther respondeu, sem certeza, que acreditava que aquela, como outras atividades envolvendo combinações de objetos, era uma criação local.
Encontramos saias e blusas, também, em uma publicação do final dos anos 1960: o segundo volume da coleção Curso moderno de Matemática para a escola elementar, da autoria de Manhúcia Perelberg Liberman, Anna Franchi e Lucilia Bechara13.
A Figura 7 mostra uma atividade a ser realizada por estudantes do segundo ano do curso primário: a partir de uma imagem, as crianças deveriam obter os números de saias, blusas e trajes. Saias e blusas são apenas um dentre muitos contextos que envolvem combinações, apresentados no livro: trajes de calça e camiseta, cores de olhos e cabelos de bonecas, composições de bebidas e comidas em uma merenda, escala de jogos em um campeonato de futebol, dentre outros. Consultamos Lucilia Bechara sobre a inspiração para essas atividades, mostrando também a Figura 1 do caderno de Cristiane Gross; ela nos respondeu que “Do que consigo lembrar, o trabalho com produto cartesiano (além da soma de parcelas iguais) na multiplicação surge na matemática moderna, particularmente com os franceses”. Comentando a atividade do caderno, observou que “A utilização de flechas foi exaustivamente explorada por George Papy da Bélgica e em Luxemburgo como se pode ver nos escritos por Robert Dieshbourg”. Poderíamos ainda nos perguntar se a imagem da coleção Curso moderno de Matemática para a escola elementar teria sido inspiradora da atividade realizada no IE; mas isso é improvável pois a multiplicação, na coleção, não é obtida pela contagem das flechas (ou pares ordenados), mas pela repetição de um deslocamento de duas unidades, como mostra a Figura 7.

Fonte: Liberman, Franchi e Bechara (1967, p. 51).
Figura 7 Atividade para aprendizagem da multiplicação no segundo ano primário
Em uma discussão sobre memória e história, Nora (1993, p. 9) aponta que “A memória se enraíza no concreto, no espaço, no gesto, na imagem, no objeto”. Nunes (2003, p. 15) fala do caráter “compósito e flexível” da memória dos indivíduos:
As memórias estão relacionadas a processos de subjetivação bastante complexos, que incluem desde sensações e imagens mentais altamente espontâneas até solenes cerimônias públicas vividas intensamente. Elas estão ancoradas em espaços e lugares nos quais circulamos, em grupos sociais de diferentes tipos aos quais pertencemos, em objetos que manipulamos. Quem recorda são os indivíduos, e essa experiência de caráter singular está presente quando se enfatiza a memória social, pois os indivíduos não são autômatos, passivos e obedientes a uma vontade social interiorizada.
Mostramos o registro do caderno (Figura 1) à sua autora e usuária: Cristiane Gross não tinha uma recordação particular daquela atividade realizada no segundo ano primário. Para os alunos, era mais uma tarefa escolar. Já para Esther Grossi e Lucilia Bechara, as imagens evocaram, de imediato, um tempo em que estavam mobilizadas para renovar o ensino de matemática na escola primária. Esther mencionou a influência de Dienes, e Lucilia, mencionou, além de Papy, “os franceses”. Em um livro da educadora francesa Nicole Picard constante do acervo do LM/IE, encontramos a recomendação da exploração da combinatória “desde a pré-escola” (PICARD, 1970, p. 68), seguida de alguns exemplos de atividades envolvendo objetos. Como referências, a autora menciona a coleção dos Papy, livros de Zoltan Dienes e uma publicação de Guy Brousseau, dentre outros. Entretanto, o intercâmbio de Esther Grossi com Nicole Picard e Dienes é posterior ao registro do caderno e ao início do Curso; o mais provável é que essas referências, amalgamadas nas reminiscências daqueles tempos, não tenham participado da elaboração da atividade com saias e blusas.
Ao mesmo tempo, e por outro lado, a evocação de diferentes autores e interlocutores nos faz pensar na Matemática Moderna como um movimento vivo, em que autores e professores engajados em experimentações ou inovações dialogavam por meio de encontros e publicações, por sua vez impregnadas por esse debate multifacetado. A concepção da multiplicação como produto cartesiano não se esgotava na definição e nas icônicas ilustrações da coleção dos Papy; a abordagem do que hoje denominamos pensamento combinatório, desde a escola elementar, foi uma das muitas proposições inovadoras do movimento da Matemática Moderna, enunciada por diferentes autores e em diferentes versões.
Saias e blusas no currículo praticado de uma escola primária
No caderno de Cristiane Gross (1968), o “Trabalho de Matemática”, envolvendo combinações de saias e blusas, e automóveis e latas de tinta, não é o primeiro registro de atividade envolvendo a multiplicação. O registro anterior, do dia 6 de agosto, é o de uma lista de exercícios de multiplicação com números de um algarismo, como 4 × 3 e 2 × 5, precedidos da instrução “Arma e resolve estas multiplicações”. O registro seguinte ao “Trabalho de Matemática”, do dia 12 de agosto, apresenta uma sequência de perguntas e respostas sobre a multiplicação. No primeiro item, a pergunta “O que é multiplicação?” é respondida com “Multiplicação é o nome de uma operação de adicionar”; o terceiro item pede o preenchimento de lacunas em uma frase, cuja escrita final é “Quando multiplicamos reunimos quantidades iguais”. A anotação “Excelente!”, na margem do caderno, nos leva a pensar que as respostas dadas pela aluna eram as esperadas, ou semelhantes às esperadas pela professora.
Pelos registros da estudante, então, vemos que a ideia da multiplicação como soma de parcelas iguais não foi abandonada naquela série, por aquela professora. Além disso, o “Trabalho de Matemática” é a única atividade constante no caderno envolvendo combinações de elementos de conjuntos distintos.
O currículo praticado naquela turma, portanto, não estava orientado por um programa amplamente reformulado ou pretensamente inovador. O “Trabalho de Matemática” pode ser considerado um traço de uma experimentação pontual de uma inovação, em que a multiplicação é abordada por meio de um problema combinatório e de uma representação gráfica. Conforme anteriormente comentado, essa experimentação poderia ter sido realizada pela iniciativa de uma estagiária normalista, pela professora da turma ou por colegas participantes do Curso de Didática.
O caráter localizado da inovação é, em parte, explicado pelos obstáculos à introdução de novos conteúdos e terminologias no curso primário, mencionados na já referida ata de 16 de março de 1967:
Qual será nossa posição para iniciar o trabalho? Não temos experiência e o campo aberto é apenas o Jardim de Infância, onde o trabalho é feito em forma de jogo e sem maior interferência da família. A melhor tentativa seria em classes de experimentação, porque é preciso enfrentar muitas dificuldades: com a administração, em tomar a responsabilidade da experiência; com os professores, pela falta de preparo, e com a comunidade, a maior delas, face à sua estruturação rígida (Item 1316 do Acervo do LM/IE, p. 1).
Podemos perceber essa experimentação pontual, também, à luz das discussões mais recentes sobre o currículo no cotidiano escolar, que apontam o caráter sempre complexo e contraditório das práticas curriculares:
[…] em nossas atividades cotidianas, os currículos que criamos misturam elementos das propostas formais e organizadas com as possibilidades que temos de implantá-las e o acordo ou desacordo que temos sobre elas. Por sua vez, essas possibilidades se relacionam com aquilo que sabemos e em que acreditamos, ao mesmo tempo que são definidas na dinâmica de cada turma, dos saberes dos alunos, das circunstâncias de cada dia de trabalho. […] É nesse sentido que entendemos as práticas curriculares cotidianas como ‘multicoloridas’, pois suas tonalidades vão depender sempre das possibilidades daqueles que as fazem e das circunstâncias nas quais estão envolvidos (ALVES; OLIVEIRA, 2002, p. 96-97).
Assim como outros registros do caderno, saias e blusas podem ser consideradas traços da Matemática Moderna em meio a essas práticas “multicoloridas” experimentadas pelas estudantes e professoras do Instituto de Educação, naqueles idos anos 1960. Não se tratava de aplicar um programa pré-estabelecido, ou de replicar as orientações de um livro didático, mas de ensinar a multiplicar, usando materiais existentes e criando novos.
Considerando as conexões apontadas entre os registros do caderno, os materiais encontrados no acervo do LM/IE e a coleção dos Papy, poderíamos pensar em saias e blusas – e automóveis e latas de tinta – como uma apropriação da ideia de produto cartesiano pelas professoras e estudantes do Instituto de Educação, entendendo apropriação “como uso particular de um sistema, uso cujo modelo é a enunciação, ou como tática, por oposição à estratégia” (NUNES; CARVALHO, 2005, p. 53).
Mais elucidativo, talvez, do que a ideia de apropriação, é pensarmos em saias e blusas como criação própria da cultura escolar. Como argumenta Chervel (1990, p. 184), “o sistema escolar é detentor de um poder criativo insuficientemente valorizado até aqui”. As criações do sistema escolar são orientadas pelas finalidades próprias da escola – como o ensino das operações aritméticas – e pelas condições em que se realizam as práticas escolares. Nessa perspectiva, ao invés de pensar que a escola se ocupou em incorporar a ideia de produto cartesiano como mais um conceito da Teoria dos Conjuntos a ser escolarizado e didatizado, podemos cogitar que a ideia de produto cartesiano foi introduzida na escola como componente da criação da atividade com saias e blusas – e outros objetos representáveis por figuras –, que permitiriam aos alunos experimentar e atribuir novos sentidos à multiplicação.
Saias e blusas como ressonâncias da Matemática Moderna
A linguagem e o simbolismo da Teoria dos Conjuntos foram, possivelmente, os elementos mais difundidos da Matemática Moderna. Algumas representações de que a Matemática Moderna teria fracassado ou teria sido descartada, a partir dos anos 1980, estão apoiadas na verificação de que livros didáticos e outros materiais foram, progressivamente, abandonando esses elementos de linguagem. Considerando a autonomia dos Estados para definirem as suas diretrizes curriculares, e os ritmos muito variados com que essas diretrizes foram atualizadas, ao longo dos anos 1970 e 1980, é difícil identificar em que medida essas mudanças nos livros responderam às alterações de documentos legais, a demandas das comunidades escolares ou outros tipos de movimentações.
Ao final dos anos 1960, a ideia de multiplicação como produto cartesiano havia sido introduzida em obras para o ginásio, como a já mencionada coleção de Sangiorgi (1968) ou a coleção Ensino moderno da Matemática elaborada pelo Núcleo de Estudo e Difusão do Ensino da Matemática (NEDEM, 1967). No manual pedagógico Matemática, metodologia e complementos para professores primários, de Ruy Madsen Barbosa (1966), a multiplicação também é definida a partir do conceito de produto cartesiano.
A linguagem dos conjuntos, conforme comentado acima, foi progressivamente descartada pelos autores de livros didáticos e pelos redatores dos documentos de orientação curricular. Entretanto, a ideia de multiplicação como produto cartesiano está presente nos Parâmetros Curriculares Nacionais para os anos iniciais do Ensino Fundamental. Mais interessante ainda é perceber que a ideia é ilustrada por um problema de combinações possíveis entre saias e blusas: “Tendo duas saias — uma preta (P) e uma branca (B) — e três blusas — uma rosa (R), uma azul (A) e uma cinza (C) —, de quantas maneiras diferentes posso me vestir?” (BRASIL, 1997, p. 73). Pela Figura 8, vemos algumas das soluções esperadas para esse problema.
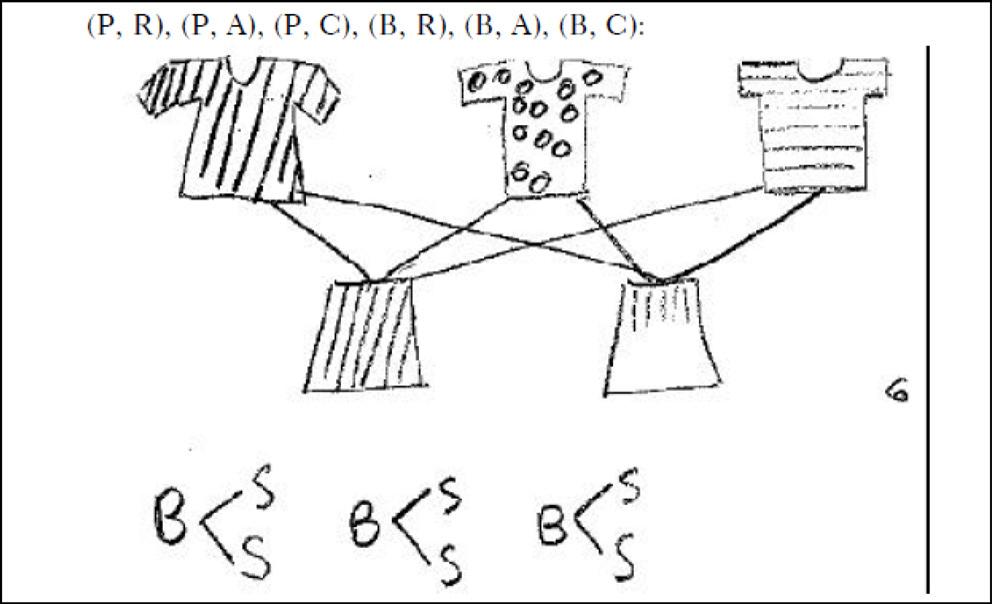
Fonte: Brasil (1997, p. 73).
Figura 8 Soluções sugeridas para o problema das combinações de saias e blusas
Na solução da Figura 8, podemos identificar vestígios do que teria sido uma solução dos anos 1960. As saias e blusas reaparecem com novos estilos e estampas; as flechas são substituídas por elos de ligação; os pares ordenados são listados, mas não aparecem entre chaves, de modo que a ideia de conjunto fica sugerida, mas não explicitada.
Considerando que os Parâmetros Curriculares Nacionais foram tomados, desde a sua publicação, como referência para a avaliação de livros didáticos, prosseguimos a investigação. Encontramos saias e blusas em uma coleção didática autorizada e distribuída pelo Programa Nacional do Livro Didático para o triênio 2016-2018 (BONJORNO et al., 2016). E, provavelmente, uma busca mais minuciosa permitiria identificar outros rastros nos livros didáticos atualmente em uso.
Podemos pensar, então, em saias e blusas como uma marca permanente daquele movimento de inovação curricular que emergiu no Brasil nos anos 1960. A valorização do pensamento combinatório em crianças e a associação entre multiplicação e produto cartesiano podem ser considerados legados do movimento da matemática moderna.
Considerações finais
A investigação apresentada neste artigo não foi organizada a partir de uma questão abrangente sobre os impactos do Curso de Didática no ensino de matemática praticado no curso primário do Instituto de Educação, ou acerca do alcance e da permanência das experimentações ali realizadas, ao tempo da Matemática Moderna. A pesquisa foi provocada por indícios que encontramos durante o trabalho simultâneo com dois acervos, e possibilitou identificar múltiplas conexões entre os esforços de renovação do ensino de matemática, nos anos 1960, em diferentes cursos da mesma instituição e em diferentes partes do país e do mundo.
A investigação indica, ainda, que aquela inovação não foi introduzida como componente de uma grande mudança curricular, mas como uma experimentação criativa e localizada de uma nova abordagem de uma operação aritmética. A persistência de uma abordagem muito assemelhada em documentos recentes sugere que a ideia era didaticamente poderosa, ao mesmo tempo em que revela uma tendência à reprodução de exercícios e contextos, ao longo do tempo. Pois, nos anos 2010, saia e blusa não é um traje comum e emblemático como era nos anos 1960.
Os achados também contribuem para a desmitificação e a desmistificação da ideia de que a Matemática Moderna teria sido uma imposição dos governos ou dos matemáticos. No Instituto de Educação, como em muitas outras partes, professores se mobilizaram para estudar, inventar e ensinar.
A preservação de acervos escolares, que está na origem da escrita deste texto, possibilitará que muitas outras investigações sejam realizadas, ampliando a rede de conexões entre os indícios e a nossa compreensão sobre as mudanças e as permanências nos currículos escolares.