Introdução
Recomendações curriculares e discussões no âmbito da Educação Matemática nas últimas décadas têm apontado o trabalho com tendências metodológicas como a resolução de problemas e a investigação matemática como promissoras para os processos de ensino e aprendizagem da Matemática. Entretanto, implementar práticas alternativas ao ensino diretivo ou expositivo tem sido ainda um desafio (STIGLER; HIEBERT, 2004; LITHNER, 2008; LAURILLARD, 2012). No caso específico do CDI (Cálculo Diferencial e Integral), Lima (2014, p. 3) reforça que, “durante muito tempo, o foco do curso foi à apresentação formal e rigorosa do conteúdo matemático, em uma abordagem centrada nela mesma”, vinculada a uma estratégia tradicional de ensino, pautada no tripé definição-exemplo-exercício.
De encontro a essa perspectiva, temos buscado caracterizar em nossa pesquisa propostas de organização de ambientes de ensino e de aprendizagem de CDI pautados em episódios de resolução de tarefas, que contemplem pressupostos das tendências metodológicas supracitadas, mas que atendam demandas rotineiras de sala de aula e a ela se ajustem. Ambiente de ensino e de aprendizagem é tomado como “um conjunto formado entre sujeitos, objetos e recursos que interagem no processo de aprendizagem” (Bragança; Ferreira; Pontelo, 2014, p. 2), previamente planejado/organizado para que ocorram “práticas de aprendizagem”, na qual o professor tem um papel fundamental, tanto na preparação, organização e sistematização das tarefas que integram esse ambiente quanto na direção e orientação de práticas pedagógicas.
Este texto, oriundo de uma reanálise de dados coletados durante uma experiência de ensino descrita na dissertação do segundo autor (FONSECA, 2017), objetiva apresentar uma reflexão sobre aspectos envolvidos na proposição de uma tarefa com uso de tecnologias digitais da informação e comunicação (TDIC), que integra um ambiente de ensino e aprendizagem de CDI. Inicialmente, apresentamos os referenciais teóricos que sustentam a experiência de ensino, bem como a conjectura que a orientou. Além disso, é apresentada uma caracterização da investigação baseada em design, mais especificamente por meio de metodologia de experiência de ensino. Como extensão à análise preliminar realizada por Fonseca (2017), apresentamos, como resultado de um trabalho articulado entre os três autores, uma análise retrospectiva da experiência, onde são discutidas diversas hipóteses relacionadas aos aspectos supracitados. Por fim, discutimos implicações dessa análise no que tange às estratégias pedagógicas na organização de ambientes de ensino e de aprendizagem de CDI que façam uso de TDIC.
Fundamentação teórica
Conforme apontam Watson et al. (2013), as tarefas matemáticas podem gerar atividade que proporciona, aos estudantes, oportunidades para elaborar conceitos matemáticos, formular ideias, desenvolver estratégias, promovendo o pensamento matemático e oportunizando a investigação. Para Ponte (2014, p. 16), a tarefa matemática é uma ferramenta norteadora essencial para o ensino e a aprendizagem da Matemática e “pode ter ou não potencialidades em termos de conceitos e processos matemáticos que pode ajudar a mobilizar”.
Inspirados nas ideias de Watson et al. (2013) e de Ponte (2014), por tarefa estamos entendendo “o amplo espectro composto por ‘coisas a fazer’ pelos estudantes em sala de aula, o que inclui desde a execução de exercícios algorítmicos até a realização de investigações ou construção de modelos matemáticos” (TREVISAN; BORSSOI; ELIAS, 2015, p. 3). Na direção de compreender essas “coisas a fazer”, respaldamo-nos em pressupostos da Educação Matemática Realística (RME)2, abordagem de ensino que compreende a matemática como oportunidade de reinvenção de conceitos, ocorrendo por meio de um processo guiado pelo professor, em que os estudantes têm um papel ativo na elaboração dos conceitos. Na perspectiva da RME, reforça-se o papel das tarefas enquanto promotoras de momentos de interação e colaboração entre professor e estudantes, respeitando sua produção, valorizando seu processo de resolução e buscando, em seu encaminhamento, promover a aprendizagem e o desenvolvimento do conhecimento matemático.
Palha, Dekker, Gravemeijer e Van Hout-Wolters (2013) e Palha, Dekker e Gravemeijer (2015), à luz de pressupostos da RME, defendem a organização de ambientes de ensino e aprendizagem pautados em episódios de resolução de tarefas (tradução que estamos adotando para shift problem lessons). Tais momentos não substituem outros presentes no contexto de uma sala de aula regular, como aqueles envolvendo a exposição de conceitos pelo professor ou o trabalho com resolução de tarefas rotineiras. Entretanto, diferem significativamente de uma aula “usual”, tendo como pressupostos: o fato de os conteúdos matemáticos serem apresentados aos estudantes fora da estrutura do “manual escolar” e por meio de sequências de tarefas com elementos que estimulem sua reflexão e a elaboração de um raciocínio conceitual, na qual cria-se um ambiente de ensino e de aprendizagem diferente do usual e propicio à resolução de problemas; o papel ativo do estudante em organizar, discutir e transformar ideias intuitivas necessárias à compreensão dos conceitos, a partir do diálogo emergente na resolução de tarefas em pequenos grupos de forma colaborativa; o papel do professor que, ao invés de fornecer explicações, estimula os grupos de estudantes a mostrar, explicar, justificar, criticar e melhorar as ideias matemáticas emergentes no grupo.
Um elemento que destacamos, ao pensar o desenho das tarefas que compõem esse ambiente, é a possibilidade de incorporação de TDIC, pois permitem ao estudante assumir um papel mais ativo na elaboração do conhecimento, conforme preconiza a RME. A incorporação da tecnologia permite que os estudantes explorem problemas mais autênticos e realísticos, apoiando a reinvenção, com base em seus conhecimentos prévios, da matemática que se espera que aprendam. Além disso, a tecnologia oferece aos estudantes mais oportunidade para interatividade, na direção do que Borba, Silva e Gadanidis (2015) caracterizam como experimentação com tecnologias. Segundo esses autores, uma tarefa elaborada nessa perspectiva deve oferecer meios para (entre outros): gerar conjecturas matemáticas e realizar testes usando um grande número de exemplos; criar e conectar diferentes (e múltiplos) tipos de representações de objetos matemáticos.
As TDIC podem contribuir para a compreensão de conceitos matemáticos, pois possibilitam a visualização, reflexão e deduções para refinar o conhecimento. Entretanto, por si só nenhuma tecnologia garante tais processos: é necessário um cuidadoso processo de planejamento para sua utilização. Em especial, o processo de elaboração, aplicação e refinamento de tarefas que façam uso desse recurso configura-se como uma importante atividade no âmbito da Educação Matemática e, mais especificamente, no caso do CDI. Tal aspecto evidencia a importância de estudos como o que aqui apresentamos.
Procedimentos metodológicos
A pesquisa da qual este artigo é recorte foi de natureza qualitativa, envolvendo um estudo em sala de aula em condições reais de ensino, e adotou pressupostos da design-based research, expressão usualmente traduzida como investigação baseada em design (PONTE et al., 2016) ou pesquisa de desenvolvimento (MATTA; DA SILVA; BOAVENTURA, 2014; BARBOSA; OLIVEIRA, 2015). De modo geral, uma pesquisa desse tipo envolve o “delineamento, desenvolvimento e avaliação de artefatos para serem utilizados na abordagem de um determinado problema, à medida que se busca compreender/explicar suas características, usos e/ou repercussões” (BARBOSA; OLIVEIRA, 2015, p. 527).
Em especial, adotamos a metodologia de experiência de ensino como um tipo especial de pesquisa baseada em design (COBB et al., 2003). O desenho (design) de uma experiência de ensino contempla o desenvolvimento de processos de planejamento e ensino e a investigação sobre tais processos em um contexto educacional (a sala de aula). Integra uma sequência de episódios guiados por conjecturas que podem ser reformuladas ou abandonadas após a análise desses episódios. Essa análise ocorre tanto no decurso da implementação da proposta (análise preliminar, quando as tarefas são formuladas e aplicadas - o que dificulta uma análise sistemática) quanto após a intervenção terminar (análise retrospectiva).
Fonseca (2017) apresentou em sua dissertação uma análise preliminar de uma experiência de ensino realizada com uma turma3 de CDI 1 no 1º semestre do ano de 2016, envolvendo o trabalho com tarefas para exploração de ideias necessárias à compreensão do conceito de derivadas. Neste artigo, propomos uma reanálise desses dados, no intuito de evidenciar a importância de um uso integrado da tecnologia, do conteúdo e da didática para criar um ambiente de ensino eficaz à aprendizagem dos conceitos matemáticos em uma das tarefas. Nesse olhar retrospectivo para a experiência de ensino que deu origem aos dados, destacamos a presença da terceira autora como parte da equipe de pesquisa que possibilita a validação colaborativa do processo (MATTA; DA SILVA; BOAVENTURA, 2014).
Para coleta de dados, fizemos uso da produção escrita dos grupos enquanto trabalhavam com as tarefas e, de forma complementar, o diário de campo organizado pelos pesquisadores. A partir de quadros contendo ideias e conceitos possíveis de serem explorados na tarefa (que serão apresentados na próxima seção), buscamos identificar na produção escrita dos 14 grupos4 (aqui nomeados como G01, G02, ..., G14) sua presença a partir do modo como a abordaram e desenvolveram5.
Uma conjectura para a experiência de ensino
O trabalho com o conteúdo matemático sequência de diferenças serviu como inspiração para o planejamento da experiência de ensino da qual este trabalho faz um recorte. Sequências numéricas são, na perspectiva de Weigand (2004; 2014), objetos fundamentais para o desenvolvimento/elaboração de conceitos do CDI. O autor defende uma “revitalização” do tema (que, há algumas décadas, constituiu o tema inicial de cursos de CDI na Europa) não como um tópico isolado, mas distribuído ao longo do currículo da Educação Básica (em nosso caso, adaptável ao longo do curso de CDI). O propósito é que uma abordagem de conjuntos discretos anteceda o estudo de derivadas de funções reais, na qual o conceito de taxa média é desenvolvido a partir da discussão de diferentes sequências de diferença e quocientes de diferenças e o conceito de integral emerge do trabalho com sequências de somas parciais, sem que o conceito de limite seja apresentado formalmente nesse momento.
Assim, o conceito de quociente de diferenças pode ser tomado como base para a compreensão do quociente diferencial; por sua vez, o estudo das sequências de diferenças pode contribuir como uma base intuitiva para a compreensão do quociente de diferenças. Dada uma sequência
Nossa conjectura para a realização da experiência de ensino foi que um trabalho sistemático na sala de aula, devidamente orientado a partir de episódios de resolução de tarefas, possibilita aos estudantes explorar de forma intuitiva “ideias básicas” necessárias à compreensão do conceito de derivadas. Temos trabalhado, em um projeto maior6, com a criação de tarefas (e, intrinsecamente associado a isso, investigado formas de utilizá-las em sala de aula, bem como aprendizagens por ela propiciadas) que oportunizem aos estudantes reinventar CDI, que permitam a criação de conceitos e teoremas fundamentais utilizados intuitivamente (por meio da organização de definições provisórias) antes que sejam descritos com precisão ou provados (TREVISAN; MENDES, 2017).
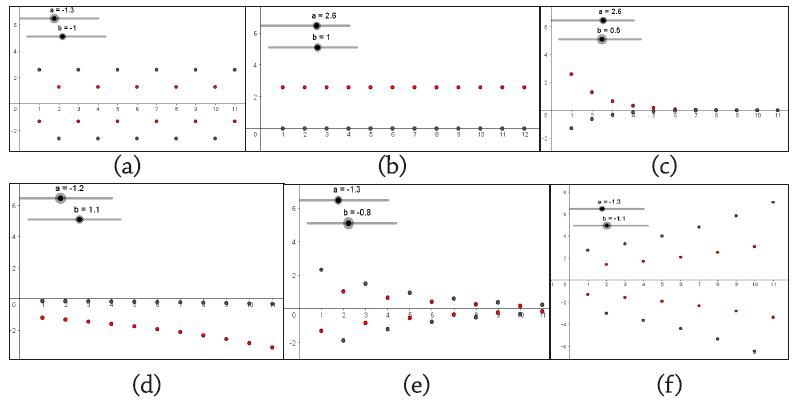
O estudo das sequências de diferenças possibilita realizar uma análise da modificação geral do comportamento das sequências (enquanto casos particulares de funções), sendo uma ferramenta importante para explorar aspectos relacionados ao crescimento/decrescimento, à diferença entre termos consecutivos e às taxas de variação, fato esse levado em conta na proposição da tarefa aqui analisada. A tarefa era de caráter “aberto”, sendo que aos estudantes foi solicitada uma análise dos parâmetros e no comportamento de duas sequências numéricas e suas sequências de diferenças associadas, por meio do seguinte comando:
Dadas as sequências definidas recursivamente por
Criados os controles deslizantes
Em um exercício de “antecipação” de resoluções, reconhecemos as múltiplas representações que, atreladas à dinamicidade possibilitada pelo movimento dos controles deslizantes do Geogebra, permitiriam investigar relações entre as sequências originais e as sequências de suas diferenças. No caso da sequência de comportamento linear: a relação do coeficiente
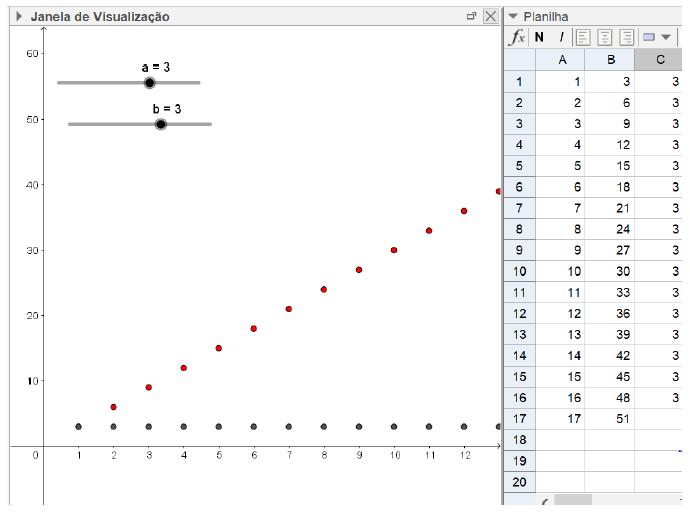
Fonte: autores.
Figura 1 Representação da sequência linear (vermelha) e da sequência de suas diferenças (azul)
Para a sequência de comportamento exponencial, há diferentes configurações possíveis, dependendo do valor escolhido para
Análise e discussão dos dados
A análise aqui apresentada está organizada em duas partes. Uma análise preliminar, recorte do trabalho de Fonseca (2017), realizada durante a implementação da experiência de ensino, que refletiu uma exploração pouco sistemática dos estudantes da tarefa proposta, e uma análise retrospectiva, momento em que é feita uma revisão dos dados no intuito de evidenciar “aspectos de qualidade” das respostas apresentadas pelos estudantes e direções para ação na sala de aula (tanto a partir de um novo desenho da tarefa quanto das discussões que dela poderiam ser originadas).
Análise preliminar
Na análise preliminar da tarefa realizada por Fonseca (2017), identificamos em todos os grupos analisados o estabelecimento de relações entre os parâmetros
No que tange às diferentes ideias e conceitos (IC) que circunscrevem o conceito de derivadas, Fonseca (2017) organizou um quadro (Quadro 1), a partir das produções escritas dos 14 grupos, nas quais encontramos em 12 deles alguma discussão acerca dos aspectos supracitados (excetuando-se aqui G03 e G04). Destaca-se que esse quadro foi construído considerando que um mesmo grupo pode ter explorado um ou mais desses conceitos.
Quadro 1 Ideias e conceitos mobilizados presentes nas produções escritas
| Ideias e conceitos | Grupos | |
| IC1 | Crescimento/Decrescimento | G01, G05, G06, G07, G08, G09, G13 |
| IC2 | Diferença entre termos consecutivos | G01, G05, G07, G09, G12 |
| IC3 | Taxa de variação | G03, G07, G08, G10, G11, G12, G13, G14 |
Fonte: Fonseca (2017).
No que tange à discussão acerca de ideias e conceitos de crescimento e decrescimento, os 7 grupos listados em IC1 reconheceram que o comportamento da sequência original relaciona-se com o sinal do parâmetro
Cinco grupos que observaram aspectos relacionados à diferença entre os termos consecutivos da sequência original e/ou sequência de diferenças são listados em IC2 e utilizaram expressões como “distância entre os pontos” ou “aumento do intervalo entre os pontos”: G01, por exemplo, aponta que a distância entre os pontos na sequência original aumenta quanto maior for o valor de
Por fim, em IC3 enquadram-se 8 grupos que destacam ideias relacionadas ao conceito geométrico de taxa de variação, em geral fazendo uso de termos como “inclinação dos pontos”, “coeficiente angular” da reta ou “amplitude” do gráfico. Na produção escrita de G03 (Figura 4), por exemplo, o valor dos parâmetros é associado à “inclinação dos pontos” (para a sequência de comportamento exponencial) sem, porém, explicitar relações entre
De modo geral, apenas uma parte dos grupos (mais especificamente, G05, G06, G07, G12 e G14) apresentou em sua produção alguma relação entre os parâmetros e o comportamento das sequências de diferenças, e nenhum deles explicitou relações entre as sequências originais e suas sequências de diferenças. Assim, nenhum conceito mais sistematizado pôde emergir das respostas obtidas e nenhuma discussão substancial pôde ser levada a cabo com a turma a partir das respostas apresentadas pelos grupos.
Análise retrospectiva
Embora todos os grupos tenham conseguido apontar o papel dos parâmetros
Desenvolver o conhecimento usando tarefas matemáticas que façam uso de TDIC requer uma boa compreensão da relação de três aspectos-chave de conhecimento: a tecnologia, a didática e o conteúdo (MISHRA; KOEHLER, 2006). Seu efetivo uso como apoio aos processos de ensino e de aprendizagem precisa considerar esses três aspectos de forma conjunta, e não de forma isolada, buscando-se relações de uns com os outros. Ou seja, exige uma boa articulação entre tecnologia, didática e conteúdo e o seu uso para desenvolver tarefas, estratégias e representações adequadas. No caso da experiência de ensino em questão, um uso efetivo de TDIC envolveria a articulação do conceito de derivada (associado ao estudo da sequência de diferenças), a utilização de vários tipos de representações (representações simbólicas, como equações ou representações visuais, como os gráficos) e o aplicativo Geogebra (usado para exibir e manipular as diferentes representações). Uma boa articulação entre estes aspectos permitiria aos estudantes interagir com o aplicativo de forma a visualizar dinamicamente e manipular representações gráficas.
Uma análise mais profunda sobre os tipos de representações que os estudantes parecem ter mobilizado (a partir das suas respostas escritas) revela que produziram e manipularam as representações visionadas, porém poucos grupos apreenderam as relações essenciais entre as representações, apontando então uma falha em interagir eficazmente com o aplicativo. Tendo por base as respostas escritas dos estudantes e as descrições proporcionadas, discutiremos a integração da tecnologia, do conteúdo e da didática a partir de quatro aspectos do meio da aprendizagem envolvidos nessa experiência de ensino, na questão de uma suposta “falha” na interação com o aplicativo.
O primeiro aspecto do ambiente de aprendizagem refere-se à tarefa propriamente. Por si só nenhuma TDIC garante processos de aprendizagem; é necessária uma tarefa que induza o estudante a agir com a ferramenta e a utilizar os resultados dessa ação interativamente na direção de alcançar o objetivo da aprendizagem. Refletindo sobre os exemplos analisados das respostas podemos questionar se o enunciado da tarefa está claramente formulado, tendo em conta o conteúdo matemático, o recurso utilizado e a forma de ser interpretado pelo aluno corretamente. No enunciado proposto, a questão é analisar o papel dos parâmetros
O segundo aspecto refere-se à TDIC utilizada, de onde se levanta o seguinte questionamento frente à tarefa: será que é o recurso mais propício para induzir o estudante na ação necessária para atingir os objetivos propostos na elaboração da conjectura que guia a experiência de ensino? Uma TDIC pode possibilitar aos estudantes mais oportunidades para interatividade (Borba; Silva; Gadanidis, 2015). Uma tarefa elaborada nessa perspectiva deve oferecer meios, para (entre outros): geração de conjecturas matemáticas e realização de testes usando um grande número de exemplos; criação e conexão entre diferentes (e múltiplos) tipos de representações de objetos matemáticos; incentivo à combinação dos diferentes tipos de raciocínios. Uma questão que se põe é se o aplicativo tem características que levam a esse tipo de experiências de aprendizagem, frente ao objetivo que se estabeleceu no desenvolvimento da tarefa. Em outras palavras: uma segunda hipótese é que a TDIC não foi a mais propícia para envolver o estudante na aprendizagem planejada pelo professor.
A análise das respostas apresentadas pelos estudantes sugere que o aplicativo é adequado para exploração, criação de conjecturas e combinação de vários tipos de raciocínios. Isso é visível na variedade de respostas apresentadas pelos grupos tal como é mostrado no Quadro 1; por exemplo o grupo G01 (Figura 4) explorou e aprofundou aspectos diferentes dos mencionados pelo grupo G07 (Figura 6). A diversidade de respostas também é visível dentro de cada agrupamento do Quadro 1. Já a resposta do grupo G07 inclui as diferentes ideias que circunscrevem o conceito de derivada elencadas no planejamento da tarefa. O grupo menciona aspectos relacionados ao crescimento e decrescimento das sequências (original e/ou de diferenças), observa a diferença entre os termos consecutivos das sequências e sua relação com os parâmetros
O terceiro aspecto tem a ver com a interpretação das ações, explicações e interação dos estudantes: será que o professor e o investigador tiveram meios suficientes para reconhecer a qualidade das respostas e da interação e diálogo ocorridos no grupo? O trabalho colaborativo é um dos aspectos importantes do ambiente de ensino e de aprendizagem que faça uso de TDIC. Uma análise das produções escritas não apresentou informação sobre as explicações e justificativas que ocorreram no grupo; que explorações foram efetuadas ou excluídas, que ideias e argumentos foram trazidos, discutidos e como foram modificados. É necessário, em um novo ciclo de aplicação da tarefa, produzir dados que permitam realizar tal análise.
O quarto aspecto refere-se à interação entre professor e estudantes no processo de formalização: será necessária a intervenção do professor para induzir os estudantes a passar da experimentação para formalização? Laurillard (2012) define conhecimento formal como um tipo de conhecimento específico no qual o professor é a autoridade e também o responsável pela sua correta apreensão. Os estudantes desenvolvem ideias e experiências matemáticas por meio da interação com as TDIC no trabalho com as tarefas propostas, e o professor ajuda-os a reformular suas ideias e interpretações, pelo diálogo e dando feedback. No caso da tarefa em tela, a intervenção do professor seria necessária para ajudá-los a passar da experimentação para a formalização, uma vez que conhecimento formal, como no caso do CDI, inclui ideias sofisticadas que precisam ser trabalhadas na interação. Além disso, as TDIC alteram a forma como aprendemos e como nos expressamos. Sem ter diálogo com o estudante seria difícil (senão impossível) para o professor interpretar corretamente a intenção dos alunos em suas respostas escritas. A tarefa “por si só” não se mostra “autossuficiente” no processo de formalização de conceitos subjacentes.
Em síntese, apresentamos no Quadro 2, como resultado da análise retrospectiva, os quatro aspectos do meio da aprendizagem envolvidos nessa experiência de ensino em aulas de CDI, envoltos na proposição de uma tarefa matemática com uso de TDIC, que procuram trazer luz às diversas facetas (aspectos do ambiente de ensino e de aprendizagem) envolvidas na interpretação da suposta “falha” na interação entre os estudantes e o software.
Quadro 2 Aspectos do ambiente de ensino e de aprendizagem envolvidos na interpretação da suposta “falha” na interação entre os estudantes e o aplicativo
| Aspectos envolvidos | Considerações |
|---|---|
| Tarefa | É necessária uma tarefa que induza o estudante a agir com a ferramenta e a utilizar os resultados desta ação interativamente na direção de alcançar o objetivo da aprendizagem. |
| Recurso tecnológico | O recurso tecnológico é adequado para exploração, mas não é o suficiente para extrair o conteúdo matemático necessário. |
| Interpretação das ações, explicações e interação dos estudantes | O professor deve ter meios suficientes para reconhecer a qualidade nas respostas dos estudantes e da interação ocorridos no grupo. |
| Interação entre professor e estudantes no processo de formalização | Será necessária a intervenção do professor para induzir os estudantes a passar da experimentação para formalização. |
Fonte: autores.
Considerações finais: ações para sala de aula
O desenvolvimento de tarefas para o uso eficaz de TDIC é um processo interativo e que consiste em elaborar, aplicar, partilhar e refinar as tarefas enquanto se faz uso desse recurso. Atendendo os resultados da experiência de ensino e de sua análise retrospectiva, um passo essencial que se reconhece no próximo ciclo iterativo de elaboração da tarefa é direcionar o foco da atenção do estudante para o conteúdo matemático objetivado. É possível que para isso acontecer seja necessário mais do que alterar o enunciado da tarefa e organizar os estudantes em grupos. As sugestões possíveis para um melhoramento da elaboração da tarefa e do ambiente de aprendizagem devem incluir os seguintes aspectos.
i. Uma elaboração mais clara do enunciado da tarefa
Sendo o objetivo sistematizar um conceito provisório de derivada a partir da discussão de diferentes sequências de diferença e, posteriormente, quocientes de diferenças, a proposição da tarefa deveria ter como foco explícito a investigação da relação entre as duas sequências (ao invés do papel dos parâmetros
Formulações do tipo aberto-controlada (expressão extraída do texto de Borba, Silva e Gadanidis (2015), porém ressignificada por Couto, Fonseca e Trevisan (2017)), ou seja, com direcionalidade ao objetivo esperado, têm se mostrado mais adequadas, ao menos nos episódios iniciais de um curso de CDI, para organização de episódios de resolução de tarefas. Por um lado, esse formato de tarefa possibilita aos estudantes a realização de experimentações com tecnologias, oferecendo meios para criar e conectar diferentes (e múltiplos) tipos de representações de objetos matemáticos, gerando conjecturas matemáticas; por outro lado, mantém um desenho ao qual os estudantes estão habituados (como se fossem “comandos” dados pelo professor).
ii. Conduzir uma discussão em nível de grupo de forma coletiva a partir da tarefa tendo por base uma lista com “boas perguntas” para direcionar a exploração dos estudantes.
Ao tentar responder questões elencadas anteriormente, os estudantes poderiam levantar conjecturas e criar tópicos de discussão em que, junto com o professor, explicassem o comportamento de variação entre os termos de uma sequência. Exemplos de conjecturas que os estudantes poderiam levantar podem ser: sendo
iii. Introduzir no meio de aprendizagem elementos que permitem aos estudantes ter feedback intrínseco.
Isso exige mais conhecimento sobre o processo de aprendizagem realizado coletivamente em grupo e sua relação com a TDIC. Como melhorar a construção proposta no Geogebra para ajudar os estudantes a focar a atenção em propriedades e elementos mais conceituais? Como potencializar a colaboração no grupo? O problema dessa sugestão é que parece haver ainda pouco conhecimento sobre formas de o professor reconhecer critérios de qualidade no diálogo entre os estudantes enquanto trabalharam com o software para estabelecer conjecturas sobre as ideias que têm e como as comunicam verbalmente. Propõe-se investigar formas de, na observação do diálogo entre os estudantes, analisar o modo como ideias importantes são discutidas, aceitas, rejeitadas ou transformadas e tentar perceber a razão disso.
iv. Reformulação da conjectura de aprendizagem.
Inicialmente, assumimos como conjectura que “um trabalho sistemático na sala de aula, devidamente orientado a partir de episódios de resolução de tarefas, possibilita aos estudantes explorar de forma intuitiva ‘ideias básicas’ necessárias à compreensão do conceito de derivadas”. No entanto isso parece não ter sido suficiente para que o estudante passasse da intuição e percepção à formalização de conceitos matemáticos. Propõe-se que a discussão coletiva da tarefa pelo professor com os estudantes seja incluída no trabalho sistemático de elaboração desses conceitos, não precisando ser conduzida de forma diretiva. O professor pode elencar contribuições dos grupos e ajudá-los na formulação matemática das suas ideias.