1 Introdução
A contagem faz parte da vida das crianças desde muito cedo. Muitas vezes, é a única forma de resolver um problema como, por exemplo: quantas balas existem em um pacote para saber se tem para todos, contar quantos brinquedos possui, quantos dias faltam para o aniversário etc. Ao perceber que balas, brinquedos, dias ou quaisquer itens podem ser contados, a criança inicia o processo de associar números a quantidades. Essa combinação pode ser feita por meio de imagens do traçado dos números associados à quantidade de algumas figuras ilustradas em cartazes, os quais se tornam um recurso ao qual a criança recorre quando precisa se certificar sobre a escrita do número e a sequência numérica.
Essas imagens, normalmente fixadas nas paredes das salas de aula, podem funcionar apenas como associação entre o número e a quantidade, indicando que objetos podem ser contados, mas também podem potencializar o ensino de aritmética, favorecendo o desenvolvimento do senso numérico, entendido como a capacidade de trabalhar com os números valorizando as relações entre eles de forma flexível e criativa.
De que modo essas representações podem fomentar algo além de simples associações entre números e quantidades, possibilitando que a criança estabeleça relações entre dois ou mais números, construa um bom senso numérico e desenvolva o raciocínio lógico?
O objetivo deste texto é apresentar o Sense Líquen, uma proposta de representação para números e quantidades que favorece a compreensão das relações entre os números e é um material manipulável para resolver operações de adição e subtração para resultados, com parcelas, minuendos e subtraendos menores que 20.
2 Números e quantidades
Nas salas de aula de primeiro ano é muito comum a presença de cartazes que representam números e quantidades expostos nas paredes. Geralmente são confeccionados pelos professores ou adquiridos pela escola e fazem parte da vida escolar dos estudantes que frequentam o Ensino Fundamental I, colorindo e alegrando o ambiente. Cada número é representado por uma figura diferente, levando às crianças a perceberam que qualquer objeto pode ser contado.
A Figura 1 apresenta dois exemplos de cartazes1 que podem ser observados nas salas de aula.

Fonte: A: https://www.americanas.com.br/produto/2638428655; B: www.elo7.com.br/banner-numeros-e-quantidades-0-a-20/dp/E12EE7.
Figura 1 Cartazes com números e quantidades.
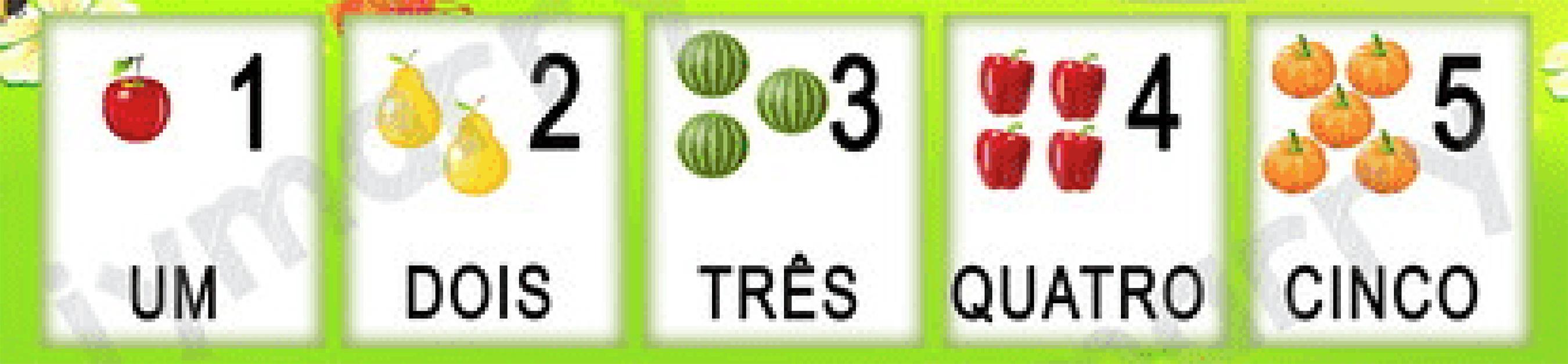
Essas representações são lindas, divertidas, coloridas, enfeitam a sala, mostrando que qualquer objeto pode ser contado, mas deixam a desejar por não construírem relações entre os números, o que é imprescindível para o entendimento da aritmética. Vamos analisar essa afirmação avaliando o recorte da Figura 1B.
Fonte:www.elo7.com.br/banner-numeros-e-quantidades-0-a-20/dp/E12EE7.
Figura 1B Recorte de números e quantidades até 5.
No recorte apresentado da Figura 1(b) temos maçãs, peras, melancias, pimentões e morangas, o símbolo do numeral que representa a quantidade e sua representação por extenso. Essa apresentação constrói a ideia de quantidade e de que podemos contar diferentes objetos, entretanto, além da noção de quantidade, precisamos construir o “sentido numérico” e estabelecer uma “rede de relações numéricas” entre os números. Analisando o número 3, por exemplo, entendemos que, por rede de relações numéricas para o número 3, no mínimo é preciso construir que 3 é 2 + 1, é 4 – 1, que o 1 e o 2 estão dentro do 3 e que o 3 está dentro do 4 e do 5. Esse é o mínimo de conhecimento necessário para a construção de uma base aritmética bem estruturada. Ao tomar consciências das relações numéricas do três e de qualquer outro número, as crianças desenvolvem o senso numérico e têm capacidade de elaborar estratégias de cálculo mental. O senso numérico é, de acordo com Sowder (1988), uma rede conceitual e bem organizada de informações numéricas que permite que uma pessoa relacione números e operações para resolver problemas de maneira flexível e criativa. Para Boaler (2018), estudantes com senso numérico bem desenvolvido conseguem interagir com os números de maneira flexível e conceitual. Greeno (1991) afirma que o senso numérico se refere a várias capacidades importantes, incluindo a computação mental flexível, a estimativa numérica e o julgamento quantitativo. A computação mental flexível envolve o reconhecimento da equivalência entre números e objetos que são decompostos e recombinados de maneira diferente. A Figura 1 não permite a construção dessas relações, visto que há objetos diferentes para cada número e uma distribuição que não facilita a visualização de que, ao passar para o próximo número, acrescentamos mais uma unidade.
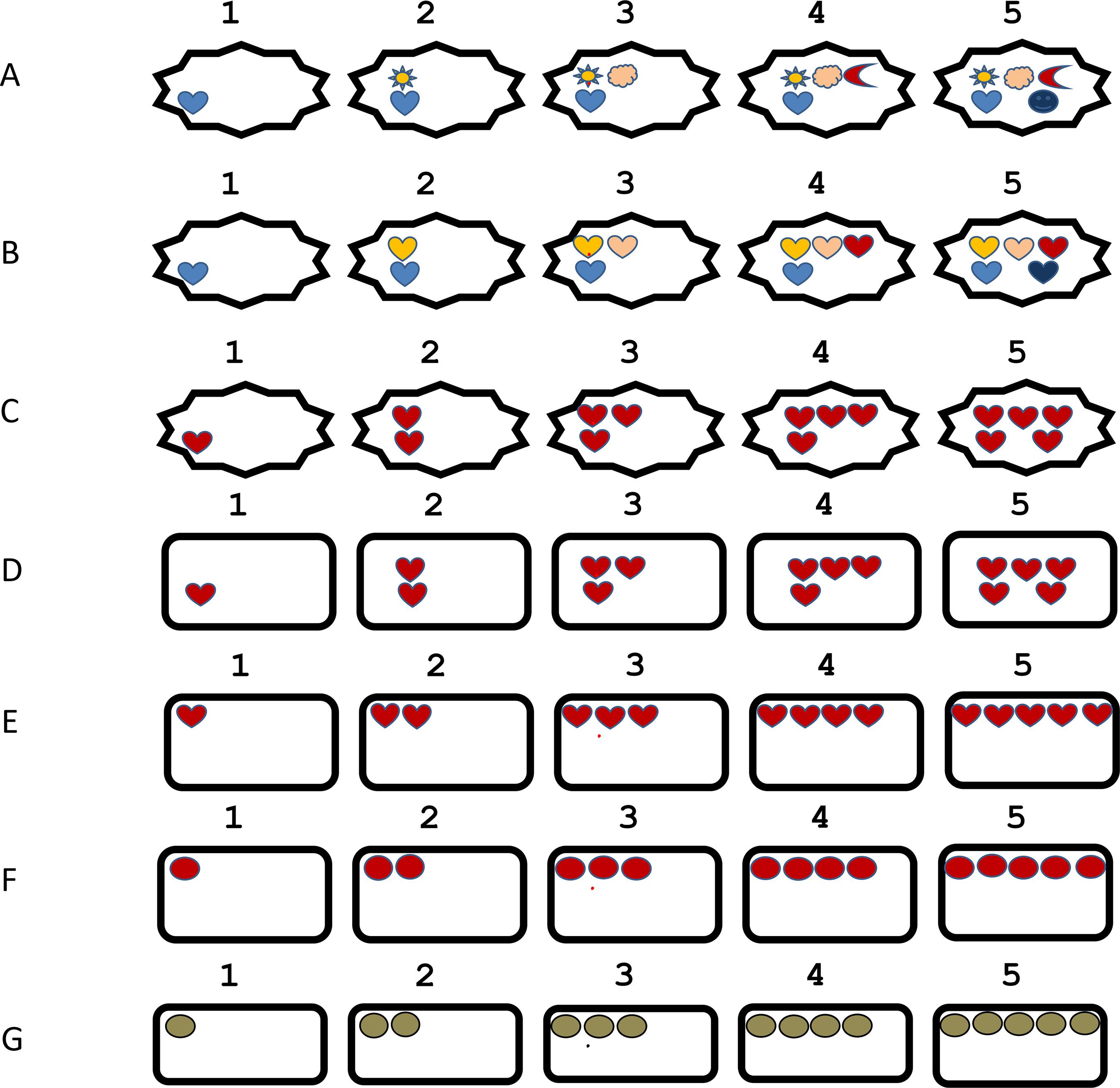
Observe a Figura 2A, na qual, a cada representação, acrescentamos um símbolo ao sucessor, mantendo a distribuição do anterior. Essa forma permite identificar a inclusão hierárquica, assim como a quantidade. A inclusão hierárquica é definida como a capacidade de perceber um número dentro do outro, como, por exemplo, que o 1 está incluído no 2 e o 2, no 3 e assim sucessivamente (KAMI e JOSEPH, 2005). Na Figura 2B, padronizamos os desenhos, mas mantivemos as cores; na Figura 2C, padronizamos as cores; na Figura 2D, colocamos em um retângulo para que o foco se mantenha nas imagens internas; na Figura 2E, fizemos um alinhamento; na Figura 2F, mudamos para círculo para ficar mais visível; e, por último, na Figura 2G, chegamos à representação que consideramos mais didática.
Fonte: Elaborado pelas autoras (2022).
Figura 2 Proposta de apresentação de números e quantidades até 5.
Em todas as representações apresentadas nessa construção, de A até G, conseguimos visualizar a inclusão hierárquica, ou seja, que o 5 contém o 4, o 3, o 2 e o 1 dentro dele, que 5 é 4 + 1, 3 + 2, 2 + 3 e 1 + 4 e entendemos que a representação da Figura 2G mostra essas relações com clareza, possibilitando a construção do sistema de numeração decimal.
Vamos ilustrar uma situação semelhante com material manipulável. Observem as figuras adiante. Se questionássemos quantos palitos há em cada grupo, o que teríamos que fazer para obter o resultado? Certamente, contar um por um ou usar um agrupamento mental. O fato é que temos que contar.
Após a contagem, podemos afirmar que, no lado esquerdo da Figura 3 temos 6 palitos e, no direito, 7 palitos. Embora o segundo monte de palitos tenha uma unidade a mais que o primeiro, a disposição não nos permite ver essa relação. Apresentando as mesmas quantidades na Figura 4, podemos inferir o resultado de forma visual, sem a necessidade da contagem de um por um.
Notem como fica visível concluir que, na Figura 4A, temos 6 bolinhas e na 4B, 7 bolinhas. Isso ocorre porque já se podem estabelecer relações: no primeiro caso temos 5 + 1 e, no segundo, 5 + 2 e diversas outras construções. Se acrescentarmos, por exemplo, outra bolinha a B, teremos 3 na segunda linha e que 5 + 3 são 8 palitos. O mais relevante na análise das figuras, porém, é o fato de que é claramente visível que B tem uma bolinha a mais que A, o que possibilita estabelecer as relações numéricas a partir dessas quantidades.
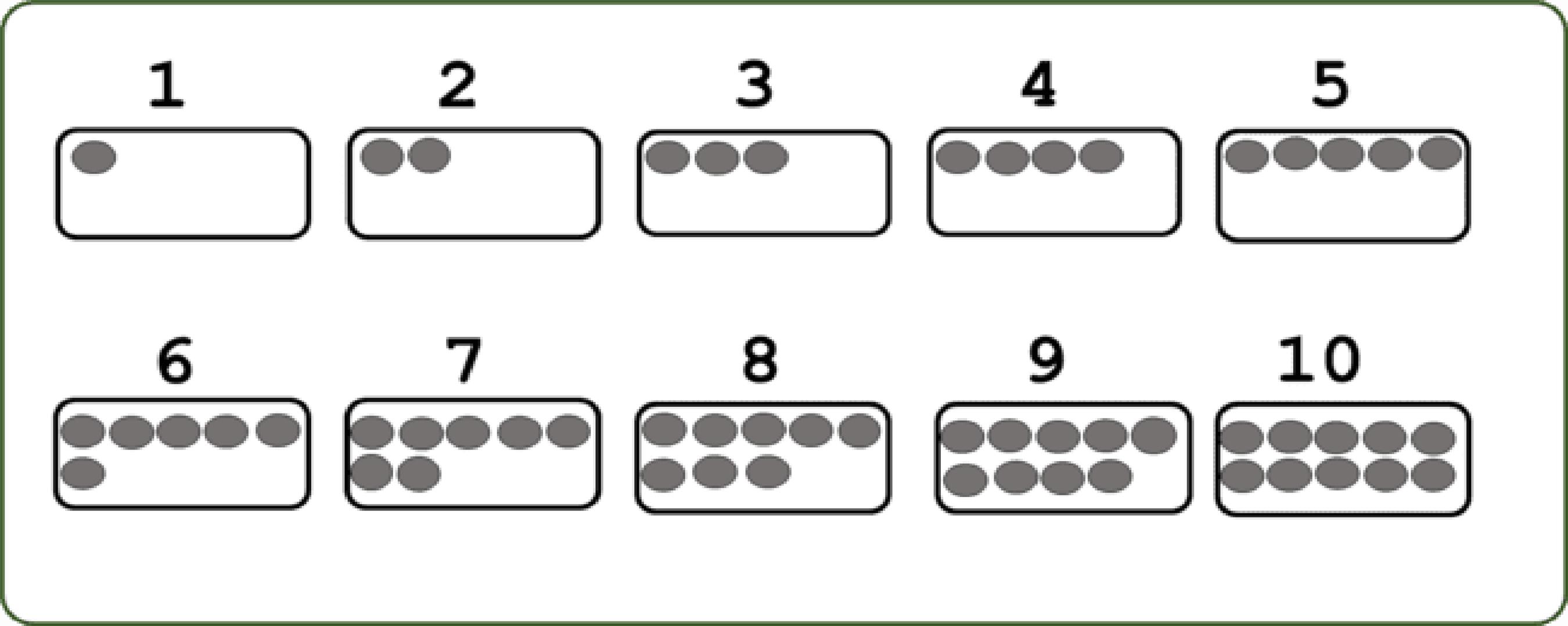
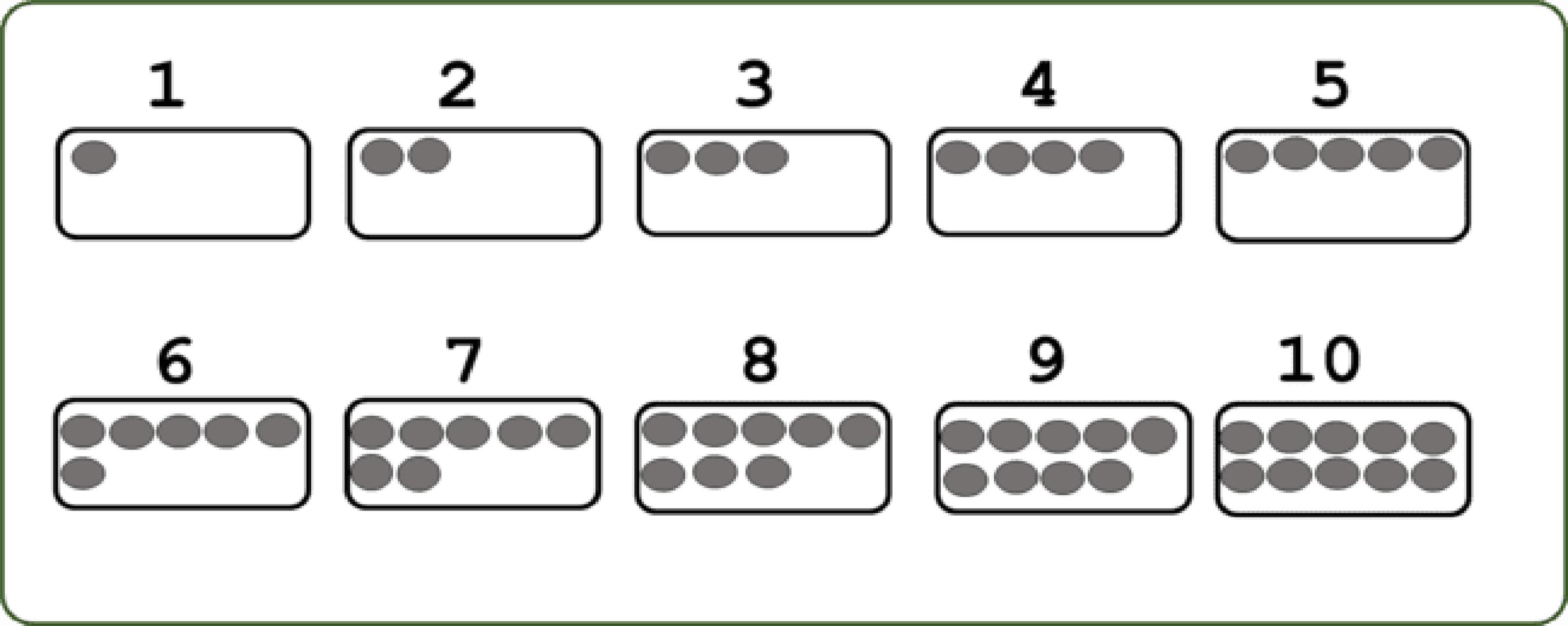
Seguindo essa lógica de construção, podemos representar os números de 6 a 10 e preenchemos a segunda linha com outras 5 unidades, tendo, assim, a representação dos números de 1 a 10. Esse modelo de representação permite que identifiquemos com o olhar, sem a necessidade de agrupamentos ou contagem da quantidade de bolinhas no retângulo. Assim, nossa proposta fica a seguinte:
Nessa apresentação, ao observarmos o número 7, é possível observar que 7 é igual a 6 + 1, 5 + 2, 4 + 3, 8 - 1, 9 - 2, 10 - 3. Podemos ter outros raciocínios, como, por exemplo, que do 7 faltam 3 unidades para 10, ou do 7 faltam 2 unidades para o 9, ou, ainda, do 7 falta uma unidade para o 8. Pode-se pensar também que o 7 é uma unidade a mais que o 6, duas unidades a mais que o 5 e assim por diante. Esse tipo de pensamento é o que permite a flexibilidade com os números e o desenvolvimento do senso numérico. Boaler (2018) assinala que “(...) o senso numérico ilustra uma compreensão profunda de Matemática, mas ele se dá por meio de uma mentalidade matemática focada em dar sentido a números e quantidades” (p. 33). Nessa proposta de apresentação de números e quantidades, acreditamos que é possível estabelecer um sentido entre números e quantidades, trabalhando com essas relações de forma flexível, como foi apresentado.
Relações como as exemplificadas no parágrafo anterior para o número 7 são extremamente relevantes, visto que representam uma rede de conhecimentos básicos para a construção de estratégias de cálculo mental (BERTICELLI e ZANCAN, 2023, no prelo), as quais não são identificáveis nas apresentações ilustradas na Figura 1. O cálculo mental está diretamente relacionado com o senso numérico, este último necessário para o desenvolvimento de habilidades como estimativa e estratégias, consideradas habilidades de um pensamento matemático flexível.
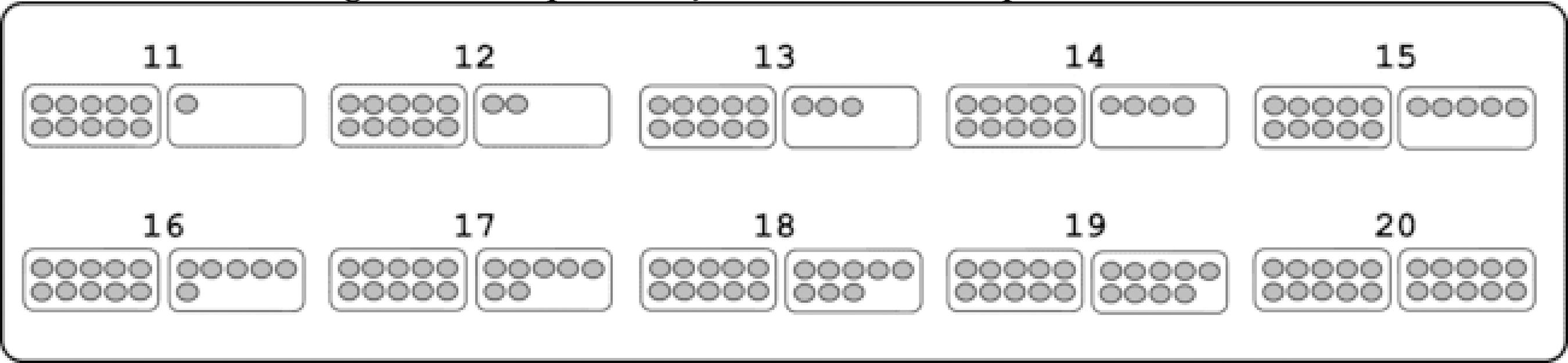
Assim como representamos os números de 1 a 10, podemos representar os de 11 a 20, ilustrando a caixa com uma dezena seguida de outra caixa com as unidades, conforme a Figura 6.
A construção do conceito de dezena é um desafio para os professores dos primeiros anos de escolarização. Os alunos demoram e têm dificuldade de compreender a construção dos números de 11 a 20. Por exemplo, o número 13 é composto por 10 + 3, ou seja, uma dezena mais 3 unidades; o número 15 é composto por uma dezena mais 5 unidades, 15 = 10+5. Essa falta de compreensão é observada quando questionamos um aluno sobre quanto é 2 + 1 e ele sabe que a resposta é 3, no entanto, quando questionamos quanto é 12 + 1, ele não sabe a resposta, indicando que não consegue ver a relação entre essas operações.
Construir uma base sólida em aritmética é a proposta da Base Nacional Comum Curricular (BNCC), como apresentado na próxima seção.
3 A Base Nacional Comum Curricular
A BNCC, documento norteador da educação básica no Brasil, traz habilidades a serem desenvolvidas nos anos iniciais e finais do Ensino Fundamental. No Quadro 1, trazemos um recorte das habilidades e dos comentários relativos a elas presentes na BNCC no que tange a números e quantidades.
Quadro 1 Habilidades para Matemática para o 1º ano do EF.
| HABILIDADES | COMENTÁRIO |
|---|---|
| (EF01MA01) Utilizar números naturais como indicadores de quantidades ou de ordem em diferentes situações cotidianas. | Utilizar os números naturais como indicadores de quantidade ou de ordem para responder a perguntas como: Quantos têm? Onde tem mais? Quantos a mais? |
| (EF01MA02) Contar de maneira exata ou aproximada, utilizando diferentes estratégias, como o pareamento e outros agrupamentos. | Essa habilidade supõe que o aluno possa resolver diferentes situações que envolvem contagens, como a distribuição de objetos e a comparação de quantidades. Dependendo das quantidades envolvidas nessas situações, surge a real necessidade de se utilizarem diferentes estratégias para a contagem, como o pareamento e outros agrupamentos, conforme previsto na habilidade. |
| (EF01MA03) Estimar e comparar quantidades de objetos de dois conjuntos (em torno de 20 elementos) por estimativa e/ou por correspondência (um a um, dois a dois) para indicar “tem mais”, “tem menos” ou “tem a mesma quantidade”. | Esta habilidade envolve estabelecer relações entre duas ou mais quantidades, expressando numericamente a diferença entre elas. Isso exige elaborar estratégias de comparação, que podem ser diretas (pareando-se um elemento de um conjunto com o elemento de outro conjunto, por exemplo) ou haver o conhecimento da ordem de grandeza do número que representa a quantidade, o que implica perceber quantas unidades há em uma quantidade. Assim, para compreender que o 8 é maior do que 6, será necessário entender que há duas unidades a mais em 8 em comparação com 6. Essa ideia de ordem de grandeza possibilitará estimar quantidades para além da noção inicial de “muito ou pouco”. |
| (EF01MA06) Construir fatos básicos da adição e utilizá-los em procedimentos de cálculo para resolver problemas. | Construir fatos básicos de adição envolve compreender que eles dizem respeito às relações estabelecidas entre números menores que 10, ou seja, são os resultados das adições de dois números menores que 10. Por exemplo, 5 + 2 = 7 é um fato básico de adição. A construção dos fatos básicos decorre do desenvolvimento de procedimentos para resolver problemas, conhecendo formas diversas de representação, inclusive com a apresentação dos sinais de adição e igualdade, sem exigência de que essa escrita seja a única forma de resolução de problemas aditivos. |
| (EF01MA07) Compor e decompor número de até duas ordens, por meio de diferentes adições, com o suporte de material manipulável, contribuindo para a compreensão de características do sistema de numeração decimal e o desenvolvimento de estratégias de cálculo. | Compor e decompor números de até duas ordens por meio de adições exige conhecer a sequência numérica escrita e falada com números maiores do que 10, bem como compreender que um número pode ser escrito como soma de outros números. Compor e decompor números não significa, ainda, a sistematização de unidades e dezenas pelos alunos, mas, sim, que eles percebam que um número de até dois algarismos pode ser representado por uma escrita aditiva. Por exemplo, são capazes de compreender que 20 pode ser representado como 10 + 10, 15 + 5 ou 5 + 5 + 5 + 5. Essa compreensão permitirá o desenvolvimento de estratégias de cálculo. A habilidade prevê o suporte de materiais manipuláveis. |
| (EF01MA08) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até dois algarismos, com os significados de juntar, acrescentar, separar e retirar, com o suporte de imagens e/ou material manipulável, utilizando estratégias e formas de registro pessoais. | A habilidade supõe resolver e elaborar problemas de adição e subtração com as ideias de: Juntar – quando juntamos um grupo de 3 objetos com outro de 8 objetos, forma-se outro grupo com 11 objetos; acrescentar – há um grupo com 8 objetos e, se a esses acrescentam-se 3 objetos, forma-se um novo grupo com 11 objetos; separar: há um grupo com 11 objetos e dele teremos que separar 8 objetos, ficando dois grupos um com 8 e outro com 3 objetos; retirar– de um grupo de 11 objetos, retiramos 3 objetos e sobra um grupo com 8 objetos. A habilidade envolve conhecimento numérico e elaboração de formas pessoais de registrar a resolução do problema, sem a obrigatoriedade da notação formal. Elaborar problemas se relaciona com a experiência de resolver problemas. A habilidade prevê o suporte de imagens ou materiais manipuláveis. |
Fonte: Elaborado pelas autoras com referência na BNCC.
Analisando-se as habilidades propostas pela BNCC, observa-se que as propostas sugeridas nas Figuras 5 e 6 possibilitam:
perceber e responder às perguntas: Quantos tem? Onde tem mais? Quantos a mais?, conforme a EF01MA01, e identificar qual conjunto tem mais e qual tem menos quantidade, segundo sugerido na EF01MA03;
contar uma quantidade de objetos, avançando do processo de contagem de um em um para um processo de contagem por pareamento ou por agrupamento, conforme solicitado na EF01MA02;
a construção dos fatos básicos, como sugerido na EF01MA06. Na Figura 5, é possível a construção de qualquer fato básico, como exemplificado o caso do 7 = 1 + 6, 7 = 2 + 5, 7 = 3 + 4, 7 = 4 + 3, 7 = 5 + 2, 7 = 6 + 1, além da percepção de que 1, 2, 3, 4, 5 e 6 estão dentro de 7, que o 7 está dentro do 8, do 9 e do 10, além de outras possibilidades desenvolvidas a partir da flexibilidade numérica;
compor e decompor números como previsto na EF01MA07;
juntar, acrescentar, separar e retirar, com o suporte de imagens e/ou material manipulável, utilizando estratégias e formas de registro pessoais, como sugerido na EF01MA08.
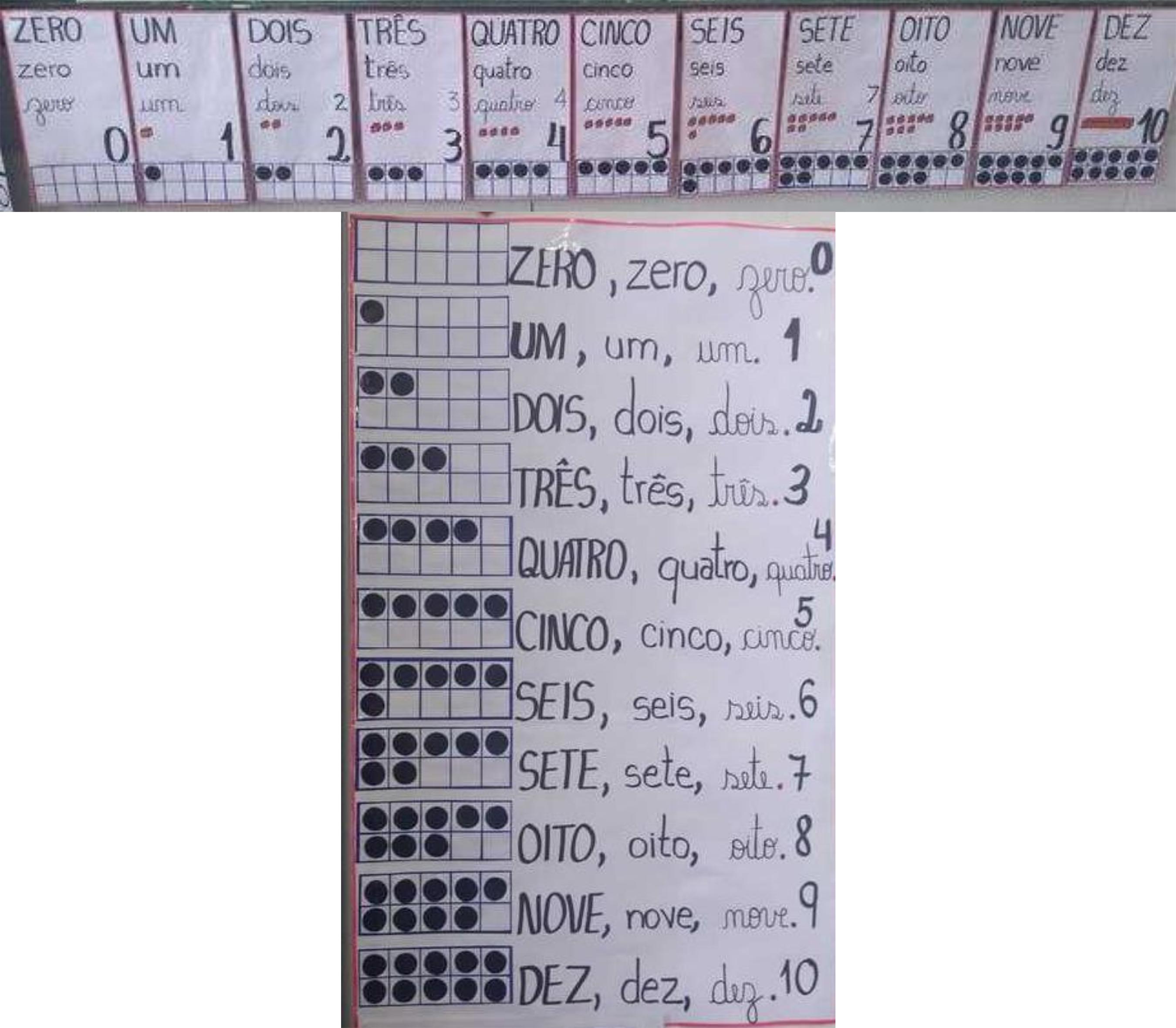
Essa forma de apresentar as relações entre números e quantidades (Figuras 5 e 6) está em concordância com o que está proposto na BNCC e pode fazer parte do ambiente escolar dos estudantes (Figura 7).
Fonte: Elaborado por professora de 1º anodo EF.
Figura 7 Foto da representação de uma sala de aula de 1º ano do EF.
Apenas representar os números e quantidades de uma forma diferente, como estamos propondo, pode se tornar, entretanto, algo vazio se o professor não tiver os conhecimentos necessários para potencializar o material. Nesse sentido, apresentamos uma forma de explorar esse recurso como um material manipulável no momento da construção das relações numéricas.
Denominamos esse material manipulável e sua forma de utilização de “Sense Líquen”, o qual conversa com o material “Ten Frame2”, disponível em forma de aplicativo no Classroom do National Conuncil of Teachers of Mathematics.
4 Sense Líquen: material manipulável do Método Líquen3
Nesta seção, vamos apresentar o Sense Líquen, sua apresentação física e sua forma de utilização e, ao mesmo tempo, fazer um contraponto com a proposta do uso de palitos de madeira ou círculos de EVA. Vejamos os exemplos adiante.
Quando desejamos que um aluno faça a operação 4 + 3 com palitos, pedimos que separe 4 palitos e 3 palitos, como na Figura 8A. Na sequência, solicitamos que ele junte todos e forneça o resultado (Figura 8B). Geralmente ele recomeça a contagem do 1. Ele conta: “1, 2, 3, 4, 5, 6 e 7”, pega um lápis e registra (Figura 8C):
Quando o professor solicita outra adição, por exemplo, 8 + 6, e pede que o aluno faça com os círculos, ele separa 8 bolinhas e 6 bolinhas (Figura 9A) e conta o montante final para encontrar o resultado (Figura 9B), iniciando em um dos montes ou contando todos.
Nessas situações, caso o aluno esqueça quantos palitos ou bolinhas colocou em cada monte, precisará recontar todas, pois a quantidade de palitos ou bolinhas em cada monte, separados ou com todos agrupados, não é visual. A conferência necessita de recontagem. Mesmo sem precisar conferir, ao juntar todas, é necessário recomeçar a contagem: “1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14”.
Para a construção do conceito de dezena, em nossas observações de sala de aula, encontramos a proposta didática de trocar a cor do palito para que este seja uma dezena, ou seja, pegamos 10 palitos, enrolamos com uma borracha e trocamos por outro de outra cor. A criança precisa acreditar que tem 10 palitos amarrados, porque a quantidade não é visível. Com os círculos, também não temos visibilidade.
Em nosso entendimento, não faz sentido termos 10 palitos que são trocados por outro de outra cor para ter uma dezena. Um palito sempre será um palito, nunca 10 palitos. Podemos dizer que as cores valem pontos, como em um jogo de varetas, mas não que ela é “10 palitos”. O número “1” representa uma dezena apenas quando estiver seguido de um único número a sua direita, como em 10, 11, 15, ou de uma unidade de medida, “1 dezena”. Essa analogia de troca por outra cor é muito utilizada em escolas, mas provocamos o questionamento sobre o quanto ela é favorável para a construção do conceito de dezena.
Vejamos agora a apresentação de um material alternativo aos palitos e bolinhas, o Sense Líquen: material manipulável do Método Líquen.
O Sense Líquen é composto por 20 círculos com duas cores, uma cor de cada lado, e uma base. A base é composta por dois conjuntos com 10 bolinhas cada, separadas em duas linhas de 5 bolinhas, conforme ilustrado na Figura 11.
O preenchimento das quantidades de 1 a 10 unidades deve ser feito com os círculos da mesma cor e acontecer da esquerda para a direita, na primeira linha, depois na segunda linha, até completar a primeira caixinha. Depois, passa-se para a primeira linha da segunda caixinha, novamente da esquerda para a direita, e para a segunda linha, sempre da esquerda para a direita. Quando completamos a primeira caixinha, temos uma dezena, e, quando completamos a segunda, temos duas dezenas. Veja a representação das quantidades de 1 a 10 unidades na base do Sense Líquen na Figura 12.
O Sense Líquen também permite que operações de adição até 20 (Figura 6) sejam ilustradas ou calculadas nele. Por exemplo, vamos ilustrar a operação 4 + 3. Colocamos as primeiras 4 bolinhas de uma cor e as 3 de outra cor na sequência (Figura 13):
Observem que, como os alunos já estão familiarizados com as imagens apresentadas na Figura 6, eles conseguem, de forma visual, compreender que 4 + 3 = 7, pois já aprenderam que uma linha completa compreende 5 unidades e, com mais 2 unidades, temos o 7. Para responder que 4 + 3 = 7 a criança utiliza o senso numérico, já que compreende que 4 + 3 = 5 + 2. Ainda, ao visualizar a distribuição das bolinhas, consegue resgatar que está realizando a operação 4 + 3.
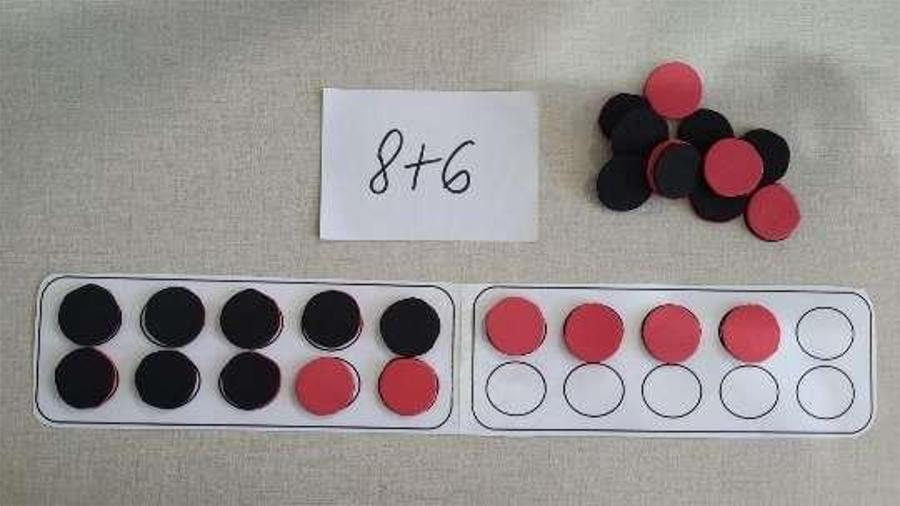
Podemos trabalhar com o mesmo raciocínio para operações que ultrapassam a dezena, como, por exemplo 8 + 6. Colocamos as primeiras 8 bolinhas de uma cor e as 6 de outra cor na sequência (Figura 14):
Da mesma forma que na anterior, os alunos já acostumados com essa representação, sabem que uma caixinha completa representa a dezena e não precisa contar todas as bolinhas novamente. Eles observam a figura e veem que temos uma caixinha completa com 10 unidades e mais 4 unidades na outra caixinha, o que totaliza 14 bolinhas. Novamente, eles conseguiram resolver 8 + 6 utilizando uma expressão equivalente, 10 + 4, sem perder de vista que estavam somando 8 + 6.
Essa distribuição das bolinhas na base torna visível o resultado da soma sem a necessidade de contagem, considerando-se que a criança esteja habituada com esse tipo de distribuição construído anteriormente, como mostrado nas Figuras 5 e 6, numerais e quantidades. A apresentação torna possível identificar e conferir qual a operação que está sendo realizada e seu resultado, sem que se precise de contagem e recontagem. Caso o aluno não esteja habituado com a distribuição e não consiga identificar a quantidade com o olhar, ele vai contar, como nos palitos ou nas bolinhas, ou seja, nenhum aluno será impedido de resolver a operação; entretanto, com a repetição, o treino e o tempo, ele se habituará e memorizará que em uma caixa cheia há 10 unidades, uma dezena, e dispensará a contagem. Desse modo, permitimos a construção de um raciocínio mais elaborado e avançado para os alunos, o que não é possível com palitos ou bolinhas.
O Sense Líquen possibilita a construção da ponte pelo 10 (BERTICELLI; ZANCAN, 2021), uma das estratégias mais utilizadas para resolver operações por meio do cálculo mental e que consiste em decompor um dos números e completar o outro para perfazer uma dezena. Por exemplo, para adicionar 8 + 6 utilizando a ponte pelo 10 fazemos 8 + 2 + 4. Essa estratégia torna-se bastante clara quando utilizamos o Sense Líquen, como se pode observar na Figura 12. Com o Sense Líquen é possível ilustrar que, partindo-se de 8 unidades, precisamos de 2 unidades para completar a dezena e que, como queremos adicionar 6 unidades, ainda restam 4 unidades para serem acrescentadas. Ficamos, assim, com uma dezena, caixa cheia, e 4 unidades, portanto 14.
Essa base com 20 unidades separadas em duas dezenas constrói a compreensão de que duas caixas cheias são duas dezenas, e os alunos conseguem ampliar seu conhecimento quando percebem que, se tiverem 3 caixas completas, terão três dezenas e assim por diante.
Podemos utilizar o Sense Líquen para ilustrar operações de subtração. Nele, em vez de retirarmos as bolinhas, nós as viramos, de modo que apareça a face de outra cor, para que a criança não esqueça o valor total do qual estamos retirando. Por exemplo, na Figura 15, ilustramos a subtração 13 - 5. Na Figura 15A representamos a quantidade de 13 unidades e na Figura 15B viramos (retiramos) as cinco unidades, sempre de trás para frente.
Na figura podemos inferir que, tendo 13 unidades e tirando 5 unidades, as 5 que estão vermelhas na Figura 15B, restam 8, as pretas da Figura 15B. As 8 unidades são visíveis pela distribuição em que aparecem, pois estão destacadas em cor diferente. Podemos construir a ideia de tirar 3, que são as unidades que temos a mais que o 10, a mais que a dezena, e precisamos tirar mais 2, pois queremos tirar 5. Transformando: 13 - 5 em 13 – 3 - 2. Conforme a criança vai abstraindo esse conhecimento, passa a realizar essas operações de cabeça, ou seja, mentalmente, utilizando a estratégia de subtração também denominada ponte pelo 10 (BERTICELLI; ZANCAN, 2021), que é a passagem pela dezena.
Também podemos formar a ideia de completar, deixando as 5 e verificando quantas temos até o 13, lembrando que uma subtração pode ser interpretada como o que falta ao subtraendo para chegar ao minuendo, nesse caso, de 5 até 13, onde pensamos: “de 5 para chegar ao 10 são 5 unidades e de 10 para chegar ao 13 são 3 unidades, ou seja 5 + 3 = 8 (Figura 16):
Com esse material é possível perceber que 13 – 5 = 8; 8 + 5=13; 5 + 8 = 13, além de perceber que do 5 faltam 8 unidade para completar o 13, ou seja, conseguimos trabalhar com os números de forma flexível, valorizando as relações numéricas da adição e subtração.
Até aqui mostramos possibilidades de ilustrar e representar adições e subtrações com, no máximo, 20 unidades com uma base e 20 círculos.
Caso os alunos não tenham a base, o professor pode orientá-los a não colocarem as bolinas de qualquer maneira, mas seguirem a distribuição conhecida das caixinhas, como mostrado na Figura 17.
Com esse estímulo os alunos passam a fazer a distribuição com as bolinhas inclusive em sua mente. Com o tempo, passam a imaginar, por exemplo, quanto falta até o 10 se tenho 8 ou 9. E, assim, unimos o numérico, o visual, as propriedades matemáticas e temos o início do cálculo mental.
Essa organização pode ser escrita no quadro, caso o professor não possua o material manipulável, de forma que todas as crianças possam ver. O professor pode desenhar com duas cores e estimular que os estudantes também desenhem as bolinhas nas caixinhas de 10, em vez de fazerem desenhos de palitinhos, como ilustrado na Figura 18.
Com a repetição, essa forma se torna natural e o desenho dos palitinhos perde a importância, pois a distribuição ordenada nas caixas facilita a visualização.
Na Figura 19, apresentamos quatro abordagens diferentes: aquela que propomos e as três mais utilizadas em salas de aula.
A primeira apresenta a possibilidade de organização e agrupamento, o que facilita encontrar o resultado de forma visual e prática, utilizando o senso numérico e a rede de relações dos números. Nas demais figuras, é necessário contar cada grupo de bolinhas e recontar (B), assim como contar os riscos que foram feitos no papel (C) ou, ainda, contar os palitos (D), primeiro os 8, depois os 5 e, no final, contar novamente, iniciando em 1, 5 ou 8. Ressaltamos que, nas Figuras 19B, C e D, a contagem é a principal ferramenta que a criança possui para chegar ao resultado.
Essa mesma distribuição pode exercitar um pensamento inverso, quando é apresentada para a criança a distribuição conforme a Figura 20 e lhe é solicitado que escreva uma expressão numérica para o que está representado.
Observando a imagem, a criança pode responder que 7 +3 + 2 ou que 7 + 5 são 12, ou uma dezena, caixa cheia, mais duas unidades; ou, ainda ,12 - 5; ou 12 – 2 - 3; ou que do 7, para completar o 12, faltam 5 unidades. Enfim, há uma série de possibilidades que podem ser exploradas nessa imagem, sendo necessário deixar a criança com a mente livre para pensar.
Para aqueles estudantes que têm construídas as operações de adição e subtração, podemos explorar diferentes formas de escrever expressões numéricas que conversem com o Sense Líquen. Por exemplo, na Figura 21, podemos pensar em doze expressões numéricas envolvendo adição e subtração. Observe a imagem e, em seguida, as expressões.
Entendemos a importância de abordar essas outras possibilidades, diferentes de 7 + 5 = 12, pois, em anos posteriores, a álgebra vai exigir essas diferentes abordagens, que podem e devem ser trabalhadas desde cedo.
Esse trabalho manipulável tem sido realizado em escolas, especialmente no 1º ano do EF, momento em que os alunos estão aprendendo a estabelecer essas relações numéricas, e tem mostrado que a Matemática pode ser fácil e compreensível. A Figura 22 ilustra estudantes utilizando o Sense Líquen em sala de aula na resolução de adições.
Observem mais uma vez que a figura permite a construção da rede de relações entre os números de forma visual, sem que o aluno necessite contar um por um para chegar ao resultado, dando início ao processo de resolução por cálculo mental, tão presente e relevante na matemática do cotidiano.
5 Considerações finais
Neste texto apresentamos o Sense Líquen, um material manipulável que oferece uma forma alternativa e padronizada de representar números e quantidades e cujos objetivos são facilitar e potencializar o aprendizado de crianças em fase de alfabetização matemática. O Sense Líquen favorece, além da associação entre número e quantidade, a construção de uma rede de relações numéricas para os números e constrói um bom senso numérico e a flexibilidade com os números, habilidades imprescindíveis para a construção de estratégias de cálculo mental.
Analisamos e comparamos o Sense Líquen com outras propostas comumente utilizadas e percebemos que esse material tem maior potencial em relação à construção de conhecimentos acerca do campo numérico quando em comparação com palitos, por exemplo. O diferencial do Sense Líquen é que ele facilita o processo de ensino e aprendizagem na construção da relação entre números e quantidades, valoriza as relações numéricas, leva os estudantes a perceberem que os números se relacionam, que um está dentro do outro, um contém o outro, e assim sucessivamente. Para nós, é fundamental trabalharmos de forma que a Matemática seja compreensível, que a aritmética tenha significado e que seja prática. Consideramos que esse material favorece essa construção.
Apesar do potencial que percebemos no Sense Líquen, entendemos a importância de o professor ter conhecer o material para ser capaz de explorá-lo, pois este não constrói, isoladamente, o conhecimento. Nosso texto é uma proposta e um convite para que mais professores utilizem o Sense Líquen em sala de aula para a construção dos conceitos básicos de aritmética, imprescindíveis para o desenvolvimento do cálculo mental.