INTRODUÇÃO
Sabemos que a matemática está presente em diversas situações em nosso cotidiano, como em idas às compras, ao prepararmos uma receita, ao analisarmos o consumo em uma conta de energia elétrica. A dificuldade fica nesse aspecto, não se consegue associar os fundamentos propostos pelos livros didáticos em experiências realmente instigantes e interessantes para o aluno.
Existem críticas ao ensino da matemática, pois vem sendo determinado por um ensino mecânico, com ênfase na memorização de fórmulas e regras, que muitas vezes são decoradas pelo aluno, fazendo com que eles se deparem com dificuldades ao longo da vida na escola. Em conformidade com Kamii (1991, p. 54),
uma educação conformista ou escola tradicional não encoraja o pensamento crítico nem o independente. As escolas precisam encorajar a autonomia do princípio, se quiserem, eventualmente, serem bem-sucedidas em ajudar indivíduos a atingirem mais altos níveis de desenvolvimento emocional e cognitivo.
Uma das mais interessantes faces do universo matemático é que tudo possui uma ligação. Aos poucos as relações matemáticas entre conteúdos vão sendo descobertas e devem ser exploradas. Nada no meio matemático está preso a um único caminho, é possível identificarmos mais de uma forma de explorar um saber matemático e este aspecto dever ser um ponto de alicerce para os professores.
Em se tratando do ensino e da construção de uma aprendizagem com sentidos e significado é preciso uma renovação em muitos aspectos. Um desses aspectos é o modo como os objetos matemáticos são trabalhados em sala de aula, muitas vezes restritos à utilização do livro didático e da lousa. Estes recursos são relevantes, mas os objetos matemáticos também podem ser trabalhados por meio de recursos manipuláveis, jogos didáticos, pesquisas, resolução de problemas com ênfase, na medida do possível, em situações do cotidiano.
A iniciativa de discutir sobre aspectos relacionados ao ensino da matemática na Educação Básica, adveio de nossa participação, como residente com bolsa, no subprojeto intitulado "Ensino de matemática no 6º ano do Ensino Fundamental: experiências formativas por meio da Residência Pedagógica" do Instituto de Educação Matemática e Científica que compõe o projeto institucional da Universidade Federal do Pará, aprovado pelo Edital CAPES nº 06/2018, que trata sobre o Programa Residência Pedagógica.
O subprojeto foi direcionado a graduandos do curso de Licenciatura Integrada em Ciências, Matemática e Linguagens para os Anos Iniciais do Ensino Fundamental, da Faculdade de Educação Matemática e Científica e apresenta como um de seus objetivos,
realizar levantamento de informações próprias do cotidiano da sala de aula no se refere as relações entre ensino-aprendizagemavaliação de matemática no 6º ano do Ensino Fundamental com fins de diagnóstico e escolhas em termos didáticos (metodologias, materiais didáticos, instrumentos de avaliação) para a melhoria das aprendizagens e dos processos de ensino (IEMCI/UFPA, 2018).
Na etapa de imersão no Programa tivemos como campo uma escola pública municipal4, em que passamos a frequentar, junto com um docente da Educação Básica, que era professor de matemática e preceptor do mencionado Programa, turmas do 6º ano do Ensino Fundamental e, a partir de então, direcionamos nossas lentes para um olhar sobre as dificuldades matemáticas dos alunos recém chegados dos Anos Iniciais do Ensino Fundamental. Logo no período denominado pelo Programa como ambientação, percebemos dificuldades quanto às quatro operações básicas, frações, múltiplos e divisores, dentre outros. A seleção da escola campo ocorreu antes da submissão do subprojeto ao Edital 06/2018 CAPES e teve como critério a proximidade do campus da UFPA e a abertura à parceria, via direção escolar e professores da Educação Básica, com a universidade.
Diante do observado, optamos por fazer um diagnóstico para identificar as reais dificuldades dos alunos quanto aos múltiplos e aos divisores. Decidimos elaborar um instrumento com questões relacionadas ao assunto e aplicamos junto a alunos do 7º ano. Essa opção pauta-se em identificar lacunas trazidas por eles referente as não aprendizagens. De posse deste diagnóstico, elaboramos um jogo didático e utilizamos com os alunos de uma turma do 6º ano e, ao final, analisamos os resultados.
Nesse sentido, o objetivo deste relato foi perceber em que termos o uso de um jogo matemático de trilha de MMC e MDC pode envolver os alunos na aprendizagem dos conteúdos de múltiplos e divisores?
Este artigo está organizado do seguinte modo: resumo, introdução, múltiplos e dividores, jogos didáticos, metodologia, observações do diagnóstico realizado, confecção e aplicação do jogo, descrição dos resultados, considerações finais e referências.
MÚLTIPLOS E DIVISORES
O consenso de usar o Mínimo Múltiplo Comum (MMC) e Máximo Divisor Comum (MDC) nos Anos Iniciais do Ensino Fundamental, vem do fato de outros conhecimentos matemáticos futuros precisarem do auxílio deste conteúdo para conseguirem ser trabalhados, além de conseguir aumentar os conhecimentos que os alunos possuem sobre a matemática, as relações que os números possuem entre operações, como multiplicação e divisão, bastante trabalhados neste assunto.
Um dos mais antigos relatos é o de Euclides, autor de Elementos, publicação que reúne treze livros. O autor mencionado fez inúmeras proposições sobre Teoria dos Números, Incomensuráveis, Geometria Plana e Geometria Espacial. A ele é atribuída a proposição sobre o Máximo Divisor Comum. No entanto, autores como Milies e Coelho (2001), afirmam que é possível que essa proposição já tenha sido feita antes de Euclides.
De acordo com Pinto (2012), embora desde a antiguidade já seja possível perceber a utilização do conceito de MMC e MDC, apenas no século XVI tal assunto tomou forte repercussão, principalmente devido a Bezout e Fermat.
O Máximo Divisor Comum (MDC) é o maior número que pode dividir vários números ao mesmo tempo. O Mínimo Múltiplo Comum (MMC) é o menor valor que pode ser múltiplo de dois ou mais números. E, mesmo tendo possibilidades para a aplicação, a utilização deste conteúdo é restrita nos Anos Iniciais do Ensino Fundamental.
Silva (2019) exemplifica algumas destas aplicações, em formato de enunciados de problemas. No que se refere ao MDC
Uma indústria de tecidos fabrica retalhos de mesmo comprimento. Após realizarem os cortes necessários, verificou-se que duas peças restantes tinham as seguintes medidas: 156 centímetros e 234 centímetros. O gerente de produção ao ser informado das medidas, deu a ordem para que o funcionário cortasse o pano em partes iguais e de maior comprimento possível. Como ele poderá resolver essa situação?
Devemos encontrar o M.D.C. entre 156 e 234, esse valor corresponderá à medida do comprimento desejado.
Decomposição em fatores primos
234 = 2 * 3 * 3 * 13
156 = 2 * 2 * 3 * 13
M.D.C. (156, 234) = 2 * 3 * 13 = 78
Portanto, os retalhos podem ter 78 cm de comprimento.
Em relação ao MMC, Silva (2019) traz a situação:
(PUC–SP) Numa linha de produção, certo tipo de manutenção é feita na máquina A a cada 3 dias, na máquina B, a cada 4 dias, e na máquina C, a cada 6 dias. Se no dia 2 de dezembro foi feita a manutenção nas três máquinas, após quantos dias as máquinas receberão manutenção no mesmo dia.
Temos que determinar o M.M.C. entre os números 3, 4 e 6.
M.M.C. (3, 4, 6) = 2 * 2 * 3 = 12
Concluímos que após 12 dias, a manutenção será feita nas três máquinas. Portanto, dia 14 de dezembro.
Tendo noção que o MMC e o MDC podem seguir uma linha de trabalho nos Anos Iniciais do Ensino Fundamental de forma lógica, ou seja, atentando para uma sequência de conteúdos que o aluno precisa saber para conseguir trabalhar de forma satisfatória com o conteúdo, que, no caso, é o processo de multiplicação e divisão. A ausência deste tipo de trabalho pode acarretar dificuldades à medida que os alunos avançam aos anos finais do Ensino Fundamental e Ensino Médio.
Em sala de aula no momento da explicação o assunto parece ser muito simples, de fácil compreensão, mas quando o aluno tenta resolver exercícios, não consegue achar um sentido ou uma conexão entre o assunto e os problemas. A não contextualização e aplicabilidade são um dos fatores cruciais para isso acontecer, em alguns problemas, por exemplo, com números muito baixos o aluno nem mesmo usa o MMC ou MDC para resolver, acaba por usar conhecimentos superficiais de matemática para conseguir êxito.
No entanto, quando se depara com uma questão mais complexa que precisa realmente de domínio do que é pedido, não consegue propor estratégia adequada de resolução. Em certas situações o educando confunde até os nomes do que é pedido por não ter compreendido o conteúdo e inverte a forma correta como devem responder o que é pedido.
Nesse sentido, consideramos que o trabalho com os múltiplos e divisores desde os Anos Iniciais do Ensino Fundamental é imprescindível. Para isto, cabe atentar para a adequação do que poderá ser trabalhado, de modo que os alunos compreendam e possam utilizar sem maiores dificuldades em anos escolares futuros.
JOGOS DIDÁTICOS: alguns aspectos pedagógicos
O termo ludicidade originado do latim "ludus", que significa jogo, é muito utilizado na educação infantil. Este conceito abrange brincadeiras e jogos, não sendo restrito a eles. Nesse sentido, a ludicidade pode permitir uma prática de ensino a crianças de forma aproximada ao modo como elas interagem e interpretam o mundo. Ao se optar por trabalho voltado ao lúdico, promove-se uma aprendizagem prazerosa, ao mesmo tempo em que é possível se individualizar as aprendizagens das crianças.
Os jogos pedagógicos, no caso o jogo matemático, torna o processo de ensino e de aprendizagem mais significativo e dinâmico. No entanto, é preciso que o mediador, ou professor, compreenda que esses jogos precisam ter um objetivo pedagógico e que, ao mesmo tempo, a mediação é relevante para que os encaminhamentos de situações levem ao aprendizado.
Almeida (2000) reflete que a educação lúdica só irá ter um sentido e fundamento se o educador estiver preparado para realizá-la, pois de nada adianta colocar em prática uma metodologia diferente se não há conhecimento suficiente dos fundamentos da educação, fundamentos estes com metodologia de fácil compreensão para quem está ensinando, para que consigam desenvolver e seguir adiante no processo de aprendizagem, em realizar as atividades e encarar problemas. Jogos criam embates, ou desafios, que conseguem desenvolver a capacidade para a busca de novas soluções engenhosas e arrojadas.
Os jogos matemáticos vêm com este intuito, funcionar como ferramenta usada como modelo didático estimulante. Os Parâmetros Curriculares Nacionais já traziam discussão acerca da utilização dos jogos no ensino. De acordo com este documento “os jogos constituem uma forma interessante de propor problemas, pois permitem que estes sejam apresentados de modo atrativo e favorecerem a criatividade na elaboração de estratégia de resolução e busca de soluções” (BRASIL, 1998, p. 46).
Conforme a Base Nacional Comum Curricular (BNCC), "a aprendizagem em Matemática está intrinsecamente relacionada à compreensão, ou seja, à apreensão de significados dos objetos matemáticos, sem deixar de lado suas aplicações" (BRASIL, 2018, p. 274). E acrescenta, "(...) recursos didáticos como malhas quadriculadas, ábacos, jogos, livros, vídeos, calculadoras, planilhas eletrônicas e softwares de geometria dinâmica têm um papel essencial para a compreensão e utilização das noções matemáticas" (BRASIL, 2018, p. 274). O jogo, neste sentido, figura como um recurso que fornece os contextos dos problemas e ao mesmo tempo, faz com que o aluno desenvolva estratégias para solucioná-lo.
O lúdico é uma das características que tem destaque ao empregar os jogos como ferramenta educativa. Vygotsky (1991), assevera que o lúdico tem forte influência no processo de aprendizagem da criança, através dele a criança interage, a curiosidade é aguçada e desenvolvida a autoconfiança. A construção da fala e do foco são aspectos fortes.
Tendo ideia de que os jogos vêm como complemento para o ensino de matemática, não somente diversão, dispersão, lúdico pelo lúdico, Grando (2000) evidencia que a disputa presente no jogo matemático tem como uma de suas funções atrair os alunos à dinâmica da temática, à interação de forma natural com o jogo por ser algo mais estimulante que uma estratégia de ensino convencional, contribuindo de forma geral para o desenvolvimento dos alunos como seres humanos. O trabalho com regras e o estímulo à criatividade podem ser considerados pontos fortes para determinar a opção por esta ferramenta para a prática pedagógica.
Nesse sentido, compreende-se que o uso de jogos como ferramenta pedagógica, tem como objetivo estimular: a criatividade, a interação e a discussão de ideias e soluções, o desenvolvimento de autoconfiança; a importância das regras tanto nos jogos como na vida, o estímulo à concentração; a afetividade, a construção de aprendizado e conhecimento realmente significativo.
Segundo Kishimoto (2005, p. 37-38),
A utilização do jogo potencializa a exploração e a construção do conhecimento, por contar com a motivação interna, típica do lúdico, mas o trabalho pedagógico requer oferta de estímulos externos e a influência de parceiros bem como a sistematização de conceitos em outras situações que não o jogo.
Com avanço nas áreas de pesquisa, como as neurociências, os jogos vêm sendo identificados como uma ferramenta que consegue trabalhar o conteúdo ao educando com espontaneidade e leveza. Em conformidade com Morales (2005), a neurociência veio para conseguir esclarecer o funcionamento do sistema nervoso, ajudando os educadores a elaborar novas ideias sobre o ensino. Uma aprendizagem mais efetiva que estimula de diferentes formas o indivíduo, que consegue aproximar o educando do conteúdo e de sua realidade, pois para quem se ensina, só aquilo que desperta seu interesse consegue ficar retido em sua memória. A propensão é que esse modelo didático seja cada vez mais presente no ambiente escolar ou até na graduação.
O jogo pode ser usado como uma ferramenta pedagógica de socialização em sala de aula, pois é um momento em que, dependendo do jogo usado, os alunos precisarão saber trabalhar em equipe, elaborando estratégias, montando planejamento de ações que possam ajudar em futuras jogadas. A utilização de jogos permite, também, trabalhar competências sociais e emocionais, contidas na Base Nacional Comum Curricular - BNCC (BRASIL, 2018), como autoconfiança, autoestima, iniciativa e questionamentos.
Neste contexto, a Teoria das Inteligências Múltiplas vem reforçar o uso dos jogos como uma ferramenta pedagógica eficaz. Essa teoria, desenvolvida pelo psicopedagogo cognitivo e educacional estadunidense Howard Gardner (1998), propõe que as inteligências são potencialmente desenvolvidas se tiverem um espaço adequado para isso, como no processo de ensino aprendizado construído em sala de aula.
Inicialmente as inteligências identificadas por Gardner (1998) foram sete, entre elas está a lógico-matemática, foco deste trabalho. Segundo Gardner (1998) a inteligência lógico-matemática é caracterizada por habilidades relacionadas à interpretação e à categorização dos fatos e de informações no cálculo, no raciocínio lógico e na busca de explicação para tudo. Perante problemas que envolvem raciocínio lógico, quem possui esse tipo de inteligência os resolve de forma metódica e persistente. Dentre as atividades que mais estimulam esse tipo de inteligência, temos os jogos, por suas características estimulantes e interessantes aos olhos do educando.
Os tempos são outros, vivemos na época dos jogos on-line que dominam, dos celulares ao computador, a atenção dos educandos. O tempo gasto no entretenimento passa de forma diferente da vista no mundo real. Quando se está imerso em um mundo virtual, o tempo passa de maneira muito mais rápida, a imaginação passeia por outros lugares, a sensação de realidade se perde com o tempo de imersão no divertimento. Esta linha de raciocínio é ratificada por alguns autores, como González (1987), para quem o jogo é o momento em que um sujeito encontra situações propícias para exercitar seus desejos, suas competências e manifestações de conseguir transformar a realidade, saborear o prazer diante da descoberta do novo e de suas possibilidades de construções inovadoras.
Neto (1992) declara que se for oferecido um ensino significativo e instigante, o que é ensinado acaba por ultrapassar a sala de aula. Entretanto, no cotidiano do educando, imerso em um processo de evolução crescente, muito bem mais interessante do que informações passadas em sala de aula, em que o aluno decora somente para fazer provas, ao serem aplicadas atividades como jogos para os alunos, notamos evidente reação do educando, com receptividade e alegria por conseguir trabalhar com algo que chega perto de sua realidade nos momentos de lazer. O interesse pelo jogo, os desafios e regras envolvem o aluno e o estimulam no processo de aprendizagem.
Esse sentimento em relação aos jogos faz todo sentido quando observamos os jovens imersos nesse mundo fantasioso da diversão, em que uma grande gama de informações e conhecimento é concentrada. Podemos observar a seriedade em boa parte no momento da participação nos jogos, foco, atenção, conversas paralelas são deixadas de lado, os alunos ficam inteiramente envolvidos na atividade. O jogo como ferramenta pedagógica, neste sentido, abrange várias competências, cabendo ao educador sensibilidade para trabalhar com jogos, tendo objetivos pedagógicos estabelecidos e adequados para mobilizar aprendizagens.
METODOLOGIA
Como metodologia para orientar a atividade optamos pela engenharia didática pois seu fundamento é a investigação, sendo baseada na experimentação em sala de aula, adequou-se aos nossos objetivos. Nesse sentido, segundo Artigue (1996), a engenharia didática é uma forma de trabalho didático comparável ao trabalho do engenheiro que, para realizar um projeto, se apoia em conhecimentos científicos da área, e se submete a um controle do tipo científico, que também trabalha objetos mais complexos que os objetos depurados pela ciência.
Almouloud (2007) explica que a engenharia didática, vista como metodologia de pesquisa, é caracterizada, em primeiro lugar, por um esquema experimental com base em realizações didáticas em sala de aula. Caracteriza-se também pelo registro em que se situa e pelos modos de validação que se dá pela comparação entre análise a priori e análise a posteriori.
Esse tipo de engenharia pode ser utilizada em pesquisas que estudam os processos de ensino e aprendizagem de um dado objeto matemático e, em particular, a elaboração de gêneses artificiais para um dado conceito. Nessa metodologia de pesquisa se identificam algumas fases de seu desenvolvimento, na seguinte sequência: (1º) análises prévias; (2º) construção das situações-problema e análises a priori; (3º) aplicação da sequência didática; e (4º) análise a posteriori e validação.
Conforme Pais (2008), nas análises prévias, o objeto de estudo é submetido a uma análise preliminar, através da qual se fazem as devidas inferências, como: levantar constatações empíricas e destacar concepções da realidade sobre a qual a experiência será realizada. Para melhor organizar essa análise, o mesmo autor recomenda proceder a uma descrição das principais dimensões que definem o fenômeno a ser estudado e que se relacionam com o sistema de ensino permeado pelas concepções epistemológica, cognitiva, pedagógica, entre outras.
Com a finalidade de analisar previamente o ensino e aprendizagem de problemas envolvendo os conceitos de múltiplos e divisores de um número natural, realizamos uma pesquisa de campo sobre o processo de ensino aprendizagem da resolução de problemas envolvendo números racionais segundo discentes do 7º ano do ensino fundamental.
A segunda fase da engenharia didática consiste na definição de certo número de variáveis de comando do sistema de ensino que supostamente interferem na constituição do fenômeno, essas devem ser articuladas e devidamente analisadas no transcorrer da sequência didática. Entendemos por sequência didática, certo número de aulas planejadas e analisadas previamente com a finalidade de observar situações de aprendizagem, envolvendo os conceitos previstos na pesquisa didática.
Ou seja, orientada pelas análises prévias, apresentaremos um conjunto de atividades para o ensino de múltiplos e divisores de um número natural que foram desenvolvidas no 6º ano do ensino fundamental da educação básica.
A terceira fase da engenharia didática é uma etapa que garante a proximidade dos resultados práticos com a análise teórica. Essa aplicação se estabelece por aulas denominadas de sessões, tendo em vista o seu caráter específico para a pesquisa, ou seja, não são aulas comuns no sentido da rotina de sala de aula.
Assim, a sequência didática a ser desenvolvida durante a segunda fase da engenharia didática de nosso estudo foi aplicada a uma turma do 6º ano do ensino fundamental de uma escola pública localizada na cidade de Belém do Pará.
A última fase de nossa pesquisa foi a análise a posteriori e validação da sequência didática. Essa fase se apoiará sobre todos os dados colhidos durante a experimentação constante das observações realizadas durante cada sessão de ensino, bem como das produções dos alunos em classe. Finalmente, será da confrontação das análises a priori e a posteriori que validaremos as hipóteses levantadas no início da engenharia.
OBSERVAÇÕES DO DIAGNÓSTICO REALIZADO
Assim sendo, foi elaborado e aplicado um questionário com os alunos do 7º ano do Ensino Fundamental para identificar quais as principais dificuldades que apresentavam em relação ao conteúdo envolvendo múltiplos e divisores (conteúdos esses do 6º ano do Ensino Fundamental).
As questões contidas nesse questionário foram retiradas do livro de matemática Dante (2015) usado na escola no ano de 2018, para turmas do 6º ano. Participaram do momento da aplicação do questionário 19 alunos.
Ressaltamos que as questões, um total de 13, foram reformuladas para que o questionário fosse objetivo, no formato múltipla escolha, com cinco alternativas e somente uma certa.
Com o material pronto, fomos à escola, local em que desenvolvemos a atividade, para que o material fosse aplicado. Explicamos aos alunos qual era o intuito do trabalho e a importância de que todos prestassem atenção no que estava escrito e fizessem sem pressa. Na sequência apresentamos as questões usadas para o teste.
QUADRO 1 Questões da atividade
Fonte: Adaptado de Dante (2015).
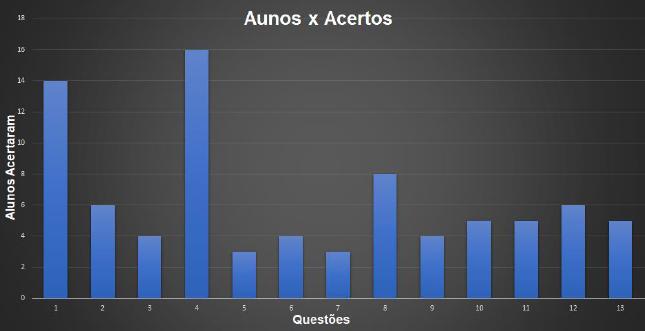
Com as informações do questionário em mãos, organizamos os resultados em tabelas e geramos gráficos. A seguir trazemos o gráfico que disponibiliza a quantidade de acertos por questão.
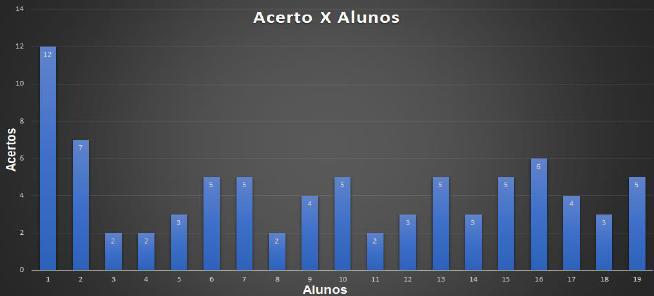
No gráfico a seguir seguem as quantidades de acertos por aluno. Podemos observar que um aluno errou somente uma questão. O desempenho desse aluno foi um comportamento isolado, tendo em consideração que os demais apresentaram quantidade de acertos que variaram entre duas e sete questões.
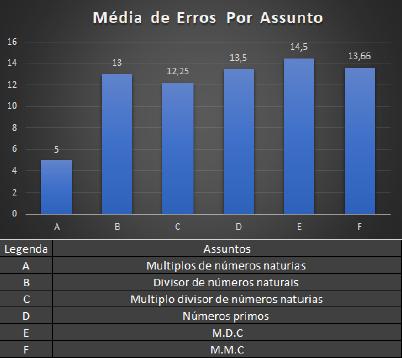
No gráfico a seguir podemos observar a quantidade de erros por assunto. Como o número de questões por assunto foi diferente, optamos por fazer a média das questões do teste. Dentre as que foram identificadas com maior quantidade de erros, identificamos as que exploravam o conteúdo MMC e MDC. A Figura 5 traz a legenda dos conteúdos organizados no gráfico a seguir, que foram identificados por letras.
A partir do desempenho apresentado pelos alunos, optamos pela elaboração do jogo de trilhas contemplando MDC e MMC. O que será descrito a seguir.
CONFECÇÃO E APLICAÇÃO DO JOGO
Antes da efetiva aplicação do jogo, realizamos buscas em livros e em sites da internet, para conhecer como vêm sendo trabalhados os conteúdos MMC e MDC, bem como para visualizar possibilidades em termos de jogos didáticos. Chamou-nos a atenção a proposta do jogo de tabuleiro e do jogo de trilha. Optamos pela elaboração de um jogo que denominamos “Trilha do MMC e MDC”.
O processo de escolha para a montagem do jogo buscou a promoção da interação dos alunos com o conteúdo e entre si. Dentre as muitas possibilidades identificadas, como por exemplo, jogos de treinamento, jogos de construção e outros, optamos pela criação baseada na dinâmica de um jogo de trilhas por considerarmos que era a que mais se aproximava aos objetivos que pretendíamos alcançar, pois este tipo de jogo estimula a interação entre jogadores, tem regras específicas, permite que sejam trabalhados aspectos variados do conteúdo, além de ser um estímulo, tendo em vista que toda a competição, finaliza com um vencedor.
Cada parte do jogo foi pensada para o aprendizado. Assim como os demais jogos, a trilha confeccionada tinha início e fim. As casas contidas na trilha apresentam questões com graus de dificuldades crescente e buscam explorar diferentes possibilidades no que concerne aos múltiplos e aos divisores. A trilha confeccionada consta a seguir.
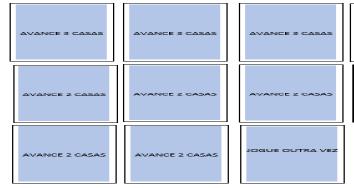
Foram confeccionadas casas especiais que remetem os jogadores à cartas especiais disponibilizadas, com informações conforme as contidas nas figuras a seguir.
Para dinamizar o jogo, consideramos adequada a participação de até seis jogadores e, para determinar o vencedor, convencionou-se atribuir tal feito ao jogador que conseguir chegar primeiro na palavra fim (última casa da trilha).
Para percorrer a trilha, os alunos jogariam um dado e percorreriam a quantidade de casas correspondentes ao numeral obtido a partir do dado. Cada casa dessa trilha contém uma pequena expressão de MMC ou MDC, na qual em uma parte há um número e na outra o jogador colocaria o número de casas que percorreu, formando, então, um problema a ser resolvido. Em cada canto da trilha existem cartas especiais que fazem o jogador, por meio de sorte avançar ou regredir na trilha, inclusive havendo a possibilidade de retornar ao início do jogo. As cartas especiais foram elaboradas no sentido de despertar maior atenção do aluno e tornar o jogo mais interessante.
Após a elaboração do jogo e definição das regras, aplicamos em uma escola municipal, em uma turma do 6° ano do Ensino Fundamental, com 40 alunos, sendo que três desses alunos possuíam Transtorno do Espectro Autista (TEA). A princípio a turma mostrou-se receptiva e curiosa a partir do momento em que visualizaram o material.
Na sequência, organizamos os alunos em grupos e, inicialmente, fizemos perguntas sobre o conteúdo. A seguir, fizemos breve explanação sobre o conteúdo que seria trabalhado por meio do jogo e, após isso, apresentamos o jogo à turma.
Esclarecemos sobre as regras e sobre a maneira correta de manipular as peças. Em cada grupo fizemos a simulação de uma primeira jogada para que não restassem dúvidas sobre como deveriam fazer para pôr em prática o jogo da trilha.
Recomendamos aos alunos que poderiam usar o caderno para o registro das resoluções dos problemas, caso tivessem dificuldade para fazerem o cálculo mental. Apesar do jogo apresentar como um dos objetivos, indicar um vencedor, observamos a colaboração entre os jogadores. Eles se ajudaram na armação dos cálculos, na resolução das expressões matemáticas, interagiram com os alunos autistas, ajudaram-nos, não discriminaram e nem excluíram esses alunos autistas, mas possibilitaram com que interagissem e participassem de todas as etapas do jogo. O jogo foi aplicado no período de uma aula de 45 minutos.
DESCRIÇÃO DE RESULTADOS
No momento do jogo, 29 alunos participaram da dinâmica e foram organizados em seis grupos, sendo 4 grupos com 6 componentes e um grupo com 5. Foram orientados a jogarem um dado para decidir quem deveria iniciar. Para efeitos de análises, serão consideradas interações ocorridas com quatro grupos que serão aqui identificados como grupos A, B, C e D. Na sequência todos os que estavam no grupo jogavam. E assim foram acontecendo a dinâmica do jogo até que um aluno conseguisse chegar ao final da trilha.
Neste item serão destacadas algumas situações identificadas durante a aplicação do jogo, especialmente quando os alunos nos chamavam para esclarecer dúvidas ou para entender as regras, seja do jogo em si, seja do conteúdo trabalhado. Na sequência serão analisados os momentos.
As situações foram selecionadas para enfatizar a interação, a colaboração, a discussão de ideias e a proposição de estratégias para a solução dos desafios encontrados durante o jogo.
Na primeira situação fomos solicitados para informar que não estavam conseguindo fazer cálculos de cabeça. Vejamos:
Situação 1
Grupo A: professor não conseguimos fazer o cálculo de cabeça!
Professor: Entenderam a aula, certo? Podem pegar seus cadernos e resolver nele!
Grupo A: Ok professor, ficamos com medo do senhor pensar que estávamos roubando no jogo.
Professor: O intuito é que vocês consigam aplicar o que foi trabalhado na aula, não tem problema algum usarem o caderno.
Na situação destacada notamos que os alunos estavam receosos de fazer uso do caderno para a resolução das operações que se colocavam. Como tínhamos como objetivo fazer com que os alunos compreendessem o modo para fazer o cálculo, seja do MDC, seja do MMC, permitimos que fizessem o uso do caderno. A interação dos alunos vai ao encontro do que Grando (2004, p.24) evidenciou
Ao analisarmos os atributos e/ou características do jogo que pudessem justificar sua inserção em situações de ensino, evidenciase que este representa uma atividade lúdica, que envolve o desejo e o interesse do jogador pela própria ação do jogo, e mais, envolve a competição e o desafio que motivam o jogador a conhecer seus limites e suas possibilidades de superação de tais limites na busca pela vitória, adquirindo confiança e coragem para se arriscar.
Os registros no caderno podem ser visualizados nas imagens a seguir.
Sobre o processo de resolução dos desafios que se colocaram a partir da interação com o jogo, os alunos foram estimulados a registrarem suas estratégias de resolução. Em conformidade com a BNCC, "no tocante aos cálculos, espera-se que os alunos desenvolvam diferentes estratégias para a obtenção dos resultados, sobretudo por estimativa e cálculo mental, além de algoritmos e uso de calculadoras" (BRASIL, 2018, p. 266).
Analisemos a próxima situação:
Situação 2:
Grupo B: Podemos usar a calculadora do celular pra fazer os cálculos grandes?
Grupo A: Também queremos usar professor!
Professor: Sim podem usar, mas somente quando a conta for com números grandes e vá demorar o cálculo, como no fim do jogo, ok?
Grupo A: Tudo bem professor era isso que pensamos.
Algumas casas do jogo continham cálculos de maior complexidade. Isto principalmente quando se aproximava do final do jogo. O uso da calculadora foi permitido por compreendermos que:
(...) o uso da máquina de calcular pode ser feito de forma proveitosa e prazerosa, principalmente por parte dos alunos. Para os alunos podendo significar uma aula diferente das que aconteciam até então, pois, com já referido anteriormente, eles podem ter mais tempo para dedicar-se ao raciocínio exigido em determinados conteúdos matemáticos, sem precisar restringir-se a aspectos "mecânico" da realização de cálculos (SCHIFFL, 2006, p. 22).
Neste sentido, consideramos que este recurso pode e precisa ser usado em momentos nos quais os alunos já tenham compreendido a lógica da situação e queiram otimizar o tempo.
Vejamos a próxima situação:
Situação 3:
Grupo C: Professor e quando erramos o cálculo, o que vai acontecer? Tem gente aqui que já errou e mesmo assim continua avançando.
Grupo D: Aqui também professor, e continua falando que está certo, fiz meus cálculos aqui e está errado sim!
Professor: Vocês não prestaram atenção na explicação, falei que quem errasse o cálculo deveria continuar na casa até conseguir acertar. Quando notarem que tem alguma coisa errada na resposta me falem que irei ver se está errado ou não, mas vocês devem ser honestos uns com os outros, pois isso não é somente uma brincadeira, estão sendo avaliados.
Nesta situação os alunos estavam em dúvida em relação a uma regra combinada antes do início do jogo, que era o fato de um aluno não conseguir acertar a resolução do cálculo solicitado pela casa do jogo. Conforme combinado, o aluno deveria permanecer na casa até que conseguisse acertar corretamente o cálculo.
Na última situação:
Situação 4:
Grupo C: Professor e quem ganhar do grupo qual a recompensa?
Grupo A: Sim todo jogo temos que conseguir alguma coisa, um incentivo pra gente fessor!
Professor: Bom falarem sobre isso ... os ganhadores de cada grupo irão vir aqui na minha mesa e jogar o jogo comigo, o que conseguir se sair melhor vou premiar com uma caixa de bombom na próxima aula!
Grupo A: Agora sim professor, o senhor vai perder feio pra mim!
Nesta situação notamos o destaque feito pelos alunos em relação à necessidade de uma premiação aos vencedores. Como forma de incentiválos e estimulá-los ao aprendizado, aumentamos o grau de dificuldade e nos colocamos como desafiante, como se estivessem em uma final de torneio. Isto deu um bom movimento. Muitos se sentiram motivados e queriam fazer a disputa final conosco. Tal qual observado por Soppelsa e Fontana (2016), o trabalho com jogos proporcionou aos grupos a troca de conhecimentos e estratégias de pensamento.
Além disso,
O conte do ensinado com o au lio de jogo fara com que o aluno entenda e não esqueça, pois toda brincadeira que aprende através do lúdico, e sempre lembrada. Mas, e importante ressaltar que este deve estar relacionado aos objetivos do ensino, sem desperdícios. Assim, os alunos aprendem de uma forma descontraída, gostosa, onde o aprendizado realmente acontecera sem uma atividade imposta e, o desafios de saber e ganhar o jogo impulsionara a aprender algo com prazer e saber cada vez mais. Neste sentido, os jogos permitem liberdade de ação (SILVEIRA, 2011, p. 20).
Ao final do jogo solicitamos aos alunos que escrevessem sobre a aula. Selecionamos dois destes registros para ilustrar.
O aluno destacou que "a aula foi muito divertida". A utilização de jogos pode contribuir com a dinâmica da aula, fazendo com que os alunos possam aprender de forma divertida. Macedo (2000), destaca que o jogo como um meio de ludicidade consegue incentivar a construção de aptidões que estimulam a racionalidade, a desmistificação do conteúdo matemático e de outras áreas, fazendo com que o educando consiga aprender regras utilizadas em todo processo de aquisição da matéria que antes parecia incompreensível, vemos a importância que a aula em conjunto com o jogo pode transformar a percepção que os alunos tem sobre a matemática.
Outro aluno faz registro semelhante ao anterior e acrescenta que "eu e meus amigos queremos mais aulas assim". Percebemos no registro a seguir, que os alunos gostaram e aprenderam de forma lúdica. E enfatizou ”aprendemos bastante".
CONSIDERAÇÕES FINAIS
O jogo "Trilha do MDC e MMC" foi uma alternativa de intervenção pensada para proporcionar aos alunos uma aprendizagem de conteúdos matemáticos de forma lúdica. Entendemos que a utilização do jogo é relevante ao processo de ensino e aprendizagem em matemática. No entanto, ressaltamos que a opção de se trabalhar com jogos precisa vir atrelada a um "por que", um "para que" e um "como", de modo que não seja o jogo pelo jogo, mas envolto em objetivos pedagógicos.
Com a aplicação do jogo pudemos notar a diferença e importância do lúdico na sala de aula, visualizamos maior interação entre os alunos e o conteúdo e a colaboração entre adversários, evidenciando que, no meio pedagógico, o foco maior precisa ser as aprendizagens dos alunos. Levando em consideração o conteúdo abordado em conjunto com o jogo, um dos aspectos a destacar foi a facilidade com que os alunos passaram a interagir com os conteúdos trabalhados, aspecto esse relevante, pois quando interagem com o mesmo conteúdo apenas a partir de uma lista de exercícios, a motivação é diferente, pois não envolve a ludicidade.
Vimos com clareza a importância de colocar o aluno como coadjuvante em relação ao seu processo de aprendizagem, não como mero espectador. Pudemos concluir que o jogo evidenciou ser um recurso didático adequado para a consolidação de conhecimento, não se opondo a parte teórica e científica, mas tendo a criatividade aliada a um processo estimulante que, certamente, pode conduzir a um aprendizado significativo.
Da experiência, aprendemos que é necessário um olhar para as aprendizagens matemáticas nos Anos Iniciais do Ensino Fundamental que dê conta de proporcionar diversidade de estratégias metodológicas que permitam aos alunos interagirem, gostarem e aprenderem a matemática de forma significativa, para que não avancem aos anos finais com tantas dificuldades.
A imersão na escola e a proximidade com a matemática mostrou que não cabe pautar o ensino desta área do conhecimento apenas na exploração exclusiva do livro didático. O aluno precisa: envolver-se com pesquisa, interagir com tarefas com características investigativo-exploratória, aprender com e a partir do uso de jogos didáticos, manusear materiais manipuláveis, dentre outras possibilidades, de modo que os conteúdos de matemáticas possam ser verdadeiramente compreendidos.
A experiência mostrou-nos também a necessidade de realização de outros estudos que possam aprofundar, sobretudo os aspectos do objeto de conhecimento matemático trabalhado, e nos aproximar do que tem sido feito em termos de pesquisa acadêmica para tratar de temas tais como a divisibilidade.