1 INTRODUÇÃO
As avaliações sistêmicas, a Prova Brasil e o Sistema de Avaliação da Educação Básica (SAEB) informam sobre rendimento escolar, indicando se os objetivos de aprendizagem estão sendo atingidos, apontando, naturalmente, para a necessidade de intervenção. Contidos no Índice de Desenvolvimento da Educação Básica (IDEB), servem como indicadores da qualidade da Educação Básica no Brasil.
Se, por um lado, o país segue melhorando seu desempenho nos anos iniciais do Ensino Fundamental, alcançando em 2019, um índice igual a 5,9 (INEP, 2019), por outro lado, as séries finais do Ensino Fundamental não atingiram a média esperada (INEP, 2019). Para o Ensino Médio, o IDEB aumentou 0,4, em 2019. O que indica, em linhas gerais: “Apesar do crescimento observado, o País ainda está distante da meta projetada” (INEP, 2019, p. 68). À medida que as séries avançam, espera-se que o aproveitamento e o desempenho sejam melhores, e não o contrário, como vem sendo demonstrado. Há quem justifique o desempenho frágil com base no precário investimento do governo. Segundo Fernandes (2017), no Brasil, gasta-se, por estudante do primeiro ciclo do Ensino Fundamental, menos da metade da quantia média investida, por ano, pelos países da Organização para a Cooperação e Desenvolvimento Econômico (OCDE).
Em contrapartida, há iniciativas que promovem e estimulam o aprendizado de Matemática, dentre elas: o Prêmio Professores do Brasil, do Ministério da Educação; o Prêmio Respostas para o Amanhã, uma iniciativa da Samsung; e as Olimpíadas Brasileiras de Matemática das Escolas Públicas (OBMEP). Ainda que tais iniciativas sejam relevantes, entende-se que são insuficientes para sanar os precários cenários de (não) aprendizagem de Matemática. O Programa Internacional de Avaliação de Estudantes (PISA), criado pela OCDE, promove uma avaliação educacional em grande escala (OCDE, 2010), estando o Brasil abaixo de Portugal em índices como equidade educacional ou na escala de Matemática. Analisando-se os países Brasil e Portugal, entre os períodos de 2006 a 2015 (OCDE, 2018), verifica-se melhor situação de Portugal em relação ao Brasil no desempenho geral. Em Matemática, Portugal atinge melhores índices, apontando melhoria contínua.
Procurando entender as relações que os números e sua representação abrangem, bem como considerando os baixos indicadores de aproveitamento escolar, foi realizada uma pesquisa de doutorado. Especificamente para este trabalho, também a partir de dados coletados do Brasil e de Portugal, formulou-se a seguinte questão: o que as avaliações diagnósticas realizadas com alunos do Brasil e de Portugal apontam? Ao responder à tal pergunta, esperava-se identificar as lacunas e eventuais discrepâncias nos sistemas educacionais desses países.
Esta pesquisa se justificou por abordar o baixo rendimento apresentado pelos estudantes nos indicadores de qualidade educacional, chegando ao terceiro grau com pouco domínio dos conceitos básicos de matemática; e a precária formação docente, em um cenário de desvalorização e desprestígio do professor. Além disso, sua relevância está em focar a necessidade de apurar e entender a forma como vem sendo trabalhado, desde as séries iniciais, um campo específico da Matemática, o SND, e as possíveis lacunas nesse processo. Sua realização procurou contribuir com a melhoria na Educação Matemática, pois se propôs a analisar relações de ensino e aprendizagem dentro de sala de aula, reveladas pelas respostas obtidas na avaliação diagnóstica. A coleta de dados, no Brasil e em Portugal, enriqueceu o processo em virtude das diferentes realidades de cada país, estabelecendo novos parâmetros de acertos e visões acerca dos erros.
A pesquisa, realizada com diferentes séries do Ensino Fundamental, partia da hipótese: na medida em que as séries avançam, o que permanece nos conteúdos matemáticos são os desdobramentos do Sistema de Numeração Decimal (SND). A partir do início dos estudos de álgebra, o trabalho sistemático com o SND vai ficando para trás, havendo poucas (ou não havendo) conexões entre os temas da série com elementos e princípios do SND.
A avaliação diagnóstica teve por objetivo “mapear” os conhecimentos matemáticos referentes ao SND, de forma direta ou indireta. Para tanto, após sua elaboração com base nos Parâmetros Curriculares Nacionais (PCN) e em livros didáticos, houve um processo de validação com a participação de professoras de diferentes séries e estados brasileiros. A aplicação da avaliação diagnóstica foi combinada previamente com as professoras e não houve aviso prévio aos estudantes. Foi explicado que a atividade fazia parte de um processo de investigação e que não seria computada na avaliação da escola.
Para se chegar a uma avaliação diagnóstica que pudesse ser aplicada nos dois países e trouxesse elementos significativos à pesquisa, foi necessário traçar um plano de ação e a aplicação de um “piloto”.
Há um paralelo entre os passos que Fernandes (2006) sistematizou em diferentes etapas o que se pretendia elaborar como avaliação diagnóstica. As etapas caracterizadas por Fernandes (2006) são: “clarificar, integrar, definir e reflectir”. Para a fase de clarificação, foram realizados estudos preliminares que consistiram na discussão com professoras atuantes no Ensino Fundamental. A pesquisadora precisou desenvolver um olhar diferenciado, um aprendizado em torno do Ensino Fundamental, uma vez que sua experiência se limitava à Educação Superior. A etapa clarificar, segundo Fernandes (2006), consiste em se valer de diferentes referenciais teóricos com o objetivo de caracterizar e integrar algumas das contribuições, as experiências e as elaborações. Com os questionamentos obtidos na aplicação da 1ª versão da avaliação diagnóstica, voltou-se o olhar para as fontes teóricas, como livros de Educação Infantil e do Ensino Fundamental, que contribuíssem para esclarecer a estrutura e o conteúdo da avaliação.
O processo definido como integrar consistiu, além de buscar em diferentes referenciais teóricos, caracterizar e integrar algumas das contribuições recebidas pelas professoras.
Na etapa definir, o processo de validação serviu para que fossem revistos e refeitos alguns tópicos. As principais alterações consistiram em diminuir o número de questões, aumentar o tamanho da fonte, utilizar caixa alta, acrescentar mais desenhos, fazer poucas perguntas em uma mesma questão e evitar a indução de respostas. Concluídas as alterações, seguiu-se para a última etapa, que se pode considerar como um processo de maturação das etapas anteriores, pois é a fase da reflexão/teorização.
Na teorização/reflexão, ocorreu a reflexão e a consequente concordância com a maioria das sugestões das professoras, com o objetivo de melhorar o instrumento de avaliação. O processo de elaboração da avaliação diagnóstica se deu a partir de várias indagações e dúvidas em diferentes etapas ao longo de sua construção. Ressalta-se que tal experiência em muito contribuiu para as demais etapas da pesquisa, pois evidenciou a necessidade de atenção aos detalhes em relação à clareza e à objetividade.
Apresenta-se, aqui, de forma mais específica, a avaliação diagnóstica, procedimento fundamental para a condução da prática docente. O processo de elaboração, validação, aplicação, correção, e conclusão trouxe elementos ricos e importantes para a visão sistêmica sobre a aprendizagem do SND.
2 A FUNÇÃO DIAGNÓSTICA DA AVALIAÇÃO
Luckesi (1997, p. 69) define avaliação “como um juízo de qualidade sobre dados relevantes, tendo em vista uma tomada de decisão”, e juízo de qualidade se refere à “qualidade do objeto que está sendo ajuizado”. Os dados relevantes dizem respeito ao referencial, aos aspectos da realidade nos quais se manifestam as propriedades “físicas” da aprendizagem. Quanto à “tomada de decisão”, está relacionada à ação posterior à ciência de que o sujeito aprendeu ou não.
Desprebitéris (2001) salienta que avaliar é confundido com medir e, logo, associa-se avaliação à nota. A atribuição desta em um instrumento de avaliação, muitas vezes desprovido de critérios, tem um caráter eliminatório e excludente. No aspecto operacional, avaliação e planejamento, segundo a autora, não podem nem devem se dissociar. Nesse sentido, a autora elucida a abrangência da avaliação: mais que atribuição de nota para o desempenho dos estudantes, precisa interconectar os diferentes componentes em um processo educativo.
Para Perrenoud (1999), a avaliação - que é muito diferente dos instrumentos avaliativos - vislumbrada como ideal é chamada de avaliação formativa. Nesse contexto, ela está longe de ser estática, pois precisa ser contínua, ao longo do processo e, mais importante, servindo para retroalimentá-lo. Para o autor, “é formativa toda avaliação que ajuda o aluno a aprender a se desenvolver, ou melhor, que participa da regulação das aprendizagens e do desenvolvimento no sentido de um projeto educativo” (PERRENOUD, 1999, p. 103). Nessa perspectiva, a avaliação diagnóstica serve para antecipar ações educativas, de maneira a intervir nos processos de aprendizagem. Pondera-se que cabe ao professor a plena consciência da forma não linear como se comportam os caminhos que levam à aprendizagem, com tentativas e erros, idas, vindas e recomeços.
3 OS NÚMEROS: EVOLUÇÃO E IMPORTÂNCIA
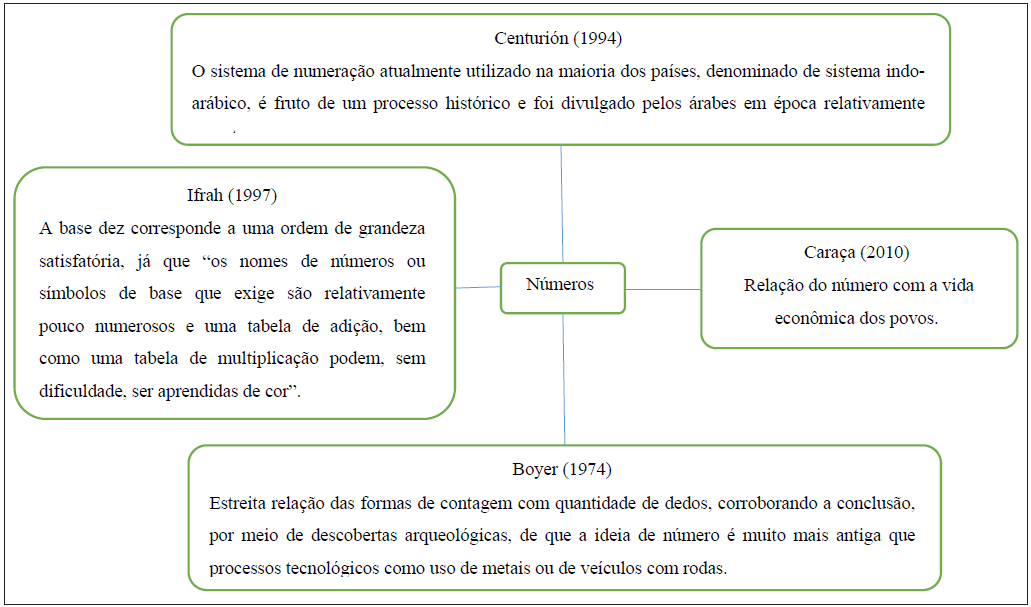
A evolução histórica dos números ocorreu em consonância com a necessidade dos povos de ordenar e contar. A Figura 1 permite visualizar diferentes autores e suas contribuições acerca dos números, seus aspectos importantes e fatores que influenciaram seu desenvolvimento.
O Sistema de Numeração Decimal é aquele cuja base é a mais difundida da História, e sua adoção hoje é quase universal, embora existam outras: sexagesimal, binária, base vinte, base trinta ou qualquer outra base que se queira representar. A ideia do sistema de numeração posicional é a variação do valor numérico dos dígitos do algarismo de acordo com a posição na composição do algarismo.
Mais especificamente, em relação ao sentido do número, Castro e Rodrigues (2008, p. 11) observam que está associado ao “intuito de compreender os números e as suas relações e desenvolver estratégias úteis e eficazes para cada um os utilizar no seu dia a dia, na sua vida profissional ou enquanto cidadão ativo”. A aproximação entre a compreensão do sentido de número e a realidade é feita por crianças e adultos. Com algum entendimento sobre o sentido dos números, qualquer pessoa é capaz de perceber as relações numéricas e seus vários significados, sentindo-se apto a interpretá-lo num determinado contexto, de modo a fazer sentido. Tal capacidade lhe fornece subsídios para interpretar dados numéricos e tomar decisões a partir deles.
É sensato considerar os fatores evolutivos de um povo atrelados à criação de sistemas de contagem de objetos e da geometria e ao uso dos recursos naturais. Nessa linha de pensamento, Caraça (2010, p. 9) afirma que “a extensão do seu conhecimento depende do grau de civilização e da intensidade da vida social do homem”.
4 O SENTIDO DO NÚMERO
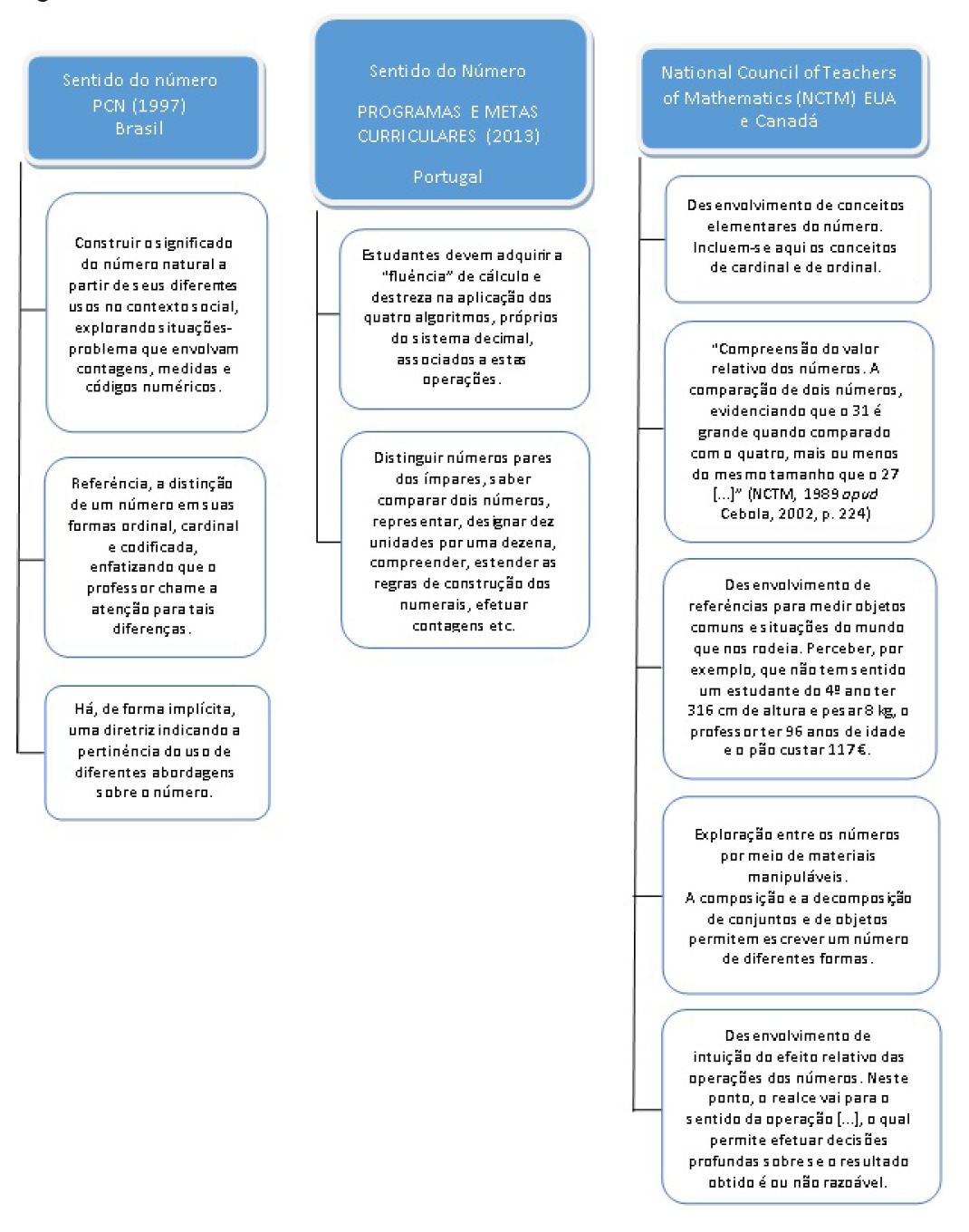
Buscou-se, nos PCNs (BRASIL, 1998), identificar a existência de alguma referência ao sentido do número, salientando-se que o termo significado (conceito) do número é menos abrangente que o sentido do número, pois, conforme Cebola (2002, p. 224),
Referir o número apenas pelas suas definições elementares é demasiado limitativo quando, sob o ponto de vista da educação matemática, pretendemos realçar quer o seu carácter utilitário no mundo actual e na vida do cidadão comum, quer o seu carácter uniforme e global.
Nessa linha de pensamento, há, de forma implícita, uma diretriz indicando a pertinência do uso de diferentes abordagens sobre o número.
Em Portugal, o documento “Programas e Metas Curriculares” para o ensino básico (PORTUGAL, 2013) foi a referência para a busca do uso do termo sentido do número. Não está explícito, assim como também nos PCNs, o termo sentido do número, mas termos correlatos, como fluência de cálculo e destreza4. Encontram-se, no documento de Portugal, termos relativos ao entendimento do número, do SND, como o “sentido de número”, a compreensão dos números e das operações e a capacidade de cálculo mental e escrito.
A Figura 2 apresenta diferentes nomenclaturas e definições relacionadas ao sentido do número em documentos e diretrizes pedagógicas:
Se nos documentos a aprendizagem do sentido de número parece simples, na sala de aula, sabe-se que, de fato, é mais complexa. Referindo-se à aprendizagem da criança, Vergnaud (2009) afirma que o trabalho da inteligência leva a deduções (ou inferências) e a construções. Tais deduções se apresentam de duas maneiras: “deduzir uma conduta ou uma regra de conduta de relações constatadas ou aceitas e deduzir novas relações a partir das relações constatadas e aceitas” (VERGNAUD, 2009, p. 35). Isso sugere que há uma sequência na construção de uma estrutura mental, que permite o encadeamento de deduções: essa sequência é denominada de transitividade.
O pensamento de Dienes (1975) e de Vergnaud (2011) sobre como ocorre a aprendizagem pode ser representado pela “metáfora” do caminho a ser percorrido, assim,
[...] os caminhos que a aprendizagem percorre parece tomar o curso de um mergulho numa massa de fenômenos aparentemente desconexos e formular as propriedades de diferentes tipos de ambientes em termos de certas regras pela inferência com estes fenômenos e pela aquisição da percepção de como induzir o acontecimento de certos fenômenos desejados. (DIENES, 1975, p. 21).
Ambos se valem da concepção de que as crianças, como qualquer sujeito, são capazes de regular sua conduta sobre as relações de estabelecer padrões, regularidades sobre o cálculo relacional que fazem.
A respeito do SND, Lerner e Sadovsky (1996) investigaram a compreensão da numeração escrita por meio de entrevistas clínicas com crianças. As pesquisadoras observaram que a necessidade de estabelecer regularidades no SND é uma premissa básica para a compreensão das regras que compõem e regem o sistema; assim sendo, as próprias crianças elaboram estratégias que se ligam diretamente aos preceitos, regras e organização do sistema. Segundo as autoras, “a avidez das crianças por desvendar os mistérios que envolvem o sistema de numeração faz deste um objeto digno de ser considerado em si mesmo” (LERNER; SADOVSKY, 1996, p. 122).
O processo de ensino e aprendizagem do SND está diretamente relacionado às práticas pedagógicas ou, melhor dizendo, à maneira como o professor faz chegar o conhecimento ao estudante.
5 METODOLOGIA E PARTICIPANTES DA PESQUISA
No Brasil (em Sorocaba) e em Portugal, a escolha das escolas participantes da pesquisa deu-se por acessibilidade. Aqui, a disponibilidade da equipe que aceitou o convite feito pela Secretaria Municipal de Educação, ao passo que lá, a escolha se deu pelos contatos do professor orientador do estágio avançado na Universidade do Minho, com as professoras de escolas de um mesmo bairro.
A pesquisa foi realizada em duas escolas no Brasil e duas escolas em Portugal - quantidade considerada satisfatória para o que se propunha investigar. No Brasil, a escola A, com 24 estudantes, no 5º ano; e a escola B, com 27 estudantes no 9º ano - e suas respectivas professoras.
No Quadro 1, estão especificadas as salas e séries em que foram aplicadas as avaliações diagnósticas no Brasil e em Portugal.
6 AS AVALIAÇÕES DIAGNÓSTICAS
Para a elaboração da avaliação diagnóstica das séries definidas (5º e 9º anos no Brasil), a fase inicial foi a escolha dos conteúdos e dos tipos de questões. Com base nos PCNs e em posse de livros didáticos da série, iniciou-se a elaboração, de acordo com o grau de dificuldade baixo, médio e alto.
A aplicação da avaliação, na fase piloto, ocorreu em uma escola particular de uma cidade próxima a Sorocaba e em uma escola municipal, em Santa Catarina. A aplicação das avaliações transcorreu como se esperava, com uma mescla de curiosidade e insegurança, até que, aos poucos, os estudantes foram se envolvendo e realizando a atividade até o final. Após a realização, os estudantes discutiram entre si sobre os acertos, resultados, dúvidas, demonstrando que o instrumento de avaliação utilizado (teste escrito) desencadeia reações diversas, como a aparente insatisfação de não ter conseguido acertar (tendo a resposta do colega como referência) e a demonstração de alegria por sua resposta ter coincidido com as de vários colegas da classe.
7 DESCRITORES E AVALIAÇÃO DIAGNÓSTICA 5º AB
Nas avaliações, a partir dos erros apresentados, procurou-se por elementos que chamassem atenção, baseados em alguns descritores oriundos do SAEB e da Prova Brasil. Os descritores foram utilizados como parâmetros por servirem de diretriz aos programas nacionais do INEP, com o objetivo de avaliar os estudantes nas áreas de Língua Portuguesa e Matemática. Os resultados das avaliações foram devolvidos aos professores do Brasil e de Portugal para que conhecessem, ampliassem e aprofundassem as habilidades de seus estudantes. Para a 5º ano, escolheram-se quatro (num total de treze) descritores, dois considerados mais simples e dois mais complexos, listados no Quadro 2:
Quadro 2 Descritores: Números e Operações 5º ano
| Descritores (D) | 5º ano |
|---|---|
| Reconhecer e utilizar características do SND, tais como agrupamentos e trocas na base 10 e princípio do valor posicional. | D13 |
| Identificar a localização de números naturais na reta numérica. | D14 |
| Identificar fração como representação que pode estar associada a diferentes significados. | D24 |
| Resolver problema com números racionais expressos na forma decimal, envolvendo diferentes significados da adição ou subtração. | D25 |
Fonte: Elaborado pelas autoras.
Buscou-se, nas avaliações diagnósticas, elementos referentes às resoluções e estratégias de cálculo utilizadas pelos estudantes. O critério para o resultado ser considerado satisfatório foi 70% de acertos do número total de estudantes. Como exemplo, a turma do 5º ano tem 28 estudantes, 70% deles correspondem a 19,6, ou seja, 19. Dessa maneira, acertos acima de 20 foram considerados satisfatórios ou domínio aceitável do tema. Os apontamentos foram organizados no Quadro 35.
Quadro 3 Avaliação diagnóstica 5º ano
| Questão/Tema/Descritores | Número de acertos | Falta dominar |
|---|---|---|
| 1- Coleta e Interpretação de dados, comparação de números, soma e subtração. (D13), (D17), (D19). | Interpretação de dados: 23. Relacionar diferença com subtração: 21. Relação parte/todo - realizar a diferença: 18. Identificar uma dezena e comparar: 21. | Relação de equilíbrio entre a compreensão de conceito e a competência de cálculo (destreza). |
| 2- Fração nas suas diferentes representações. (D21), (D24) | Equivalência de frações: 20. Classe de equivalência e simplificação: 7. Comparação de frações: 7. Representar fração: 7. | Parte/todo, representação fracionária, equivalência e comparação de frações |
| 5- Porcentagens. Interpretação de dados em uma tabela. (D26). | Interpretação de dados de uma tabela; obter a porcentagem: 1 acerto. Obter o total de porcentagem de um determinado valor: nenhum. |
Conceito de porcentagem. A relação na qual um número na forma percentual é uma fração com denominador 100. |
| 7- Estratégias de resolução de problemas. (D20). | Raciocínio lógico sobre as possíveis posições dos pedaços de madeira: 24. Depois de colocadas as madeiras, em cada encontro entre as madeiras, pregar um prego: oito. | Situações de uso do raciocínio lógico. O uso do cálculo de combinações diferentes em um mesmo problema. |
Fonte: Elaborado pelas autoras.
Como é possível observar nos quadros apresentados, os estudantes apresentaram dificuldades em: leitura e escrita numérica, a priorização da multiplicação em relação à adição; estratégias de cálculo, como interpretação e posterior cálculo em relação aos problemas propostos (a contar pelos cálculos apresentados, vê-se que houve equívocos na interpretação e na comparação de números e na relação parte/todo (em uma parcela da subtração ou em partes de uma fração), sendo que as frações revelaram o menor número de acertos.
8 DESCRITORES E AVALIAÇÃO DIAGNÓSTICA 9º AB
No 9º ano, os descritores da Prova Brasil também serviram de parâmetro. Diferentemente do 5º ano, eles se diferenciam, pois foram introduzidos novos descritores, que são: Números e Operações/Álgebra e Funções (D16 a D35).
Estão apresentados, no Quadro 4, os descritores mais relacionados aos números, escolheram-se quatro (de um total de 14) referentes a números inteiros, frações e equações.
Quadro 4 Descritores para o 9º ano
| Descritores (D) | 9º ano |
|---|---|
| Efetuar cálculos com números inteiros, envolvendo as operações (adição, subtração, multiplicação, divisão, potenciação). | D18 |
| Identificar fração como representação que pode estar associada a diferentes significados. | D22 |
| Resolver problema que envolva equação do 2º grau. | D31 |
| Identificar um sistema de equações do 1º grau que expressa um problema. | D34 |
Fonte: elaborado pelas autoras.
Em relação ao critério para o resultado ser considerado satisfatório, sendo 70% do total com 26 estudantes, ou seja, 18,2 estudantes, trabalhando-se com um valor inteiro, têm-se 19 estudantes (ou acertos).
A partir dos dados apresentados no Quadro 5, alguns aspectos podem ser observados em relação aos erros apresentados: má interpretação das questões, questões deixadas em branco, não conseguiram resolver um sistema linear, operações com número racionais sem o entendimento da relação parte/todo, equivalência de frações.
Quadro 5 Avaliação Diagnóstica 9º ano
| Questão/Tema Descritores | Acertos | Falta dominar |
|---|---|---|
| 3- Raciocínio lógico; equação incompleta de segundo grau. | Acerto total: nenhum aluno. Acertos parciais: 12. Erros totais (ou em branco): 14. |
Passagem da linguagem coloquial para a linguagem matemática. |
| 4- Interpretação de texto; sistemas de equações lineares. | Interpretação: 13. Resolver o sistema de equações: 4. Erros totais (em branco): 9. |
Interpretação de texto. Resolução de sistema de equações lineares. |
| 6- Sistema de numeração decimal. | Acertos totais: 24. Erros totais (ou em branco): 4. | Classes e ordens representativas do SND. |
| 8- Reta numerada. Relação de ordem nos números reais. | Acertos totais: 19. Erros totais: (ou em branco): 7. | Localizar números inteiros na reta numerada. Ordem crescente da reta. |
| 11- Conjuntos Numéricos: relação de inclusão. | Acerto total: 1. Acertos parciais: 10. Erros totais (ou em branco): 15. |
Conjuntos numéricos. Relação de inclusão. |
Fonte: Elaborado pelas autoras.
Dos descritores D21 ao D28, são abordados os números racionais, como também se encontram nos PCNs: “Os estudos dos números racionais, nas suas representações fracionária e decimal, merecem especial atenção no terceiro ciclo, partindo da exploração de seus significados, tais como: a relação parte/todo, quociente, razão e operador” (BRASIL, 1998, p. 66, grifo nosso). De uma maneira geral, o conceito de número racional, na representação fracionária, não está completamente dominado no 5º ano, vindo a aparecer novamente no 9º ano, como não totalmente aprendido.
Para as séries finais, o que precisaria ficar retido dos aspectos principais do SND são suas regularidades, para alicerçar conhecimentos futuros. O domínio das regras e dos algoritmos trabalhados nas séries anteriores poderá determinar o maior ou menor entendimento dos temas das séries seguintes, por uma vida inteira.
As avaliações diagnósticas não apresentaram discrepâncias significativas, uma vez que a quantidade de erros (em termos percentuais) foi parecida. Em números, no 9º ano, diferentemente do 5º ano, os estudantes deixaram muitas questões em branco, não se dando ao trabalho de responder, o que remete ao questionamento: não sabiam resolver ou não se envolveram a ponto de esboçar algum raciocínio em torno do que era solicitado? Desconheciam o assunto requerido ou faltou comprometimento com o instrumento avaliativo? Tal diferença suscita pensar sobre o que acontece com esse estudante que, com o passar dos anos, vem perdendo o entusiasmo, o comprometimento com as questões propostas. A motivação diminui? Ou os interesses mudam de foco?
9 DESCRITORES DAS APRENDIZAGENS ESSENCIAIS - PORTUGAL: 4º AP
Em posse do material coletado nas avaliações de 18 estudantes, a partir dos erros apresentados, procurou-se por elementos que chamassem atenção, baseados em alguns descritores oriundos das Aprendizagens Essenciais (AE)6.
Para o 4º ano do 1º Ciclo do Ensino Básico, foram selecionadas as AE referentes aos Números e às Operações que são apresentados no Quadro 67:
Quadro 6 Aprendizagens Essenciais: números e operações: 4º ano
| AE: Objetivos essenciais de aprendizagem | Perfil do Aluno (PA) |
|---|---|
| Ler e representar números no sistema de numeração decimal até o milhão, identificar o valor posicional de um algarismo e relacionar os valores das diferentes ordens e classes. | Conhecedor/Sabedor/Culto/Informado |
| Comparar e ordenar números naturais, realizar estimativas do resultado de operações e avaliar a sua razoabilidade. | Criativo |
| Reconhecer relações numéricas e propriedades das operações e utilizá-las em situações de cálculo. | Crítico/Analítico |
| Reconhecer e memorizar fatos básicos da multiplicação e da divisão. | Indagador/Investigador |
| Calcular com números racionais não negativos na representação decimal, recorrendo ao cálculo mental e a algoritmos. | Respeitador da diferença do outro |
| Representar números racionais não negativos na forma de fração, decimal e percentagem, estabelecer relações entre as diferentes representações e utilizá-los em diferentes contextos, matemáticos e não matemáticos. | Sistematizador/ Organizador |
| Conceber e aplicar estratégias na resolução de problemas com números racionais não negativos, em contextos matemáticos e não matemáticos, e avaliar a plausibilidade dos resultados. | Questionador/ Comunicador/ Autoavaliador |
| Reconhecer regularidades em sequências e em tabelas numéricas; formular e testar conjeturas. | Participativo/colaborador/ Responsável/autônomo |
Fonte: elaborado pelas autoras.
As AE estão elencadas juntamente a objetivos/descritores atitudinais que se quer obter, considerando a maturidade cognitiva e social de cada série. A partir desses parâmetros, a análise se direciona para as avaliações diagnósticas, focando-se os erros apresentados.
Usou-se o mesmo critério do Brasil, considerados 70% do total, um índice satisfatório de aproveitamento. Sendo assim, na avaliação diagnóstica, com 18 estudantes, o número de acertos acima de 13 foi considerado satisfatório.
Para efeito de organização e melhor visualização, os apontamentos foram organizados no Quadro 7.
Quadro 7 Avaliação diagnóstica: 4º ano
| Questão/Tema | Acertos | Falta dominar |
|---|---|---|
| 2- Fração nas suas diferentes representações | Equivalência de frações: 15. Classe de equivalência e simplificação: 18. Comparação de frações: 12. Representar fração: 10. | Relação parte/todo, representação fracionária, equivalência e comparação de frações. |
| 3- Interpretação de texto, adição. Uso do conectivo “e” como agrupamento de parcelas | Interpretação de texto; transcrição direta: 15. Entender a prioridade de antes multiplicar para depois somar: 12. Somar as quantidades: 12. | Interpretação do problema (texto); hierarquia das operações. |
| 5- Porcentagens. Interpretação de dados em uma tabela | Interpretação de dados de uma tabela; obter a porcentagem: 2. Obter o total de porcentagem de um determinado valor: nenhum acerto. Obter o total de porcentagem e somar os resultados: nenhum acerto. | Conceito de porcentagem. A relação na qual um número na forma percentual é uma fração com denominador 100. |
| 7- Estratégias de resolução de problemas | Raciocínio lógico sobre as possíveis posições dos pedaços de madeira: 10. Depois de colocadas as madeiras, em cada encontro entre as madeiras, pregar um prego: oito. | Situações de uso do raciocínio lógico. O uso do cálculo de combinações diferentes em um mesmo problema. |
Fonte: elaborado pelas autoras.
Após a tabulação dos dados e com os apontamentos surgidos acerca das avaliações, segue-se a análise dos aspectos que despertaram mais atenção. Os erros mais comuns foram em: interpretação de texto, operação de multiplicação e operações feitas na questão não condizentes com o que foi pedido. Foi possível observar fragilidade na comparação de números: 25% dos estudantes ainda não têm o domínio da relação de ordem entre os números. Além disso, a relação parte/todo, seja numa parcela da subtração, seja em uma representação fracionária, ainda não foi totalmente compreendida por estudantes nesse estágio.
10 DESCRITORES DAS APRENDIZAGENS ESSENCIAIS - PORTUGAL: 9ºAP
Em posse do material coletado, 20 estudantes (de um total de 24) fizeram a avaliação diagnóstica. Nas avaliações, a partir dos erros apresentados, procuraram-se elementos que chamassem atenção, baseados em alguns descritores oriundos das AE, consideradas como parâmetros principais do que é necessário dominar no final de cada período. Para o 9º ano do 3º Ciclo do Ensino Básico, foram selecionadas as AE para os Números e Operações apresentados no Quadro 8, salientando os números racionais positivos e negativos, introdução dos números racionais, expandindo para o conjunto dos números reais, além do uso de estratégias de cálculos para a resolução de problemas.
Quadro 8 Aprendizagens Essenciais 9° ano: Números e Operações: 9º ano
| AE: objetivos essenciais de aprendizagem | Perfil do Aluno (PA) |
|---|---|
| Reconhecer números inteiros, racionais e reais nas suas diferentes representações, incluindo a notação científica, em contextos matemáticos e não matemáticos. | Conhecedor/ sabedor/culto/ informado |
| Comparar números reais, em contextos diversos, com e sem recurso à reta real. | Criativo |
| Calcular, com e sem calculadora, com números reais, recorrendo a valores exatos e aproximados e em diferentes representações, avaliar os efeitos das operações e fazer estimativas plausíveis. | Crítico/ Analítico |
| Resolver problemas com números reais em contextos matemáticos e não matemáticos, concebendo e aplicando estratégias de resolução, incluindo a utilização de tecnologia, e avaliando a plausibilidade dos resultados. | Respeitador da diferença/do outro |
| Exprimir oralmente e por escrito ideias matemáticas, com precisão e rigor, para justificar raciocínios, procedimentos e conclusões, recorrendo ao vocabulário e à linguagem próprios da matemática (convenções, notações, terminologia e simbologia). | Comunicador Autoavaliador |
Fonte: elaborado pelas autoras.
Os descritores apresentados no PA revelam a preocupação com a maturidade do estudante, considerando elementos que vão além dos aspectos cognitivos, por exemplo: a autonomia, a preocupação com o outro, a criatividade e a capacidade de indagar.
11 ANÁLISE DOS RESULTADOS
11.1 Brasil
As avaliações diagnósticas aplicadas no quinto ano apontam lacunas na compreensão de conceitos de leitura e escrita numéricas; as estratégias de cálculo ainda precisam ser reforçadas antes que se conclua a resposta a um problema, bem como a interpretação de problemas necessita ser mais (bem) trabalhada. Os estudantes revelaram, também, dificuldades na comparação de números, na relação parte/todo, e nos problemas com porcentagem. A operação de multiplicação, prioritária em relação à adição, não foi totalmente compreendida.
As avaliações diagnósticas aplicadas nos 9º anos revelaram: falhas na compreensão dos termos algébricos, na interpretação de problemas e na resolução de sistemas lineares; significativa dificuldade na resolução de equações de segundo grau; em questões com valor posicional dentro de um número, foi demonstrado domínio por parte da maioria dos estudantes; dificuldade em operar com números racionais.
Ainda nas avaliações do 9º ano, alguns aspectos podem ser salientados em relação às aprendizagens: há, na maior parte dos estudantes que fizeram a avaliação, o domínio da relação de ordem nos números reais, com um significativo número de erros em questões que tratavam da regra de três, que, por sua vez, envolve a fração. A questão com equações (montar a equação) do segundo grau apresentou erros significativos. Nesse caso, há a interpretação e a necessidade da linguagem algébrica para representar o termo a ser encontrado. Na questão envolvendo o cálculo de porcentagem e de desconto, foram requeridos conhecimentos de regra de três, porcentagem e interpretação, que, a ver pelos erros apresentados, não estão totalmente dominados.
11.2 Portugal
As avaliações diagnósticas dos 4° anos apontaram para o fato de que estratégias de cálculo ainda precisam ser trabalhadas antes que se oficialize a resposta de um problema (talvez uma leitura mais atenta); foram verificadas poucas tentativas de cálculo antes de responder ou mesmo respostas sem cálculo. Em relação à desenvoltura matemática para a resolução de problemas, alguns estudantes apresentaram cálculos que em nada condiziam com a questão; em contrapartida, a maioria apresentou bom desempenho em relação à comparação de números. Vinte e cinco por cento dos estudantes ainda não têm o domínio desta estrutura numérica, que é a relação de ordem entre os números.
As avaliações diagnósticas do 9° ano revelaram dificuldades nos problemas de interpretação e na resolução de equações do 2º grau e de sistemas lineares. Observou-se maior concentração dos estudantes portugueses em relação aos brasileiros, ainda assim, deixando questões em branco. A postura dos portugueses em relação ao momento da avaliação foi diferente: rapidamente se posicionaram e fizeram silêncio, diferentemente da agitação e da demora em iniciar a avaliação ocorrida aqui no Brasil, na série equivalente.
12 AS AVALIAÇÕES DIAGNÓSTICAS APLICADAS NOS DOIS PAÍSES
As avaliações diagnósticas não apresentaram significativas discrepâncias, uma vez que a quantidade de erros (em termos percentuais) não foi muito diferente. Na questão envolvendo soma e subtração nos Naturais, por exemplo, as duas turmas (Brasil e Portugal) apresentaram o domínio do tema arguido, mas, em relação à questão que pedia o quanto faltava para uma dezena, em Portugal, não houve erros e, no Brasil, de 28, houve 21 acertos (75%). Com base nos dados coletados, os estudantes convivem com situações de leitura e interpretação de dados. Ressalta-se a necessidade de explorar mais situações nesse contexto, para que o estudante possa ler um texto, interpretá-lo com ênfase no significado matemático do contexto.
É natural que, com a passar das séries, os elementos mais diretos ao SND deixem de ser trabalhados e, em contrapartida, outros temas sejam apresentados, apoiando-se em seus fundamentos. Toda a lógica que perpassa o SND, se bem trabalhada e compreendida nas séries iniciais, servirá de base para o entendimento dos diversos temas nas séries futuras. Corroborando este pensamento, estão as orientações trazidas pelo NCTM (2000), em relação ao nono ano, quando afirma:
Durante estes anos de escolaridade, a compreensão que os alunos têm de número constitui o alicerce para a compreensão da álgebra, enquanto que a destreza com as operações numéricas constitui a base para a aprendizagem da utilização e manipulação hábil dos símbolos. (NCTM, 2000, p. 347, grifo nosso).
Dessa forma, as diagnósticas trouxeram à tona elementos que sinalizam para os conteúdos que necessitam ser mais bem trabalhados.
Considera-se que, sob o ponto de vista da função da avaliação como balizador das práticas pedagógicas, retomamos o que afirma Desprebitéris (2001) sobre “a abrangência da avaliação”, por não estar restrita à simples atribuição de notas de acordo com o desempenho dos estudantes, mas ir além, buscando interconectar os diferentes componentes em um processo educativo. Porém salienta-se que, em posse dos dados levantados, os tópicos não dominados precisariam ser retomados e abordados de uma forma diferente, com estratégias diversas, buscando garantir a aprendizagem dos estudantes.
As etapas caracterizadas por Fernandes (2006), “clarificar, integrar, definir e reflectir”, foram vivenciadas nesta pesquisa e contribuíram para que, de forma sequencial e organizada, cada fase fosse cumprida e elementos importantes ao escopo deste trabalho fossem recolhidos.
13 CONSIDERAÇÕES FINAIS
A pesquisa em sala de aula é um fenômeno complexo, que requer múltiplos olhares. A riqueza da experiência consistiu também em oportunidades de repensar a Matemática que se trabalha em sala de aula; de forma inevitável, fazer paralelos entre o que se vivenciou nas salas de aula observadas e a prática da pesquisadora.
A metodologia oportunizou que se fosse a campo, objetivando compreender os aspectos da prática pedagógica no ensino de SND. A bibliografia consultada permitiu esclarecer, fundamentar e interpretar as experiências e análises. Buscou-se evidenciar, à luz da teoria, aspectos das relações didáticas e da aprendizagem de conceitos matemáticos.
A aplicação de uma avaliação diagnóstica como parte da pesquisa de doutorado reverberou de maneira significativa e provocativa. Dois aspectos se destacaram: um relacionado à recepção de pesquisa empírica na escola e outro aos resultados.
No Brasil, houve quem aceitasse a pesquisa e houve (escola) quem não “acolhesse a proposta”. Foi necessária muita persistência para realizá-la. Entendemos que a cultura escolar em vigor, que parece considerar a sala de aula como a um “santuário”, precisa ser desmistificada, repensada e mudada. O sentido da mudança envolve a abertura para a interlocução com outros agentes educativos e para a pesquisa comprometida com a busca de melhoria da prática pedagógica e da aprendizagem.
Em Portugal, a acolhida foi diferente, sem dificuldade, parece que as professoras se sentiram satisfeitas de poderem contribuir com uma pesquisa que envolvesse dois países. O que faz com que, no Brasil, haja tanta dificuldade? Será que se atribui uma soberania ao professor, a ponto de não aceitar que sua prática pedagógica seja observada, questionada, discutida?
Quanto aos resultados, a aplicação e a análise das avaliações diagnósticas revelaram lacunas na compreensão dos conteúdos já vistos, as quais comprometem ou, na melhor das hipóteses, dificultam o aprendizado de novos conceitos, os quais podem estar relacionados com as práticas pedagógicas que, nas séries iniciais, voltam-se para aspectos do SND de forma efetiva, por ser natural e previsto. Nas séries seguintes, outros temas vão surgindo (além dos números), como a álgebra, a geometria, e, muitas vezes, as práticas pedagógicas priorizam outros temas e, por consequência, deixam de abordar aspectos relacionados aos números. Com essa mudança, os princípios aditivos e multiplicativos são pouco trabalhados, podendo vir a comprometer a aprendizagem de matemática no Ensino Médio e no Ensino Superior, modalidade em que a pesquisadoraatua e constata dificuldades.
Outro resultado foi de que as avaliações diagnósticas não apresentaram discrepâncias em relação aos dois países. Os temas que apresentaram maior número de erros, como as frações e estratégias de cálculo na resolução de problemas, foram constatados no Brasil e em Portugal. A diferença significativa foi na postura dos alunos no momento da avaliação. Em Portugal, maior seriedade, rápida organização da turma, silêncio com pouca interferência do professor, poucos questionamentos, numa postura autônoma, de quem entra no jogo e sabe que é sua a responsabilidade de (tentar) resolver as questões. Em contrapartida, no Brasil, a demora em organizar a sala, em fazer silêncio; muitas perguntas que poderiam ter sido evitadas, uma vez que as instruções iniciais tinham sido dadas; e depois já com a avaliação na mão, uma certa resistência em iniciar a prova, ler as questões. Também, aqui no Brasil, especialmente no 9º ano, estudantes querendo ver a prova do colega, alegando não saberem fazer “nada”.
Tais constatações descortinam um delicado cenário de uma cultura passiva por parte dos estudantes, na qual estes não se sentem capazes de realizar uma avaliação com seriedade e competência, pois é seu papel naquele momento demonstrar o conhecimento adquirido até então. O que precisa ser melhorado? Implantarmos cultura mais dialógica entre professor e estudante? Uma cultura de um aluno mais ativo, mais comprometido com o “seu” processo de aprendizagem, no qual ele é capaz de se autoavaliar, questionar e pedir ajuda ao professor nos temas não aprendidos?
Entende-se ter atingido o objetivo desta pesquisa: levantar aspectos a serem melhorados em relação a conteúdos referentes aos números e ao SND, uma vez que foi possível perceber lacunas em conteúdos não dominados pelos estudantes das séries nas quais a avaliação foi aplicada.
O nível de exigência do professor, observado nas escolas de Portugal, era maior do que no Brasil. O professor exigia postura do estudante diante da realização das atividades, tarefas, estudo e comprometimento. Considera-se que, independentemente da série a lecionar, é fundamental que haja um amplo conhecimento do objeto matemático a ser abordado.
Considera-se necessário sensibilizar os professores para a necessidade de explorar e trabalhar com os padrões de regularidades do SND nas séries finais, por meio de desafios, atividades diferenciadas, buscando evidenciar elementos da estrutura dos diversos Sistemas Numéricos, bem como trabalhar com outras bases (especialmente as menores).
Por fim, retoma-se a questão de que o professor é o agente que conduz o sujeito à aprendizagem, e está em suas mãos essa tarefa, que se inicia muito antes de colocar os pés em sala de aula, da mesma forma que sua abrangência vai além dos muros escolares.