1 Introdução

A inserção da álgebra como unidade temática para os anos iniciais do Ensino Fundamental na nova Base Nacional Comum Curricular (BRASIL, 2018) intensificou as discussões acerca do ensino deste campo de conhecimento da matemática, aproximando da realidade escolar questões colocadas em pauta no campo da pesquisa desde a década de 1980. Nesse sentido, pesquisas como as de ^{Fiorentini, Miorim e Miguel (1993}), ^{Lins e Gimenez (2005}) e Lanner de Moura e Sousa (²⁰⁰⁸) já vinham corroborando estudos de âmbito internacional (^{Kaput, 2007}; ^{Canavarro, 2007}; ^{Kieran, 2004}; Kieran et al., 2016) relacionados à temática Early Algebra, em que se propõe o desenvolvimento do pensamento algébrico já nas séries iniciais do Ensino Fundamental. Mais recentemente, outros pesquisadores também vêm se debruçando sobre este tema, trazendo muitas contribuições a este campo de pesquisa (Sousa, 2004; ^{Panossian, 2014}; ^{Radford, 2018}; ^{Moretti; Radford, 2021})

Considerando a intrínseca relação entre os processos de ensino e aprendizagem, cumpre destacar a relevância de estudos relacionados à formação do professor que ensina matemática nos anos iniciais, tendo em vista tal necessidade de se pensar numa organização do ensino voltado ao desenvolvimento do pensamento algébrico já nesta fase. Nesse contexto, desenvolvemos uma pesquisa de mestrado (^{Santos, 2020}) que buscou investigar, no contexto da formação continuada, o desenvolvimento do pensamento algébrico de professores que ensinam matemática nos anos iniciais.

A pesquisa se fundamentou na perspectiva Histórico-Cultural, sobretudo a partir das contribuições de ^{Vigotski (2004 3}, ²⁰⁰⁷, ²⁰¹⁰) relacionadas à formação e desenvolvimento humano, sentidos e significados e atividade; além da Teria da Atividade (^{Leontiev, 1978}, ¹⁹⁸³, ¹⁹⁸⁸) e Teoria Desenvolvimental (^{Davidov, 1983 1988}; ^{Davidov; Márkova, 1987}).

Considerando, sob tais lentes teóricas, que a escola tem como finalidade a apropriação de conhecimentos científicos e culturais historicamente produzidos pela humanidade a partir do desenvolvimento do pensamento teórico, buscou-se proporcionar um espaço formativo, intencionalmente planejado, que corroborasse a atividade de ensino dos professores, mas que também potencializasse o desenvolvimento do pensamento teórico dos docentes. Em outras palavras, o objetivo era investigar o processo de desenvolvimento do pensamento algébrico dos professores em atividade de ensino, articulando o movimento de formação continuada de matemática, e especificamente da álgebra, com a organização do ensino para os anos iniciais do Ensino Fundamental.

O processo de investigação amparou-se no materialismo histórico-dialético, com a realização de um experimento formativo (^{Davidov, 1988}; ^{Vigotski, 2004}; ^{Cedro, 2008}). Adotou-se como base teórico-metodológica a Atividade Orientadora de Ensino (^{Moura, 1996}; ^{Moura et. al, 2016}) e, com isso, foram propostas Situações Desencadeadoras de Aprendizagem que proporcionassem ações coletivas voltadas à apropriação dos nexos conceituais algébricos e ao desenvolvimento do pensamento algébrico, que compreendemos coincidir com o pensamento teórico mediado por conceitos do campo de conhecimento da álgebra.

Neste artigo apresentaremos uma síntese desta compreensão acerca do pensamento algébrico como pensamento teórico mediado por conceitos algébricos. Em seguida, evidenciaremos algumas contribuições metodológicas da Atividade Orientadora de Ensino para a pesquisa na organização do movimento formativo dos professores, tendo em vista a apropriação dos nexos conceituais e desenvolvimento do pensamento algébrico. O recorte de análise acompanhará o processo formativo de uma das professoras analisadas na pesquisa, trazendo sua participação em vários momentos das propostas coletivas, buscando evidenciar movimentos de superação dialética em seu pensamento a partir de indícios de sua aproximação aos nexos conceituais algébricos e de seu processo de desenvolvimento do pensamento algébrico. Finalizaremos apresentando algumas considerações acerca da pesquisa e do processo de formação continuada para o desenvolvimento do pensamento algébrico de professores que ensinam matemática nos anos iniciais do Ensino Fundamental.

2 O pensamento teórico mediado por conceitos algébricos

Com base em Davidov (1988), compreende-se que o pensamento permite a compreensão racional da realidade pelo ser humano a partir da idealização e planejamento do objeto e de sua reestruturação após as experiências práticas, movimento que reflete a unidade entre o concreto e o abstrato. Diante disso, o pensamento pode se pautar nas práticas sobre a realidade, atendo-se aos aspectos aparentes, externos e sensíveis do objeto, denominando-se como pensamento empírico; ou pode manifestar-se a partir da busca por estabelecer conexões internas e externas no intuito de revelar a essência do objeto, a partir da qual se formam todas as particularidades e especificidades deste, constituindo-se, assim, o pensamento teórico.

O pensamento empírico parte de casos particulares tomados repetidamente e transformados em representações gerais a partir de uma regularidade no campo abstrato, realizando a generalização empírica, tomada a partir das experiências sensoriais do objeto.

Ao contrário, o pensamento teórico parte da apreensão de casos concretos e caóticos, reduzindo-os ao campo abstrato a fim de realizar experimentos mentalmente a partir de reflexão e racionalidade, buscando, nesse movimento, aproximar-se de seus elementos essenciais, isto é, os nexos conceituais deste objeto de conhecimento, a fim de revelar sua essência, a lei geral que rege tal objeto. Em seguida, tais relações ascendem novamente ao concreto dito pensado, em que a relação geral revela o objeto em seu sistema integral na medida em que possibilita a manifestação da essência na resolução dos casos particulares relacionados a esta lei geral. Esse processo é ilustrado pela tríade concreto-abstrato-concreto (^{Romeiro; Moretti, 2016}), movimento que permite a reprodução mental de um objeto em seu sistema integral, isto é, a formação do conceito teórico sobre este objeto (^{Davidov, 1988}). Em síntese, é a unidade entre abstração, generalização e formação de conceitos, partindo do geral para o particular, que constitui o desenvolvimento do pensamento teórico.

O estabelecimento de nexos conceituais, como possibilidade de concretização do pensamento teórico, permite a compreensão do estudo lógico (do movimento do pensamento) e histórico (do movimento dos fenômenos do mundo objetivo) dos conceitos, por meio de formas de pensamento teórico (processos de abstração, generalização e formação de conceitos), de análise e síntese, e no movimento de ascensão do abstrato ao concreto, movimento da lógica dialética (^{Panossian, 2014}, p.110).

Atrelado ao movimento de apreensão dos nexos conceituais e da essência do objeto, compreende-se que o movimento lógico-histórico permite desvelar o percurso das experiências humanas ao longo da história, refletindo a ação lógica do pensamento humano acerca do percurso constituinte do objeto (^{Kopnin, 1966}). Com a impossibilidade de reproduzir a história em sua integralidade, o movimento lógico-histórico possibilita evidenciar os elementos essenciais do conceito, desta forma, imprescindíveis ao desenvolvimento do pensamento teórico.

Do mesmo modo que o pensamento teórico permite a compreensão racional de objetos da realidade “identificando a essência do objeto e criando conexões mentais sobre as propriedades que compõem a forma universal do mesmo” (^{Santos, 2020}, p.34), o pensamento algébrico é o pensamento voltado à compreensão da realidade em movimento e de seus fenômenos (^{Sousa, 2004}; ^{Lanner De Moura; Sousa, 2008}), que se dá a partir do estabelecimento de relações entre as grandezas quantitativamente variáveis, sendo esta a essência da álgebra (^{Panossian, 2014}).

Nesta perspectiva, o pensamento algébrico também se desenvolve a partir da identificação e apropriação dos nexos conceituais algébricos, por meio da compreensão das relações gerais relacionadas às grandezas variáveis, sendo que nos anos iniciais esse processo pode se dar a partir da compreensão e manipulação das estruturas das operações de modo analítico, garantindo a indissociabilidade entre aritmética, geometria e álgebra.

Nesse contexto, ao longo do processo de desenvolvimento do pensamento algébrico, a partir de situações concretas e caóticas a priori, a relação geral é abstraída e manifestada novamente nos casos particulares relacionados a cada fenômeno, possibilitando sua ressignificação e generalização, expressando-se o conhecimento algébrico por meio de conceitos. Diante disso, compreendemos o pensamento algébrico como o pensamento teórico mediado por conceitos algébricos (^{Moretti; Virgens; Romeiro, 2020}; ^{Santos, 2020}; ^{Moretti; Virgens; Romeiro, 2021}). Cumpre salientar que a aritmética, nessa perspectiva, não é compreendida como o empírico da álgebra, uma vez que há generalizações teóricas no campo da aritmética. No entanto, a aritmética é compreendida como outro campo de conhecimento que deve estar intrinsecamente articulado ao ensino da álgebra, sobretudo nos anos iniciais. Compreender as estruturas aritméticas corroboram o movimento de apreensão das relações algébricas, assim como a aproximação dos nexos conceituais e o desenvolvimento do pensamento algébrico podem ressignificar cálculos aritméticos outrora cristalizados e mecanizados; logo, na relação entre o conhecimento aritmético e conhecimento algébrico, um não é precedente do outro e seu ensino podem e devem coexistir.

Mediante o exposto, foram desenvolvidas Situações Desencadeadoras de Aprendizagem ao longo do experimento formativo com os professores que buscaram aproximá-los de alguns nexos conceituais a fim de que se apropriassem de elementos do conhecimento algébrico com vistas ao desenvolvimento do pensamento algébrico. Amparamo-nos, nesse sentido, nas contribuições de Sousa, ^{Panossian e Cedro (2014}) que, a partir do movimento lógico-histórico da álgebra, evidenciaram a fluência, o campo de variação e a variável como principais nexos conceituais algébricos, sendo estes adotados em nossa pesquisa naquele momento de investigação.

Em síntese, a fluência remete à ideia de constante transformação e evolução do mundo e dos fenômenos presentes nele; a “variável vai representar as possibilidades de valores para uma determinada grandeza” (^{Santos, 2020}, p. 112) e o campo de variação vai delimitar o movimento de variação da variável. Ao longo de pesquisas posteriores, temos ampliado nossa perspectiva acerca dos nexos e elementos conceituais algébricos, expandindo a compreensão de nexos como o “movimento, valor desconhecido (incógnita); reconhecimento de padrões e generalizações; variáveis; relações entre grandezas variáveis; e relação algébrica funcional” (^{Moretti; Virgens; Romeiro, 2021}, p.1469).

3 Sobre os aspectos metodológicos da pesquisa

Dialogando com os pressupostos teóricos da pesquisa, adotou-se o método materialista histórico-dialético, em que, com base na dialética, busca-se a superação da lógica formal entendendo-se que “o fenômeno estudado deve ser apresentado de tal modo que permita a sua apreensão em sua totalidade” (^{Cedro, 2008}, p.96). Assim, o pesquisador, a partir de um olhar teórico sobre a realidade do fenômeno estudado, busca acompanhá-lo em movimento de modo a revelar sua essência (^{Gamboa, 2000}; ^{Frigotto, 2000}). Tal concepção pressupõe a superação descritiva da análise dos dados produzidos, considerando os pares dialéticos e as contradições inerentes a esse processo.

A fim de objetivar uma investigação de tal natureza, desenvolveu-se um experimento formativo com planejamento intencional por parte da pesquisadora voltado à atividade de ensino dos professores, seu processo de aprendizagem e seu desenvolvimento psíquico, uma vez que “um dos pontos essenciais dessa perspectiva é que ela pressupõe a intervenção ativa do pesquisador nos processos psíquicos que ele estuda” (^{Cedro, 2008}, p.105).

O experimento formativo foi desenvolvido na forma de uma ação de extensão da Universidade Federal de São Paulo (UNIFESP), em parceria com uma escola pública do município de Guarulhos, na qual uma das pesquisadoras atuava como professora polivalente da Educação Infantil e dos anos iniciais do Ensino Fundamental. Ao todo se inscreveram 23 professores dessa mesma escola, que participaram dos 17 encontros propostos com uma hora de duração cada um.

A Atividade Orientadora de Ensino (AOE) foi utilizada como base teórico- metodológica para o planejamento e organização do experimento, uma vez que esta é compreendida como a unidade entre a atividade de ensino e de aprendizagem e pode orientar tanto a organização do ensino pelo professor (^{Moura, 2010}) como o percurso de investigação pelo pesquisador, permitindo “usar sua estrutura para identificar motivos, necessidades, ações desencadeadas e sentidos atribuídos pelos sujeitos no processo de ensino” ^{(Moura et al., 2016}, p.125).

Preconizando aspectos como a ludicidade, interação e coletividade como constituintes do processo de aprendizagem, a AOE prevê a elaboração e desenvolvimento de Situações Desencadeadoras de Aprendizagem (SDA) (^{Moura, 1996}), propostas que buscam colocar os sujeitos diante de uma necessidade relacionada ao movimento lógico-histórico do conceito, de modo a atender a necessidade de aproximação da essência de um conhecimento a partir da apropriação de seus nexos conceituais.

Utiliza-se como recursos para a SDA a história virtual (fictícias e relacionadas a necessidades humanas no movimento de produção de conhecimento); o jogo, que supera a aparência por si só e desencadeia uma necessidade teórica a ser resolvida no âmbito da coletividade; e a situação emergente do cotidiano, suscitando questões do cotidiano atrelados ao contexto em que se dá a aprendizagem. É fundamental que, além de carregar em si a síntese histórica do conceito, a SDA permita discussões em grupo e sínteses coletivas com a mediação do professor (ou pesquisador) e dos pares, a fim de despertar a necessidade de aprender e corroborar a atividade dos sujeitos envolvidos, com vistas ao desenvolvimento do pensamento teórico (^{Moura et al., 2016}).

Ao longo dos encontros do experimento formativo proposto na pesquisa, os professores se depararam com Situações Desencadeadoras de Aprendizagem relacionadas a elementos do conhecimento algébrico, sendo desafiados a lidarem com “elementos potencialmente mobilizadores dos sujeitos para a solução de um problema relativo aos conteúdos [...]” (^{Moura, 1996}, p.4), nesse caso relacionados a alguns nexos conceituais da álgebra.

O experimento foi dividido em três módulos, sendo o primeiro para identificar o perfil do grupo e os sentidos iniciais dos participantes acerca da álgebra e seu ensino; o segundo módulo buscou aproximar os professores dos nexos conceituais algébricos com vistas ao desenvolvimento do pensamento algébrico; e o terceiro teve o intuito de articular a atividade de ensino e de aprendizagem do professor, isto é, seu processo formativo com a organização do ensino voltado ao pensamento algébrico dos alunos dos anos iniciais do Ensino Fundamental.

Para a produção de dados, foram utilizados diversos instrumentos como registros em questionário, transcrição de audiovisual, diário de campo, registros coletivos. E, a partir dos dados produzidos, a análise buscou incorporar e superar o aspecto descritivo, a fim de acompanhar o fenômeno investigado (o desenvolvimento do pensamento algébrico dos professores) em movimento, apreendendo os indícios de superação no modo de pensar que pudessem estar relacionados à aproximação dos nexos conceituais algébricos e ao processo de desenvolvimento do pensamento algébrico.

4. Processo de desenvolvimento do pensamento algébrico do professor dos anos iniciais no contexto da formação continuada

Para este artigo, vamos apresentar como recorte de análise o percurso formativo de uma professora dos três que foram analisados na pesquisa. Traremos uma síntese do movimento de aproximação dos nexos conceituais pela professora Bia (nome fictício), a fim de revelar alguns indícios de um processo de desenvolvimento do pensamento algébrico pela docente. Para isso, daremos ênfase aos dados produzidos no segundo módulo do experimento. No entanto, traremos algumas cenas do primeiro módulo, a fim de observar a compreensão inicial da professora acerca do que é álgebra. Além disso, em alguns momentos aparecerão falas transcritas referentes a outros professores, por estarem interagindo com a professora Bia e, assim, corroborarem seu movimento formativo.

Ao início do experimento formativo, questionamos os professores e pedimos para que eles registrassem e posteriormente compartilhassem com os pares o que eles entendiam ser a álgebra. A professora Bia, assim como os outros professores, apontou uma dificuldade em definir o que é álgebra, demonstrando nem mesmo compreendê-la como um campo da matemática distinto da aritmética.

Bia: Pra ser sincera eu vi muito pouco essa discriminação álgebra, tudo para mim era matemática. O que discriminava era geometria... a palavra álgebra não fez parte da minha formação. Então pra mim é difícil colocar o que é a álgebra exatamente. São os jogos? As situações-problema? É tudo? [...].

Bia indica uma problemática relacionada à sua formação como professora, o que corrobora pesquisas que apontam uma limitação na formação inicial e continuada de professores que ensinam matemática nos anos iniciais (^{Nacarato et al., 2023}), que na maioria das vezes não garantem uma compreensão e articulação entre os campos de conhecimento da matemática, se voltando mais a uma perspectiva tecnicista, não rompendo com a resistência que muitos professores já trazem desde a educação básica.

No quarto encontro, os professores foram convidados a refletir sobre o sinal de igualdade e seu papel no ensino da matemática. Apesar de não ser um nexo conceitual algébrico, entendemos que a compreensão da igualdade como equivalência e garantia de equilíbrio, e não apenas como indicador estático de um resultado, é fundamental para o desenvolvimento do pensamento algébrico.

Bia: Igual é... igual? (risos) Então...é pra mostrar o resultado (risos).

A professora Bia e nenhum dos outros professores reconheceram a igualdade como equivalência ou equilíbrio, mas como uma ação, um resultado estático para situações problemas, inclusive presentes nos livros didáticos, em que se coloca, de um lado, um valor somado a outro desconhecido e do outro lado da igualdade o resultado. Nesses casos, os estudantes precisam encontrar o valor que está faltando, o que é plenamente possível de se realizar a partir de contagem discreta, sem demandar que se amplie a compreensão acerca do sentido das manipulações de quantidades conhecidas ou desconhecidas dos dois lados da igualdade, reconhecendo a estrutura para além da aparência. A ampliação da compreensão para além da aparência da igualdade, implicando na compreensão do sentido da equivalência, permite reconhecer que independentemente das operações realizadas e de quais quantidades estejam sendo manipuladas, o princípio da igualdade será garantido, mantendo-se sempre os dois lados em equilíbrio.

De modo geral, ao longo dos primeiros encontros, com seus registros e falas, a professora Bia deu indícios de que seus conhecimentos e forma de pensar estivessem limitados ao campo da aritmética. Não indicou em nenhum momento, assim como os outros professores, elementos que remetessem ao conhecimento algébrico, como grandezas variáveis, campo de variação ou mesmo no campo da linguagem, quando é mais comum indicar-se letras ao se referir a variáveis, incógnitas etc. Retomando que, de acordo com Davidov (¹⁹⁸⁸), o pensamento teórico pressupõe a compreensão da essência do objeto e de seus nexos conceituais, entende-se que, naquele momento, a professora Bia parecia não pensar teoricamente sobre o campo algébrico por não ter conceitos formados sobre esse objeto. Desse modo, ainda não pensava algebricamente.

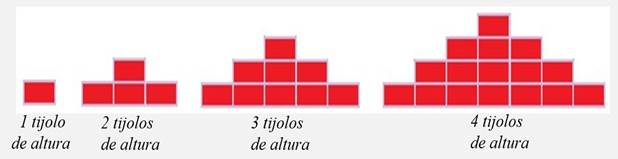
Ao longo do segundo módulo, foi proposta aos professores uma SDA sob a forma de uma história virtual denominada de “O jovem construtor”, em que se apresentava um padrão e algumas situações problemas envolvendo tal sequência. Na história virtual, o jovem construtor Pedro é estudante do curso de edificações e precisa elaborar o projeto de construção de uma escada, em que se possa subir de um lado e descer do outro, sem que se saiba a quantidade de tijolos usada no total.

Fonte: ^{Santos, 2020}, p.82.

Figura 1 Padrão apresentado na SDA “O jovem construtor” 

Ao resolverem uma das situações propostas, em que se perguntava qual a quantidade de tijolos na altura e quantidade total de tijolos utilizada na parede de uma escada cuja base tivesse 39 tijolos, a professora Bia manifesta a necessidade de uma regra geral que possibilite a resolução dos casos particulares, sem necessariamente ter que ficar resolvendo cada situação aritmeticamente, considerando a inviabilidade ou até impossibilidade disso em alguns casos, sobretudo aqueles com valores significativamente altos.

Bia: [...] quando a pergunta trouxe a base 39, a gente foi fazendo bem manualmente, sabe, desenhando mesmo. A gente pegou o 39, que era a base, e fomos somando mais dois desde a primeira posição até chegar nele...aí a gente viu que a altura era 20...mas eu questionei que isso só deu certo porque foi pra responder com poucos tijolos, porque se fosse mais ia ficar difícil...se fossem centenas de tijolos a gente não poderia ficar fazendo manualmente....mas aí gerou aquele conflito, porque a gente não conseguia pensar em algo que servisse pra achar a quantidade pela base, sem ter que calcular um por um.

A necessidade apontada pela professora remete ao movimento de generalização algébrica, em que uma regra geral é abstraída a partir daquela situação concreta (dita caótica) e depois retorna ao concreto de modo pensado; isto é, uma regra geral para encontrar a altura e quantidade de tijolos para qualquer base de escada. A primeira condição para esse movimento de ascensão do pensamento é a que a professora Bia manifesta nesse momento: a identificação de que é necessário partir do geral para o particular (Davidov, 1988), nesse caso, expresso pela Bia como a necessidade de “pensar em algo que servisse pra achar a quantidade pela base, sem ter que calcular um por um”. Na SDA proposta existem duas variáveis intrinsecamente relacionadas, isto é, a base e a altura da parede, sendo que, a partir desta relação entre as duas, resulta uma terceira variável: a quantidade total de tijolos. No excerto apresentado e ao longo do encontro, Bia reconhece claramente duas variáveis: a altura, representada pela palavra “quantidade”, e a base, além da necessidade de se estabelecer uma relação funcional entre elas a partir de uma regra geral, o que indica uma aproximação do conceito de variável, que é um nexo conceitual algébrico, apesar de, naquele momento, não conseguir nomeá-la.

A cena seguinte refere-se a uma SDA denominada “Altura da pirâmide” (^{Sousa, 2004}), em que um chefe de construção do antigo Egito precisa estabelecer como calcular a altura da coluna mestra de uma pirâmide, sem que o faraó tenha estabelecido sua altura. O que ele já sabe é que já foram colocadas 12 pedras na coluna mestra e ainda restam 60 pedras no depósito disponíveis para uso.

A partir das discussões sobre a SDA em um grupo menor, Bia parece começar a perceber a possibilidade de variação e relação funcional entre grandezas.

Alice: Se ele usasse tudo, por exemplo, a altura seria 60 mais 12. Bia: Mas aí a gente tem que ver o que que ele tá pedindo...é a altura que ele quer saber? Porque o faraó ainda não escolheu.

Alice: Então h vai ser igual a x mais 12. H é a altura...o x é quantas pedras ele vai usar a mais.

Bia: Sim... porque ele não precisa usar todas...pode usar mais 10, mais 15, mais 35...depende da altura que o faraó pedir.

Alice: É.

Bia: Entendi.

A professora Bia, em conversa com a professora Alice que é formada em matemática, indica alguns valores que a variável pode assumir, isto é, a possibilidade de variação da grandeza relacionada à quantidade de pedras que ainda podem ser utilizadas. Apesar de indicar valores específicos, ela demonstra, ao longo do encontro, compreender que estes valores devem, necessariamente, estar submetidos à delimitação desta variação, expressa pelo campo de variação que vai de zero a sessenta, assim como o campo de variação da altura vai de 12 a 72, se aproximando, assim, de mais um nexo conceitual algébrico.

Além disso, neste mesmo excerto apresentado, observa que a quantidade de pedras a ser utilizada para complementar a coluna mestra da pirâmide “depende da altura que o faraó pedir”, estabelecendo, assim, uma relação entre as duas grandezas variáveis envolvidas, ainda que de modo inicial, o que remete à essência do conhecimento algébrico.

Outra SDA, “O jogo Fantan” (Panossian; ^{Moura, 2010}), é um jogo de tabuleiro com quatro jogadores representados por uma cor diferente. O tabuleiro é quadrado e tem seus quatro cantos demarcados por numerais de zero a três. Cada jogador recebe 20 fichas de sua respectiva cor e aposta de zero a três fichas a cada rodada em um dos cantos do tabuleiro, sendo que a quantidade de fichas das apostas não pode coincidir entre os jogadores. Um dos jogadores apanha uma quantidade aleatória de feijões e espalha sobre a mesa. Formam-se grupos de quatro feijões e quem apostou no canto em que a quantidade coincide com a sobra de feijões após os agrupamentos é o vencedor da rodada, recebendo de cada jogador a quantidade de ficha que ele mesmo apostou ou a quantidade do adversário, caso seja um valor menor.

Nas discussões sobre o jogo, Bia traz em sua fala alguns aspectos que parecem remeter aos nexos conceituais algébricos.

Bia: Eu vejo novamente a ideia das possibilidades. É legal que a gente sabe de quanto a quanto eles podem ir. A sobra do feijão vai de 0 a 3, as fichas que a gente podia ganhar por rodada também...porque se eu ganhasse o máximo de todos, que era 5, eu teria 20... aí tem o resto, a quantidade de feijões, quantidade de fichas, enfim... é a gente entender o que pode estar acontecendo durante o jogo.

A professora Bia começa a reconhecer que a álgebra está relacionada à previsibilidade e controle de movimento das grandezas, destacando, inclusive, a fluência e o campo de variação das grandezas envolvidas, dois nexos conceituais algébricos. Da mesma forma, junto a seu grupo, estabeleceu oralmente uma regra que pudesse controlar ou calcular a quantidade total de qualquer punhado de feijões a partir dos agrupamentos realizados, recorrendo e ressignificando o conceito aritmético da divisão a partir de uma abordagem algébrica.

Jonas: Acho que a gente poderia usar a letra q pra representar a quantidade total de feijões.

Pesquisadora: E quanto vai valer esse q?

Jonas: Tem muitas possibilidades. A gente não sabe quantos feijões vão ser pegos em cada punhado.

Bia: Pensando nesse sentido, a quantidade de grupos que vai ter em cada rodada também poderia ser representada por outra letra. Só que aí tem que ser vezes 4, não é, Jonas? Igual você tinha falado, multiplicando a quantidade de grupo por quatro.

Pesquisadora: Então como que a gente registraria isso? Alice: Q é igual a 4g mais o resto. O resto pode ser o r. Pesquisadora: E essa seria a única forma de registrar?

Elisa: A gente poderia escrever ao invés de usar letras. Escrever que a quantidade total de feijões é igual a quantidade de grupos vezes 4 mais o que sobrar.

Além de pensarem numa regra geral para satisfazer todos os casos particulares, os professores parecem reconhecer as variáveis e expressá-las utilizando diferentes linguagens, inclusive a alfanumérica. Trata-se de um momento de produção e apropriação coletiva, mas que parece corroborar o movimento do pensamento da professora Bia.

Também foi utilizada como SDA uma adaptação do jogo de pega-varetas, com a intenção de aproximar os professores de nexos conceituais algébricos como a variável e as incógnitas; destacar a possibilidade de controle e expressão do movimento das grandezas por meio das linguagens (escrita ou simbólica); além de apresentar, de modo geral, a ideia de sistemas de equações, retomando a importância de se estabelecer relações entre as grandezas variáveis em questão.

Os professores foram divididos em grupos menores, como de costume, e receberam um jogo de pega-varetas sem as instruções padrão. A pesquisadora estabeleceu que as regras seriam aquelas já conhecidas culturalmente, porém, eles determinariam todos juntos o valor da pontuação para cada cor de vareta resgatada, exceto as cores amarela e vermelha, cujos valores seriam decididos sigilosamente por cada grupo menor. Foi estabelecido que os valores estipulados estariam no conjunto dos números naturais, entre 0 e 60. Ao final do jogo, cada grupo deveria anotar quantas varetas de cada cor cada participante conseguiu e suas respectivas pontuações finais.

Fonte: ^{Santos, 2020}, p.88.

Quadro 1 Jogo de pega-varetas 

O grupo da professora Bia caminha em direção à compreensão dos nexos conceituais algébricos e se aproximam de uma relação mais geral envolvendo a necessidade de desvendar os dois valores desconhecidos.

Bia: Mas e agora, como que a gente calcula? Pode ser qualquer valor de 1 a 60?

Jonas: É, mas 60 não é, porque é o preto. E 30 e 10 também não. Então é qualquer número de 1 a 60 menos esses três... Aqui sobrou 160 para o vermelho e para o amarelo.

Bia: Deixa eu ver... A gente soma os que a gente já sabe o valor e vê quanto fica para o vermelho e o amarelo.

Jonas: Isso. Mas a pontuação de cada uma é diferente...

Olga: Sim... cada uma tirou uma quantidade de cada cor.

Bia: Mas o valor da amarela e da vermelha é a mesma para todas. Jonas: Então a gente precisaria achar um valor que desse certo pra todas as pontuações. O duro é achar isso (risos).

A professora Bia reforça, ainda que em forma de pergunta, o campo de variação das grandezas quando diz “Pode ser qualquer valor de 1 a 60?”. Além disso, percebe que os valores da pontuação das varetas amarelas e vermelhas deveriam ser iguais para todas as integrantes do grupo que eles analisavam, já que naquele momento utilizavam a pontuação de apenas uma das jogadoras do grupo adversário. Esse pressuposto, corroborado pela fala do professor Jonas, está relacionado a uma das condições essenciais do conceito de sistema de equações, em que os valores das incógnitas devem satisfazer todas as equações relacionadas.

Jonas: Aí a gente tem que descobrir os valores, ou pensar numa fórmula que ajude a encontrar esses valores? Porque deve ter. A gente sabe que é comparando, mas como que resolve?

Bia: Aqui acho que a gente tem que encontrar os valores mesmo...porque a gente tem que saber quanto que vale o amarelo e o vermelho para o grupo delas. Mas deve ter um jeito que sirva para qualquer pontuação.

Jonas: Também acho ... mas, olha aqui (começa a registrar) ... se eu pensar que eu tenho 60 pro amarelo, então cada vareta vale 20. Aí sobra 100 para a vermelha...como são 4, então cada uma valeria 25. Não é isso?

Bia: É, mas aí a gente tem que ver se dá certo para as outras pontuações.

Jonas: Quero aprender logo essa fórmula (risos).

Neste caso do jogo, eles percebem que deveriam encontrar valores para as varetas de cor amarela e vermelha que coincidissem nas pontuações de todas as jogadoras do grupo analisado, satisfazendo suas respectivas pontuações finais, o que remete a uma aplicação prática do conceito de sistema de equações num movimento de ascensão do abstrato ao concreto, ainda que o foco naquele momento não fosse que os professores dominassem os algoritmos de resolução de sistemas. A professora Bia também levanta a necessidade de buscar uma regra geral que atenda a necessidade de formação do conceito do geral para o particular, quando indica que “deve ter um jeito que sirva para qualquer pontuação”.

Após juntar todos os grupos, a pesquisadora toma a pontuação de duas professoras do mesmo grupo, com a primeira pontuação representada como 1A + 1V = 20 e a segunda como 3A + 5V = 90. Nesse caso, A representava o valor atribuído a cada vareta da cor amarela e V o valor correspondente a cada vareta da cor vermelha. A partir disso, os professores foram questionados sobre quanto valeria a vareta vermelha da primeira e, em seguida, da segunda professora, se a de cor amarela valesse 1.

Jonas: Se a gente pensar no equilíbrio, vai ficar três mais cinco V igual a 90. Então o 5V teria que valer 87, não é isso?

Bia: Mas aí seria cinco vezes alguma coisa igual a 87... não dá....

Alice: Gente, vai dar um número quebrado.

Pesquisadora: Qual o conjunto numérico que nós estabelecemos para ser usado?

Jonas: Naturais...então esse resultado não serve...o A não vale 1.

Pesquisadora: Por quê?

Jonas: Porque vai dar um número quebrado...

Bia: Também porque o resultado deu diferente do [resultado] da Olga. Elas são do mesmo grupo, então eu entendo que o resultado tem que ser igual.

Bia reitera sua compreensão acerca do campo de variação e de que os valores atribuídos às varetas de cor amarela e vermelha devem atender à pontuação de todas as integrantes do respectivo grupo.

A pesquisadora elabora um quadro com as possíveis respostas para a pontuação de cada professora e questiona aos professores quais seriam os valores que atenderiam essa condição nas pontuações apresentadas.

Jonas: Vai ser o 5 e o 15. Pesquisadora: Por quê?

Jonas: Porque são os dois valores iguais que aparecem para as duas. Pesquisadora: E se mudasse o valor de uma cor?

Jonas: O da outra cor também mudaria... Pesquisadora: Por quê?

Bia: Porque elas estão dentro da pontuação da pessoa. Então se mudar o valor de uma cor, muda a outra e toda a pontuação.

Jonas: A gente entendeu que tinha que comparar, mas a gente foi jogando valores aleatórios de 1 a 60. Não prestamos atenção que talvez não fosse até 60.

Edna: Mas tem o seguinte...a gente estava trabalhando com valores até 60...se fosse um número maior teria muito mais possibilidades... até achar um valor que desse certo para as duas...

Bia: Mas eu acho que essa questão da comparação é pra gente ver de onde vem...como que funciona. Lá no nosso grupo a gente imaginou que tivesse algum jeito de resolver mais fácil.

Bia, assim como Jonas, dá indícios de compreensão do movimento de variação das grandezas e de que, nesse momento, as variáveis assumem valores específicos (incógnitas); percebem o campo de variação destas grandezas e reconhecem que, a partir da compreensão da forma geral de resolução, pode-se estabelecer regras a serem aplicadas em qualquer situação particular que podem ser manifestadas por meio de algoritmos, por exemplo. Bia também indica a possibilidade de as grandezas variarem e a relação que existe entre tais grandezas variáveis ao afirmar que “se mudar o valor de uma cor, muda a outra e toda a pontuação”, dando indícios de compreender elementos do conhecimento algébrico relacionados à essência da álgebra e aos seus nexos conceituais.

Ao longo da síntese coletiva, também foram discutidas as diversas formas de registro, em que alguns grupos escreveram o nome das cores seguidas da quantidade de varetas de cada jogador, enquanto outros escreveram utilizando letras para simbolizar. A partir disso, a pesquisadora foi problematizando e retomando com os professores questões como a relação entre variável e incógnita, de que modo a variável pode expressar o movimento das grandezas e as formas de representar essa variável.

No final do segundo módulo do experimento, a pesquisadora volta a pedir aos professores que escrevam e depois falem o que eles entendiam ser álgebra.

Bia (escrita): Álgebra é a relação entre grandezas. É trabalhar com o número desconhecido que pode variar.

Bia (fala): Eu escrevi que a álgebra envolve as coisas que podem variar. E pra mim, eu aprendi que também é trabalhar sem o número. E eu comecei a entender, porque pra mim isso era mecânico, era calcular o x e só. Tanto que eu nem sabia que isso que era álgebra (risos).

Nesse momento, a professora Bia demonstra uma grande superação no modo de pensar, manifestando em sua fala e escrita aspectos relacionados ao valor desconhecido, à variação das grandezas e à possibilidade de se estabelecer relações entre elas. Tais indícios remetem a um movimento de aproximação à essência da álgebra e aos nexos conceituais algébricos, movimento constituinte do processo de desenvolvimento do pensamento algébrico.

5 Considerações finais

Neste artigo apresentou-se um recorte de uma pesquisa com professores que ensinam matemática nos anos iniciais do Ensino Fundamental, na qual investigou- se o desenvolvimento do pensamento algébrico desses professores no contexto da formação continuada. A pesquisa foi fundamentada nos pressupostos da Perspectiva Histórico-Cultural, sobretudo com as contribuições de Vigotski, Leontiev e Davidov e o pensamento algébrico foi apresentado como pensamento teórico mediado por conceitos algébricos.

O movimento de produção dos dados se deu a partir de um experimento formativo amparado na Atividade Orientadora de Ensino, no qual foram propostas Situações Desencadeadoras de Aprendizagem que tinham em vista a aproximação dos professores à essência da álgebra e aos nexos conceituais algébricos. O recorte de análise dos dados apresentou o movimento formativo da professora Bia, destacando algumas cenas que davam indícios do processo de compreensão de elementos algébricos relacionados aos nexos conceituais e ao movimento de generalização partindo do geral para o particular.

Compreende-se que a organização de movimentos formativos de professores dos anos iniciais que busquem aproximá-los da essência da álgebra e dos nexos conceituais algébricos a partir de ações coletivas e significativas com as contribuições da Atividade Orientadora de Ensino pode potencializar o desenvolvimento do pensamento teórico mediado por conceitos algébricos, isto é, o pensamento algébrico.

Uma vez que os nexos conceituais algébricos são elementos essenciais relacionados ao movimento lógico-histórico dos conceitos e à formação do pensamento algébrico, a compreensão destes nexos, a saber: fluência, variável e campo de variação, foi prioridade ao longo do experimento formativo realizado na pesquisa apresentada. Além disso, a aproximação de tais nexos pela professora Bia ao longo de seu processo formativo foi o objeto principal de análise neste artigo.

A professora Bia, ao longo do trabalho coletivo para resolução das Situações Desencadeadoras de Aprendizagem, indicou mudanças no modo de reconhecer a álgebra como campo de conhecimento relacionado ao movimento de variação das grandezas e às relações estabelecidas entre elas. Pareceu também se aproximar da ideia de fluência, campo de variação e valor desconhecido (variável e incógnita), isto é, dos nexos conceituais algébricos, movimento que remete ao processo de desenvolvimento do pensamento algébrico.