Serviços Personalizados
Journal
Artigo
Compartilhar
Cadernos de Pesquisa
versão impressa ISSN 0100-1574versão On-line ISSN 1980-5314
Cad. Pesqui. vol.53 São Paulo 2023 Epub 07-Jun-2023
https://doi.org/10.1590/1980531410031
BASIC EDUCATION, CULTURE, CURRICULUM
DIDACTIC ANALYSIS OF CURRICULAR MATERIALS BY FUTURE TEACHERS
IUniversidad Nacional del Altiplano (UNA), Puno, Peru; bcotrado@unap.edu.pe
IIUniversidad de Granada (UGR), Granada, Spain; mariaburgos@ugr.es
IIIUniversidad de Zaragoza (Unizar), Zaragoza, Spain; pbeltran@unizar.es
IVUniversidad Nacional del Altiplano (UNA), Puno, Peru; acastroq@unap.edu.pe
The design and implementation of a training experience with future Peruvian mathematics teachers is described, aimed at developing the competence of analyzing the didactic suitability of curricular materials on probability. From a qualitative approach and with the support of the guidelines of didactic engineering based on the Ontosemiotic Approach, the protocols of written responses of 38 participants are available. The results show limitations in the assessment of suitability indicators and difficulties to elaborate a reasoned judgment on it. It is concluded that there is a need to promote reflective practice on the use of curricular materials and proposals for improvement changes in all facets of didactic suitability in a joint manner.
Key words: PROFESSIONAL COMPETENCE; TEACHING MATERIALS; TEACHER; SECONDARY SCHOOL
Se describe el diseño e implementación de una experiencia formativa con futuros profesores de matemáticas peruanos, destinada a desarrollar la competencia de análisis de la idoneidad didáctica de materiales curriculares sobre probabilidad. Desde un enfoque cualitativo y con el apoyo de las pautas propias de la ingeniería didáctica basada en el Enfoque Ontosemiótico, se dispone de los protocolos de respuestas escritas de 38 participantes. Los resultados muestran limitaciones en la valoración de indicadores de idoneidad y dificultades para elaborar un juicio razonado sobre esta. Se concluye la necesidad de potenciar la práctica reflexiva en torno al uso de los materiales curriculares y las propuestas de cambios de mejora en todas las facetas de la idoneidad didáctica de manera conjunta.
Palabras-clave: COMPETENCIA PROFESIONAL; MATERIAL DIDÁCTICO; MAESTRO; ESCUELA SECUNDARIA
Descrevemos a concepção e implementação de uma experiência de treinamento com futuros professores de matemática peruanos, destinada a desenvolver a competência de analisar a adequação didática dos materiais curriculares sobre probabilidade. A partir de uma abordagem qualitativa e com o apoio das diretrizes da engenharia didática baseada na Abordagem Ontosemiótica, foram gerados e analisados os protocolos de respostas escritas de 38 participantes. Os resultados mostram limitações na avaliação dos indicadores de idoneidade e dificuldades na elaboração de um julgamento fundamentado de idoneidade. Conclui-se que existe a necessidade de promover uma prática reflexiva no uso de materiais curriculares e propostas de melhoria em todas as facetas da adequação didática de forma conjunta.
Palavras-Chave: COMPETÊNCIA PROFISSIONAL; MATERIAL DIDÁTICO; PROFESSOR; ENSINO MÉDIO
On décrit la conception et la mise en place d’une expérience d’entraînement avec de futurs enseignants de mathématiques péruviens, destinée à développer leur compétence d’évaluation de l’adéquation didactique des matériaux curriculaires portant sur la probabilité. A partir d’un approche qualitatif et avec l’appui des lignes directrices de l’ingénierie didactique basée sur l’Approche Ontosémiotique, on a examine les protocoles de réponses écrites de 38 participants disponibles. Les résultats dévoilent des limitations dans l’évaluation des indicateurs d’idonéité, et des difficultés à formuler un jugement fondé sur l’idonéité. On conclue qu’il faut encourager/une pratique réflexive compréhensive sur l’emploi des matériaux curriculaires, et des propositions de perfectionnement dans toutes les facettes de l’adéquation didactique.
Key words: COMPÉTENCE PROFESSIONNELLE; MATÉRIAL DIDACTIQUE; PROFESSEUR; LYCÉE
Several research perspectives in mathematics education assume that the teacher must have the mathematical and didactic knowledge to describe, explain and systematically assess the instructional processes, foreseen, planned, or actually implemented, as well as to competently apply such knowledge in their improvement (Giacomone et al., 2018).
The importance of curricular materials as a support for the teaching task has motivated that, in the last decades, the analysis of these resources has received special attention from the research community in mathematics education (Burgos et al., 2020; Thompson, 2014). Curricular materials are “tools” (Stein et al., 2007) or “artifacts” (Brown, 2009) that support teacher planning and practice. Within this “specific set of resources, designed to support a particular program of teaching and student learning over time” (Remillard & Kim, 2020, p. 3, own translation), are curricular programs, textbooks, student workbooks, and teaching guides, designed for teachers.
Faced with the design of an instructional process proposed in a textbook or in student workbooks, the teacher must be able to analyse, establish criticisms and make adaptations that solve its limitations considering the particularities of the content (Thompson, 2014; Yang & Liu, 2019). Assessing curricular materials according to their ability to help students achieve the learning objectives established in the curricular guidelines requires an in-depth analysis. Such an analysis should make it possible to identify potentially conflicting elements that, during their implementation, require a modification of the planned didactic path.
Given this demand, previous research (Breda et al., 2017; Giacomone et al., 2018) proposes the application of the tools of the Ontosemiotic Approach (OSA) to mathematical knowledge and instruction (Godino et al., 2007), to develop in teachers the specific competence of didactic analysis of instructional processes (Burgos & Godino, 2021; Giacomone et al., 2018; Godino et al., 2017). This competence involves the teacher’s ability to describe and explain the mathematical practices put into play when solving problems and studying the intended mathematical contents (ontosemiotic analysis competence), as well as the global reflection on teaching practice, its assessment and progressive improvement (didactic suitability analysis competence) (Godino et al., 2017). This will allow the teacher to use curricular materials critically as a guide for instructional design in each context, assessing and making adaptations to solve their limitations (Yang & Liu, 2019).
Although student workbooks are regarded as curricular resources for practice, assessment, and monitoring (Hoadley & Galant, 2016) much of the literature on curricular materials has focused on textbooks. We have not found research with prospective teachers that explores the development of didactic analysis competence on student workbooks. This motivates that in this study we pay attention to such resource. Furthermore, given that the mathematical content addressed by these workbooks is broad, it is pertinent to focus on a specific topic: probability. Scarce research on the treatment of probability in the curriculum and in textbooks, reveal important deficiencies that hinder an adequate probabilistic literacy: the priority context is that of games of chance, the proposed situations are not sufficiently representative and balanced of other meanings different from the classical one, situations involving experimentation and simulation with manipulatives or software are missing, among others (Cotrado et al., 2022; Vásquez & Alsina, 2015).
This paper describes the design and implementation of a formative experience with future secondary education mathematics teachers, aimed at developing their competence in analysing the didactic suitability of workbooks on probability, using the guide designed and developed in Cotrado et al. (2022).
Theoretical framework and research problem
The research is based on the model of Didactic-Mathematical Knowledge and Competences (DMKC) of the mathematics teacher developed in the OSA framework (Godino et al., 2017). The two key competences of the mathematics teacher are the mathematical competence and the didactic analysis and intervention competence that consists of “designing, applying and assessing own and others’ learning sequences, through didactic analysis techniques and quality criteria, to establish cycles of planning, implementation, assessment and to raise proposals for improvement” (Breda et al., 2017, p. 1897, own translation). This competence is articulated through five subcompetences, associated with conceptual and methodological tools of OSA: analysis of global meanings, ontosemiotic analysis of practices, management of didactic configurations and trajectories, normative analysis, and analysis of didactic suitability (Godino et al., 2017). In this paper we attend to the subcompetence of didactic suitability analysis.
Didactic suitability is defined as the degree to which an instructional process (or a part of it) meets certain characteristics that allow qualifying it as optimal or adequate to attain the adaptation between the personal meanings achieved by students (learning) and the intended or implemented institutional meanings (teaching), considering the circumstances and available resources (environment). It involves the systematic and coherent articulation of epistemic, cognitive, affective, interactional, mediational, and ecological facets that interact with each other and can be particularized to each instructional unit of study (Godino, 2013). For each of these facets, systems of components and general empirical indicators are developed that guide the analysis and provide criteria for the progressive improvement of teaching and learning processes (Breda et al., 2018; Godino, 2013).
The suitability criteria, understood as “a standard of correctness that establishes how a teaching and learning process should be carried out” (Breda et al., 2018, p. 264, own translation), arise from the consensus of the scientific community in mathematics education, which on the one hand guide how things should be done and on the other hand, allow us to assess the instructional processes planned or implemented in relation to a specific content. Below is a description of the criteria in relation to the processes of studying probability (the reader can find more information in Cotrado et al., 2022):
Epistemic suitability: the intended institutional meanings must be representative of the reference meaning that must articulately contemplate the meanings: intuitive, subjective, frequentist, classical and axiomatic (Batanero & Borovcnik, 2016; Beltrán-Pellicer et al., 2018). In particular, this implies making explicit the definition of favourable, unfavourable and possible cases prior to the introduction of Laplace’s rule, insisting on the need for finiteness and equiprobability of elementary events in order to apply this rule, differentiating between theoretical probability and its estimated value by means of relative frequencies, as well as emphasizing that the stability of frequencies requires repeated trials with different sample sizes.
Cognitive suitability: it is necessary to guarantee that the study of probability is achieved in a progressive and integral manner, from its diverse meanings, considering the necessary prior knowledge of the students. This implies starting the didactic path with problem-situations in which simple random experiments are conjectured, distinguishing between random and deterministic situations, determining relative frequencies using different information representation registers (e.g., bar charts and tables); applying Laplace’s rule in simple cases. Curricular materials should propose situations to detect biases or previous difficulties that students may have when solving probability problems will facilitate overcoming frequent errors.
Affective suitability: there should be spaces to make explicit emotional states in the face of problem solving, situations that highlight the aesthetic and precision qualities of mathematics, as well as contextualized situations and elements that can be motivating, such as humour or games. It is also valued that there are situations that motivate the student to participate actively and feel confident to explore ideas, formulate hypotheses and propose different solution strategies.
Interactional suitability: a clear and well-organized presentation of the problem-situations, emphasizing the key concepts of probability and facilitating interaction through questions that require shared reflection, should be observed. Specifically, the sequence should allow students to initially express their idea about the outcome of a random experiment or games where chance plays a key role. As they experiment and simulate, opportunities arise to elaborate conjectures and nuance the initial ideas, seeking that students take responsibility for autonomous work.
Mediational suitability: a high degree of mediational suitability involves promoting the relevant use of resources such as dice, coins, cards, roulette wheels, random number tables, calculators, virtual resources, or interactive applets, which allow both exploring basic concepts of probability and producing graphic representations with greater formality and abstraction.
Ecological suitability: it is valued that the contents are in line with the curricular guidelines and establish intra and interdisciplinary connections to promote probabilistic literacy.
From the DMCK model, it is considered that the mathematics teacher must know, understand and value this tool and acquire competence for its appropriate use (Godino et al., 2017). The competence in analysing the didactic suitability of mathematical study processes allows the teacher to reflect on the planned or implemented instructional processes and make informed decisions for improvement (Godino et al., 2017). This has motivated that, in recent years, numerous investigations have been conducted in the field of teacher education using the construct didactic suitability and its breakdown into components and indicators (Breda et al., 2018; Burgos et al., 2020; Castillo Céspedes & Burgos, 2022; Esqué & Breda, 2020; Giacomone et al., 2018; Seckel & Font, 2020). Didactic suitability has also been applied to analyse and evaluate training programs or curricular materials (Castillo Céspedes et al., 2022; Cotrado et al., 2022). In that sense, this research has the purpose of developing in future mathematics teachers their competence in analysing didactic suitability, using as a resource the student workbooks on the topic of probability. The following questions are raised:
What observations do the future teachers make when assessing the indicators of didactic suitability? What difficulties do they encounter?
What is the level of relevance of their assessments for each one of the partial suitability facets and in general for the didactic suitability of the material?
Do they consider the assessment of didactic suitability when deciding how to use the workbook? How they do it?
Next, we describe the design of the training action and the analysis process of the reports submitted by the participants.
Methodology
In the training experience, we followed the methodology of didactic engineering understood in the generalized sense proposed by the OSA (Godino et al., 2014). This leads to distinguish four phases: preliminary study in its different dimensions, design of the experiment, implementation, and retrospective analysis. We adopted a qualitative methodological approach characterized by the systematic analysis of data whose interpretation allows us to explain social phenomena, such as that of an educational experience (Strauss & Corbin, 1990). In that sense, we applied content analysis (Cohen et al., 2011) to examine the response protocols of prospective teachers.
Research context, participants, and data collection
The training experience is developed with 38 future teachers (FT onwards) of the Specialty of Mathematics, Physics, Computer Science, and Informatics at the Universidad Nacional del Altiplano (Peru) during the year 2022,1 in the context of the subject of Descriptive Statistics in virtual mode. This format contemplates synchronous actions through videoconferencing (Google Meet) and asynchronous actions to provide study material and upload assignments through the Google Classroom platform. The implementation of the workshop comprised three virtual synchronous sessions of two hours each: 38 FT participated in the first session, while the second and third sessions were attended by 35 FT, of which only 30 were able to complete the assessment task.
The trainer conducting the workshop also plays the role of researcher. As data collection instruments, the trainer’s notes and the protocols of the participants’ written responses are available.
Session design and implementation
Each of the synchronous sessions is complemented by asynchronous activities in which the PF must work on guided readings and develop their reports individually. At any time, he/she can ask the trainer any questions as needed.
Session 1: Initial exploration and introduction to a tool for reflection
The participants reflect and share their opinions on the possible ideal characteristics of a curriculum material, answering the question: what should a good mathematics curriculum material be like? Next, the trainer shows worksheet 9 dedicated to probability in the workbook for first grade of secondary education (Ministério de Educación [Minedu], 2019) and asks them:
Could you say whether worksheet 9 of the first-grade workbook is a good curricular material? Would you use it in a mathematics classroom? Why?
The FT, individually, reflect, describe, and explain the reasons why they think this worksheet should or should not be used in a classroom. The goal is for the FT to make an analysis based on their personal meanings without any guideline that might influence their assessment. They then share their answers in class.
After the sharing, the trainer introduces the notion of didactic suitability and its structure in criteria as norms emanating from consensus in the educational and research community. The components and indicators for the different facets are then briefly presented and specified in the case of probability. The corresponding asynchronous activity consists of reading a document on the criteria and indicators of didactic suitability of curricular materials in probability elaborated by the authors based on Cotrado et al. (2022).
Sessions 2 and 3: Implementation of the didactic suitability guide of curricular materials in probability
The session opens with a reflection on the reading proposed in the previous session. Then, three didactic configurations are identified as units of analysis in worksheet 9: Application (UA1), Verification (UA2) and Evaluation (UA3). The FT must respond individually to the instructions:
Considering the analysis units into which worksheet 9 of the workbook is broken down, identify and justify whether the indicators of each partial suitability described in the previously provided reading are met.
Elaborate a reasoned assessment on the didactic suitability of worksheet 9 in each of the facets.
How do you think the use of worksheet 9 should be managed to increase its didactic suitability? Describe the changes or improvements you could introduce for each gap or conflict you identified in the section.
Considering the complexity of the task, two sessions are dedicated for the FT to complete the three questions. In addition, to support and oversee the participants’ productions, they are asked to share their work file with the trainer.
Results
The analysis of the FT’s evaluations of the didactic suitability of worksheet 9 allows us to observe the difficulties in understanding the tasks, the possibilities offered by each activity and, finally, the achievements of the participants.
Initial exploration and introduction to a tool for reflection
The intention of the first task was to explore the prior conceptions of the FT about what a curricular material is. The participants in this session conceived it as any element, tool or resource used by teachers. They gave as examples of curricular materials: books, educational videos, software, blackboard, web pages, simulators and encyclopaedias, but not workbooks, which are also considered curricular materials according to Remillard and Kim (2020).
At this point, the question arises: what should a good mathematics curricular material be like? As a result, we obtained the opinions of 19 FT out of 38, summarized in Table 1.
Table 1 FT opinions on characteristics of good curricular material according to facets
| Facets | Description | Frequencies |
|---|---|---|
| Epistemic | Meaningful, concrete tasks, brief definitions | 4 |
| Affective | Attractive, well-illustrated, catches the student’s attention, motivational | 9 |
| Interactional | Clear and precise, instructive | 5 |
| Promotes interaction between teacher and student | 1 | |
| Cognitive | Appropriate to the student’s age and interest, connects with the student’s real life | 5 |
| Mediational | Easy to use or handle | 5 |
| Ecologic | Aim or purpose well defined | 3 |
| Others | General, does not specify characteristics | 4 |
Source: Authors’ elaboration.
After this general reflection, the FT had to initially assess worksheet 9 (without prior instruction on didactic suitability) and justify whether it appeared to them as a good material, whether and why they would use it in mathematics class. In this case, 15 FT rated the worksheet as adequate or good, two FT rated it as moderately good, and only FT19 considered that the worksheet was not adequate and would not use it in the classroom. In the evaluations of these 18 FT, incipient features of indicators can be recognized, although they are not very precise and are based on superficial characteristics of the curricular material. These are summarized by facet in Table 2.
Table 2 Incipient features of didactic suitability indicators by facet
| Facets | Incipient features of indicators | Frequencies |
|---|---|---|
| Epistemic | Includes problems contextualized and from everyday life. | 7 |
| Propose several exercises | 2 | |
| Makes use of graphical representations | 7 | |
| Presents some definitions of probability | 3 | |
| Explains the formulas and use Laplace’s rule | 3 | |
| The steps are very well explained | 2 | |
| Allows students to justify their answers | 1 | |
| Affective | Contains attractive images and colours | 12 |
| Motivates the student with simple exercises | 7 | |
| Encourages an active role of the student | 2 | |
| Interactional | Shows open-ended questions, examples and solutions to guide subsequent problems | 6 |
| Problems are clear and well-ordered | 6 | |
| Shows interaction between teacher and student | 2 | |
| Cognitive | The statements are understandable and for different learning levels | 4 |
| It includes and evaluation | 2 | |
| The problems contain questions that generate cognitive conflicts | 1 | |
| Use errors as a source of learning | 1 | |
| Mediational | It includes spaces to solve the problems | 6 |
| Ecological | The material is in accordance with Minedu guidelines | 2 |
Source: Authors’ elaboration.
From the epistemic point of view, seven FT prioritize the contextualization of the problem-situations (“The problem-statement is related to the student’s context, and this makes it possible to apply the knowledge learned in any situation of daily life”, FT20) and another seven FT highlight the relevance of the graphic representations (“It uses graphics from mathematics, such as the pie or circle graph”, FT21).
To a lesser extent, they point out that the worksheet includes concise definitions of probability (“Presents some definitions of probability so that the student understands the differences of each one”, FT24), the correct use of Laplace’s Rule (“Shows the correct use of the formula of the topic”, FT33), the procedural detail (“The steps of the development of the solutions of each problem are very well explained for the better understanding of the student”, FT20) and the possibility of arguing (“the students can justify the results of the problem”, FT26).
Most of the FT consider the worksheet “good” because its design is eye-catching (“it is attractive to the student, it has images and colours”, FT22). Seven other FT observe that the problem-situations foster motivation and positive attitude (“it has problems that are easy to answer and that helps the student to be motivated to answer the exercises”, FT31; “this worksheet has several exercises with few letters so that it does not generate boredom”, FT21). These are aspects referred to the affective dimension.
From an interactional perspective, they believe that the worksheet provides examples and solutions that assist students (“It presents the solutions to certain exercises to guide the resolution of similar situations”, FT24); it presents activities in a logical sequence (“It has a good order, which facilitates understanding and prevents confusion when reading”, FT20); and it promotes interaction between the teacher and student.
To a lesser extent, they recommend the use of the worksheet for cognitive reasons: it contains problems that respond to different complexity degrees (“The statement is understandable and adequate for the students’ learning level”, FT20) or contemplates evaluation (“It has a self-evaluation section”, FT25).
On the other hand, the few opinions that showed features related to the mediational facet referred to the space to work on problem solving (“it has spaces to develop problems”, FT27) and in the ecological aspect the mention to the curriculum (“the worksheet presents didactic sequences proposed by the ministry”, FT24).
FT19 did not consider the lesson adequate based on the fact that “it proposes many worded and boring exercises that students are no longer ready to do those problems”.
Application of didactic suitability indicators to evaluate curricular materials
The second session focused on the criteria and indicators of didactic suitability for probability curricular materials. The traits mentioned by the participants in the previous session were taken as a starting point for reflection. Afterwards, the FT conducted the analysis of the curricular material through the application of the didactic suitability guide (Cotrado et al., 2022). The activity was delivered by 30 FT. In this section we show the result of the analysis performed by the 30 FT who submitted the task.
Epistemic dimension
The FT were able to identify and apply the indicators of epistemic suitability in a specific way, which was a great advance with respect to the generic descriptions of the previous session. The particularization of the components in situations-problems, languages, concepts, procedures, propositions and arguments, relations and epistemic conflicts to analyse the worksheet was also observed. The 30 FT recognized 14 problem-situations in all the curricular material and related them mostly to the classical meaning of probability. However, they did not justify it on the basis of equiprobability conditions, nor on the finiteness of the sample space, although some participants mentioned the gambling context. Table 3 summarizes the indicators correctly assessed and justified by the FT.
Table 3 Epistemic suitability indicators correctly identified by the FT
| Components | Evidence of use of indicators | Frequency |
|---|---|---|
| Problem-situation | Lack of problem situations relating different meanings of probability | 4 |
| Absence of situations from a context familiar to the student | 2 | |
| Lack of situations where the student can generate, experiment, and simulate problems | 9 | |
| Components | Evidence of use of indicators | Frequency |
| Languages | Uses different registers and representations | 19 |
| The linguistic registers are appropriate to the educational level to which they are addressed | 19 | |
| Concepts | Concepts are relative to the educational level of the students, but are not clear | 4 |
| Absence of situations where the student can generate or negotiate definitions | 5 | |
| Procedures | Some steps are not explained or justified | 2 |
| Lack of situations where the student can generate or negotiate procedures | 1 | |
| Propositions | Laplace’s rule is used, the other properties are insufficient (they do not involve impossible and certain events) | 2 |
| There are no situations in which the student generates propositions | 4 | |
| Arguments | There are few arguments to justify propositions and procedures | 1 |
| Relations | The meanings of probability are not articulated | 2 |
| Mathematical objects are connected to each other | 1 | |
| Epistemic conflicts | Some epistemic errors or conflicts are present | 6 |
| Absence of definitions (probable event, impossible event) | 5 |
Source: Authors’ elaboration.
Out of the 22 FT that referred to indicators of the problem-situations component, only four correctly noted the absence of tasks relating different meanings of probability. For example:
In all three units of analysis, only problems of the classical type are presented. There are no problems of frequential meaning, only in UA3 problem 3 presents a circular sector graph that can be related to the frequential meaning. (FT8).
In fact, the worksheet only proposes situations-problems that prioritize classical meaning over intuitive and frequential meaning, without relating them to each other. Likewise, the absence of situations in a context close to the student in which the differences between random and deterministic experiment are discussed was correctly noted by two FT (“the situations do not necessarily include real contexts of the student where the random and the deterministic can be distinguished”, FT21). Nine other FT conveniently specified that the card lacks situations where the student can generate, experiment and simulate problems.
Most of the FT (19) indicated that the worksheet uses different languages, specifying: verbal, symbolic-numeric (inequality, equality, integers, decimals, fractions, percentages, and probability scale), graphic (tree diagram and circular sector graph) and tabular (double-entry table), considering their appropriateness to the educational level at which the resource is aimed. However, they did not observe the use of tree diagrams and double-entry tables, which are not contemplated in the curriculum of the first grade of secondary education.
Regarding the concepts component, 23 FT identified their diversity, linking them to the different situations-problems. Among the most cited were probability, events, simple event, compound event, certain, probable and impossible event, favourable and possible cases, chance, sample space. Of these, four FT correctly stated that the concepts are appropriate to the corresponding educational level, although the notions of simple and compound random experiment and compound event are not recognized in the curriculum. In addition, the FT failed to recognize the lack of references to deterministic situation, simulation, trials and experimentation that should be contemplated in the first grade to ensure adequate epistemic suitability.
In UA2, three solved situations are presented, in which different procedures are observed with the usual prevalence of the classical meaning as opposed to the frequential one. In this regard, 23 FT identified as procedures: listing of elementary events, construction of the sample space, distinction of favourable and possible cases, calculation of probability using Laplace’s rule. However, only two of them correctly noted that some procedures lack explanation and justification. No FT reflected on the absence of important procedures for an adequate teaching of probability. Among them, distinguishing random phenomena from deterministic ones, qualitatively comparing probabilities, or those characteristics of frequentist meaning such as making predictions from observations of experiments or data, estimating probabilities from repetitions of the same random experiment, and simulating random experiments.
Most FT had difficulty in identifying and adequately assessing the indicators in the propositions and arguments components. While 16 FT recognized Laplace’s rule, “the sample space is finite”, “the probability of the certain event is 1” (or “the most probable sum is 7” in UA2) as propositions, no participant referred to equiprobability, nor did they miss the properties of the frequentist meaning or if they did, it was imprecisely. On the other hand, three of them commented incorrectly and without justification, that the worksheet includes all propositions and proposes situations where the student can generate or negotiate propositions.
Few arguments justifying the propositions and procedures are observed in the worksheet (“the procedures are explained and argued in a vague way”, FT8), although these are supported in different registers: natural language, numerical-symbolic, tabular, and graphic (tree diagram). In this sense, only five FT mentioned that the arguments are based on tables or graphs (referring to the proposition of UA2 “the most probable sum is 7”) or Laplace’s rule (“It is based on the application of Laplace’s rule, also other arguments are based on the definition of elementary and compound event, in some cases it is not justified”, FT8).
The indicator related to the relations component was applied by 19 FT. However, only two of them adequately identified the lack of articulation between the different meanings (“the different meanings of probability are not articulated in the situations presented in the worksheet”, FT8), while the others gave a positive evaluation without reflection or in a vague manner.
Finally, the FT had to evaluate whether the curricular material presents epistemic conflicts, that is, ambiguities or errors in the definitions, procedures, propositions or problem statements. This was the only indicator on which the participants raised any questions to the trainer. Of the 28 FT who reflected on this indicator, three identified the lack of clarity in the definitions (of event, probable event, certain event, and impossible event) and commented that Laplace’s rule is not justified.
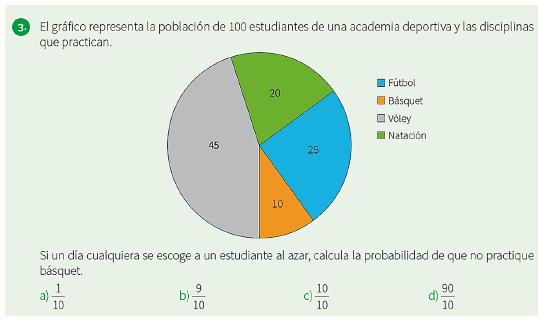
Nine FT recognized the absence of title in the circular diagram of the situation-problem corresponding to UA3 (see Figure 1).
For example, FT21 refers “In problem 3 of AU3, you can see that the statistical pie chart does not have a title which is a serious error in statistics”. Five FT noted the confusion that can be caused by the use of “case”, “result” and “event” interchangeably (see Figure 2). In this regard, FT24 reflects:
In AU2, in the first example, to a certain extent it talks about events, event A, event B, that is allowed because according to the classical meaning it is a concept that one should have of events, but when applying Laplace’s rule it talks about the number of favourable cases, wouldn’t it be there to put favourable events? This would be a conflict because there is no difference between what is a case and what is an event.
They also frequently pointed out that the mistake of multiplying by 100 % is frequently made when the correct way is to multiply by the number 100, and to write the symbol % at the end to indicate that it is expressed as a percentage (see Figure 3).
On the other hand, eight FT made inaccurate or incomprehensible comments, just as eight others stated that they found no errors or ambiguities in the record (“from my point of view I find no errors or ambiguities in the record”, FT20).
Cognitive dimension
In general, the participants showed no doubts in the interpretation of the indicators to be examined in this facet. Only FT23 asked how it should assess the degree of difficulty.
Table 4 Cognitive suitability indicators correctly identified by the FT
| Components | Evidence of use of indicators | Frequency |
|---|---|---|
| Evaluation | UA3 presents evaluation situations with different levels of comprehension | 16 |
| Lack of self-assessment situations | 3 | |
| Individual differences | The situations respond to different difficulty level | 11 |
| Previous knowledge | There is a shortage of introductory situations that lead to the differentiation between random and deterministic experiments | 3 |
| Cognitive conflicts | In AU2, error is used as a source of learning | 2 |
| Equiprobability biases are not anticipated | 3 |
Source: Authors’ elaboration.
As shown in Table 4, most of the FT correctly identified the presence of assessment situations with different levels of comprehension but did not appreciate that these situations refer only to the application of Laplace’s rule. They also correctly identified that the proposed situations respond to several degrees of difficulty, as well as that extension and reinforcement situations are included. However, the assessment of the indicators on prior knowledge was more limited. Only three FT pertinently recognized that the worksheet does not present introductory situations to differentiate random from deterministic experiments, nor situations where the convergence of the relative frequency under the repetition of an experiment can be recognized. For example, FT24 observes that the worksheet: “Does not indicate the definition of probability or what it refers to, does not present an example of a deterministic situation explicitly so that the student can distinguish between random and deterministic experiments”. For the other FT, prior knowledge is covered by showing the definition of sample space, event, favourable and possible cases, or Laplace’s rule.
Similarly, the FT had difficulties in recognizing the indicators on cognitive conflicts in the worksheet. Only two participants explicitly identified that in UA2 a situation is proposed that uses error as a means of reflection (Figure 4) and three other FT indicated that no situations are proposed to detect equiprobability bias. Certainly, the most common errors and biases of probabilistic reasoning are not foreseen in the worksheet, since the proposed situations are oriented to the application of Laplace’s rule, even in situations where the events are not equiprobable. Some FT failed to identify any cognitive conflict, e.g., FT13 states “I do not find any conflict, because the whole card is expressed in a clear way”. In addition, 11 FT confused cognitive conflicts with epistemic conflicts.
Affective dimension
The assessment results for this aspect were quite poor. However, with regards to the emotions component, 12 FT noted that the worksheet presents contextualized situations and problems that could motivate students and foster positive emotions. Nevertheless, these situations do not allow us to assess the actual usefulness of probability in students’ daily and socio-professional lives. As FT24 points out: “There is no significant mathematical value provided, only the use of unconventional games in the situations”.
Five FT point out the consideration of the aesthetic and precision qualities of mathematics in the worksheet, although they do not justify their statement, possibly referring to the illustrations that accompany the situations (“In some situations if aesthetic qualities are presented”, FT8). Nine FT indicate that the worksheet offers opportunities for creative problem solving (“there are spaces where the student has to solve the problems according to his/her analytical criteria”, FT27). However, the absence of experimentation and simulation situations impedes the flexibility to explore mathematical ideas in solving problems on probability. Likewise, the students’ emotions, attitudes and beliefs about problem solving are not explicitly considered. Only FT4 was able to partially observe these indicators and FT8 pointed out that: “Beliefs about probability or something related to this concept are not taken into account at all”.
Interactional dimension
The indicator of the interaction component among students was correctly assessed by only nine FT who pointed out the absence of tasks that allow working in groups and promote dialogue. The rest of the FT did not respond or made imprecise comments.
Seven FT noted that the worksheet proposes questions and solved situations that allow the student to assume the responsibility of study. Although the worksheet facilitates the autonomous work of the student, especially in AU1 and AU2 through these activities, there are few opportunities for students to investigate on their own about the proposed issues.
In the curricular material-student interaction component, only five FT pointed out that some key concepts of probability are not highlighted in the worksheet and the presentation is not clear enough. Although this is especially important regarding the conditions for the application of the classical and the frequentist meanings of the probability, the participants did not perceive this deficiency in the material, despite having the guide.
Mediational dimension
In this dimension, ten FT correctly identified that the worksheet sufficiently promotes the temporal space, even dedicating more space to situations that present greater difficulty of understanding. Regarding the material resources, only three FT consistently pointed out that the worksheet does not provide for the use of manipulative or computer resources. In the worksheet, situations are described verbally, and it is the student who must imagine the random situation without indications of the use of resources for experimentation or simulation. However, 17 FT mistakenly considered that the worksheet encourages the use of manipulative materials, referring to the illustrations (urns, dice, roulettes) and descriptions that present the situations. For example, FT22 mentions: “The worksheet shows roulettes, coins, dice, which encourages teachers and students to use them”.
Ecological dimension
Most of the FT do not consistently apply the indicators of the various components to the curriculum material. However, ten of them recognized and affirmed that the curriculum material does not show discriminatory verbal expressions, three observed the lack of connection with other mathematical contents, and two correctly stated that research or the use of technological innovation strategies is not encouraged through the proposed situations. In addition, 11 FT recognize (although partially and without details) that the purposes of the worksheet correspond to curricular regulations. Even though, as we mentioned, the concepts of simple and compound random experiment are not provided for in the curriculum, but are developed in the worksheet, only FT8 pointed out a certain mismatch between the meanings of probability and evaluation with the curriculum (“The meanings, concepts, and evaluation presented in the worksheet are not sufficiently in line with the curriculum”, FT8).
Value judgments and management proposals on curricular material
The FT were supposed to take into account the previous analysis through the didactic suitability components and indicators to make a reasoned judgment about the relevance of the worksheet in each of the facets. Twelve FT (out of 30) did not respond to this instruction, and another seven did so in a general way, considering the importance of the material meeting the didactic suitability indicators, but without specifying how they are observed in the worksheet or if it is the same in all facets. Only three of them show a certain tendency to consider it of high suitability (“In the affective facet, it is developed in a very present way, like the other dimensions”, FT20). In Table 5, the frequencies in the assessment of didactic suitability by the 11 FT who did provide a more precise judgment are shown.
Table 5 Assessment of the didactic suitability of the worksheet by the FT (n=11)
| Dimensions | ||||||
|---|---|---|---|---|---|---|
| Categories | Epistemic | Cognitive | Affective | Interactional | Mediational | Ecological |
| High | 6 | 6 | 9 | 4 | 7 | 8 |
| Average | 5 | 3 | 2 | 6 | 4 | 3 |
| Low | 0 | 2 | 0 | 1 | 0 | 0 |
Source: Authors’ elaboration.
The research team’s analysis of the suitability through the application of the guide led us to consider (based on the number of indicators that were fully, partially, or not met in each facet) the suitability as average in all facets (with a tendency towards low in the interactional and mediational facets), except for the ecological facet, which was considered low. When the FT rated the suitability as high in each facet, they based it on the complete fulfilment of the associated indicators. When they rated it as average or low (on rare occasions), they mentioned the deficiencies they found in the different facets based on the partial or non-compliance of certain indicators. For example, in the epistemic facet, they based it on the fact that the worksheet omits or incompletely defines important concepts of probability. FT5 mentions, “It should explicitly define the definition of favourable, unfavourable, and possible cases prior to the introduction of Laplace’s rule. Therefore, in this facet, it is in the middle of didactic suitability”.
They also considered the lack of representativeness (“[the epistemic suitability] refers to the degree of representativeness of the institutional meanings implemented or anticipated, with respect to a reference meaning; in this case, it was presented as average”, FT22). The other FT rated the epistemic suitability of the worksheet as adequate or made imprecise comments on the matter. The deficiencies in the cognitive facet mainly refer to not considering all previous knowledge or not addressing individual differences. For example, FT24 states, “As mentioned earlier, the indicators of previous knowledge, individual differences, cognitive conflicts, and evaluation do not match what should be shown for material of good suitability”.
The shortcomings identified in the affective facet have to do with the lack of more motivating images or illustrations to accompany the proposed situations. In the interactional facet, the FT felt that problem-solving situations that should be addressed as a group were missing. On the other hand, five FT rate the worksheet positively because they consider that it presents problem situations in a clear and well-organized manner. However, this assessment is not appropriate because, as mentioned, the presentation of the worksheet regarding the different meanings of probability and how they are articulated is not sufficiently clear or complete. The shortcomings in the mediational aspect emphasized the lack of technological tools as a means to solve or verify the results of the exercises. In the ecological aspect, deficiencies were observed in relation to interdisciplinary and intradisciplinary connections (“the ecological suitability meets the indicators except for the intra and interdisciplinary connections”, FT7).
Table 6 Improvement proposals indicated by the FT
| Dimension | Improvement proposal | Frequency |
|---|---|---|
| Epistemic | Include a complete theoretical explanation of the concepts Address the different meanings of probability Correct errors in the statements (titles in the graphics, eliminate confusing images) and take care in the use of symbols, tables, graphics Pose situations with multiple solutions |
11 |
| Interactional | Propose activities to work in groups, promoting dialogue and communication | 5 |
| Mediational | Include the use of physical or technological materials and resources | 3 |
| Affective | Emphasize the usefulness of the content Use situations closer to the student, motivating Foster emotional reflection of the student on mathematics |
5 |
| Cognitive | Consider previous knowledge required or give a warning about it Use various problem-solving methods Provide more examples with greater diversity and progressively increasing complexity Use incorrect solutions to emphasize errors as a learning source Use self-evaluation rubric |
9 |
Source: Authors’ elaboration.
Finally, the FT had to make decisions about the use of the worksheet and propose changes or improvements to increase its didactic suitability. As shown in Table 6, out of the 30 FT, eight did not respond to this assignment and five did so inconclusively, indicating that it is an applicable worksheet in the classroom or that “it can be improved in many aspects” (FT25) without indicating which ones. These FT had not responded to the overall assessment of the lesson or had done so confusingly. The remaining 17 FT proposed relevant improvement proposals, in the epistemic, interactional, cognitive, affective, and to a lesser extent, mediational facets.
Conclusion
In conclusion, carrying out a critical analysis that guides the use of curricular materials, such as student workbooks, is a challenging task that requires specific training and knowledge (Beyer & Davis, 2012; Godino et al., 2017). Therefore, teacher training programs should focus on developing the necessary knowledge and skills that enable teachers to critically reflect on the management of mathematics curricular materials, using specific criteria to successfully carry out this task (Beyer & Davis, 2012).
With this interest in mind, in this work we have described the implementation and results of a training action aimed at developing the critical analysis competence of Peruvian mathematics teacher trainees regarding probability curriculum materials. The prior reflection of the teacher trainees has allowed us to identify their prior knowledge and beliefs about what defines a good curriculum material and how they identify it in a specific one. In this case, the facets that were mentioned less were the epistemic one (mathematical content) and the ecological one (correspondence with the curricular, academic, and social environment), highlighting partial aspects of the affective facet (being attractive and motivating for students). When focusing on the workbook for analysis, except for one of them who did not consider it appropriate, all of them valued it as a suitable material to use in their classroom. In these evaluations, the aspects that were mainly highlighted were of an epistemic and affective nature, followed by the interactional one (the last two not mentioned in the general characteristics of a good material, which suggests that having a specific example helps them to concretize their reflection).
After the training, providing the FT with a guide with the indicators of didactic suitability to analyse the worksheet aimed to direct their attention towards fundamental aspects that condition instructional processes. We observed that even with this instrument, participants had difficulties in assessing the degree of compliance of indicators in the different facets. This led them to overlook important deficiencies in the epistemic facet (prevalence of the classical meaning over the frequentist one, omission of the applicability conditions of Laplace’s rule and the properties of probability, lack and disarticulation of the different meanings of probability), cognitive (lack of attention to prior knowledge and prediction of probabilistic biases), interactional (confusing and deficient presentation of content), mediational (absence of activities to incorporate material and technological resources), and ecological (lack of connection with other disciplines, content not included in the curriculum). Only one-third of the participants managed to express a reasoned judgment of didactic suitability, which was considered high in all facets except interactional. In this case, it is observed that their discourse is based on the degree of compliance with indicators and the deficiencies found.
In the third prompt, more than half of the participants propose relevant improvement proposals, which means that some of the FT who did not respond or did so inconclusively to the issuance of a value judgment on didactic suitability did consider the indicators to make change proposals based on their degree of fulfilment. However, there are important deficiencies in the worksheet to be corrected: expanding the range of problems with tasks that connect the different meanings of probability, promoting experimentation and simulation of random experiments, avoiding the predominant use of equiprobable devices (dice, coins) that leads students to extend the application of the Laplace rule to all probabilistic situations, among others. In addition, it is observed that the ecological facet is still absent when there is a mismatch between what is contemplated in the worksheet and the curricular guidelines.
In summary, providing teachers with opportunities to reflect on their teaching practice is not enough; they need tools to direct their attention towards relevant elements of the teaching and learning processes (Seckel & Font, 2020; Sun & Van Es, 2015). These tools should be incorporated into initial and continuing teacher education activities, where other deficiencies in the future teacher’s knowledge can also be observed. In our case, the research results lead us to the need to reinforce didactic-mathematical knowledge in probability from an epistemic perspective (practices, objects, and processes characteristic of the different meanings of probability and how they relate), cognitive (factors that influence the complexity of probability situations and biases), as well as in the other facets, where a confused idea of affective aspects is observed, such as student autonomy or the importance of adopting the curriculum in materials to guarantee a progression of learning without gaps.
Acknowledgments
Work developed within the PID2019-105601GB-I00/AEI/10.13039/50110001103 project, with the support of the research groups: S60_20R - Investigación en Educación Matemática (Gobierno de Aragón y Fondo Social Europeo) and FQM126 (Junta de Andalucía).
REFERENCES
Batanero, C., & Borovcnik, M. (2016). Statistics and probability in high school. Sense Publishers. https://doi.org/10.1007/978-94-6300-624-8 [ Links ]
Beltrán-Pellicer, P., Godino, J., & Giacomone, B. (2018). Elaboración de indicadores específicos de idoneidad didáctica en probabilidad: Aplicación para la reflexión sobre la práctica docente. Bolema: Boletim de Educação Matemática, 32(61), 526-548. https://doi.org/10.1590/1980-4415v32n61a11 [ Links ]
Beyer, C., & Davis, E. (2012). Learning to critique and adapt science curriculum materials: Examining the development of preservice elementary teachers’ pedagogical content knowledge. Science Education, 96(1), 130-157. https://doi.org/10.1002/sce.20466 [ Links ]
Breda, A., Font, V., & Pino-Fan, L. (2018). Criterios valorativos y normativos en la didáctica de las matemáticas: El caso del constructo idoneidad didáctica. Bolema: Boletim de Educação Matemática, 32(60), 255-278. https://doi.org/10.1590/1980-4415v32n60a13 [ Links ]
Breda, A., Pino-Fan, L., & Font, V. (2017). Meta Didactic-Mathematical knowledge of teachers: Criteria for the reflection and assessment on teaching practice. Eurasia Journal of Mathematics, Science and Technology Education, 13(6), 1893-1918. https://doi.org/10.12973/eurasia.2017.01207a [ Links ]
Brown, M. (2009). The teacher-tool relationship: Theorizing the design and use of curriculum materials. In J. Remillard, B. Herbel-Eisenmann, & G. Lloyd (Eds.), Mathematics teachers at work: Connecting curriculum materials and classroom instruction (pp. 17-36). Routledge. [ Links ]
Burgos, M., Castillo Céspedes, M. J., Beltrán-Pellicer, P., Giacomone, B., & Godino, J. (2020). Análisis didáctico de una lección sobre proporcionalidad en un libro de texto de primaria con herramientas del enfoque ontosemiótico. Bolema: Boletim de Educação Matemática, 34(66), 40-68. https://doi.org/10.1590/1980-4415v34n66a03 [ Links ]
Burgos, M., & Godino, J. (2021). Assessing the epistemic analysis competence of prospective primary school teachers on proportionality tasks. International Journal of Science and Mathematics Education, 20, 367-389. https://doi.org/10.1007/s10763-020-10143-0 [ Links ]
Castillo Céspedes, M. J., & Burgos, M. (2022). Reflexiones de futuros maestros sobre la idoneidad didáctica y modo de uso de una lección de libro de texto. Bolema: Boletim de Educação Matemática, 36(72) 555-579. https://doi.org/10.1590/1980-4415v36n72a25 [ Links ]
Castillo Céspedes, M. J., Burgos, M., & Godino, J. (2022). Elaboración de una guía de análisis de libros de texto de matemáticas basada en la teoría de la idoneidad didáctica. Educação e Pesquisa, 48, Artículo e238787. https://doi.org/10.1590/S1678-4634202248238787esp [ Links ]
Cohen, L., Manion, L., & Morrison, K. (2011). Research methods in education. Routledge. [ Links ]
Cotrado, B., Burgos, M., & Beltrán-Pellicer, P. (2022). Idoneidad didáctica de materiales curriculares oficiales peruanos de educación secundaria en probabilidad. Bolema: Boletim de Educação Matemática, 36(73), 888-922. https://doi.org/10.1590/1980-4415v36n73a13 [ Links ]
Esqué, D., & Breda, A. (2020). Valoración y rediseño de una unidad sobre proporcionalidad, utilizando la herramienta idoneidad didáctica. Uniciencia, 35(1), 38-54. http://dx.doi.org/10.15359/ru.35-1.3 [ Links ]
Giacomone, B., Godino, J., Wilhelmi, W., & Blanco, T. (2018). Desarrollo de la competencia de análisis ontosemiótico de futuros profesores de matemáticas. Revista Complutense de Educación, 29(4), 1109-1131. https://doi.org/10.5209/RCED.54880 [ Links ]
Godino, J. (2013). Indicadores de la idoneidad didáctica de procesos de enseñanza y aprendizaje de las matemáticas. Cuadernos de investigación y formación en educación matemática, (11), 111-132. https://revistas.ucr.ac.cr/index.php/cifem/article/view/14720 [ Links ]
Godino, J., Batanero, C., & Font, V. (2007). The onto-semiotic approach to research in mathematics education. ZDM, 39(1-2), 127-135. https://doi.org/10.1007/s11858-006-0004-1 [ Links ]
Godino, J., Giacomone, B., Batanero, C., & Font, V. (2017). Enfoque ontosemiótico de los conocimientos y competencias del profesor de matemáticas. Bolema: Boletim de Educação Matemática, 31(57), 90-113. https://doi.org/10.1590/1980-4415v31n57a05 [ Links ]
Godino, J., Rivas, H., Arteaga, P., Lasa, A., & Wilhelmi, M. (2014). Ingeniería didáctica basada en el enfoque ontológico-semiótico del conocimiento y la instrucción matemáticos. Recherches en Didactique des Mathématiques, 34(2-3), 167-200. https://www.ugr.es/~jgodino/eos/JDGodino_ID-EOS_31mayo2014.pdf [ Links ]
Hoadley, U., & Galant, J. (2016). An analysis of the grade 3 Department of Basic Education workbooks as curriculum tools. South African Journal of Childhood Education, 6(1), 1-12. https://doi.org/10.4102/sajce.v6i1.400 [ Links ]
Ministerio de Educación (Minedu). (2019). Cuaderno de trabajo de matemática: Resolvamos problemas secundaria 1. Minedu. https://repositorio.minedu.gob.pe/handle/20.500.12799/6862 [ Links ]
Remillard, J., & Kim, O. K. (2020). Elementary mathematics curriculum materials: Designs for student learning and teacher enactment. Springer Nature. https://link.springer.com/book/10.1007/978-3-030-38588-0 [ Links ]
Seckel, M. J., & Font, V. (2020). Competencia reflexiva en formadores del profesorado de matemática. Magis: Revista Internacional de Investigación en Educación, 12(25), 127-144. https://doi.org/10.11144/Javeriana.m12-25.crfp [ Links ]
Stein, M. K., Remillard, J., & Smith, M. (2007). How curriculum influences student learning. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 319-370). Information Age Publishing. [ Links ]
Strauss, A., & Corbin, J. (1990). Basics of qualitative research: Grounded theory procedures and techniques. Sage Publications, Inc. [ Links ]
Sun, J., & Van Es, E. (2015). An exploratory study of the influence that analyzing teaching has on preservice teachers’ classroom practice. Journal of Teacher Education, 66(3), 201-214. https://doi.org/10.1177/0022487115574103 [ Links ]
Thompson, D. (2014). Reasoning-and-proving in the written curriculum: Lessons and implications for teachers, curriculum designers, and researchers. International Journal of Educational Research, (64), 141-148. https://doi.org/10.1016/j.ijer.2013.09.013 [ Links ]
Vásquez, C., & Alsina, A. (2015). El conocimiento del profesorado para enseñar probabilidad: Un análisis global desde el modelo del conocimiento didáctico-matemático. Avances de Investigación en Educación Matemática, (7), 27-48. https://dialnet.unirioja.es/servlet/articulo?codigo=5682820 [ Links ]
Yang, K., & Liu, X. (2019). Exploratory study on Taiwanese secondary teachers’ critiques of mathematics textbooks. Eurasia Journal of Mathematics, Science and Technology Education, 15(1), 1-16. https://doi.org/10.1007/s10857-019-09453-0 [ Links ]
1The training of secondary mathematics teachers in Peru is carried out in public and private universities, as well as in Higher Pedagogical Institutes, with a ten-semester duration.
Received: January 22, 2023; Accepted: March 22, 2023










 texto em
texto em