Introdução

Segundo ^{D’Ambrosio (2005, p. 30)}: “As ideias matemáticas, particularmente comparar, classificar, quantificar, medir, explicar, generalizar, inferir e, de algum modo, avaliar, são formas de pensar, presentes em toda a espécie humana.” Nos causa estranheza a forma como esses assuntos são abordados nas escolas, enfatizando a memorização de regras e técnicas, uma vez que as habilidades matemáticas perpassam a essência da própria humanidade.

Nesse sentido, este artigo objetiva discutir a relevância do raciocínio na matemática escolar e os elementos necessários a uma atividade que privilegie o raciocínio proporcional. Com este intuito, discutimos que a sequência definição → exemplos → exercícios tem tido lugar de destaque na matemática escolar. Abordamos que, historicamente, a memorização tem sido valorizada na educação brasileira e tem roubado do raciocínio o papel de protagonista. Especificamente na matemática escolar, a memorização de regras e técnicas tem acarretado consequências à aprendizagem matemática de nossos alunos.

Assim, argumentamos sobre a relevância do raciocínio proporcional para a matemática escolar e a relação que pode ser estabelecida entre a matemática, o cotidiano e outras disciplinas escolares para o desenvolvimento e exploração desse tipo de raciocínio nos anos finais do ensino fundamental. Discutimos ainda, que para desenvolver e explorar o raciocínio proporcional dos alunos de matemática da educação básica, é necessário realizar atividades intencionais nas aulas e, por isso, tratamos dos elementos necessários para elaboração dessas atividades.

A sequência definição → exemplos → exercícios

Conforme ^{Nacarato, Mengali e Passos (2009)}, nos anos finais do ensino fundamental a aprendizagem de matemática não ocorre por repetições e mecanizações, mas consiste em uma prática social que requer envolvimento do aluno em atividades que estabeleçam relações e que façam parte de um processo gradual, em que definir, exemplificar e fazer exercícios não devem ser as tarefas centrais.

A prática escolar pautada em “definição → exemplos → exercícios” em matemática está relacionada ao ensino tradicional e foi historicamente incentivada no Brasil. Segundo ^{Souza (1998)}, esse modelo de prática teve motivação inicial a partir da dependência que o ensino tinha da Igreja. Nesse contexto, os alunos eram vistos como catecúmenos e a memorização mecânica era necessária, pois a permissão para raciocinar e desenvolver suas próprias ideias e interpretações produziria o risco de os jovens criarem uma heresia de cunho doutrinário ou ideológico. Isso implicou que, na escola, o ensino fosse reduzido à prática de memorização, de forma que:

Memorizar era uma forma de o professor ensinar aquilo que não sabia, de o aluno aprender o que não entendia, de os examinadores avaliarem o que não compreendiam, na esperança de que um dia encontrariam o sentido do que aprenderam de cor (^{SOUZA, 1998, p. 88}).

Esse formato claramente se refletiu no ensino da disciplina de matemática e, ainda hoje, o encontramos nas escolas brasileiras. Mas, além da influência dos métodos educacionais implementados pela igreja, ^{Oliveira (2007)} aponta para outro método.

No decorrer dos anos, a Matemática tem sido ensinada obrigando o aluno a estudar e resolver problemas fora de sua realidade e, até sem aplicação no seu cotidiano. Tal ensino é remanescente do método tecnicista onde se ensinavam técnicas para o aluno aprender, a partir do memorizar, se contrapondo aquela que considera o conhecimento em constante construção (^{OLIVEIRA, 2007, p. 13}).

Muitas vezes, nas aulas de matemática, o ensino é iniciado pela explanação da definição de um determinado conteúdo, seguido de exemplos que já foram matematicamente comprovados. Por fim, as questões são praticadas por meio de exercícios análogos ao exemplo dado, que retomam fórmulas e métodos decorados nas etapas anteriores. Ao final se corrige o exercício na lousa, com a explicação da solução ideal.

No ensino de Matemática, predominam aulas com uma introdução, pelo professor, com explicações teóricas e formais sobre um novo tópico matemático, alguns exemplos de questões e/ou aplicações resolvidos no quadro e, em seguida, uma lista de exercícios que, em função da quantidade, acabam, em parte, ficando como trabalho de casa. Variações deste mesmo modelo, dando maior ou menor ênfase às explicações do professor, com alunos trabalhando ora individualmente, ora em grupo, em atividades com seminários ou a partir de propostas fundamentadas em aplicações matemáticas, em muitos casos, também fazem parte das aulas. No entanto, todas têm um forte apego às listas de exercícios que os professores propõem muitas vezes por julgarem que praticando o aluno compreenderá o conteúdo. Por outro lado, nos programas curriculares, encontramos objetivos educacionais como: desenvolver o raciocínio lógico e a criatividade (^{BENNEMANN, ALLEVATO, 2012, p. 103-104}).

Esse modelo se assemelha ao que ^{Freire (1981)} denominou de educação bancária, uma relação em que o professor é o detentor do conhecimento, o sujeito ativo da relação, e que por ter o conhecimento em seu poder, deposita-o no aluno. Esse, por sua vez, é sujeito passivo e, por isso, recebe o conhecimento seguindo as indicações do professor. O foco na educação bancária é a formação de sujeitos obedientes, disciplinados e submissos, que compõem uma população subordinada, que não questiona e se acomoda com a falta de criatividade, de raciocínio e de liberdade. Especificamente na matemática, a educação bancária acontece há décadas.

Sabe-se que a típica aula de Matemática a nível de primeiro, segundo ou terceiro graus ainda é uma aula expositiva, em que o professor passa para o quadro negro aquilo que ele julgar importante. O aluno, por sua vez, cópia da lousa para o seu caderno e em seguida procura fazer exercícios de aplicação, que nada mais são do que uma repetição na aplicação de um modelo de solução apresentado pelo professor. Essa prática revela a concepção de que é possível aprender Matemática através de um processo de transmissão de conhecimento (^{D’AMBROSIO, 1989, p. 15}).

Embora esse apontamento tenha sido feito há trinta anos, infelizmente ainda é realidade (^{VALENTE, 2016}). As práticas ligadas à reprodução de ideias e conceitos contribuem para que as compreensões matemáticas se reduzam à memorização de regras e técnicas que são repetidas nas avaliações e que surtem pouco efeito no cotidiano dos alunos. Segundo Freire,

Um dos equívocos de muitos educadores que insistem em demasiado numa coisa importante, e que a escola tradicional usou muito, é a repetição. A repetição da definição, a repetição do conceito, da descrição do conceito. É como se repetindo o educando aprendesse. A repetição se dando como meio de se possibilitar a memorização. Obviamente que não há aprendizagem sem memorização, não há conhecimento sem memorização. O equívoco está em que não se memoriza para aprender, aprende e por isso memoriza. Só é possível memorizar na medida em que eu aprendo o objeto. É porque eu sei o objeto que eu memorizo o objeto, não o contrário (^{FREIRE, 2018, p. 71}).

^{Freire (2018)} ainda destaca que, se as práticas mecânicas de memorização da descrição do conceito fossem substituídas pela aprendizagem pautada no entendimento do objeto, “[...] ensinar seria uma coisa mais séria, mais complexa do que a gente pensa que é” (^{FREIRE, 2018, p. 71}). Para que o cenário atual seja mudado, ^{Valente (2016, p. 5)} afirma que “[...] as práticas ligadas à memorização devem ser abandonadas em favor de métodos em que haja uma participação ativa do aluno”. Assim, a educação não pode ser eficaz por meio de “depósitos”, como acontece no modelo da educação bancária. A prática precisa ser pautada na ação e reflexão sobre o mundo de forma problematizadora e não mecanizada. Homens e mulheres precisam ser corpos conscientes. De modo que:

[...] a educação libertadora, problematizadora, já não pode ser o ato de depositar, ou de narrar, ou de transferir, ou de transmitir ‘conhecimentos’ e valores aos educandos, meros pacientes, à maneira da educação “bancária”, mas um ato cognoscente. O antagonismo entre as duas concepções, uma, a ‘bancária’, que serve à dominação; outra, a problematizadora, que serve à libertação, toma corpo exatamente aí. Enquanto a primeira, necessariamente, mantém a contradição educador-educando, a segunda realiza a superação (^{FREIRE, 1981, p. 78}).

É nesse sentido que ^{Ponte, Oliveira e Varandas (2008, p. 166)} afirmam que “[...] o papel do professor, em muitas situações, é visto, sobretudo, como o de fornecer informações aos alunos, controlar o discurso e o desenvolvimento da aula, procurando que todos os alunos atinjam os mesmos objetivos no mais curto espaço de tempo”. Embora essa seja a prática vigente, Maltempi e Mendes afirmam que:

Atualmente, alunos e professores pressionam por mudanças no ensino de Matemática. Os primeiros ao manifestarem insatisfação com uma Matemática difícil, desinteressante e dissociada do mundo em que vivem; e os professores por estarem frustrados por não conseguirem estimular seus alunos a aprenderem matemática (^{MALTEMPI; MENDES, 2016, p. 87}).

Segundo ^{Valente (2016)}, para que haja mudança é necessário abandonar formas de instruir alunos nos conteúdos matemáticos e passar a educar de acordo com as suas necessidades e possibilidades. Para isso, devemos nos empenhar em criar metodologias que tornem os alunos responsáveis pelo próprio aprendizado. Formar cidadãos criativos, competentes e autônomos no que diz respeito à pesquisa e à ciência que perpassam as disciplinas escolares e a vida. Mas, para que isso ocorra, é necessário dar prioridade ao desenvolvimento e à exploração do raciocínio nas aulas de matemática, conforme discutiremos na próxima seção.

Memorização e raciocínio

É comum que as pessoas se recordem de ter decorado regras nas aulas de matemática. Desde pequenos somos levados a decorar a tabuada. Com o passar do tempo somos apresentados às fórmulas, expressões e a frases que nem sempre fazem sentido, como “a ordem dos fatores não altera o produto”, “mais com mais dá mais”, “a ao quadrado mais b ao quadrado é igual a c ao quadrado”, “a mais b ao quadrado é igual ao quadrado do primeiro, mais duas vezes o primeiro vezes o segundo, mais o quadrado do segundo”, dentre tantas outras.

Ao iniciar os estudos algébricos, conhecemos o x e nos surpreendemos com quantos significados diferentes pode haver para uma única letra. No vídeo intitulado “Romanos”¹, do canal de humor ”Porta dos Fundos”, os atores ironicamente questionam “quem foi o gênio que teve essa brilhante ideia de colocar letras e números iguais?”. No vídeo é possível analisar pelo menos três significados que o x, em suas diferentes formas de escrita, pode representar na matemática, como o número dez romano, o símbolo da multiplicação, e uma incógnita. O x também é usado para representar um erro na resolução da questão colocada, e as críticas não param por aí. Um dos personagens, ao ser questionado sobre o valor do “xizinho” responde prontamente que, como o X (em letra maiúscula) é dez, então o valor de “xizinho” ( x em letra minúscula) é cinco, o que mostra que decorar valores sem entender o significado, não faz sentido. Técnicas de cálculo como “isolar o x e passar o resto pro outro lado” são lembrados pelo personagem do professor que encena “Romanos”, que se mostra enfurecido com o fato de seus alunos ainda não terem decorado a regra.

A cena da aula em “Romanos” possui muitas semelhanças com as salas de aula de matemática. Segundo ^{Valente e Pinheiro (2015)}, é preciso estar ciente que decorar não é uma boa forma de favorecer a aprendizagem do aluno. Repetir regras e técnicas até pode ser eficiente, mas certamente não levará à fixação na memória de nossos alunos se não houver preocupação com a compreensão.

Não queremos aqui dizer que memorizar é algo ruim. Seria terrível se, todos os dias, esquecêssemos tudo o que memorizamos no dia anterior. Ter uma boa capacidade de armazenar informações é uma qualidade indiscutível. O que defendemos é que as atividades de memorização estejam relacionadas ao raciocínio, ao cálculo mental e à identificação de padrões que levem à formulação de esquemas capazes de resultar em algo que seja válido em diversas situações, com a sistematização do que foi aprendido. Explicar o caminho encontrado e compartilhar com a turma o procedimento para chegar a um resultado é uma forma dos alunos desenvolverem a autonomia, a criticidade, a criatividade e a capacidade de tomar decisões. Ao raciocinar, conectamos argumentos, fazemos deduções e estabelecemos relações que nos conduzem a reflexões, análises e sínteses. No lugar de exigir a insistência e o esforço de nossos alunos para decorar podemos valorizar o raciocínio.

Assim, passamos a discutir que, especificamente no ensino de matemática na educação básica, temos muito a ganhar se reconhecermos a relevância do raciocínio proporcional.

Relevância do raciocínio proporcional para a matemática escolar

O raciocínio proporcional se relaciona com formas de raciocínio, identificação de situações proporcionais e não proporcionais, desenvolvimento e aprimoramento de habilidades e aptidões concernentes à lógica necessária ao raciocínio matemático (^{FERNÁNDEZ; LLINARES, 2012}; ^{LAMON, 2005}; ^{FARIA, 2016}). Faria explicita que o raciocínio proporcional pode ser entendido como:

[...] a capacidade de raciocinar, estabelecendo uma relação entre duas ou mais grandezas em termos relativos, mobilizando para tal raciocínio a habilidade de analisar qualitativamente situações, estabelecer relações, julgar com equidade e distinguir circunstâncias proporcionais das não proporcionais (^{FARIA, 2016, p. 49}).

Pela sua abrangência, o raciocínio proporcional é de extrema importância para a formação matemática dos alunos dos anos finais do ensino fundamental. Ao estimulá-los, trabalham-se questões que instigam o senso de justiça; o reconhecimento das proporções nas relações estruturais que envolvem escalas e a constante de proporcionalidade; a capacidade de analisar dados quantitativos e como interpretá-los qualitativamente; a escolha por termos relativos oriundos de uma estrutura multiplicativa, mesmo com a possibilidade de escolher termos absolutos provenientes da estrutura aditiva; e a habilidade de relacionar grandezas, e de diferenciar circunstâncias proporcionais das não proporcionais.

O raciocínio proporcional é mais abrangente do que realizar cálculos baseados em expressões do tipo ab=cd , ele é primordial para que elaboremos argumentos e explicações diante de contextos e aplicações baseados na proporcionalidade. Do mesmo modo que afirmamos que a memorização tenha o seu valor, esta não deve ser exigida em detrimento do raciocínio. Reforçamos a ideia de que saber operar cálculos proporcionais é importante, mas raciocinar é muito mais abrangente e, por isso, deve ser prioridade na no ensino da matemática escolar.

Não negamos a importância da mobilização das noções de cálculo proporcional para raciocinar proporcionalmente. No entanto, consideramos o raciocínio proporcional mais profundo e mais amplo do que a proporcionalidade, pois, enquanto este envolve dados quantitativos, para os quais resultados puramente numéricos já satisfazem, aquele exige que interpretações qualitativas emerjam na compreensão de aplicações e contextos baseados na proporcionalidade, sejam na matemática, em outras ciências ou em situações do cotidiano (^{LAMON, 2005}).

A relevância do raciocínio proporcional para a matemática escolar ainda compreende o fato de que é extremamente útil na interpretação dos fenômenos reais, pois muitos aspectos de nossas vidas operam sob essa estrutura (^{FERNÁNDEZ; LLINARES, 2012}). Esse é mais um fator que indica que desenvolver a capacidade de raciocinar proporcionalmente é importante para os alunos dos anos finais do ensino fundamental. Assim, ao explorar o raciocínio proporcional, contribuímos para que os alunos estabeleçam relações entre a matemática e situações do cotidiano fora da escola, ao calcular as compras, ao identificar investimentos mais lucrativos, ao explorar desenhos e mapas, ao executar medições, ao converter moedas ou ajustar uma simples receita de bolo ao número de convidados de uma festa.

Além disso, o aluno que raciocina proporcionalmente poderá ter um melhor desempenho em outras disciplinas escolares, pois será capaz de entender as escalas dos mapas proporcionais à realidade estudada em geografia; de interpretar o crescimento dos seres vivos, por vezes proporcionais ao tempo de vida, trabalhada nas aulas de ciências; de compreender a escala musical e as proporções entre os elementos que compõem os quadros de Leonardo da Vinci, estudados em artes; e em inúmeras outras situações que emergem no âmbito dos mais distintos conteúdos escolares.

É nesse sentido que defendemos o desenvolvimento e exploração do raciocínio proporcional e indicamos, na próxima seção, elementos necessários a uma atividade que o privilegie.

Processo de elaboração de atividade que estimula o raciocínio proporcional

Para desenvolver e explorar o raciocínio proporcional dos alunos de matemática da educação básica é necessário formular atividades intencionais, ou seja, questões que tenham por objetivo estimular este peculiar raciocínio. Partindo do pressuposto que “[...] desenvolver o raciocínio matemático dos alunos é, sem dúvida, um dos grandes objetivos da Matemática escolar [...]” (^{MATA-PEREIRA; PONTE, 2018, p. 782}), temos o intuitode discutir os elementos necessários à uma atividade que privilegie o raciocínio proporcional e, para isso, compartilhamos o processo de elaboração de uma atividade de seu desenvolvimento e exploração do nos anos finais do ensino fundamental com o GeoGebra, intitulada “Frações Equivalentes e Porcentagem”.

Essa atividade é uma das quatro que compõem as atividades de desenvolvimento e exploração do raciocínio proporcional propostas e disponíveis em ^{Faria (2016)} e no GeoGebraBook². Ressaltamos que não buscamos esgotar os elementos necessários a uma atividade que estimule o raciocínio proporcional, a finalidade aqui consiste em destacar os elementos que se sobressaíram na experiência de elaboração das atividades descritas em ^{Faria (2016)}.

A atividade (Quadro 1), cujo processo de elaboração será analisado a seguir, descreve a situação de uma loja que fez uma liquidação, anunciando 40% de desconto, mas que, alguns dias antes, aumentou os preços em 30%. Ainda é investigado o que ocorreu com o preço de um fogão que passou pelo mesmo processo de aumento seguido de desconto.

Elaborar o enunciado é parte importante do processo, pois, para que uma atividade estimule o raciocínio proporcional é necessário que tenha um caráter transdisciplinar, no sentido de que transite por territórios não restritos às disciplinas escolares e contribua para a formação epistemológica e para o desenvolvimento da capacidade de raciocinar proporcionalmente em situações relativas ao cotidiano. A transdisciplinaridade, “leva o indivíduo a tomar consciência da essencialidade do outro e da sua inserção na realidade” (^{D’AMBROSIO, 2011, p. 10}), e pode dar origem, “[a]o despertar da consciência na aquisição do conhecimento” (^{D’AMBROSIO, 2011, p. 10}). Assim, a relação de disciplinas com o contexto social, cultural, histórico e político de uma comunidade pode ser entendida como transdisciplinaridade, que incentiva uma nova compreensão da realidade, articuladora de elementos que passam entre, além e através (ideia de trans) das disciplinas em busca de compreensão da complexidade que abrange o ser humano, o conhecimento e a consciência (^{FARIA, 2016}).

De acordo com ^{Boavida, Paiva, Cebola, Vale e Pimentel (2008)}, é preciso envolver os alunos em atividades que abordam situações do cotidiano para, assim, estimular o seu raciocínio. Para tanto, é recomendado que sejam elaboradas atividades diversificadas e significativas, que promovam investigação, comunicação matemática, argumentação e conexões matemáticas.

Com o intuito de melhorar a compreensão da situação matemática proposta, toda a atividade foi elaborada na perspectiva intradisciplinar, que possibilita uma visão abrangente dos conceitos explorados, dando a atenção necessária às particularidades das vertentes aritmética, geométrica e algébrica. A intradisciplinaridade corresponde às rigorosas relações das ramificações de uma mesma disciplina. Sendo assim, a matemática pode ser entendida como disciplina matriz, e a aritmética, a geometria e a álgebra como disciplinas derivadas ou ainda como ramificações da disciplina matriz (^{FARIA, 2016}).

Nesse sentido, um arquivo do GeoGebra (duas-operações-consecutivas.ggb) (Figura 1) é utilizado, pois este software otimiza e viabiliza a abordagem matemática intradisciplinar do raciocínio proporcional, evidenciando características específicas de cada vertente matemática, o que contribui para o entendimento do todo e para a compreensão de conceitos e relações que ocorrem concomitantemente. Além disso, o GeoGebra possibilita a exploração de múltiplas representações que destacam particularidades das ramificações matemáticas por meio de seus diversos recursos e janelas que apresentam os objetos matemáticos dinamicamente conectados, o que contribui para que as desvantagens de cada representação sejam supridas pelas vantagens das outras, no que se refere ao ensino e à aprendizagem de matemática (^{FARIA; MALTEMPI, 2018}).

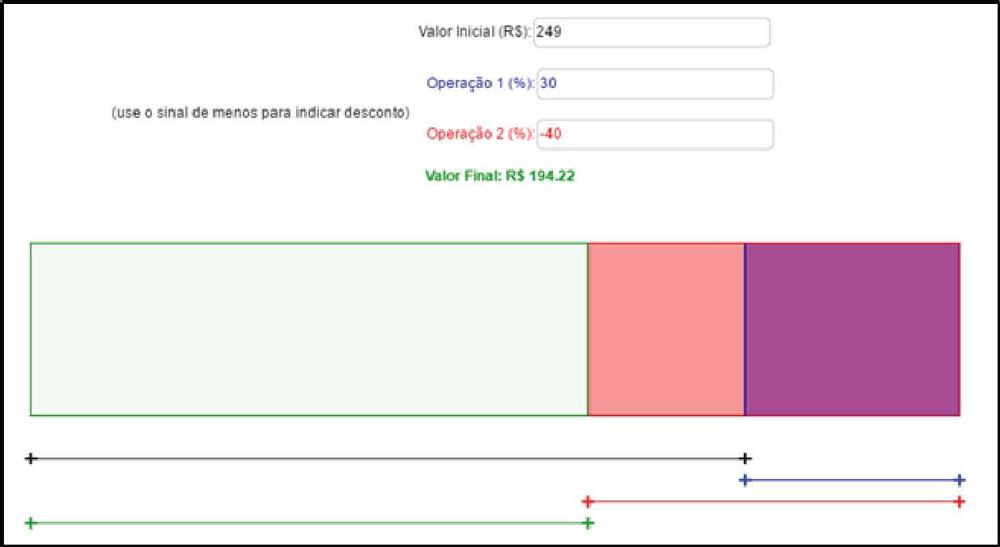
Fonte: Elaborada pelos Autores (2020).

Figura 1 Construção no GeoGebra da situação descrita no Quadro I 

No item a, é dado que um micro-ondas que durante todo o ano custava R$ 249,90 entrou em liquidação. Os controles deslizantes do GeoGebra mostram que o produto, que sofreu um aumento de 30% e um desconto consecutivo de 40%, era vendido na liquidação por R$194,22. Assim, se percebe que houve um desconto no produto ao entrar em liquidação. Contudo, o desconto realmente dado ao produto foi de R$ 55,68, obtido pela subtração do valor inicial pelo valor final. Assim, se comparado ao valor inicial de R$ 249,90, o desconto não foi de 40% e sim de 22%. Mas, para chegar à resposta, é necessário que o professor intervenha e estimule seus alunos para que façam inferências justificadas, utilizando conhecimentos matemáticos prévios para obter novas conclusões. Nesse processo,

[...] o professor deve resistir ao impulso de dar indicações para a resolução de tarefas e problemas, tentando apoiar o raciocínio e o trabalho do aluno. Se o professor apresenta demasiadas indicações aos alunos e não os desafia, a resolução da tarefa é simplificada e não apoia o desenvolvimento do raciocínio (^{MATA-PEREIRA; PONTE, 2018, 785}).

Assim, o professor deve questionar os alunos e organizá-los de modo que consigam compartilhar suas dúvidas e ouvir os colegas para que possam construir suas ideias em colaboração. No processo de desenvolvimento e construção do raciocínio, as justificativas devem ser resultado de uma tarefa coletiva permeada da discussão, esclarecimento e refutação de possíveis respostas aos questionamentos propostos pelo professor.

Embora seja uma atividade simples, é preciso raciocinar proporcionalmente para se chegar à conclusão. Nesse sentido, o raciocínio quantitativo, pautado na estrutura aditiva não é suficiente, é necessário raciocinar qualitativamente, ou seja, em uma estrutura multiplicativa. Pensar desse modo envolve mais do que a comparação de valores absolutos, deve-se levar em consideração valores relativos por meio de uma comparação entre o valor inicial e os valores que sofreram aumento e desconto.

Nesse sentido, elaborar atividades que estimulem o raciocínio proporcional implica em muito mais do que fazer questões que empreguem algoritmos ou cálculos mecânicos. As questões precisam estimular a capacidade de pensar, analisar e explorar relações entre quantidades, que devem ser expostas por meio de comentários, explicações e argumentos sobre as relações proporcionais (^{LAMON, 2005}).

^{Freire (1981, p. 80)} afirma que “[...] quanto mais se problematizam os educandos, como seres no mundo e com o mundo, tanto mais se sentirão desafiados. Tão mais desafiados, quanto mais obrigados a responder ao desafio [...]”. Por isso, atividades de desenvolvimento e exploração do raciocínio proporcional devem desafiar nossos alunos a raciocinar matematicamente, e não repetir o modelo de prática escolar em matemática que segue a sequência “definição → exemplos → exercícios”. Para que se tenha um ensino que privilegie o raciocínio, as atividades devem estar centradas em “[...] criar situações de aprendizagem estimulantes, desafiando os alunos a pensar, apoiando-os no seu trabalho, e favorecendo a divergência e a diversificação dos percursos de aprendizagem” (^{PONTE; OLIVEIRA; VARANDAS, 2008, p. 166}).

Conclusão

Neste artigo, debatemos a relevância do raciocínio na matemática escolar. Discutimos, também, os elementos necessários a uma atividade que privilegie o raciocínio proporcional.

Defendemos que para estimular o raciocínio proporcional são necessários alguns elementos. É preciso formular atividades intencionais, com foco no raciocínio qualitativo. É indispensável ter claro o que se quer alcançar com a atividade para pensar no exemplo a ser explorado, nos recursos necessários para desenvolvimento da atividade, nos conteúdos matemáticos que se quer ensinar, dentre outros fatores que permeiam o raciocínio proporcional. Para isso, o enunciado deve instigar a capacidade de pensar, analisar e explorar relações.

Também é necessário que a atividade seja elaborada de modo que se consiga explorar a estrutura multiplicativa, distinguindo-a da estrutura aditiva e trabalhando com o aluno a capacidade de julgar em quais ocasiões cada estrutura é adequada. Também consideramos necessário privilegiar situações relativas ao cotidiano, com caráter transdisciplinar para que uma atividade estimule o raciocínio proporcional. É o interesse e o envolvimento dos alunos com atividades investigativas, diversificadas e significativas, que promovem o desenvolvimento do raciocínio proporcional. Ademais, adotar a perspectiva intradisciplinar, utilizando tecnologias digitais, é uma alternativa para que se tenha uma visão abrangente dos conceitos explorados quanto às particularidades das vertentes aritmética, geométrica e algébrica.