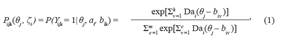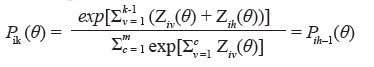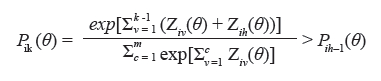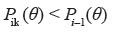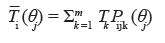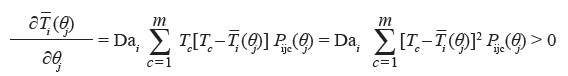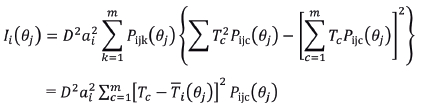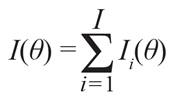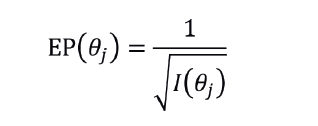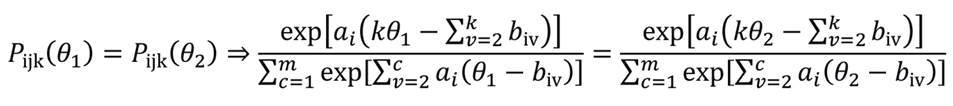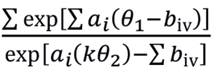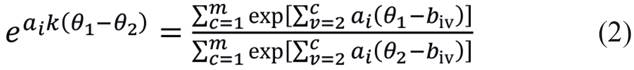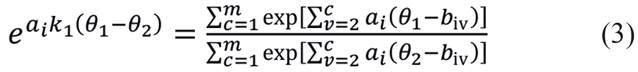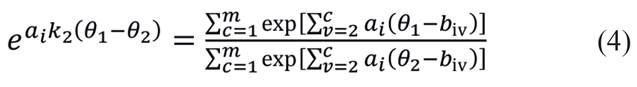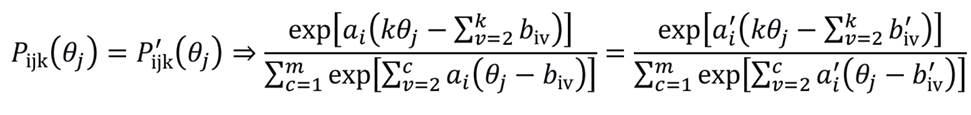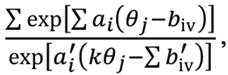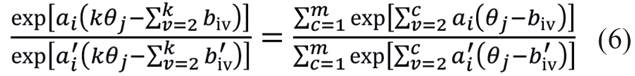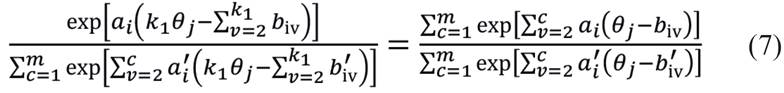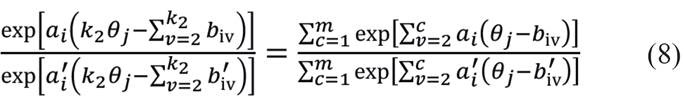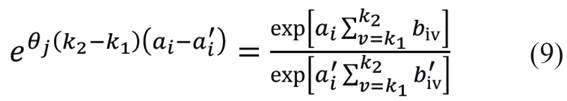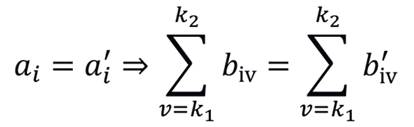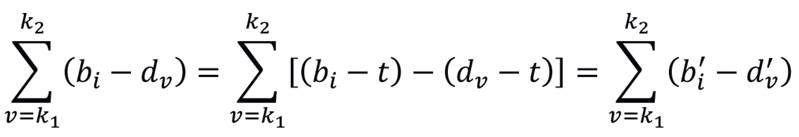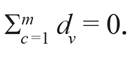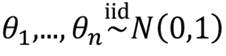INTRODUÇÃO

É cada vez mais frequente o uso dos modelos da Teoria da Resposta ao Item (TRI) para estudar certas características de indivíduos, as quais, muitas vezes, são representadas por quantidades denominadas como traços latentes, que são características que não podem ser medidas diretamente, tais como nível de estresse, nível de depressão, proficiência em determinada área de conhecimento, entre outras. Em muitos instrumentos de medida, os itens (questões) que os compõem apresentam alternativas que pertencem a alguma escala gradual (ordinal). Por exemplo, num questionário de avaliação de um produto por parte de consumidores, as categorias de resposta podem variar de zero (ruim) a cinco (excelente), de modo discreto (^{MURAKI, 1992}); ou, numa avaliação cognitiva, como no vestibular da Universidade Estadual de Campinas (Unicamp),¹ são incluídas questões dissertativas, cujas respostas recebem escores que variam de zero (erro total) a quatro (acerto total), no conjunto {0,1,2,3,4}. Nessas situações, tem-se interesse em avaliar os traços latentes (dos indivíduos) envolvidos. Na primeira, seria o grau de qualidade do produto atribuído pelos consumidores, enquanto, na segunda, seria o conhecimento dos vestibulandos. Em ambos os casos, o Modelo de Crédito Parcial Generalizado (MCPG) poderia ser utilizado para analisar tais dados (^{MURAKI, 1992}, ¹⁹⁹⁷). O MCPG, pertencente à família dos modelos para as respostas politômicas graduais da Teoria de Resposta ao Item (TRI), considera as probabilidades de escolha para cada uma das categorias (^{MURAKI, 1997}).

A literatura brasileira existente sobre o MCPG é escassa. Mesmo na literatura internacional, alguns pontos não têm sido estudados adequadamente, ainda que estes sejam de grande importância. Em parte, isso se deve a uma relativa dificuldade de interpretação dos parâmetros do modelo (^{ANDRADE; TAVARES; VALLE, 2000}), como comentaremos adiante. Em face desse quadro, o presente trabalho tem por objetivo estudar, mais detalhadamente, alguns dos principais aspectos relacionados ao MCPG: interpretação dos parâmetros, principalmente por meio de análises gráficas da função de resposta à categoria do item (FRCI) que caracteriza tal modelo (^{ANDRADE; TAVARES; VALLE, 2000}); avaliação de como mudanças nos parâmetros dos itens afetam a função de informação do item e do teste (^{MURAKI, 1993}); e aspectos ligados à identificabilidade (tema este que por vezes é abordado de modo casual e inadequado). Salientamos que tais resultados são importantes para uma correta utilização de qualquer modelo, em particular do MCPG, bem como na escolha de um método de estimação apropriado.

MODELO DE CRÉDITO PARCIAL GENERALIZADO

O Modelo de Crédito Parcial Generalizado, formulado por ^{Muraki (1992}), pertence à família dos modelos de resposta ao item (MRI) para respostas politômicas graduais, sendo, portanto, apropriado na modelagem de itens cuja resposta está relacionada a algum tipo de escala gradual. Em outras palavras, o respondente ganha mais crédito (teria um maior valor para seu traço latente) à medida que sua resposta se aproxima da completa. A probabilidade de um indivíduo j, com traço latente θj, escolher a categoria k do item i tem por expressão:

em que: i = 1,2,..., I; j = 1,2,..., n e k = 1,2,..., m_i; Y^ijk é igual a 1, se o indivíduo j escolhe a categoria (recebe o escore) _k no item i e 0 em caso contrário; ai é o parâmetro associado à discriminação do i-ésimo item (seu valor também influencia na discriminação do item como um todo); b_ik = b_i - d_k está associado à dificuldade da categoria k do item _i; d_k é a dificuldade relativa da categoria _k em comparação com as outras categorias; θ_j é o traço latente do _j-ésimo indivíduo; ζ_i = (a_i, b_i1,..., b_imi); D é um fator de escala, sendo que D = 1,7 é utilizado quando se deseja que a função logística - equação (1) - forneça resultados semelhantes aos da ogiva normal; P_ijk(θ_j , ζ_i ) é chamada de Função de Resposta à Categoria do Item (FRCI).

Interpretação dos parâmetros

No MCPG, devido à complexidade de sua formulação matemática, a interpretação dos parâmetros dos itens, por meio da visualização (análise gráfica) das curvas características do item (CCI), se torna de extrema importância, mais ainda do que no caso dos modelos para respostas dicotômicas. Nesta subseção, avalia-se como os valores dos parâmetros dos itens afetam o comportamento das curvas (probabilidade de escolha) de cada categoria, bem como seus significados. Nos exemplos apresentados, consideraremos b_i0 ≡ 0, i = 1, 2,…,I, por razões que explicaremos mais adiante.

Parâmetro a_i

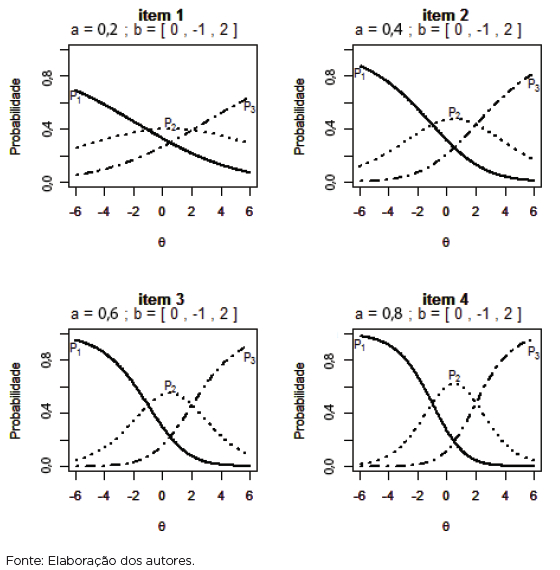
O parâmetro ai é denominado parâmetro de discriminação do item, embora, para o MCPG, afete o comportamento de cada categoria, em relação a esse aspecto. Para o modelo em estudo não são esperados valores de a_i negativos, uma vez que isso indicaria que a probabilidade de atingir categorias “mais difíceis” diminuiria com o aumento do traço latente.

Como ilustrado pela Figura 1, fixando os parâmetros b_ik, quanto maior o valor do parâmetro ai mais as probabilidades de escolha de cada categoria distinguem-se entre si e maior é a distância entre as probabilidades de escolha de duas categorias para indivíduos com traços latentes diferentes. Note-se que a diferença entre as probabilidades de dois indivíduos com traços latentes -2 e 0, por exemplo, escolherem uma determinada categoria de resposta é maior no item 4 (que apresenta maior valor do parâmetro “a”) do que no item 1 (com menor valor do parâmetro “a”), ou seja, o item 4 é mais apropriado para discriminá-los. Assim, quanto maior é o valor do parâmetro “a” de um item, mais diferente é a FRCI entre suas categorias e maior é o seu poder de discriminação.

Parâmetro b_ik

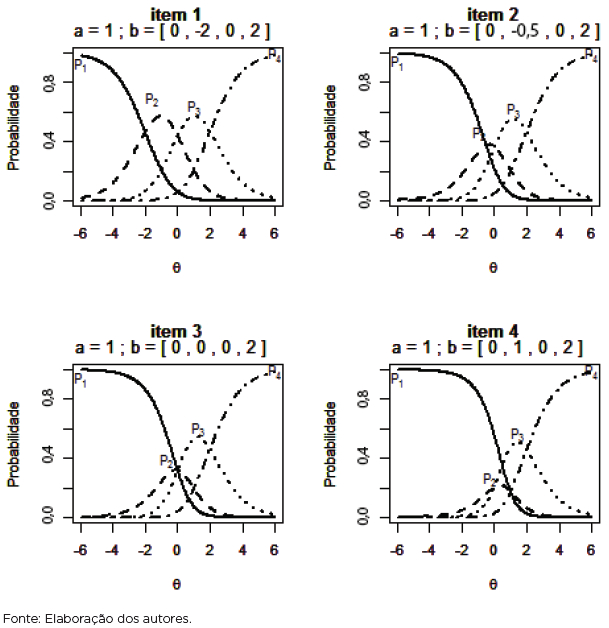
Os parâmetros b_ik, k = 1,..., mi estão associados à dificuldade de cada categoria do item e apresentam valores na mesma escala do traço latente, com espaço paramétrico igual a R. O fato de o traço latente e os parâmetros de dificuldade aparecerem como uma diferença entre si - ver equação (1) - os coloca na mesma escala (há uma relação direta entre a natureza dos dois). Isso permite compreender melhor o que cada nível (categoria) está medindo em relação ao traço latente de interesse. Assim, se os diferentes níveis de dificuldade estiverem vinculados a uma definição de operações cognitivas ou do conteúdo da tarefa, as informações obtidas na avaliação, na maioria das vezes, se tornam qualitativamente mais refinadas (^{SANTOS et al., 2002}).

A Figura 2 apresenta o gráfico da FRCI do MCPG de quatro itens com quatro categorias de resposta, em que se considerou a = 1 para todos os itens, enquanto que os parâmetros de dificuldade variam assim: b_i = (b_i1,b_i2,...,b_imi) com b₁ = (0, -2,0,2), b₂ = (0, -0.5,0,2), b₃ = (0,0,0,2) e b₄ = (0,1,0,2). Em alguns casos (em geral, quando os valores dos parâmetros de dificuldade estão ordenados de forma crescente, em função do valor da categoria), o intervalo (b_ik; b_{ik + 1}) representa o conjunto de valores de θ_j, no qual a probabilidade de escolha da categoria “k” é maior do que a das outras k - 1 categorias. Observando o item 1, nota-se que um indivíduo com traço latente entre -2, por exemplo, tem maior probabilidade de optar pela categoria 2. O mesmo indivíduo, no item 4, tem maior probabilidade de optar pela categoria 1.

Temos ainda que os parâmetros de dificuldade do item podem ser decompostos como b_ik = b_i - d_k, em que d_k serão chamados de parâmetros de categoria (ou d_ik, quando assumimos parâmetros de categoria diferentes para cada item), e que eles correspondem aos pontos na escala do traço latente (θ) em que as curvas associadas à P_ijk-1 e P_ijk se interceptam. Essas duas funções igualam-se somente uma vez, o que pode ocorrer em qualquer ponto na escala de θ. Então, a partir da hipótese de que a_i > 0, tome-se Z_ik (θ) = Da_i (θ - b_ik), portanto: Se θ = b_ih, temos que:

Se θ > b_ih, temos que:

Pode ser considerado um raciocínio análogo, tal como o caso anterior, agora para θ < b_ih, em que:

Parâmetro θ

Como apontado por ^{Andrade, Tavares e Valle (2000}), teoricamente o traço latente pode assumir qualquer valor entre -∞ e ∞. Assim, é necessário estabelecer uma escala na qual ele será medido. Em geral, tal escala é definida fixando-se a média e a variância dos traços latentes, denotando-a por (valor da média, valor do desvio padrão). Ainda, os resultados obtidos em uma métrica podem ser transportados para outra, por meio de transformações lineares (^{ANDRADE; TAVARES; VALLE, 2000}). Por exemplo, o Sistema de Avaliação da Educação Básica (Saeb)/Prova Brasil usa a métrica (250,50). Assim, na escala (0,1), um indivíduo com traço latente 1,5 está a 1,5 desvio padrão acima do traço latente médio, enquanto na escala (250,50) esse mesmo indivíduo teria um traço latente de 325, valor também correspondente a 1,5 desvio padrão acima do traço latente médio (^{ANDRADE; TAVARES; VALLE, 2000}).

Função de Resposta do Item

Como definido em Muraki (1993), a função de resposta ao item para uma dada função de escore (pontuação) T_k = k, k=1,2...,m_i é dada por:

Essa função pode ser vista como a regressão dos escores do item na escala do traço latente (LORD, 1980), apresentando um comportamento estritamente crescente em θ_j e T_k = k, o que pode ser visto a partir de:

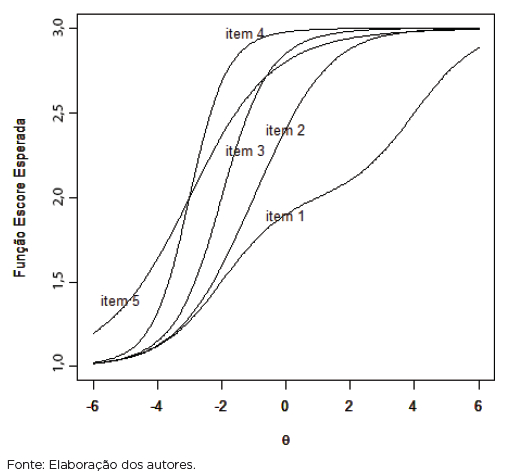
A Função de Resposta do Item (FRI) de cada um dos itens analisados anteriormente (referentes à Figura 2) é apresentada na Figura 3, a qual representa a relação entre o escore esperado de um determinado item, em função do traço latente. Vale ressaltar que o item 1 mostra dois pontos de inflexão (como atestado na Figura 4).

Função de Informação do Item

A Função de Informação do Item (FII) permite avaliar o quanto o item apresenta de informação a respeito do traço latente, ou seja, a qualidade do item para, apropriadamente, estimar os traços latentes e distinguir indivíduos que possuem valores diferentes para estes. A informação do item para a classe de modelos de resposta ao item politômicos foi apresentada por ^{Samejima (1974}) e tem por expressão:

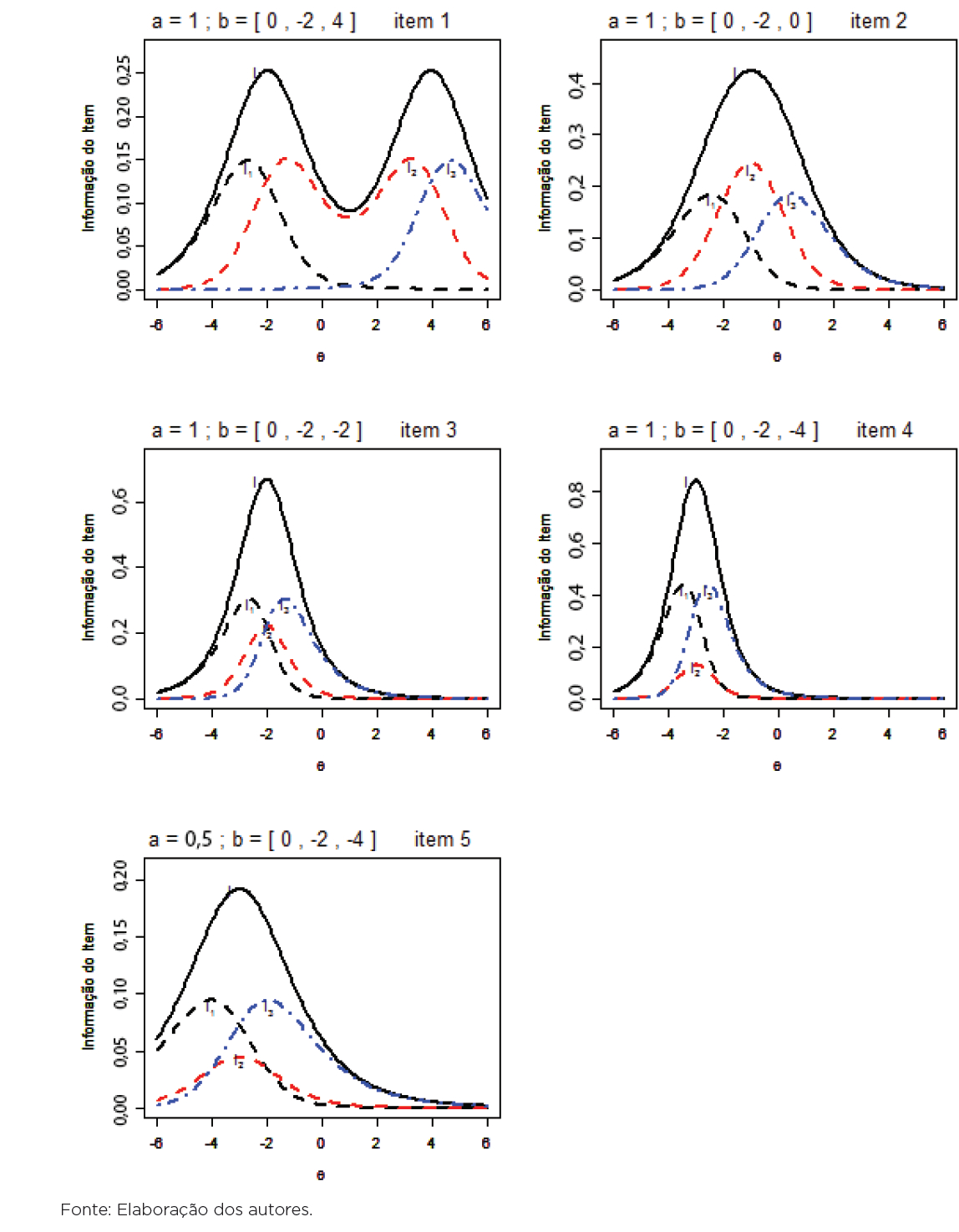
Para melhor entender o comportamento da função de informação do item, a Figura 4 apresenta a FII de cinco itens, com a₁ = 1, b₁ = (0, -2,4); a₂ = 1, b₂ = (0, -2,0); a₃ = 1, b₃ = (0, -2,-2); a₄ = 1, b₄ = (0, -2,-4); e a₅ = 0,5, b₅ = (0, -2,-4). A partir do item 1, nota-se que a FII para o MCPG não é, necessariamente, unimodal e, quanto maior for a distância entre dois parâmetros de dificuldade de categorias adjacentes, menor é a informação na faixa ao redor da mediana (lembremos que estamos considerando uma escala (0,1)) da distribuição de θ. Por outro lado, o item 2, entre todos os apresentados, é o mais apropriado quando se quer estimar o traço latente de indivíduos de uma população em que há grande concentração de indivíduos em torno da mediana. Além disso, a informação do item tende a ser maior em torno dos valores dos seus parâmetros de dificuldade.

Função de Informação do Teste

A Função de Informação do Teste (FIT) é representada pela soma das informações de cada item:

A informação do teste está associada ao erro padrão relativo à estimativa do traço latente do j-ésimo indivíduo (nos casos da estimação por máxima verossimilhança e moda a posteriori), da seguinte forma:

Ou seja, quanto maior for a informação do teste, menor será o erro padrão associado à estimativa do traço latente.

IDENTIFICABILIDADE

Na TRI, o problema de falta de identificabilidade aparece com frequência, porém são escassos na literatura textos que viabilizem a compreensão de um tema que, no desenvolvimento inferencial, de acordo com ^{Rivers (2003}), “é por vezes abordado de modo casual e inadequado”. O autor afirma também que a identificabilidade, apesar de não ser suficiente, é condição necessária para garantir a consistência dos estimadores de máxima verossimilhança. ^{Andrade, Tavares e Valle (2000}) ladeiam a questão, destacando que a falta de identificabilidade ocorre porque diferentes valores dos parâmetros dos itens e/ou do traço latente podem produzir a mesma probabilidade de um indivíduo escolher certa categoria, o que inviabiliza o desenvolvimento de qualquer procedimento de utilização direta da verossimilhança.

De acordo com ^{Matos (2008}), a solução para a não identificabilidade depende basicamente do modelo em estudo e do método de estimação adotado. Na TRI, existe um tipo de falta de identificabilidade em função da invariância a transformações lineares, mais conhecido como um problema de indeterminação da escala de medida, que muitas vezes é solucionado estabelecendo-se uma métrica para os traços latentes (fixando-se sua média e seu desvio padrão) ou impondo restrições aos valores dos parâmetros dos itens.

Particularmente, no MCPG, devido à sua estrutura complexa, na maioria das vezes, é necessário restringir ambas as classes de parâmetros. A seguir são apresentadas algumas definições que serão úteis para a compreensão do texto e que podem ser vistas, por exemplo, em ^{Matos (2008}). Posteriormente, discutiremos como elas se encaixam nos aspectos de identificabilidade do MCPG.

Definição 1 (Parâmetros Observacionalmente Equivalentes). Dois pontos do espaço paramétrico ψ₁, ψ₂ ∈ θ são ditos observacionalmente equivalentes se P_ψ1 = P_ψ2. A igualdade P_ψ1 = P_ψ2 significa dizer que dois modelos probabilísticos são ponto a ponto iguais, ou seja, P_ψ1(y) = P_ψ2(y) para todo valor y.

Definição 2 (Parâmetro e Modelo Globalmente Identificável). Um ponto do espaço paramétrico ψ₀ ∈ θ é dito identificável ou globalmente identificável se não existe outro ponto do espaço paramétrico observacionalmente equivalente a ψ₀. Nesse caso, dizemos que o modelo probabilístico P_ψ0 é globalmente identificável.

Como mencionado em “Interpretação dos parâmetros”, uma condição imprescindível para assegurar a identificabilidade do modelo é fixar um dos parâmetros de dificuldade de cada item, por exemplo, b_i,₀ = 0, i = 1,2,...,I. Do ponto de vista teórico, a estimação dos parâmetros dos itens e dos traços latentes dos indivíduos é dividida em três situações, nomeadamente:

Para cada um desses cenários, será feito um estudo de modo analítico, estabelecendo condições necessárias (e suficientes) para assegurar a identificabilidade do modelo, impondo restrições em uma classe de parâmetros ou em ambas, quando necessário.

θ_j desconhecido, a_i e b_ik conhecidos

Na prática, esta situação ocorre quando os parâmetros dos itens já foram calibrados (estimados) e o que se pretende é estimar o traço latente dos indivíduos. Nesse caso, o modelo é globalmente identificável (Definição 2).

Demonstração. Considerem-se dois pontos do espaço paramétrico, θ₁, θ₂ ∈ θ, observacionalmente equivalentes (Definição 1), ou seja, P_ijk (θ₁) = P_ijk(θ₂). Será provado que θ₁ = θ₂:

Multiplicando ambos os lados por:

obtém-se:

Note-se que o lado direito da equação (2) é constante para todo k ∈ (1,...,m). Sendo assim, seja k₁ e k₂ ∈ (1,...,m) e tal que k₁ < k₂.

Para k = k₁:

Para k = k₂:

Igualando (3) e (4), passa-se a ter:

Como a_i > 0 e k₁ < k₂, a equação (5) é verdadeira quando θ₁ - θ₂ = 0, ou seja, quando θ₁ = θ₂. Chega-se assim ao resultado de interesse. Portanto, em se querendo fazer inferência sobre os traços latentes, não é necessário restringir qualquer classe de parâmetros, pois uma métrica já fora definida, uma vez que os parâmetros dos itens são conhecidos, e o modelo está globalmente identificado.

θ_j conhecido, a_i e b_ik desconhecidos

Agora, com θ_j conhecido, o MCPG é função apenas dos parâmetros ai e b_ik. Para itens com resposta dicotômica (duas categorias), ambos os parâmetros de discriminação e dificuldade podem ser estimados sem a necessidade de impor restrições. Nesse caso, d₁ já estaria definido como zero. Porém, quando se tem mais de duas categorias, existe uma indeterminação entre os parâmetros de categoria e o de dificuldade, ou seja, o modelo não é identificável.

Demonstração. Para provar a falta de identificabilidade do modelo, é suficiente exibir um exemplo de dois conjuntos de parâmetros observacionalmente equivalentes (Definição 1). Para tal, considerem-se dois modelos probabilísticos P_ijk (θ_j) e P'_ijk(θ_j), análogos ponto a ponto, cujos parâmetros do item não são todos iguais, por conseguinte:

Multiplicando ambos os lados por

obtém-se:

Note-se que o lado direito da equação (6) é constante para todo k ∈ (1,...,m). Sendo assim, seja k₁ e k₂ ∈ (1,...,m) tal que k₁ < k₂.

Para k = k₁:

Para k = k₂:

Igualando-se o lado direito de (7) e (8), obtém-se a forma:

Como o lado direito da equação (9) é constante para todo

θ_j e k₁ < k₂, resulta que:

Assim, decompondo biv = bi - dv, seja b'i = bi - t e d'v = dv - t, com t ≠ 0. É fácil constatar que tais parâmetros são observacionalmente equivalentes, o que mostra, particularmente, que o modelo não é identificável, isto é:

Assim, no caso em que se conhece o traço latente dos indivíduos, a fim de garantir unicidade dos parâmetros dos itens, devem-se impor restrições lineares aos mesmos, por exemplo,

Ambos desconhecidos

No caso em que todos os parâmetros são desconhecidos, não há uma métrica definida e, portanto, deve-se estabelecê- -la. Porém, devido à complexidade do modelo, impor restrições somente aos parâmetros do item ou apenas aos traços latentes, isoladamente, não é suficiente, fazendo-se necessário impor restrições para ambas as classes. Com intuito de realizar a estimação dos parâmetros dos itens, sem a presença dos traços latentes, por exemplo, integrando- se a verossimilhança em relação a estes, é comum considerar para eles uma distribuição de probabilidade latente, e que os n indivíduos constituem uma amostra aleatória simples de uma população com essa distribuição. Com isso, em vez de se trabalhar com a verossimilhança completa, utiliza-se, numa primeira etapa, uma verossimilhança marginal (integrada), que possui as mesmas propriedades da verossimilhança genuína (^{CORDEIRO, 1992}). Sendo assim, considere-se que g(θ|η) denota uma função densidade de probabilidade (fdp), duplamente diferenciável. Uma escolha comum para g(θ|η) consiste em:

Sob a verossimilhança marginal, o cenário mostra-se similar ao apresentado na subseção anterior, cujo desenvolvimento já foi mostrado. Dessa forma, no caso em que se desconhecem todos os parâmetros do modelo, é condição suficiente impor restrições tanto aos traços latentes quanto aos parâmetros dos itens. Também é possível restringir a soma dos valores observados e dos valores observados ao quadrado dos traços latentes, embora essa abordagem seja menos frequente.

CONCLUSÃO

No presente trabalho, foi apresentada uma discussão sobre diversos aspectos de interesse do MCPG. A fim de melhor entender o significado dos parâmetros dos itens, avaliou-se, graficamente, como mudanças nos valores dos parâmetros influenciam o comportamento da CCI relacionada a cada categoria, bem como a função de informação do item e do teste. A partir das discussões sobre falta de identificabilidade do modelo, foi possível observar, de forma detalhada, as causas assim como as melhores estratégias para eliminá-la, seja restringindo os parâmetros dos itens, os traços latentes ou ambos, ampliando os conhecimentos sobre um assunto ainda pouco discutido na literatura estatística.

AGRADECIMENTOS

Os autores agradecem ao Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) pela bolsa concedida por meio do Programa Institucional de Bolsas de Iniciação Científica/Universidade Estadual de Campinas (Pibic/Unicamp) ao primeiro autor, sob orientação do segundo, bem como ao parecerista anônimo pelos comentários que contribuíram para melhorar substancialmente o artigo.