INTRODUÇÃO
Ernica et al. (2023), Soares e Delgado (2016) e Soares et al. (2018) argumentam contra o uso do índice de Gini e das medidas T e L de Theil1 para analisar a desigualdade de aprendizagem entre alunos, e defendem o uso da divergência de Kullback-Leibler (KL) para isso. Vamos discutir os argumentos desses autores e criticar a proposta de usar a divergência de Kullback-Leibler para comparar distribuições de medidas de proficiência entre estudantes. Defendemos o uso de uma combinação de medidas usuais de tendência central (média e mediana) e de dispersão (desvio padrão e diferença absoluta média), complementada, eventualmente, por medidas de desigualdade, como o índice de Gini e/ou o coeficiente de variação e comparações gráficas das funções de densidade, curvas de quantis, curvas de Lorenz e curvas de Lorenz generalizadas.
Cabe explicitar que não será feita aqui uma avaliação abrangente de todos os temas abordados nos trabalhos citados. Vamos nos limitar ao problema de medir a desigualdade em uma distribuição de notas e, mais especificamente, à proposta de usar a divergência de Kullback-Leibler para comparar duas distribuições de notas.
O USO DE MEDIDAS USUAIS DE DESIGUALDADE PARA NOTAS
O índice de Gini e as medidas T e L de Theil são comumente usados para avaliar a desigualdade da distribuição da renda. É certo que uma distribuição de notas em uma matéria tem várias características diferentes de uma distribuição de renda entre pessoas, e isso exige cuidados na interpretação de qualquer medida estatística calculada. Mas vários argumentos dos autores citados contra o uso do índice de Gini e das medidas de Theil são inválidos.
De Ernica et al. (2023, pp. 18-19), consta que:
Tanto o coeficiente de Gini como o índice de Theil podem ser entendidos como medidas que comparam distribuições estatísticas e sintetizam a distância entre uma situação observada e uma distribuição na qual todos indivíduos têm a mesma renda. Essas medidas assumem, implicitamente, três pressupostos: primeiro, que a distribuição observada deve ser comparada com uma distribuição na qual há igualdade de resultados entre indivíduos; segundo, que há uma quantidade total e fixa de renda que está sendo distribuída entre indivíduos; terceiro, que pode haver transferência de quantidades de renda de um indivíduo para outro, diminuindo a renda dos que concentram mais para aumentar a dos que concentram menos, de modo a se produzir situações menos desiguais. Esses pressupostos, contudo, não podem ser assumidos para a realidade educacional.
É certo que os limites inferiores para o índice de Gini (G) e o T de Theil (T) são zero e correspondem ao caso de perfeita igualdade. Mas, em praticamente todos os estudos, G e T são usados para comparar a desigualdade entre regiões, entre países ou entre diferentes anos. E, quando se diz que o G da distribuição da renda domiciliar per capita no Brasil, de acordo com os dados da Pesquisa Nacional por Amostra de Domicílios (Pnad), em 2015 é substancialmente menor do que em 2001, não se está, de nenhuma maneira, pressupondo que o ideal (em qualquer sentido) seja G = 0. Mesmo quando se afirma que a desigualdade da distribuição de renda no Brasil é elevada, está implícita uma comparação com outros países, particularmente os da Europa Ocidental, e não um “pressuposto” G = 0.
E também não é válida a afirmativa de que ao calcular G ou T precisamos pressupor “que há uma quantidade total e fixa de renda que está sendo distribuída entre indivíduos” (Ernica et al., 2023, p. 19). É óbvio que isso não ocorre quando comparamos a desigualdade de distribuição de renda no Brasil em 2001 e 2015.
O terceiro pretenso “pressuposto” também é falso. Se a desigualdade em um país cresce de um ano para outro, isso não se deve, necessariamente, a uma transferência regressiva de renda, podendo ser consequência de um crescimento proporcionalmente maior da renda dos relativamente ricos do que o da renda dos relativamente pobres. É usual analisar a sensibilidade das medidas de desigualdade da distribuição da renda avaliando sua alteração em consequência de hipotéticas transferências regressivas (ou progressivas) de renda, mas isso não significa que a possibilidade de realizar tais transferências seja um pressuposto para o cálculo de G ou T. Concordamos, obviamente, que no caso da distribuição de notas não faz sentido pensar em “transferências” regressivas ou progressivas.
Ao tratar da distribuição de renda, considera-se que uma boa medida de desigualdade deve obedecer à condição de Pigou-Dalton, isto é, seu valor deve aumentar quando transferimos renda de uma pessoa para uma outra que tenha renda maior ou igual. No caso de escolaridade ou avaliações de aprendizado, a ideia de transferir valores entre pessoas não faz sentido. Mas é fácil formular o princípio de Pigou- -Dalton de maneira a evitar a ideia de transferência: dada uma distribuição discreta, uma medida de desigualdade deve aumentar sempre que ocorrer, simultaneamente, a redução de um valor e um aumento igual em outro valor da variável que era igual ou maior do que o primeiro.
A DIVERGÊNCIA DE KULLBACK-LEIBLER
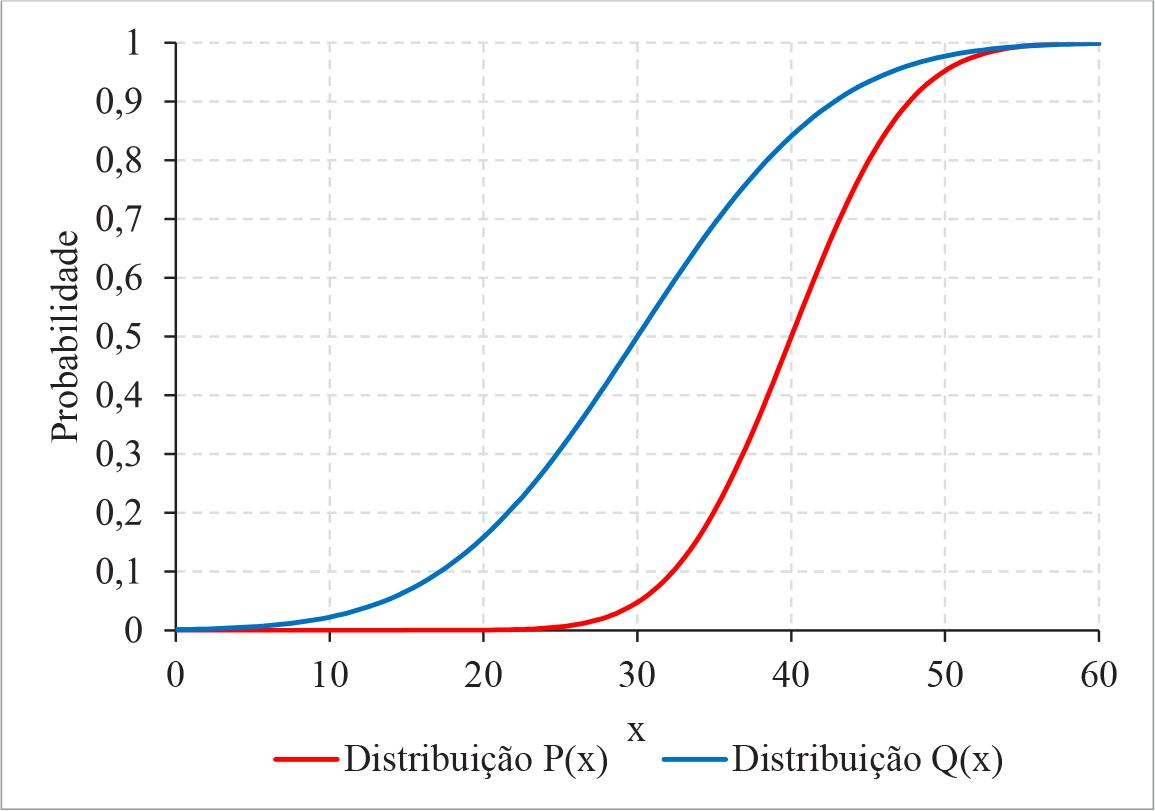
Soares et al. (2018), depois de argumentarem que as medidas de desigualdade usuais na análise da distribuição da renda são inapropriadas para avaliar desigualdades educacionais, propõem-se a encontrar uma boa medida da divergência entre distribuições de medidas do aprendizado. Observam que uma opção óbvia seria considerar a área entre as funções de distribuição, como ilustra a Figura 1. Pode-se provar que, qualquer que seja a distribuição, a área entre o eixo das ordenadas e a curva da função de distribuição é igual à média da distribuição. Consequentemente, a área entre as duas curvas é igual à diferença entre as médias das duas distribuições .
Soares et al. (2018) consideram essa uma maneira limitada (“a limited option”) de medir a distância entre as duas distribuições, porque leva em conta apenas um tipo de diferença entre elas. Também descartam o uso de uma área delimitada pela curva que mostra como uma função de distribuição varia em função da outra (a função de distribuição acumulada relativa), uma medida de distância entre distribuições, proposta por Soares e Marotta (2009), que é igual à média da distribuição relativa. Soares et al. (2018) defendem, então, o uso da divergência de Kullback- -Leibler para comparar distribuições de notas de alunos.
No caso de duas distribuições discretas de uma variável com valores xi(i = 1,...n), com probabilidades Q(xi) e P(xi) para cada um dos diferentes valores de , a divergência de Kullback-Leibler de Q para P, ou ganho de informação quando se passa da distribuição Q para a distribuição P, é dada por
No caso de distribuições contínuas com funções de densidade de probabilidade q(xi) e p(xi), a divergência é dada por
A divergência de Kullback-Leibler nunca é negativa, isto é, K(P ‖ Q) ≥ 0, com K(P ‖ Q) = 0 apenas se as duas distribuições são iguais.2
Uma vez que, em geral, K(P ‖ Q) ≠ K(Q ‖ P), é necessário sempre explicitar se se trata da divergência de Q para P ou da divergência de P para Q.
Ao usar a expressão (1), se P(xi) = 0 e Q(xi) > 0, considera-se que a respectiva parcela é nula, tendo em vista que para uma variável z qualquer
Vamos examinar o caso da divergência de Kullback-Leibler de uma distribuição uniforme (P) de x = a a x = a + ω para uma outra distribuição uniforme (Q) definida sobre um intervalo mais estreito, dentro do intervalo de a a + ω, isto é, no intervalo de b a b + θ, de maneira que e a ≤ b e b + θ ≤ a + θ, com desigualdade estrita em pelo menos um dos casos. Pode-se deduzir que a referida divergência é
Se, por exemplo, ω é dez vezes o valor de θ, quando se passa da distribuição de maior amplitude para a de menor amplitude, há um ganho de informação de ln(10) nats ou log2(10) bits.
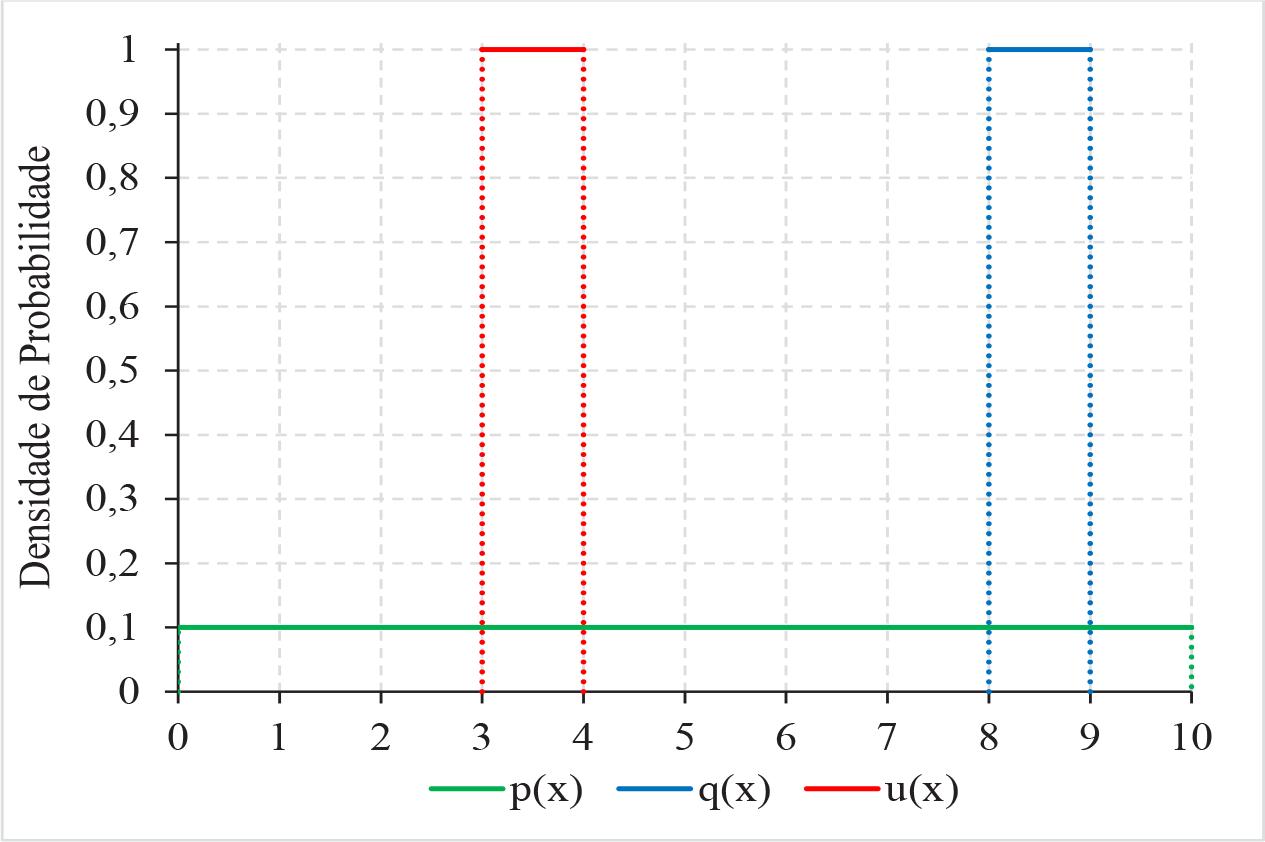
A Figura 2 mostra as funções de densidade de probabilidade [p(x), q(x) e u(x)] de três distribuições uniformes (P, Q e U, respectivamente). De acordo com a expressão (3), a divergência de P para Q é exatamente igual à divergência de P para U, isto é, ln(10) nats.
Vamos imaginar que a Figura 2 represente três possíveis distribuições de pluviosidade em algum dia futuro, de 0 a 100 mm (multiplicando por 10 os valores indicados no eixo das abscissas). A distribuição P seria o esperado antes de uma previsão, e as distribuições Q e U seriam duas diferentes previsões de meteorologistas. Quando passamos de P para Q ou de P para U, o intervalo de variação da pluviosidade é reduzido a 1/10 do admitido a priori; é razoável, portanto, dizer que as duas previsões têm um valor informativo de nats. Mas, se considerarmos que a Figura 2 se refere a três distribuições de notas, a tendência é considerar absurda a afirmativa de que a divergência de P para Q é igual à divergência de P para U.
Um procedimento simples e apropriado de comparar as distribuições é comparar suas médias ou medianas e alguma medida de dispersão (como o desvio padrão) e/ou de desigualdade (como o coeficiente de variação). É claro que média e desvio padrão não constituem uma descrição completa de uma distribuição. Trata-se de comparar as características mais relevantes. E a tentativa de descobrir um único número que sintetize as diferenças relevantes entre duas distribuições pode trazer confusão, em lugar de contribuir para uma análise mais clara do tema.
A Tabela 1 mostra três distribuições hipotéticas de frequência de 110 alunos conforme notas de 0 a 10 em determinada prova, ilustradas na Figura 3. As médias das distribuições P, Q e U, nesta ordem, são 5, 4,2 e 7. As respectivas variâncias são 10, 6,96 e 12. As divergências de Kullback-Leibler de P para Q e de P para U têm exatamente o mesmo valor: 0,453. As divergências em sentido inverso, de Q para P e de U para P, são ambas iguais a 0,318. No entanto, de P para Q a média e a variância diminuem e de P para U a média e a variância aumentam. Esse simples exemplo numérico mostra que não é razoável usar a divergência de Kullback-Leibler para comparar distribuições de notas.
TABELA 1 Três distribuições de frequências fictícias de 110 alunos conforme notas de 0 a 10
| Nota (x) |
DISTRIBUIÇÃO | ||
|---|---|---|---|
| P | Q | U | |
| 0 | 10 | 6 | 6 |
| 1 | 10 | 6 | 6 |
| 2 | 10 | 6 | 6 |
| 3 | 10 | 50 | 6 |
| 4 | 10 | 6 | 6 |
| 5 | 10 | 6 | 6 |
| 6 | 10 | 6 | 6 |
| 7 | 10 | 6 | 6 |
| 8 | 10 | 6 | 6 |
| 9 | 10 | 6 | 6 |
| 10 | 10 | 6 | 50 |
Fonte: Elaboração do autor.
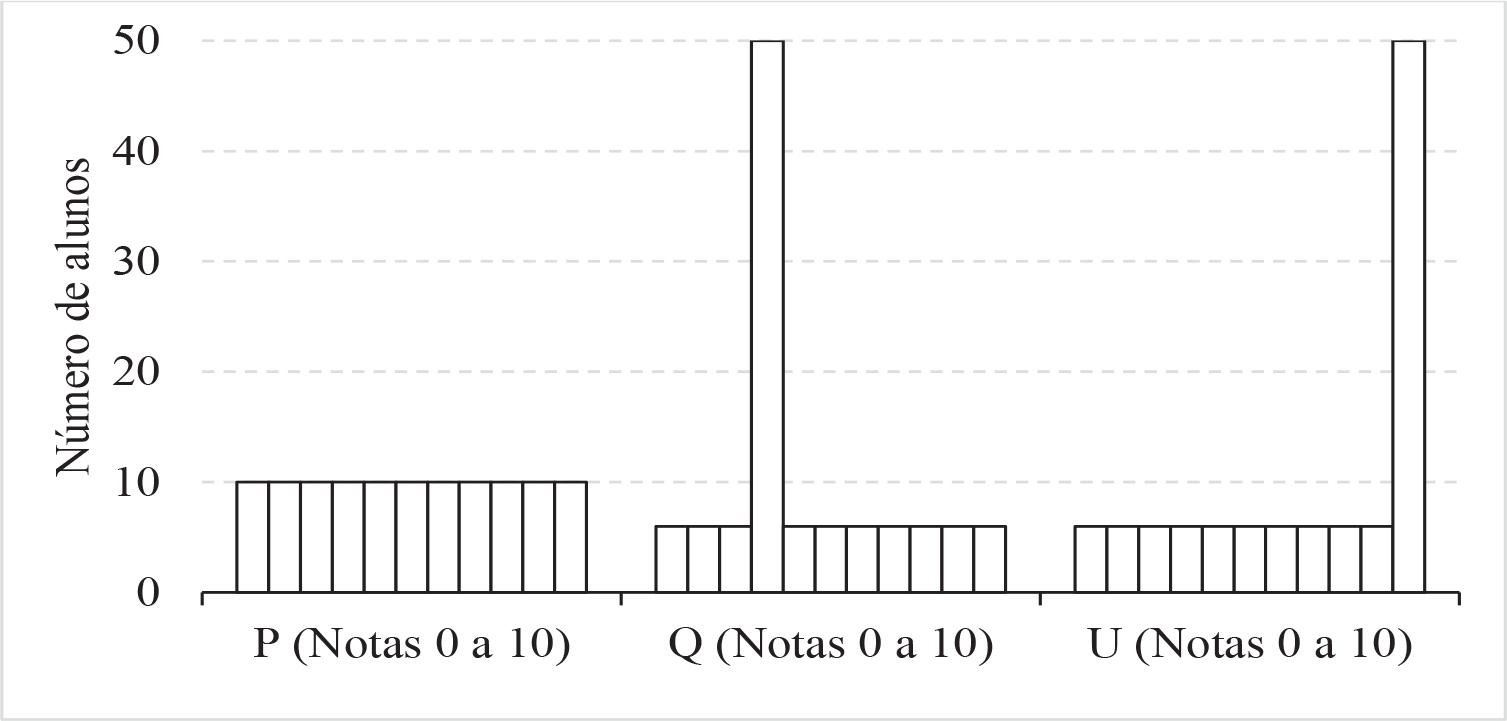
Fonte: Elaboração do autor.
FIGURA 3 Gráficos das distribuições de frequências apresentadas na Tabela 1
Consideremos, agora, as três distribuições de 100 alunos conforme notas de 0 a 10 apresentadas na Tabela 2 e representadas graficamente na Figura 4. As notas médias nas distribuições P, Q e U são, respectivamente, 6,80, 5,45 e 3,20. A variância é a mesma (9,56) nas distribuições P e U e é menor (5,85) na distribuição Q. A assimetria é negativa nas distribuições P e Q, mas é positiva na distribuição U. Comparando as distribuições duas a duas, verifica-se que a divergência de Kullback-Leibler, nos dois sentidos, é sempre a mesma (0,797).
TABELA 2 Três distribuições de frequências fictícias de 100 alunos conforme notas de 0 a 10
| Nota (x) |
DISTRIBUIÇÃO | ||
|---|---|---|---|
| P | Q | U | |
| 0 | 5 | 5 | 10 |
| 1 | 5 | 5 | 40 |
| 2 | 5 | 5 | 10 |
| 3 | 5 | 5 | 5 |
| 4 | 5 | 5 | 5 |
| 5 | 5 | 10 | 5 |
| 6 | 5 | 40 | 5 |
| 7 | 5 | 10 | 5 |
| 8 | 10 | 5 | 5 |
| 9 | 40 | 5 | 5 |
| 10 | 10 | 5 | 5 |
Fonte: Elaboração do autor.

Fonte: Elaboração do autor.
FIGURA 4 Gráficos das distribuições de frequências apresentadas na Tabela 2
Em total desacordo com a proposta de Soares et al. (2018), não vemos nenhuma vantagem em utilizar a divergência de Kullback-Leibler na análise das notas. Soares et al. (2018, p. 14) notam que o fato de a divergência de Kullback-Leibler nunca ser negativa impede que essa medida indique qual das duas distribuições está “acima” da outra e dizem que para resolver esse problema irão utilizar a posição da curva de distribuição acumulada relativa.4 Note-se que isso absolutamente não resolve o problema de interpretar a igualdade das divergências de U para P e de U para Q na Tabela 2.
A divergência de Kullback-Leibler é o ganho de informação quando se passa de uma distribuição para outra, não pode ser negativa e certamente é útil em vários contextos, mas parece totalmente inapropriada para a análise do desempenho de alunos em provas.
Cabe comentar a afirmativa de Soares e Delgado (2016, p. 767), contrapondo uma diferença de médias à divergência de Kullback-Leibler (denominada “medida KL” no referido artigo):
Como é amplamente conhecido, as médias registram um aspecto muito específico das distribuições que, entretanto, pode ser dominante em alguns casos. A medida KL, por outro lado, é capaz de captar qualquer tipo de diferença, o que justifica seu uso apesar de seu hermetismo matemático.
É óbvio que nenhuma medida, isoladamente, pode captar todas as diferenças entre duas distribuições quaisquer. Até quando se trata de um mesmo conceito geral, como “tendência central”, cada medida específica tem suas qualidades e limitações. É fácil imaginar duas distribuições, das quais a primeira tem média menor, mas mediana maior, do que a segunda. Em princípio, a divergência de Kullback- -Leibler de uma distribuição de notas observada para uma distribuição de referência é um resultado adicional que pode ser acrescentado às diferenças ou razões entre médias, medianas, variâncias, etc. Conforme argumentamos anteriormente, trata-se de uma medida inapropriada para os objetivos usuais em análises comparativas de distribuições de notas. Basta considerar as três distribuições apresentadas na Tabela 2 e admitir que Q(x) e U(x) são duas distribuições observadas e P(x) é a distribuição de referência. É relevante constatar que as médias de Q(x) e U(x) ficam, respectivamente, 1,35 e 3,6 pontos abaixo da média da distribuição de referência. Qual é a relevância de saber que as divergências de Kullback-Leibler de Q(x) para P(x) e de U(x) para P(x) são iguais?
QUE MEDIDAS USAR E A DESIGUALDADE ENTRE CATEGORIAS
O simples cálculo de uma média só é estritamente válido se a escala de medida for intervalar, isto é, se diferenças (intervalos) puderem ser comparadas. A média entre 5 metros e 11 metros é igual a 8 metros, porque a diferença 8 m - 5 m = 3 m é igual à diferença 11 m - 8 m = 3 m. Mas, a rigor, não é válido dizer que a média entre as escolaridades 5 e 11 seja 8, pois o percurso para passar de 8 para 11 anos de escolaridade é diferente do percurso para passar de 5 para 8 anos de escolaridade. Considerando que escolaridade e notas são variáveis ordinais, deveríamos usar a mediana, e não a média, como medida de tendência central de uma distribuição. Entretanto é generalizado o uso de médias de notas e de escolaridades. Aceitando-se tal falta de rigor e admitindo que notas e escolaridade são medidas com escala razão,5 não há impedimento para o uso de medidas usuais de desigualdade de renda, como o índice de Gini e as medidas de Theil, na avaliação da desigualdade de distribuições de notas ou de escolaridade.
Ao analisar a distribuição da renda, pode-se argumentar que é inconveniente usar o coeficiente de variação (a razão entre o desvio padrão e a média), porque ele é muito sensível ao que ocorre na cauda superior da distribuição. Mas esse problema está associado à fortíssima assimetria positiva usual na distribuição da renda. Como escolaridade e notas não apresentam, usualmente, forte assimetria positiva, o coeficiente de variação pode ser uma medida de desigualdade perfeitamente apropriada para essas variáveis.
Ernica et al. (2023, p. X) afirmam que, para “caracterizar e medir as situações de equidade ou de desigualdade”, eles calculam
. . . a distância entre as distribuições de aprendizagens de grupos no interior do município, formados pelos indivíduos que têm determinadas características que são correlacionadas às proficiências: nível socioeconômico, raça e sexo. Assim, para cada série e disciplina, são calculadas as distâncias entre a distribuição das proficiências de pessoas de nível socioeconômico mais baixo e a de pessoas de nível socioeconômico mais alto, entre a distribuição das proficiências das pessoas autodeclaradas pretas e a das pessoas autodeclaradas brancas, entre a distribuição das proficiências de meninas e a de meninos.
As “distâncias” mencionadas são as divergências de Kullback-Leibler.
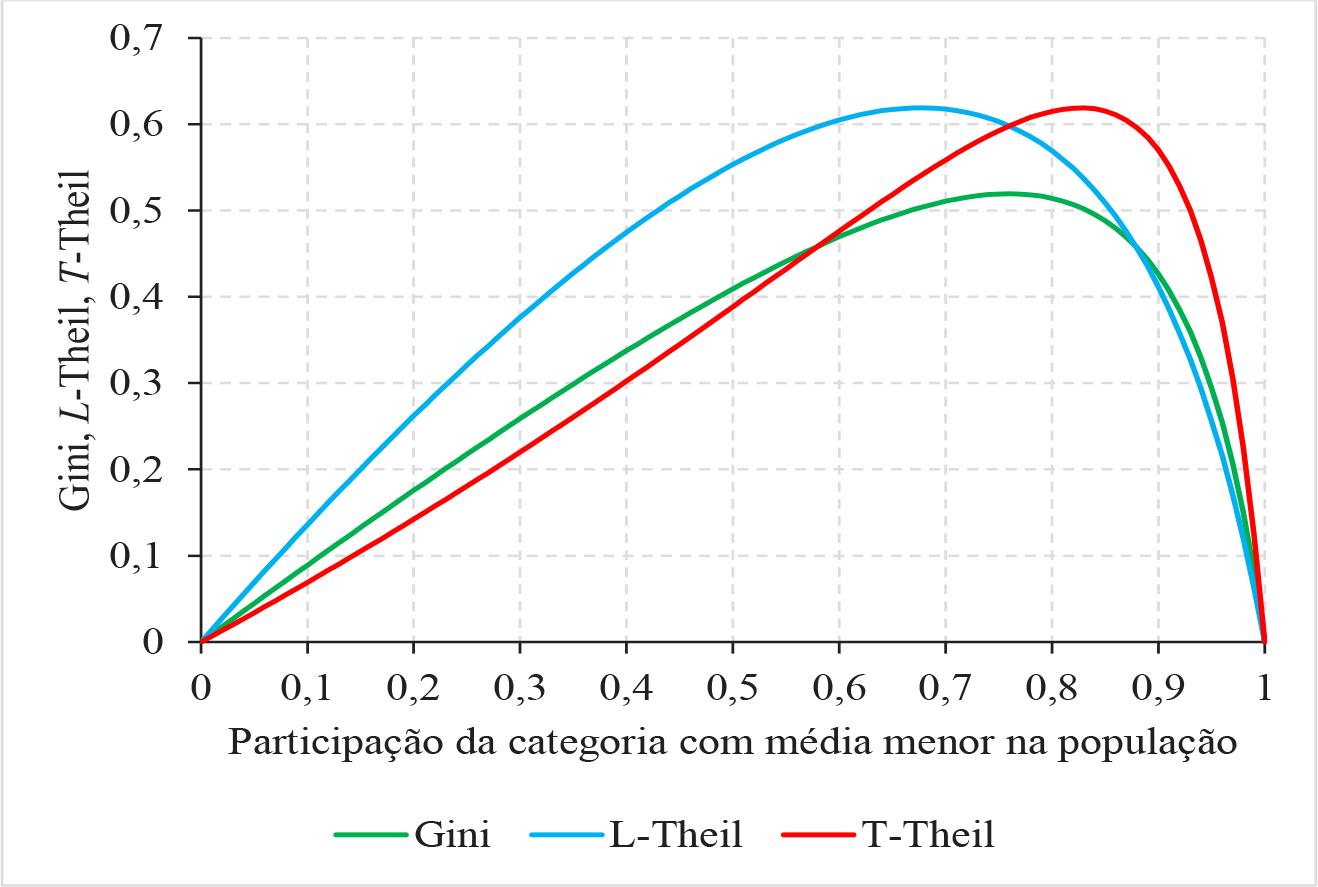
Essa maneira de medir desigualdade é claramente inapropriada por não levar em consideração a participação de cada categoria na população. Para avaliar a desigualdade da distribuição de qualquer variável entre diferentes categorias de uma população, as medidas consagradas de desigualdade (como o índice de Gini e as medidas T e L de Theil) levam em conta a participação de cada categoria na população. A desigualdade entre duas categorias não depende apenas da “distância” entre as respectivas médias; depende, também, da participação de cada categoria na população. Consideremos um exemplo simples em que o próprio valor da variável (1 ou 10) caracteriza as duas categorias. Definimos dois conjuntos de seis elementos: o conjunto A = {1, 10, 10, 10, 10, 10} e o conjunto B = {1, 1, 1, 1, 10, 10}. Nos dois conjuntos a distância entre categorias é 10 - 1 = 9, mas no conjunto A apenas um dos seis elementos pertence à categoria com valor individual 1, ao passo que no conjunto B isso acontece com quatro dos seis elementos. Note-se que nesse caso a desigualdade na população se confunde com a desigualdade entre categorias, já que não há desigualdade dentro das categorias, e verifica-se que as medidas usuais de desigualdade são bem menores para o conjunto A do que para o conjunto B. O índice de Gini é 0,147 para o conjunto A e é 0,5 para o conjunto B. No Apêndice, mostra-se como os valores do índice de Gini e das medidas T e L de Theil entre duas categorias, fixada a relação entre as duas médias, variam em função da participação de cada categoria na população.
O caráter limitado da medida de desigualdade calculada por Ernica et al. (2023) é mais grave no caso dos cinco estratos de nível socioeconômico. Eles levam em consideração apenas a “distância” (medida pela divergência de Kullback-Leibler) entre o primeiro e o quinto estrato, enquanto uma medida apropriada de desigualdade entre os cinco estratos seria calculada com base nas notas médias e nas participações dos cinco estratos na população. Fixada a diferença de nível de notas entre o primeiro e o quinto estrato, o grau de desigualdade entre os cinco estratos será maior se os dois estratos extremos concentrarem a maior parte da população, em comparação com uma situação na qual os estratos extremos têm participação diminuta na população.
Cabe notar que, dependendo do problema analisado, interessa avaliar a dispersão da escolaridade (ou de notas), e não sua desigualdade. No caso do coeficiente de variação e do índice de Gini (que pode ser definido como a razão entre a diferença absoluta média e duas vezes a média), a medida de desigualdade se confunde com uma medida de dispersão relativa. A escolaridade de uma pessoa é um condicionante básico do rendimento que ela tende a auferir no seu trabalho e, de imediato, pensa-se que a desigualdade da distribuição da renda deve estar associada à desigualdade da escolaridade. Mas, no modelo consagrado de uma equação de rendimento, o logaritmo da renda é uma função da escolaridade (E). Desprezando os termos associados aos efeitos de todas as demais variáveis (gênero, cor, idade, setor de ocupação, etc.), a equação, com parâmetros α e β, seria:
Diferenciando, segue-se que:
Isso mostra que variações na escolaridade correspondem a variações relativas na renda, ou seja, é a dispersão na escolaridade, e não a desigualdade da escolaridade, que está diretamente associada à desigualdade na renda.6
ANALISANDO DISTRIBUIÇÕES DE ESCOLARIDADE NO BRASIL E NAS UNIDADES DA FEDERAÇÃO EM 2022
Nesta seção, tendo em vista ilustrar com dados reais os procedimentos para comparar distribuições, vamos analisar a distribuição de pessoas ocupadas conforme sua escolaridade, usando os dados da Pnad Contínua de 2022, no Brasil e nas unidades da Federação.
Na amostra da Pnad Contínua anual de 2022 (IBGE, 2023), baseada na quinta entrevista, há 160.222 pessoas ocupadas. Considerando os pesos ou fatores de expansão fornecidos pelo Instituto Brasileiro de Geografia e Estatística (IBGE), verifica-se que esse número corresponde a uma população de 96,98 milhões de pessoas ocupadas.
A variável VD3005 da Pnad Contínua, com valores de 0 a 16, informa a escolaridade (ou número de anos de estudo) de cada pessoa. O 0 indica pessoa sem instrução ou com menos de um ano de estudo; 1 indica que a pessoa tem um ano de estudo; e assim por diante, até 15 para pessoa com 15 anos de estudo e 16 para pessoa com 16 ou mais anos de estudo. Nos resultados apresentados a seguir, adotamos 18 como a escolaridade média dessa última categoria.
Sempre usando os fatores de expansão fornecidos pelo IBGE, verificamos que as escolaridades média (μ) e mediana são, respectivamente, 11,67 e 12 anos. Como medidas de dispersão da distribuição, podemos usar o desvio padrão (σ) ou a diferença absoluta média (∆), iguais, respectivamente, a 4,49 e 4,90. As correspondentes medidas de desigualdade são o coeficiente de variação (C = σ / μ) e o índice de Gini [G = ∆ / (2μ)], iguais a 0,385 e 0,210, respectivamente. Note-se que essas duas medidas de desigualdade são medidas de dispersão relativa.
A Figura 5 mostra a curva de quantis da distribuição da escolaridade das pessoas ocupadas no Brasil, de acordo com os dados da Pnad Contínua de 2022 (IBGE, 2023). Tendo ordenado as pessoas conforme valores não decrescentes da escolaridade, a linha do gráfico mostra como varia a escolaridade com a proporção acumulada de pessoas. A linha em forma de degraus se deve ao fato de a escolaridade ser medida em números inteiros. Note-se o grande patamar com escolaridade 12, de pessoas que completaram o segundo grau e que são 35,3% da população. Outro patamar é observado para os que têm escolaridade igual ou maior que 16 anos, constituindo pouco mais de 21% da população. Observa-se que 20,6% das pessoas ocupadas não completaram o ensino fundamental e 34,6% não completaram o ensino médio. É evidente que a Figura 5 mostra características da distribuição que nenhum índice, isoladamente, poderia revelar.
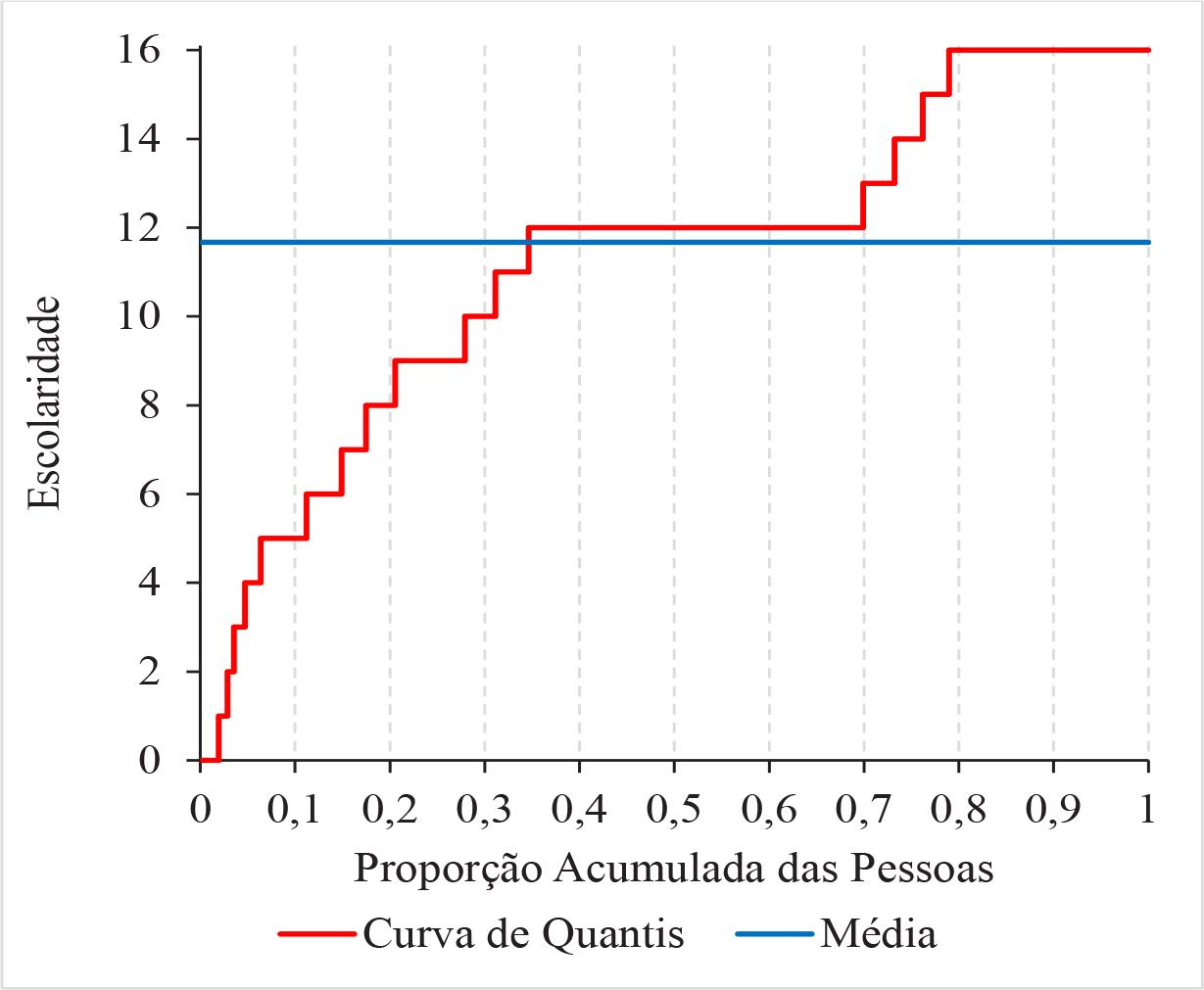
Fonte: Elaboração do autor, com base em microdados da Pnad Contínua de 2022 (IBGE, 2023).
FIGURA 5 Quantis e média da distribuição da escolaridade das pessoas ocupadas no Brasil em 2022
Tendo em vista o cálculo da divergência de Kullback-Leibler, vamos criar uma distribuição de referência na qual a escolaridade é igual a 9 para 30% das pessoas, é igual a 12 para outros 30% e é igual ou maior que 16 para os demais 40%. A média dessa distribuição é igual a 13,5. Verifica-se que a divergência de Kullback-Leibler da distribuição da escolaridade das pessoas ocupadas no Brasil em 2022 para essa distribuição de referência é igual a 0,630.
Ao analisar a distribuição da escolaridade das pessoas ocupadas em cada unidade da Federação em 2022, nota-se que a mediana é sempre igual a 12 anos. A Tabela 3 apresenta, para cada unidade da Federação, a população de pessoas ocupadas, a escolaridade média, dois percentis, duas medidas de dispersão (desvio padrão e desvio absoluto médio), duas medidas de desigualdade (coeficiente de variação e índice de Gini) e a divergência de Kullback-Leibler da distribuição observada para a distribuição de referência.
TABELA 3 Características da distribuição da escolaridade das pessoas ocupadas por unidade da Federação (UF) brasileira em 2022
| UF | N | Média | P10 | Q3 | DP | ∆ | CV | G | KL |
|---|---|---|---|---|---|---|---|---|---|
| RO | 849 | 10,93 | 5 | 12 | 4,70 | 5,20 | 0,430 | 0,238 | 0,666 |
| AC | 324 | 11,30 | 4 | 15 | 5,05 | 5,55 | 0,447 | 0,245 | 0,694 |
| AM | 1.685 | 11,21 | 5 | 12 | 4,41 | 4,72 | 0,393 | 0,211 | 0,704 |
| RR | 248 | 12,26 | 7 | 14 | 4,19 | 4,38 | 0,342 | 0,179 | 0,655 |
| PA | 3.766 | 10,19 | 4 | 12 | 4,66 | 5,17 | 0,457 | 0,253 | 0,836 |
| AP | 359 | 11,87 | 5 | 15 | 4,79 | 5,22 | 0,403 | 0,220 | 0,661 |
| TO | 717 | 11,44 | 5 | 13 | 4,60 | 4,99 | 0,402 | 0,218 | 0,683 |
| MA | 2.458 | 10,53 | 4 | 12 | 4,73 | 5,15 | 0,449 | 0,245 | 0,730 |
| PI | 1.269 | 10,86 | 3 | 14 | 5,23 | 5,85 | 0,481 | 0,269 | 0,705 |
| CE | 3.527 | 10,87 | 4 | 12 | 4,71 | 5,11 | 0,434 | 0,235 | 0,730 |
| RN | 1.376 | 11,31 | 5 | 13 | 4,65 | 5,10 | 0,412 | 0,225 | 0,717 |
| PB | 1.445 | 10,38 | 3 | 12 | 5,01 | 5,57 | 0,483 | 0,269 | 0,793 |
| PE | 3.591 | 10,91 | 4 | 12 | 4,76 | 5,18 | 0,436 | 0,238 | 0,711 |
| AL | 1.166 | 10,49 | 3 | 12 | 4,99 | 5,54 | 0,476 | 0,264 | 0,749 |
| SE | 975 | 10,52 | 3 | 12 | 5,03 | 5,61 | 0,478 | 0,267 | 0,814 |
| BA | 6.019 | 10,50 | 4 | 12 | 4,76 | 5,21 | 0,453 | 0,248 | 0,826 |
| MG | 10.363 | 11,28 | 5 | 13 | 4,41 | 4,87 | 0,390 | 0,216 | 0,644 |
| ES | 1.982 | 11,55 | 5 | 14 | 4,43 | 4,87 | 0,384 | 0,211 | 0,602 |
| RJ | 7.710 | 12,61 | 7 | 18 | 4,22 | 4,56 | 0,335 | 0,181 | 0,553 |
| SP | 23.493 | 12,60 | 7 | 18 | 4,05 | 4,35 | 0,322 | 0,172 | 0,585 |
| PR | 5.757 | 11,70 | 5 | 14 | 4,41 | 4,84 | 0,377 | 0,207 | 0,584 |
| SC | 3.829 | 11,80 | 5 | 14 | 4,38 | 4,80 | 0,372 | 0,203 | 0,533 |
| RS | 5.749 | 11,83 | 6 | 14 | 4,20 | 4,66 | 0,355 | 0,197 | 0,568 |
| MS | 1.350 | 11,67 | 5 | 15 | 4,53 | 5,02 | 0,389 | 0,215 | 0,643 |
| MT | 1.712 | 11,27 | 5 | 13 | 4,49 | 4,91 | 0,398 | 0,218 | 0,674 |
| GO | 3.616 | 11,58 | 5 | 14 | 4,44 | 4,84 | 0,383 | 0,209 | 0,656 |
| DF | 1.567 | 13,33 | 8 | 18 | 4,20 | 4,54 | 0,315 | 0,170 | 0,590 |
Fonte: Elaboração do autor, com base em microdados da Pnad Contínua de 2022 (IBGE, 2023).
Nota: População de pessoas ocupadas em milhares (N), escolaridade média (Média), décimo percentil (P10), terceiro quartil (Q3), desvio padrão (DP), diferença absoluta média (∆), coeficiente de variação (CV), índice de Gini (G) e divergência de Kullback-Leibler (KL).
É fato bem conhecido que o nível de escolaridade está associado ao desenvolvimento econômico e ao nível de renda. Observa-se, na Tabela 3, que, nas unidades da Federação do Nordeste, a região mais pobre do país, a escolaridade média está sempre abaixo de 11,4 (quase sempre abaixo de 11), ao passo que nas unidades do Sudeste, Sul e Centro-Oeste a escolaridade sempre supera 11,2. O Distrito Federal se destaca com uma escolaridade média igual a 13,33.
Como esperado, medidas referentes ao mesmo conceito são positiva e fortemente correlacionadas. Considerando os valores obtidos para as 27 unidades da Federação e usando a população de pessoas ocupadas de cada unidade como fator de ponderação, verifica-se que a correlação entre as duas medidas de dispersão (o desvio padrão e a diferença absoluta média) é igual a 0,991, e a correlação entre as duas medidas de desigualdade (o coeficiente de variação e o índice de Gini) é igual a 0,998.
Observa-se que há uma relação entre a média e a dispersão da escolaridade. No estudo de Hoffmann e Oliveira (2014), os dados da Pnad de 1992 a 2012 mostram que a variação da diferença absoluta média da escolaridade em função da escolaridade média das pessoas ocupadas é bem representada por uma parábola côncava que passa por um ponto de máximo quando essa média é aproximadamente 7,5. Mas, no caso dos dados da Tabela 3, como as escolaridades médias estão substancialmente acima de 7,5, os pontos estão todos no ramo descendente da parábola, de modo que, para as 27 observações, a correlação entre a diferença absoluta média e a escolaridade média é igual a -0,900 e a correlação entre o desvio padrão e a escolaridade média é igual a -0,889. Cabe ressaltar que essa relação empiricamente constatada entre dispersão e média da distribuição da escolaridade é usada por Hoffmann e Oliveira (2014) e Hoffmann e Jesus (2020) para explicar, em parte, a evolução diferente da desigualdade da distribuição da renda no setor agrícola do Brasil, em comparação com a sua evolução no setor não agrícola.
Tentando entender o que capta a divergência de Kullback-Leibler da distribuição da escolaridade observada para a distribuição de referência, calculamos as correlações dessa divergência com a média e com as medidas de dispersão e de desigualdade apresentadas na Tabela 3, com ponderação pela população de pessoas ocupadas de cada unidade da Federação. Os resultados estão na Tabela 4. Para as cinco correlações, o valor p referente ao teste de nulidade é inferior a 0,01%.
TABELA 4 Correlações entre a divergência de Kullback-Leibler (KL) e medidas apresentadas na Tabela 3 para a distribuição da escolaridade em cada unidade da Federação
| MEDIDA | CORRELAÇÃO COM KL |
|---|---|
| Escolaridade média | -0,866 |
| Desvio padrão (DP) | 0,801 |
| Diferença absoluta média (∆) | 0,774 |
| Coeficiente de variação (CV) | 0,878 |
| Índice de Gini (G) | 0,860 |
Fonte: Elaboração do autor, com base em microdados da Pnad Contínua de 2022.
Cabe ressaltar que, sendo a escolaridade média na unidade da Federação e sendo a escolaridade média da distribuição de referência, a correlação entre a divergência de Kullback-Leibler e a diferença é igual à correlação entre a divergência e , com o sinal trocado, pois é constante. Assim, a correlação entre a divergência de Kullback-Leibler e é 0,866: quanto maior a divergência, mais a média observada está abaixo da média da distribuição de referência. As demais correlações apresentadas na Tabela 4 mostram que, ao mesmo tempo, a divergência de Kullback-Leibler tende a crescer com a dispersão e a desigualdade da distribuição da escolaridade. Mas isso faz dessa divergência uma medida especialmente útil? Em nossa opinião, é melhor usar medidas de conceitos bem conhecidos, como tendência central e dispersão, e inclusive analisar possíveis relações entre essas variáveis.
Vale enfatizar que nenhum número, isoladamente, pode caracterizar bem as diferenças entre duas distribuições. Com perdão pela tautologia, a comparação das médias mostra apenas a grandeza e o sentido da diferença nos níveis médios das duas distribuições. Se compararmos médias, desvios padrões e o coeficiente de assimetria, já captamos o que podem ser consideradas as principais características das duas distribuições, mas ainda não se trata de uma análise exaustiva. Alguns tipos de gráfico podem ser muito úteis para completar a análise. Como exemplo desse tipo de procedimento, mostramos, na Figura 6, os quantis da distribuição da escolaridade em Minas Gerais (MG), São Paulo (SP) e no Distrito Federal (DF). MG e SP são as unidades da Federação com as maiores populações, e optamos por incluir o DF por ele se destacar, na Tabela 3, pela maior escolaridade média.
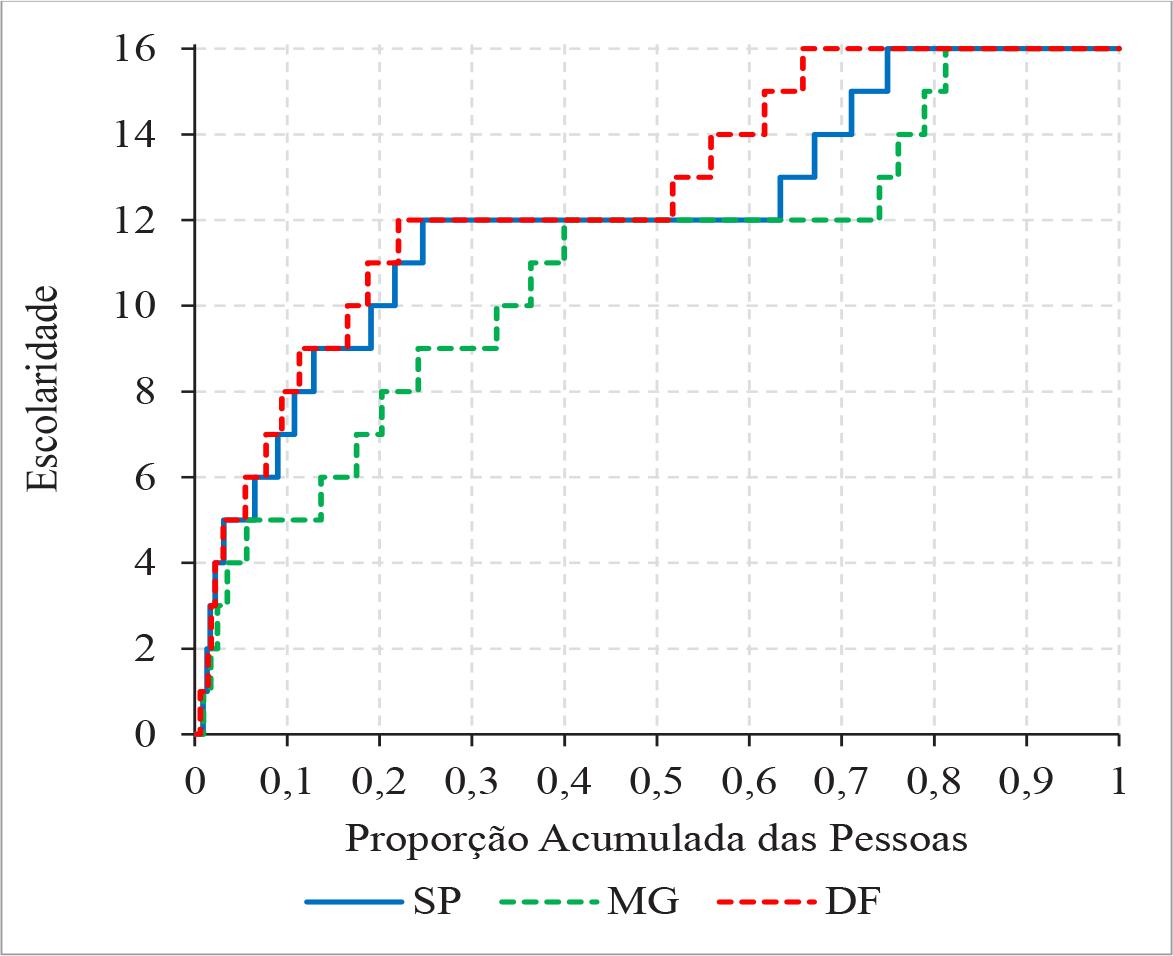
Fonte: Elaboração do autor, com base em microdados da Pnad Contínua de 2022 (IBGE, 2023).
FIGURA 6 Quantis das distribuições de escolaridade das pessoas ocupadas em MG, SP e DF em 2022
Observa-se, na Figura 6, que a linha para SP sempre coincide ou fica acima da linha para MG, ou seja, que a distribuição da escolaridade em SP domina, em primeira ordem, a distribuição em MG. Observa-se também que a distribuição da escolaridade no DF domina, em primeira ordem, a distribuição em SP. Então, necessariamente, a escolaridade média do DF é maior que a de SP, que, por sua vez, é maior que a de MG. A dominância em primeira ordem garante que, fixado um nível de escolaridade qualquer, a proporção de pessoas que alcançaram esse nível na distribuição dominante é maior ou igual à proporção correspondente na outra distribuição.
CONCLUSÃO
Nossa recomendação é abandonar totalmente o uso da divergência de Kullback- -Leibler na análise de notas.
Se considerarmos que escolaridade e notas são variáveis ordinais e não têm as propriedades de uma escala intervalar, nem o cálculo de médias é rigorosamente válido; a medida de tendência central apropriada é a mediana e devemos nos limitar aos métodos estatísticos não paramétricos. Se, por outro lado, admitirmos que notas e escolaridade têm escala razão, podemos usar médias e também as medidas usuais de dispersão (como a variância e o desvio padrão) e de desigualdade (como o coeficiente de variação, o índice de Gini e as medidas T e L de Theil).
Dada a dificuldade de encontrar uma medida sintética que leve em consideração os diversos aspectos relevantes na comparação entre distribuições de notas (ou de escolaridade), recomenda-se adicionalmente o uso de gráficos para fazer as comparações, como aqueles referentes às estimativas das suas funções de densidade, às curvas de quantis, às curvas de Lorenz e às curvas de Lorenz generalizadas.