1 Introducción
Uruguay registra, desde hace más de una década, una sostenida inversión en tecnologías digitales en centros educativos de Educación Primaria, secundaria y en formación docente mediante la implementación del Plan de “Conectividad Educativa de Informática Básica para el Aprendizaje en Línea” (Ceibal). Los estudios y principales investigaciones realizados en relación al Plan Ceibal señalan un avance significativo en términos de reducción de la brecha digital, acceso universal a la tecnología, aumento de las expectativas de los padres con respecto a la Educación de sus hijos y una alta valoración social de la iniciativa (RIVOIR, 2013).
A pesar del avance importante en términos de equidad de acceso y universalización de los recursos digitales, el Plan Ceibal enfrenta importantes desafíos para favorecer una mayor inclusión social e impulsar la mejora sostenida del sistema educativo de Uruguay (COBO, 2016; VAILLANT, 2013). Algunos de esos desafíos refieren al uso con sentido pedagógico de las tecnologías digitales y a su incorporación por parte de los profesores uruguayos.
Entre los antecedentes referidos a la temática, se destaca una investigación (VAILLANT; BERNASCONI, 2012) que identificó y analizó las expectativas, las prácticas de enseñanza y el desarrollo profesional de los profesores de Matemática de Educación Secundaria en Uruguay. Entre los principales hallazgos del estudio está que el uso de herramientas digitales se asocia a la enseñanza de conceptos específicos del campo matemático. Además, se pudo constatar que para un adecuado uso de las computadoras personales XO 1 , son fundamentales buenas condiciones de acceso, capacidades y actitudes favorables de los profesores, así como liderazgo pedagógico del director del centro. Y es en esa línea de investigación que se inscribe el estudio que se presenta en este artículo.
El análisis que compartiremos, se basa en el avance de resultados de la investigación en curso titulada “Claves para incorporar las herramientas y plataformas digitales en la enseñanza de la Matemática en el Ciclo Básico: percepciones de docentes y caminos de mejora”. El estudio fue diseñado e implementado por los tres autores con el apoyo de la Agencia Nacional de Investigaciones e Innovaciones de Uruguay (Anii) 2 . Se expone la información empírica de algunas de las variables y dimensiones consideradas en la encuesta digital realizada a profesores de Matemática en el primer semestre del año 2018. Por limitaciones de espacio, se han descartado los datos cualitativos del estudio resultantes de las entrevistas realizadas.
2 Notas conceptuales
2.1 ¿Qué dice la literatura internacional?
La incorporación universal de tecnologías digitales en los sistemas educativos de América Latina, la región del Caribe y resto del mundo es un fenómeno relativamente reciente y que busca promover, entre otros efectos, la alfabetización digital, las habilidades digitales y las competencias tecnológicas tanto de profesores como de estudiantes (ORGANIZACIÓN PARA LA COOPERACIÓN Y EL DESARROLLO ECONÓMICOS [OCDE], 2015).
Diversos informes y estudios reportan un crecimiento sostenido de las políticas referidas a las Tecnologías de la Información y de la Comunicación (TIC) en la última década (CHAIA et al ., 2017). Los avances han sido notorios y se han logrado, a través de programas uno a uno a escala nacional o sub nacional (tal es el caso de Argentina, Brasil, Costa Rica y Uruguay), o por la promoción del acceso y uso de diversos dispositivos, aplicaciones en red, plataformas de apoyo a la enseñanza o usos de estándares como apoyo de recursos TIC para la docencia y desarrollo de destrezas con tecnología digital ubicua (CABROL; SZÉKELY, 2012; UNESCO, 2016).
A pesar de la decidida promoción de gobiernos y organismos internacionales para la inclusión de tecnología con sentido pedagógico en las aulas, la mayoría de los profesores todavía prefieren aún el uso de métodos tradicionales de enseñanza y resisten la innovación de los métodos de enseñanza en ambientes tecnológicos (CABEZAS GONZÁLEZ; CASILLAS MARTÍN, 2019). Esta es una de las conclusiones principales de la encuesta internacional sobre la enseñanza y el aprendizaje del año 2013 según Teaching and Learning International Survey (Talis). El reporte destaca que el uso de las TIC es un factor clave para promover prácticas pedagógicas más activas que favorezcan la adquisición de conocimientos y competencias en los estudiantes (OCDE, 2015).
El Informe Talis (OCDE, 2015) señala avances significativos en la cobertura digital de los sistemas educativos, pero al mismo tiempo las opiniones de los profesores de los 36 países participantes en el estudio confirman que aún predominan los métodos tradicionales de enseñanza. Un 70% de los profesores encuestados declaran basar su enseñanza en un resumen de contenidos mientras que un 38% afirma usar las TICs en su práctica docente diaria (OCDE, 2015). Por otra parte, la encuesta revela que los profesores reclaman una adecuada formación en TIC para facilitar el uso pedagógico que hacen en las aulas (OCDE, 2015).
La revisión de la literatura internacional específica sobre enseñanza de la Matemática y tecnologías brinda potente evidencia basada en estudios de pequeña escala con modelos cuasi experimentales respecto a los beneficios del uso de las herramientas digitales en la docencia (BANSILAL, 2015; FURIÓ et al. , 2014). Por otra parte, diversos investigadores (ATTARD, 2015; GOEHLE; WAGAMAN, 2016) analizaron la efectividad que tienen para el aprendizaje de la Matemática el uso de herramientas y plataformas digitales por parte del profesor. Sin embargo, esos resultados deben ser considerados con prudencia pues dependen de una serie de factores entre los cuales están la preparación, formación y el compromiso de los docentes en el uso pedagógico de la tecnología digital (CHAUHAN, 2017).
Finalmente, la competencia Matemática del profesor se vincula con la habilidad de poner en acción una serie de destrezas tecnológicas que hacen referencia al razonamiento matemático para resolver situaciones del mundo cercano al alumno. El énfasis está en las capacidades, habilidades y destrezas para llevar adelante procesos tales como pensar, razonar, argumentar, modelar, y resolver situaciones problemáticas en las que son necesarios los conocimientos, las operaciones, el lenguaje simbólico de la Matemática y las herramientas tecnológicas (GARCÍA PERALES, 2014, 2018; OCDE, 2013).
2.2 La evidencia nacional
En el caso de Uruguay y a pesar de la expansión y masificación de los recursos tecnológicos, existe un escaso uso de las tecnologías en los cursos de Matemática, por parte de los estudiantes y profesores de Educación Secundaria (RODRÍGUEZ ZIDÁN; TÉLIZ, 2013). Algunos estudios evidencian que son escasos los apoyos que recibe el profesor para el uso de las herramientas digitales y para la consolidación de sus competencias y habilidades en Matemática (BENTANCOR BIAGAS, 2017). Esa es una de las razones que justifica la puesta en marcha de la Plataforma Adaptativa de Matemática (PAM), implementada por Plan Ceibal. Se trata de una iniciativa para que el profesor y el estudiante tomen contacto con una amplia gama de actividades, diferenciadas por niveles de dificultad.
En el año 2015, un estudio sobre el uso de PAM permitió identificar patrones de uso de la plataforma, perfiles de los profesores y patrones actitudinales de los estudiantes. La investigación evidenció que la plataforma se utilizó solo por parte de un 30% de los profesores observados. Además, se constató en un 96% de los casos, que los profesores tenían problemas en el uso de la plataforma. El recurso se utilizaba más como revisión de conceptos que como herramienta de apoyo pedagógico (PLAN Ceibal, 2015). A esa conclusión llegan otras investigaciones en Uruguay, las cuales evidencian que la variable con mayor incidencia referida a la probabilidad de uso es el “factor profesor” (ABOAL et al ., 2018).
Parecería que, entre otros factores, el liderazgo del director del centro educativo es esencial para promover el uso pedagógico efectivo de las tecnologías por parte de los profesores. También influyen los procesos y los planes curriculares en la formación de los profesores (MAZZOTTI, 2016). Y en ese sentido, la realidad es preocupante ya que solo el 40% de los formadores incorporan la enseñanza del uso de plataformas digitales en los cursos de formación inicial docente (RODRÍGUEZ ZIDÁN et al ., 2017).
Con respecto al diseño curricular y la formación inicial de profesores de Uruguay, una investigación indica que los planes de estudio no identifican cuáles son las competencias digitales que los futuros profesores deben incorporar y que por lo tanto resulta muy difícil adoptar cambios curriculares que posibiliten la inclusión genuina de las tecnologías digitales en la formación de los profesores (CABRERA BORGES et al., 2018).
3 Metodología
La investigación que se describe en este artículo tiene por objetivo identificar y describir el nivel de uso de aplicaciones, plataformas y dispositivos digitales que realizan en sus clases los profesores de Matemática del 1er. nivel de Educación Secundaria de Uruguay. Además, busca analizar si existen diferencias significativas de los niveles de uso de las tecnologías en función del género, la edad, la formación pedagógica específica para la disciplina, la experiencia como docente y la zona geográfica donde se desempeñan los profesores.
Tal como fue ya explicitado en la introducción de este artículo, el enfoque empleado fue cuantitativo y cualitativo. Por razones de espacio solo se presentan los datos cuantitativos resultantes de un diseño descriptivo no experimental transeccional, tipo “survey” (HERNÁNDEZ SAMPIERI; FERNÁNDEZ COLLADO; BAPTISTA LUCIO, 2010). El principal instrumento fue una encuesta digital que consideró los aportes de la traducción y adaptación a Uruguay del estudio Survey of Mobile device use during (WITECKI; NONNENCKE, 2015), la encuesta para la evaluación de plataformas digitales de Marcelo y Zapata (2008) y el inventario para el registro y descripción de las competencias tecnológicas en eLearning de Yot y Marcelo (2016).
Se implementó como estrategia de campo el envío del cuestionario digital vía formulario de LimeSurvey cuyas ventajas han sido reportadas por varios estudios internacionales (DÍAZ DE RADA, 2012; HOLMBERG et al ., 2010). Se trata de un procedimiento que tiene poco costo y permite un rápido acceso de poblaciones altamente dispersas geográficamente. Además ese tipo de encuesta en línea auto administrada implica una mayor garantía de anonimato (HEERWEGH; LOOSVELDT, 2008).
Entre sus debilidades, debe mencionarse los errores de cobertura, escasa aleatoriedad de la muestra y menor tasa de respuesta. Estos tres factores fueron especialmente considerados como amenazas a la validez y se consideraron para disminuir los sesgos de la investigación. En la planificación y puesta en práctica del procedimiento, se buscó maximizar las tasas de respuesta y la tasa de retención mediante estrategias como la personalización, la frecuencia semanal de envíos y la generación de incentivos para los profesores encuestados (HEERWEGH; LOOSVELDT, 2008).
Para el proceso de validación del cuestionario, se realizaron dos procedimientos: a) prueba piloto aplicada a 8 profesores de Matemática que no integraban la muestra y b) evaluación de las propiedades métricas de las escalas utilizadas. La prueba piloto fue efectuada por la plataforma Limesurvey para poder testear las condiciones de aplicación y los procedimientos. El proceso de validación permitió identificar las dificultades en la aplicación de las preguntas y mejorar aquellos aspectos que daban lugar a confusiones. Así, la pregunta original “ ¿Planifica estrategias pedagógicas para alumnos con necesidades educativas especiales utilizando herramientas y plataformas digitales? ” fue sustituida por “¿Planifica el uso de herramientas y plataformas digitales de acuerdo a las experiencias y aprendizajes previos de sus alumnos?”.
3.1 Población
El universo de estudio está delimitado por la condición de ser profesor de Matemática en el 1er Nivel de Educación Secundaria de Uruguay. El marco que se utilizó como insumo para la definición del procedimiento de muestreo, se constituyó a partir de los registros y bases de datos disponibles con información estadística de la población de docentes de Matemática en Uruguay (ADMINISTRACION NACIONAL DE EDUCACION PUBLICA, 2015, 2017; CONSEJO DE EDUCACION SECUNDARIA, 2017; INSTITUTO NACIONAL DE EVALUCI´N EDUCATIVA [INEED], 2014).
La muestra cuantitativa fue por conveniencia (HERNÁNDEZ SAMPIERI; FERNÁNDEZ COLLADO; BAPTISTA, 2010). Para el estudio descriptivo y explicativo, se conformó una muestra de profesores de Matemática de 1er Nivel de Educación Secundaria que constituyó nuestra población de estudio. Se enviaron 1.593 3 invitaciones por vía mail entre 24/8/2018 y 12/9/2018. Finalmente, la muestra voluntaria quedó integrada por 176 docentes que respondieron la invitación. La media de edad es de 42 años (< 21, > 63 y DS = 9,69), con una experiencia docente promedio de 14,8 años (< 1 y > 40 años y DS = de 8,48). El perfil sociodemográfico de la muestra puede apreciarse en la Tabla 1 .
Tabla 1 – Distribución de la muestra según Género y Titulación
| Variable | Valor | Frecuencia | Porcentaje (%) |
|---|---|---|---|
| Género | Femenino | 135 | 76,7 |
| Masculino | 41 | 23,3 | |
| Titulación | Sí | 111 | 63,1 |
| No | 65 | 36,9 |
Fuente: Elaboración propia (2019)
El perfil de distribución por género de la muestra es muy similar a la distribución nacional de profesores en Uruguay, donde existe una tendencia histórica de feminización de la matricula, ya que el 75% de los profesores son mujeres y el 25% hombres (ANEP, 2008). La titulación docente en Matemática en el país es una de las más bajas del sistema educativo, ya que se cuenta solamente con un 41% de docentes titulados (GONZÁLEZ MORA; GONZÁLEZ BURGSTALLER; MACARI, 2013).
3.2 Instrumento
El cuestionario diseñado se estructuró en ocho secciones, aunque solamente fueron consideradas para este artículo las dimensiones referidas a las competencias tecnológicas de los docentes. En particular, se analizó la frecuencia con que los docentes utilizan dispositivos digitales con sus alumnos en el aula de Matemática. Este procedimiento se realizó mediante una escala tipo Likert (respuestas categorizadas entre extremos de “Nunca” y “Todos los días”). Además se utilizó una escala que permitió determinar el nivel de uso de aplicaciones específicas para Matemática (respuestas categorizadas entre los extremos “No competente” y “Avanzado”). En la Tabla 2 se incluyen las dimensiones y subdimensiones del cuestionario así como el tipo de preguntas realizadas.
Tabla 2 – Estructura del cuestionario
| Dimensión (Sección) | Subdimensión | Ítem | Tipo de preguntas |
|---|---|---|---|
| A. Perfil profesional | Género, edad, antigüedad, subsistema, zona, titulación, centro y carácter del cargo | 1, 2, 3, 4, 5, 6, 7 y 8 | Politómicas y cuantitativas |
| B. Competencia y uso de tecnología | Desempeño en herramientas tecnológicas Acceso desde el hogar y el centro educativo a las herramientas tecnológicas Frecuencia de uso de herramientas tecnológicas | 9, 10, 11 y 12 | Politómicas y escala tipo Likert |
| C. Aplicaciones para la enseñanza de la Matemática | Nivel de uso de aplicaciones: PAM, GeoGebra, Moodle, Derive, Edmodo, Tortugarte | 13 | Escala tipo Likert |
| D. Mejora de los aprendizajes | Inclusión o no de herramientas digitales en su práctica | 14 | Dicotómica |
| E. Apoyo a la enseñanza | Elabora material didáctico digital, usa material extraído de un portal educativo, actividades domiciliarias que implican el uso de herramientas digitales | 15 | Escala tipo Likert |
| F. Necesidad de formación | PAM, otras plataformas, software específico de Matemática | 16 | Politómica |
| G. Limitaciones | Dificultades encontradas para incorporar software | 17 | Politómica |
| H. Actividad e aprendizaje basada en tecnología | Buenas prácticas de enseñanza con tecnología | 18 y 19 | Dicotómica y pregunta abierta |
Fuente: Elaboración propia (2019)
Los resultados acerca del grado de fiabilidad y consistencia interna de las dos escalas analizadas en este artículo se presentan en la Tabla 3 .
Tabla 3 – Niveles de confiabilidad de las escalas de medición utilizadas
| Escalas | N | Alpha de Cronbach | Decisión |
|---|---|---|---|
| Escala para medir frecuencia de uso de herramientas y plataformas digitales | 176 | 0,717 | Alta |
| Escala para medir el nivel de uso de aplicaciones para la enseñanza de la Matemática | 176 | 0,870 | Muy Alta |
| Se aplica el criterio interpretativo sugerido por: Ruiz Bolívar (2002) y Palella y Martins (2003) quienes indican que; de 0,81 a 1,00 la confiablidad es Muy Alta, de 0,61 a 0,80 es Alta y de 0,41 a 0,60 es Moderada. | |||
Fuente: Elaboración propia (2019)
El análisis de datos se realizó utilizando técnicas estadísticas descriptivas y coeficientes: frecuencias, análisis de diferencias significativas de medias y proporciones, aplicación de coeficientes no paramétricos. La base de datos se estructuró inicialmente en una planilla Excel y posteriormente el tratamiento estadístico se efectúo con el software SPSS V21.
4 Resultados
“¿Cuál es el uso que los docentes hacen de las plataformas digitales y de las aplicaciones matemáticas asociadas a la enseñanza de su disciplina?” es una de las preguntas que nos formulamos en la investigación. La encuesta realizada proporcionó respuestas en una escala tipo Likert de 5 puntos (desde 1- “No competente hasta 5- “Avanzado”), ya que los profesores debían indicar sus preferencias de uso en una lista con diferentes aplicaciones informáticas y plataformas educativas a emplear para el abordaje de contenidos curriculares del Ciclo Básico de Educación Secundaria.
El listado de aplicaciones fue agrupado en tres categorías: Plataformas, Geometría y Análisis y Programación. Los resultados se procesaron a partir de la construcción de un indicador que resulta de la suma de los valores porcentuales de la escala adjudicados a las categorías “Muy Avanzado” (valor 5) y “Avanzado” (valor 4) en cada ítem de la escala. El Gráfico 1 muestra la distribución porcentual de este indicador en el cual se destaca el uso de la aplicación GeoGebra y de PAM.
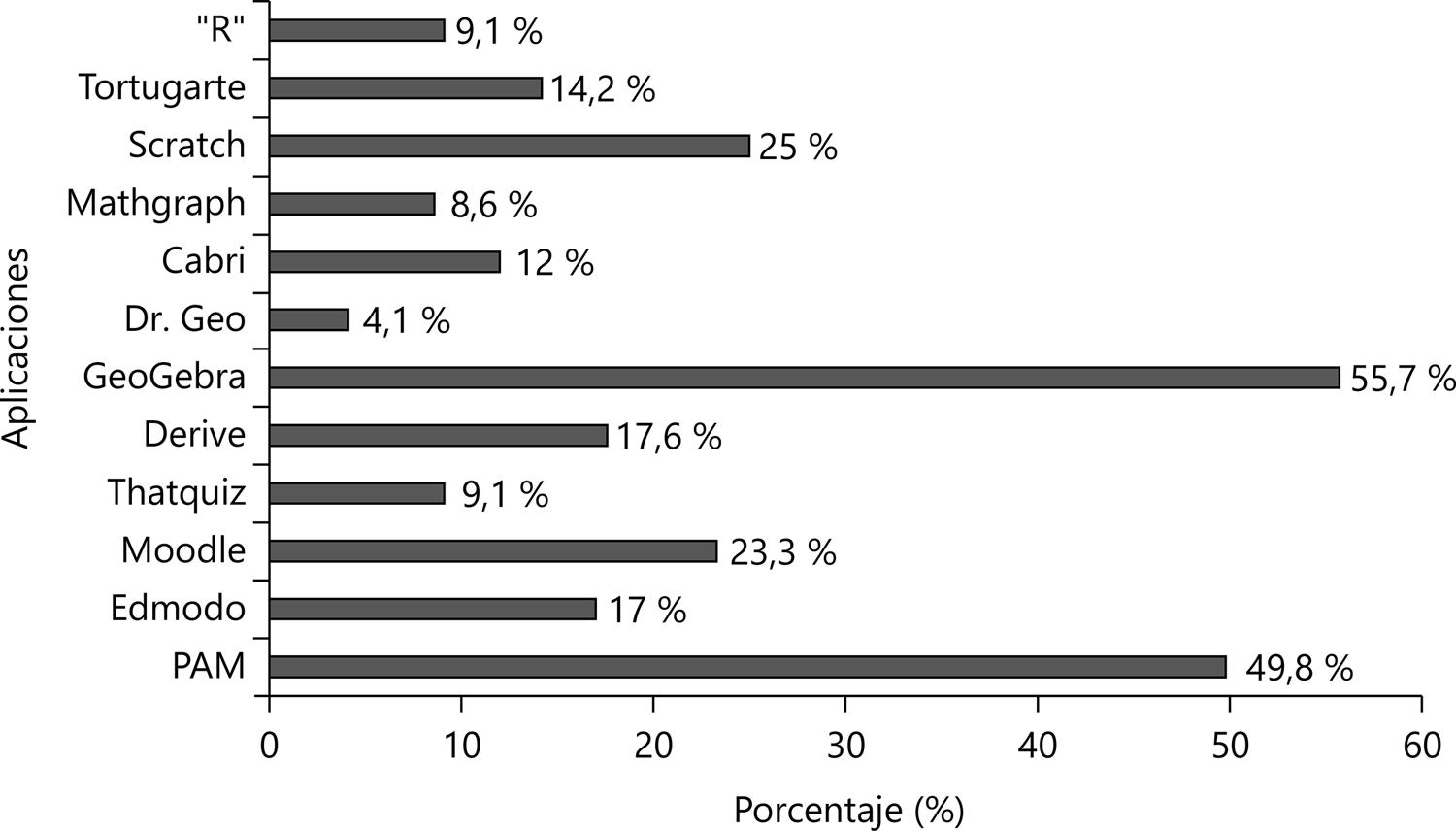
Fuente: Elaboración propia (2019)
Gráfico 1 – Porcentaje de profesores con un nivel de uso avanzado o muy avanzado de las aplicaciones específicas para la enseñanza de la Matemática (*)(*) Suma de porcentajes de respuestas de las dos categorías de la escala Likert en cada variable.
Un análisis más detallado se presenta en la Tabla 4 , donde se incluyen las estadísticas descriptivas de las variables evaluadas. Se elaboró una clasificación de estas en tres categorías: Plataformas, Geometría y Análisis y Programación.
Tabla 4 – Uso de aplicaciones matemáticas y herramientas digitales: estadísticas descriptivas según dimensión considerada
| Dimensión | Variables | N | Mínimo | Máximo | Media | Desvío Estándar | Porcentaje Muy avanzado uso |
|---|---|---|---|---|---|---|---|
| Plataformas | PAM | 176 | 1,00 | 5,00 | 3,2898 | 1,18133 | 49,8 |
| Edmodo | 176 | 1,00 | 5,00 | 2,4148 | 1,14323 | 17,0 | |
| Moodle | 176 | 1,00 | 5,00 | 2,3807 | 1,29944 | 23,3 | |
| Thatquiz | 176 | 1,00 | 5,00 | 1,8068 | 1,10952 | 9,1 | |
| Geometría y Análisis | Derive | 176 | 1,00 | 5,00 | 2,4318 | 1,17396 | 17,6 |
| GeoGebra | 176 | 1,00 | 5,00 | 3,5568 | 0,86001 | 55,7 | |
| Dr. Geo | 176 | 1,00 | 5,00 | 1,6307 | 0,98849 | 4,1 | |
| Cabri | 176 | 1,00 | 5,00 | 2,1932 | 1,09396 | 12,0 | |
| Mathgraph | 176 | 1,00 | 5,00 | 2,0966 | 1,07267 | 8,6 | |
| Programación | Scracth | 176 | 1,00 | 4,00 | 1,7841 | 0,93746 | 25,0 |
| Tortugart | 176 | 1,00 | 4,00 | 1,4716 | 0,82065 | 14,2 | |
| ‘R’ | 176 | 1,00 | 4,00 | 1,2841 | 0,73210 | 9,1 |
Fuente: Elaboración propia (2019)
Como se puede apreciar en la Tabla 4 , GeoGebra (55,7%) y la Plataforma Adaptativa de Matemática (PAM, 49,8%), aparecen como las aplicaciones específicas para Matemática que consignan los mayores niveles de uso según la autopercepción declarada por los docentes consultados. Hemos encontrado, además, que existe una correlación fuerte y significativa entre el uso de PAM y la predisposición a usar la aplicación GeoGebra (N = 176, “r”, 0.43, p.000).
En el otro extremo, programas más específicos como R (9,1%), que requieren el dominio de destrezas tecnológicas más avanzadas para su utilización, Mathgraph (8,6%), Dr. Geo (4,1%) registran bajos porcentajes de utilización. Estos programas interactivos para la enseñanza de geometría aparecen relegados, posiblemente por el uso institucionalizado que en Uruguay tiene la aplicación GeoGebra. Este hecho se constata en iniciativas como la organización del curso semipresencial de GeoGebra dirigido a profesores de enseñanza secundaria del Uruguay con el objetivo de capacitar a los docentes en el uso del software (MACHADO et al ., 2012) y en la elaboración de un estudio, realizado por docentes del Consejo de Formación en Educación de la Anep, que recoge algunas experiencias didácticas del uso de GeoGebra para el trabajo en la escuela primaria (DAMISA; DODINO; PIEDRA CUEVA, 2017).
Esta predisposición a usar GeoGebra que tienen los profesores sobre otro software dinámico coindice con los hallazgos de estudios nacionales (TÉLIZ 2014; VAILLANT; BERNASCONI, 2012) e internacionales (BULUT; BULUT, 2011; REISA, 2010; SUMMAK; BAGLIBEL; SAMACIOGLU; 2010), que han reconocido sus fortalezas para la enseñanza de la geometría sobre otros programas de la misma disciplina.
4.1 Uso de dispositivos para el trabajo con herramientas y plataformas digitales
“¿Qué dispositivos utilizan con mayor frecuencia los profesores de la muestra analizada como soporte para el trabajo con herramientas y plataformas digitales?”, es otra de las preguntas que nos formulamos en el estudio. Para responderla, indagamos en la frecuencia con la que los profesores utilizan herramientas y plataformas digitales con sus alumnos en los siguientes dispositivos: sala de Informática o Laboratorio del centro educativo, con las computadoras brindadas por el Plan Ceibal, con tablet y con smartphones . Los profesores expresaron su frecuencia de uso, teniendo en cuenta la siguiente escala: 1 – Nunca, 2 – Algunas veces al mes, 3 – Algunas veces a la semana, y 4 – Todos los días.
Los datos colectados permitieron realizar dos tipos de análisis: la frecuencia de uso que hacen los profesores de los dispositivos digitales y los diferentes niveles de intensidad de uso de cada uno de los dispositivos digitales relevados. La frecuencia fue estudiada a partir de un índice que resulta de la suma de las puntuaciones de las respuestas obtenidas en la consulta sobre el uso de cuatro dispositivos digitales. El índice tiene un rango de variación que oscila entre los 4 y los 16 puntos y para para su representación gráfica y visualización se presenta en el Gráfico 2 un Índice resumen con tres categorías: frecuencia baja (4, 9), frecuencia media (9, 13), frecuencia alta (13, 16).
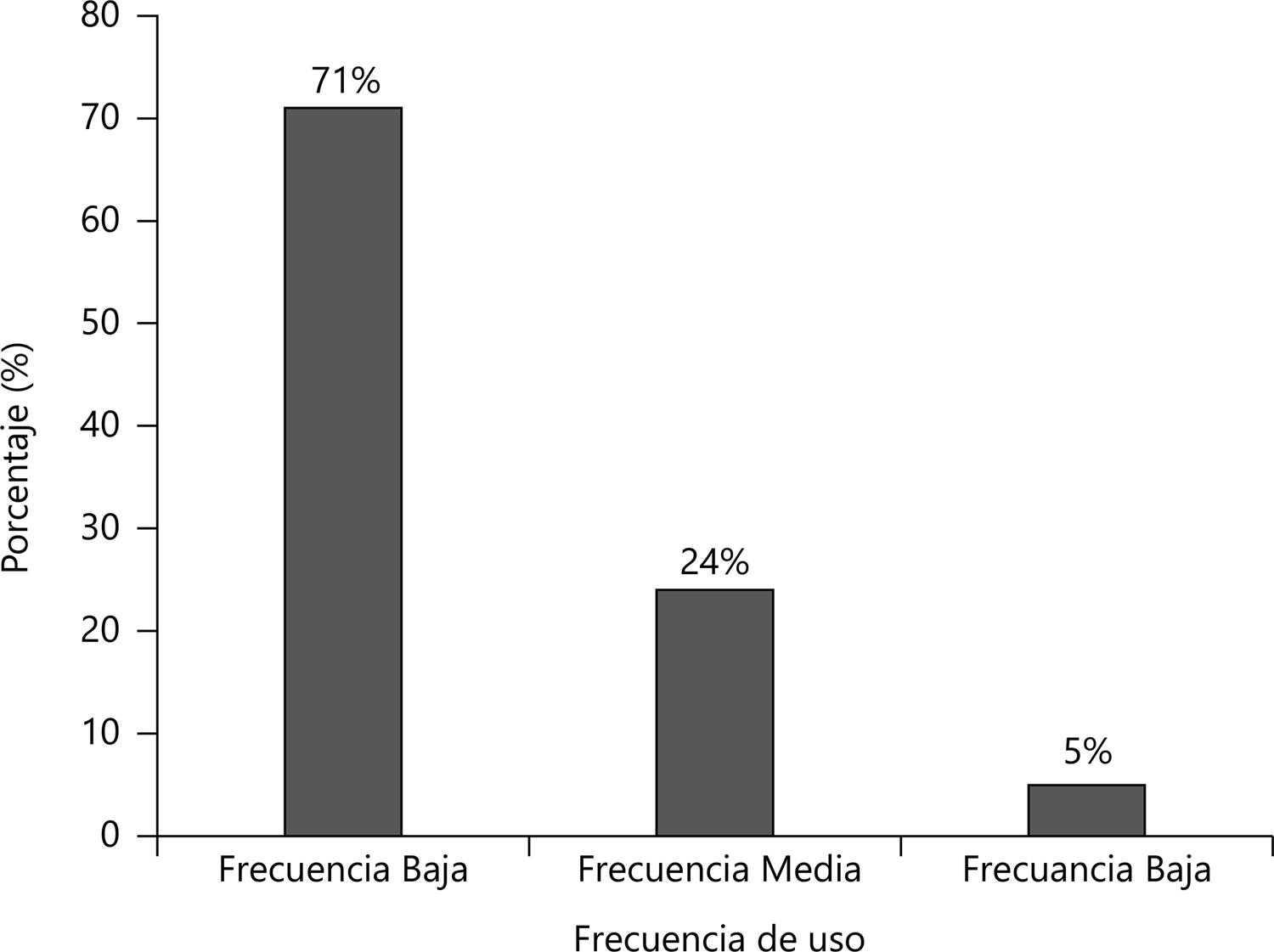
Fuente: Elaboración propia (2019)
Gráfico 2 – Índice resumen de frecuencia de uso de dispositivos digitales
Las evidencias que figuran en el Gráfico 2 son concluyentes. Se constató una escasa orientación de los profesores de Matemática de la muestra hacia la promoción de un trabajo pedagógico en el aula apoyado con tecnología. El 71% de los profesores relevados manifiesta una baja predisposición para el trabajo con tecnología digital con sus alumnos.
Posteriormente para indagar la intensidad con la que los profesores usan los diferentes dispositivos digitales relevados, se diseñó un nuevo indicador a partir de la suma de los porcentajes correspondientes a los valores 3 “Algunas veces a la semana” y 4 “Todos los días” de la variable.
En el Gráfico 3 podemos observar que los profesores de Matemática utilizan con diferente intensidad los dispositivos digitales relevados como instrumentos de apoyo a la enseñanza. El uso del teléfono Smartphone es el soporte preferido de los docentes (39,2%). Con base en los datos relevados en este estudio, y para el caso de la docencia de Matemática en el 1er nivel de Educación Secundaria, este recurso estaría desplazando, tal como las evidencias lo indican, al uso de la computadora personal que brinda el Plan Ceibal a los estudiantes, la tablet y el recurso de trabajar con los estudiantes fuera de salón de clase en la sala de informática.
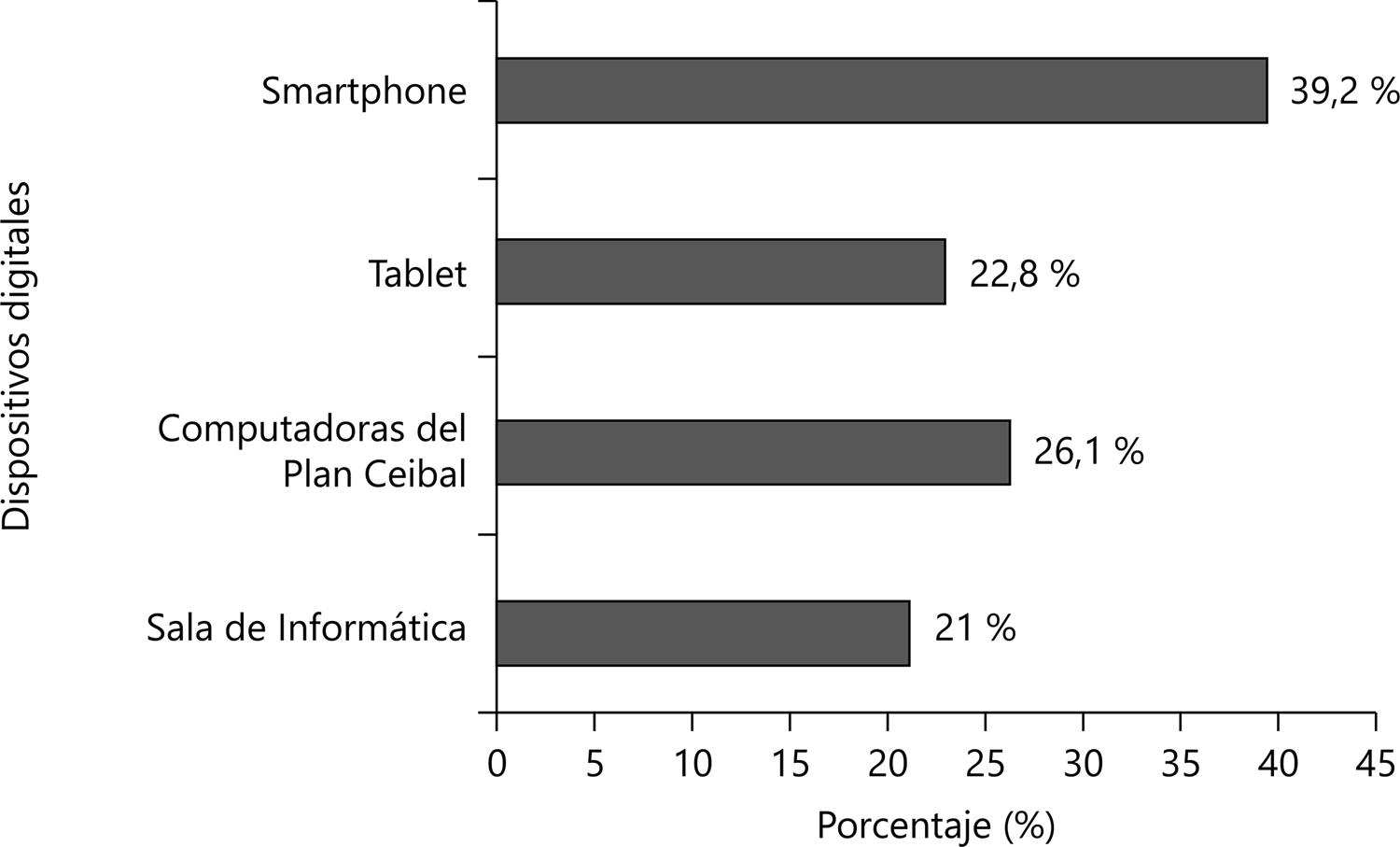
Fuente: Elaboración propia (2019)
Gráfico 3 – Frecuencia de uso de dispositivos digitales preferidos para la enseñanza de la Matemática** La frecuencia de uso se expresa en porcentaje de respuestas positivas sobre cada dispositivo
Estos datos coinciden con otros estudios nacionales referidos al uso de tecnologías ubicuas en la formación docente (CABRERA BORGES et al. , 2018) resultados de reportes de organismos internacionales (UNESCO, 2016) y análisis empíricos que estudiaron de qué manera cambian los procesos de enseñanza y aprendizaje a partir de la inclusión de recursos y plataformas digitales que posibilitan el aprendizaje ubicuo (LEFOE et al., 2009; SANG et al., 2010).
4.2 ¿Qué factores explican los diferentes niveles de uso de las tecnologías?
Además del abordaje descriptivo, nos propusimos estudiar si existen diferencias significativas del nivel de uso de aplicaciones y dispositivos en función de factores sociodemográficos y profesionales. En este caso, optamos por aplicar un coeficiente no paramétrico ya que partimos de la constatación de que las observaciones en la variable dependiente no cumplen con el supuesto de normalidad (ya que la “p” asociada a los contrastes de K-S (0,003) y S-W (0,039) da por debajo del nivel de significación alfa prefijado de 0,05). Las pruebas U de Man Whitney y la prueba H de Kruskal-Wallis son una excelente alternativa a las pruebas paramétricas basadas en el t de Student, ya que posibilitan contrastar la hipótesis de que K muestras cuantitativas se han obtenido de la misma población.
A tales efectos se seleccionaron para el análisis dos aplicaciones (GeoGebra y Scratch) y dos plataformas (PAM y Moodle) de mayor uso docente, además de los cuatro dispositivos digitales relevados.
La Tabla 5 muestra los valores significativos (sig. bilateral) de los coeficientes no paramétricos aplicados. El procedimiento seleccionado para el análisis relaciona cada uno de los cinco factores sociodemográficos considerados con las ocho variables dependientes incluidas en el modelo.
Tabla 5 – Contraste de hipótesis U de Man Whitney y Kruskall y Wallis según las variables consideradas en el modelo (valores de p .)
| Variables | Principales aplicaciones matemáticas y plataformas utilizadas | Uso de dispositivos para la enseñanza de la Matemática | ||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| PAM | GeoGebra | Scratch | Moodle | Sala de Informática | XO | Tablet | Smartphone | |
| Edad(**) | 0,109 | 0,27 | 0,307 | 0.564 | 0.090 | 0.586 | 0.378 | 0.436 |
| Género(*) | 0.376 | 0.955 | 0.929 | 0.619 | 0.112 | 0.872 | 0.310 | 0.999 |
| Título(*) | 0.312 | 0.030 | 0.019 | 0.226 | 0.236 | 0.403 | 0.255 | 0.191 |
| Experiencia(*) | 0.814 | 0.637 | 0.621 | 0.244 | 0.224 | 0.045 | 0.836 | 0.348 |
| Zona | 0.530 | 0.696 | 0.209 | 0.696 | 0.044 | 0.000 | 0.259 | 0.180 |
Fuente: Elaboración propia (2019)
(*) Valores p. de U de Man Whitney, (**) Valores p. de Kruskall y Wallis
El contraste estadístico realizado nos permitió identificar que la titulación pedagógica incide favorablemente en la promoción del uso de GeoGebra (p.0030) y de Scratch (p.0.019). Hemos encontrado diferencias estadísticamente significativas con respecto a la zona geográfica que determinan un mayor uso del laboratorio o la sala de informática (p.004) y un aumento en la preferencia de las computadoras personales (p.000). Los profesores que se desempeñan en Montevideo parecen enfrentar mayores dificultades para el uso de tecnologías que sus colegas del resto del país. Para el primer caso, los profesores de la región metropolitana utilizan más el recurso de trabajar con sus alumnos en la sala de computadoras del centro educativo. En lo referido a la segunda hipótesis, los profesores de Matemática que se desempeñan en la región geográfica más distante de la zona metropolitana utilizan con mayor frecuencia las computadoras otorgadas por el Plan Ceibal. Probablemente el tamaño del centro educativo y la mayor frecuencia en estas zonas de centros educativos de pequeña escala favorezca el uso de tecnologías en el aula de Matemática. Finalmente, la experiencia docente explica el mayor uso de las computadoras personales del Plan Ceibal (p.0.045), lo que podría ser interpretado como la necesidad de implementar políticas a largo plazo para sostener el cambio educativo con tecnologías.
Otro hallazgo encontrado es que las evidencias confirman la no incidencia del sexo y la edad en las preferencias de uso de tecnologías para la docencia de la Matemática. Los datos coinciden con los resultados de estudios antecedentes (RODRÍGUEZ ZIDÁN et al. , 2017). En un listado de 43 actividades de aprendizaje con tecnologías relevadas entre estudiantes de Uruguay de diferentes especialidades de profesorado, en solo tres se hallaron diferencias significativas según las edades y el sexo. Una conclusión similar se ve reflejada en los resultados de estudios previos realizados por Marcelo et al. (2016) quienes encontraron que no existen diferencias significativas en el nivel de uso de tecnologías como apoyo a actividades de aprendizaje entre docentes universitarios españoles en función del sexo o de la edad.
La no existencia de relación entre edad y uso de tecnologías pone en duda la teoría de los nativos digitales (PRENSKY, 2001). Casi la mitad de la muestra de profesores de Matemática (45%), tienen 38 años o menos, límite establecido como la barrera entre nativos e inmigrantes digitales. Sin embargo, a pesar de esta condición, este subgrupo docente tiene un bajo desempeño de competencias digitales. Tal como se ha establecido en estudios previos acerca del uso de tecnología digitales en los estudiantes, un grupo importante de los nativos digitales no están familiarizados con habilidades digitales altas (GALLARDO ECHENIQUE, 2012).
Ese hallazgo nos sirve de insumo para reflexionar acerca del diferente nivel de desarrollo de competencias y de uso de recursos digitales en los profesores de Matemática. En nuestro estudio nos encontramos con dos tipos de usabilidad de las tecnologías según las percepciones de los docentes: un grupo caracterizado por el uso 2.0 de la tecnología digital y que está en condiciones de desarrollar habilidades digitales avanzadas con sus estudiantes en la clase de Matemática (aprendizaje en línea, uso de plataformas virtuales, uso de Smartphone en clase) y otro grupo de docentes con bajo desempeño en el uso de tecnologías, cuyo perfil está más ligado las prácticas tradicionales con bajo uso de tecnologías de tipo 1.0. En los dos grupos de docentes, la edad no es un factor determinante.
5 Conclusiones
Tanto el análisis descriptivo como el estudio de hipótesis mediante correlaciones entre factores sociodemográficos y variables de uso de las tecnologías en el aula de Matemática, nos permitió comprobar la existencia de diferencias en el perfil de uso, tanto en la frecuencia como en la preferencia de dispositivos. Los hallazgos encontrados ponen de manifiesto que el aprovechamiento pedagógico en la clase de Matemática de los recursos, herramientas y plataformas examinadas es de nivel bajo y moderado. Para potenciar este impacto, es necesario crear nuevos modelos disruptivos de formación tecno pedagógica del profesorado (MARCELO; VAILLANT, 2018).
Se destaca entre los resultados alcanzados la incorporación del teléfono celular como el dispositivo que más utilizan los profesores en sus clases de Matemática, 13 puntos porcentuales por encima de la computadora que brinda Plan Ceibal y casi 17 puntos por encima de la tablet. En este sentido, nuestros hallazgos coinciden con los resultados de investigaciones que demuestran que los dispositivos móviles devienen en escenarios educativos nuevos, tanto formales como informales (HINOSTROZA et al ., 2015; UNESCO, 2016).
Si bien la edad no es un factor que incida en el uso de las tecnologías por parte de los profesores de Matemática participantes del estudio, se halló que otros factores contextuales como el hecho de disponer de un título de pedagogía para el nivel donde se desempeñan o la experiencia profesional como profesores de secundaria son elementos que contribuyen a aumentar la efectividad en el uso de TIC en Educación Básica.
Los datos presentados en este artículo refieren a un estudio empírico de corte descriptivo. Los hallazgos deber ser interpretados en el marco de las limitaciones propias del enfoque, principalmente las referidas al tamaño de la muestra y la autoselección voluntaria de los participantes a responder el cuestionario en línea. En el futuro, seria relevante contrastar los resultados con estudios apoyados en metodologías mixtas, a efectos de enriquecer los hallazgos desde una perspectiva que articule métodos cuantitativos y cualitativos.















