INTRODUÇÃO
O desenvolvimento científico-tecnológico e a inovação de um país passam pelos portões da apropriação, por parte dos estudantes, desde a educação básica, dos conhecimentos matemáticos em nível científico. Mas, de modo geral, o sistema educacional brasileiro vem promovendo o desenvolvimento do pensamento empírico, a partir do ensino dos conhecimentos fragmentados e simplificados, apresentados aos estudantes já em sua forma abstrata, por meio de uma sequência de passos prontos para serem memorizados (Amaral, 2018; Lemes e Cedro, 2015; Silva, 2018; Souza e Esteves, 2018).
Como resultado, os dados do Sistema de Avaliação da Educação Básica (Saeb), divulgados pelo Ministério da Educação (MEC), em 2017, indicam que sete de cada dez alunos, ao concluírem a educação básica, demonstram nível insuficiente em matemática (Brasil, 2016). Resultado similar também foi constatado pelo Programa Internacional de Avaliação de Alunos (Pisa), principal avaliação educacional internacional, na qual, entre os 79 países avaliados em 2018, o Brasil ficou na 71ª posição em matemática.
Com todas as ressalvas a esse tipo de avaliação, esse baixo desempenho dos estudantes brasileiros decorre, dentre outros fatores, do modo de organização do ensino vigente, no qual predomina o pensamento empírico (Rosa e Antunes, 2021). As consequências para o desenvolvimento do pensamento em nível teórico/científico são danosas e impactam negativamente vários aspectos, inclusive os resultados das avaliações oficiais.
Isso significa que devemos organizar o ensino em função de tais avaliações? Óbvio que não. Isso significa que devemos organizar o ensino de modo que possibilite a apropriação da essência dos conhecimentos, da relação genética inicial, essencial, nuclear, que permita a aplicação dos respectivos conhecimentos nas diversas situações particulares (Davýdov, 1982). Tal relação nuclear também não é considerada no ensino brasileiro, geralmente são ensinados exemplos particulares, empiricamente. E, então, os estudantes só conseguem resolver exercícios parecidos com aqueles vistos em sala, seja nas provas oficiais ou em situações do dia a dia (Rosa, 2012).
É neste contexto educativo (educação básica) que são formados os futuros professores. Nos cursos de licenciatura, a lógica não tem sido muito diferente daquela que sustenta a educação básica e os professores recém-formados tendem a repetir o conteúdo e o método de ensino que receberam na educação básica e no ensino superior (Matos, 2017).
Portanto, é necessário repensar, no sistema educacional brasileiro, o modo de organização de ensino vigente, tanto o conteúdo quanto a metodologia, desde a educação básica até a formação de professores (Freitas, 2016 e Isidoro, 2019; Fontes, 2019). Uma das possibilidades para subsidiar o repensar consiste no ensino desenvolvimental (Libâneo e Freitas, 2017).
A Teoria do Ensino Desenvolvimental foi formulada por Vasily Vasilyevich Davýdov com o objetivo de promover o desenvolvimento do pensamento teórico contemporâneo nos estudantes. Para o autor em referência, o pensamento humano caracteriza-se pelas “particularidades da generalização, em unidade com os processos de abstração e formação de conceitos” (Davídov, 1988, p. 100, tradução nossa). Ele pode ocorrer de duas formas: pela lógica formal (aspecto imediato, direto e externo) ou pela lógica dialética (aspecto mediatizado, interno, ligado à essência do objeto).
Para Davídov (1988, p. 104, tradução nossa), “o pensamento que se realiza com a ajuda das abstrações e generalizações de caráter lógico-formal somente leva a formar os chamados conceitos empíricos”. Eles revelam apenas a aparência em seu aspecto imediato e direto, descrevem somente os resultados do pensamento empírico por meio de tarefas que classificam, comparam e identificam os objetos em seus traços comuns, externos. Porém, o pensamento empírico não é o caminho mais efetivo para os dias atuais (Davídov, 1988).
O nível requerido atualmente é o do pensamento teórico moderno, em que “[...] põe em evidência as passagens, o movimento, o desenvolvimento, graças ao qual pode examinar as coisas de acordo com a natureza própria destas” (Davídov, 1988, p. 108, tradução nossa). O pensamento teórico decorre dos conceitos científicos. Esse possibilita revelar a essência do objeto, sua conexão interna, e requer que os estudantes considerem os objetos e fenômenos em um sistema que contemple as relações dentro de uma totalidade.
Em síntese, Davýdov (1982) propõe que a educação escolar organize o ensino com a finalidade de promover o desenvolvimento do pensamento teórico dos estudantes, a partir da apropriação de conhecimentos científicos.
No que se refere à matemática, o ensino desenvolvimental prevê que os conceitos sejam abordados a partir da revelação e modelação do núcleo conceitual no estudo das relações entre grandezas discretas e contínuas, na indissociabilidade entre aritmética, álgebra e geometria (Davýdov, 1982; Davídov, 1988; Rosa, Moura e Damazio, 2019).
Por outro lado, no modo de organização de ensino predominantemente desenvolvido no Brasil, as significações aritméticas, algébricas e geométricas geralmente são apresentadas aos estudantes de forma fragmentada. O estudo das grandezas aparece ao final dos livros didáticos ou diluído em capítulos isolados, sem interconexão com os demais conceitos que comumente emergem da contagem de grandezas discretas e da dicotomia entre concreto e abstrato (Rosa e Galdino, 2017).
Faz-se necessário, portanto, repensar o modo de organização de ensino predominantemente desenvolvido no Brasil de modo que ocorra o processo de redução do concreto ao abstrato e a ascensão do concreto ao abstrato (Rosa e Hobold, 2016). “O movimento do sensorial-concreto ao concreto por meio do abstrato no pensamento é a lei universal do desenvolvimento do conhecimento humano, a qual ocupa posição especial na dialética materialista” (Kopnin, 1978, p. 163).
No estágio da percepção sensorial da realidade, o conhecimento recebe os dados, o material, sem o qual não se pode avançar nem um passo. No estágio do pensar abstrato, se busca o que constitui a base, a unidade da diversidade. No estágio da reprodução mental do concreto, o círculo em certo modo de fecha no ponto de partida, porém, sobre uma nova base: a diversidade se nos apresenta já não como um conjunto caótico de aspectos e relações, mas como uma unidade organizada subordinada a determinadas leis. O concreto mentalmente reproduzido aparece já não em forma de somas de diversos dados, observações, fatos, proposições separadas, etc., mas como um saber sobre os fenômenos iluminados por uma ideia única. (Ilienkov, 2006, p. 160)
O movimento do pensamento de redução concreto ao abstrato consiste na separação do universal como essência e lei do desenvolvimento do sistema e leva à formação do conceito. “Só no processo de ascensão ao concreto mental, e dentro dele, o conceito revela sua genuína importância teórica e seu conteúdo inicial, elaborando em si os dados da contemplação e representação, de todo o conjunto de referências fáticas sobre o objeto.” (Davídov, 1988, p. 357)
A passagem do concreto ao abstrato e deste ao concreto não pode ser empírica, não pode ser fragmentada, não pode ser rasa. É preciso considerar, desde o concreto ponto de partida, as reflexões em nível teórico. Para tanto, ao realizar experiências práticas, objetais, o estudante deve refletir sobre elas teoricamente (Davýdov, 1982; Davídov, 1988; Rosa, Moura e Damazio, 2019).
Mas como organizar o ensino de matemática a partir de experiências práticas na unidade entre concreto e abstrato no âmbito teórico? Como articular as significações aritméticas, algébricas e geométricas em um único conceito ou sistema conceitual? De que forma o estudo das grandezas pode dar origem a diferentes conceitos matemáticos? Em outras palavras, como organizar o ensino de matemática com base na Teoria do Ensino Desenvolvimental?
Em busca de respostas aos questionamentos anteriormente apresentados, acompanhamos, durante o segundo semestre de 2017, as aulas da disciplina relacionada ao ensino de matemática do curso de pedagogia de uma universidade comunitária localizada no Sul do Brasil que segue os princípios teóricos e metodológicos da Teoria do Ensino Desenvolvimental (Rosa e Santos, 2020).
Dentre os diversos sistemas conceituais abordados na disciplina, focamos naquele constituído pelas relações de multiplicação e divisão, dada a sua relevância para a educação matemática básica. A relação de multiplicidade e divisibilidade dá origem à tabuada e, portanto, interfere no estudo de vários conceitos ao longo de todo o ensino fundamental e médio (Rosa e Hobold, 2019).
Tais delineamentos nortearam o processo de constituição do objetivo de pesquisa, que consiste em investigar a origem e o desenvolvimento de elementos característicos do ensino desenvolvimental durante a introdução dos conceitos de multiplicação e divisão em um curso de pedagogia.
Para tanto, realizamos uma investigação experimental, por meio de um experimento didático desenvolvimental. Essa metodologia de pesquisa, proposta por Davídov (1988), permite ao pesquisador investigar o processo de ensino e aprendizagem no contexto em que ele ocorre. De acordo com Davídov (1988), o experimento didático desenvolvimental caracteriza-se pela intervenção ativa do pesquisador nos processos que ele investiga e “aparece como metodologia de educação e ensino experimentais que impulsionam o desenvolvimento.” (Davídov, 1988, p. 196, tradução nossa, grifo do autor)
Para a apreensão da realidade pesquisada, acompanhamos os 15 encontros semanais, com duração de 3 horas cada. Assumimos a docência em 2 encontros, nos quais refletimos sobre o modo de organização do ensino sobre os conceitos de multiplicação e divisão, com 23 acadêmicas, todas do sexo feminino, matriculadas na 4ª (quarta) fase do curso. A turma era bem diversificada do ponto de vista de idade, com acadêmicas de 18 a 48 anos. No início do semestre, a maioria da turma já estava em início da carreira docente, por meio de estágios remunerados e atuando como professora auxiliar de estudante com necessidades especiais. A maioria relatou que passou por dificuldades com a matemática na educação básica e que essas dificuldades se tornaram, no decorrer dos anos, em aversão a essa disciplina. Tal aversão provocou ansiedade e preocupação com o início da unidade de aprendizagem de matemática no curso de pedagogia. Ao longo do semestre, as inseguranças provocadas pelas experiências negativas anteriormente vivenciadas foram gradual e parcialmente arrefecidas. No 7º e 8º encontros assumimos a docência em caráter investigativo. Esses 2 encontros constituem o recorte da presente pesquisa, porém sem desconsiderar as relações dele com os demais momentos da disciplina.
O recorte para o presente artigo foi detalhado por meio da apreensão de 3 episódios formativos capturados em 3 momentos distintos, mas interconectados: 1. primeiro dia de aula do semestre letivo (avaliação inicial); 2. decorrer do semestre (experimento didático desenvolvimental com dois dias de duração) e 3. ao final do semestre (avaliação das compreensões finais), por meio da elaboração de um novo plano de ensino e desenvolvimento com estudantes dos anos iniciais do ensino fundamental.
No decorrer do semestre, estruturamos e reestruturamos o experimento didático desenvolvimental, com uma sequência de tarefas, a partir dos estudos de Crestani (2016) sobre o ensino desenvolvimental, e desenvolvemos com as acadêmicas no 7º e 8º encontros.
Esses três momentos foram capturados em gravações de áudio, vídeo e registro fotográfico, por meio dos seguintes instrumentos: gravador de voz, filmadora, máquina fotográfica e diário de campo. Registramos as manifestações orais e escritas das acadêmicas nas conversas individuais e coletivas durante o desenvolvimento das tarefas. Os dados apreendidos foram organizados e analisados conforme expomos na sequência.
O EXPERIMENTO DIDÁTICO DESENVOLVIMENTAL
Durante a realização do experimento, apreendemos os dados de pesquisa e sistematizamos por meio de episódios formativos compostos por cenas, que foram organizadas em flashes: falas transcritas, fotografias e figuras captadas no experimento didático desenvolvimental. As cenas e os correspondentes flashes refletem as manifestações das acadêmicas no processo de resolução e correção de tarefas sobre os conceitos de multiplicação e divisão. Os flashes estão seguidos do nome de cada acadêmica, por solicitação das próprias colaboradoras da pesquisa, que optaram por serem identificadas.
O recorte da pesquisa, para o presente artigo, incide nas manifestações das acadêmicas durante o desenvolvimento da primeira tarefa sobre os conceitos de multiplicação e divisão, conforme segue.
EPISÓDIO FORMATIVO - INTRODUÇÃO DOS CONCEITOS DE MULTIPLICAÇÃO E DIVISÃO
O presente episódio formativo é constituído por 2 (duas) cenas, nas quais expressamos o movimento realizado durante a resolução coletiva da primeira tarefa sobre os conceitos de multiplicação e divisão. A primeira tarefa consistia na medição, com uma xícara tomada como unidade de medida básica, de um volume de líquido que estava em um recipiente maior. Tomamos como ponto de partida o objeto concreto sensorialmente dado aos órgãos dos sentidos. Esse movimento teve como ponto de partida a relação entre medidas, a partir de um experimento objetal que envolvia a medição da grandeza volume. Nesse episódio ocorreram a revelação e a transformação dos elementos da relação nuclear dos conceitos de multiplicação e divisão bem como sua modelação nas formas objetal, gráfica e literal, por meio de elementos algébricos, geométricos e aritméticos.
• Cena 1 - O pensamento teórico como ponto de partida do experimento objetal
É composta por sessenta e um flashes (61F), capturados durante a resolução da tarefa 1, no contexto coletivo. Nesse dia, as carteiras estavam organizadas em forma de U, desse modo as acadêmicas estavam uma ao lado da outra e, ao lado, na mesa da professora, dispusemos os recipientes que possibilitaram a reflexão no plano objetal. Refletimos sobre a origem do pensamento teórico no contexto do experimento objetal, por meio da prática da medição. Essa cena é composta pela análise da primeira parte do processo de resolução coletiva da tarefa, na qual apresentamos, primeiramente, o volume de líquido a ser medido (K) e a unidade de medida básica (A), conforme Fotografia 1.

Fonte: Acervo da pesquisa, 2017
Fotografia 1 - Volume de líquido a ser medido (K) e unidade de medida básica (A).
A partir dessa informação, surge a questão central: o volume de líquido de medida K é formado por quantas unidades A? O ponto de partida para a resolução da tarefa é a relação entre grandezas, ou seja, a medição da grandeza volume (volume de líquido na cor azul). Nesse sentido, há necessidade de revelar o valor aritmético do volume de líquido cuja medida algébrica é K, a partir da unidade de medida A, expressa pela capacidade do recipiente menor (unidade de medida básica). Assim, não há um valor específico para K. Poderia ser 10, 20, 30, enfim, qualquer valor. Trata-se, portanto, de uma tarefa particular, porém de caráter geral, dada por meio do seguinte enunciado: o volume de líquido de medida K é formado por quantas unidades A?
Para o processo de solução, as acadêmicas sugeriram que realizássemos a transferência do líquido de volume K por meio do recipiente com capacidade A para outro recipiente (experimento objetal). Durante o processo, direcionamos as reflexões a fim de gerar a necessidade de realizar a transferência com um recipiente maior que A, denominado unidade de medida intermediária. Assim, a relação nuclear dos conceitos de multiplicação e divisão foi revelada, a partir do experimento objetal, conforme flashes a seguir:
01· Nilma: - [...] a gente não sabe a quantidade que tem.
02· Fabiana: - Então, precisa de uma medida maior.
03· Mestranda: -Tá, uma medida intermediária. Mais alguma sugestão? [sic]
04· Silvia: - Mas a medida intermediária já é o A, né [sic]?
05· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
06· Mestranda: - A Fabiana sugeriu...
07· Fabiana: - Uma outra medida. Uma medida intermediária que não seja A.
08· Mestranda: - Mas para que uma outra medida?
09· Fabiana: - Para não ter que fazer tantas vezes, porque o A é muito pequeno.
10· Mestranda: - Mais alguém tem alguma outra sugestão?
11· Margarida: - Precisava de um outro recipiente para passar o líquido.
12· Mestranda: - Então, eu tenho aqui um outro recipiente como a Margarida sugeriu, do mesmo formato e tamanho, certo? Qual é a sugestão agora?
13· _________:Introdução do terceiro recipiente a partir da sugestão de Margarida
14· Mestranda: - Já temos outro recipiente. Vou utilizar a capacidade de A para fazer a transferência?
15· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
16· Mestranda: - Então, a sugestão de vocês é fazer a transferência [com a medida A]. Mas será que vai ser demorado?
17· Acadêmicas: - Eu acho que vai.
18· Mestranda: - Trabalhoso?
19· Acadêmicas: - Vai.
20· Mestranda: - Então, qual seria a sugestão?
21· Ana Carolina: - Eu acho que tem que ser outro recipiente maior que A e não do tamanho do K.
22· Mestranda: - Então, eu tenho outro recipiente de capacidade C.
23· _________: Introdução da unidade de medida intermediária.
24· Mestranda: - Como que nós podemos denominá-la? Já surgiu essa questão na sala.
25· Acadêmicas: -Unidade de medida intermediária.
26· Mestranda: - Unidade de medida intermediária, porque nós temos K que representa o quê?
27· Acadêmicas: - O total.
28· Mestranda: - Comparando C com K, ele é intermediário. E comparando com A também é intermediário. Então temos três medidas diferentes, quais são elas?
29· Acadêmicas: - K, C e A.
30· Mestranda: - O que representa o K?
31· Acadêmicas: - O total.
32· Mestranda: - Temos C?
33· Acadêmicas: - Medida intermediária.
34· Mestranda: - Qual é a outra?
35· Acadêmicas: - A.
36· Mestranda: - A, unidade de medida básica. Então, para fazer uma transferência mais rápida, do que nós precisamos?
37· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
38· Mestranda: - Vamos ver quais são as opiniões?
39· Margarida: - Eu acho que tu usa a básica para colocar em C pra ver quanto vai dar [sic].
40· Mestranda: - E depois?
41· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
42· Mestranda: - Então, a sugestão é transferir o líquido com C?
43· Júlia: - Acho que seria pegar o C para ver quantos A cabe em C e depois quantos C cabe dentro do K [sic].
44· Mestranda: - Como que eu faço para saber quantos C têm em K?
45· Ana Carolina: -Eu acho que é duas vezes o C, né [sic].
46· Mestranda: - Então, eu pego o líquido, passo para o C e passo para cá (aponta para o recipiente igual a K que está vazio) até acabar o líquido. É isso?
47· Acadêmicas: - Isso.
48· Margarida: - Isso, mas primeiro passa o A para o C.
49· Mestranda: - Preciso de uma ajudante aqui. Quem pode ser voluntária?
50· _________: Participação de Clarice no experimento objetal.
51· ________: Momento da transferência do líquido do recipiente K, por meio da unidade básica A para o recipiente C, unidade de medida intermediária. Em síntese, A coube três vezes em C.
52· Mestranda: - Então, sabemos que A cabe quantas vezes em C?
53· Acadêmicas: - Três vezes.
54· Mestranda: - Qual é o próximo passo?
55· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
56· Fabiana: - Passar o líquido do C para o recipiente vazio.
57· _________: Momento da transferência do líquido do recipiente K, por meio da unidade de medida intermediária C para o recipiente vazio, igual a K.
58· Mestranda: - Então, C coube quantas vezes em K?
59· Acadêmicas: - Cinco.
60· Mestranda: - Uma vez, duas vezes, três vezes, quatro vezes, cinco vezes.
61· _________: Contagem da quantidade de unidades de medidas intermediárias.
As reflexões desencadeadas pelo processo de resolução da tarefa geraram a seguinte necessidade: “Precisava de um outro recipiente para passar o líquido” (Margarida, 11F). Nesse momento, apresentamos outro recipiente de mesmo formato e capacidade de medida K. Instigamos as acadêmicas a pensarem se a transferência com a unidade de medida A seria demorada e trabalhosa, por ser muito pequena (16F; 18F). As acadêmicas concluíram que sim, e surge a reflexão sobre como agilizar o processo.
A partir da necessidade de transferir o líquido de modo mais rápido, Ana Carolina (21F) sugere: “Eu acho que tem que ser outro recipiente maior que A, e não do tamanho do K”. Assim, apresentamos o recipiente com capacidade de medida C (22F; 23F). “Como que nós podemos denominá-la? Já surgiu essa questão na sala” (Mestranda, 24F). Essa questão foi uma sugestão de Fabiana (7F) no início da resolução coletiva, a inserção de “uma outra medida. Uma medida intermediária que não seja A”, a qual surgiu da necessidade de “[...] não ter que fazer tantas vezes, porque o A é muito pequeno” (Fabiana, 9F). O contexto da tarefa instigou as acadêmicas a refletirem sobre a superação de uma necessidade gerada no processo de resolução. Essa necessidade de transferir o líquido com mais agilidade orientou o pensamento das acadêmicas no sentido de explicar o ainda não conhecido e de buscar uma possibilidade de solução.
Portanto, é a partir da necessidade de uma unidade de medida maior, tal como ocorreu historicamente (Caraça, 1951), que surgiu a unidade de medida intermediária (C). Em relação à medida K (todo) e à medida A (unidade de medida básica), a medida C (unidade de medida intermediária) tem tamanho intermediário. Assim, com base nos elementos revelados (K, C e A), surge outro questionamento: “[...] temos três medidas diferentes, quais são elas?” (Mestranda, 28F). A síntese coletiva foi de que K representa o todo, C representa a unidade de medida intermediária e A representa a unidade de medida básica.
Nesse momento foram revelados os elementos que compõem o núcleo interno da multiplicação e divisão. Mas qual a relação entre eles? Como eles estão interconectados de modo a possibilitar o movimento interno da multiplicação para a divisão e vice-versa? Tal relação também é revelada durante o experimento objetal.
Ao retomar como seria realizado o procedimento de transferência de líquido de modo mais rápido, Margarida (39F) sugere: “Eu acho que tu usa a básica [A] para colocar em C pra ver quanto vai dar [sic]”. Na sequência, Júlia (43F) complementa: “Acho que seria pegar o C para ver quantos A cabe em C e depois quantos C cabe dentro do K [sic]”. Por sugestão das acadêmicas, a mestranda (51F) transfere uma parte do líquido do recipiente com medida K, com unidade básica A, para o recipiente com medida C, unidade de medida intermediária. A partir da análise dessa transferência, as acadêmicas concluíram que a unidade de medida intermediária C corresponde a 3 vezes a unidade de medida básica A (C=3A ou
O próximo passo, conforme expressou Júlia (43F), foi verificar quantas vezes C (unidade de medida intermediária) coube dentro do K (todo). Desse modo, o volume de líquido com medida K foi transferido para o recipiente vazio, por meio da unidade de medida intermediária C. Após a transferência, as acadêmicas concluíram que C coube 5 (cinco) vezes em K (
A questão central da tarefa ainda não foi respondida, mesmo após o experimento objetal de transferência de líquido, a resposta ainda não está apresentada. O experimento objetal possibilitou que as acadêmicas realizassem a transformação dos dados. Primeiramente, afirmaram que a transferência do líquido por meio da unidade de medida A (de um em um) seria mais demorada e trabalhosa. A partir da necessidade de realizar a transferência de líquido de modo mais rápido, elas sugeriram a unidade de medida intermediária (contagem por agrupamentos).
Durante o experimento objetal, concreto ponto de partida, o foco das reflexões era para a grandeza volume, e não para os objetos envolvidos. As acadêmicas revelaram os elementos que constituem a relação nuclear dos conceitos de multiplicação e divisão: unidade de medida básica (A), unidade de medida intermediária (C) e o todo (K). A relação entre esses elementos (medidas distintas de uma determinada grandeza), revelada no experimento objetal, geradora dos conceitos de multiplicação e divisão, será reproduzida por meio de símbolos, para auxiliar a compreensão coletiva da resposta para a questão central da tarefa.
Aqui cabe refletir, o experimento objetal anteriormente relatado é empírico ou teórico? Em outras palavras, o empírico é ponto de partida para se chegar ao teórico? De acordo com Davídov (1988, p. 132, tradução e grifo nossos), o pensamento teórico
sempre está internamente ligado com a realidade dada em forma sensorial. Exatamente o pensamento teórico (e de nenhuma maneira o empírico) realiza em plena intensidade as possibilidades cognoscitivas que a prática objetal-sensorial, recriadora em sua essência experimental das ligações universais da realidade, abre perante ao ser humano. (Davídov, 1988, p. 132, tradução e grifo nossos)
Desse modo, no contexto do ensino desenvolvimental, o experimento anteriormente apresentado é teórico, pois vai além de sua aparência e adentra em sua essência ao possibilitar a revelação dos elementos que constituem a relação essencial do conceito ou sistema conceitual em estudo (Rosa, Moura e Damazio, 2019).
Na tarefa em análise, a resposta não está empiricamente (explicitamente) dada no plano objetal concreto. Será revelada por meio de elementos abstratos, conforme adiantamos ao leitor quando apresentamos os modelos C=3A, C/A=3, e K=5C.
Isso porque o movimento de redução do concreto ao abstrato aparece “como momento subordinado, como meio” para o posterior procedimento de ascensão do abstrato ao concreto (Davídov, 1988, p. 148, tradução nossa, grifo nosso), conforme movimento apresentado a seguir (Cena 2).
• Cena 2 - Redução do concreto ao abstrato e ascensão do abstrato ao concreto
Essa cena é composta por quarenta e cinco flashes (45F), extraídos do segundo momento de resolução da tarefa 1, no contexto coletivo, como continuidade dos flashes expostos na cena 1. Na presente cena, evidenciamos o movimento de redução do concreto ao abstrato como meio para o procedimento de ascensão do abstrato ao concreto. Esse movimento representou uma etapa significativa percorrida pelas acadêmicas no processo de modelação da relação nuclear dos conceitos de multiplicação e divisão, desde o plano objetal até as representações gráficas (esquema e reta numérica).
01· Mestranda: - Então, a partir dessas informações [apresentadas na cena 1] respondemos à questão? [O volume de líquido de medida K é formado por quantas unidades A?]
02· Acadêmicas: - Ainda não.
03· Mestranda: - Mas a partir dessas informações, com a transferência do líquido, conseguimos responder?
04· Acadêmicas: - Sim, conseguimos.
05· Mestranda: - Como vocês fariam?
06· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
07· Clarisse: - C é igual a 3A.
08· Mestranda: - Certo.
09· Clarisse: - K é igual a 5C. E depois tenho que multiplicar o cinco pelo três.
10· Mestranda: - Todo mundo concorda?
11· Professora titular da disciplina: - Eu não entendi.
12· Algumas acadêmicas: - Eu também não entendi.
13· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
14· Juliana: - A lógica é essa, mas as crianças não vão ter essa lógica que tem na explicação da Clarisse.
15· Nilma: - Eu nem entendi o que a Clarisse falou.
16· Clarisse: - Ai, gente! Eu falei que C é igual a 3A, e que o C é igual [pausa de reflexão], não, é que um K é igual a 5C. Só isso que eu falei.
17· Nilma: - Ah, tá, te entendi [sic]. Então, aí tem que montar o problema.
18· Clarisse: - Tem que fazer na reta.
19· Mestranda: - Mais alguma sugestão?
20· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
21· Professora titular da disciplina: - Patrícia, vai lá e faz como você está sugerindo para a gente conseguir te ouvir.
22· Fotografia 1 - Patrícia faz um esboço do esquema no quadro.
23· Patrícia: - Eu pensei isso, mas não é.
24· Mestranda: - Por que tu achas que não é?
25· Patrícia: - Porque teria que fazer a fórmula, [...]. Não sei se é A dividido, não sei se é dividido por C que é igual a K. Não sei.
26· Professora titular da disciplina: -Será que não dá para fazer por aquele esquema lá?
27· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição.
28· _________: Silvia vai até o quadro e representa os dados da tarefa por meio de outro esquema (Fotografia 3).
29· Fotografia 2 - Reelaboração do esquema.
30· Professora titular da disciplina: - Ou seja, a Patrícia tinha razão, dava para partir do esquema, ok?
31· Acadêmicas: - Sim.
32· Mestranda: - Vocês concordam com o que a Silvia está fazendo?
33· _________: Duplas e trios conversam ao mesmo tempo, de modo que impossibilita a transcrição. Algumas responderam que sim e outras que não. Não houve um consenso.
34· Nilma: - A cabe dentro do C.
35· Silvia: - A cabe três vezes dentro do C. C cabe cinco vezes dentro do K.
36· Acadêmicas: -Isso mesmo (aplausos).
37· Nilma: - O nosso raciocínio foi o mesmo.
38· Mestranda: - Muito bem representado. Mas chegamos à resposta para essa questão?
39· _________: Momento de silêncio.
40· Mestranda: - O volume de líquido de medida K é formado por quantas unidades A? Está representado. Mas, que operação podemos utilizar?
41· Acadêmicas: - Multiplicação.
42· _________: Na sequência, as acadêmicas discutem sobre a operação de multiplicação: 3×5. Essa operação é representada na reta numérica.
43· Mestranda: -Então, agora vamos verificar como fica na reta numérica [a reta já tinha sido objeto de reflexão nas aulas anteriores].
44·_________: Após concluímos que 3×5=15 unidades de A, refletimos sobre a operação da divisão a fim de analisar o movimento operacional inverso que possibilita a averiguação do resultado (Fotografia 4).
45· Fotografia 3 - Averiguação do resultado da operação 3×5=15 por meio de sua inversa 15÷3=5.

Fonte: Acervo da pesquisa, 2017.
Fotografia 4 - Averiguação do resultado da operação 3×5=15 por meio de sua inversa 15÷3=5.
Os flashes apresentados na cena 2 mostram a continuidade da resolução da tarefa. A partir das informações reveladas na cena 1, questionamos como fariam para responder ao problema central da tarefa (5F). Clarisse sintetizou que “C é igual a 3A” (7F), “K é igual a 5C” (9F) e concluiu: “E depois tenho que multiplicar o cinco pelo três” (9F). A fala de Clarisse é constituída de significações algébricas, aritméticas e geométricas. A fala, como um todo, está sustentada na significação geométrica, que consiste na grandeza contínua volume e a ligação interna de suas medidas. Quando a acadêmica se refere aos valores das medidas na forma literal (C ou K), trata-se de elementos algébricos, pois utiliza letras para representar um valor desconhecido. A significação aritmética é expressa quando esta sugere multiplicar o cinco pelo três.
Contudo, algumas acadêmicas ainda não haviam compreendido a síntese apresentada por Clarisse. Ao conversarem com o intuito de compreenderem o movimento operacional gerador do resultado (20F), observamos que Patrícia propõe a representação dos dados por meio de um esquema e sugerimos que ela fosse ao quadro (21F) apresentar sua reflexão para a turma, conforme Figura 1.
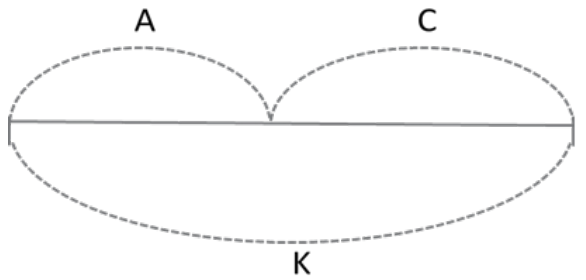
Fonte: Elaboração da mestranda, com base na produção de Patrícia, 2017.
Figura 1 - Esquema elaborado pela acadêmica Patrícia (22F).
Após representar os elementos que compõem a tarefa no esquema, Patrícia (23F; 25F) expressa: “Eu pensei isso, mas não é” [...] “porque teria que fazer a fórmula, [...]. Não sei se é A dividido, não sei se é dividido por C que é igual a K. Não sei”. Patrícia utiliza o modelo da relação interna da adição e subtração (Rosa, 2019), estudado nas aulas anteriores, constituído por duas partes e o todo (A + C=K; K-A=C; e K-C=A). Porém a própria estudante constata o equívoco; no entanto, é importante destacar a relevância da proposição de Patrícia para o início do processo de abstração e para a revelação do movimento operacional realizado no plano objetal. Destaca-se, ainda, a clareza da acadêmica ao concluir que seu esquema não representa a relação revelada no plano objetal. Na tentativa de mostrar que é possível representar por meio de esquema, no flash 28F, Silvia vai até o quadro e elabora o esquema a seguir (Figura 2).
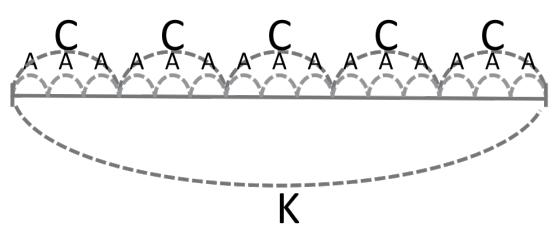
Fonte: Elaboração da mestranda, com base na produção de Silvia, 2017.
Figura 2 - Esquema proposto pela acadêmica Silvia (29F).
Silvia, ao fazer o esquema no quadro, modela geometricamente, com o auxílio, inclusive, de elementos algébricos, a relação revelada no plano objetal entre os valores A, C e K: “A cabe três vezes dentro do C. C cabe cinco vezes dentro do K” (Silvia, 35F). As demais acadêmicas constatam que o esquema elaborado por Silvia expressa o movimento operacional realizado na transferência do líquido (36F). Tal esquema é importante para evidenciar a relação interna dos elementos que compõem a tarefa.
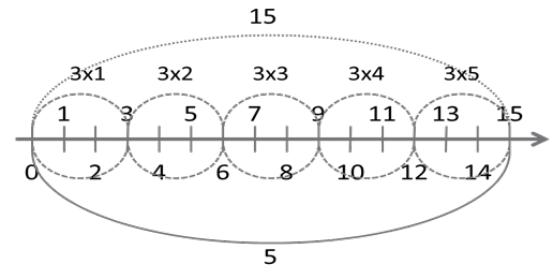
Nesse momento, questionamos: “[...] mas chegamos à resposta para essa questão?” (38F) “[...] que operação podemos utilizar?” (40F). As acadêmicas respondem que é a multiplicação (41F). E discutem sobre tal operação (3×5) e sua inversa (15÷3). Ambas foram expressas na reta numérica, conforme Figura 3.
Fonte: Elaboração da mestranda, 2017.
Figura 3 - Representação na reta numérica das operações 3×5=15 e 15÷3=5.
A Figura 2 consistia na representação geométrica (esquema composto por segmento de reta e arcos) dos valores algébricos (A, C e K). Agora, na Figura 3, os mesmos valores foram representados na forma aritmética, na reta numérica (contexto geométrico do conceito de número). A mesma relação objetal, representada na forma mais geral (Figura 2), depois é expressa na forma singular (Figura 3), com o intuito de evidenciar um resultado concreto (15). A partir da análise do movimento operacional, expresso na reta numérica, as acadêmicas concluem que o volume de líquido de medida K é formado por 15 unidades A.
Em síntese, no episódio em análise, as acadêmicas percorreram o movimento de redução do concreto ao abstrato e ascensão do abstrato ao concreto. A partir do experimento objetal, os dados foram revelados, transformados e modelados. O movimento de abstração do modelo teve como ponto de partida a forma objetal e, depois, seguiu para as formas gráfica e literal, na interconexão das significações aritméticas, algébricas e geométricas. Essas representam, em âmbito teórico, a forma universal do objeto.
O PONTO DE PARTIDA: COMPREENSÕES INICIAIS
A fim de analisar as compreensões iniciais, no primeiro dia de aula do semestre, propusemos às acadêmicas a seguinte situação (Figura 4).
Com base nos planos de ensino elaborados pelas acadêmicas, a partir da situação exposta (Figura 5), constatamos a presença de elementos do pensamento empírico nesse primeiro momento. A seguir, apresentamos o plano de ensino elaborado pela acadêmica Margarida (Figura 6), como expressão geral dos planos de ensino elaborados pela turma.

Fonte: Acervo da pesquisa, 2017.
Figura 5 - Plano de ensino elaborado pela acadêmica Margarida no primeiro dia de aula.

Fonte: Acervo da pesquisa, 2017.
Figura 6 - Representação da unidade de medida básica (A) e o todo (C).
Margarida, em seu primeiro plano de ensino considera as experiências do dia a dia das crianças, como dividir a turma em grupos e até mesmo a divisão de balas. Nessas situações cotidianas, a formação dos estudantes limita-se às bases da consciência e do pensamento empírico.
O cultivo, na escola, do pensamento empírico é uma das causas objetivas de que o ensino escolar influencia fracamente no desenvolvimento psíquico das crianças, no desenvolvimento de suas capacidades intelectuais, porquanto o pensamento empírico origina-se e pode mais ou menos desenvolver-se fora da escola, já que suas fontes estão vinculadas à vida cotidiana das pessoas. (Davídov, 1988, p. 06, tradução nossa)
Assim, se as crianças desenvolvem o pensamento cotidiano/empírico fora da escola, cabe-nos questionar a finalidade do ensino empírico, no qual, conforme Davydov (1982, p. 14, tradução nossa), uma de suas finalidades principais consiste em “inculcar nas crianças generalizações e conceitos [...]” empíricos.
No plano de ensino em análise (Figura 5), a resposta aritmética estava dada visualmente nos desenhos. Um recurso que também poderia ser utilizado é a distribuição dos objetos concretamente dados (estudantes), um a um, até chegar ao último estudante, para a formação de 5 (cinco) grupos iguais, sem necessariamente proceder à operação de divisão.
Outra limitação foi considerar apenas a significação aritmética e a contagem da grandeza discreta com foco para o algoritmo. Desconsiderou-se a significação algébrica por meio de letras e as reflexões na reta numérica, contexto geométrico do conceito de número e sua operacionalização.
Trata-se de um exemplo empírico que já toma como ponto de partida uma quantidade predefinida de estudantes e grupos, e que, durante o processo de solução, não possibilita a revelação, no plano objetal, do movimento de solução. Afinal, como se divide, no plano objetal, dez estudantes em cinco grupos iguais? Como esse movimento objetal poderia ser representado geometricamente e algebricamente? Qual a relação interna dos elementos que compõem tal proposição? Estas e outras questões não são respondidas nos limites de uma proposição empírica.
Em síntese, nas produções apresentadas no primeiro dia de aula pelas estudantes, houve o predomínio de problemas em que a resposta estava dada visualmente aos órgãos dos sentidos com a representação básica e direta da situação envolvida por meio de desenhos. De modo geral, o processo de resolução era a partir da distribuição, um a um, dos objetos, com ênfase para a introdução do algoritmo nos limites da significação aritmética, das grandezas discretas e das situações-problemas de caráter particular.
PONTO DE CHEGADA: COMPREENSÕES FINAIS
Ao término do semestre, as acadêmicas elaboraram um novo plano de ensino e desenvolveram com estudantes do segundo e terceiro anos do ensino Fundamental I em escolas de educação básica da região. Nesse momento, observamos o envolvimento, o comprometimento, a criatividade e a preocupação em estudar, compreender e possibilitar às crianças a aprendizagem dos conceitos em âmbito teórico.
Vamos continuar com o exemplo de Margarida, por entendermos que o movimento percorrido por essa acadêmica representa as demais. Dessa forma, apresentaremos a seguir o relato de Margarida sobre como foi desenvolvida sua tarefa com as crianças. Margarida fez seu relato por meio de slides do Power Point. As imagens a seguir foram extraídas, com autorização, de seus slides.
Para desencadear as reflexões, ela elaborou uma história intitulada “Era uma vez uma barata independente.”
Dona Baratinha é uma barata independente. Ela quer muito reformar o ateliê dela, porque ela faz os laços de fita e resolveu dar uma melhorada na parede do ateliê. Ela está com um problemão. [...] Ela tem no porão da casa dela uma caixa de azulejo pequeno. Só que ela não tem noção da quantidade de azulejo que vai nessa parede. (Margarida, 2017)
A partir do enredo exposto, Margarida apresentou a parede de Dona Baratinha (superfície de média C) e o azulejo (unidade de medida básica A), e questionou: quantos azulejos Dona Baratinha vai precisar para preencher esta parede? (Figura 6).
A partir da situação proposta, Margarida provocou a necessidade de utilizar uma medida intermediária (maior que A), uma vez que a contagem um a um (de A em A) seria demorada. A partir das várias sugestões apresentadas pelas crianças, Margarida escolheu uma delas (a contagem de quatro em quatro), pois já tinha confeccionado uma unidade com medida B, na qual cabia 4 vezes a medida A, ou seja, B=4A (Figura 7).
De posse da unidade de medida intermediária, verificou-se quantas vezes essa medida intermediária (B) cabia no todo (C) e concluiu-se que era 6 (seis) vezes: C=6B. (Figura 8)

Fonte: Acervo da pesquisa, 2017.
Figura 8 - Representação da unidade de medida básica (A), medida intermediária (B) e todo (C).
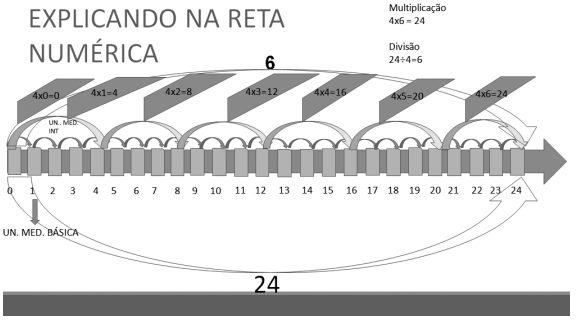
A partir dos dados revelados e transformados na situação desencadeadora, Margarida direcionou as reflexões para chegar à operação de multiplicação ao propor a representação na reta numérica da contagem dos azulejos de quatro em quatro, realizada no plano objetal. Na sequência, questionou sobre como seria o movimento operacional inverso (divisão), também representado na reta numérica (Figura 9).
Fonte: Acervo da pesquisa, 2017.
Figura 9 - Representação do movimento realizado no experimento objetal na reta numérica.
Após refletirem sobre as operações de multiplicação (4 × 6) e divisão (24÷4) na reta numérica, Margarida retomou o problema inicial: Dona Baratinha vai precisar de 24 (vinte e quatro) azulejos pequenos para preencher a parede.
Na experiência de docência desenvolvida e relatada por Margarida, ela já não toma como ponto de partida a divisão, mas a contagem, passa pela multiplicação e, finalmente, atinge o conceito de divisão. Não considera o conceito isoladamente, tal como procedeu no primeiro momento, mas em seu sistema conceitual. Toma o concreto (sistema conceitual) como ponto de partida e de chegada, enquanto integridade revelada a partir do elo que interconecta diferentes conceitos a uma única relação nuclear. Em sua proposta de ensino, a acadêmica sugeriu um problema que envolvia a medição da área da superfície, ou seja, de uma grandeza contínua, enquanto no primeiro momento considerou apenas a contagem de grandezas discretas. Tomou como ponto de partida o experimento objetal e, a partir do sistema de relações entre as medidas, revelou os elementos que constituem a relação que dá origem aos conceitos de multiplicação e divisão em âmbito teórico.
A essência do pensamento teórico consiste em que se trata de um procedimento especial com o que o homem enfoca a compreensão das coisas e os acontecimentos por via da análise das condições de sua origem e desenvolvimento. Quando os estudantes estudam as coisas e os acontecimentos do ponto de vista deste enfoque, começam a pensar teoricamente. (Davídov, 1988, p. 06, grifos do autor)
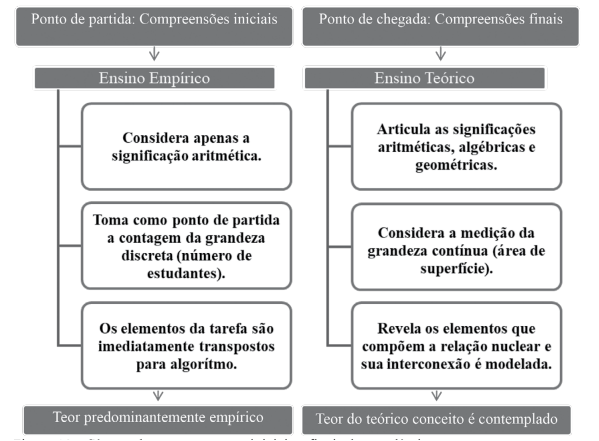
O experimento objetal de medição da superfície proposto por Margarida, ao final do semestre, possibilita a análise das condições de origem e desenvolvimento dos conceitos de multiplicação e divisão. Diferentemente do primeiro dia de aula, agora Margarida considera uma grandeza contínua (área de superfície). A partir do experimento objetal com essa grandeza, revela e modela a relação nuclear, nas formas objetal, gráfica e literal, por meio da interconexão entre as significações geométricas, aritméticas e algébricas. Embora não contemple o esquema com valores representados na forma algébrica, há diferenças substanciais entre as duas produções de Margarida, conforme sistematizamos no esquema da Figura 10.
Fonte: Elaboração nossa, 2018.
Figura 10 - Síntese das compreensões iniciais e finais das acadêmicas.
É importante ressaltar que, durante o experimento também chegamos no algoritmo da divisão, mas só depois das estudantes compreenderam o que cada elemento significava, para que pudessem interpretar os problemas e elaborar corretamente o algoritmo.
CONSIDERAÇÕES FINAIS
Analisamos o processo de origem e o desenvolvimento de elementos característicos do ensino desenvolvimental durante a introdução dos conceitos de multiplicação e divisão em um curso de pedagogia por meio de um experimento didático desenvolvimental.
Constatamos que o ensino de matemática pode ser organizado a partir de experiências práticas, por meio do estudo das relações entre grandezas. As grandezas, concretamente dadas, permitem a delimitação de elementos que possibilitam a revelação e a modelação da relação nuclear dos conceitos e sistemas conceituais. Tal relação nuclear consiste na essência conceitual que pode ser revelada por meio do estudo das relações entre as grandezas, tanto discretas quanto contínuas. Embora no plano concreto, a revelação da essência requer um processo de análise teórica que vai além da aparência das grandezas e possibilita revelar suas conexões internas. Isso só é possível por meio da dissociabilidade das significações aritméticas, algébricas e geométricas. A ausência de uma destas significações implica fragmentação do sistema conceitual.
Para finalizar, é importante ressaltar que estamos no início de uma longa e árdua caminhada na busca por uma educação promotora do desenvolvimento do pensamento teórico matemático, a partir da apropriação do conhecimento científico por estudantes, professores e futuros professores.
Desse modo, esperamos que a presente pesquisa contribua com reflexões sobre o modo de organização do ensino de matemática, em nível teórico, para todos e todas. Acreditamos que este é um dos caminhos importantes para atingirmos a transformação do ensino de matemática no Brasil, porém, insuficiente. Fazem-se necessárias novas pesquisas que avancem, inclusive, no enunciado das tarefas, a fim de contemplar problemas reais que afligem a humanidade na contemporaneidade.