Introdução
No âmbito da formação de professores, ao tratarmos de temáticas que envolvem os conceitos matemáticos ensinados na Educação Básica, temos nos preocupado em estudar, juntamente com professores e futuros professores, as possíveis contribuições que a História da Matemática e suas diferentes vertentes historiográficas podem trazer aos processos de ensino-aprendizagem de conceitos matemáticos, dentre eles, o de função.
Nesse sentido, consideramos os estudos de Ríbnikov (1987), uma vez que, para o autor, a História da Matemática explica a natureza da Matemática, bem como o desenvolvimento do pensar matemático, a partir de diversos pontos de vista, ou seja, há diferentes modos de ver e conceber a Matemática e, consequentemente, os conceitos matemáticos.
Assim, ao se ter contato com uma variedade de historiografias, podemos ter dúvidas, tanto sobre os conceitos matemáticos, quanto sobre as verdades matemáticas que muitas vezes memorizamos sem compreensão.
Ensinar e aprender Matemática não deveria nos dar a oportunidades de refletir sobre as diversas interpretações que matemáticos e educadores matemáticos construíram e continuarão construindo ao longo da história sobre o desenvolvimento dos conceitos matemáticos? Não deveria nos possibilitar ter contato com movimentos lógico-históricos dos conceitos matemáticos que frequentam nossas vidas? Não deveria nos possibilitar a compreensão dos nexos conceituais (internos e externos) que se apresentam nos conceitos matemáticos?
Questões como essas fizeram parte de uma pesquisa desenvolvida no período de março de 2015 a dezembro de 2016, que contou com financiamento do Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). Aqui, pressupõe-se que, ao estudarmos a História da Matemática e suas versões historiográficas, podemos perceber que as relações quantitativas e formas espaciais, por exemplo, têm relações indissolúveis com as exigências da técnica e as ciências naturais. Podemos nos conscientizar, a partir de vários exemplos, de que as verdades matemáticas não foram construídas em um processo harmonioso de “desenvolvimento contínuo e gradual” (RÍBNIKOV, 1987, p. 15). Assim, a história do conhecimento dos conceitos matemáticos só tem sentido quando compreendemos os diversos movimentos das abstrações do pensamento que compuseram as formalizações que estudamos, as quais, por sua vez, comporão os nexos conceituais (internos e externos) dos conceitos que são estudados em sala de aula.
As abstrações, demonstrações e aplicações são os principais traços característicos da Matemática e são esses traços que, ainda hoje, fundamentam a maioria das aulas de Matemática. Estudam-se, por exemplo, o conceito de função, tendo como fundamento a Teoria dos Conjuntos. No entanto, esses traços, quando estudados a partir dos elementos perceptíveis do conceito (DAVYDOV, 1982), destacam apenas os nexos externos dos conceitos. Os nexos internos perdem a importância. Aqui, os nexos conceituais (internos e externos) da Matemática são definidos como elos. São construídos historicamente e ligam os conceitos de várias formas, não necessariamente lineares. São definidos por historiadores, matemáticos, educadores matemáticos e professores que ensinam Matemática, a partir de seus modos de ver e conceber os conceitos.
No caso da função, os nexos externos são predominantes nas aulas de Matemática e podem ser representados pela expressão f(x). A não compreensão desse conceito, por parte dos alunos do Ensino Médio, explicita-se nas aulas de Física e Química, por exemplo, quando a função deixa de ser apresentada na forma de f(x). Os alunos se perdem. Não conseguem relacionar os nexos externos apresentados pelos professores de Matemática com os nexos internos apresentados pelos professores de Física e de Química, tais como os movimentos (regulares e irregulares) e variações (quantitativa e qualitativa).
Quando Dias e Saito (2009, p. 9) chamam a atenção para “o contexto no qual conceitos matemáticos são desenvolvidos” e para “o movimento do pensamento no contexto”, desafiam-nos a pensar sobre os nexos internos dos conceitos que ensinamos e sobre quais historiografias poderiam nos auxiliar a compreendê-los, de forma a desenvolvê-los, juntamente com os alunos, em sala de aula. Aqui tem-se “[...] por pressuposto a possibilidade do estudo no movimento do pensamento, no sentido de apreensão do objeto, isto é, do desenvolvimento do conceito [...].” (DIAS; SAITO, 2009, p. 9).
Ou seja, é para ter acesso às histórias dos conhecimentos dos conceitos matemáticos, elaborados pelas diversas civilizações e narradas em diversas versões, sob diferentes pontos de vista, nas historiografias de Matemática, que defendemos que os cursos de formação de professores e, consequentemente, as escolas da Educação Básica, considerem os movimentos lógico-históricos dos conceitos nas aulas de Matemática. No entanto, faz-se necessário conhecer e analisar algumas historiografias já publicadas.
Se as historiografias da Matemática abordam a história dos conhecimentos matemáticos, ao conhecê-las, temos condições de compreender os nexos conceituais (internos e externos) que cada historiador, matemático, educador matemático ou professor que ensina Matemática prioriza. Há aqui uma relação direta entre historiografias, História da Matemática e movimentos lógico-históricos. O elo comum entre esses três conceitos estaria nos modos de ver e conceber a história do conhecimento humano sobre determinados objetos. Nesse caso, estamos tratando dos objetos matemáticos que se materializam, a partir de diversas linguagens, dentre elas, a aritmética, a algébrica e a geométrica.
É sobre as historiografias de Karlson (1961), Ríbnikov (1987), Eves (1997) e Caraça (1998) e os modos de ver e conceber o conceito de função desses quatro autores que trata este artigo. Escolhemos esses autores porque, do nosso ponto de vista, suas historiografias representam um modo de ver e conceber a História da Matemática, a partir do paradigma iluminista da História, mais especificamente por indicarem uma concepção marxista da História, conforme descrevemos no Quadro 1 que será apresentado no próximo item. Ao analisá-las, pudemos identificar os contextos e os vários nexos conceituais que os referidos autores explicitam ao apresentarem suas versões historiográficas sobre os movimentos lógico-históricos do conhecimento do conceito de função. Nesse contexto, há nexos que podem ser definidos como internos e outros externos, e vice-versa, porque formam uma unidade dialética. Temos como pressuposto que o estudo da função, a partir de seus nexos conceituais, pode contribuir com a organização do ensino por parte dos professores de Matemática da Educação Básica.
Quadro 1 Paradigmas e suas respectivas concepções do conceito de História
| Paradigma "iluminista" |
Concepção marxista da história Foi adequadamente sintetizada por Adam Schaff (19-- apud CARDOSO; VAINFAS, 2011, p. 4), o qual estabelece: Que a realidade social é mutável. Que essa mudança é submetida a leis cujo reflexo são as leis dinâmicas da ciência (histórica). Que as mudanças conduzem a estados periódicos de equilíbrio relativo, cuja característica não é [...] a ausência de qualquer mudança, mas sim a duração relativa de suas "formas" e "relações recíprocas" (hoje expressaríamos isto mais precisamente com as palavras: da estrutura do sistema). |
|
Concepção dos Annales da história Autodenominada de Nova História, o grupo construiu a "história-problema". Trata-se daquilo que Eric Hobsbawn (19-- apud CARDOSO; VAINFAS, 2011, p. 7) chamou de nouvelle vague da historiografia francesa. Ponto básicos: A crença no caráter científico da história que, no entanto, é uma ciência em construção: isso conduziu, em especial, à afirmação da necessidade de passar de uma "história-narração" a uma "história-problema" mediante a formulação de hipóteses de trabalho. O debate crítico permanente com as ciências sociais, sem reconhecer fronteiras entre elas que sejam estritas e definitivas; sendo menos estruturada que tais ciências, a história delas importou problemáticas, conceitos, métodos e técnicas, incluindo, desde 1930, a quantificação sistemática e o uso de modelos de certas áreas – cada vez mais numerosas – de estudos históricos, movimento ampliado ainda pela generalização dos computadores. A ambição de formular uma síntese histórica global do social, explicando a vinculação existente entre técnicas, economia, poder e mentalidades, mas também as oposições e as diferenças de ritmo e fase entre os diferentes níveis do social. O abandono da história centrada em fatos isolados e também uma abertura preferencial aos aspectos coletivos, sociais e repetitivos do histórico, substituindo a anterior fixação em indivíduos, elites e fatos "irrepetíveis": daí o interesse maior pelas temáticas econômicas, demográficas e relativas às mentalidades coletivas. Uma ênfase menor do que no passado nas fontes escritas (embora elas continuem sendo as mais usadas, no conjunto, pelos historiadores, sem excluir os dos Annales), favorecendo a ampliação do uso da história oral, dos vestígios arqueológicos, da iconografia, etc. A tomada de consciência da pluralidade dos níveis da temporalidade: a curta duração dos acontecimentos, o tempo médio (e múltiplo) das conjunturas, a longa duração das estruturas; além de que o próprio tempo longo, estrutural, é diferencial em seus ritmos dependendo de quais estruturas se trate (o mental, por exemplo, muda mais lentamente do que o econômico, e este mais do que o técnico). A preocupação com o espaço, primeiro por meio da tradicional ligação com a geografia humana; depois, através da história, ainda mais espacialmente pensada, inaugurada com os estudos de mares e oceanos: o Mediterrâneo, de Fernand Braudel; o Atlântico, de Frédéric Mauro; o Atlântico e o Pacífico, de Pierre e Huguette Chaunu etc.; e, o tempo todo, a sólida tradição francesa da história regional. A história vista como "ciência do passado" e "ciência do presente" ao mesmo tempo: a história-problema é uma iluminação do presente, uma forma de consciência que permite ao historiador – homem de seu tempo –, bem como aos seus contemporâneos a que se dirige, uma compreensão melhor das lutas de hoje, ao mesmo tempo em que o conhecimento do presente é condição sine qua non da cognoscibilidade de outros períodos históricos (CARDOSO; VAINFAS, 2011, p. 7-8). | |
| Pontos comuns entre as concepções Marxista e dos Annales O reconhecimento da necessidade de uma síntese global que explique tanto as articulações entre os níveis que fazem da sociedade humana uma totalidade estruturada quanto as especificidades no desenvolvimento de cada nível. A convicção de que a consciência que os homens de determinada época têm da sociedade em que vivem não coincide com a realidade social da época em questão. O respeito pela especificidade histórica de cada período e sociedade (por exemplo, as leis econômicas só valem, em princípio, para o sistema econômico em função do qual foram elaborados). A aceitação da inexistência de fronteiras estritas entre as ciências sociais (sendo a história uma delas), se bem que o marxismo seja muito mais radical quanto à unidade delas. A vinculação da pesquisa histórica com as preocupações do presente. Alguns dos membros do grupo dos Annales – mas nem todos, nem a maioria – se aproximaram à noção marxista da determinação em última instância pelo econômico (CARDOSO; VAINFAS, 2011, p. 9). | |
| Paradigma "pós-moderno" | Concepção da história (ou melhor, das histórias) Definição do que seria a história-disciplina formulada por Keith Jenkins (19-- apud CARDOSO; VAINFAS, 2011, p. 14): A história é um discurso mutável e problemático – ostensivamente a respeito de um aspecto do mundo, o passado –, produzido por um grupo de trabalhadores cujas mentes são de nosso tempo (em grande maioria, em nossa cultura, historiadores assalariados) e fazem seu trabalho em modalidades mutuamente reconhecíveis que são posicionadas epistemológica, ideológica e praticamente; e cujos produtos, uma vez em circulação, estão sujeitos a uma série de usos e abusos logicamente infinitos mas que, na realidade, correspondem a uma variedade de bases de poder existentes em qualquer momento que for considerado, as quais estruturam e distribuem os significados das histórias ao longo de um espectro que vai do dominante ao marginal (CARDOSO; VAINFAS, 2011, p. 14). |
Fonte: Elaborado pelos autores.
Aspectos teóricos e metodológicos que fundamentam a pesquisa
A pesquisa está caracterizada como documental e qualitativa, com inspiração em “estudos históricos”, conforme apontam Fiorentini e Lorenzato (2007, p. 103), considerando-se que, para levantar as informações necessárias, fizemos uso de fontes primárias, tais como: textos impressos e manuscritos, fichamentos de livros e textos teóricos que tratam de temáticas como: historiografia, historiografias da Matemática, História da Matemática, movimentos lógico-históricos e conceito de função.
Nesse sentido, quando Cardoso e Vainfas (2011) nos apresentam o conceito de História, chamam a atenção para o fato de que, ao estudá-lo, devemos considerar pelo menos dois paradigmas: iluminista e pós-moderno, os quais fundamentam as principais vertentes teóricas estudadas, atualmente. As concepções marxista e dos Annales fazem parte do paradigma iluminista e têm pontos comuns. O paradigma pós-moderno considera uma nova concepção da História, na realidade, uma nova concepção das Histórias (no plural), conforme mostra o Quadro 1.
No caso das quatro historiografias estudadas podemos inferir, a partir do que foi descrito no Quadro 1, que nenhuma delas se fundamenta na concepção dos Annales da história ou, ainda, no denominado paradigma pós-moderno da História.
Quando o assunto é a História da Matemática, chamamos a atenção para os estudos de D’Ambrósio (1999), o qual considera que não há como desvencilhar a História da Matemática da Filosofia da Matemática. Isso quer dizer que as historiografias da Matemática escritas por matemáticos e educadores matemáticos estão fortemente relacionadas tanto às fontes históricas consultadas quanto às interpretações dessas fontes, as quais dependem diretamente das ideologias assumidas, considerando-se que:
[...] uma vez identificados os objetos do estudo, a relação de fatos, datas e nomes depende de registros, que podem ser de natureza muito diversa: memórias, práticas, monumentos e artefatos, escritos e documentos. Essas são as chamadas fontes históricas. E a interpretação depende de ideologia, na forma de uma filosofia da história. Essa é a essência do que se chama historiografia. (D’AMBRÓSIO, 1999, p. 4).
Nesse contexto, ao considerar a História da Matemática e as diversas vertentes historiográficas, no que diz respeito à formação dos professores, entendemos que não há como desconsiderar os aspectos apresentados tanto por Cardoso e Vaifans (2011), quanto por D’Ambrósio (1999). Por esse motivo, há de se considerar os movimentos lógico-históricos, que têm seus fundamentos teóricos no materialismo histórico dialético, uma das vertentes das historiografias.
Dessa forma, ao articular história da matemática e ensino, não procuramos fazer a história guiar o pensamento de tal modo a impor o processo histórico, mas permitir que a formação das ideias componha a lógica do movimento do pensamento [...]. A partir da categoria do lógico e do histórico como forma de pensamento, observamos a possibilidade didática que busca relacionar o histórico de conceitos e sua essência, o lógico, com a finalidade da formação do conceito para si. Ao reproduzir a criação e o desenvolvimento de um conceito, além de compreender sua necessidade, e as aptidões humanas nele sintetizadas, novos aspectos e novas relações do movimento do objeto no pensamento são descobertos. Desse modo, ao explorar o movimento lógico-histórico do conceito como investigação didática também contribuímos na aprendizagem da forma de construção do conhecimento, possibilitando que o indivíduo compreenda a inexistência de verdades absolutas, concepções frequentes de estudantes em relação à matemática, gerada pelo método de ensino que aborda somente a lógica formal. (DIAS; SAITO, 2009, p. 11).
Assim, considerando-se o que foi apresentado até aqui, para desenvolver, a pesquisa selecionamos quatro historiografias: Karlson (1961), Ríbnikov (1987), Eves (1997) e Caraça (1998), que têm diferentes modos de ver e conceber a Matemática, o conceito de função e, consequentemente, o ensino de conceitos matemáticos. Apesar de suas diferenças, os autores têm pelo menos um aspecto em comum: concebem e veem a História, a partir do paradigma iluminista, segundo as três características apresentadas no Quadro 1. Ríbnikov (1961) é o único que se assume materialista dialético, portanto, sua historiografia explicita a concepção marxista da História da Matemática.
Ao analisar as historiografias escritas em diferentes contextos, tivemos como foco indicar os movimentos lógico-históricos da função. Para tanto, em termos metodológicos, a análise dos dados da pesquisa seguiu uma linha interpretativa cuja característica é a particularização, em vez da generalização de resultados. Nesse contexto, a busca não é de universais abstratos, aos quais se chega, segundo Moreira (1990), a generalizações estatísticas, mas de universais concretos, que se atinge através do estudo detalhado de um caso específico, localizado culturalmente. Aqui, o caso específico está relacionado às historiografias específicas e os universais concretos se materializam no delineamento dos nexos conceituais (internos e externos) do conceito de função, os quais podem contribuir com a formação dos professores que ensinam Matemática.
A historiografia de Paul Karlson: primeiro modo de ver e conceber o conceito de função
Ao descrever, de uma forma poética e divulgar o pensamento dos conhecimentos matemáticos, na década de 1940, Karlson, segundo indicações de Bauer (1961), ao escrever o livro A magia dos números: a matemática ao alcance de todos, preocupou-se em apresentar a história do desenvolvimento dos conceitos matemáticos para todos aqueles que, de alguma forma, desprezavam e odiavam a Matemática.
Teve como propósito escrever os movimentos lógico-históricos dos conceitos matemáticos de uma forma simples, para que todas as pessoas pudessem compreendê-los. Não é a toa que, para alguns, matemáticos ou não, o livro de Karlson pode ser enquadrado como um tipo de divulgação científica. Um livro que não precisa ser levado muito sério, em termos de aprofundamento matemático e, por esse motivo, não deve frequentar as aulas de Matemática, especialmente, no Ensino Superior.
No entanto, quando começamos a analisar o livro, constatamos que o autor não deixa nada a desejar, no que diz respeito à apresentação das argumentações que fundamentam o desenvolvimento dos conceitos matemáticos. Ainda que não tenha preocupações em enfatizar as demonstrações lógicas e formais, elas estão lá. Os movimentos lógico-históricos dos conceitos estão presentes para que, leigos no assunto, professores e, porque não, os matemáticos possam ter acesso aos nexos conceituais dos números, da álgebra, do cálculo, da geometria, e, principalmente, do conceito de função. O autor nos apresenta o reino das funções, mostrando-nos sua paixão sobre as funções. Das 608 páginas, 239 delas, ou seja, 39% do livro, foram dedicadas aos movimentos do desenvolvimento lógico-históricos do conceito de função.
Ao nos apresentar a história do conhecimento sobre o conceito de função, o autor nos indica que há um reino que luta insistentemente para representar os movimentos da vida. Para Karlson (1961), não há como separar o conceito de função dos movimentos mais gerais da vida.
Nesse contexto, a função nos permite conhecer os movimentos regulares e irregulares que permeiam nossas vidas. Ao adentrarmos o reino das funções, somos informados de que se faz necessário considerar que, “se existisse uma taquigrafia especial para os matemáticos, onde as palavras mais frequentes estivessem representadas por símbolos particulares, deveríamos começar por uma palavra e somente uma: a palavra função” (KARLSON, 1961, p. 375-376), considerando-se que, desde que os conceitos: infinito, vida, movimento, ação e reação passaram a dominar o mundo, a palavra-chave da matemática passou a ser: função.
Ao surgir pela primeira vez nas ciências matemáticas como conceito perfeitamente definido, a função possuía êste caráter dinâmico, vivo, em formação; ela rompeu o império rígido da clássica geometria grega e, lançando-se através dos vestíbulos dos templos, tomara de assalto a terra virgem das verdades jamais pisadas, qual um incêndio brutal e impetuoso. Era desta maneira que mestres como Newton, Leibniz, Euler manejavam a função - não é debalde que ela deriva do círculo de idéias da época de mais intenso movimento intelectual, da Renascença; não é em vão que Newton a chama pelo belo nome de genila: a pequena criadora. (KARLSON, 1961, p. 387, grifo do autor).
A taquigrafia é um modo de escrever, de forma sintética, resumida, por símbolos especiais. Assim, ao nos apresentar o reino das funções, o autor, além de nos chamar a atenção para os movimentos da vida e para o conceito de infinito, indica-nos que há um “segrêdo da variação” (KARLSON, 1961, p. 373) e se faz necessário não ignorar a importância que o conceito de infinito numérico, definido a partir de observações que consideraram tanto “a imensidão do céu” quanto as “lentes polidas do primeiro microscópio, para os novos e inexplorados mundos do infinitamente pequeno” (KARLSON, 1961, p. 376) passa a ter, a partir da Renascença. É nesse período que “Giordano Bruno finalmente arranca o véu que até então cobria o infinito, proclamando a existência de miríades de outros mundos” (KARLSON, 1961, p. 376). Ou seja, é durante o Renascimento que se quebra a
[...] harmonia e a paz, pois tudo era de natureza divina. Luta, litígio e discórdia ficavam circunscritos à baixa esfera terrestre, domínio dos homens, que perdera a felicidade divina pelo pecado original” [...] e talvez mais de um dêstes pioneiros tenha imaginado que também aqui um mundo minúsculo se equipararia ao outro - descendo ao infinitamente pequeno: também aqui sem princípio e sem fim. (KARLSON, 1961, p. 375-376).
Em seguida, por meio de uma poesia, define o conceito de função. Convida-nos a pensar sobre “o sentido matemático da ação” que envolve um possível movimento da vida: a caminhada de um “viandante distraído na floresta” e de um “soldado em férias que tem no sangue a cadência constante das marchas” (KARLSON, 1961, p. 376). Chama a nossa atenção para que possamos aprender “alguns vocábulos” que se apresentam nessa ação, tais como: função; variável independente ou variável arbitrária; representação formal; valores admissíveis para uma função; gráfico da função (representação concreta da função).
Ao tratar das “funções e suas representações”, Karlson (1961, p. 380) destaca a “imagem” e as “relações” que podem ser descritas através das funções. Apresenta-nos exemplos que envolvem trajetos de pessoas ou de trens; guaritas dos guarda-chaves; funcionamento das grandes estações ferroviárias; movimento dos comboios de cargas; movimentos durante a escalada de montanhas; problemas de economia; movimento de altura e pressão atmosférica nos aviões. Para o autor, faz-se necessário que: “consideremos as funções como sêres vivos, e procuremos familiarizar-nos com os seus costumes” (KARLSON, 1961, p. 387). Por último, apresenta-nos os conceitos de polinômios; sociologia das funções; função algébrica, contínuo, máxima e mínima, e cálculo diferencial.
Se os polinômios, ou funções racionais inteiras, eram comparáveis aos números racionais inteiros, muito razoável é procurarmos também pelas analogias existentes neste nosso novo reino, os números fracionários. Aliás, devemos acostumar-nos a ver nas funções uma espécie de “supernúmeros”, assim como podemos considerar os estados ou os povos como “superindivíduos”, estruturas de ordem superior, compostos de um sem número de sêres, dotados êles mesmos de personalidade própria. (KARLSON, 1961, p. 392-393).
Karlson (1961) nos convence de que as funções descrevem leis que não se podem facilmente generalizar. Como representam os movimentos da vida de todos nós, têm vida própria. Logo, faz-se necessário estudar seus movimentos para que possamos representá-las de forma sintética, ou seja, analiticamente ou graficamente.
Ao analisarmos os movimentos lógico-históricos do desenvolvimento da função do ponto de vista de Karlson (1961), podemos chamar a atenção, primeiramente, para os seguintes nexos conceituais (internos e externos): movimentos; infinito numérico; variação; campo de variação; relação; números e representações (analítica e gráfica). Em seguida, a partir de uma análise um pouco mais aprofundada, podemos perceber que, ao definir o conceito de função, a partir dos modos de ver e conceber o conceito, do referido autor, há de se considerar nexos conceituais (internos e externos): o movimento regular, o movimento irregular, a variação, a variável dependente, a variável independente, as leis, a imagem, o domínio, o contradomínio, a relação, o polinômio, a representação analítica e a representação gráfica.
A historiografia de Konstantin Ríbnikov: segundo modo de ver e conceber o conceito de função
Ríbnikov (1987), professor da Universidade Estatal “Lomonosov” de Moscou e doutor em Ciências Fisicomatemáticas, ao contrário de Karlson (1961), que escreveu para os leigos que odiavam Matemática, teve como público-alvo os estudantes e especialistas em Matemática. Sua historiografia se fundamenta nos pressupostos do Materialismo Histórico Dialético, considerando-se que:
[...] naturalmente, o estudo da História das Matemáticas pode ser frutífero só se as investigações se realizam baseando-se na ciência marxista-leninista com a aplicação do método do materialismo dialético e com o completo conhecimento do conteúdo especial das questões estudadas. A História da Matemática, como se deduz da definição de seu objeto dada mais acima, tem a ver com todo o conjunto desta ciência, com todos os ramos da matemática e com grande número de outras ciências. Esta circunstância ressalta a dificuldade dos problemas da História da Matemática e a singularidade dos métodos histórico-científicos de investigação (RÍBNIKOV, 1987, p. 10, tradução nossa). [...] Uma correta compreensão materialista do objeto das matemáticas e o conhecimento de sua história é uma condição necessária para a compreensão cabal do lugar desta ciência na atividade produtiva e social dos homens, é uma garantia para saber encontrar seu lugar no trabalho comum e compreender a relação do conteúdo de seu trabalho com as tarefas gerais. (RÍBNIKOV, 1987, p. 12, tradução nossa).
Um dos objetivos de sua historiografia é apresentar aos futuros professores os movimentos lógico-históricos do desenvolvimento do conhecimento científico, dentre eles, o desenvolvimento do conhecimento da Matemática, destacando-se as “forças motrizes” e as “vias de seu desenvolvimento” (RÍBNIKOV, 1987, p. 8, tradução nossa), as quais contêm os nexos conceituais (internos e externos). Ao tratar do “objeto e método da História da Matemática”, indica-nos que:
A composição da matemática, como a de outra ciência, é a seguinte: a) FATOS, acumulados no transcurso de seu desenvolvimento; b) HIPÓTESES, isto é, suposições científicas, baseadas nos fatos, que se submetem posteriormente a uma verificação experimental; c) os resultados da generalização do material real expresso, neste caso, por TEORIAS E LEIS MATEMÁTICAS; d) a METODOLOGIA da matemática, isto é a interpretação teórica geral das leis e teorias matemáticas, as que caracterizam o enfoque geral no estudo do objeto das matemáticas. Todos estes elementos estão inter-relacionados e se encontram em desenvolvimento constante. (RÍBNIKOV, 1987, p. 9-10, tradução nossa, grifos do autor).
Têm certa exigência: a inseparabilidade entre o lógico e o histórico. Conhecer esse par dialético:
[...] requer em matemática o conhecimento dos fatos fundamentais da história das matemáticas e dos trabalhos clássicos, a compreensão das leis do desenvolvimento das ciências matemáticas e do caráter histórico da correspondência entre as disciplinas matemáticas particulares. Esta exigência é provocada e apoiada também pelo exemplo dos principais cientistas matemáticos. Sua atividade em ramos concretos das matemáticas como regra, se conjuga com investigações de problemas históricos (RÍBNIKOV, 1987, p. 18, tradução nossa).
[...] a relação entre o histórico e o lógico no desenvolvimento das matemáticas, [...] confirma a conhecida tese marxista de que o lógico na ciência é o histórico, porém, só assimilado e posto em certa ordem (RÍBNIKOV, 1987, p. 107, tradução nossa).
A forma de ver e conceber o conceito de função de Ríbnikov (1987, p. 218) considera o ponto de partida a “transformação dos fundamentos da análise infinitesimal”, bem como “dois aspectos: a função como correspondência e expressão analítica”. Esses aspectos não estão dissociados ao “conjunto de meios” que envolvem as expressões matemáticas que foram construídas, historicamente, uma vez que:
A apreciação intuitiva de dependência funcional como revelação da relação causal dos fenômenos em diferentes modificações foi apropriada pela humanidade desde épocas remotas. Uma grande história tem também tentativas de expressar estas dependências com os recursos da matemática. Uma das primeiras tentativas foi o estudo pelos antigos matemáticos dos lugares geométricos e a formação de numerosas tábuas. Sucessivamente, o conjunto de meios de expressão matemática das funções se foi enriquecendo. Nela se inclui o aparato simbólico da análise diofantina, as funções algébricas e trigonométricas, os logaritmos e outros dados concretos sobre umas ou outras funções ou classes de funções. (RÍBNIKOV, 1987, p. 220, tradução nossa).
Para o referido autor, e também para Karlson (1961), a história do conhecimento do conceito de função não está dissociada dos estudos feitos por Descartes, Newton e Leibniz. Do ponto de vista de Ríbnikov (1987), Descartes via e concebia o conceito de função como correspondência. Newton procurava dar às funções um “tratamento mecânico”, a partir da sua “teoria das fluxões” e Leibniz se preocupou em indicar o uso do termo e expressá-lo, a partir de curva:
A ideia geral de função como correspondência de uma natureza relativamente ampla foi enfatizada por Descartes. Contudo, a possibilidade de operar com funções inevitavelmente se relacionava com suas expressões concretas: com os meios da geometria ou as expressões analíticas simbólicas. I. Newton, a este, acrescentou o tratamento mecânico da função em sua teoria das fluxões. A parte operacional desta teoria se baseava, como se conhece, nos desenvolvimentos das funções em séries de potências. Por sua vez, Leibniz expressou a ideia geral de dependência funcional, introduzindo o termo “função” e o símbolo correspondente para todos os segmentos relacionados com a curva de tal modo que o seu comprimento depende da posição do ponto sobre a curva (ordenadas, segmentos de tangentes, subtangentes, normais, subnormais). (RÍBNIKOV, 1987, p. 220, tradução nossa).
Para o autor em questão, “os êxitos práticos da análise infinitesimal impulsionaram os cientistas a colocar mais atenção ao tratamento do conceito de função, o qual permitia a operabilidade com funções concretas” (RÍBNIKOV, 1987, p. 220, tradução nossa). Em 1718, Bernoulli considerou “que uma função é simplesmente uma expressão analítica” e Euler, nesta mesma linha de raciocínio, fez a seguinte definição:
Uma função de uma quantidade variável é uma expressão analítica, composta de alguma maneira por esta quantidade variável e números ou quantidades constantes [...]. Todas as funções podem ser representadas por uma série de potências: f(z) ~ a0 + a1z + a2z2 ... (onde z, em termos gerais, é complexo). (RÍBNIKOV, 1987, p. 220-221, tradução nossa).
A partir dos estudos de Descartes, definiram-se os conceitos de função e funções contínuas:
Da definição de função como expressão analítica surgiu uma definição especial de continuidade. Uma função se considerava contínua se, se dava, em todo seu domínio de existência, por uma única expressão analítica. Assim, resultavam contínuas as funções: y=1/x; y= tg x, etc. A propriedade de continuidade de uma função no sentido usual para nós se denominava conexidade da função [...]. Por isso, depois da classificação de funções e a introdução dos conceitos fundamentais na teoria das funções do século XVIII, imediatamente seguem as seções de caráter operativo, onde se incluem os métodos de desenvolvimento de funções em séries e as propriedades das últimas. (RÍBNIKOV, 1987, p. 220-222, tradução nossa).
Nesse sentido, ao analisarmos os movimentos lógico-históricos do conceito de função, do ponto de vista de Ríbnikov (1987), pudemos constatar que as formas de ver e conceber o conceito de função, para o autor, não estão dissociadas dos movimentos científicos que fazem parte de outras áreas do conhecimento, como a Física, por exemplo, bem como de conhecimentos gerados historicamente, no interior da própria Matemática, tais como: a álgebra não simbólica, especialmente, a álgebra sincopada de Diofanto; a álgebra simbólica, a trigonometria, os logaritmos e a continuidade.
A partir dessa constatação, delineamos os seguintes nexos conceituais (internos e externos): movimento científico, variação, campo de variação, com especial atenção para o conjunto dos números complexos, fazer corresponder, expressão analítica, dependência, relação, representação, lugar geométrico, e variáveis (palavra, letra e, a mistura entre palavra e letra, denominada de sincopação).
A historiografia de Howard Eves: terceiro modo de ver e conceber o conceito de função
Em sua historiografia que compõe o livro Introdução à história da matemática, composto por 15 capítulos, cuja segunda edição foi publicada, aqui no Brasil, no final da década de 1990, Eves (1997) nos indica que suas narrativas historiográficas são elaboradas a partir de sete “períodos matemáticos”, a saber:
1.º) Egípcio e Babilônico (3000 a.C. - 260 d.C.); 2.º) Grego (600 a.C. - 450 d.C.); 3.º) Chinês (1030 a.C. - 1.644 d.C.); 4.º) Hindu (200 a.C. - 1250 d.C.); 5.º) Baixa Idade Média (450 - 1120 d.C.); 6.º) Moderno (Primeira metade, 1450 a 1700 d.C.) e 7.º) Moderno (Segunda metade, 1700 d.C. até o presente) (EVES, 1997, p. 2-3).
O autor, assim como Ríbnikov (1987), mostra-nos que tem preocupações com os alunos dos cursos de graduação. Escreve para eles e, ao final de cada capítulo, apresenta o que denominou “expedientes pedagógicos”, que são materializados nos exercícios, temas e bibliografias. A historiografia de Eves (1997) procura dar ênfase ao desenvolvimento das ideias matemáticas elaboradas ao longo dos séculos. Nesse sentido, defende que se faz necessário conhecer o panorama cultural de cada grupo que contribuiu para que os conceitos matemáticos fossem desenvolvidos.
Aqui, o conceito de função evoluiu a partir de fatos que se relacionam com as “noções de espaço e geometria” (EVES, 1997, p. 660). O foco do conceito de função estaria no desenvolvimento do termo. Significa que o autor está preocupado em fazer com que os estudantes conheçam os movimentos lógico-históricos da palavra função, diferentemente do que ocorre com Karlson (1961) e Ríbnikov (1987). É claro que, ao analisarmos os movimentos lógico-históricos da palavra, podemos conhecer, através da forma, o seu conteúdo. Isso não significa que o fato de os alunos de graduação, dentre eles os futuros professores de Matemática, conhecerem a história da palavra função faz com que aprendam a fazer generalizações e possam ampliar alguns dos conceitos que já conhecem.
O Quadro 2 sintetiza os estudos de Eves.
Quadro 2 Síntese dos movimentos lógico-históricos da palavra função
| Leibniz (1694) | Introduziu a palavra função, na sua forma latina equivalente. Expressava qualquer quantidade "associada a uma curva, como por exemplo, as coordenadas de um ponto da curva, a inclinação de uma curva e o raio da curvatura de uma curva" (EVES, 1997, p. 660). |
| Johann Bernoulli (1718) |
"Havia chegado a considerar uma função como uma expressão qualquer formada de uma variável e algumas constantes" (EVES, 1997, p. 660). |
| Euler (em seguida) | "Considerou uma função como uma equação ou fórmula qualquer envolvendo variáveis e constantes. Conceito que a maioria dos alunos dos cursos elementares de matemática tem" (p. 661). |
| Fourier (1768-1830) | "Foi levado a considerar, em suas pesquisas sobre a propagação do calor, as chamadas séries trigonométricas. Estas séries envolvem uma forma de relação mais geral entre as variáveis que as que já haviam sido estudadas anteriormente" (EVES, 1997, p. 661). |
| Lejeune Dirichlet (1805-1859) |
"Chegou à seguinte formulação: uma variável é um símbolo que representa qualquer um dos elementos de um conjunto de números; se duas variáveis x e y estão relacionadas de maneira que, sempre que se atribui um valor a x, corresponde automaticamente, por alguma lei ou regra, um valor a y, então se diz que y é uma função (unívoca) de x. A variável x, à qual se atribuem valores à vontade, é chamada variável independente e a variável y, cujos valores dependem dos valores de x, é chamada variável dependente. Os valores possíveis que x pode assumir constituem o campo de definição da função e os valores assumidos por y constituem o campo de valores da função" (EVES, 1997, p. 661). |
| Teoria dos Conjuntos (século 20) |
"Propiciou ampliar o conceito de função de maneira a abranger relações entre dois conjuntos de elementos quaisquer, sejam esses elementos números ou qualquer outra coisa. Assim, na teoria dos conjuntos, uma função f é, por definição, um conjunto qualquer de pares ordenados de elementos, pares esses sujeitos à condição seguinte: se (a1, b1) Є f, (a2, b2) Є f e a1 = a2, então b1 = b2. O conjunto A dos primeiros elementos dos pares ordenados chama-se domínio da função e o conjunto B de todos os segundos elementos dos pares ordenados se diz imagem da função. Assim, uma função é simplesmente um tipo particular de subconjunto do produto cartesiano A x B. Uma função f se diz injetora se, de (a1, b1) Є f, (a2, b2) Є f e b1 = b2, decorre a1 = a2. Se f é uma função e (a,b) Є f, escreve-se b= f(a)" (EVES, 1997, p. 661). |
Fonte: elaborado pelos autores.
O autor enfatiza ainda que:
O conceito de função permeia grande parte da matemática e, desde as primeiras décadas do século presente [20], muitos matemáticos vêm advogando seu uso como princípio central e unificador na organização dos cursos elementares de matemática. [...]. Enfim, é inquestionável que quanto antes se familiarize um estudante com o conceito de função, tanto melhor para sua formação matemática. (EVES, 1997, p. 661).
Os movimentos lógico-históricos apresentados por Eves (1997) no conceito de função, a partir da Teoria dos Conjuntos, podem ser encontrados na maioria dos livros didáticos de Matemática utilizados pelos estudantes nas salas de aula do Ensino Médio, uma vez que, ao analisá-los, constataremos que os autores desses livros sugerem que o conceito de função seja introduzido aos alunos, a partir do seu último estágio de rigor, ou seja, construído no século 20.
Ao nos apresentar esse estágio, Eves (1997) não consegue nos indicar os teóricos que fizeram a última definição, porque são muitos. Prefere nos indicar que, no século 20, o conceito de função, ao ser reelaborado, considerou a Teoria dos Conjuntos. No entanto, defendemos que, sem a compreensão dos nexos conceituais (internos e externos) que foram construídos, a partir do século 17, conforme indica o Quadro 2, fica muito difícil a compreensão do conceito de função, a partir da Teoria dos Conjuntos, considerando-se que tal conceito descreve movimentos regulares da vida.
É por esse motivo que nos arriscamos a dizer que, quando se vê e se concebe a função, somente a partir do último estágio de rigor, ou seja, a partir da Teoria dos Conjuntos, a forma do conceito, ou seja, a palavra, assume o conteúdo. Há aqui a separação da unidade dialética forma-conteúdo. É como se, ao ouvir a palavra função, os jovens, de todas as classes sociais e que frequentam as escolas da Educação Básica, assim como os matemáticos, já tivessem clareza de que estão diante de um instrumento criado, historicamente, durante pelo menos três séculos, final do XVII ao XX, para nos auxiliar a descrever os movimentos da vida, desde que sejam regulares. Aqui, priorizam-se os nexos externos do conceito. Não se priorizam os nexos internos do conceito: variação, dependência, interdependência, campo de variação, relação, representação (analítica e gráfica). Não é à toa que, nesta perspectiva, à qual denominamos lógica-formal, cujo ponto de partida para o ensino do conceito de função é a Teoria dos Conjuntos, poucos jovens escolarizados conseguem relacionar o conceito de função com os movimentos de suas próprias vidas. Há uma distância muito grande entre os movimentos da vida e o conceito lógico-formal da função.
A historiografia de Bento de Jesus Caraça: quarto modo de ver e conceber o conceito de função
Almeida (1998), ao fazer a introdução da segunda edição do livro Conceitos fundamentais da Matemática, publicado por Bento de Jesus Caraça, em Portugal, em 1941, em um contexto que pode ser considerado sombrio - a ditadura militar portuguesa, onde “vivia-se num clima de medo generalizado em que se por um lado o Estado aterrorizava os cidadãos, por outro vivia no terrível temor de eles se libertarem” (ALMEIDA, 1998, p. xiv) -, destaca-se que:
Logo no prefácio do Autor, faz-se uma clara opção entre duas atitudes possíveis: [olhar para a Ciência] “tal como vem exposta nos livros de ensino, como coisa criada” ou “assistir à maneira como foi sendo elaborada”, aparecendo então “como um organismo vivo, impregnado de condição humana, com as suas forças e as suas fraquezas”, sendo no livro adoptada a segunda atitude. Usando ainda os termos de Bento de Jesus Caraça, este ponto de vista revela [as] “hesitações, dúvidas, contradições, que só um longo trabalho de reflexão e apuramento consegue eliminar, para que logo surjam outras hesitações, outras dúvidas, outras contradições”. Espelham estas palavras a atitude arraigadamente científica do Autor, apontando nelas o mecanismo fundamental do progresso científico, em que a dúvida assume um papel crucial. Já Platão considerava que a valorização da dúvida distinguia os homens dos outros animais [...]. (ALMEIDA, 1998, p. vii-viii).
Assim, em sua historiografia, ao justificar a escolha pela segunda atitude em relação à Ciência, a qual é definida como um “instrumento forjado pelos homens para conhecer a Realidade”, Caraça (1998) afirma que a Matemática é:
Como uma ciência à parte, desligada da realidade, vivendo na penumbra do gabinete, um gabinete fechado, onde não entram os ruídos do mundo exterior, nem o sol nem os clamores dos homens. Isto, só em parte é verdadeiro. Sem dúvida, a Matemática possui problemas próprios, que não têm ligação imediata com os outros problemas da vida social. Mas não há dúvida também de que os seus fundamentos mergulham tanto como os de outro qualquer rumo da Ciência, na vida real; uns e outros entroncam na mesma madre. Mesmo quanto aos seus problemas próprios, raramente acontece, se eles são de facto daqueles grandes problemas que põem em jogo a sua essência e o seu desenvolvimento, que eles não interessem também, e profundamente, a corrente geral das ideias. (CARAÇA, 1998, p. xxiii-xxiv).
Nesse sentido, Caraça (1998) faz opção pelo “carácter libertador da ciência, convite a pensar e que vive da correcção constante dos seus erros, não poderia alhear-se ao regime ditatorial, obviamente ameaçado pela cultura e pela liberdade” em Portugal (ALMEIDA, 1998, p. xiv).
Isso quer dizer que, Caraça (1998), através de sua historiografia, defende que, o conhecimento científico, enquanto organismo vivo, dentre eles, o conhecimento matemático, pode libertar os homens das algemas da opressão.
Constatamos que o autor em questão, embora seja matemático, é reconhecido como humanista do século 20, título que conquistou devido à sua atuação política e por defender que a Matemática, enquanto bem cultural, deveria ser conhecida por todas as pessoas.
Não obstante, quando o autor trata dos movimentos lógico-históricos dos conhecimentos matemáticos, dentre eles, o de função, assim como Karlson (1961) enfatiza os movimentos da realidade, da vida e, consequentemente, ao conceito de Ciência que abraça. Para ele:
A introdução do conceito de função como instrumento necessário para o estudo da nova realidade da Ciência - a noção de lei natural - traz consigo, como não poderia deixar de ser, um conjunto de ideias e concepções que lhe são inerentes. Recorda-se o leitor do que dissemos [...] sobre a natureza do conceito de variável e a sua ligação à filosofia da fluência? [...] o próprio nome que Newton dá às funções revela bem a sua atitude mental - chama-lhes fluentes; o uso do nome função só mais tarde se generaliza. (CARAÇA, 1998, p. 190-191).
Caraça (1998) chama a atenção para o primeiro nome que Newton dá à função: fluentes, o qual está diretamente relacionado à fluência, ao movimento. Para ele, a função deve estar atrelada aos conceitos de fluência e interdependência, que são conceitos filosóficos. Nesse sentido, quando o assunto é a variável, o autor faz a seguinte afirmação:
A variável é, portanto, uma entidade que, dizendo respeito a um nível de isolado - o conjunto - superior ao do número, é ela própria, de uma natureza superior [...]; no entanto, o caráter contraditório do conceito - a variável é e não é cada um dos elementos do conjunto - deu origem a que a sua introdução na Ciência seja relativamente recente. Pelo seu caráter essencial - síntese do ser e não ser -, ela sai daquele quadro de ideias que quer ver na realidade uma permanência e irrompe ligada à corrente do pensamento que, expressa ou tacitamente, vê na fluência, a primeira das suas características. Uma variável é o que for determinado pelo conjunto numérico que ela representa - a sua substância, o seu domínio [...]. (CARAÇA, 1998, p. 120).
A substância que pode ser compreendida enquanto um dos nexos internos, o domínio da função está diretamente ligado a um determinado campo numérico. Ao mesmo tempo, “o conceito de função aparece-nos, no campo matemático, como o instrumento próprio para os estudos das leis” (CARAÇA, 1998, p. 121), quantitativas e qualitativas., considerando-se que:
[...] o conceito de função permite estabelecer uma correspondência entre as leis matemáticas e as leis geométricas, entre as expressões analíticas e os lugares geométricos (conjuntos de todos os pontos que gozam de uma mesma propriedade). Para estabelecer essa correspondência não há mais que, a cada expressão analítica, fazer corresponder aquele lugar que define a mesma função que ela. A expressão analítica, ou melhor, a igualdade y = expressão analítica chama-se equação do lugar que lhe corresponde [...]. (CARAÇA, 1998, p. 130).
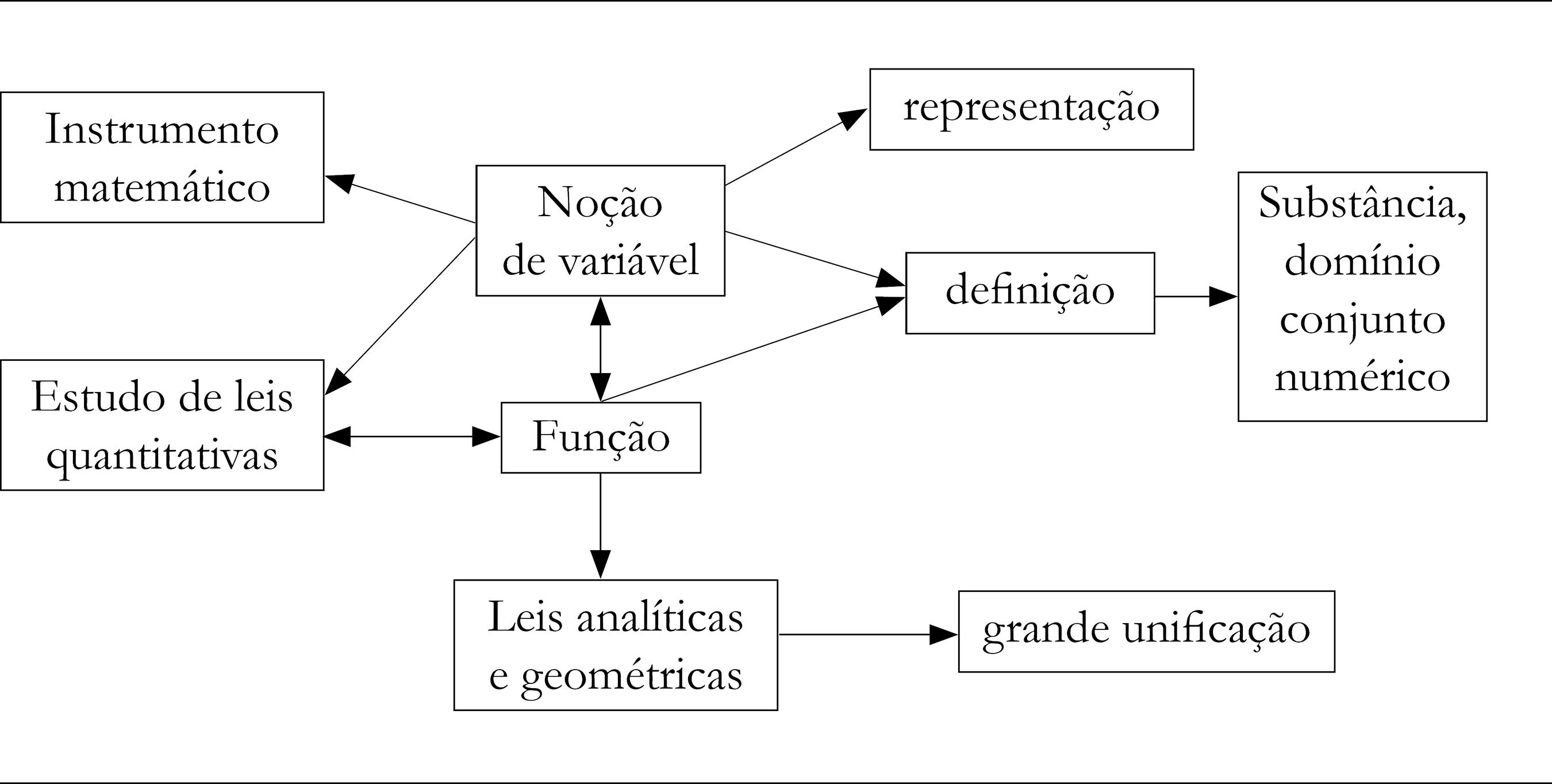
Ou seja, para Caraça (1998), assim como para Karlson (1961), Ríbnikov (1987) e Eves (1997), os movimentos lógico-históricos da função estão relacionados a outras áreas de conhecimento e podem ser definidos como um excelente instrumento para a leitura da realidade, científica ou não. Podem ser sintetizados, da seguinte forma, conforme mostra a figura 1.
Ao analisarmos os movimentos lógico-históricos descritos na historiografia de Caraça (1998) podemos delinear os seguintes nexos conceituais (internos e externos): fluência, interdependência, variação, leis (qualitativas, quantitativas, analíticas e geométricas), fazer corresponder, campos numéricos, equação e representação.
Nesse sentido, não podemos deixar de mencionar que, ao contrário de Eves (1997), o ponto de partida de Caraça (1998) para nos apresentar os movimentos lógico-históricos da função está fincado à realidade, à fluência e à interdependência. Não está atrelado à Teoria dos Conjuntos. Podemos dizer que o modo de ver e conceber o conceito de função de Caraça (1998) se aproxima aos modos de ver e conceber a função de Karlson (1961) e de Ríbnikov (1987).
Considerações finais
Ao analisarmos as quatro historiografias, pudemos constatar que não há como negar que os conceitos matemáticos, dentre eles, o conceito de função, são constantemente reelaborados, nas diversas civilizações, em momentos e contextos distintos, na medida em que novas necessidades surgem e nos obrigam a lançar diferentes olhares para a realidade fluente e interdependente que nos cerca. Aqui, a realidade é ampla e considera os movimentos da vida e os científicos que também fazem parte de nossas vidas.
Os nexos conceituais (internos e externos) comuns às historiografias de Karlson (1961), Ríbnikov (1987), Eves (1997) e Caraça (1998) são: movimento, movimento irregular, movimento regular, interdependência, variação, campo de variação, relação e representações (analítica e geométrica). Tais nexos podem ser associados às realidades que nos cercam, sejam científicas ou não.
Os movimentos lógico-históricos descritos pelos quatro autores nos mostram que o conceito de função é muito mais amplo do que os nexos externos tratados nas escolas da Educação Básica, especialmente, no Ensino Médio: representações nas formas analítica, f(x) e gráfica. Embora esses nexos também sejam construídos historicamente, eles congelam os principais nexos internos da função: os movimentos, especialmente, aqueles que são regulares. Aqui, o lógico se sobrepõe ao histórico.
Quando emprestamos as formas de ver e conceber o conceito de função de Karlson (1961), Ríbnikov (1984), Eves (1997) e Caraça (1998), podemos delinear os nexos conceituais (internos e externos) e perceber que esses nexos nos possibilitam: (1) analisar e compreender movimentos regulares e irregulares da vida; (2) elaborar leis de formação que regem os movimentos regulares da vida; (3) compreender um poderoso instrumento de leitura e compreensão das diversas variações que insistem em dominar a nossa realidade, seja ela científica ou não; e, (4) pensar cientificamente, de forma a elaborarmos pensamento teórico sobre a realidade que nos cerca. Isso porque, com o conceito de função, podemos conhecer e fazer previsão sobre a realidade que nos cerca. Não estaria aqui o foco do pensamento científico, do pensamento teórico?
Nesse sentido, podemos compreender melhor o que são os pares dialéticos: teoria e prática; interdisciplinaridade e disciplinaridade; regularidade e irregularidade; fluência e permanência, dentre outros. E esse não seria o principal papel da Matemática, auxiliar-nos a compreender a realidade que nos cerca? Ou, pelo menos, parte dessa realidade?
É por esse motivo que, defendemos que as historiografias sobre conceitos matemáticos façam parte da formação de professores que ensinam Matemática, para que possam conhecer melhor os nexos conceituais (internos e externos) que compõem os conceitos que ensinarão em sala de aula. Dessa forma, os movimentos lógico-históricos poderão fazer parte de suas práticas educativas e serem compreendidos como unidade dialética entre ensino e aprendizagem e, consequentemente, contribuir com a organização do ensino de Matemática.
Defendemos que os professores que ensinam Matemática na Educação Básica podem ampliar o estudo das funções, incorporando os nexos conceituais (internos e externos) que levam ao entendimento do pensamento teórico da função, a partir de sua gênese conceitual que é a compreensão da realidade, enquanto movimentos da vida, os quais, quando isolados para serem estudados com maior profundidade, podem ser transformados em leis: qualitativas, quantitativas, analíticas e geométricas, por exemplo. Tais leis regem os conhecimentos científicos, os quais se manifestam em diversas áreas do conhecimento, denominadas exatas e humanidades, por exemplo.
Ou seja, áreas como a medicina fazem uso do conceito de função quando precisam compreender determinados fenômenos, tal qual, a economia, a física, a química, a história, a geografia, dentre outras. No nosso entendimento, apenas alguns estudantes conseguem compreender os nexos externos da função quando o ponto de partida do ensino é a Teoria dos Conjuntos. Tal teoria congela os movimentos fluentes e interdependentes da vida por estar em seu último estágio de rigor. É por esse motivo que, para a maioria dos escolarizados, cabe apenas memorizar e decorar o conceito de função, através das fórmulas.