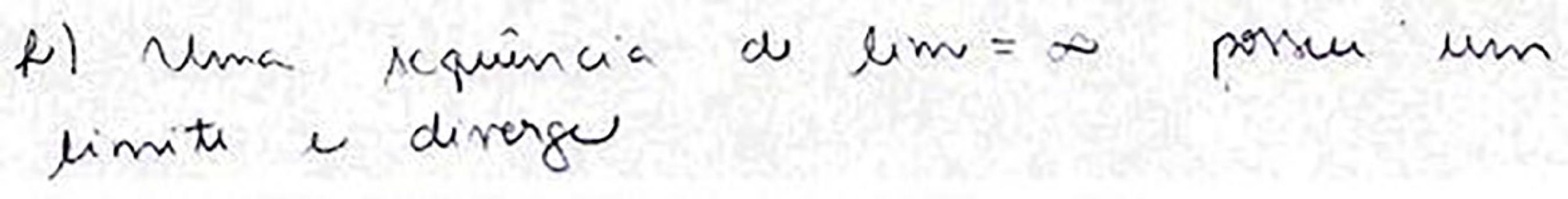Introdução
Apresentamos uma análise das percepções de um grupo de estudantes de um curso de Licenciatura em Matemática sobre prova e justificativa em Matemática, com foco no assunto sequências numéricas. A investigação envolveu a aplicação de duas questões do tipo Verdadeiro/Falso e entrevistas semiestruturadas, em dois momentos distintos do Curso, um deles ao final da disciplina Sequências e Séries (6º semestre) e o outro, ao final da disciplina Introdução à Análise Real (8º semestre). Para a elaboração dos instrumentos de coleta de dados, entrevistamos sete docentes que ministram essas disciplinas para o Curso de Licenciatura em Matemática.
Os referenciais teóricos usados foram os processos do Pensamento Matemático Avançado (DREYFUS, 1991), a interação de aspectos algorítmicos, intuitivos e formais em Matemática (FISCHBEIN, 1994) e os aspectos intuitivo-numérico e lógico-formal (SOUZA, 2008).
Entendemos que é fundamental, para o desenvolvimento do Pensamento Matemático Avançado (DREYFUS, 1991), a elaboração de provas, justificativas e contraexemplos de afirmações matemáticas e exploramos isso com os participantes, em questões do tipo Verdadeiro/Falso, acompanhadas de justificativas que julgassem pertinentes. O interesse e a preocupação com essa problemática não são recentes. Pinto (1998) coloca, como uma questão a ser investigada, o fato de estudantes de Licenciatura em Matemática evitarem o formalismo e aceitarem explanações informais ou pouco rigorosas como comunicação e justificativa para resultados em Matemática.
Gomes (2013) entrevistou licenciandos e professores de Matemática da Educação Básica sobre o papel da disciplina Análise Real no currículo de Licenciatura em Matemática e as palavras mais citadas foram ‘reproduzir’, ‘decorar’, ‘difícil’, ‘teórica’ e ‘abstrata’. Também não souberam apontar a importância dessa disciplina na formação do futuro professor. Um participante destacou que “[...] foi muito difícil mesmo, principalmente as demonstrações. [...] as demonstrações não é pra qualquer um; não é pra mortal demonstrações de teorema”. (GOMES, 2013, p. 228).
Moreira e Vianna (2016) destacam que há uma convergência entre as posições de grupos de matemáticos e de educadores matemáticos sobre o papel que a disciplina Análise Real desempenha na formação de professores de Matemática. A maioria dos entrevistados por esses autores defende a obrigatoriedade dessa disciplina no currículo e aponta que “[...] o aluno da licenciatura precisa conhecer a natureza do pensamento matemático, seus modos de proceder, suas demonstrações, a forma como a matemática organiza-se em conhecimento específico, precisa ter uma cultura matemática”. (MOREIRA; VIANNA, 2016, p. 12).
As perspectivas colocadas por esses autores evidenciam uma dicotomia entre o que docentes e estudantes de Licenciatura em Matemática esperam e recebem da disciplina Análise Real. Pretendemos acirrar este debate, ao relacionar visões de docentes com as respostas dadas por estudantes em questões que precisam de justificativas e contraexemplos, no assunto sequências numéricas, após as disciplinas Sequências e Séries e Introdução à Análise Real.
Referenciais Teóricos
Interação de Aspectos Formais, Intuitivos e Algorítmicos
Fischbein (1994) argumenta que precisamos observar se há ou não a interação de aspectos formais, algorítmicos e intuitivos num sujeito em atividade matemática, o que significa olhar a Matemática como um processo criativo, uma atividade humana, com momentos de "[...] iluminação, hesitação, aceitação e refutação" (FISCHBEIN, 1994, p. 231). Entendemos que essa interação deve guiar escolhas e práticas, para que estudantes possam produzir afirmações e provas matemáticas e avaliar, formal e intuitivamente, a validade dessas produções.
O aspecto formal refere-se a axiomas, definições, teoremas e demonstrações e Fischbein (1994) reitera que "[...] têm de penetrar como um componente ativo do processo de raciocínio. Devem ser inventados ou aprendidos, organizados, checados e usados ativamente pelo estudante" (FISCHBEIN, 1994, p. 232). E aponta ainda que o pensamento proposicional e as construções hipotético-dedutivas não são adquiridos espontaneamente.
O aspecto algorítmico corresponde às técnicas e procedimentos de resolução, que têm caráter fundamental no entendimento e na criação em Matemática, pois apenas aspectos formais não são suficientes para conferir a habilidade de resolver problemas. Segundo Fischbein (1994, p. 232), "[...] Esta profunda simbiose entre significado e habilidades é uma condição básica para o produtivo e eficiente raciocínio matemático".
O aspecto intuitivo diz respeito a uma intuição cognitiva, um entendimento intuitivo, uma solução intuitiva, aquilo que um sujeito considera autoevidente e para o qual não vê necessidade de prova ou justificativa (FISCHBEIN, 1994, p. 233), como "a parte é menor que o todo" ou resolver uma inequação como se fosse uma equação. Esse conhecimento intuitivo exerce papel coercivo no raciocínio, definindo caminhos e estratégias que podem facilitar o processo de aprendizagem ou gerar dificuldades e conduzir a contradições e equívocos.
Fischbein (1994) defende a interação de aspectos intuitivos e formais ao afirmar que uma informação não é processada apenas por estruturas lógicas, mas também por modelos intuitivos, que agem de maneira implícita, restringindo e definindo caminhos. A influência desses modelos no pensamento matemático é importante e decisiva e permanece agindo, mesmo após as estruturas formais do raciocínio estarem desenvolvidas.
Também usamos aspectos intuitivo-numéricos e aspectos lógico-formais (SOUZA, 2008). Os primeiros se relacionam à necessidade que indivíduos sentem de se apoiar em alguns valores numéricos para desenvolver o raciocínio e validar, conferir e generalizar resultados, ao determinar um limite, por exemplo, ou construir uma tabela para traçar o gráfico de uma função, dada pela expressão algébrica. Aspectos lógico-formais (SOUZA, 2008) dizem respeito ao entendimento de sentenças como p ⇒q e p ⇔ q, presentes na elaboração de justificativas e no reconhecimento de hipóteses e teses em Matemática, como resolver (x − 1) (x − 3) = 1, fazendo x − 1 = 1, ou x − 3 = 1 sem perceber que as respostas obtidas não são soluções da equação.
Processos do Pensamento Matemático Avançado
Segundo Dreyfus (1991), o Pensamento Matemático Avançado é uma inter-relação de processos cognitivos como visualização, representação, classificação, tradução, generalização, justificativa, síntese e abstração. Envolve toda a atividade matemática, desde criar um problema, elaborar conjecturas e estratégias de resolução, até chegar aos níveis de refinamento e prova.
No Ensino Superior, pode haver uma supervalorização de processos de abstração e de métodos dedutivos, em detrimento de processos heurísticos e Tall (1991) reforça que esta 'apresentação' da Matemática não mostra o poder do pensamento avançado, na sua multiplicidade de processos e abordagens. Defende que o conhecimento matemático seja abordado de forma a privilegiar a aquisição de insights dos métodos e processos da Matemática avançada, por caminhos que respeitem a estrutura e o processo de pensamentos individuais.
Com esse panorama de características psicológicas relacionadas ao desenvolvimento do pensamento matemático, escolhemos, para nossas análises, os processos de representação, visualização, mudança entre representações, generalização e síntese.
O processo de representação é de especial importância para a produção e o ensino de Matemática, uma vez que só temos acesso aos objetos dessa ciência por meio de representações (DREYFUS, 1991), que são de dois tipos: simbólica e mental. Uma representação simbólica está associada a signos e a significados que um indivíduo tem para explicitar um conhecimento implícito e pode ser exteriorizada pela escrita ou pela fala. Uma representação mental refere-se a esquemas internos ou sistemas de referência que uma pessoa usa para interagir com o mundo exterior.
Um dos processos pelos quais as representações mentais podem passar a existir é o de visualização, que depende de sistemas de representação e de produções externas, concretas, materialmente percebidas pelo sujeito. Dreyfus (1991) destaca que, em Matemática, é necessário ter muitas representações mentais, relacionadas a vários e diferentes aspectos desse conceito.
Nesse sentido, o processo de mudança entre representações tem papel de destaque, uma vez que a existência de várias representações não é suficiente para conferir um uso flexível e articulado de um conceito, é preciso saber transitar entre essas representações, de acordo com as situações que a resolução de um problema impõe. Dreyfus (1991) sustenta que ele não é trivial e, para ser apropriado pelos estudantes, que estão construindo esquemas mentais, precisa ser reiteradamente trabalhado pelos professores.
O processo de representação está presente em todos os níveis do pensamento matemático, mesmo nos mais elementares. Outros processos, como generalização e síntese, são desenvolvidos a partir do refinamento de habilidades e experiências, à medida que se entra em contato com conteúdos matemáticos mais avançados. O processo de generalização consiste em deduzir ou induzir resultados gerais a partir de casos particulares e de características semelhantes identificadas, expandindo os domínios de validade das conclusões originais para contextos mais amplos.
O processo de síntese refere-se à capacidade de combinar ou compor partes de maneira a formar um todo coerente, que frequentemente agrega mais do que a soma das partes que o compõem. Trata-se de um processo que busca inter-relacionar resultados, ideias e algoritmos que foram aprendidos de maneira isolada, fragmentada e que ressurgem fundidos, mesclados em um novo resultado, um novo conhecimento, mais coeso e poderoso.
Os processos de generalização e síntese, aliados ao de representação, constituem a base para o desenvolvimento da abstração, fundamental para o Pensamento Matemático Avançado. O processo de abstração é construtivo, vai da compreensão de propriedades de objetos matemáticos para a de estruturas mais gerais. Essa construção pressupõe uma mudança no foco de atenção, que deve migrar de objetos particulares para estruturas específicas e próprias, que consideram relações entre objetos. Por exemplo, no estudo de certo conceito ou ideia, acreditamos que um único exemplo, seguido de uma definição formal, não evita que se cometam erros no futuro. O trabalho com diversos exemplos e situações pode fazer com que semelhanças sejam percebidas e se foque a atenção nas propriedades e relações, possibilitando as abstrações pretendidas; para isso, os exemplos não podem ser muito complexos, nem envolver muitas propriedades (DREYFUS, 1991).
Observamos que os processos de visualização e de representação exercem papel importante no desenvolvimento de abstrações, pois imagens visuais podem apresentar características globais e enfatizar aspectos estruturais dos conceitos, que contribuem para a construção de abstrações. Além disso, representações e abstrações são processos complementares, pois um conceito muitas vezes é abstraído a partir de várias representações e uma representação está sempre associada a propriedades de um conceito. Dessa forma, o uso conjunto de várias representações pode favorecer a abstração das relações e propriedades de um conceito (DREYFUS, 1991).
Procedimentos Metodológicos
Para a elaboração dos instrumentos de coleta de dados, entrevistamos sete docentes que ministram as disciplinas Sequências e Séries e Introdução à Análise Real para o Curso de Licenciatura em Matemática. Todos trabalham em uma instituição pública de ensino do Estado de São Paulo. Os professores Bete , Carlos, Dione e Fátima têm Mestrado em Matemática; a professora Fátima cursa Doutorado em Educação Matemática; o professor Carlos, Doutorado em Matemática; e a professora Geise possui Mestrado e Doutorado em Computação Matemática. Todos já ensinaram sequências numéricas no Ensino Superior e possuem mais de 10 anos de atuação docente.
Das análises das entrevistas com os docentes, identificamos duas principais dificuldades dos estudantes, relativas à elaboração de justificativas em Matemática: (1) A definição de limite de sequências e (2) A estrutura lógica de demonstrações, as quais nortearam a elaboração de duas questões do tipo Verdadeiro e Falso, relacionadas ao estudo de sequências numéricas, por meio das quais avaliamos como estudantes percebem a construção de justificativas em Matemática. As questões foram respondidas individualmente, sem nenhum tipo de consulta a materiais externos e sem intervenção do pesquisador, a não ser no esclarecimento de dúvidas relativas aos enunciados.
A aplicação da Questão 1 ocorreu ao final da disciplina Sequências e Séries (6º semestre); foram convidados 17 estudantes do curso de Licenciatura em Matemática da instituição escolhida e que haviam cursado os ensinos Fundamental e Médio em escolas públicas. A partir da análise das respostas dadas por escrito, os estudantes Bia, Camilo, Débora e Franciele foram selecionados para a realização de entrevistas semiestruturadas (BONI; QUARESMA, 2005) individuais, nas quais foram discutidas as suas respostas a cada um dos itens da Questão 1.
A Questão 2 foi aplicada ao final da disciplina Introdução à Análise Real (8º semestre) e foram convidados 15 alunos, dos quais 10 haviam respondido a Questão 1. Os estudantes Bia, Camilo e Débora foram novamente entrevistados, nos mesmos moldes da primeira entrevista.
As respostas dos participantes, para cada uma das questões, foram analisadas com base na Análise de Erros (CURY, 2007), procedimento metodológico que propõe uma análise de conteúdo para identificar classes de erros recorrentes nas resoluções dos problemas propostos, seguida de quadros com as frequências e os percentuais de cada tipo de erro identificado.
Discussão dos Resultados da Investigação
Apresentamos, a seguir, uma análise das entrevistas individuais realizadas com os docentes, por meio das quais procuramos identificar o papel que cada um deles atribui à elaboração de justificativas em Matemática e as dificuldades que eles apontam na aprendizagem dos alunos.
Iniciamos as entrevistas pedindo que falassem como introduzem sequências numéricas e se fazem alguma revisão sobre limites. A partir das respostas, identificamos dois grupos. As professoras Bete e Geise preferem abordagens iniciais baseadas em aspectos algorítmicos e intuitivos, pelo uso de problemas que solicitam, a partir de uma sequência dada, o estabelecimento da lei algébrica ou a identificação de termos consecutivos e problemas aplicados. Os professores Carlos, Dione e Fátima, ao contrário, adotam abordagens iniciais que privilegiam mais aspectos formais, marcados principalmente pelo uso de definições. Nesse sentido, a fala da professora Dione é bastante emblemática: !"Definição! Sequência numérica, define...".
A professora Fátima é a única que explicita fazer uma revisão de limites; para ela, o resgate de aspectos formais justifica essa revisão com épsilons e deltas. Na disciplina Sequências e Séries, constatou que os estudantes não sabiam lidar com esses conceitos e justifica que isso ocorre pelo fato de serem tratados, nas disciplinas iniciais de Cálculo, de forma apenas intuitiva, com regras e técnicas de cálculo, em detrimento de aspectos formais. E diz “[...] ah, conforme o x se aproxima desse valor a função se aproxima deste, né, então matematicamente o que significa se aproximar de x, o que é se aproximar da função?”.
As abordagens intuitivas dispensadas à introdução de limite foram caracterizadas por Robert (1982) como ‘modelos dinâmicos’. Essa perspectiva do ensino de limite, apontada pela professora Fátima, coloca em discussão o nível de formalismo adotado nas disciplinas iniciais de Cálculo e as implicações disso em disciplinas matemáticas futuras.
O professor Carlos, embora expresse preferir abordagens iniciais mais formais, mostrou uma perspectiva flexível. Tem bastante experiência no ensino de Análise e aspectos formais presentes nessa disciplina o influenciaram ao ministrar Sequências e Séries. Segundo ele "[...] algumas coisas que eu fiz lá eu poderia não ter feito e gasto mais tempo [...] em aprender os critérios de convergência e aplicar [...] pra poder avançar mais e chegar mais longe [...] seria melhor justificar menos". Reitera que o principal papel de Análise é que os estudantes aprendam técnicas de demonstração e o funcionamento de estruturas lógicas como ‘se, então’ e ‘se, e somente se’. E destaca que futuros professores de Matemática devem conhecer certos conceitos, como a cardinalidade dos conjuntos numéricos, posição que está em consonância com as apontadas pelos docentes de Matemática e Educação Matemática entrevistados por Moreira e Vianna (2016).
No estudo de convergência de sequências, o professor Carlos percebeu que alunos que tiveram contato com a definição formal de limites em cursos iniciais de Cálculo têm mais facilidade e se saem melhor nas disciplinas avançadas, posição também assumida pelas professoras Dione e Fátima. O professor Carlos pondera, ainda, que não se trata ‘apenas’ de dar uma definição formal, mas de mostrar o funcionamento do épsilon e do delta. Entendemos que este relato evidencia a necessidade da interação de aspectos intuitivos e formais relativos às sequências desde as primeiras abordagens, além de apontar para os benefícios que essa interação pode trazer para o desenvolvimento de processos como generalização e síntese.
Sobre o nível de formalismo adotado no curso de Licenciatura em Matemática, a professora Dione reiterou que, na disciplina Sequências e Séries, acredita que se o aluno souber bem a parte formal "[...] acaba conseguindo se virar na parte mais prática, na parte de conta."
Em oposição à fala da professora Dione, não acreditamos que apenas um bom conhecimento de aspectos formais relativos a um assunto seja capaz de conferir habilidade em resolver problemas; conforme defendemos anteriormente, entendemos ser essencial que exista uma interação de aspectos algorítmicos, intuitivos e formais para que um sujeito possa se apropriar de conceitos e técnicas e resolver problemas com autonomia. Além disso, a disciplina Análise deveria retomar o estudo de sequências numéricas para possibilitar o desenvolvimento de processos como generalização e síntese, essenciais para a formação de professores de Matemática.
Sobre abordagens formais na disciplina Análise, o professor Carlos percebeu que uma aluna estava apenas reproduzindo as técnicas de demonstração, sem entender o que de fato estava fazendo. A professora Fátima também identificou esse comportamento em alguns estudantes "[...] sabem que tem que pegar aqueles épsilons, aquele n a partir dali, mas eles sabem porque é aquela sequência didática que ele aprendeu pra resolver aquilo. Mas não porque ele entendeu o conceito". As falas dos professores Carlos e Fátima reiteram as dificuldades manifestadas pelos licenciandos e professores de Matemática da Educação Básica entrevistados por Gomes (2013), que também apontaram ter reproduzido e decorado procedimentos e demonstrações sem entendê-los plenamente, quando cursaram a disciplina de Análise Real.
Entendemos que as colocações dos professores Carlos e Fátima evidenciam um tipo de ensino que não parece cumprir o papel de formar os estudantes. Essa dificuldade no ensino de aspectos formais de Matemática, acreditamos, está relacionada à dicotomia que permeia as disciplinas, entre abordagens algorítmico-intuitivas e formais.
Os estudantes, privados do ensino de aspectos formais, terão dificuldade em enfrentar o formalismo matemático das disciplinas avançadas, o que acarreta as situações trazidas pelos docentes entrevistados. Essas dificuldades estão relacionadas ao conhecimento e ao uso de estruturas lógicas e também foram identificadas por Souza (2008) que, em seu trabalho, destaca que "[...] nenhum dos pesquisados conseguiu mostrar que entendeu como funciona, na prática, o ‘se... então'". (SOUZA, 2008, p. 250).
Em geral, os relatos apontam que há uma dicotomia entre abordagens algorítmico-intuitivas e formais e não o trabalho com os três aspectos simultaneamente, o que seria, defendemos, necessário para o aprendizado de conceitos e ideias matemáticas. Essa dicotomia ainda acaba por dificultar o desenvolvimento de processos relativos ao Pensamento Matemático Avançado, como os de generalização e de síntese, pois ou persistem as abordagens intuitivas, que não possibilitam ao estudante avançar nos aspectos formais do conceito, ou trazem uma abordagem formal que não valoriza uma articulação com os conhecimentos intuitivos que os alunos trazem.
Apresentamos, a seguir, a Questão 1 e a análise das respostas dadas para cada um dos itens.
Questão 1: Classifique as seguintes afirmações em verdadeiras (V) ou falsas (F). Apresente um argumento ou um contraexemplo para justificar cada uma das respostas dadas (VIEIRA, 2016)
( ) Toda sequência de termos estritamente positivos que converge para 0 é decrescente.
( ) Toda sequência limitada é convergente.
( ) Os termos de uma sequência convergente nunca superam o valor de seu limite.
( ) Dada uma sequência an, sempre é possível encontrar um intervalo numérico do tipo ]a, b[ que, a partir de certo índice n, contenha todos os termos dessa sequência.
( ) Uma sequência decrescente, cujos termos cabem em um intervalo numérico do tipo ]a, b[ , tem limite.
( ) Uma sequência pode ter limite e não ser convergente.
( ) Toda sequência que converge para um determinado número L tem limite.
Apenas o item e exige uma 'demonstração' um pouco mais trabalhosa, nos demais, era esperado um contraexemplo ou o reconhecimento de uma definição, no caso do item g .
O Quadro 1 traz as estatísticas das respostas apresentadas e a classificação adotada, que considera a importância da elaboração de justificativas e contraexemplos. A coluna Em branco (B) indica respostas sem justificativa, a coluna Erradas (E) , as respostas com justificativas erradas ou sem sentido, e a coluna Corretas (C) indica respostas com justificativas corretas.
Quadro 1 Classificação das respostas da questão 1
| Itens | B | E | C |
|---|---|---|---|
| (a) (F) Toda sequência de termos estritamente positivos que converge para 0 é decrescente. | 29% | 71% | 0% |
| (b) (F) Toda sequência limitada é convergente. | 29% | 42% | 29% |
| (c) (F) Os termos de uma sequência convergente nunca superam o valor de seu limite. | 30% | 35% | 35% |
| (d) (F) Dada uma sequência an, sempre é possível encontrar um intervalo numérico do tipo ]a, b[ que, a partir de certo índice n, contenha todos os termos dessa sequência. | 47% | 18% | 35% |
| (e) (V) Uma sequência decrescente, cujos termos cabem em um intervalo numérico do tipo ]a, b[ tem limite. | 59% | 18% | 23% |
| (f) (F) Uma sequência pode ter limite e não ser convergente. | 29% | 29% | 42% |
| (g) (V) Toda sequência que converge para um determinado número L tem limite. | 24% | 6% | 70% |
Fonte: Vieira (2016).
Quadro 1 indica muitas dificuldades dos participantes em classificar as afirmações e em apresentar justificativas para as decisões tomadas, uma vez que apenas no item g o percentual de respostas corretas é maior do que o de respostas em branco ou erradas somadas.
A análise das respostas erradas revelou quatro classes de erros, destacadas no Quadro 2.
Quadro 2 Erros identificados na primeira questão
| Descrição do Erro | Freq. | % |
|---|---|---|
| A1 – Apresentar um exemplo para justificar uma afirmação considerada verdadeira | 4 | 24% |
| B1 – Confundir a expressão 'limitada' com 'ter limite' | 7 | 41% |
| C1 – Enquadrar limites infinitos (divergência) na expressão 'ter limite' | 7 | 41% |
| D1 – Apresentar argumentos sem sentido nas justificativas | 11 | 65% |
Fonte: Vieira (2016).
O erro tipo A1 aconteceu principalmente na justificativa para o item a. As respostas dos estudantes José e Franciele (Fig. 1) são exemplos dessa situação.
Durante a entrevista, as explicações de Franciele confirmam suas confusões para a construção de justificativas em Matemática. Sobre a resposta dada ao item a, diz "Logo que eu saí disso aí, dessa avaliaçãozinha, eu conversei com várias pessoas [...] que falaram que na verdade eu teria que dar um exemplo meio que genérico pra dizer que era verdadeira e na falsa dar um contraexemplo". Sobre o que significa ser genérico, explica "Que é válido pra tudo, se eu colocar qualquer valor lá ele vai [...] sempre convergir pra zero e ele vai ser decrescente".
Cometido por 24% dos estudantes, esse tipo de erro nos parece bastante grave e está além do estudo de sequências numéricas, pois indica falta de aspectos lógico-formais, que estão na base do pensamento matemático e não deveriam mais acontecer com estudantes do 6o semestre de Licenciatura em Matemática. Abordagens algorítmico-intuitivas de resultados e verdades matemáticas podem explicar esse tipo de erro e reforçam o caráter danoso que o abandono de aspectos formais pode causar à formação matemática de estudantes.
As respostas de Camilo e Franciele (figura 2) mostram o erro tipo B1.
Camilo, ao comentar a resposta dada para o item b , diz "Eu confundi. Porque sequência limitada não quer dizer que ela tem um limite. Tem uma outra definição que eu não lembro agora mas eu sei que tem". Entendemos que esse tipo de erro não pode ser explicado simplesmente pelas semelhanças entre as palavras, mas por incompreensões que parecem ter raízes na falta de compreensão de aspectos formais. Franciele corrobora essa leitura, quando diz que "[...] se existe uma sequência que está ali no número L que está superiormente e um outro número n, sei lá, que está inferiormente ele vai ser como o sanduíche ele vai sempre apertar, ele sempre vai tender a algum número L”. Além das confusões conceituais, chama-nos a atenção a maneira descuidada ou 'pouco formal' com que a estudante expressa suas ideias matemáticas.
O índice de 41% de ocorrência dos erros tipo B1 e C1 nos parecem altos e indicam falta de compreensão de aspectos formais, pois há evidências de que os conceitos de função limitada e de limite de funções não foram apropriados pelos participantes, assim como a definição de convergência de sequências, que se refere à aproximação dos termos da sequência para um número real L. A resposta de Bia para o item f mostra o erro tipo C1 (Figura 3).
O comentário de Bia sobre o item f , durante a entrevista, exemplifica as incompreensões de natureza formal que destacamos. Segundo ela,
Também fiquei na dúvida nessa. Coloquei falsa, depois coloquei verdadeira. Porque eu pensei: se ela tem limite, ela converge, então não tem cabimento. [...] eu fiquei na dúvida porque eu pensei, tipo, se um limite é infinito, você está dizendo que o limite é infinito... Tem limite. Então, e ela não é convergente, aí eu fiquei meio na dúvida, mas no final coloquei verdade. [Bia, primeira entrevista].
Acreditamos que notações do tipo limn→∞ a n = + ∞ , aliadas a abordagens algorítmico-intuitivas, são os principais responsáveis por esse erro. De qualquer forma, entendemos que a valorização e o uso da definição formal poderiam minimizar este tipo de dificuldade.
O erro tipo D1, apresentar respostas ou justificativas sem sentido, foi uma tônica para 65% dos participantes. A Figura 4 exemplifica respostas enquadradas nessa classe de erros.
Os altos índices dos erros tipos B1, C1 e D1 (Quadro 2), somados aos percentuais de questões deixadas em branco (Quadro 1), desenham um panorama de muitas dificuldades dos participantes na Questão 1 e nem mesmo o êxito de 70% dos estudantes no item g consegue mudar essa leitura.
De maneira geral, as dificuldades em lidar com a definição de limite de sequências e com a estrutura lógica de demonstrações, identificadas nas falas dos docentes, se confirmam, de fato, na análise do desempenho dos estudantes que participaram da pesquisa, ao final da disciplina Sequências e Séries.
A Questão 2 foi aplicada um ano depois, ao final da disciplina Introdução à Análise Real.
Questão 2: Classifique as seguintes afirmações em verdadeira (V) ou falsa (F). Apresente um contraexemplo para justificar as afirmações falsas e demonstre os resultados no caso das afirmações verdadeiras. (VIEIRA, 2016).
( ) Toda sequência de termos estritamente positivos que converge para 0 é decrescente.
( ) Toda sequência limitada é convergente.
( ) Dada uma sequência an, sempre é possível encontrar um intervalo numérico do tipo ]a, b[ que, a partir de certo índice n, contenha todos os termos dessa sequência.
( ) Uma sequência pode ter limite e não ser convergente.
( ) Toda sequência convergente é limitada.
( ) Se uma sequência an satisfaz |an|<∞, então an é limitada.
Alguns itens da Questão 1 aparecem na Questão 2 e acrescentamos os itens e e f , com o objetivo de avaliar se houve progresso dos participantes em aspectos lógico-formais, relacionados à elaboração de justificativas e de argumentações matemáticas. Entendemos que a comparação entre as respostas dadas nas duas ocasiões fornece elementos para observar o desenvolvimento dos estudantes e a permanência, ou não, de dificuldades identificadas na Questão 1. Além disso, a partir das justificativas apresentadas, podemos verificar se houve evolução de processos do Pensamento Matemático Avançado, como generalização e síntese.
Apresentamos no Quadro 3 os percentuais de respostas em branco, erradas e corretas para cada uma das afirmações da Questão 2 . Como antes, foram consideradas Corretas (C) respostas que apresentaram justificativas adequadas; a coluna Em branco (B) indica respostas sem justificativa e Erradas (E) corresponde às respostas com justificativas erradas ou sem sentido.
Quadro 3 Classificação das respostas da Questão 2
| Itens | B | E | C |
|---|---|---|---|
| (a) (F) Toda sequência de termos estritamente positivos que converge para 0 é decrescente. | 47% | 53% | 0% |
| (b) (F) Toda sequência limitada é convergente. | 53% | 20% | 27% |
| (c) (F) Dada uma sequência an, sempre é possível encontrar um intervalo numérico do tipo ]a, b[ que, a partir de certo índice n, contenha todos os termos dessa sequência. | 67% | 20% | 13% |
| (d) (F) Uma sequência pode ter limite e não ser convergente. | 60% | 20% | 20% |
| (e) (V) Toda sequência convergente é limitada. | 60% | 40% | 0% |
| (f) (F) Se uma sequência an satisfaz | an | < ∞ , então an. é limitada. | 73% | 7% | 20% |
Fonte: Vieira (2016).
Uma análise dos protocolos revelou um aumento no percentual de itens sem nenhum tipo de justificativa (B ). Além disso, 33% dos participantes não responderam nenhum item da Questão 2, índice bem maior do que os 12% da Questão 1. A análise das justificativas consideradas erradas indicou as mesmas classes de erros encontradas na análise da Questão 1. Para facilitar a leitura, repetimos as estatísticas identificadas na análise da Questão 1, que são indicadas na coluna %Q1 do Quadro 4. As colunas Freq e %Q2 referem-se aos dados da Questão 2.
Quadro 4 Erros identificados nas Questões 1 e 2
| Descrição do Erro | Freq. | %Q2 | %Q1 |
|---|---|---|---|
| A2 – Apresentar um exemplo para justificar uma afirmação considerada verdadeira | 5 | 33% | 24% |
| B2 – Confundir a expressão 'limitada' com 'ter limite' | 5 | 33% | 41% |
| C2 – Enquadrar limites infinitos (divergência) na expressão 'ter limite' | 3 | 20% | 41% |
| D2 – Apresentar argumentos sem sentido nas justificativas | 6 | 40% | 65% |
Fonte: Vieira (2016).
A resposta de Débora (Figura 5) é exemplo do uso de casos particulares para justificar afirmações consideradas verdadeiras pelos respondentes, situações agrupadas no erro tipo A2.
Na entrevista, Débora disse que o exemplo não justifica a afirmação, porque é um caso particular e que, durante a atividade, não conseguiu demonstrar o resultado nem achar um contraexemplo, então deixou a resposta da Figura 5 como exemplo da veracidade da afirmação. Embora essas observações de Débora indiquem alguma clareza com relação ao uso de exemplos para justificar afirmações verdadeiras, a resposta escrita parece contradizer isso, pois colocações do tipo "a sequência procurada" se opõem à afirmação "Toda sequência ...", proposta no item a, o que indica uma percepção nebulosa sobre a elaboração de justificativas em Matemática.
A comparação entre os índices de erros nas Questões 1 e 2 (ver Quadro 4), indica que houve um aumento dos que cometeram o erro tipo A2, de 24% para 33%. Essa situação não era a esperada, pois ao final da disciplina Análise Real é desejável que os estudantes atinjam um melhor nível de maturidade matemática, que articulem e trabalhem com mais facilidade aspectos lógico-formais relativos às estruturas da lógica matemática e à elaboração de justificativas. Moreira e Vianna (2016) apontam que matemáticos e educadores matemáticos concordam que essas habilidades deveriam ser desenvolvidas na disciplina Análise Real, conforme destacamos anteriormente.
O erro tipo B2 agrupa os estudantes que confundiram a expressão limitada com ter limite nas respostas dadas para os itens b e e . As respostas de José e Teo (Figura 6) exemplificam isso.
A redução de 41% do erro tipo B1 para 33% do erro B2 (ver Quadro 4) é ilusória e não indica que houve uma superação dos estudantes nessa dificuldade, uma vez que os percentuais de 53% e de 60% de participantes que não responderam aos itens b e e , respectivamente, são altos (ver Quadro 3). Dessa forma, entendemos que esse tipo de dificuldade parece persistir para boa parte dos participantes e, conforme destacamos anteriormente, pode ser explicado por abordagens de ensino que se detêm na exploração de técnicas algébricas e no desenvolvimento intuitivo de ideias e que não promovem a interação com aspectos formais associados a esses conceitos.
O erro tipo C2, cometido por 20% dos estudantes, foi identificado na análise do item d . Esse índice, somado aos 60% dos que deixaram a questão em branco (Quadro 3), desenha um panorama de muitas dificuldades dos participantes. De fato, a comparação desses percentuais com os 29% de respostas em branco da Questão 1(f) (Quadro 1) e os 41% do erro tipo C1 aponta para um desempenho pior na Questão 2, neste item.
A resposta de Bia (Figura 7) é um exemplo do erro tipo C2. Essa estudante repete o erro cometido na Questão 1(f), ou seja, não houve nenhum progresso dela nos conceitos abordados neste item.
Na entrevista, questionada sobre o que significa ter limite, Bia explicou que "É... ter um... resultado... pera [pausa] É ter um limite que existe". Em seguida, reafirmou que o exemplo lim n →∞ (n + 1) = +∞ é um caso que tem limite e é divergente e que isso justifica a afirmação verdadeira do item, e emendou "Não ter limite é quando o limite não existe. No caso do seno". Neste caso, Bia confunde o limite infinito com a expressão "possuir limite".
Os erros tipo B2 e C2 indicam incompreensões de natureza formal e um conhecimento restrito da definição de convergência de sequências e do conceito de sequência limitada. Como defendemos, notações do tipo lim n →∞ an = +∞, aliadas a abordagens de ensino que supervalorizam técnicas de cálculo de limites e ideias intuitivas desse conceito, em detrimento dos aspectos formais que os sustentam, são os principais responsáveis por esses tipos de erro.
O erro tipo D2 concentra os estudantes que apresentaram argumentos sem sentido nas justificativas. A resposta de Eva (Figura 8) é exemplo desse tipo de erro.
Assim como na análise do erro tipo B2, entendemos que a redução de 60% do erro tipo D1 da Questão 1 para os 40% do erro tipo D2 é aparente, pois houve um número maior de itens deixados em branco na Questão 2. Com essa perspectiva, podemos afirmar que o índice de 40% do erro tipo D2, somado aos altos percentuais de itens deixados em branco (Quadro 3), desenha um panorama de muitas dificuldades dos participantes em construir justificativas em Matemática.
As análises dos erros tipo A2 e D2 indicam que não houve uma melhora dos participantes da pesquisa em aspectos lógico-formais relacionados à argumentação matemática e à elaboração de justificativas, o que, reiteramos, seria uma evolução esperada para estudantes que estão terminando o curso de Licenciatura em Matemática.
Nas entrevistas da segunda etapa, solicitamos aos estudantes Bia, Camilo e Débora que identificassem a hipótese e a tese dos itens da Questão 2 e todos apresentaram respostas corretas, para todos os itens. Bia disse que os professores das disciplinas Geometria e Álgebra ensinaram e solicitaram que os estudantes fizessem esse tipo de reconhecimento. É interessante observar que, mesmo sendo capazes de fazer isso com clareza, não conseguiram apresentar nenhuma demonstração correta na Questão 2. Entendemos que essa falha indica que não se trata apenas de ter conhecimento das estruturas formais, mas de saber colocá-las em funcionamento ou, como sustenta Fischbein (1994), de inter-relacionar aspectos algorítmicos, intuitivos e formais, relativos ao desenvolvimento dos conceitos e ideias em Matemática.
De maneira geral, a análise da Questão 2 e a comparação com os resultados da Questão 1 indicam que a maioria dos participantes não superou dificuldades em lidar com a definição de limite de sequências e com resultados que abordam propriedades como ser decrescente e limitada. Os percentuais de itens errados e em branco, apresentados no Quadro 3, e os índices dos erros tipo B2 e C2 corroboram essa análise.
Entendemos que uma abordagem que não valoriza a exploração de aspectos formais relacionados aos conceitos e definições e que não promove a interação dessas características formais com aspectos algorítmico-intuitivos de procedimentos e ideias seja responsável por muitas dificuldades encontradas pelos estudantes nas tarefas propostas por essa questão.
Além disso, as dificuldades dos participantes, relacionadas à elaboração de justificativas e de argumentações em Matemática, parecem ser um grande obstáculo para o desenvolvimento de processos do Pensamento Matemático Avançado, pois parte essencial da atividade matemática exige a capacidade de elaborar justificativas e contraexemplos para resultados e afirmações.
Considerações Finais
De maneira geral, as dificuldades em lidar com (1) a definição de limite de sequência e (2) a estrutura lógica de demonstrações, analisadas nas Questões 1 e 2, foram identificadas para os estudantes que participaram da pesquisa.
Na Questão 2, o erro tipo A2, com 33% de ocorrência, e o erro tipo D2, com 40% de ocorrência, são as principais evidências da dificuldade dos estudantes com a estrutura lógica de demonstrações. A resposta da estudante Débora (Figura 5) para a Questão 2(a) é um exemplo desse tipo de dificuldade, pois apresenta um caso particular para justificar a veracidade considerada por ela neste item.
Reiteramos que era esperada maior maturidade dos participantes com relação ao emprego de aspectos lógico-formais relativos à construção de provas e na argumentação matemática, ao final da disciplina Introdução à Análise Real, uma das disciplinas finais do curso de Licenciatura em Matemática. Seguindo a posição de Pinto (1998), essa realidade indica que esses futuros professores de Matemática ainda não entendem a natureza da prova matemática em sua essência.
Entendemos que todas as incompreensões, erros e limitações dos estudantes na elaboração de justificativas e argumentações em Matemática são dificultadores do desenvolvimento de processos mais sofisticados do Pensamento Matemático Avançado, como generalização e síntese, uma vez que tendem a restringir a expansão de resultados e de domínios de validade e inviabilizam a composição de conhecimentos fragmentados.
Observamos, uma vez mais, que o trabalho com demonstrações e com a lógica subjacente não está atrelado somente ao estudo de sequências numéricas, mas a todas as disciplinas matemáticas e as dificuldades apontadas em nossa análise indicam que a formação lógico-formal de estudantes de Licenciatura em Matemática deve ser mais amplamente investigada.
Nesse sentido, parece-nos muito importante que as classificações de afirmações em Verdadeiro ou Falso, acompanhadas de justificativa, propostas nas questões apresentadas neste artigo, sejam usadas em disciplinas de Matemática em geral, pois podem propiciar aos estudantes uma visão mais profunda sobre a natureza do pensamento matemático, por meio de demonstrações e da elaboração de contraexemplos. Reiteramos que questões que explorem aspectos formais dos conceitos envolvidos no estudo de sequências devem ser valorizadas nos processos de ensino e de aprendizagem, sob pena deste tema se constituir em um amontoado de técnicas, algoritmos e ideias vagas, que pouco contribuirão para a formação dos estudantes.
Entendemos que as dificuldades formais apontadas reiteram a necessidade do desenvolvimento de processos do Pensamento Matemático Avançado durante toda a formação dos estudantes. Generalização, síntese e abstração não devem ser trabalhados apenas nas disciplinas finais que, como Análise, devem coroar o uso desses processos, para a compreensão da Matemática como uma construção lógica, inter-relacionada, coerente e consequente de conceitos e ideias.