Introdução
O presente estudo se insere em um campo crescente de pesquisas que, valendo-se de ferramentas teóricas foucaultianas, pretende problematizar discursos que têm circulado na área de Educação Matemática (KNIJNIK; DUARTE, 2010; MAGNUS; CALDEIRA; DUARTE, 2016; SANTOS; SILVA, 2019; SARTOREI; DUARTE, 2015; SOUZA; SILVA, 2017). Discurso, segundo Foucault (2016), não deve ser associado a uma frase, expressão verbal ou a qualquer conjunto de signos que remetem à suposta essência de um conteúdo específico. Ou seja, o termo discurso não é apenas uma simples combinação de palavras que descrevem as coisas do mundo; eles a constituem, pois são "[...] práticas que formam sistematicamente os objetos de que falam" (FOUCAULT, 2016, p. 60).
Dentre os diferentes discursos que circulam na área, interessamo-nos em investigar aqueles que se apresentam em torno das noções de Mathematical Knowledge for Teaching (MKT), Mathematics Teacher's Specialized Knowledge (MTSK) e Mathematics for Teaching (MfT). Estes foram traduzidos, respectivamente, como Conhecimento Matemático para o Ensino (CME), Conhecimento Especializado do Professor de Matemática (CEPM) e Matemática para o Ensino (MpE). Em linhas gerais, os discursos do CME, CEPM e MpE referem-se a um conhecimento que é tido como específico para o ensino de Matemática, compreendendo que ele difere do conhecimento matemático requerido por outros profissionais, por exemplo, um matemático, um engenheiro, uma enfermeira (BALL; BASS, 2003; NYIKAHADZOYI, 2015). Desse modo, na tentativa de capturar a variabilidade desses discursos em uma única expressão, tomamos a noção de discurso da Matemática específica para ensinar.
De acordo com o nosso aporte teórico, essas práticas discursivas buscam imprimir regimes de verdade. A "verdade", segundo Foucault (1989), é produzida historicamente no interior de discursos que não são em si nem verdadeiros nem falsos, ou seja, o que há são discursos que são acolhidos e passam a funcionar como "verdadeiros". Do mesmo modo, há mecanismos e instâncias habilitadas/reconhecidas como capazes de distinguir e sancionar discursos verdadeiros ou falsos; há técnicas e procedimentos valorizados para a obtenção da verdade, como o método científico, por exemplo; e há aqueles que têm a função de dizer o que funciona como verdadeiro (FOUCAULT, 1989). Os estudos que fazem circular o discurso da Matemática específica para ensinar são associados a instituições de pesquisa. Por meio de métodos científicos, com financiamento público ou privado, buscam aperfeiçoar cada vez mais seus instrumentos de pesquisa para manterem o seu encargo de dizer o que seria a "verdade" sobre a Matemática específica para ensinar.
Não obstante, essas práticas discursivas demandam modos de ser professor(a) de Matemática ao disponibilizar condições de possibilidades para uma variabilidade de tipos de sujeito. O sujeito, segundo Foucault (2006, p. 275), "[...] é uma forma, e essa forma nem sempre é, sobretudo, idêntica a si mesma". Para Foucault (2016), um discurso disponibiliza um espaço de exterioridade para diversas posições de subjetividades. A subjetividade é "[...] a maneira pela qual o sujeito faz a experiência de si mesmo em um jogo de verdade" (FOUCAULT, 2006, p. 236), ou seja, pode ser compreendida como produto do processo de subjetivação que constitui o sujeito quando este se identifica ou é identificável com determinado discurso.
Montecino e Valero (2015), analisando os resultados de pesquisas produzidas sobre professores de Matemática e documentos oficiais, mostram como os discursos expressam características de um(a) professor(a) de Matemática "desejado(a)" que permitem identificar o objeto discursivo que chamamos de "professor(a) de Matemática". Nesta direção, diremos que os discursos que circulam em torno, por exemplo, da categoria "bom professor de Matemática", fornecem aos(às) professores(as) possibilidades de serem reconhecidos(as) por si mesmos ou pelos outros, como: um sujeito em constante atualização; um sujeito que tem domínio do conteúdo matemático; um sujeito masculino; um sujeito rigoroso; um sujeito atencioso com seus alunos, dentre tantos outros. Quando um indivíduo é reconhecido ou se reconhece em determinado discurso, ele é assujeitado a esse discurso, tornando-se um sujeito do discurso, constituído em meio a práticas que "[...] não são, entretanto, alguma coisa que o próprio indivíduo invente. São esquemas que ele encontra em sua cultura e que lhe são propostos, sugeridos, impostos por sua cultura, sua sociedade e seu grupo social" (FOUCAULT, 2006, p. 276).
Desse modo, "[...] nos constituímos como sujeitos de determinado tipo, com certas características, com certos modos de ser e de viver ao ocupar determinadas posições de sujeito que são disponibilizadas nos discursos" (RIBEIRO, 2013, p. 51). Entendemos que posição de sujeito se define pela condição que é possível de ser ocupada por um sujeito em relação a diversos discursos. Face ao exposto, desenvolvemos um ensaio teórico com o objetivo de identificar posições de sujeito disponibilizadas pelo discurso da Matemática específica para ensinar. Segundo Barbosa (2018), os ensaios teóricos se caracterizam por apresentar uma argumentação lógica, rigorosa, coerente e crítica sobre um determinado tema, de modo que os estudos mobilizados visam subsidiar a construção dessa argumentação. Assim, além dos estudos foucaultianos, recorremos a literatura sobre CME, CEPM e MpE no intuito de circunstanciar a nossa construção argumentativa. No estudo, as teorizações foucaultianas foram utilizadas como uma caixa de ferramentas, o que permitiu uma construção do nosso objeto, transformando-o e possibilitando uma nova forma de compreendê-lo.
Problematizar esse discurso no intuito de pôr sob exame como ele se engendra para produzir o sujeito-professor(a)-de-Matemática requer a compreensão de que M. Foucault abandonou a noção de "sujeito desde sempre aí" (VEIGA-NETO, 2016, p. 107) e trabalhou para mostrar de que maneiras tipos de sujeito são produzidos como efeitos de discursos. Quando nos referimos a sujeito-professor(a)-de-Matemática através de uma única expressão conectada por hífen, não estamos afirmando que esse discurso forma um sujeito uno. Queremos demarcar um sujeito em sua descontinuidade e dispersão, o seu caráter fabricado, múltiplo e incessante de sua subjetivação diante das múltiplas posições de sujeito que um indivíduo pode assumir. Mesmo considerando que as posições de sujeito não são fixas e nem unitárias, pois são instáveis, cambiantes e permanentemente modificáveis, quando um sujeito é identificado como professor(a) de Matemática é porque ele foi capturado, assujeitado, por diferentes discursos que o identificam e o fazem reconhecer-se como um(a) professor(a) de Matemática num determinado tempo e espaço.
Situando Estudos da Área
Apoiados nos estudos sobre o conhecimento profissional do professor desenvolvidos por Shulman (1987), pesquisadores da área de Educação Matemática têm dedicado esforços para investigar o conhecimento necessário para ensinar Matemática. Sobre o tema, destacam-se os estudos desenvolvidos pelo grupo liderado pela pesquisadora Deborah Ball, de quem identificamos trabalhos datados do início dos anos 2000 (BALL; BASS, 2003; STYLIANIDES; BALL, 2004). Essas pesquisas têm recorrido ao estudo de L. Shulman para desenvolver a noção de Conhecimento Matemático para o Ensino (CME) com o objetivo de construir uma teorização capaz de mapear o conhecimento matemático necessário para executar as tarefas recorrentes no ensino de Matemática (BALL; THAMES; PHELPS, 2008).
Segundo essa perspectiva, a prática docente requer um conhecimento que entrelaça aspectos do ensino e da aprendizagem com o conteúdo e sustenta que a descompactação de ideias matemáticas é uma das características distintivas desse conhecimento (BALL; BASS, 2003). Em linhas gerais, o "descompactar" é compreendido como a capacidade que o(a) professor(a) tem de detalhar, tornando explícitas as ideias e os procedimentos matemáticos.
Além do descompactar, Ball e Bass (2003) afirmam que o ensino requer que os(as) professores(as) auxiliem os(as) estudantes a conectar ideias matemáticas como, por exemplo, conectar noções algébricas com noções geométricas. Requer ainda que os(as) professores(as) antecipem como as ideias matemáticas evoluem e mudam. Ou seja, espera-se que os(as) professores(as) estejam atentos(as) para afirmações generalizantes do tipo: não é possível subtrair um número maior de um menor, ou, em uma divisão, o resultado é sempre menor, levando em consideração que afirmações como essas mudam à medida que se amplia o estudo sobre os conjuntos numéricos. Ainda segundo as autoras, é esperado que os(as) professores(as) representem as ideias matemáticas de diferentes formas e que sejam capazes de avaliar a qualidade matemática dos materiais de ensino (um livro didático, por exemplo).
Em busca de delinear o conhecimento matemático necessário para o ensino, Ball, Thames e Phelps (2008) argumentam em favor de um entendimento que evite uma assunção estritamente reducionista e utilitarista do termo "necessário". Essa concepção mais generosa do termo permitiria englobar habilidades, hábitos mentais e percepções que importam para o ensino efetivo da disciplina e, em busca de identificá-las, os autores propuseram um refinamento das categorias de Shulman (1987), conforme a Figura 1.
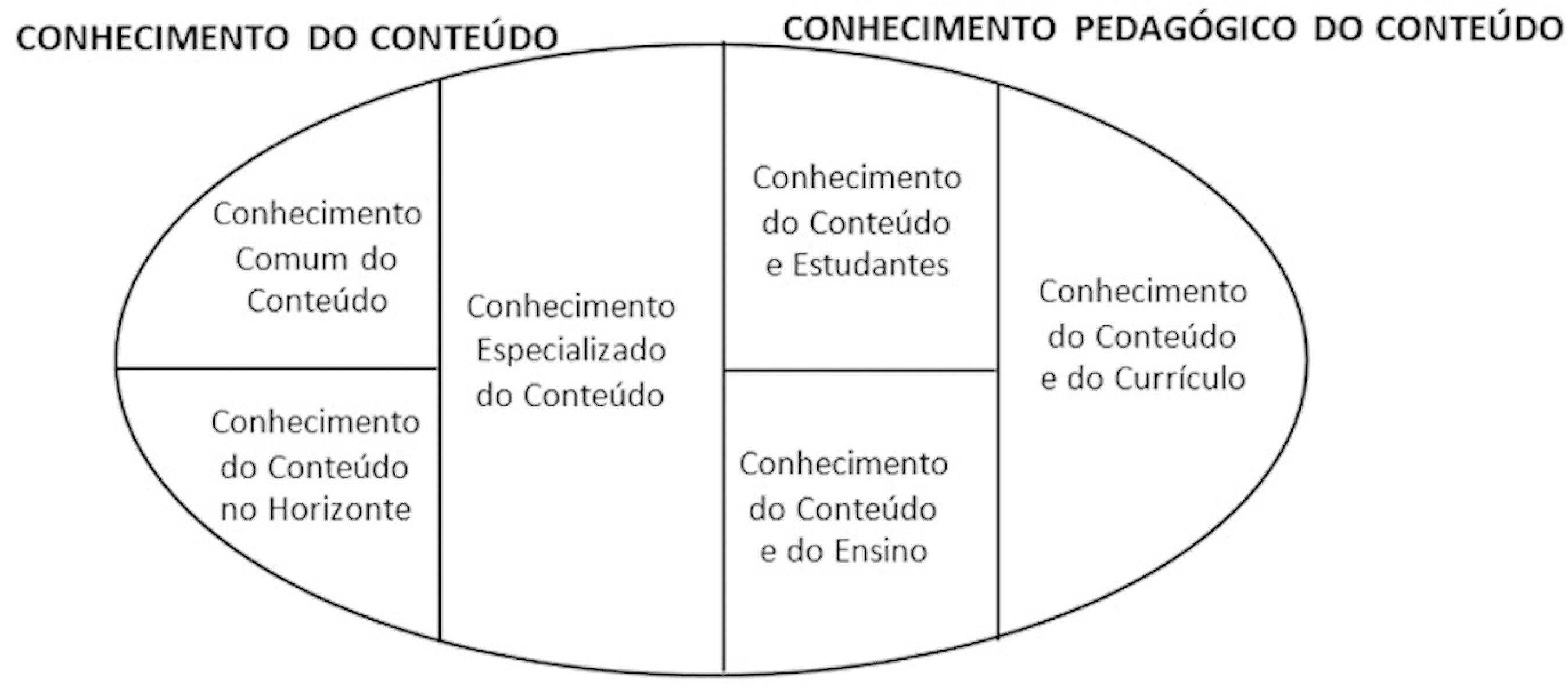
Fonte: traduzido de Ball, Thames e Phelps (2008, p. 403).
Figura 1 Domínios do Conhecimento Matemático para o Ensino (CME)
Os domínios propostos por Ball, Thames e Phelps (2008) para identificar o CME aparecem divididos em Conhecimento do Conteúdo e em Conhecimento Pedagógico do Conteúdo. O primeiro deles é subdividido em Conhecimento Comum do Conteúdo, Conhecimento Especializado do Conteúdo e Conhecimento do Conteúdo no Horizonte. O segundo subdivide-se em Conhecimento do Conteúdo e Alunos, Conhecimento do Conteúdo e Ensino, e Conhecimento do Conteúdo e do Currículo. Como a caracterização desses domínios é de fácil localização na literatura da área (LAUTENSCHLAGER; RIBEIRO, 2017; RIBEIRO, 2011), não a mencionaremos para evitar repetições desnecessárias.
A configuração desses domínios estabeleceu uma agenda de pesquisas na área de Educação Matemática em diversos países com o propósito de identificar e caracterizar tais conhecimentos. No Brasil, por exemplo, destacamos os estudos de: Ribeiro (2012) que discute o conhecimento matemático para o ensino de equações; Rangel, Giraldo e Maculan Filho (2015) sobre o conhecimento de matemática para o ensino do conceito de número racional; Ferreira, Ribeiro e Ribeiro (2017), que discutem o ensino de álgebra para os anos iniciais do Ensino Fundamental; Lautenschlager e Ribeiro (2017) que discorrem sobre o conhecimento matemático de professores para o ensino de polinômios na Educação Básica; e Pazuch, Lima e Albrecht (2018) sobre os conhecimentos relativos ao conceito de função. Entre os estudos que recorrem a esses domínios, é comum a sinalização de necessidade de maior refinamento dos mesmos, seguindo o entendimento de Ball, Thames e Phelps (2008) de que eles não significam uma classificação exaustiva do conhecimento matemático do(a) professor(a).
No intuito de contribuir com esse refinamento, o grupo de pesquisa liderado por José Carrillo propõe que o conhecimento dos(as) professores(as) é especializado, configurando a noção de Conhecimento Especializado de Professores de Matemática, eliminando a referência ao Conhecimento Comum do Conteúdo (CARRILLO et al., 2013), conforme Figura 2.
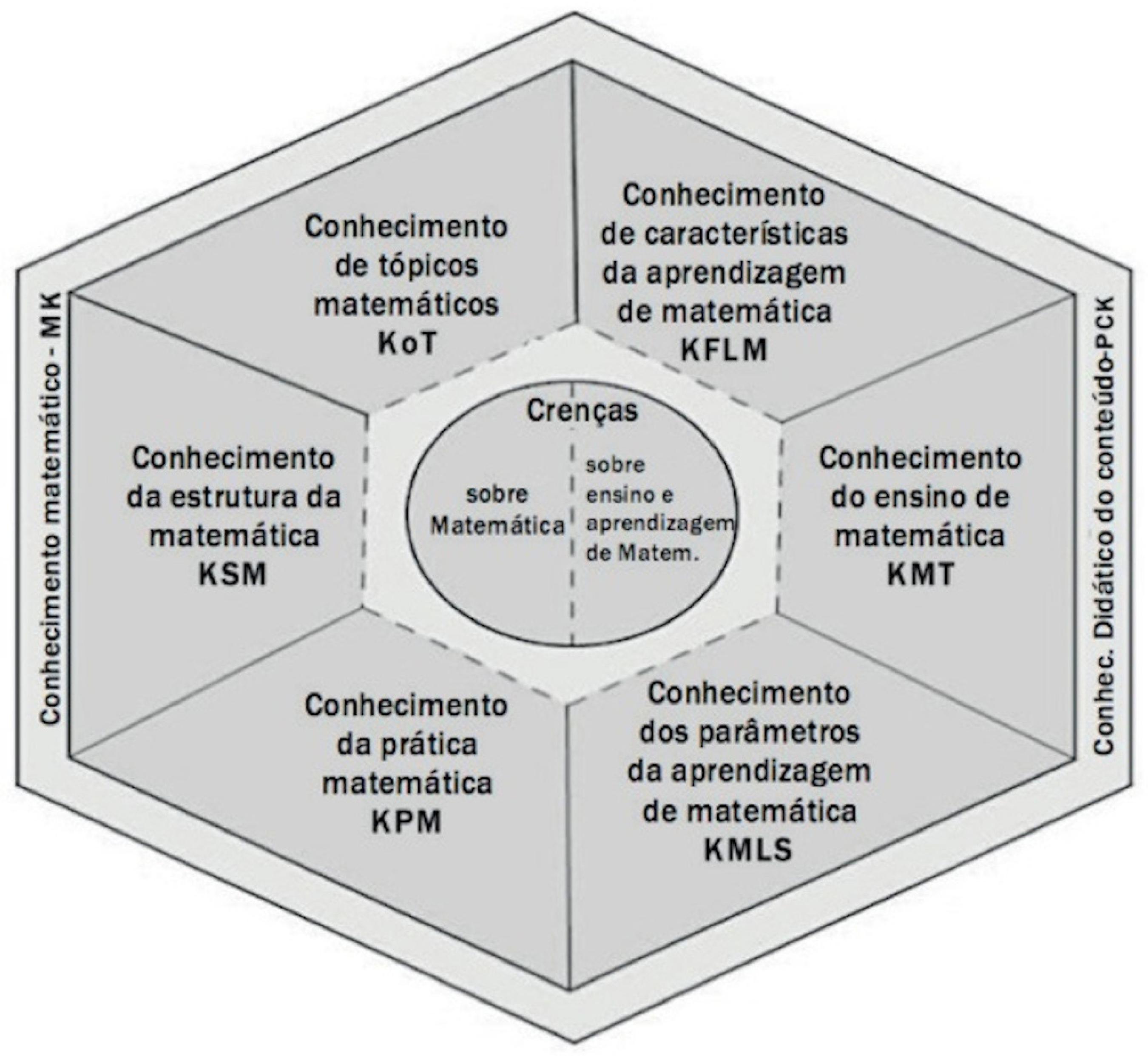
Fonte: Mello, Moriel Junior e Wielewski (2017).
Figura 2 Domínios do Conhecimento Especializado de Professores de Matemática
Como observamos, o CEPM também se organiza em domínos e subdomínios que focalizam demandas relacionadas ao ensino de Matemática em particular. O domínio Conhecimento Matemático é subdividido em: Conhecimento dos Tópicos Matemáticos; Conhecimento da Estrutura da Matemática; e Conhecimento da Prática Matemática. O domínio Conhecimento Pedagógico do Conteúdo é subdividido em: Conhecimento do Ensino de Matemática; Conhecimento das Características de Aprendizagem de Matemática; Conhecimento dos Parâmetros de Aprendizagem de Matemática. Para mais detalhes sobre esses domínios, ver os trabalhos de Carrillo et al. (2013) e Mello, Moriel Junior e Wielewski (2017).
Como um contraponto aos domínios do conhecimento matemático para o ensino, pesquisadores(as) passaram a adotar o termo Matemática para o Ensino (MpE). Argumentam que esse termo tem o intuito de apreender em uma única categoria o Conhecimento do Conteúdo e o Conhecimento Pedagógico do Conteúdo (POURNARA et al., 2015), de mostrar que, de uma perspectiva epistemológica social, os domínios Conhecimento Especializado do Conteúdo e Conhecimento Comum do Conteúdo são controversos (ADLER; HULLIET, 2008), e de evidenciar que as conceptualizações do CME são demasiadamente focadas no indivíduo, não contemplando o caráter dinâmico, emergente, tácito e em constante desenvolvimento que envolve o trabalho de ensino (DAVIS, 2010; DAVIS; RENERT, 2014).
Esses estudos procuram explicar a MpE afastando-se das discussões sobre as demandas de conhecimento do(a) professor(a) (DAVIS; SIMMT, 2006) para aproximar-se de uma análise da atividade de ensino em si (DAVIS; ADLER; PARKER, 2007). Defendem que a matemática para o ensino é tácita (DAVIS; SIMMT, 2006) e buscam explorá-la por meio de ações efetivamente desenvolvidas nas aulas de Matemática, de discussões realizadas por professores(as) em cursos de formação continuada e na análise de material didático.
Para Davis, Adler e Parker (2007), a MpE está inserida numa prática pedagógica e é constituída a partir de múltiplos objetos que se inter-relacionam, dos quais se destacam a Matemática e o ensino, por não haver separação entre eles. Desse modo, a MpE seria regulada pelas regras e normatizações da prática pedagógica na qual é desenvolvida. Neste sentido, os autores argumentam que as pesquisas que buscam investigar a MpE, necessariamente, precisam ser sensíveis ao contexto e as condições nas quais ela se desenvolve.
Barwell (2013) sugere que o conhecimento dos(as) professores(as) de matemática é organizado socialmente e estruturado discursivamente. Esta compreensão o faz considerar que o ensino de matemática in situ não seria bem captado por domínios de conhecimento definidos a priori. Nesta mesma direção, Davis e Renert (2014) defendem que a MpE exige compromissos coletivos e participativos, de modo que o conhecimento individual e o coletivo não podem ser dicotomizados; é muito vasta e volátil para ser considerada em termos de domínios; no nível individual, os entendimentos de conceitos e saberes de matemática são emergentes e, no nível dos coletivos sociais, é, em grande parte, tácito; no nível cultural, os(as) professores(as) são participantes vitais na criação da Matemática, principalmente quando selecionam e/ou dão ênfases a determinadas interpretações em detrimento de outras.
Para compreender o que está em jogo na constituição de uma MpE, Davis e Renert (2014), propuseram uma metodologia participativa através da qual os(as) professores(as) questionam e elaboram a matemática com vistas ao ensino, conforme a Figura 3, denominada de Concept Study, o qual traduzimos como Estudo do Conceito. Os autores organizaram o Estudo do Conceito em torno de quatro ênfases para a discussão coletiva de conceitos matemáticos. São elas: realizações, panoramas, vinculações e combinações conceituais. Assim, como os domínios propostos por Ball, Thames e Phelps (2008) e Carrillo et al. (2013), essas ênfases vêm sendo divulgadas em investigações da área (RANGEL; GIRALDO; MACULAN FILHO, 2015; SANTOS; BARBOSA, 2016) e não são tratadas como etapas ou níveis que seguem um processo linear. São consideradas imprevisíveis, decorrentes de interesses comuns, de conhecimentos divergentes e encontros acidentais.
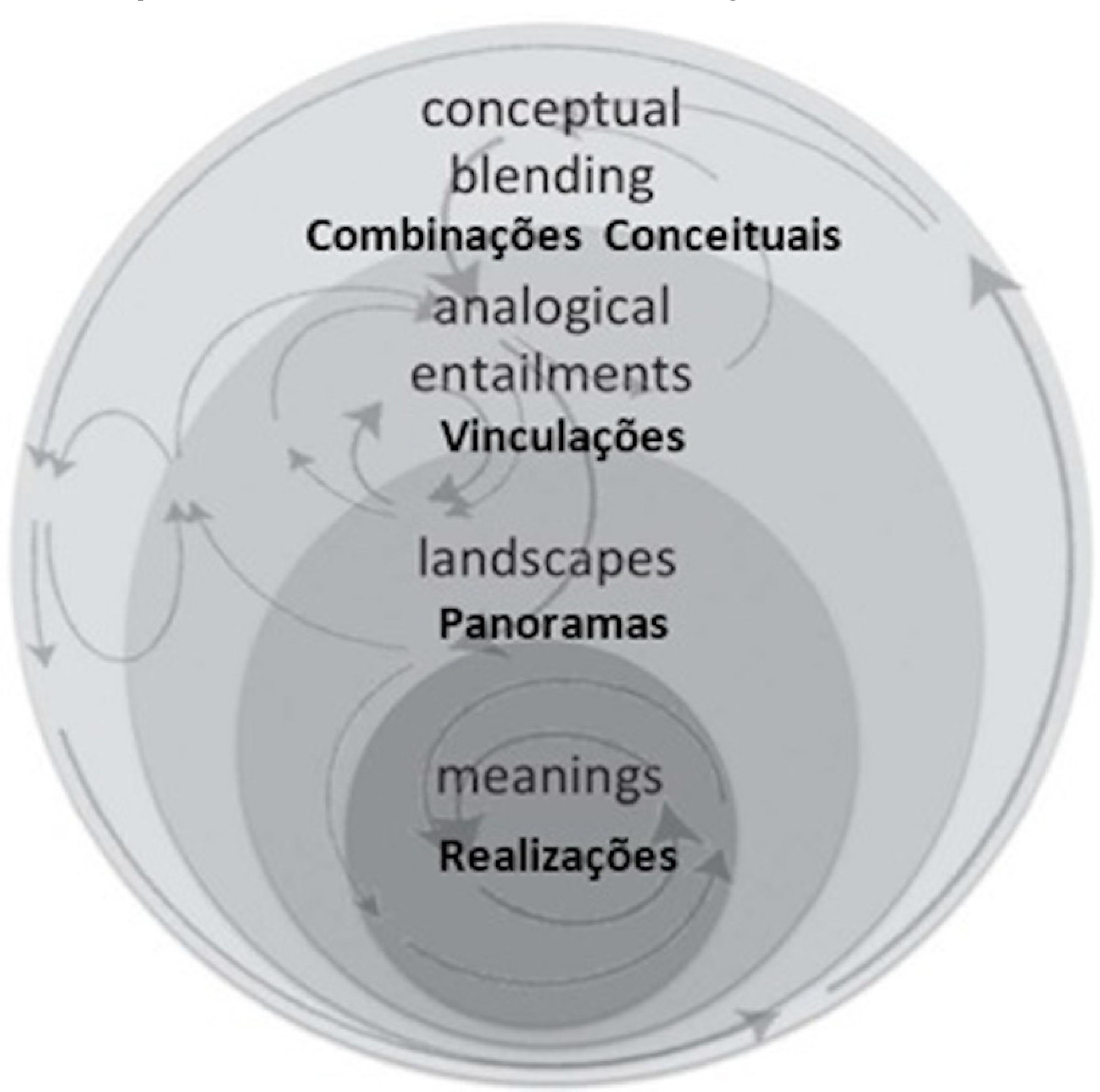
Fonte: adaptado de Davis e Renert (2014, p. 57).
Figura 3 Uma metáfora visual para descrever as relações entre ênfases de estudo de conceito
Segundo Davis e Renert (2014, p. 35, tradução nossa), a Matemática para o Ensino (MpE) "[...] é melhor interpretada como uma disposição aberta em relação à matemática em ambientes educacionais, do que como uma coleção específica de habilidades ou competências". Até aqui, tivemos o propósito de situar os estudos sobre o conhecimento matemático para ensinar no intuito de perguntar e examinar como ele acontece e se engendra nos discursos que circulam nas pesquisas da área.
Identificação de Posições de Sujeito
Investigar de que modo vem se dando a constituição desse sujeito-professor(a)-de-Matemática, uma "analítica do sujeito" nas palavras de Veiga-Neto (2016), requer examinar as práticas discursivas que o constituem. Assim, nos propomos a problematizar discursos que circulam nas investigações da área e que configuram as noções de CME, CEPM e MpE, examinando-os em sua produtividade.
Com o objetivo de identificar posições de sujeito disponibilizadas pelo discurso da Matemática específica para ensinar, optamos por separá-los em dois grupos: cognitivo-representacional e sociodiscursivo1. O primeiro grupo reúne discursos que tomam o conhecimento matemático como parte de processos cognitivos, portanto, é individual e representam as ações de professores(as). No segundo grupo estão os discursos que consideram o conhecimento matemático como tácito e emergente de uma prática social. Essa estratégia analítica visa demarcar que esses discursos partem de filiações epistemológicas distintas, independentemente das terminologias adotadas pelos seus autores, e não descarta que eles podem se influenciar mutuamente. Além disso, para cada posição de sujeito identificada buscamos exemplificá-las em termos das supostas capacidades e habilidades que o sujeito precisa ter para assumi-la, tornando-se capaz de ensinar adequadamente a Matemática.
Posições de sujeito disponibilizadas por discursos cognitivo-representacionais
Após mais de uma década de pesquisas sobre o CME, a revisão de literatura realizada por Hoover et al. (2016) apontou que os estudos liderados por Deborah Ball estabeleceram uma agenda de pesquisas na área, mas, ao mesmo tempo, a ausência de uma perspectiva teórica bem definida sobre o tema possibilitou refinamentos como o CEPM, por exemplo. Tomando como base os estudos seminais, Ball e Bass (2003) e Ball, Thames e Phelps (2008), e o trabalho de Carrillo et al. (2013), identificamos posições de sujeito disponibilizadas pelos discursos cognitivo-representacionais.
Com base no exposto em Ball e Bass (2003), a primeira posição de sujeito identificada é o sujeito descompactador do conteúdo. Essa posição associa-se a um(a) professor(a) que tem a capacidade de detalhar, desempacotar, todos os procedimentos que geralmente são omitidos, tornando-os acessíveis aos(as) estudantes. Por exemplo, na resolução de uma operação de multiplicação, é comum que qualquer pessoa alfabetizada matematicamente saiba resolvê-la pelo algoritmo tradicional (Figura 4A). Entretanto espera-se que o(a) professor(a), além do algoritmo tradicional, saiba explicar a propriedade distributiva que é “compactada” pelo algoritmo tradicional e possa decompor os números que compõem os fatores para mostrar aos(as) estudantes o que foi "compactado" pelo algoritmo tradicional (Figura 4B).
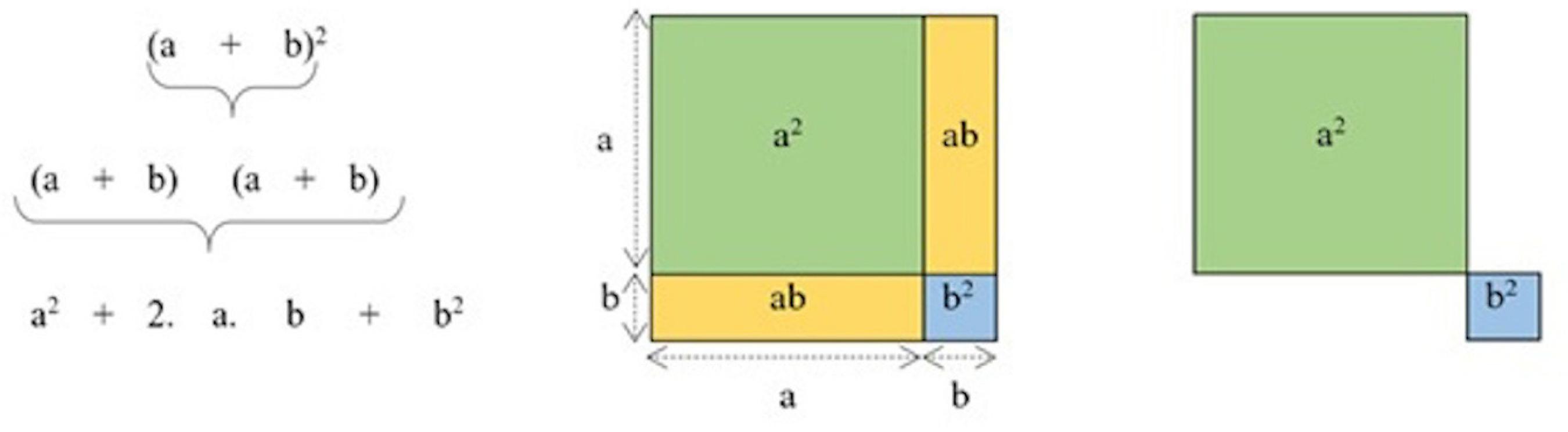
Dos estudos de Ball e Bass (2003) e Carrillo et al. (2013), identificamos a posição de sujeito conectador de diferentes áreas da Matemática tal que o(a) professor(a) seria capaz de articular diferentes campos da Matemática de forma compreensível aos(as) estudantes. Para exemplificá-la tomamos como referência o conteúdo Produtos Notáveis, geralmente apresentado no 8o ano do Ensino Fundamental, quando o(a) professor(a) ao tratar do Quadrado da soma de dois termos (Figura 5A) o faz associando à representação geométrica (Figura 5B) o que lhe permite diferenciar (a + b)2 de a2 + b2 (Figura 5C), como segue:
Vimos em Ball e Bass (2003) que aos(as) professores(as) também é disponibilizada a posição de sujeito antecipador de dificuldades, ou seja, que demonstra conhecer como os estudantes se relacionam com os conteúdos identificando que etapas de um procedimento matemático é mais comum a incidência de erros, seja de ordem conceitual ou mesmo procedimental. Isso pode ser percebido, por exemplo, quando um(a) professor(a) apresenta as propriedades da potenciação e antecipa aos(as) estudantes que (a+b)2 ≠ a2+b2. Esta diferença pode ser ilustrada algebricamente pela Figura 5B e geometricamente pela Figura 5C. Nesta mesma direção, é disponibilizada a posição de sujeito que escolhe atividades adequadas: um(a) professor(a) que monitora a aprendizagem dos estudantes ao escolher adequadamente questões sobre o conteúdo estudado, conforme ilustra a Figura 6.
Como mostram Ball e Bass (2003), para saber se os estudantes sabem ordenar corretamente números decimais2, o(a) professor(a) deveria escolher questões que exigem a comparação desses números verificando a sua parte decimal. Assim, entre as opções da atividade apresentada na Figura 6, o(a) professor(a) deveria saber que a melhor delas é o item (c), pois exige atenção às casas decimais que, se ignoradas, podem levar a uma ordenação incorreta dos números. O mesmo não ocorre nos itens (a) e (b), pois caso o estudante ignore o ponto ou, no nosso caso, a vírgula, ainda assim os ordenariam corretamente.
Identificamos ainda em Ball e Bass (2003) a posição de sujeito crítico dos materiais didáticos. Essa posição informa que os(as) professores(as) deveriam ser capazes de avaliar criticamente os materiais didáticos que lhes são disponibilizados, para que possam escolher o que melhor se adapta a sua realidade. Citamos como exemplo a escolha dos livros didáticos a partir do guia disponibilizado pelo Programa Nacional do Livro Didático (PNLD), ou seja, espera-se que os(as) professores(as) sejam capazes de avaliar os livros disponíveis e identificar o de melhor qualidade para ser utilizado com os(as) estudantes.
Ball e Bass (2013) destacam também que os(as) professores(as) devem ser capazes de compreender métodos não-convencionais utilizados pelos estudantes ao resolver questões para informar se eles fazem ou não sentido matematicamente, disponibilizando a posição de sujeito que compreende resoluções não-convencionais. Assim, defendem que ter habilidades para analisar e avaliar as características matemáticas e a validade de métodos alternativos são importantes para um(a) professor(a) de Matemática. Para exemplificar essa situação, os autores apresentam duas formas de resolução de uma operação de subtração (Figuras 7A, 7B e 7C) que desafiam aquilo que corriqueiramente é realizado no algoritmo tradicional.

Fontes: Figuras 7A e 7B: Ball e Bass (2013, p. 10); Figura 7C: Ball, Thames e Phelps (2008, p. 396).
Figura 7C Resolução não-convencional da subtração
Ball e Bass (2003) e Ball, Thames e Phelps (2008) argumentam que diante de um erro cometido pelo estudante, os(as) professores(as) precisam mais do que identificar uma resposta incorreta: requer a capacidade de rapidamente dimensionar a fonte de um erro matemático de maneira eficiente e fluente. Ainda segundo os autores, a análise de erros, muitas vezes de provas fracassadas, é uma prática comum entre os matemáticos, mas difere daquela requerida aos(as) professores(as), porque esta se concentra nos erros produzidos por estudantes, enquanto aquela decorre de seu próprio trabalho.
Neste contexto, vê-se também disponibilizada a posição de sujeito eficiente. Ou seja, o(a) professor(a) deve ser ágil e rápido em identificar as demandas matemáticas de seus estudantes. Para Ball, Thames e Phelps (2008, p. 397, tradução nossa), "[...] este é um trabalho que os professores devem fazer rapidamente, muitas vezes na hora, porque em uma sala de aula, os alunos não podem esperar enquanto um professor se intriga sobre a matemática em si", os(as) professores(as) precisam processar tais análises com fluência e rapidez.
A posição de sujeito articulador didático também é disponibilizada aos(às) professores(as). Um(a) professor(a) que mobiliza diferentes estratégias de ensino com o objetivo de superar as dificuldades dos(as) estudantes ou de explorar certos aspectos de um conteúdo demonstrando ter conhecimento do conteúdo e das possíveis dificuldades dos(as) estudantes. Podemos ilustrar essa situação quando um(a) professor(a), no contexto da Geometria Euclidiana, necessita provar que a soma das medidas dos ângulos internos de um triângulo é igual a 180o. Neste caso, pode recorrer à demonstração (Figura 8A), a utilização recursos manipuláveis (Figura 8B), ao uso de um software (Figura 8C), dentre outros.
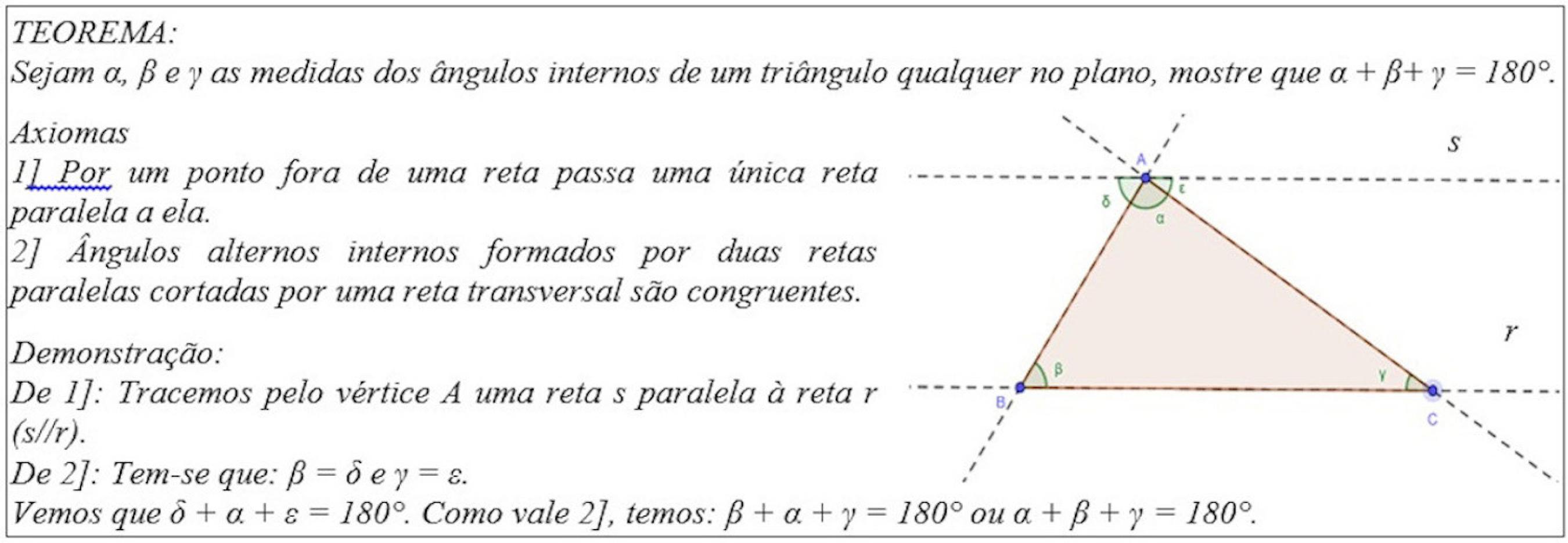
Fonte: elaborado pelos autores.
Figura 8A Uma possível demonstração para o Postulado das Paralelas de Euclides

Fonte: elaborado pelos autores.
Figura 8B Uso de material manipulável para constatar o Postulado das Paralelas
Fonte: elaborado pelos autores.
Figura 8C Animações no software GeoGebra para mostrar o Postulado das Paralelas
Quando Ball e Bass (2003), Ball, Thames e Phelps (2008) e Carrillo et al. (2013) argumentam sobre o conhecimento do conteúdo e sua relação com o ensino, disponibilizam a posição de sujeito regente, ou seja, aquele que relaciona o conteúdo com a prática de ensino. Para os autores, durante uma discussão em sala de aula, o(a) professor(a) deve decidir quando fazer uma pausa para obter mais esclarecimentos, quando usar a observação de um(a) estudante para fazer um questionamento e quando fazer uma nova pergunta ou colocar uma nova tarefa para promover o aprendizado dos(as) estudantes como se regesse uma orquestra.
Ball, Thames e Phelps (2008) e Carrillo et al. (2013), ao tratarem da importância do(a) professor(a) conhecer como o currículo organiza os conteúdos, disponibilizam a posição de sujeito conhecedor dos guias curriculares. Ou seja, aquele(a) que conhece como os conteúdos aparecem nos guias curriculares e, portanto, são capazes de articulá-los, antecipando aos(as) estudantes como as ideias matemáticas evoluem e mudam. Citamos como exemplo uma situação na qual um(a) professor(a) discute a solução da equação x2+4x+5=0, em uma turma do 9o ano do Ensino Fundamental, que pelos guias curriculares opera com o Conjunto dos Números Reais, e alerta os estudantes sobre a existência do Conjunto dos Números Complexos, que será discutido no Ensino Médio e no qual a solução da equação existe.
Além das posições elencadas até aqui, destacamos os estudos de Stylianides e Ball (2008), Steele e Rogers (2012) e Carrillo et al. (2013) por tratar de um método próprio da área de Matemática - demonstração - dos quais emerge a posição de sujeito que sabe provar. Ou seja, um(a) professor(a) que conhece diferentes estratégias de prova e sabe avaliar que tarefas envolvendo provas podem ser propostas ou não aos(as) estudantes e que tipo de prova os(as) estudantes serão capazes de realizar. O Quadro 1 mostra a sistematização elaborada por Steele e Rogers (2012) sobre o Conhecimento Matemático para o Ensino de Provas (CME-P). Segundo os autores, essa sistematização não representa o corpo completo do CME-P, mas constitui ponto de partida para a sua identificação.
Quadro 1 Sistematização do conhecimento matemático para o ensino de provas
| Component of proof knowledge | Criteria for evaluating component |
|---|---|
| Defining proof | Proof as a mathematical argument |
| Proof as based on mathematical facts | |
| Proof as valid for a general class | |
| Proof as stablishing truth | |
| Identity proofs and non-proofs | Distinguishing proofs from non-proofs |
| Link features of an argument to aspects of the definition of proof | |
| Recognize proof across representations | |
| Create mathematical proofs | Be able to write proofs in a variety of forms |
| Understanding the roles of proof in mathematics | Proof as verifying truth os a known fact |
| Proof as explaining why | |
| Proof as communicating mathematical ideas | |
| Proof as creating new mathematical knowledge | |
| Proof as systematizing the domain |
Fonte: Steele e Rogers (2012, p. 161).
Além do destaque à especificidade do CME-P, chama-nos a atenção a revisão de literatura realizada por Hoover et al. (2016). Nela, os autores destacam que a área tem começado a despertar para a necessidade de abordar a persistente desigualdade na aprendizagem da Matemática, tanto produzidas como reproduzidas na escola, disponibilizando a posição de sujeito minimizador desigualdades. Ou seja, os(as) professores(as) devem permitir que grupos historicamente marginalizados acessem o conhecimento matemático, além de reconhecer que existem diferentes Matemáticas em circulação dentro e fora da sala de aula.
Nesta categoria, identificamos posições de sujeito disponibilizadas por discursos cognitivo-representacionais da Matemática específica para ensinar. Esses discursos fornecem modos de ser professor(a) de Matemática que se engendram para constituir um sujeito capaz de: descompactar, conectar, antecipar, articular, compreender e provar ideias matemáticas de forma associada às demandas específicas do ensino. Por isso, é um sujeito: que escolhe atividades adequadas, crítico de materiais didáticos e curriculares, eficiente, regente das tarefas vinculadas ao ensino e minimizador de desigualdades.
Posições de sujeito disponibilizadas por discursos sociodiscursivos
Como vimos, há discursos da Matemática específica para ensinar que consideram que este conhecimento é de caráter dinâmico, tácito, emergente e dependente do contexto. Argumentam que o(a) professor(a) é indissociável dos contextos sociais dos quais participa e, portanto, precisa ser sensível a esse contexto. Face ao exposto, inferimos que qualquer posição de sujeito a ser disponibilizada por discursos sociodiscursivos está enviesada pela dimensão contextual como apontam os estudos nos quais circulam esses discursos.
Nesta direção, Davis, Adler e Parker (2007) afirmam que a MpE é regulada/controlada por princípios da prática pedagógica na qual é elaborada. Neste sentido, esse discurso disponibiliza a posição de sujeito regulado, uma vez que estes princípios regulam, por exemplo, o sequenciamento dos conteúdos, o tempo destinado à aprendizagem dos mesmos pelos estudantes, a relação entre diferentes disciplinas, muitas vezes influenciados por fatores externos, a exemplo das avaliações padronizadas, por exemplo.
Admitindo que a MpE se dá em contextos controlados, Davis e Renert (2014) destacam que ela pode ser tanto mais vasta, evolutiva e distribuída, quanto mais flexíveis forem as relações entre a Matemática e as questões de ordem social, cultural, política, econômica, etc. Os autores citam como exemplo o fato de novas tecnologias, como as calculadoras gráficas, estarem substituindo as antigas (por exemplo, o lápis e papel), permitindo que os(as) estudantes resolvam problemas mais sofisticados e realistas (DAVIS; RENERT, 2014).
Os autores acreditam que "[...] uma questão crítica (se não a principal) aqui é a falta de capacidade dos professores para lidar com o novo conteúdo matemático, e mesmo com o conteúdo atual, de maneira convincente" (DAVIS; RENERT, 2014, p. 13, tradução nossa), disponibilizando assim a posição de sujeito flexível. Um sujeito flexível mostra uma atitude crítica em relação à Matemática, sintonizando-a com a rápida transformação da sociedade; é atento às competências matemáticas requeridas atualmente.
Considerando que a MpE é tácita (DAVIS; SMMIT, 2006) e que se explica por meio das ações efetivamente desenvolvidas nas aulas (BARWELL, 2013), espera-se que um(a) professor(a) saiba lidar com o imprevisível diante de questionamentos realizados por estudantes, conseguindo explorar a situação de modo a criar novas formas de comunicar um conceito matemático em estudo, disponibilizando a posição de sujeito explorador de oportunidades. No modelo proposto por Coutinho e Barbosa (2016), ao abordar o conceito de Combinação Simples, um(a) professor(a) deveria ser capaz de recorrer a diferentes realizações a depender dos questionamentos dos estudantes, tais como: "[...] diagramas de árvores, definição formal, listagem dos agrupamentos, fórmula, ordenação irrelevante dos elementos, contagem dos agrupamentos usando modelos concretos e comparação com arranjo" (COUTINHO; BARBOSA, 2016, p. 793).
O estudo de Davis e Renert (2014), bem como aqueles que seguiram o modelo analítico do Estudo do Conceito por eles elaborado, têm disponibilizado posições de sujeito em torno da natureza complexa do conhecimento matemático para ensinar. Davis e Renert (2014) exploram o conceito de substructing na intenção de discorrer sobre o que significa uma compreensão profunda de um conceito. Segundo os autores, essa compreensão requer mais do que separar um conceito em partes, diferindo da ideia de descompactar, pois envolveria a análise de como essas partes se mantêm ou não unidas a depender do contexto sugerindo uma (re)formulação do conceito. Assim, à ideia de substructing disponibiliza-se a posição de sujeito reformulador de conceitos. Um(a) professor(a) capaz de desenvolver uma compreensão profunda sobre um conceito a ponto de poder reformulá-lo, reconstruí-lo, transformá-lo de maneira criativa e não apenas descritiva/interpretativa como no processo de descompactar.
Podemos ilustrar essa posição com a situação explorada por Davis e Renert (2014) diante do questionamento de um professor sobre a primalidade do número 1. A situação mostra que diferentes metáforas e interpretações sobre a multiplicação podem levar a conclusão indesejável de que 1 é primo (Quadro 2), mas também revela que, antes do século XIX, a maioria dos matemáticos considerava 1 primo, o que faz os(as) professores(as) ponderarem sobre a necessidade de os(as) estudantes também se envolverem em estudos desse tipo, já que poderiam verificar como a Matemática se desenvolve.
Quadro 2 Resultado parcial do estudo sobre a primalidade do número 1
| Ifmultiplicationis ... | ... then afactor is ... | ... thena productis ... | ... then aprime numberis ... | ... then a composite numberis ... | Is 1 prime? |
|---|---|---|---|---|---|
| Doing a Sequence of Folds | an n- fold | the count of regions bounded by creases from folding | a product that can only be reached by folding directly | a product that requires a combination of folds | No. Since no folds are involved in making a product of 1, it is neither prime nor composite |
| Making a Rectangular Array | a dimension | the count of objects / cells in the array | a product that will always have a dimension of 1, no matter how you arrange it | a product that can be arranged in an array in which neither dimensions is 1 | Yes. A product of 1 must have a dimension trat is 1. |
Fonte: Davis e Renert (2014, p. 37).
Na perspectiva de Davis e Renert (2014), a MpE é resultado de desdobramentos de entendimentos coletivos sobre determinados conceitos matemáticos decorrentes da participação do(a) professor(a) em contextos comunicativos, tais como: cursos de formação inicial ou continuada, interação com materiais curriculares, dentre outros. Assim, se disponibiliza a posição de sujeito participativo, ou seja, aquele que participa de contexto nos quais se discute formas de comunicar um conceito sempre disponível para compartilhar com outros professores o seu modo de comunicar conceitos matemáticos. Um(a) professor(a) comprometido(a) com o grupo do qual participa, que busca variados recursos para aprimorar o modo como comunica conceitos matemáticos, é comunicativo(a), proativo(a).
A partir do modelo analítico proposto por Davis e Renert (2014) identificamos a posição de sujeito de repertório evolutivo-coletivo. Um(a) professor(a) que não existe em separado, como se através dele(a) fosse possível representar todo o conhecimento matemático que está distribuído entre os(as) professores(as), pois participa de coletivos sociais nos quais as realizações coletivas se desdobram em realizações individuais, sem dicotomizá-las. Por exemplo, para comunicar o conceito de Função o grupo de professores(as) investigado por Santos e Barbosa (2016) recorre a diferentes realizações, que não se referem ao repertório de um(a) único(a) professor(a), mas do coletivo de professores(as), conforme a Figura 9.
Fonte: Santos e Barbosa (2016, p. 163).
Figura 9 Representação de panoramas sobre as realizações do conceito de Função
Segundo Santos e Barbosa (2016), a disposição separada dos panoramas visa demarcar que eles têm identidade e fronteiras específicas, mas que não há entre eles hierarquia e, portanto, recomenda-se que haja ligação entre eles de modo a promover uma variabilidade de realizações do conceito em estudo. O repertório não é fixo, pois comunica um determinado conceito de diferentes formas que variam de acordo com os coletivos sociais dos quais o(a) professor(a) participa. O que existe é uma compreensão coletiva da Matemática, na qual cada professor(a) é um sujeito com predisposição para evolução de seus entendimentos pessoais.
Nesta categoria, identificamos posições de sujeito disponibilizadas por discursos sociodiscursivos da Matemática específica para ensinar. Esses discursos fornecem modos de ser sujeito-professor(a)-de-Matemática que se engendram para constituir um sujeito regulado, flexível, explorador de oportunidades e reformulador de conceitos matemáticos de acordo com o contexto do qual participa. Um sujeito que se constitui coletivamente, portanto, é complexo, participativo e engajado e sua prática resulta de um repertório evolutivo uma vez que é coletivo e instável.
Considerações Finais
Com o objetivo de identificar posições de sujeito disponibilizadas pelo discurso da Matemática específica para ensinar, nossa problematização de inspiração foucaultiana incidiu sobre estudos do Conhecimento Matemático para o Ensino, do Conhecimento Especializado do Professor de Matemática e da Matemática para o Ensino. Ao incidir o nosso olhar sobre os discursos que circulam nas pesquisas da área, optamos por analisá-los separando-os em dois grupos: os discursos cognitivo-representacionais e os discursos sociodiscursivos. Sobre a nomenclatura adotada para estes últimos, ponderamos que, em uma perspectiva foucaultiana, ambos os grupos são de ordem discursiva e que o uso da palavra "discursivo" se deu para registrar que os adeptos desses discursos admitem que a Matemática a ser ensinada emerge das interações discursivas que ocorrem em uma prática social.
No estudo identificamos 12 (doze) posições de sujeito disponibilizadas por discursos cognitivo-representacionais. Tais discursos disponibilizam modos de ser professor(a) de Matemática que se engendram para constituir um sujeito capaz de: descompactar, conectar, antecipar, articular, compreender e provar ideias matemáticas de modo a torná-las mais acessíveis aos estudantes. Todas essas "capacidades" atenderiam demandas específicas relacionadas ao ensino de uma Matemática que pode vir a minimizar desigualdades sociais, especialmente, por dar oportunidade a grupos historicamente excluídos. Por isso, é um sujeito que escolhe atividades adequadas, é crítico de materiais didáticos e curriculares, regendo com eficiência as tarefas vinculadas ao ensino.
Em relação aos discursos sociodiscursivos, foram identificadas 6 (seis) posições possíveis que se engendram para constituir um sujeito controlado pelas regras do contexto em que se insere, flexível, explorador de oportunidades e capaz de (re)formular conceitos matemáticos. Um sujeito complexo, que se constitui coletivamente. Logo, espera-se que seja participativo e engajado em situações coletivas nas quais possa discutir e, consequentemente, aumentar/reconfigurar o seu repertório conceitual. Portanto, a sua prática de ensino resultaria de um repertório evolutivo, uma vez que é coletivo e instável.
Cada uma dessas posições identificadas define a condição que é demandada, possível de ser ocupada pelo sujeito-professor(a)-de-Matemática, pelos discursos cognitivo-representacionais e sociodiscursivos. Os discursos cognitivo-representacionais disponibilizam posições que demandam tornar a matemática acessível aos estudantes e que visam diminuir a incidência de erros. Os discursos sociodiscursivos, disponibilizam posições que relacionam a prática do(a) professor(a) de Matemática a fatores externos, e que se entrelaça com posições demandadas pelo discurso cognitivo-representacional, a exemplo do sujeito minimizador de desigualdades.
Decorre da nossa opção teórica que discursos são apreensíveis, porém os seus efeitos não são esgotáveis, uma vez que a produção discursiva não acaba. Desse modo, não tivemos a pretensão de esgotar todas as posições de sujeito disponibilizadas pelo discurso da Matemática específica para ensinar, haja vista que constantemente tantas outras posições estão sendo disponibilizadas. Entretanto, consideramos que as posições aqui identificadas nos permitem mostrar como vem se dando a produção desse sujeito-professor(a)-de-Matemática em meio aos discursos que circulam na área de Educação Matemática.
Como vimos, as posições de sujeito identificadas fazem surgir semelhanças e diferenças entre discursos cognitivo-representacionais e sociodiscursivos. Olhar esses discursos em torno de suas dispersões nos permite inferir que discursos cognitivo-representacionais demandam um sujeito-professor(a)-de-Matemática que se nutre da teoria e aperfeiçoa a sua prática de maneira não dicotômica, com base em uma epistemologia da prática. Outrossim, os discursos sociodiscursivos demandam um sujeito-professor(a)-de-Matemática que se institui peça por peça cotidianamente, não sendo possível demarcar situações práticas que não fossem também teóricas.
Por fim, o estudo mostrou o quanto se demanda de um(a) professor(a) de Matemática para que ele(a) seja considerado(a) apto(a) a ensinar, o quanto precisa saber para reconhecer-se e ser reconhecido(a) como um(a) bom(boa) professor(a) de Matemática, o quanto que a questão da docência, em especial à docência em Matemática, não é uma questão trivial.