Introdução
A formação de professores em modelagem matemática tem sido temática recorrente nas pesquisas da área de Educação Matemática nas últimas décadas, particularmente, o ensino e a aprendizagem desta área do conhecimento (BLUM, 2015; FERRI, 2018; SILVA; OLIVEIRA, 2018). Os resultados das investigações, por um lado, indicam que a modelagem matemática já consta nas estruturas curriculares de diferentes cursos e de diferentes níveis de escolaridade (FERRI, 2018). Por outro lado, os desafios relativos à introdução da modalidade na sala de aula ainda devem ser mais discutidos nos cursos de formação de professores (MALHEIROS; FORNER; SOUZA, 2020; MAASS; ENGELN, 2018).
Perante esses desafios, Blum (2015) e Ferri (2018), entre outros, têm abordado de forma explícita a questão: a modelagem matemática pode ser ensinada e aprendida? Embora a questão possa parecer retórica, as discussões a seu respeito estão em constante movimento.
No presente artigo, inserido no movimento inerente ao enfrentamento da necessidade de associar uma discussão teórica às práticas de modelagem matemática na sala de aula, e também em concordância com a resposta afirmativa para a questão apresentada, investigamos o processo comunicacional que se estabelece em um contexto em que o foco é ensinar e aprender o fazer modelagem matemática. A pesquisa empírica é realizada em uma disciplina denominada Modelagem Matemática na Perspectiva da Educação Matemática, em um curso de formação inicial de professores de Matemática.
Nossa interpretação da comunicação na sala de aula com modelagem matemática se dá à luz de pressupostos da semiótica peirceana. Charles Sanders Peirce (1839-1914) foi um filósofo e matemático americano que, segundo Santaella (2008), dedicou-se à configuração de uma doutrina capaz de compreender as estruturas do conhecimento por meio de suas deliberações sobre signos, caracterizando a semiótica como ciência dos signos.
O pensamento de Peirce tem merecido atenção, nas últimas décadas, no âmbito da Educação Matemática (HOFFMANN, 2007; KADUNZ, 2016; PRESMEG, 2006; PRESMEG et al., 2016; SÁENZ-LUDLOW; SILVA; ALMEIDA 2015), e um aspecto relevante, neste contexto, refere-se à argumentação de Sáenz-Ludlow e Kadunz (2016) sobre o uso do signo e sua intermediação no processo de comunicação. Neste sentido, o objeto da semiótica não é precisamente o próprio signo, mas o seu uso, ou o comportamento semiótico associado a processos de comunicação.
Neste trabalho, levamos em consideração a natureza triádica do signo estabelecida por Peirce, e o papel dos signos interpretantes produzidos e usados na comunicação entre professor e alunos, no decorrer de alguns episódios das aulas na disciplina Modelagem Matemática na Perspectiva da Educação Matemática, em um curso de Licenciatura em Matemática.
Modelagem matemática
A modelagem matemática diz respeito à investigação, por meio da Matemática, de uma situação-problema cuja origem, de modo geral, não é a própria matemática. Durante o desenvolvimento de uma atividade de modelagem associam-se etapas e procedimentos, algumas vezes, expressos por meio de esquemas reconhecidos como ciclos de modelagem matemática (ALMEIDA, 2020). A imagem apresentada no quadro 2, relativa ao Episódio 2, refere-se a um ciclo de modelagem apresentado em Bassanezi (2002). Nestes esquemas (ou ciclos) identificam-se o que este autor chama de etapas da modelagem, e compreendem procedimentos tais como, a identificação do problema a ser resolvido, a coleta de dados, a seleção de variáveis, a elaboração de hipóteses, a simplificação, a obtenção de um modelo matemático, e sua interpretação - o que implica na validação do modelo -, identificando a sua pertinência para a obtenção de uma solução para o problema. O modelo matemático, neste contexto, é um sistema conceitual, descritivo ou explicativo, expresso por meio de uma linguagem ou de uma estrutura matemática, não se restringindo a expressões algébricas, podendo ser um gráfico, uma tabela, um texto, uma imagem (ALMEIDA; SILVA; VERTUAN, 2012).
A introdução de atividades de modelagem matemática nas salas de aula pode assumir diferentes configurações, dependendo do conhecimento que estudantes e professores possuem, e dos objetivos com que as realizam. Neste sentido, no desenvolvimento de atividades de modelagem, uma etapa pode receber mais ênfase do que outra, de acordo com as finalidades com que são introduzidas na sala de aula (ALMEIDA, 2018).
Levando em consideração as finalidades da introdução de atividades de modelagem matemática na sala de aula, Galbraith (2012) aponta que há, essencialmente, dois modos de compreendê-la: modelagem como conteúdo, e modelagem como veículo. No primeiro modo, a finalidade é desenvolver habilidades de construir e utilizar modelos matemáticos, e, neste caso, as etapas são traduzidas em termos de competências a serem desenvolvidas pelos alunos no ato de fazer. A modelagem como veículo, por sua vez, caracteriza-se pela finalidade de construir modelos para aprender matemática, e, neste caso, a ênfase está nas potencialidades das atividades para aprender matemática. Ainda, segundo Galbraith (2012), a modelagem como conteúdo e como veículo têm orientações distintas, dependendo de quem é fim e de quem é meio. Em comum, entretanto, elas apontam a aprendizagem como aspecto estrutural no desenvolvimento de atividades de modelagem.
Assim, ainda que Galbraith (2012) tenha identificado especificidades na modelagem como veículo e na modelagem como conteúdo, o que se apreende em cada um destes modos pode não ser tão facilmente identificado. Desta forma, podemos vislumbrar que aprender o fazer modelagem matemática não é independente do fazer per si. Tendo em vista que, neste artigo, dirigimos nossa atenção ao fazer - em um curso de formação de professores -, também consideramos as argumentações de Almeida e Dias (2007), de que a formação de professores para a modelagem precisa dar oportunidades aos alunos - professores em formação -, de aprender sobre, aprender por meio, e ensinar usando modelagem matemática.
Neste contexto, podemos ponderar que a comunicação entre aquele que ocupa o papel de ensinar e aqueles que estão no papel de aprendizes, pode ser relevante para a conjunção entre ensinar e aprender o fazer modelagem matemática. De fato, conforme defendem Alro e Skovsmose (2006), a aprendizagem é uma experiência pessoal, mas ela ocorre em contextos sociais repletos de relações interpessoais que só se firmam por meio da comunicação.
A comunicação sob a perspectiva da semiótica peirceana
A noção de signo ocupou mentes de grandes pensadores como Platão, Aristóteles, Locke, Kant, Peirce, Saussure, que, ao longo de séculos, trataram da conceitualização, da natureza, e da função do signo, no pensamento e na interação entre pessoas (NÖTH, 1990). Conforme consideram Sáenz-Ludlow e Kadunz (2016), a história e a evolução da semiótica parece andar lado a lado com a história e a evolução da comunicação.
Comunicar é uma ação para entrar em contato com algo ou alguém, de maneira escrita, falada ou gesticulada. Essa ação necessita de um sistema de códigos constituído por signos que sejam compreensíveis, tanto para o enunciador, quanto para o intérprete da mensagem comunicada (PIETARINEN, 2003; SILVA, 2013).
Conforme sugere Pietarinen (2003, p. 82, tradução nossa), Peirce entende a comunicação como "[...] um diálogo entre interlocutores que trazem à tona signos". Neste sentido, a comunicação cria um vasto sistema semiótico que requer a realização de interpretações, para possibilitar a construção de conhecimentos, em que o signo é o resultado da interpretação que uma mente - um intérprete - dá a um objeto.
Bartolotti (2003) sugere que poderíamos perguntar: o que Peirce entende por signo? Em sintonia com grande parte dos que se interessam pela teoria peirceana, este autor também considera que Peirce apresentou diferentes definições para o signo no decorrer de sua trajetória filosófica.
Em termos gerais, a concepção de signo para Peirce (1972) repousa em uma ligação triádica, inter-relacionando representámen, objeto e interpretante. O representámen remete às características do signo, independentemente de sua função representativa, que deve ser diferente do pensamento que o sucede. O objeto refere-se à coisa exterior. Por fim, o interpretante refere-se à função representativa do signo, à capacidade do signo de endereçar-se a outro signo.
Sobre essa relação triádica, Peirce (1998, p. 13, tradução nossa) expressa que "[...] o signo ou representámen é algo que serve para produzir conhecimento sobre alguma outra coisa para a qual o signo está [stands for], ou representa. Essa outra coisa é chamada de objeto do signo". Esse conhecimento é produzido por uma mente - um intérprete - que produz outro signo - o interpretante.
Peirce dedicou grande parte de seus investimentos para a estruturação e a classificação de signos interpretantes, apresentando-os com diferentes denominações, decorrentes de processos de análise dos intérpretes. Como considera Santaella (2008), os signos interpretantes na teoria peirceana são meios utilizados para representar algo para alguém, são meios de pensamento, de compreensão, de raciocínio, de aprendizagem.
No processo de comunicação, o interpretante constitui um ato comunicativo produzido por meio de uma relação estabelecida entre um enunciador para com um intérprete, e se efetiva quando esses dois parceiros "[...] atingem uma compreensão mútua do signo[...] " (SANTAELLA, 2008, p. 68). Considerando justamente essa relação entre enunciador e intérprete, Peirce (1998) caracteriza o interpretante como: (i) intencional, oriundo de um enunciador; (ii) efetual, produzido pelo intérprete em reação a outro signo; (iii) comunicacional, que é a conjunção necessária entre enunciador e intérprete, a fim de que a comunicação possa ocorrer. Este interpretante comunicacional conduz ao que Peirce denomina commens, e consiste em tudo o que é bem compreendido entre enunciador e intérprete.
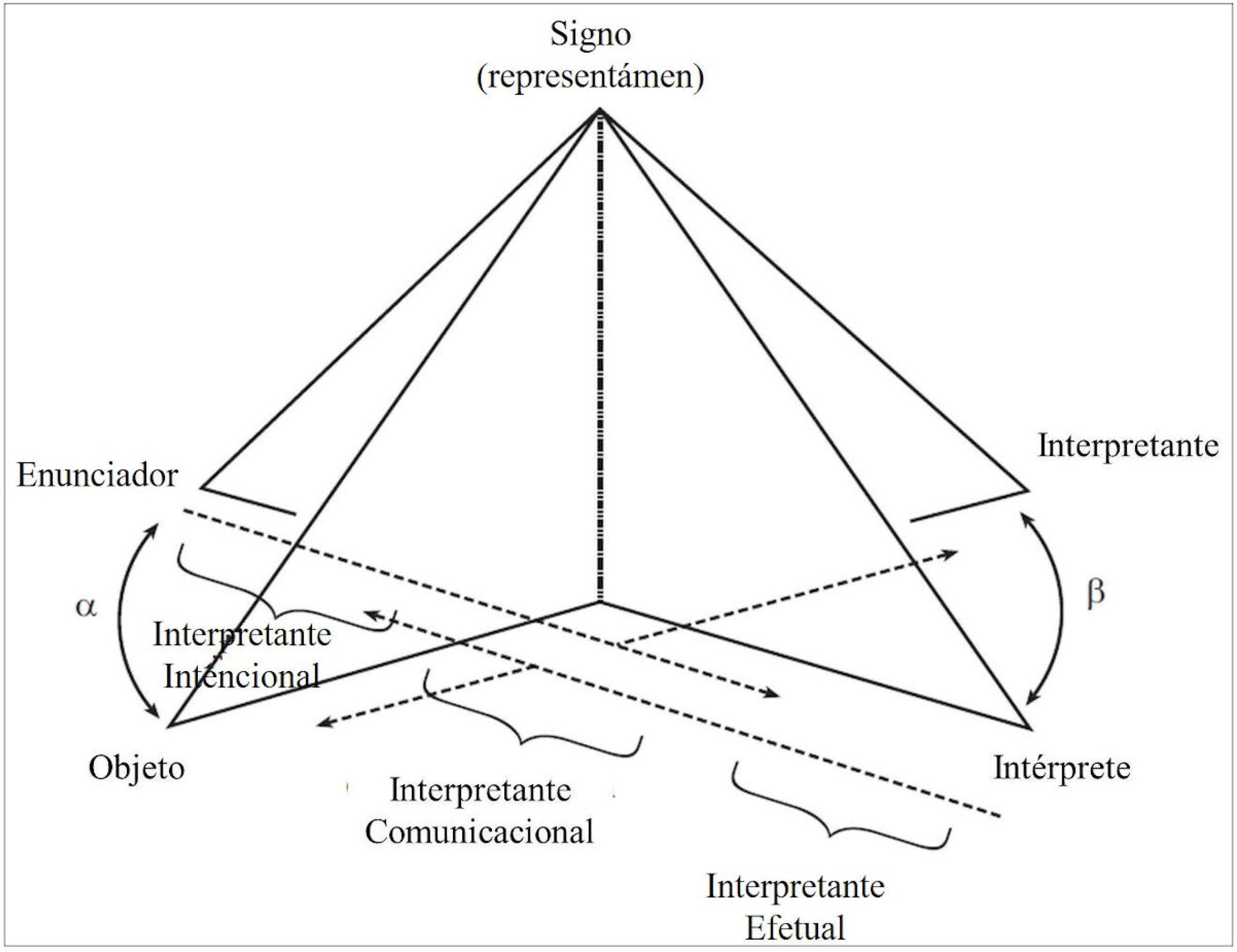
Em atos de comunicação pode-se observar "[...] duas escalas dinâmicas dentro da divisão triádica de signos, uma representando o continuum objeto-interpretante, e o outro representando o continuum enunciador-intérprete" (PIETARINEN, 2003, p. 86, tradução nossa). As duas escalas são esquematizadas na figura 1. As setas representadas em linhas tracejadas representam o aumento ou a diminuição de estados de informação dos enunciadores e dos intérpretes; as áreas que se sobrepõem representam fundamentos em comum, e é nestas sobreposições que os interpretantes comunicacionais são determinados; α indica a convergência entre os objetos e os enunciadores, e β, a convergência entre os signos interpretantes e seus intérpretes.
Segundo Presmeg (2008), na sala de aula tais convergências decorrem da comunicação entre alunos e professor no desenvolvimento das atividades. Os commens são os resultados da comunicação e, essencialmente, são os indícios do que se tornou conhecido em cada atividade.
A modelagem matemática na sala de aula
Nossas argumentações referentes à mediação por signos, na comunicação entre professor e alunos, no ensinar e aprender o fazer modelagem matemática, consideram três episódios relativos a três instantes no decorrer das aulas da disciplina de Modelagem Matemática na Perspectiva da Educação Matemática. Trata-se de uma disciplina anual com carga horária de 75 horas, e foi ministrada por uma das autoras do presente artigo, no ano de 2018. A turma era formada por vinte alunos. Os episódios estão descritos no quadro 1, quadro 2, quadro 3, e quadro 4.
Quadro 1 Episódio 1
Fonte: elaborado pelas autoras.
Quadro 2 Episódio 2: parte 1
| Episódio 2 - parte 1 |
|---|
| Refere-se ao início do estudo sobre modelagem matemática em que, tanto os aspectos teóricos, como os aspectos relativos à implementação da modelagem nas aulas de matemática, viriam à tona. As atividades iniciaram-se com o estudo do capítulo 1 do livro Ensino-aprendizagem com modelagem matemática, de Rodney Carlos Bassanezi (BASSANEZI, 2002). A partir de uma leitura preliminar do capítulo realizada pelos alunos, foram formados grupos para a discussão do texto. Essa discussão foi orientada por questões entregues pela professora, que contemplam elementos considerados por ela essenciais no que se refere à caracterização, uso e implementação da modelagem matemática na sala de aula. Após a estruturação de respostas para as questões por cada um dos grupos, ocorreu a apresentação e a discussão das respostas pelos grupos, com todos os alunos da disciplina. Durante este episódio, as atividades foram gravadas em áudio e vídeo, e os alunos entregaram os slides usados em suas apresentações, bem como um relatório completo com as respostas das questões, elaborado após as aulas do episódio. Partes das respostas foram apresentadas no quadro pelos alunos, especialmente aquelas relativas aos modelos matemáticos que constavam no texto, ou solicitados pelas respostas das questões. O nosso foco são as questões que, em alguma medida, referem-se ao como fazer modelagem matemática. |
Fonte: elaborado pelas autoras.
Quadro 3 Episódio 2: parte 2
| Episódio 2 - parte 2 |
|---|
| Estudo do capítulo 1 do livro Ensino-aprendizagem com modelagem matemática, de Rodney Carlos Bassanezi (BASSANEZI, 2002). |
| Título do capítulo: Modelagem matemática: um método científico de pesquisa ou uma estratégia de ensino e aprendizagem? |
| Parte 1: questões gerais (todos os grupos farão apresentações) |
| 1. Qual parece ser a intenção do autor com este capítulo? |
| 2. A partir da leitura do texto, caracterize Matemática. |
| 3. A partir da leitura do texto, caracterize Modelagem Matemática. |
| 4. Qual o papel da Matemática nas outras áreas do conhecimento? |
| 5. Apresentar as relações que, a partir da leitura do capítulo, podem ser estabelecidas entre Modelagem Matemática e Como ensinar Matemática, de maneira que se torne um assunto agradável para a maioria, incluindo alunos e professores. |
| 6. Fale sobre o histórico da 'tratória' e resolva a equação diferencial (modelo matemático) cuja solução representa esta curva. |
| Parte 2: questões específicas (cada grupo vai apresentar uma questão) |
| 1. O que é modelo matemático? Como são classificados os modelos matemáticos? |
| 2. Discuta, com base no capítulo estudado, a eficiência da modelagem e do modelo matemático. |
| 3. Dê um exemplo de Modelo Matemático diferente daqueles do texto, e classifique-o conforme o tipo de matemática utilizada. |
| 4. Quais são os argumentos favoráveis à inclusão da modelagem nas atividades escolares? Explique. |
| 5. Que tipos de obstáculos à inclusão da modelagem matemática nas atividades escolares são discutidos pelo autor? |
| 6. O desenvolvimento de atividades de modelagem matemática na sala de aula requer a inter-relação entre matemática, a área do conhecimento em que se situa o problema investigado, e a educação matemática. A figura abaixo é apresentada no livro do autor cujo capítulo está sendo estudado. Identifique, nessa figura, etapas do desenvolvimento de uma atividade de modelagem matemática. |
Fonte: elaborado pelas autoras.
Quadro 4 Episódio 3
Fonte: elaborado pelas autoras.
A atividade semiótica nos episódios de modelagem matemática
Para buscar indícios de mediação por signos na comunicação entre professor e alunos no ensinar e aprender o fazer modelagem matemática, realizamos uma análise interpretativa dos três episódios, considerando os registros escritos e de áudio e vídeo coletados no decorrer das aulas da disciplina, bem como dos relatórios entregues pelos alunos sobre cada uma das atividades dos episódios. Os vinte alunos que cursaram a disciplina em que os episódios foram desenvolvidos são aqui indicados por A1, A2, [...] A20. Quando nos referimos à professora na transcrição de diálogos usamos P1. Do ponto de vista metodológico, trata-se de uma pesquisa qualitativa com cunho interpretativo.
Nossas argumentações, sobretudo, consideram que, em se tratando de episódios de sala de aula, participam professor e alunos. O nosso esforço analítico sobre os episódios pauta-se nos signos interpretantes produzidos no processo comunicacional estabelecido na dinâmica.
O episódio 1, sobre a atividade relativa ao horário de verão descrito no quadro 1, representa o primeiro contato dos alunos com a modelagem matemática, na disciplina. Neste caso, a obtenção dos dados necessários para a abordagem da situação, bem como o encaminhamento de como poderia ser estudada por meio da matemática foram orientados pela professora. Os interpretantes intencionais da professora (enunciador) lançam luz para que os estudantes iniciem a sua familiarização com o fazer modelagem matemática; e os alunos - intérpretes - tiveram suas experiências com o fazer, mediadas pelas orientações e colaborações da professora.
As informações, neste caso, são mais centradas na professora do que nos alunos. Os procedimentos dos alunos são relativos à construção do modelo matemático, obtendo, a partir dos dados da situação, os parâmetros desse modelo, conforme indica o quadro 1. Os interpretantes efetuais são produtos de atenção a interpretantes intencionais. No continuum professora-alunos, a dinâmica ainda está apoiada nos interpretantes intencionais. A resposta ao problema, que não é o próprio modelo nesta situação, mas o que dele se pode fazer, vai se delineando pela comunicação entre professora e alunos, de modo que o modelo construído passa a ser usado para determinar os dias de início e término do horário de verão. Os procedimentos matemáticos dos alunos são resultados da sobreposição de interpretantes intencionais e efetuais, caracterizando aí os interpretantes comunicacionais. De fato, neste episódio o que os alunos efetivamente iriam conhecer refere-se diretamente à resposta ao problema para a determinação dos dias de início e término do horário de verão. No entanto, indiretamente, estes alunos estavam se apropriando de etapas e procedimentos inerentes ao desenvolvimento de uma atividade de modelagem matemática. Neste sentido, o que se tornou conhecido, para além do problema estudado, refere-se ao fazer modelagem matemática.
Durante as aulas relativas ao episódio 2, descrito no quadro 2 e no quadro 3, as discussões tiveram como foco as questões apresentadas na descrição deste episódio. Estão no escopo deste artigo os elementos dessas discussões, que dizem respeito ao fazer modelagem matemática, uma vez que é sobre isto que a professora espera que os alunos aprendam no episódio. Neste caso, os interpretantes efetuais são as argumentações dos alunos apresentadas pelos grupos, ou individualmente, perante a turma. Todavia, a discussão também foi subsidiada por intervenções e colaborações da professora (do enunciador), visando estabelecer uma comunicação formativa em que características do objeto fazer modelagem matemática fossem evidenciadas. Estas evidências configuram-se, na sala de aula, como interpretantes comunicacionais - os commens -, uma vez que são resultados de sobreposições entre interpretantes intencionais e interpretantes efetuais.
Os registros captados por áudio e vídeo dão indícios de elementos que os alunos consideram relevantes para o fazer modelagem matemática. Um desses elementos refere-se à relevância vislumbrada na abordagem de situações não matemáticas por meio da matemática, como indica, por exemplo, a fala de um aluno:
A11: Com a modelagem a gente consegue juntar, por exemplo, a geografia, igual a gente fez com o horário de verão, associar física e tantas outras matérias num problema que a gente vai conseguir resolver com a modelagem né? Então, também acho que torna a aula mais atrativa para os alunos, porque daí entra na questão do estudar algo que é do cotidiano do aluno.
As discussões também revelam a expectativa de que, em atividades de modelagem, os alunos podem desenvolver sua autonomia para agir na abordagem das situações, conforme indica parte de um diálogo entre professora e alunos.
A6: Não sei se alguém falou, mas quando você ensina matemática com a modelagem você dá autonomia para o aluno.
P1: Exatamente.
A6: Esse é o principal foco do estudo, autonomia de pensamento para o aluno raciocinar por si só, para resolver os problemas do mundo, do cotidiano.
P1: Isso. Muito interessante! Esse é um fato importante da modelagem, o aluno sentir essa capacidade de fazer as coisas com criatividade, com estilo próprio.
Neste ato de comunicação, o estado de informação dos alunos - intérpretes - está estruturando um continuum da relação objeto-interpretante, e os interpretantes já passam a ser commens, resultantes do diálogo entre professora e alunos.
A questão 2, relativa às deliberações sobre a eficiência da modelagem matemática, gerou uma discussão que levou em consideração diferentes possibilidades para ponderar sobre a eficiência.
A7: A modelagem é eficiente a partir do momento que nos conscientizamos que estamos sempre trabalhando com aproximações da realidade, ou seja, que estamos elaborando sobre a representação do sistema [...] Além disso, a eficiência da modelagem eu acho que ela também se encaixa no campo educacional, no sentido que a gente já discutiu, porque a gente consegue trabalhar com situações do cotidiano do aluno, consegue despertar a autonomia do aluno a partir de trabalhos utilizando a modelagem. A eficiência da modelagem tá também nisso! Você conseguir dar liberdade para o outro responder, dar liberdade para o outro se tornar pesquisador mesmo no âmbito escolar.
A10: Quando você fez esse questionamento de eficiência, professora, você pensou em que? [dirigindo-se à professora].
P1: Justamente nas duas coisas que vocês parecem apontar: como avaliar se o modelo é eficiente, mas também se a modelagem é eficiente. Fiquei muito satisfeita com essa compreensão de vocês!
O diálogo indica que um fazer modelagem matemática eficiente leva em consideração características do modelo matemático produzido, e também o conjunto de ações no decorrer dessa produção.
A questão 6 (identificada no esquema do quadro 3) foi a que mais diretamente levaria os alunos a refletir sobre práticas do fazer modelagem matemática. Nela, os grupos identificaram diferentes etapas do desenvolvimento de uma atividade de modelagem, e fizeram-no considerando o esquema (ciclo) apresentado no texto em estudo (episódio 2).
O grupo de alunos que se dispôs a liderar a discussão dessa questão organizou slides e, a partir das imagens, passou a discutir o tema com os colegas.
A3: A primeira etapa que ele [referindo-se ao texto] apresenta é a experimentação. Nesse momento é que a gente olha para os dados obtidos para a situação que a gente quer estudar [...] Aí a segunda etapa é a da abstração [...] Aí a gente tem a seleção de variáveis e daí a formulação de hipóteses implica em considerar o que sabe da situação. A gente estava até comentando como fizemos isso, no exemplo do horário de verão que a gente estudou [...]
A20: E daí a próxima etapa é a obtenção do modelo matemático e resolução usando esse modelo. Aí dependendo da complexidade, pode se usar métodos computacionais para chegar à solução. E a partir do momento que pode ser que o modelo não traga uma solução, a modelagem possibilita usar outras técnicas ou talvez outras hipóteses. Uma vez construído o modelo, vem a etapa da validação que define se aceita ou não o modelo. Nessa etapa as hipóteses e os modelos podem ser contestados e os resultados que foram encontrados são comparados com os dados experimentais obtidos na primeira etapa. Quanto mais próximo os resultados obtidos pelo modelo forem dos dados experimentais, mais chances de se validar esse modelo. Mas também não depende mais só dos dados, depende da intenção do modelador e do contexto.
A8: O autor diz no texto que o interessante é que nenhum modelo é definitivo e que um modelo bom é um modelo que pode proporcionar a criação de outros modelos. Então no quadrinho que ele colocou aqui [aponta para o slide] a experimentação é a etapa que às vezes não é o matemático que faz. Daí, já a abstração e resolução é o matemático que executa e a validação do modelo não é feita somente pelo matemático, mas também pelo pesquisador de outra área. Uma das coisas que o autor diz no texto é que o intercâmbio da matemática com esses pesquisadores é o que proporciona a obtenção de modelos coerentes e úteis. A quinta etapa que é a modificação, a gente pode ver dentro desse quadro [apontando para o esquema do slide] que ele faz, porque, se você observa, esse quadro tem uma setinha que ele faz então na validação de modo que se ele não for validado eu posso voltar aqui [apontando para a etapa de abstração] e faço todo o processo matemático de novo. Quem faz esse processo aqui dentro desse quadro é o matemático e fora desse quadro o pesquisador de outra área. Claro que pode ser em conjunto ou não com o matemático.
P1: Isso... a modelagem matemática é um processo dinâmico.
A comunicação expressa no diálogo relativo a esse episódio nos permite afirmar que os interpretantes intencionais (produzidos pela professora) atuam como referência para que os intérpretes (os alunos), aumentem o seu estado de informação sobre o objeto - o fazer modelagem matemática -, constituindo, assim, o continuum enunciador-intérprete a que nos referimos na figura 1.
O episódio 3, descrito no quadro 4, refere-se ao desenvolvimento de uma atividade de modelagem que ocorreu após o estudo do texto e das discussões a respeito de um problema levados pela professora. Nesse sentido, os interpretantes intencionais da mente da professora (enunciador) lançam luz para que os alunos comecem a ter autonomia na construção da atividade.
Para resolver o problema, os alunos, divididos em grupos de até seis integrantes, buscaram padrões por meio da observação de suas mãos, concluindo que "[...] a mão do ser humano tem algumas regularidades" (registro dos alunos). Essa constatação levou-os a selecionar diferentes medidas para a criação do algoritmo. Essas medidas, por sua vez, foram submetidas a operações, de forma a que cada grupo desenvolvesse um algoritmo. Os interpretantes intencionais seriam compreendidos na medida em que cada desafio fosse enfrentado pelos alunos. Assim, nos atos de comunicação no continuum objeto (problema) - interpretante (meio para chegar à solução), e no continuum enunciador (professora) - intérprete (aluno), os estados de informação iam se transformando na medida em que cada etapa da modelagem ia sendo construída: coleta de dados (medidas das mãos); hipóteses (quais medidas usar); matematização (quais ferramentas matemáticas poderiam ser usadas); construção do modelo (o algoritmo desenvolvido); validação do modelo (a testagem do algoritmo para identificação de intrusos).
O que parece fundamental nessa atividade é a possibilidade de inferir-se que os interpretantes intencionais foram transformados em interpretantes efetuais (na mente dos alunos) e conduzindo a commnens (resultados da comunicação entre professora e alunos). De fato, o êxito dos alunos na obtenção e na validação do algoritmo, nesse caso, é um indicativo, do ponto de vista semiótico, de que ocorreu a comunicação. Os resultados dos alunos são interpretantes comunicacionais, que indicam que houve construção de conhecimento ao fazer modelagem matemática, ou seja, commens se constituíram.
Esta inferência pode ser associada a dois aspectos observados nos dados coletados. Um deles é um trecho do relatório dos alunos em que afirmam que "[...] a atividade nos proporcionou conhecer como os sistemas biométricos funcionam e como ferramentas matemáticas podem ser usadas para combinar medidas. Um aspecto fundamental é caracterizar bem a margem de erro aceitável para aumentar a segurança do sistema". O outro é a apresentação de um esquema em que os alunos identificam e caracterizam os diferentes procedimentos associados ao desenvolvimento da atividade, conforme indica a figura 2.
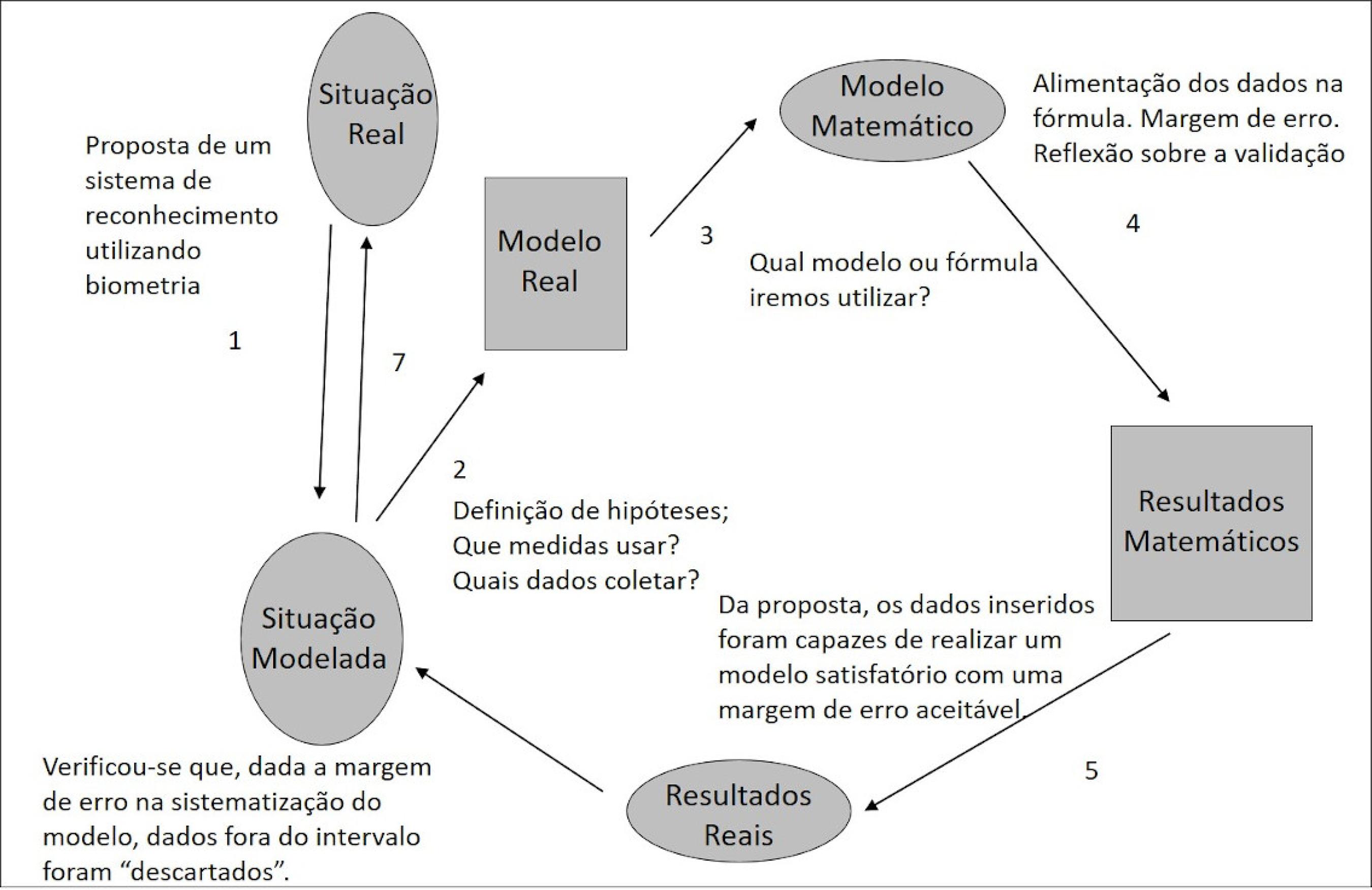
Fonte: elaborada pelas autoras a partir dos relatórios dos alunos.
Figura 2 Esquema construído por um aluno para a atividade da biometria da mão
Do ponto de vista do fazer modelagem matemática, este é um indicativo de que os três episódios, que individualmente sinalizam uma ação de signos interpretantes mediando a comunicação na sala de aula, se articulam para a construção de conhecimento.
Implicações para ensinar e aprender o fazer modelagem matemática
Olhar para as possibilidades de ensinar e aprender o fazer modelagem matemática à luz da semiótica peirceana nos permite apresentar contribuições para a questão que ainda merece atenção no debate acadêmico: como ensinar e aprender o fazer modelagem matemática?
Considerando que a comunicação na sala de aula é mediada por signos, e o uso e a produção de signos são essenciais para que algo possa ser aprendido, a identificação de diferentes signos interpretantes dá indícios de configurações para ensinar e aprender o fazer modelagem matemática na sala de aula.
Um resultado relevante, neste contexto, refere-se à ação do professor. A análise do processo comunicacional entre professor e alunos vem ao encontro do que propõe Blum (2015), de que no ensinar e no aprender o fazer modelagem matemática é fundamental o constante equilíbrio entre orientação do professor e ações independentes dos alunos. De fato, cabe ao professor orquestrar as atividades para que aquilo que tem a intenção de ensinar possa ser aprendido, e oferecer aos alunos vastas oportunidades de envolvimento, permanente ativação cognitiva, e oportunidades de comunicação.
Sob esta ação do professor, o fazer modelagem matemática é mediado por uma configuração de uso e de produção de signos que intermedeiam a conjunção entre enunciador (professor) e objeto (fazer modelagem matemática), e entre signos interpretantes e intérpretes (alunos). Desta interpolação decorrem commens (indícios de aprendizagem), como resultados do processo comunicacional evocado.
A análise de signos interpretantes, no decorrer dos três episódios, nos permite indicar que, para o fazer modelagem matemática é relevante, entre outros aspectos: gerar, com os estudantes, atividades que possam levar à identificação de alguns encaminhamentos da modelagem; associar, na sala de aula, ações e discussões que viabilizam aos alunos interações com grupos e apresentação de suas ideias. Por outro lado, a análise semiótica das produções de signos pelos alunos nos leva a ver indícios de que estes são capazes de identificar que podem ser autônomos e criativos, produzindo diferentes resoluções para os problemas e usar diferentes conteúdos matemáticos. Além disso, também indicam que diferentes etapas podem ser caracterizadas durante as atividades, e que ações relativas a elas podem ser discutidas no interior de cada grupo.
Do ponto de vista semiótico, o que é aprendido sobre o fazer modelagem matemática se revela nos interpretantes comunicacionais que resultam da sobreposição de interpretantes intencionais e interpretantes efetuais, considerando o professor, os alunos, e o processo comunicacional que entre eles se desencadeia. Os processos comunicacionais verificados nos episódios se modificam e se incrementam na medida em que interpretantes intencionais e interpretantes efetuais se combinam, e resultam dessa combinação, os interpretantes comunicacionais.
No episódio 1 grande parte do que se pode considerar como interpretante comunicacional é resultado da atenção dos intérpretes (alunos) aos interpretantes do enunciador (professora).
No caso do episódio 2, em que a ação se volta diretamente ao aprender sobre modelagem matemática, o que se tornou conhecido é efeito da ação de interpretantes intencionais, como referência para os intérpretes aumentarem o seu estado de informação relativa ao fazer modelagem.
Por fim, no episódio 3, os interpretantes intencionais constituíram um desafio para os intérpretes. Nesse caso, os próprios alunos deveriam identificar e executar ações relativas ao fazer modelagem, configurando-se um estado indicativo de que para aprender a fazer requer fazê-lo. Este fazer, todavia, é produto de sobreposição de interpretantes intencionais e interpretantes efetuais, e o esquema da figura 2 pode se caracterizar como um interpretante comunicacional resultante desta sobreposição.
Podemos conjecturar que os episódios assim entrelaçados configuram um ambiente comunicacional profícuo para a ocorrência dos commens relativamente ao fazer modelagem matemática.
Considerando que, na formação de professores em modelagem matemática, deve-se incluir o aprender sobre, e o aprender por meio da modelagem matemática, conforme sugerem Almeida e Dias (2007), a análise da atividade semiótica que conjuga interpretantes de um enunciador (professora) com interpretantes produzidos pelos alunos - e, a partir desses, gera interpretantes comunicacionais -, nos leva a ponderar que a interlocução constante entre aprender sobre, e o aprender por meio, pode ser eficiente. Um aprender assim configurado pode vislumbrar que o ensinar usando modelagem matemática, terceira etapa a que se referem Almeida e Dias (2007), pode ser bem sucedido em práticas docentes futuras. Assim, se para Galbraith (2012) há uma dualidade entre modelagem como veículo e modelagem como conteúdo, na presente pesquisa, a análise do processo comunicacional leva-nos a ponderar que aprender o fazer modelagem matemática não é independente do fazer modelagem matemática.
A interpretação semiótica oferece meios de compreensão de como ocorre aprender o fazer modelagem matemática da perspectiva do intérprete (aluno), da perspectiva do enunciador (professor), indagando, a todo instante, o potencial do processo de comunicação, e levando em consideração que as posições (de enunciador e de intérprete) são móveis. De fato, o interpretante intencional da professora se movimenta, na medida em que o aluno também enuncia, para além de ser um intérprete passivo. A sala de aula constitui o que Silva (2013) chama de explosão de signos, em que o professor, com signos intencionais, provoca nos alunos a geração de signos, conforme suas experiências e suas interpretações. Neste sentido, o conhecimento sobre o fazer modelagem matemática em um curso de formação de professores vai sendo construído, na medida em que a comunicação entre o professor e os alunos se torna alinhada de tal maneira que um pode compreender e atender às expectativas do outro. É justamente neste sentido que se deve buscar o que Blum (2015) denomina de equilíbrio entre o trabalho independente dos alunos e a colaboração do professor.