Introdução

As tentativas de aproximação entre o ensino e a história da matemática não são recentes, embora o tema ainda suscite muitas dúvidas e diferentes compreensões. Fried ( ²⁰⁰¹) destaca que, apesar de o tema ter ganhado força na discussão acadêmica nas décadas de 1960 e 1970, o valor da história da matemática para o ensino já era objeto de pesquisas e debates no começo do século XX (por exemplo, ^{BARWELL, 1913}apud^{FRIED, 2001}). Atualmente, tais pesquisas têm sido identificadas com a linha da história e pedagogia da matemática ( History and Pedagogy of Mathematics – HPM) e têm perpassado a discussão acerca do “por quê” e “como” a história da matemática pode desempenhar um papel no ensino, como bem analisam Barbin ( ¹⁹⁹⁷) e Jankvist ( ²⁰⁰⁹).

Enquanto alguns autores, como Barbin ( ¹⁹⁹⁷) e Fauvel e Maanen ( ²⁰⁰⁰), propõem a leitura de originais em sala de aula, outros ponderam que o uso da história nesse contexto demandaria algum tipo de adaptação, uma vez que história e educação, embora dialoguem, são campos de conhecimentos e de atividades distintos ( ^{FRIED, 2001}; ^{RADFORD, 1997}). Como decorrência, pesquisas nessa linha têm apontado implicações dessa articulação para a formação de professores que ensinam matemática ( ^{CLARK, 2019}; ^{FURINGHETTI, 2020}; ^{GUILLEMETTE, 2017}). No cenário nacional, tivemos, na década de 1990, produções que se propuseram a discutir as potencialidades e objeções do uso pedagógico da história da matemática, entre as quais destacamos Vianna ( ¹⁹⁹⁵) e Miguel ( ¹⁹⁹⁷). Nessa direção, o último autor defende que o uso da “história da matemática pedagogicamente orientada”, entendida como

[…] uma história viva, humana, esclarecedora e dinâmica, vindo substituir as enfadonhas histórias evolutivas das ideias matemáticas, quase sempre desligadas das necessidades externas e/ou internas que estiveram na base de sua origem e transformação, poderia constituir-se em ponto de referência para uma prática pedagógica problematizadora em matemática que tivesse por meta uma problematização, entendida como simultaneamente lógica, epistemológica, metodológica, sociológica, política, ética, estética e didática. ( ^{MIGUEL, 1997, p. 103}).

Em consonância com Miguel ( ¹⁹⁹⁷) acerca da potencialidade da história pedagogicamente orientada, desenvolvemos uma pesquisa teórica que investigou possíveis implicações da relação entre filogênese e ontogênese para organização do ensino da matemática. Tal relação, embora tenha permeado algumas pesquisas em educação matemática ( ^{FURINGHETTI, 2020}; ^{FURINGHETTI; RADFORD, 2008}; ^{RADFORD; PUIG, 2007}), constitui-se como uma abordagem ainda pouco explorada. Assim, partindo de uma fundamentação teórica na perspectiva histórico-cultural ( ^{KOPNIN, 1978}; ^{LEONTIEV, 1983}; ^{VIGOTSKI, 2002}) e na teoria cultural da objetivação [RADFORD ( ²⁰⁰⁶), RADFORD ( ^{2011 2013}), buscamos estabelecer relações entre uma abordagem pedagógica dos conceitos matemáticos, a história do conceito e sua significação cultural. Para os fins deste artigo, focamos a discussão teórica sobre a relação entre atividade humana, prática social e história dos conceitos. Como resultado, apresentamos algumas possíveis implicações desta relação para a organização do ensino e para a formação de professores que ensinam matemática.

Entendemos que pensar a organização do ensino em uma perspectiva histórico-cultural passa pela tomada de consciência de conceitos históricos, o que só é possível em atividades humanas envolvendo signos e instrumentos, em um movimento dialético entre processos inter e intrapsíquicos ( ^{VIGOTSKI, 2002}). Tal tomada de consciência é produzida na atividade dos sujeitos ( ^{LEONTIEV, 1983}) e resulta da produção crítica de sentido dos conceitos históricos em jogo, o qual pode se relacionar a uma mudança de motivo na atividade desenvolvida pelo sujeito, a partir de uma certa necessidade.

Entendendo a sala de aula como uma “comunidade de aprendizagem” ( ^{RADFORD, 2006}), a teoria da objetivação assume que o processo de aprendizagem envolve o encontro entre sujeitos e saberes, o conhecimento das práticas nas quais esses conceitos são integrados, os valores que os conceitos expressam, e os modos de agir e refletir que envolvem e dotam com significados tais conceitos. Tal encontro só é possível por meio da atividade humana conjunta entre alunos e professores, chamada “labor conjunto”. O saber, na teoria da objetivação, não é uma entidade ideal. Nas palavras de Luis Radford, o saber é compreendido como “[…] uma síntese de generalização codificada da ação humana – o trabalho humano –, de modo que, para o aluno, o saber aparece como pura potencialidade” ( ^{MORETTI; PANOSSIAN; MOURA, jan./mar. 2015, p. 246}). Assim, a aprendizagem é entendida como o encontro com o saber e sua transformação subjetiva em algo que aparece à consciência; esta transformação é o que chamamos objetivação ( ^{RADFORD, 2017b}).

Consequentemente, a aprendizagem docente implica o concomitante processo de tomada de consciência – isto é, tornar-se consciente dos significados culturais (matemáticos e outros), o que resulta na transformação do sentido e, portanto, do motivo e das necessidades na atividade de ensino do sujeito. Assim, a atividade de ensino deve ser capaz de dar vida à significação cultural do conceito em sala de aula ao desencadear a atividade conjunta dos sujeitos. Nesse sentido, um poderoso recurso para a organização do ensino que favoreça esse movimento em sala de aula é a história dos conceitos e práticas sociais a ele relacionadas.

Atividade humana, prática social e história dos conceitos

Em uma perspectiva histórico-cultural apoiada nas produções de Vygotsky ( ²⁰⁰⁰, ²⁰⁰²), Leontiev LEONTIEV ( ²⁰⁰¹), Moura et al. ( ²⁰¹⁰), Radford RADFORD ( ²⁰¹³), entre outros, os conceitos matemáticos são compreendidos como produções humanas que plasmam, cristalizam e expressam respostas às necessidades dos sujeitos em um determinado lugar e tempo histórico ( ^{VYGOTSKY, 1998}).

Longe de uma compreensão ingênua da noção de necessidade que poderia levar o leitor a assumir a defesa da recapitulação ⁴ ( ^{MIGUEL, 2004}), segundo a qual haveria uma relação direta entre “[…] o desenvolvimento histórico do pensamento matemático e a aprendizagem matemática dos alunos” ( ^{RADFORD, 2000, p. 145}), entendemos o conceito de necessidade a partir de uma perspectiva dialética, o que significa se afastar de qualquer paralelismo biogenético ⁵ ( ^{VYGOTSKY, 1998}). O conceito de necessidade em uma perspectiva dialética amplia-se para além da relação imediata entre indivíduos, necessidade e objetivo e passa a carregar um significado ontológico que Fraser ( ¹⁹⁹⁸), ancorado nos trabalhos de Hegel e Marx, vincula às dimensões ética, social e estética. Seres humanos aqui são vistos como seres de necessidade. A distinção entre necessidades naturais (por exemplo, respirar, comer e dormir) e necessidades socialmente criadas indica a alteração na forma como cada pessoa as satisfaz ( ^{FRASER, 1998}). Além disso, distingue-se necessary need de luxury need e explicita-se seu movimento de transformação, ou como, “necessidades prementes” se relacionam como “necessidades supérfluas” (não urgentes). Para o campo da educação, é de importância especial o conceito de higher needs (algo como “necessidades mais elevadas ou necessidades superiores”) e sua relação com a realização da essência humana mediada pela consciência ( ^{FRASER, 1998, p. 143}).

Um exemplo da relação entre a produção do conhecimento matemático e as suas correspondentes atividades humanas e práticas sociais pode ser encontrado no estudo desenvolvido por Høyrup ( ¹⁹⁹⁴) sobre a história da medida, números e peso em culturas da Mesopotâmia e da Grécia, no qual estes conceitos são especialmente abordados. Ao superar uma compreensão platônica de matemática, Høyrup ( ¹⁹⁹⁴) mostra como as instituições culturais medeiam a influência de forças socioculturais gerais sobre os sujeitos ao mesmo tempo em que esses indivíduos também contribuem para modelar a interação com as forças socioculturais. Para explicitar essa mediação cultural, o autor identifica o sentido do trabalho dos escribas naquele contexto social e histórico. Mais especificamente, demonstra que, apesar da demanda relacionada às necessidades imediatas do cotidiano, a motivação dos escribas para a resolução de problemas passava por um reconhecimento social e pela identidade profissional dessa atividade, de forma que “[…] tudo tem a ver com a prática dos escribas, mas a prática de escriba transposta da região da necessidade prática para a do virtuosismo” ( ^{HØYRUP, 1994, p. 66}), o que só foi possível em uma sociedade que valorizava e encorajava tal aspecto de forma imbrincada ou subsumida a sistemas sociais de produção de sentido. Outro aspecto explorado pelo autor é a constituição da matemática como entidade e campo de conhecimento no “[…] ponto onde as práticas matemáticas pré- existentes e anteriormente independentes são coordenadas através, pelo menos, de um mínimo de compreensão intuitiva de relações formais” ( ^{HØYRUP, 1994, p. 67–68}).

Tais exemplos nos permitem compreender que as necessidades que movem as atividades humanas se relacionam com diferentes motivos e mudam em diferentes culturas no que diz respeito a diferentes práticas sociais e o sentido que essas têm em culturas determinadas. Tal compreensão acerca da relação entre práticas sociais e conceitos matemáticos abstratos remete à discussão de Kopnin ( ¹⁹⁷⁸) sobre os aspectos históricos e lógicos do conceito. O conceito de história tal como assumido pelo autor, ao diferenciar-se de uma visão positivista, vai ao encontro do conceito que subjaz a perspectiva histórico- cultural e que compreende que

O primeiro ato histórico é, portanto, a produção dos meios que permitam a satisfação dessas necessidades, a produção da própria vida material, e de fato este é um ato histórico, uma condição fundamental de toda a história, que ainda hoje, como há milhares de anos, deve ser cumprido todos os dias e todas as horas, simplesmente para manter os seres humanos vivos. […] O segundo ponto é que, satisfeita essa primeira necessidade, a ação de satisfazê-la e o instrumento de satisfação já adquirido conduzem a novas necessidades — e esta produção de novas necessidades é o primeiro ato histórico. ( ^{MARX; ENGELS, 1993, p. 39–40}).

O conceito de história é compreendido como uma categoria ontológica e diretamente conectado ao modo como os indivíduos produzem sua vida e suas existências através da produção de novas necessidades, que superam as necessidades naturais. Essas novas necessidades, intrinsicamente humanas, são sociais, culturais e históricas ( ^{ORTEGA Y GASSET, 2002}) ⁶ . Imerso nessa compreensão dialética da história, Kopnin ( ¹⁹⁷⁸) compreende que o movimento histórico da produção humana de conceitos se dá por meio de atividade material e sensível. Segundo o autor, tal movimento histórico, ao ser apropriado pelo pensamento humano, constitui-se no aspecto lógico do conceito. Assim, a história por ele referenciada “[…] não é só a história do objeto, sua produção e desenvolvimento, mas também a história de como a humanidade se apropriou desse objeto, ou seja, a história de seu conhecimento” ( ^{MORETTI, 2014, p. 35}).

Dentro desse contexto, a produção de ideias matemáticas é compreendida em unidade com seu significado manifestado em práticas sociais no ambiente cultural em que são produzidas. A produção e o refinamento de ideias matemáticas (por exemplo, o conceito de número ou de figura geométrica) constituem-se, ao longo da filogênese e do desenvolvimento histórico, no sentido dialético da história mencionado acima. A sua ontogênese é o desenvolvimento dessas ideias no curso da vida dos indivíduos, mas a ontogênese não é a mera repetição do caminho histórico dos conceitos ( ^{FURINGHETTI; RADFORD, 2008}; ^{RADFORD; PUIG, 2007}): como destacou Vygotsky ( ²⁰⁰⁰), em um manuscrito escrito em 1929, é apenas no reino orgânico que semelhante repetição pode ocorrer, uma vez que, no desenvolvimento orgânico, a filogênese é repetida na ontogênese. Por outro lado, o desenvolvimento cultural teria a relação entre filogênese e ontogênese como sua força motriz. Nas palavras do autor,

[…] lá a filogênese está incluída em potencial e se repete na ontogênese, aqui a inter-relação real entre filo- e ontogenia: a pessoa como biótipo não é necessária: para o embrião no útero da mãe desenvolve-se em filhote humano, o embrião não interage com o biótipo adulto. No desenvolvimento cultural esta inter-relação é a força motriz básica do desenvolvimento (aritmética dos adultos e infantil, fala etc.). ( ^{VYGOTSKY, 2000, p. 27}).

Em síntese, o autor defende que é na unidade entre filogênese e ontogênese que nós encontramos a força motriz do desenvolvimento cultural. Para ele, essa força motriz reside na interação entre as “[…] formas ideais desenvolvidas, elaboradas pela humanidade”, forma ideal na cultura, encarnada no sujeito “[…] porque essa pessoa é membro de um certo grupo social, é uma certa unidade da história, vive numa determinada época histórica e em determinadas condições históricas” ( ^{VYGOTSKY, 2010, p. 698}). Desta forma, essa força motriz é a atividade humana que dá vida ao potencial histórico e social da cultura humana ( ^{LEONTIEV, 1983}). Nesse sentido, o movimento filogenético de produção de conceitos e valores éticos e estéticos objetiva-se na ontogênese por meio da atividade humana. Ou seja, é assim que a ontogênese é sustentada pela filogênese por meio da atividade humana, que, por sua vez, não apenas repete o movimento histórico, mas, de maneira autoral e criativa, o constitui de forma dialética. A ontogênese, portanto, sustenta-se na filogênese ao mesmo tempo em que a constitui e é por ela constituída.

Tais ideias centrais da abordagem histórico-dialética nos permitem afirmar a importância da interação entre o desenvolvimento histórico-cultural, as práticas sociais e o desenvolvimento conceitual na ontogenênese, de modo que “[…] para entender desenvolvimentos conceituais precisamos colocar o sujeito cognoscente e toda a atividade matemática em estudo dentro da sua concepção cultural da matemática e da ciência em geral” ( ^{RADFORD, 1997, p. 28}). Sob esse ponto de vista, é necessário reconhecer a importância de estudar os conceitos no seu processo de produção, juntamente com as significações culturais intrínsecas à cultura em que estão inseridas, uma vez que, ontogeneticamente, o pensamento humano é subsumido a uma realidade cultural RADFORD ( ²⁰¹⁴).

Acerca da relação entre o desenvolvimento histórico e o pensamento humano, Kopnin ( ¹⁹⁷⁸) entende que o conceito é a unidade dialética de seus aspectos lógicos e históricos. Para esse autor, os aspectos históricos, ao serem apropriados pelo pensamento humano, constituem o aspecto lógico, de modo que este seria “[…] a reprodução da essência do objeto e da história do seu desenvolvimento no sistema de abstrações” (p. 183). Assim, o lógico seria a apropriação do histórico pelo pensamento humano e, “[…] por isso, o lógico é o histórico libertado das casualidades que o perturbam” (p. 184).

Neste sentido, [para Kopnin] a unidade entre os aspectos lógicos e históricos do objeto de conhecimento, que chamamos de enfoque lógico-histórico do conceito, alinha-se epistemologicamente à compreensão histórico-cultural sobre o desenvolvimento psíquico como constituído na unidade dialética entre o individual e o coletivo, entre o intrapsíquico e o interpsíquico. ( ^{MORETTI, 2014, p. 36}).

Retomando a linha de argumentação que compreende a unidade dialética entre ontogênese e filogênese como força motriz do desenvolvimento cultural apenas se produz na atividade humana, aquela que dá vida ao potencial histórico e social do saber humano, assim também é possível compreender que a unidade entre os aspectos lógico e histórico do objeto de conhecimento se objetivam para o ser cognoscente por meio da atividade humana de caráter coletivo. Essa compreensão tem implicações para a forma de organização do ensino, como veremos a seguir.

Implicações para a organização do ensino

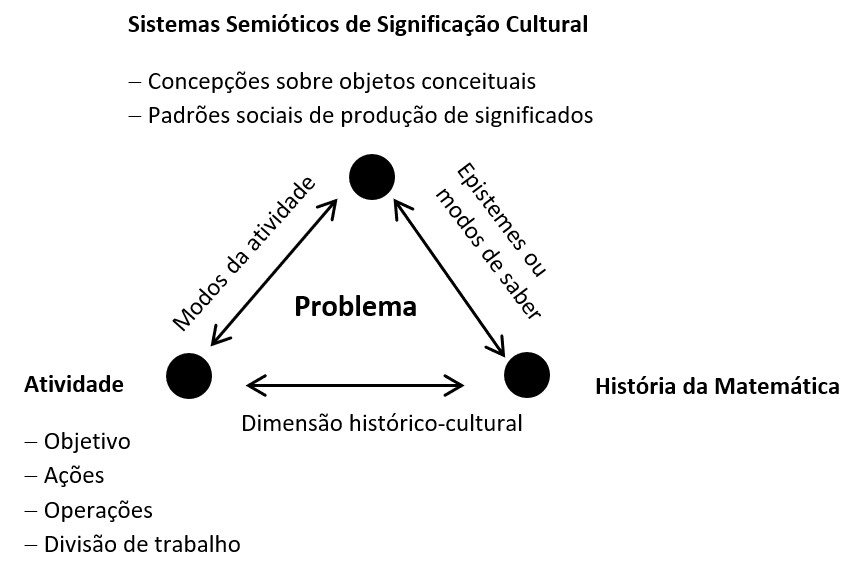
A relação dialética entre filogênese e ontogênese, tal como se manifesta na relação entre a atividade humana e o saber matemático social e historicamente constituído, indica o potencial da história da matemática como suporte para a organização do ensino que visa desenvolver o pensamento teórico dos alunos – com problemas cotidianos, mas também para além do foco nas situações do dia a dia. Assim, propomos que o sentido dos problemas matemáticos escolares tome uma dimensão que associe elementos lógico- históricos da história da matemática (a sua historicidade no entendimento dialético do termo), o conceito da atividade de sala de aula (como aquela que busca relacionar aspectos da unidade dialética da filogênese e ontogênese), e o que chamamos sistemas semióticos de significações culturais ( Figura 1).

[…] é através da prática social que [os seres humanos] produzem suas ideias (matemáticas ou não), é claro que a prática social não opera autonomamente por si só: a prática social está impregnada de sistemas simbólicos que a organizam de diferentes maneiras. A estes sistemas simbólicos chamamos sistemas semióticos de significação cultural. ( ^{RADFORD, 2014, p. 10}).

Sistemas semióticos de significações culturais referem-se a uma estrutura dinâmica suprassimbólica, na qual encontramos concepções culturais sobre objetos matemáticos, sua natureza, os padrões sociais de produção de significados, a forma como as investigações matemáticas devem ocorrer etc. Sistemas semióticos de significações culturais organizam, em um nível simbólico, a atividade de ensino e aprendizagem em sala de aula, em particular por meio dos modos de produção de conhecimento e das formas de colaboração humana que são cultivadas na sala de aula.

Fonte: Moretti e Radford (²⁰¹⁵).

Figura 1 – Dimensões do problema: história da matemática, atividade e sistemas semióticos de significações culturais 

As dimensões de problema tais como estamos propondo pressupõem compreendermos tanto o uso didático da história da matemática, quanto o conceito de atividade, no contexto teórico no qual transitamos ao longo desse artigo. Assim, a atividade humana mediada ( ^{LEONTIEV, 1983}) permite ao sujeito atribuir sentido pessoal às significações sociais, sendo que “[…] a significação é a forma pela qual um homem determinado chega a dominar a experiência da humanidade, refletida e generalizada” ( ^{LEONTIEV, 1983, p. 225}, tradução nossa). Assim é que os conhecimentos se transformam para o sujeito em “conhecimentos vivos” que medeiam a sua relação com o mundo (p. 246).

O aspecto coletivo da atividade humana é destacado por diferentes pesquisadores, em especial, no tocante aos processos de aprendizagem. Rubtsov ( ^{1996, p. 134}) destaca o papel do coletivo na atividade de aprendizagem ao afirmar que “[…] a atividade de aprendizagem se apresenta, essencialmente, sob a forma de uma atividade realizada em comum”. O autor destaca ainda alguns elementos que compreende como essenciais à atividade coletiva, tais como:

a reflexão, permitindo ultrapassar os limites das ações individuais em relação ao esquema geral da atividade (assim, é graças à reflexão que se estabelece uma atitude crítica dos participantes com relação às suas ações, a fim de conseguir transformá-las, em função de seu conteúdo e da forma do trabalho em comum). ( ^{1996, p. 136}).

Na mesma linha teórica, Moura et al. ( ²⁰¹⁰) destacam a importância do trabalho coletivo em sala de aula na solução do que chamam de situações desencadeadoras de aprendizagem, que visam proporcionar “[…] ao aluno envolver-se na solução de um problema como se fosse parte de um coletivo que busca solucioná-lo, tendo como fim a satisfação de uma determinada necessidade” ( ^{MOURA, 2010, p. 2010}, p. 224).

A importância da atividade coletiva ou de trabalho conjunto em sala de aula também é considerada por Radford ( ^{2019, p. 3069}), que compreende que é por meio do chamado “labor conjunto” ( joint labour) que o saber é colocado em movimento e “[…] se materializa em algo sensível; isto é, conhecimento”. Ao defender a objetivação do saber como conhecimento por meio da atividade conjunta em sala de aula, o autor assume que

Um conceito é precisamente a refracção subjetiva do saber na consciência através da mediação do conhecimento. Um conceito permite-nos fazer coisas e pensar sobre elas de certas maneiras. Enquanto o saber e conhecimento são entidades histórico-culturais, um conceito é de ordem subjetiva: a subjetiva e parcial versão do saber cultural. ( ^{RADFORD, 2019, p. 3069}, tradução nossa).

Na busca para compreender o saber como uma entidade objetiva – histórica e culturalmente – e a sua relação com os indivíduos à medida que estes se deparam com tal saber e tentam agarrá-lo e dar-lhe sentido, Radford (2002) propõe o conceito de objetivação:

Mais precisamente, os processos de objetivação são aqueles processos sociais, coletivos de se tornar progressivamente consciente de um sistema de pensamento e de ação – um sistema que vamos percebendo gradual e parcialmente e ao mesmo tempo dotamos de significado. Os processos de objetivação são aqueles processos de tentativa de notar algo culturalmente significativo, algo que é revelado à consciência de forma não passiva, mas por meio da corpórea, sensível, afetiva, emocional, artefatual, semiótica e criativa atividade dos indivíduos. Neste contexto, a aprendizagem é definida como o resultado de processos de objetivação. E como os sistemas de pensamento (matemáticos, etc.) são sempre revelados parcialmente, estes processos são sempre infinitos – e, portanto, também o é a aprendizagem. ( ^{RADFORD, 2019, p. 3065}, grifo do autor).

Assim, ao dialogar com uma produção cultural e histórica, a atividade coletiva em sala de aula relaciona-se com algum aspecto do desenvolvimento histórico do conceito em jogo na relação didática que se estabelece entre os sujeitos nesse espaço de aprendizagem. Considerar a relevância do conhecimento da história do conceito e, em particular, da história da matemática não significa compactuar com o discurso da recapitulação, da repetição da história no processo de ensino e de aprendizagem, como alguma leitura superficial poderia sugerir. Reconhecer o diálogo com a história da matemática na organização didática do ensino significa reconhecer que

[…] esse saber tem uma trajetória, uma história e o estudo dessa história, o estudo de suas condições de possibilidades, de transformação, de generalização, de refinamento, dá-nos uma ideia da densidade epistemológica do saber, que pode ser muito importante no momento de desenhar atividades didáticas e interpretar o que se passa na sala aula. (RADFORD em entrevista a ^{MORETTI; PANOSSIAN; MOURA, jan./mar. 2015, p. 254}).

Assim, considerar a história da matemática na organização didática do ensino pressupõe considerar que, para todo conceito, sempre há uma possibilidade já constituída, formas já trilhadas, de pensá-lo. Por outro lado, se entendemos que o encontro do sujeito com essas formas culturais, históricas e sociais de saber se dão por meio da atividade coletiva, a proposta didática que desencadeia a atividade dos sujeitos pode possibilitar também o encontro destes com uma forma de atividade humana relacionada ao conceito. Esse é um ponto especialmente delicado de se considerar na elaboração didática de situações desencadeadoras de aprendizagem, uma vez que considerar uma atividade humana relacionada à produção histórica do conceito implica reconhecer que a “[…] matemática não tem um significado cultural invariável, nem se desenvolve no mesmo sentido e em uma só direção” ( ^{RADFORD, 2017a, p. 152}, tradução nossa).

Olhar para a história da matemática como recurso didático implica sempre uma escolha temporal, histórica e cultural. Para qual cultura e momento histórico deslocamos a nossa atenção? Podemos falar da generalidade de conceitos matemáticos quando olhamos para a organização lógica atual do conceito, porém, compreender seu movimento histórico significa reconhecer caminhos, continuidades e rupturas. Tal forma de compreender a produção histórica da matemática e seu diálogo com a educação matemática – mais especificamente, com a organização didática do ensino – traz o desafio de propor aos pesquisadores da educação matemática a busca para compreenderem o contexto histórico de produção de textos e conceitos matemáticos, de modo que “[…] os textos matemáticos de outras culturas são investigados tendo em conta as culturas em que estavam embutidos” ( ^{FURINGHETTI; RADFORD, 2008, p. 646}).

Explorando essa relação entre a produção histórica da matemática como atividade humana e seu diálogo com a educação matemática, Radford ( ^2017b) apresenta um exemplo no qual utiliza sequências de figuras geométricas para introduzir os estudantes dos anos iniciais ao estudo da álgebra, por meio da generalização de padrões. A ideia é que, a partir de alguns termos iniciais da sequência, os estudantes reconheçam a regularidade e construam os termos seguintes. Nesse caso, o que se propõe é que os estudantes tomem consciência de formas de pensar algebricamente ao se depararem coletivamente com formas históricas de fazer matemática e lidar com generalizações de sequências aritméticas. Radford ( ^2017b) destaca que a atividade humana de investigar sequências aritméticas já era presente em civilizações antigas, como a mesopotâmica, e ganhou especial interesse entre os neopitagóricos com o estudo dos números poligonais (triangulares, quadrados, pentagonais etc.), cuja generalização teórica foi posteriormente expressa por Diofanto no século III a. C., de modo que “[…] as formas algébricas de refletir, perceber e tratar sequências são formas codificadas de pensar e fazer […] codificadas e refinadas na história cultural humana” ( ^{RADFORD, 2017b, p. 104}).

Na sala de aula, o encontro dos estudantes com essas formas historicamente codificadas da atividade humana de generalizar sequências é possível na atividade coletiva entre estudantes e professor, ao lidarem com objetivações desse saber cultural e histórico que é entendido como potencialidade. Nesse processo, temos a ascensão do abstrato – entendido como potencialidade histórica do saber – ao concreto multideterminado e atualizado como conhecimento pela atividade humana.

Nesse contexto, o apoio à história busca trazer para a sala de aula uma situação desencadeadora de aprendizagem que permita a objetivação de formas codificadas de se pensar sobre sequências, de modo que o trabalho coletivo com essas formas codificadas de reconhecer e generalizar padrões pode desencadear o movimento do pensamento algébrico que implica a investigação sobre o movimento de grandezas e sua variabilidade, o reconhecimento da relação de dependência e regularidade e o trabalho com quantidades indeterminadas de forma analítica, como já discutido em Radford ( ²⁰¹⁸).

Algumas conclusões

Neste artigo, sugerimos que uma história culturalmente significada de conceitos na educação matemática implica compreender que a história não é a mera sucessão de eventos ( ^{RADFORD, 2016}); assumir essa concepção também inclui o reconhecimento da importância de levar em conta a produção de ideias matemáticas em unidade com sua significação manifestada em práticas sociais em um ambiente culturalmente específico – tanto no nível filogenético como no ontogenético. Neste contexto, o estudo da história da matemática deve permitir o reconhecimento das práticas sociais relacionadas à produção histórica e cultural de conceitos, bem como o reconhecimento por parte do educador dos limites e das mudanças qualitativas dessas práticas – o que pode indicar um pensamento teórico sobre a prática, sem o qual a produção do conceito não seria possível. Desta forma,

[…] apresentamos uma interpretação diferente da recapitulação baseada na ideia de conexões conceituais entre desenvolvimentos ontogenéticos e filogenéticos. Estas conexões – induzidas pelo complexo sistema de aprendizagem da escola – aparecem como partes do processo de objetivação dos alunos ( ^{RADFORD, 2002}) e dão sentido a um saber histórico e culturalmente constituído depositado e mobilizado pela escola. ( ^{FURINGHETTI; RADFORD, 2008, p. 649}).

Tal saber permite a elaboração de situações desencadeadoras de aprendizagem e, potencialmente, move os estudantes na direção de uma necessidade coletiva do conceito, já que exigem um pensamento teórico sobre a prática e o reconhecimento de maneiras de conhecer significados histórica e culturalmente. Tal necessidade não está necessariamente relacionada a problemas históricos reais e pode emergir por meio de diferentes tipos de situações problema, tais como “[…] um jogo, um problema contextualizado, ou mesmo um problema de compatibilidade lógica dentro da própria matemática” ( ^{MORETTI; MOURA, 2011, p. 443}). As necessidades, à medida que surgem na sala de aula, podem não estar diretamente relacionadas a problemas históricos reais. No entanto, eles estão profundamente enredados aos desejos que motivam a atividade, uma vez que, como Leontiev ( ^{1974, p. 22}) observou, “[…] um objeto de atividade pode obviamente ser tanto material quanto ideal. O ponto chave é que por trás do objeto [da atividade] sempre existe uma necessidade ou um desejo, ao qual [a atividade] sempre responde”.

Outro aspecto relacionado à contribuição da história da matemática para a organização do ensino, a partir de uma perspectiva histórico-cultural, refere-se ao reconhecimento do professor de uma perspectiva histórica e epistemológica do saber, sem a qual

[…] arriscamo-nos a não entender as dificuldades que muitos estudantes podem atravessar em seu encontro com essas formas condensadas de refletir e atuar e também perdemos possibilidades para a geração de desenhos sofisticados das atividades que queremos trazer para a sala de aula. (RADFORD em entrevista a ^{MORETTI; MOURA, 2011, p. 254}).

Focando a organização do ensino da matemática, destacamos que não há uma formulação de problema matemático que, por si própria, faça emergir um determinado conceito ou conhecimento e, nesse sentido, o que apresentamos neste texto distingue-se da teoria das situações didáticas ( ^{BROUSSEAU, 2008}), segundo a qual, para todo conceito matemático, corresponde uma situação – um problema matemático que, de certa forma, vai forçar o aluno a utilizar o conceito. Assim, entendemos que não há qualquer formulação de problemas matemáticos que possa trazer à tona um determinado conceito ou alguns conhecimentos por “si só”.

Ao partirmos da proposta vigotskiana da unidade dialética entre ontogênese e filogênese como força motriz do desenvolvimento cultural na atividade humana, defendemos que, na organização do ensino da matemática, também é possível compreender que a unidade entre os aspectos lógicos e históricos do objeto de conhecimento se objetivam para o ser cognoscente por meio da atividade humana de caráter coletivo.

Assim, a proposição dos problemas com base na história da matemática, como nós entendemos, só pode ser desencadeadora de aprendizagem por meio de um “trabalho conjunto” com o professor. Neste sentido, a história da matemática é esclarecedora tanto ao inspirar atividades impregnadas de necessidades humanas do conceito, quanto ao permitir ao professor compreender os limites dos problemas matemáticos que podem ser formulados, bem como a mediação necessária para que os estudantes se tornem criativamente conscientes dos caminhos teóricos de pensar matematicamente.