Introduction
A deep understanding of students’ learning processes and mathematical learning difficulties along with their various causes are one of the core challenges of research in Mathematics Education ( FRITZ; HAASE; RÄSÄNEN, 2019). In this article, we show the analysis of a class episode on the resolution of an arithmetic-algebraic problem from two different theoretical perspectives: the Semiotic Bundle Approach (SBA) and the Onto-Semiotic Approach (OSA). The focus of this research is to investigate the dialogue generated by connecting these two theories; in other words, it is about observing a meeting space between the SBA and OSA drawing from the comparison of their respective analysis of a mathematical situation. Thus, such networking effort is a first study of a shared space of dialogue (a Semiosphere—-in the words of Lotman 1990) and then Radford ( 2008) in the analysis of mathematical situations. This space identifies and is generated by the asymmetries found between the two different lenses, i.e., the pivots around which dialogue is generated: in fact, information is generated by asymmetric semiotic mechanisms ( LOTMAN, 1990, p. 74; MANOLINO, 2021). The Semiosphere, generated by the networking between SBA and OSA, allows us to read the mathematical meta-discussion describing the reality of the class situation in its completeness and complexity, and goes beyond the simple analysis of the level of integration between the two theories ( PREDIGER; BIKNER-AHSBAHS; ARZARELLO, 2008).
The use of multiple theoretical frameworks in mathematics education has long been recognized as a need due to the multidisciplinary characterization of this field of studies (see the ZDM issue of May 2008). The common work, notably European, of the scholars in working group 11—-Different theoretical perspectives and approaches in research in Mathematics Education, started at CERME 4 in February 2005 (see ARTIGUE et al., 2006 ). Indeed, other similar examples spring up in the group, such as the Symposium of the Spanish Society of Mathematics Education Research held in 2018—-entitled Knowledge and teaching competence: establishing relationships between theoretical perspectives ( RODRÍGUEZ-MUÑIZ et al., 2018 , p. 15-80). The research community has focused its attention in order to progress towards understanding, and possibly coordinating, different theories ( ARTIGUE; MARIOTTI, 2014; KIDRON, 2016; FLORES et al., 2020 ): the purpose is to develop conditions for a productive dialogue between theories within Mathematics Education and beyond.
Several studies from the SBA contribute to the growth of this field of research ( ARZARELLO; ROBUTTI; SABENA, 2007; DREYFUS et al., 2014 ; MAFFIA; SABENA, 2015). More incipient are the initiatives by the OSA to engage in a serious dialogue to explain their own theoretical approach to others and to understand those of others, using specific educational problems ( BORJI et al., 2018 ; D’AMORE; GODINO, 2007; FONT et al., 2016 ; GRUGEON-ALLYS; GODINO; CASTELA, 2016).
The research works proposed by Godino et al. ( 2016), Pino-Fan et al. ( 2015), Drijvers et al. ( 2013), and Borji et al. ( 2020) argue that networking is a promising route in order to understand the observed phenomenon in the mathematics classroom. Continuing this research line, our starting point is the analysis of a mathematics class episode involving an arithmetic-algebraic task utilizing two theoretical lenses: SBA (with its essential in cognition dynamic genesis of signs) and OSA (as a hybrid, dynamic, and inclusive theoretical system). However, we go further. We focus on the dialogue between the constructs as a new way to look at intertwining the two theories, using Radford’s ( 2008) vision of the Semiosphere: “a dynamic set of connection” (p. 319), where integration and identity are the two dynamic axes (plots) of our script.
We acknowledge the need to really understand theories, not only by addressing theoretical foundations and concepts, but also by discussing concrete examples and cases. The two sections below, Semiotic Bundle Approach and Onto-Semiotic Bundle Approach, summarize the SBA and OSA’s main theoretical notions, respectively. The following section, the Networking of Theories, describes the respective research theoretical framework. In the next and last section, we apply the Networking notion around the classroom episode. Observing the possible asymmetries between the two theoretical approaches, the following research questions were raised: what are the characteristics of SBA and OSA that shape the Semiosphere generated by their networking? In particular, without limiting ourselves to the degree of interaction but rather drawing on the identity plot dimension, are there theoretical elements of one approach that enable us to improve tracing the identity of the other? We looked for observable elements to answer this in the idea (paraphrased by Derrida, who refers to words and Saussure, who refers to signs, but perfectly consistent in the dialogue between our two approaches) that the significance of a theoretical approach is not intrinsic but rather determined through the difference quotient between the approaches. Finally, our main conclusions are highlighted.
Semiotic Bundle Approach
The Semiotic Bundle Approach (SBA) is a theoretical framework elaborated by Arzarello ( 2006a), which enlarges the classical notion of semiotic register (DUVAL, 2006) attributing a central role to the body and to the signs within a socio-cultural (Vygotskian) and multimodal perspective. Arzarello extends the definition by Ernest ( 2006) of a semiotic system, supported by the notion of semiotic set on three key components: “signs, modes of production/transformation, and relationships” ( ARZARELLO, 2006b, p. 281).
A collection of semiotic sets, which changes over time, and a collection of relations between the sets, that can be converted into each other, frames the notion of Semiotic Bundle, or bundle of semiotic sets. As Arzarello et al. ( 2009) pointed out, the Semiotic Bundle is a dynamic construct that allows the micro-analysis of signs (conceived in a Vygotskian perspective) in both synchronic–considering the relationships among different semiotic resources simultaneously activated by the subjects at a certain moment, and diachronic ways–focusing on the evolution of signs and its genetic function in successive moments, to highlight the roles that different resources play in students’ multimodal cognitive processes.
Mathematical objects are naturally not directly accessible to the senses, but always mediated by representations or signs. These two bedrocks make it necessary to have a lens capable of observing the mathematical concepts arising and evolving together with their signs. The multimodal nature of the human sense-motor system perceives the sensory modalities as integrated with each other and with the cognitive system, so perceptual-motor and “embodied” activity in a mathematics classroom context, such as gestures, tool’s manipulation, drawing and body movements, come to take on a prominent role also for the abstract thought and cognitive processes. Considering the Semiotic Bundle, it is possible to “fully grasp the evolution of learning processes” ( ARZARELLO et al., 2009 , p. 100).
Onto-Semiotic Approach
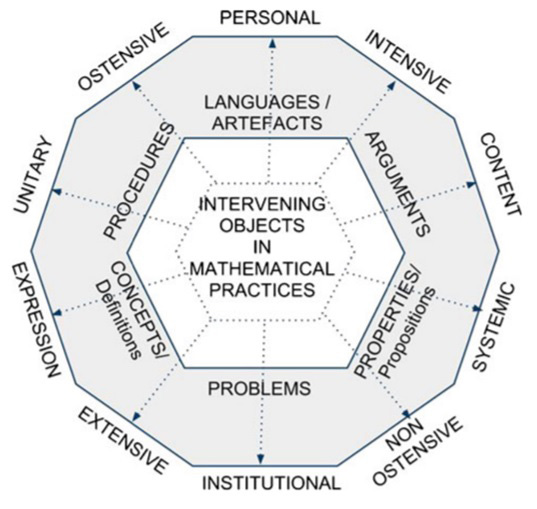
Key elements of the epistemological and cognitive modelling of mathematical knowledge proposed by OSA are the notions of practices (or sequence of practices), objects, processes, and semiotic function. OSA holds a pragmatist perspective of the mathematical activity offering some theoretical constructs to handle with the meaning issue of the mathematical objects. These meanings emerge from the mathematical practices, in which one can identify the use of different languages (in a wide sense, as linguistic registers). Then, in order to achieve a fine characterization of such meanings, OSA has introduced the notion of onto-semiotic configuration of practices, objects, and processes ( figure 1).
In OSA, the various types of objects, according to their nature and function, are classified into the following categories: languages (expressions, graphics) in their various registers (written, oral, gestural); situations-problems (extra-mathematical applications, exercises); concepts-definitions (these are not the mathematical concepts in a wide sense, but concepts as definitions introduced by a rule); propositions (statements about concepts-definitions); procedures (algorithms, operations); arguments (statements used to validate or explain propositions and procedures).
These objects can be considered from different viewpoints (or dualities): ostensible objects (material, perceptible) and non-ostensible objects (abstract, ideal, immaterial); extensive objects (particular) and intensive objects (general); personal (relating to individual subjects) and institutional (shared within an institution or community of practices); expression and content (antecedent or consequent of a semiotic function); unitary (objects considered globally as a whole) and systemic (considered as systems formed by structured components).
All objects are interconnected by semiotic functions, forming onto-semiotic configurations. In other words, interpreting the notion by Hjemslev ( 1943) of sign function and of semiotic function by Eco ( 1976), in the OSA a semiotic function is understood as the correspondence or dependency relation between an antecedent entity (expression, significant) and a consequent one (content, meaning) established by a subject (person or institution) according to a certain rule, habit or criterion, established in an act of communicative interaction ( GODINO, 2017). These semiotic functions can be of two types: referential (related to objects and processes referred to or mobilized in mathematical practices) or pragmatic-operational (related to the role of these practices in the resolution of the task). Consequently, both primary and secondary objects (derived from the application of dualities) can be considered from the process-product perspective, which provides criteria for distinguishing types of primary and secondary mathematical processes, leading to achieve problematization, definition, enunciation, argumentation, particularization-generalization, representation-meaning processes, etc. In the next section, these key elements are put to work in the analysis of the mathematical situation.
Networking of theories
The Networking of Theories can be accomplished in various ways, focusing on different aspects of theories “at the level of principles, at the level of methodologies, at the level of research questions, or as combination of these” ( RADFORD, 2008, p. 322), and for different purposes: “to understand other theories (and their own), to better understand a given empirical phenomenon, to develop a given theory, and, more generally, to improve teaching practice” ( PREDIGER et al., 2008 , p. 176).
In this study, we adopt the way Radford ( 2008) understands Networking of Theories as “a dynamic set of connection subsumed in the Semiosphere” (p. 319). The Semiosphere is a semiotic space where different languages and cultures meet and interact, giving rise to a dialogue. This is where one theory, reacting to the dialogue with the other, reaches the essence of the semiotic point of view, organically intrinsic to the human consciousness, according to Lotman ( 1990): the unfolding of naive knowledge within scientific ideas, the expression of what “we have always known”. With this aim, Radford ( 2008) suggests submitting, alongside integration ( PREDIGER et al., 2008 ), also identity. The dialectical tension between these two plots, in fact, generates a meta-language in which the asymmetries between the two theories are revealed and the dialogue begins. Lotman ( 1990) asserts that dialogue and asymmetries constitute the elements enabling vision and access to the Semiosphere. The asymmetries are the observables of the process of mutual knowledge and insertion into a certain common cultural world (between the two theories); which causes not only a rapprochement of the different cultures, but also their specialization: by entering a certain cultural community, culture begins to cultivate its own peculiarity more strongly. In turn, other cultures also codify it as ‘peculiar’, ‘unusual’. Instead, ‘for itself’, the isolated culture is always ‘natural’ and ‘common’ ( LOTMAN, 1990). Only by becoming part of a larger whole, it assimilates the external vision of itself and is perceived as specific. Thus, there is a functional asymmetry: ‘that works’, generates, extracts.
In the following sections, we study the dialogue between the SBA and the OSA and their asymmetries, in order to extract (to use Radford’s terms) what is often taken for granted but unnoticed.
Networking around a classroom episode
The episode
A narrative related to Penelope’s myth ( ARZARELLO, 2006a) was presented to pupils attending the final (5th) grade of an Italian Primary school. Students working in a small group were videotaped, and the videos and the children’s written productions constituted the data for the analysis from the SBA perspective in several works ( BAZZINI; SABENA; VILLA, 2009).
The problem was posed through this narration:
On the island of Ithaca, Penelope had been waiting for ten years for the return of her husband Ulysses from the war. On Ithaca, however, a lot of men wanted to take the place of Ulysses and marry Penelope. One day, the goddess Minerva told Penelope that Ulysses was returning and that his ship would arrive at Ithaca in 50 days. Penelope immediately summoned the suitors and told them: “I will choose my bridegroom among you, and the wedding will be celebrated when I have finished weaving a new piece of cloth for the nuptial bed. I will begin today, and I promise to weave [a span] every two days; and when I have finished, the cloth will be my dowry”. The suitors accepted. The cloth had to be 15 spans in length. Penelope immediately began to work, but one day she wove a span of cloth, while the following day, in secret, she undid half a span. Will Penelope choose another bridegroom? Why?
The full didactical objectives are three: social construction of mathematical knowledge; consolidation of crucial concept of grade 5; recursivity and covariance between variables (time and length) and its graphical representation, suitably coordinated for producing a mathematical model to solve the problem.
The activity has been examined by two original video recordings of the group composed of five pupils in the class: Danilo, Eugenio, Maddalena, Olivia, and Sandra (fictitious names). Essential video transcription units (Ui), whose indexes are set in chronological order, has been produced. The choice of the units to transcribe is about those that describe the class episode and the cognitive and epistemological environment developed in it.
The case study was analysed ex novo by the authors of this paper, with both the SBA and OSA theoretical lenses. Despite the fact that the former lens had already been extensively exploited for the analysis of this case study, the authors tried again with such theoretical tools, the latter – the analysis with the Onto-Semiotic Approach of the case study – was absolutely new. The two analyses with the two theoretical lenses were carried out collaboratively among the authors. Once the two analyses were carried out, both independently, the authors each on their own account applied networking strategies to what the two lenses brought as knowledge. Subsequently, in specifically dedicated meetings, the authors were able to verify that the description of the dialogue between the two theories provided by each of the three authors led to the same conclusions, which are then presented in this paper.
The genetic Semiotic Bundle enlargement and the generative function of the basic gesture
To untangle the issue, students respond with gesture, gaze, speech and drawings as they interact with one another ( ARZARELLO et al., 2006b ). Thus, the interpretation of the semiotic resources within the Semiotic Bundle allows to describe the didactical phenomena as a multimodal system developing in time. Gestures, utterances, and written signs are combined to create a cognitive environment, offering the children an opportunity to substantiate their knowledge in relation to the problem. In this instance, the mutual and multimodal interactions among the different semiotic resources form the basis of the objectification of a key idea that may grow. The development of the genetic process, in three phases, of this idea (the covariance between time and length) is shown as follows.
• Gestures only: the embodiment phase
The children read the text and then begin rephrasing, discussing, and interpreting it ( table 1). In order to contextualize the story, they focus on the actions of weaving and unravelling a span of cloth. They use different gestures: a hand sweeping on the desk, the thumb and the index or the thumb and the pinkie extended, as well as the rotation of the wrist to the right or left. Gestures allow children to identify themselves with Penelope; namely, students embody the problem.
Table 1 - Transcription units for the Gestures only phase
| U1 | Sandra: In my opinion, the cloth doesn’t come out in the end. Because, undoing and doing it again and then undoing… |
| U2 |
Eugenio : As if the cloth had to come out large like that (open and parallel hands, one in front of the other, are indicating a space interval: gesture in figure 2a) Sandra: So, she had to do the cloth to be married, but... |
| U3 | Eugenio: Yes: it is as if you had to make a piece like this […] (gesture in figure 2a): you make a piece like this (gesture in figure 2b); then you take away a piece, like this (gesture in figure 2c); then you make again a piece like this (gesture in figure 2b) and you take away a piece like this (gesture in figure 2c) |
Source: Prepared by the authors.
A peculiar gesture, two hands placed in parallel on the desk ( figure 2a) to indicate the weaving and unravelling of a piece, is introduced by a student and it is soon imitated by all the other children ( figure 2d). It becomes a shared sign for the whole group and in the semiotic bundle within which the pupils’ knowledge is about to evolve. It is called basic gesture ( ARZARELLO et al., 2006b ).
• Gestures and speech: the appraisal phase
The function of gestures is not only to immerse students into the problem, but also to create situations of the discourse where content is accessible to everyone in the group. Echoing gestures with analogous and synchronic words ( table 2), the students evolve the semiotic bundle and so the shared knowledge. The students make the narrative’s words resonate in them.
Table 2 - Transcription units for the Gestures and speech phase
| U4 |
Olivia: No, look ... because if she was making a span (basic gesture: figure 2d) and then, the day after, she was half undoing it (shifting her left hand rightward: her hands are repeating the same gesture as Eugenio, first representing doing and then undoing) and a half was left… Right? Then the day after (moving her left hand leftward and repeating the gesture) … Danilo: (interrupting) A half was always left Sandra: No, she always took away a half Danilo: Yes Olivia: Yes, but… |
| U5 |
Eugenio: It increased, yes, it increased. But imagine that she arrived at the end and took off a piece. Danilo: By a half, it increased. She does a span and takes away a half, then she does another one and she cuts it in the half, and it comes to one. Olivia: Yes, and then she does another one, takes off a half: one and a half |
| U6 |
Eugenio: Yes, but imagine that she arrives at the end and we take the calculation… but once she has finished the cloth, if it didn’t take her all the days, the fifty days … she didn’t get married, yet Olivia: It didn’t take her fifty days... because... Sandra: Because we have to count the nights, how many there are… |
Source: Prepared by the authors.
Together, gestures and words make it possible to attribute lengths to those “pieces”: the children speak about span, about half and one, and the gestures embody them. However, the named lengths—-embodied, are not yet free from their coexistence with the passage of time. Nevertheless, this coexistence and the repetition and coordination between gestures and words allow children to identify a regularity of Penelope’s production: A half was always left.
• Gestures, speech and drawing: the clue phase
A half is always left. But when? The variation in time must be separated from the variation in length. Counting time. Sandra feels the need to write down gestures, thoughts and words. She draws a representation of Penelope’s work, using her hand to measure a span on paper ( figure 3a). The previous basic gesture ( figure 2), Olivia’s “span” (U4 in table 2), becomes now a written sign. As occurred previously, also the sketch contribute to the growth of the semiotic bundle ( figure 3).
To promote understanding in this key phase, table 3 translates the dialogue into the units of analysis U7-U13.
Table 3 - Transcription units for the Gestures, speech, and drawing phase
| U7 |
Sandra: A span would be this one ( figure 3a) Olivia: Yeah, but it doesn’t matter Danilo: Five spans divided by half a span … How long is a span more or less? 10 cm? Olivia: But it doesn’t matter how long it is |
| U8 |
Sandra: A span plus another one, (she repeats the gesture of figure 3a by moving her hand to the right and tracing a second vertical mark) plus...a half and a half (she marks the middle of each span) .. . so it is one half anyway! So, in two nights she makes… Eugenio: Sorry but, with a span she reaches a point, with two spans… Sandra: … in two years... |
| U9 |
Sandra: … there are two spans! Eugenio: A span is 25 cm long Olivia: Yes, but it doesn’t matter how long it is! You don’t have to measure! |
| U10 | Sandra: There we go! These are two spans. (She traces a line, the mid of figure 3b, indicating the separation between a span and the other. At this moment, in the figure there are only 5 vertical marks and the separation mark just drawn down). |
| U11 | Eugenio: Yeah . . . It does matter, because you make a half of 25, getting… |
| U12 |
Sandra: Wait! If I do take off one half, so this part disappears. (She traces a sort of deleting marks on the first half of each of the two spans drawn, see figure 3b.) It still remains a span. Therefore, in two days she makes a span. Eugenio: Yeah! She makes one in other two days |
| U13 |
Olivia: No, four [days]...four, because... Sandra: In four [days] she makes two [spans] Olivia: No Sandra: Because … plus this one (she traces the curve under the traits in figure 3b)… it’s a span with this one (indicating the last part) Olivia: In four [days] she makes one [span], because (she reads the text): one day she weaves a span and the day after she undoes a half |
Source: Prepared by the authors.
During the discussion, the children turn the sketch ( figure 3a) into a diagram ( figure 3b). The white space indicates the weaving act, oblique lines (deletion marks) symbolize the unravelling, vertical lines signalize the elapsed time. Sandra is forced to represent the cloth with gaps due to the inherent rigidity of the drawing: to indicate that the half-spans were linked together over time a curve was added at the bottom. Getting to know the problem, previously embodied in gestures, is now drawn: parallel swiping hands and wrist rotation are now written signs. A genetic relationship between the basic gesture, its synchronic words, and the diagram is manifest. Using the written signs, the children climb the crucial step of understanding that it takes Penelope four days to weave one span of cloth. The entire generated semiotic bundle has had the generative function in the correct management of the covariance of the variables; early algebra processes can be detected. Indeed, starting from Olivia’s local rule: “In four [days] she makes one [span],” children are able to reach the end of the story, integrating the tools that they have made up (gestures, speech and drawing) by using some arithmetic.
Within the SBA, the blossoming of different semiotic resources is observed, and they grow together in an integrated way. A richer and richer semiotic bundle is generated, where the students can act and interact to grasp the problem, to explore it, and to elaborate solutions. Students develop and share their semiotic activities and generate different signs to cope with the problem. This process allows students to internalize its mathematical competencies.
Analyzing the Semiotic Bundle enlargement with the OSA theoretical tools
This section shows the knowledge put into play by the students using the onto-semiotic configuration tool. The resolution process is developed as a succession of practices that are gradually manifested, which progressively provides arguments for the various propositions expressed by the children. The sequence of the decisive steps has a deductive justification that can be grasped only by looking at the whole system of practices. table 4, table 5, and table 6 synthetize the onto-semiotic configuration and the semiotic functions involved in the mathematical practices. The column on the right indicates the role, or function, that each practice plays in the resolution process; the central column describes the objects referred to in the mathematical practices of the left column.
The Gestures only phase of the Semiotic Bundle evolution over time comprises three transcription units (U1, U2, and U3 in table 1). In U1, we find, above all, a translation from the natural language of the problem text to the gestural and natural/oral language of children. In the sense of Duval’s (2006) theory, a transformation is witnessed from the natural register to the gesture, and a treatment within the gestural register. Weaving and unravelling, adding, and removing: this gestural repetition allows a – perhaps premature and acerbic – birth of the concept of variable, which begins to feel the need coming from the physical process of building the cloth, Penelope´s action. U2 and U3 hold linguistic registers, but the use and purpose of the practices differ from U1. In U2, Sandra’s discursive practice has the role of conforming and reaffirming her own U1 proposition and Eugenio’s expression. The child is trying to evoke and set a total and final length, in order to later compare the partial length that develops during the addition and subtraction of spans and half spans. We can also denote an interpretation of gestural language (segment idea, parallel hands) to oral language. U3 shows an advance compared to the current configuration; gestures allow to describe Penelope’s weaving procedure. In each case, in onto-semiotic terms, the concept is an emergent of a mathematical practices system carried out by the student regarding the proposed task, thus highlighting the personal dimension of meaning; in this system of practices a specific onto-semiotic configuration is activated ( table 4).
Table 4 - OSA practice units associated with the Gestures only phase of the Semiotic Bundle enlargement
| Operative and discursive practices | Objects referenced in the practices | Use and purpose of the practices |
| U1 |
Languages: natural; gestural Concepts: magnitude (length); quantity Proposition: “the cloth doesn’t come out” |
To give a first interpretation of the problem and its intuitive solution. |
| U2 |
Languages: natural; gestural Concepts: segment; extremes: origin and end; fixed length; quantity; size Propositions: “it had to come out large like that”; “had to do the cloth” Procedure: comparison of lengths |
To locate the final length, the reference, in order to confirm and reaffirm the first interpretation and solution. |
| U3 |
Languages: natural; gestural Concepts: variables (length and time); repetition; variation |
To express the quantities of lengths and their variations |
Source: Prepared by the authors.
table 5 shows the OSA interpretation for the Gestures and speech phase of the Semiotic Bundle evolution (transcription units U4, U5, and U6 in table 2).
Table 5 - OSA practice units associated with the Gestures and speech phase
| Operative and discursive practices | Objects referenced in the practices | Use and purpose of the practices |
| U4 |
Languages: natural; gestural Concepts: covariation: relation; unit of measure (span); fraction (half) Procedure: a sequence of steps expresses the increased length as a function of time Propositions: “she was making a span... A half was always left” |
To express/describe the process of length variation as a function of time. |
| U5 |
Languages: natural; gestural Concepts: quantities; sums and subtractions Propositions: “It increased… By a half” Argumentation: fixed i=1/2 span, (1-1/2)+(1-1/2)= i+i=1 span; 1+(1-1/2)=1+i… |
To qualify the covariation and to quantify the increase. |
| U6 |
Language: natural Concepts: magnitude (time); quantities (50 days and final length of the cloth) Proposition: “It didn’t take her fifty days.” Argumentation: “Because we have to count the nights, how many there are...” |
To qualify covariation: describing the maximum amount of time and counting the used time. |
Source: Prepared by the authors.
Finally, table 6 considers the Gestures, speech and drawing phase of the Semiotic Bundle genetic process. U7, U9, and U11 transcription units are merged, although they do not occur sequentially: these units are, at times, contextualized into the problem itself and, at other times, they adopt an institutional character. In addition, the children estimate the length in centimeters of a span, but this procedure turns out to be an obstacle in solving the problem; yet, this leads them to a drawing for which the sketch proposed by Sandra in U8 and U10 will be the turning point. Sandra proposes a drawing representing two half-split spans as a resolution procedure. To get to the new linguistic register, transformation is not immediate in the girl (she reasoned out loud), but rather spontaneous. By relating gestures, drawings and words, the children discover a constant that correlates time and length within U12. Finally, in U13 they find the local rule for the resolution of the problem. The system of practices includes re-reading the text, so the students understand the covariation between the time interval and the length of the cloth, choices unitary variables (ostensive facet).
Table 6 - OSA practice units associated with the Gestures, speech, and drawing phase
| Operative and discursive practices | Objects referenced in the practices | Use and purpose of the practices |
| U7/U9/U11 |
Languages: natural; gestural; graphic Concept: units of measure (span and cm) Proposition: “A span is 25 cm long” Procedure: estimation Argumentation: empirically: sketch of a span and measurement with tool (ruler) |
To estimate a unit of measure that is concrete, known and practical. |
| U8/U10 |
Languages: natural; gestural; graphic Concept: units of measure (length and time) Procedure: draw (graphic representation) |
To explain graphically and visually the unit of measurement sought. |
| U12 |
Languages: natural; gestural; graphic Concepts: increase; ratio; function (covariation) Proposition: “in two days she makes a span” Argumentation: (1-1/2)+(1-1/2)=1 span, in 2 days |
To discover a constant, a ratio, that relates time and length: to set the covariation. |
| U13 |
Languages: natural; gestural; graphic Concepts: variables; function (covariation); ratio. Proposition: “No, four [days]…four, because…” Argumentation: 1-1/2=1/2 span, in 2 days |
To correct Sandra’s erroneous argumentation and to make a new argument for a correct solution. |
Source: Prepared by the authors.
The outlined systems of practices above reveal configurations of mathematical objects that can be considered non-ostensive (abstract) or ostensive (material), as shown in figure 1. Thus, the meanings of the mathematical objects are characterized in terms of these epistemic configurations. However, these meanings are not static entities since there are processes involved through the mathematical practices. These processes allow to achieve a holistic view of the class episode, considering the different ways in which individuals build or negotiate the meaning of the emerging objects:
• Meaning-representation processes
Practices and objects reveal processes of meaning and representation that the subject that solves the problem implicitly performs, in this case, the children. The transcription units refer to the ostensive objects making up the elementary practices that are the expression or antecedent of the semiotic function that is established with the objects identified in the second column in table 4, table 5, table 6, which are the corresponding contents or meanings of those semiotic functions. They are semiotic functions of pragmatic-operational type: each practice is interpreted in terms of its role in the resolution process. This analysis of the semiotic functions, and therefore of the mathematical knowledge that are put at stake in the resolution process, is not thorough. Each elementary practice can, in turn, be decomposed into other constituent elements, which play their own role within each practice and refer to other non-ostensible objects.
• Institutionalization-personalization processes
Children are spontaneously brought to work in a strictly personal environment, so it is necessary to contextualize the exercise. The context helps the child to move in a space that he or she knows or could know naturally and think spontaneously. However, children are influenced by an institutional frame they know they have to come to. Therefore, for example, they are distracted by the idea of measuring the length of a span in centimeters, that is, using an institutional reference system.
• Idealization-materialization processes
The identified objects have an ostensible (visible) and a non-ostensive (ideal, abstract) facet ( GIACOMONE, 2018). In our case, we can see an idealization of an empirical object, Penelope’s cloth, which will serve as a reference for constructing the concept of covariation between length (spans) and time. Children need ostensible objects to communicate the solution to the problem, so by using gestures and drawings, we see them representing the two concepts many times. Thus, the drawings and gestures are a materialization of an ideal object, based on which we intend to perform the mathematical modelling required for the resolution of the task.
• Decomposition-reification processes
The unitary-systemic duality is linked to the processes of reification (constitution of objects as a whole) and decomposition (inverse). In this case, the previously studied configuration has to be considered as a system in order to be learned (systemic perspective). However, it is important that, gradually, the children make progress towards a unitary perspective that must be decomposed into different elements; such a process is required. This process is clear when children switch from describing what happens day by day to, at the end of the episode, describing what happens every two or four days.
• Generalization-particularization processes
In this case, the children struggle to reach a generalization. We start to appreciate it only in the last line. Primary school children are brought to work on special cases, so the teacher’s intervention is needed to develop this process, but this was not the goal of this work phase.
These processes take into account how the meanings of the objects which emerge from the mathematical practices are negotiated. For instance, the personal meanings of the students are confronted with the institutional meaning, from which the teacher has implemented the didactical sequence.
Asymmetries and dialogue on mathematical objects and processes: networking consideration
In our research work, we have referred to the networking of theories both as a tool to grasp and interpret the learning processes of mathematics in their complexity (with reference to the specific classroom episode taken in analysis) and as a tool to analyze and reflect on the theories themselves (meta-reflection). In particular, from the methodological point of view, the analyses have been carried out at a micro-analytical level. The discussion among the students was transcribed and codified, focusing on mathematical objects and processes, but also taking into account the modality and context in which they are expressed. The transcriptions of the dialogues have been enriched with the freeze-frames of the video recording to which they correspond, in an effort to highlight the correspondence between the different semiotic resources in play. The resulting “multimodal transcription” was then analyzed in detail through the interweaving of the methodological tools of the two theories, SBA and OSA, starting from the fundamental assumption that both are immersed in a Semiosphere. The latter is a founding element, an environment, the context, which allows the dialogue and collaboration between the two approaches.
The analysis with OSA tools favors a description of the institutional practices to solve the required task and of the configuration of mathematical objects and processes involved, by which it reveals the onto-semiotic complexity of these configurations (a priori epistemic analysis). The aim of this a priori analysis, which has not been presented in this paper, is to identify and express the constructs that the task intended the students to grasp.
On this foundation, the onto-semiotic configuration of practices, objects, and processes can enrich the semiotic bundle since these configurations articulate the dialectic between ostensive objects and non-ostensive objects (concepts, propositions, procedures and arguments) highlighted by the OSA. In fact, SBA is a lens for reading multimodal and non-modular cognitive activity: neurons, in learning processes, are activated both at the level of action and perception and are already integrated at the level of the sensory-motor system and not “via higher association areas” ( GALLESE; LAKOFF, 2005, p. 459). Attention to multimodality enables to grasp the coexistence and importance of different modalities or resources in learning and teaching processes related to the embodied nature of mathematical knowledge. Then, the semiotic analysis considers each of these resources as important signs for learning and teaching processes. Perceptive-motor and embodied activities play a prominent role also in abstract thought (non-ostensive), which is characteristic of mathematical discourse. So, alongside embodied cognition a pillar of the SBA, which has provided an operational analysis tool for relating the body to concepts in cognitive learning, the onto-semiotic configuration allows a zoom in on the situational (situation-problems, phenomena), conceptual, propositional, procedural, and argumentative elements.
The multimodality of the studied phenomena, because of its relevance in pupils’ learning processes, includes a focus on the learners’ gestures in addition to the other signs. The analysis of gestures through the semiotic bundle has provided a basis for a reconstruction of epistemic processes, integrating gestures as part of the multimodal intervention in which they were produced epistemically. For this, paying attention also to gestures enriches the concept of semiotic function and allows a thrust on the teaching and learning processes in their multimodality. The notion of semiotic function, introduced by OSA, allows to provide a detailed explanation about what is the pupils’ cognitive activity to give their answers.
Does this dialogue between SBA and OSA, as we have so far discussed, allow to look at gestures as mathematical objects? Mathematical objects, in OSA analysis, are like the characters of a story that develops over time through various practices. As an example, we intend to draw attention to the U2 unit of practice when Eugenio says “...large like this” and makes the gesture shown in figure 2a: open and parallel hands, indicating the final fixed length. In this gesture (type of language) the following objects could be recognized (see the second column in table 4): concepts of segment, edges, origin and end, fixed length etc.; proposition “...large like that”; and it seems natural to insert the gesture in figure 2a. In fact, here we go beyond simply emphasizing the systematic aspect of representations in mathematics, gestures are also considered signs. So, from the OSA point of view, gestures, as part of language, are primary objects that contribute to the emerging meaning from a particular mathematical practice, and therefore they are called mathematical objects, at the same level as propositions, arguments, etc. However, gestures in SBA play a central role, and they are interpreted considering all the other elements in the bundle. This interpretation of a gesture, however, strictly depends on the referential context of the activity and of the subjects (here, the children) involved in the activity. The cultural aspects they reveal cannot be ignored. The cultural, social, and historical dimension in which mathematical concepts are born and evolve, including gestures, is of paramount importance ( RADFORD et al., 2008). Moreover, in its presuppositions on the mathematics’ nature, the OSA is supported by an anthropological approach, in line with the philosophy of the mathematics of Wittgenstein ( 1953). Although the theoretical role played by gestures is different in each framework, both of them share this pragmatist view of the mathematical activity.
In the collaboration between these two frameworks, one can certainly see a fruitful repercussion for the analysis of teaching and learning processes as we have been able to identify inspirational asymmetries (to keep use Lotman’s terms).
Final remarks
In this article, a theoretical reflection has been raised from the analysis of a problem-situation considering two theoretical lenses for didactic analysis: Semiotic Bundle and Onto-Semiotic Approaches. By presenting an empirical case of Networking of Theories, our effort has been to bring the two approaches into dialogue, reading the asymmetries found between their languages, with the aim of getting some new insights into the problem of analyzing episodes of the resolution of arithmetic-algebraic tasks.
In the didactic analysis shown on Penelope’s problem, the two approaches shared some conclusions and complemented one another in other aspects. The findings were often in agreement with each other but offered different perspectives. On the one hand, it is revealed how two different theories can frame in a complementary way the semiotic (or ostensive) dimension of mathematical activity in how they approach teaching and learning phenomena. The two perspectives coincide in the same subject: the importance given to ostensive objects (gestures, discourses, written symbols, etc.) not only as signs but also as essential tools of mathematical practices. It was helpful to explain explicitly that OSA is a theoretical approach to Mathematics Education, which incorporates a system of conceptual notions for different facets involved in the teaching and learning of mathematics.
On the other hand, SBA has a strong cognitive orientation insofar as it looks at the learning and teaching of mathematics through the integrated lens of the embodied semiotic resources used. Differences between OSA and SBA, and this has been a major achievement of our dialogue, lie mainly in the ontological accommodation of gestures, but both of them recognize the role of gesture in the process of constructing meaning and share a pragmatist point of view. Therefore, the two theories meet in focusing on the specific components that make mathematics learning possible, and particularly pointing out the micro and macro processes that support it.
Of course, we are aware of the limits of our efforts. In order to delve into the complementarities between theories, we should also explore other contents (algebra, geometry, probability), using other kinds of problem as well as other educational levels. In fact, it is possible that, for some of these contents, gestures do not have as much relevance in classroom episodes. Each theory emphasizes some aspects to the detriment of others; hence, establishing a dialogue between them is certainly useful for research. The general idea of networking is not intended to limit the theories within a single framework, but to observe their Semiosphere, within which it is possible to capture the continuous flow from one language to another. In this regard, the different intuitions that those approaches can give to specific learning problems are made explicit and thus functional.