Introdução
Sabe-se que a Estatística e a Probabilidade são componentes de extrema importância nos dias atuais, pois a todo o momento as pessoas se deparam com incertezas e variabilidades que influenciam diretamente na tomada de decisões, bem como com elementos que requerem a interpretação e organização de dados, leitura de gráficos e afins, tornando-se esse, assim, um saber indispensável para a melhor compreensão do mundo.
No entanto, destaca-se que o estudo e a apropriação efetivos desses componentes perpassam pela inclusão da Estatística e da Probabilidade no currículo de Matemática e pela formação de professores que atuam lecionando em turmas desde os anos iniciais da educação básica. É o que aponta Lopes (2008, p. 61) ao defender que “os conceitos probabilísticos e estatísticos devem ser trabalhados desde os anos iniciais da educação básica para não privar o estudante de um entendimento mais amplo dos problemas ocorrentes em sua realidade social”.
Lopes (2008) propõe que esses conceitos devem ser trabalhados de modo que as atividades propostas partam de uma problematização, desenvolvendo uma prática pedagógica em que sejam exploradas ações que possibilitem uma experimentação concreta, de coleta e de organização de dados, considerando situações vinculadas ao cotidiano dos alunos.
Além disso, a autora destaca que a inclusão da Estatística e da Probabilidade como um tópico “à parte” a ser estudado em um ou outro ano da escolaridade da educação básica apenas reforça o uso de fórmulas, o que pode comprometer o desenvolvimento dos pensamentos estatístico e probabilístico. Nesse ponto, cabe lembrar que, tradicionalmente, o ensino de Matemática tende à exatidão e ao determinismo em detrimento a situações que abordem a aleatoriedade e a aproximação, o que, segundo a autora, além de limitar a visão matemática que o aluno poderá desenvolver, pode ainda “dificultar suas possibilidades de estabelecimento de estratégias para a resolução de problemas diversificados que lhe surgirão ao longo de sua vida” (Lopes, 2008, p. 63).
Cumpre destacar que a Matemática e a Estatística são ciências diferentes. Enquanto a Matemática lida com a certeza, a Estatística lida com dados que só fazem sentido dentro de um contexto. Desse modo, um outro ponto a ser discutido refere-se às lacunas deixadas durante os processos de formação tanto inicial quanto continuada de professores da educação básica. Nesse sentido, Lopes (2014) relata que:
[...] pesquisas atuais denunciam o pouco preparo do professor para efetivar o ensino e a aprendizagem da estocástica. A formação inicial e contínua dos professores que ensinam Matemática na Educação Básica não tem preparado esses profissionais para o domínio teórico-metodológico da Educação Estatística (Lopes, 2014, p. 527).
Ainda nesse sentido, Echeveste et al. (2005) comentam que a falta de preparo dos professores, aliada à escassez de recursos pedagógicos, faz com que os docentes prefiram não trabalhar com esse conteúdo. De fato, se pensarmos que os educadores não se sentem preparados para inserir atividades problematizadoras em suas aulas, o ensino da Probabilidade e da Estatística poderia se estabelecer de modo errôneo, ou mesmo abrir espaço para blocos “mais convencionais” como os relacionados à álgebra e à geometria, deixando os conteúdos de Estatística e Probabilidade em “segundo plano”.
Nessa perspectiva, Lopes (2008) aponta que a formação do educador matemático que atuará na educação básica deve abarcar um processo de ensino e aprendizagem que contemple a resolução de problemas, simulações e experimentos, que permitam ao profissional construir conhecimentos enquanto estabelece relações com informações adquiridas.
É nesse sentido que o presente artigo visa apresentar e discutir uma proposta para o ensino de Probabilidade considerando o jogo campo minado. Apresentam-se duas atividades que podem ser implementadas em espaços formativos envolvendo licenciandos e/ou professores da educação básica ou, ainda, podem ser utilizadas por professores que ensinam Probabilidade e Estatística na educação básica.
O que está previsto para o ensino e aprendizagem de Probabilidade na educação básica brasileira?
Visando compreender o que está previsto curricularmente acerca do ensino de Probabilidade na educação básica, recorreu-se aos documentos curriculares brasileiros, sendo eles: os Parâmetros Curriculares Nacionais (PCN) (Brasil, 1997, 1998); as Orientações Curriculares Nacionais para o Ensino Médio (PCNEM) (Brasil, 2006) e a Base Nacional Comum Curricular (BNCC) (Brasil, 2017).
No Quadro 1 é apresentada uma comparação acerca das prescrições curriculares para os anos iniciais e finais do ensino fundamental e do ensino médio.
Quadro 1. Documentos curriculares brasileiros e orientações quanto ao Ensino de Probabilidade nos anos iniciais do Ensino Fundamental.
| Documento | Ciclo/Ano | Citação/Habilidade | |
| Anos iniciais do Ensino Fundamental | PCN | 1º e 2º Ciclos* | Com relação à Probabilidade, a principal finalidade é a de que o aluno compreenda que grande parte dos acontecimentos do cotidiano são de natureza aleatória e é possível identificar prováveis resultados desses acontecimentos. As noções de acaso e incerteza, que se manifestam intuitivamente, podem ser exploradas na escola, em situações nas quais o aluno realiza experimentos e observa eventos (em espaços equiprováveis) (Brasil, 1997, p. 40). |
| BNCC | 1º Ano | Classificar eventos envolvendo o acaso, tais como “acontecerá com certeza”, “talvez aconteça” e “é impossível acontecer”, em situações do cotidiano (Brasil, 2017, p. 281). | |
| 2º Ano | Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis”, “muito prováveis”, “improváveis” e “impossíveis” (Brasil, 2017, p. 285). | ||
| 3º Ano | Identificar, em eventos familiares aleatórios, todos os resultados possíveis, estimando os que têm maiores ou menores chances de ocorrência (Brasil, 2017, p. 289). | ||
| 4º Ano | Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações (Brasil, 2017, p. 293). | ||
| 5º Ano | Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não (BRASIL, 2017, p. 297). Determinar a Probabilidade de ocorrência de um resultado em eventos aleatórios, quando todos os resultados possíveis têm a mesma chance de ocorrer (equiprováveis) (Brasil, 2017, p. 297). | ||
| Anos Finais do Ensino Fundamental | PCN | 3º e 4º Ciclos** | Com relação à Probabilidade, a principal finalidade é a de que o aluno compreenda que muitos dos acontecimentos do cotidiano são de natureza aleatória e que se podem identificar possíveis resultados desses acontecimentos e até estimar o grau da possibilidade acerca do resultado de um deles. As noções de acaso e incerteza, que se manifestam intuitivamente, podem ser exploradas na escola, em situações em que o aluno realiza experimentos e observa eventos (em espaços equiprováveis) (Brasil, 1998, p. 52) |
| 6º Ano | Calcular a Probabilidade de um evento aleatório, expressando-a por número racional (forma fracionária, decimal e percentual) e comparar esse número com a Probabilidade obtida por meio de experimentos sucessivos (BRASIL, 2017, p. 305). | ||
| BNCC | 7º Ano | Planejar e realizar experimentos aleatórios ou simulações que envolvam cálculo de Probabilidades ou estimativas por meio de frequência de ocorrências (Brasil, 2017, p. 311). | |
| 8º Ano | Calcular a Probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das Probabilidades de todos os elementos do espaço amostral é igual a 1 (Brasil, 2017, p. 315). | ||
| 9º Ano | Reconhecer, em experimentos aleatórios, eventos independentes e dependentes e calcular a Probabilidade de sua ocorrência, nos dois casos (Brasil, 2017, p. 319). | ||
| Ensino Médio | PCNEM | 1º ao 3º ano | Ao estudar Probabilidade e chance, os alunos precisam entender conceitos e palavras relacionados à chance, incerteza e Probabilidade, que aparecem na nossa vida diariamente, particularmente na mídia. Outras ideias importantes incluem a compreensão de que a Probabilidade é uma medida de incerteza, que os modelos são úteis para simular eventos, para estimar Probabilidades, e que algumas vezes nossas intuições são incorretas e podem nos levar a uma conclusão equivocada no que se refere à Probabilidade e à chance (Brasil, 2006, p. 79). |
| BNCC | 1º ao 3º ano | Identificar situações da vida cotidiana nas quais seja necessário fazer escolhas levando-se em conta os riscos probabilísticos (usar este ou aquele método contraceptivo, optar por um tratamento médico em detrimento de outro etc.) (Brasil, 2017, p. 533) Identificar e descrever o espaço amostral de eventos aleatórios, realizando contagem das possibilidades, para resolver e elaborar problemas que envolvem o cálculo da Probabilidade (Brasil, 2017, p. 537) Resolver e elaborar problemas que envolvem o cálculo de Probabilidade de eventos em experimentos aleatórios sucessivos (Brasil, 2017, p. 537) Reconhecer a existência de diferentes tipos de espaços amostrais, discretos ou não, e de eventos, equiprováveis ou não, e investigar implicações no cálculo de Probabilidades (Brasil, 2017, p. 541). |
Notas: *1º Ciclo (faz referência a 1ª e 2ª série; 2º Ciclo (faz referência a 3ª e 4ª série); ** 3º Ciclo (faz referência a 5ª e 6ª série); 4º Ciclo (faz referência a 7ª e 8ª série).
Fonte: Elaborado pelos autores (2022)
Os documentos curriculares aqui apresentados têm o objetivo de nortear, ser um referencial, durante a elaboração de currículos regionais e locais. A BNCC, documento curricular mais atual, ainda estabelece competências (gerais e específicas) e habilidades que os alunos precisam desenvolver ao longo da educação básica.
Com relação à definição das habilidades, a BNCC diz que “[...] a progressão ano a ano se baseia na compreensão e utilização de novas ferramentas e também na complexidade das situações-problema propostas, cuja resolução exige a execução de mais etapas ou noções de unidades temáticas distintas” (Brasil, 2017, p. 275).
Ao observar as citações e habilidades trazidas pelos dos documentos curriculares presentes no Quadro 1, percebe-se que há indicações para que o ensino e a aprendizagem de Probabilidade sejam articulados desde os anos iniciais do ensino fundamental. A BNCC de Matemática do ensino fundamental (Brasil, 2017) propõe cinco unidades temáticas, assim designadas: Números, Álgebra, Geometria, Grandezas e Medidas, Probabilidade e Estatística.
Olhando em particular para a unidade temática Probabilidade e Estatística, de acordo com a BNCC, o estudo desse componente nos anos iniciais do ensino fundamental tem a finalidade de:
[...] promover a compreensão de que nem todos os fenômenos são determinísticos. Para isso, o início da proposta de trabalho com Probabilidade está centrado no desenvolvimento da noção de aleatoriedade, de modo que os alunos compreendam que há eventos certos, eventos impossíveis e eventos prováveis. É muito comum que pessoas julguem impossíveis eventos que nunca viram acontecer. Nessa fase, é importante que os alunos verbalizem, em eventos que envolvem o acaso, os resultados que poderiam ter acontecido em oposição ao que realmente aconteceu, iniciando a construção do espaço amostral (Brasil, 2017, p. 274).
Já para os anos finais do ensino fundamental, a BNCC sinaliza que:
O estudo deve ser ampliado e aprofundado, por meio de atividades nas quais os alunos façam experimentos aleatórios e simulações para confrontar os resultados obtidos com a Probabilidade teórica - Probabilidade frequentista. A progressão dos conhecimentos se faz pelo aprimoramento da capacidade de enumeração dos elementos do espaço amostral, que está associada, também, aos problemas de contagem (Brasil, 2017, p. 274).
No âmbito do ensino médio, a BNCC propõe a construção de uma visão integrada da Matemática, aplicada à realidade dos estudantes. Nessa perspectiva, almeja-se “[...] a consolidação, a ampliação e o aprofundamento das aprendizagens essenciais desenvolvidas no Ensino Fundamental” (Brasil, 2017, p. 527). Assim, os conceitos que envolvem a unidade temática Probabilidade e Estatística podem ser abordados numa perspectiva espiral de conhecimento ao longo do período de escolarização.
Os PCN, por sua vez, propõem os seguintes blocos de conteúdo: Números e Operações, Espaço e Forma, Grandezas e Medidas e Tratamento da Informação. Abordar-se-á, em especial, o bloco Tratamento da Informação, que é constituído por “[...] estudos relativos a noções de Estatística e de Probabilidade, além dos problemas de contagem que envolvem o princípio multiplicativo” (Brasil, 1997, p. 52). Em relação aos anos iniciais do ensino fundamental, os PCN sugerem que: “[...] a principal finalidade é a de que o aluno compreenda que grande parte dos acontecimentos do cotidiano são de natureza aleatória e é possível identificar prováveis resultados desses acontecimentos” (Brasil, 1997, p. 40).
Já em relação aos anos finais do ensino fundamental, os PCN seguem a mesma linha apresentada anteriormente, porém com certo aprofundamento, no sentido que
[...] a principal finalidade é a de que o aluno compreenda que muitos dos acontecimentos do cotidiano são de natureza aleatória e que se podem identificar possíveis resultados desses acontecimentos e até estimar o grau da possibilidade acerca do resultado de um deles (Brasil, 1998, p. 52).
Nessa etapa, as situações relacionadas à ideia de Probabilidade devem abarcar a construção do espaço amostral como referência para estimar a construção desse conceito, utilizando-se de uma razão. Durante os anos finais do ensino fundamental, os conceitos relacionados à Probabilidade continuam a ser explorados de maneira informal, por meio de investigações que culminem em previsões a respeito do sucesso de um evento (Brasil, 1998).
Por meio das habilidades e citações até aqui destacadas, é possível inferir que o estudo de Probabilidade, nos anos iniciais do ensino fundamental, converge para proposições de situações problematizadoras do cotidiano que envolvam os conceitos de acaso e que possibilitem identificar, classificar e compreender eventos de natureza aleatória. Posteriormente, nos anos finais, percebe-se que alguns conceitos são inseridos gradativamente, como a representação, por meio de um número racional (forma fracionária, decimal e percentual), da probabilidade de acontecer um evento aleatório, conceitos de Análise Combinatória (como o princípio multiplicativo) e reconhecimento de eventos dependentes e independentes. Por fim, o ensino médio insere-se numa perspectiva de aprofundamento e consolidação dos conceitos estudados anteriormente.
Até o presente momento, alguns assuntos importantes foram abordados: análise do que dizem as pesquisas que tratam do estudo de Probabilidade na formação de professores; uma investigação sobre o que está previsto para ser ensinado na educação básica sobre Probabilidade, além de uma breve discussão acerca da educação Estatística.
Diante do exposto, dessas demandas de formação e das habilidades e competências que os documentos curriculares trazem, a elaboração de uma proposta que ajude a atenuar o cenário anteriormente descrito mostra-se pertinente. Dessa forma, com essas informações em mente e com o aporte teórico em mãos, será apresentada e discutida uma atividade para o ensino de Probabilidade baseada no jogo campo minado
O campo minado
De acordo com Viensci (2009), a primeira aparição do jogo desenvolvido por Robert Donner ocorreu em 1989, com o lançamento do Windows 3.1. Desde então esteve sempre incorporado ao sistema operacional Windows (ou disponível para download), possuindo ainda versões para outros sistemas operacionais e para celulares.
Salienta-se que há várias opções do jogo campo minado disponíveis, como o multijogador (online), na qual é possível jogar em dupla, desafiar e ser desafiado por pessoas de diferentes regiões e até mesmo de outros países. Algumas outras opções possuem características únicas, como a possibilidade de habilitar ou desabilitar o tempo disponível para se efetuar uma jogada (o que, a depender da versão, pode gerar um acréscimo na pontuação quando essa função é ativada), entre outras coisas. Neste trabalho, particularmente, será usada uma alternativa do jogo que se joga individualmente, mas que ainda, no decorrer das atividades, possibilita discussões coletivas. Além disso, a opção utilizada possui tempo livre para efetuar as jogadas, de modo que os participantes tenham tranquilidade para pensar e desenvolver suas estratégias.
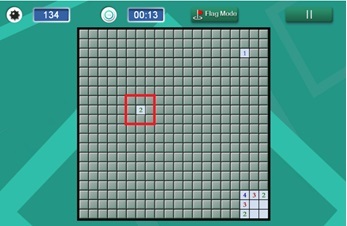
O jogo, em geral, consiste em um tabuleiro retangular (constituído por quadrados de tamanhos iguais) de tamanho variável em que uma quantidade também variável de bombas é disposta de maneira aleatória. Por exemplo, um tabuleiro de dimensão 20 por 20, 400 “quadradinhos”, nos quais 134 bombas estarão distribuídas aleatoriamente. O objetivo do jogo é descobrir todos os quadrados que não contenham minas. Cada casa (quadrado) pode ser revelada clicando sobre ela; caso o jogador acerte uma casa que contém uma bomba, o jogo termina e as demais bombas são reveladas. Por outro lado, caso o quadrado não contenha uma mina, uma destas duas coisas acontecerá:
Um número entre 1 e 8 aparece, indicando quantas minas existem ao redor dessa casa. Na Figura 1, na região em vermelho, observa-se que existem duas minas adjacentes à casa com o número 2;
Nenhum número aparece. Quando isso acontece, significa que não há bombas ao redor do quadrado em que foi efetuado o clique, daí o jogo automaticamente abre todas as casas ao redor daquela até encontrar alguma(as) casa(s) que possua uma mina ao redor.
O jogador ganha se conseguir revelar todas as casas que não contenham bombas. Considerando esse recurso e as discussões apresentadas acerca das prescrições curriculares para o ensino de Estatística e Probabilidade, a seguir é apresentado o percurso de elaboração da proposta.
Processo de elaboração da proposta
O objetivo do presente artigo é apresentar e discutir uma proposta para o ensino de Probabilidade envolvendo o jogo campo minado. A proposta leva em consideração a perspectiva da pesquisa qualitativa que, segundo Garnica (2004), possui as seguintes características:
(a) a transitoriedade de seus resultados; (b) a impossibilidade de uma hipótese a priori, cujo objetivo da pesquisa será comprovar ou refutar; (c) a não neutralidade do pesquisador que, no processo interpretativo, vale-se de suas perspectivas e filtros vivenciais prévios dos quais não consegue se desvencilhar; (d) que a constituição de suas compreensões dá-se não como resultado, mas numa trajetória em que essas mesmas compreensões e também os meios de obtê-las podem ser (re)configuradas; e (e) a impossibilidade de estabelecer regulamentações, em procedimentos sistemáticos, prévios, estáticos e generalistas (Garnica, 2004, p. 86).
A proposta se apresenta com a intencionalidade de contribuir com espaços de formação de professores e, também, com os processos de ensino e de aprendizagem de Probabilidade e Estatística no ensino médio. Além disso, como a presente proposta apresenta elementos tanto dos anos inicias quanto dos anos finais do ensino fundamental, pode-se adaptá-la de modo a atender as demandas desses respectivos níveis de ensino.
Devido à grande proximidade do par tecnologia-jogo com a realidade dos alunos e, considerando sua importância para o currículo de Matemática, procurou-se estruturar duas atividades que valorizassem a experimentação e que possibilitassem o desenvolvimento do pensamento probabilístico e do raciocínio lógico.
Para elaborar essa proposta, os autores buscaram respaldo nos pressupostos da autora Lopes (2008), além de terem tentado contemplar as diretrizes da BNCC de modo a resgatar elementos previstos para os anos iniciais do ensino fundamental e introduzindo elementos dos anos finais do mesmo ciclo. Além disso, destaca-se aqui que, ao fazer uso de dispositivos móveis (ou computadores) que dinamizam o ensino de Matemática, “[...] o estudo da Probabilidade em particular, transforma-se em alternativas que possam ser acrescentadas significativamente às atividades escolares para alunos e professores nas aulas de matemática” (Souza, 2015, p. 95), o que favorece o estabelecimento de uma relação professor-aluno que torna o aluno protagonista nos processos de ensino e aprendizagem.
A seguir, será detalhada cada uma das duas atividades e os aspectos conceituais e procedimentais que cada uma delas demanda serão discutidos.
Apresentação e discussão da atividade 1 da proposta para o ensino de Probabilidade envolvendo o jogo campo minado
A partir da experimentação dos elementos/recursos presentes no jogo, será apresentada uma proposta de atividade que possibilite desenvolver conceitos de Probabilidade de modo a auxiliar o professor na inserção do tema nas aulas de Matemática, bem como “Identificar, em eventos familiares aleatórios, todos os resultados possíveis, estimando os que têm maiores ou menores chances de ocorrência” (Brasil, 2017, p. 289), retomando conceitos previstos na BNCC relativos aos anos iniciais e introduzindo outros novos, previstos para os anos finais - como a representação da probabilidade de acontecer um evento aleatório por meio da forma fracionária.
Com a utilização do jogo campo minado como recurso didático, pretende-se atingir os seguintes objetivos:
Desenvolver uma atividade exploratória em que os alunos estabeleçam estratégias para vencer o jogo;
Mobilizar o pensamento probabilístico e o raciocínio lógico;
Estimular métodos intuitivos para o cálculo de probabilidade;
Definir empiricamente os conceitos de Probabilidade (evento, espaço amostral etc.);
Classificar eventos como: “pouco prováveis”, “muito prováveis”, “improváveis” e “impossíveis”;
Apresentar os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não;
Identificar a probabilidade de um evento ocorrer ou não, entre outras coisas.
A seguir, apresentar-se-á a proposta da primeira atividade envolvendo o jogo campo minado:
O campo minado é um popular jogo de computador para um jogador. Foi inventado por Robert Donner em 1989 e tem como objetivo revelar um campo de minas sem que alguma seja detonada.
Regras
A área de jogo consiste num campo retangular formado por quadrados. Cada quadrado pode ser revelado clicando sobre ele, e, se o quadrado clicado contiver uma mina, então o jogo acaba! Se, por outro lado, o quadrado não contiver uma mina, uma de duas coisas poderá acontecer:
Um número aparece, indicando a quantidade de quadrados adjacentes que contêm minas, ou nenhum número aparece. Nesse caso, o jogo revela automaticamente os quadrados que se encontram adjacentes ao quadrado vazio, já que não contêm minas.
O jogo é ganho quando todos os quadrados que não têm minas são revelados.
Pergunta inicial: Você já jogou o jogo campo minado? Caso a resposta seja sim, costuma adotar alguma estratégia? Descreva-a.
Proposta de atividade 1 - adaptada de Souza e Garcia (2016, p. 133).
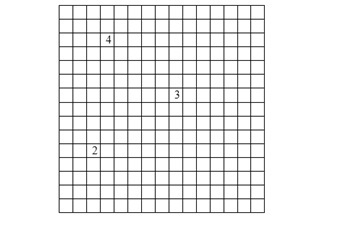
Considere um campo que possui 225 quadradinhos e que contém 30 minas escondidas. Um jogador clicou em 3 quadradinhos em que não haviam minas: no 1º apareceu o número 3, indicando que há 3 bombas adjacentes a ele; no 2º apareceu o número 2, indicando que há 2 bombas adjacentes a ele; no 3º apareceu o número 4, indicando que há 4 bombas adjacentes a ele, conforme a figura a seguir.
1) Qual das jogadas a seguir é a mais indicada para o próximo clique?
Jogada A: clicar em um dos quadradinhos adjacentes ao número 3;
Jogada B: clicar em um dos quadradinhos adjacentes ao número 2;
Jogada C: clicar em um dos quadradinhos adjacentes ao número 4;
Jogada D: clicar em um dos quadradinhos restantes, não indicados nas jogadas anteriores. Justifique.
Como a proposta advém de uma experiência prática com o jogo, é importante que o professor se certifique de que todos os alunos possuam a mesma versão (ou similar) do jogo caso opte por reproduzi-lo em celulares ou de que os computadores possuam o jogo disponível caso for utilizar algum laboratório de informática.
Dessa forma, a etapa inicial da aula deve ser destinada à apresentação, exploração e conhecimento dos elementos do jogo, realizando a leitura das regras e instigando-os a jogarem e pensarem em estratégias.
Num momento seguinte, após experimentarem o jogo, os alunos devem responder a pergunta do início do roteiro da atividade: “Você já jogou o jogo campo minado? Caso sim, costuma adotar alguma estratégia? Descreva-a”.
O intuito dessa pergunta é tentar identificar se os alunos possuem algum conhecimento prévio acerca de Probabilidade e se esse conhecimento está sendo utilizado de alguma forma; se desenvolveram alguma estratégia atrelada a algum raciocínio lógico ou se jogaram apenas contando com sorte. Essas informações são de suma importância, pois a ideia é retomá-las para discussão e fechamento da atividade (última etapa da segunda atividade proposta).
Na atividade 1 há quatro possíveis jogadas para serem analisadas. A seguir, tem-se uma análise inicial:
| A situação da jogada A indica que há três minas escondidas em um total de oito quadradinhos. Em termos fracionários, tomando a parte do todo, é possível escrever essa situação como |
| A jogada B configura uma situação em que há duas bombas em oito quadradinhos. Isso significa que |
| Ao observar a jogada C, verifica-se que há quatro bombas em oito quadradinhos. Logo, existem 4 quatro quadradinhos que possuem bombas e 4 quatro quadradinhos que não possuem bombas. Isso significa que é igualmente provável clicar em uma bomba ou não. |
| Por fim, da jogada D infere-se que há (30 − 9) = 21 minas escondidas nos 225 − (3 . 9) = 198 quadradinhos restantes (não incluídos nas jogadas A, B e C). Daí conclui-se que |
A partir dessas informações, vê-se que a jogada que apresenta menor risco de o jogador clicar em uma mina é a jogada D, já que
Assim, as melhores jogadas, em ordem, seriam: D, B, A e C.
Como a ideia é clicar em quadradinhos que não possuem minas para continuar prosseguindo no jogo, outra forma de ilustrar essa situação e que pode ser abordada pelo professor seria verificar qual jogada propiciaria a maior chance de clicar em um quadradinho vazio (que não contém uma mina). Usando as informações anteriores, tem-se que:
Com isso, conclui-se que as jogadas, em ordem, nas quais há maior chance de o jogador clicar em um quadrado vazio são: D, B, A e C (como esperado).
Observe-se que o conceito de Probabilidade ainda não foi formalmente definido; apenas o conceito de fração (que já deve ser de conhecimento da turma) foi utilizado e, com isso, tentou-se significar o que teria maior ou menor chance de acontecer, procurando desenvolver o pensamento probabilístico antes de apenas definir uma “fórmula” e aplicá-la.
Nesse sentido, o professor pode ainda ilustrar algumas outras situações como essa, que, além de possibilitarem a classificação de eventos como “pouco prováveis” e “muito prováveis”, podem facilitar (em uma futura definição) o entendimento do que seria a probabilidade de acontecer um evento complementar.
Ao ilustrar essa situação, o professor pode propor uma discussão sobre o que é mais provável acontecer ao escolher em uma casa adjacente ao número 7: se é clicar em uma mina ou em uma casa vazia. Sabe-se que há sete minas escondidas em oito casas; logo, é muito provável encontrar uma mina ao executar a operação.
Como visto anteriormente, essa probabilidade pode ser representada como
Outra possibilidade seria discutir com os alunos o que seria mais provável de ocorrer ao executar o primeiro clique: clicar em uma mina ou não. A seguir, discorrer-se-á sobre a segunda atividade que compõe a proposta que está sendo apresentada e discutida no presente artigo.
Apresentação e discussão da atividade 2 da proposta para o ensino de Probabilidade envolvendo o jogo campo minado
Proposta de atividade 2 - Adaptada de Souza e Garcia (2016, p. 133)
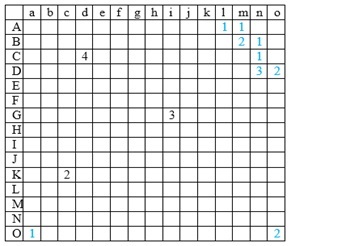
Considere que o jogador tenha feito mais algumas jogadas (destacadas em azul) de modo que a continuação do jogo tenha assumido a seguinte forma:
Obs. 1: As letras servem apenas para orientar a explicação de uma possível jogada.
Obs. 2: Os quadrados de posições (A, n), (A, o), (B, o) e (C, o) são quadrados que já foram revelados e não possuem minas; portanto, não são passíveis de efetuar uma jogada.
Suponha que você deva realizar o próximo clique. Com este cenário e segundo sua análise, qual seria a melhor jogada? Justifique.
A estratégia que você apontou (na primeira pergunta) se enquadra nos procedimentos que utilizou ao realizar esta atividade? Discuta com seus colegas.
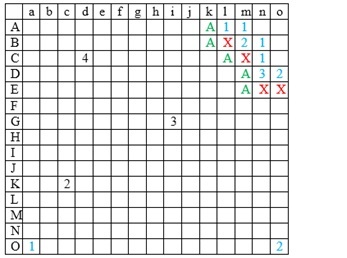
Na Atividade 2, nota-se que, pelas regras do jogo, existem duas minas ((E, n) e (E, o)) nas posições adjacentes ao número 2 de posição (D, o). As letras maiúsculas representam a “linha” e as minúsculas, a “coluna” da respectiva posição. Para melhor entendimento, a posição (H, d) foi destacada em verde. Observa-se que a letra “H” representa a linha e a letra “d”, a coluna (Figura 2).
Prosseguindo, observa-se que o número 1 da posição (B, n) diz que há uma mina na posição (C, m). Por outro lado, o número 2 da posição (B, m) revela que há duas minas adjacentes a ele. Sabe-se da existência de uma das duas minas. Nota-se ainda que a outra mina não pode estar na posição (C, l), pois, dessa maneira, não cumpriria a obrigatoriedade de existência da mina adjacente aos números 1 de posições (A, m) e (A, l), respectivamente. Logo, essa outra mina estará na posição (B, l).
Para melhor entendimento, denomina-se “X” o local em que as minas estão escondidas e “A” as posições seguras onde não há minas, como ilustrado na Figura 2. Assim, as posições das minas encontradas são: (E, o), (E, n), (C, m) e (B, l). Por outro lado, as melhores jogadas, em que há 100% de probabilidade de não encontrar uma mina são: (E, m), (D, m), (C, l), (B, k) e (A, k).
Observe-se que, como foram descobertas as minas de posições (E, n) e (E, o), a probabilidade de clicar em uma mina adjacente ao número 2 de posição (D, o) configura-se como um evento certo e a jogada “clicar em um quadrado vazio adjacente à posição (D, o)” caracteriza-se como um evento impossível, pois não há essa possibilidade. Assim, pode-se ir trabalhando a ideia de probabilidade sem necessariamente defini-la.
Para finalizar, os alunos devem responder à questão número 2 do roteiro: “A estratégia que você apontou (na primeira pergunta) se enquadra nos procedimentos que utilizou ao realizar essa atividade? Discuta com seus colegas.”
A ideia é retomar as respostas dos alunos às perguntas que compunham o questionário preenchido antes da execução da atividade propriamente dita e discutir as percepções adquiridas ao longo dela; se as estratégias se mantiveram, o que mudou e, principalmente, se ocorreu um aprendizado dos conceitos objetivados, possibilitando que o aluno tenha uma visão melhor do que sucedeu antes, durante e depois da prática e que professor tenha elementos que o ajude a refletir sobre sua prática.
Com base em Souza e Garcia (2016, p. 128, grifos próprios), “chamamos de evento ou acontecimento, e geralmente indicamos por uma letra maiúscula, cada subconjunto do espaço amostral de um experimento aleatório.”. Dessa forma, utilizando ainda a Figura 2, o evento “não clicar em uma mina adjacente ao 3” da posição (G, i)”, por exemplo, terá como elemento os cinco “quadrados vazios”, enquanto o evento “clicar em uma mina adjacente ao 3” terá como elementos as seis minas adjacentes ao número 3.
Considerando a Atividade 2, o evento “clicar em uma mina adjacente ao número 2 da posição (D, o)” é representado pelo próprio espaço amostral da jogada, pois observa-se que os quadrados adjacentes ao número 2 (passíveis de que uma jogada seja feita) contêm apenas minas - logo, o espaço amostral dessa jogada é constituído por essas minas. Nesse caso, diz-se que esse evento é certo.
Outro exemplo disso pode ser visto em relação ao espaço amostral no lançamento de um dado de seis faces cujo evento é “o número da face superior ser menor ou igual a que 6”, em que claramente os elementos que constituem esse evento são representados pelo próprio espaço amostral.
Por outro lado, ainda considerando o espaço amostral do lançamento de um dado de seis faces, o evento “o número da face superior ser maior ou igual a que 7” é representado pelo conjunto vazio, uma vez que o espaço amostral não possui esse resultado. Nesse caso, diz-se que esse evento é impossível.
Considerando ainda o experimento que consiste em lançar um dado não viciado, verifica-se que cada face tem probabilidade de 1/6 de ocorrer. Observe-se que a probabilidade é a mesma para todos os eventos unitários. Quando isso ocorre, diz-se que o espaço amostral é equiprovável. Em uma situação do campo minado, em que é possível reduzir o espaço amostral para o “universo” da jogada considerada, que será equiprovável quando o número de minas for igual ao número de casas vazias (como ocorre na jogada C da Atividade 1).
Baseado em Souza e Garcia (2016), é trazida a seguinte definição “formal” de probabilidade: “considere um evento A de um espaço amostral Ω finito e equiprovável. A razão entre a quantidade de elementos de A (indicada por n(A)) e a quantidade de elementos de Ω (indicada por n(Ω)) é a Probabilidade P(A) de o evento A ocorrer.” (Souza; Garcia, 2016, p. 131). De outra forma, é possível escrever que
Informalmente, com relação à razão anterior, costuma-se dizer que “a probabilidade de ocorrer um determinado evento é dada pelo quociente entre o número de casos favoráveis (casos de nosso interesse) e o número de casos possíveis (total de casos)”.
Considerando A um evento qualquer de certo espaço amostral Ω, para Ø, A e Ω, vale:
Dividindo cada membro dessa desigualdade por n(Ω) > 0, obtem-se o seguinte:
Desse resultado, conclui-se que a probabilidade de um evento ocorrer é um valor de 0 a 1; ou seja, de 0% a 100%. Daí, conclui-se que:
Se A é um evento impossível, tem-se P(A) = 0
Se A é um evento certo, tem-se P(A) = 1
Usando esses conceitos, percebe-se, por exemplo, que ao executar a jogada A da atividade 1, clicar em um dos quadradinhos adjacentes ao número 3”, a probabilidade de o jogador clicar em uma mina (considerando o evento “clicar em uma mina adjacente ao número 3”) é de
Pode-se ainda calcular a probabilidade de um evento não ocorrer (ou a probabilidade de acontecer um evento complementar). Usando ainda o exemplo anterior, vê-se que a probabilidade de o jogador “não clicar em uma mina adjacente ao número 3” é dada por
De modo geral, seja Ā o conjunto formado pelos elementos de Ω que não pertencem a A ou seja, Ā = Ω − A. Diz-se que Ā é complementar de A em relação a Ω.
Como Ā = Ω − A e Ā ∩ A, tem-se:
Ao dividir ambos os membros dessa igualdade por n(Ω) > 0, tem-se:
Logo, a probabilidade de não ocorrer o evento A (indicado por P(Ā)) é: P(Ā) = 1 − P(A).
Outra situação que exemplifica isso é: considere como espaço amostral os números naturais de 1 a 10 e o evento A, a ocorrência de sair um número maior do que 7 no sorteio de um desses número. Tem-se que Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} e A = {8, 9, 10}. Daí, Ā = Ω − A = {1, 2, 3, 4, 5, 6, 7}.
A probabilidade de não aparecer um número maior do que 7 vai ser:
Por fim, pode-se ainda realizar um experimento associado à frequência relativa. Considere-se uma configuração com 30 minas espalhadas aleatoriamente em 100 quadradinhos. Sabe-se que, ao executar o clique que dará início ao jogo, o jogador não sabe se encontrará uma mina ou não. Observe-se ainda que é possível refazer esse experimento sob as mesmas condições - isto é, reiniciar o jogo e executar um novo clique.
Imagine-se, por exemplo, que esse exercício tenha sido realizado 100 vezes, das quais 37 resultaram em encontrar uma mina e 63 em encontrar um quadrado vazio. Nesse caso, a razão
A ideia é que se verifique que, à medida que o número de jogadas (realização do experimento) aumenta, as frequências relativas correspondentes às ocorrências de “encontrar uma mina” ficam cada vez mais próximas do valor
Para realizar o experimento como descrito anteriormente, deve-se observar se a versão do jogo utilizada permite que o jogador perca o jogo ao realizar o primeiro clique (pois algumas versões são programadas para que isso não ocorra). Caso isso não seja possível (encontrar uma mina já no primeiro clique), pode-se efetuar o primeiro clique e ver quantas casas foram abertas e, posteriormente, efetuar o experimento a partir da segunda jogada (como se a segunda jogada virasse o “primeiro clique”). Suponha-se, por exemplo, que foram abertas nove casas. No segundo clique (segunda jogada), serão 30 minas em quadradinhos (considerando ainda a situação anterior). Por outro lado, se, ao realizar o primeiro clique, fossem abertas 12 casas, então no segundo clique haveriam 30 minas em 100 − 9 = 91 quadradinhos - e assim por diante. Logo, pode-se registrar os resultados (encontrar uma mina ou não) de cada situação em que o segundo clique foi efetuado (segunda jogada com 30 minas em 88, 89 ou 90 quadradinhos etc.) e comparar a frequência relativa associada a cada situação com a sua respectiva probabilidade de ocorrer, procedendo como foi descrito no experimento exemplificado inicialmente.
Considerações Finais
Cabe ressaltar que neste artigo foram apresentadas algumas sugestões, e não imposições. O professor, enquanto educador e/ou formador, possui liberdade para adaptar as situações propostas ou complementar com outras abordagens que por acaso não tenham sido apresentadas. Como mencionado anteriormente, esta proposta se apresenta como mais uma alternativa e não deve ser encarada como algo definitivo (assim como qualquer outra), pois é dever do professor/educador refletir constantemente sobre sua ação docente e adaptar o que melhor se enquadra à sua realidade e à de seus alunos.
Para a implementação da atividade, deixa-se como sugestão aquilo que foi adotado na experiência dos autores à época em que o artigo foi escrito . Apesar de as recomendações terem sido escritas considerando um espaço para a formação de professores, as ideias aqui inseridas podem ser replicadas e reproduzidas num contexto de sala de aula para o ensino médio.
Recomenda-se que o formador agrupe os futuros professores em duplas (caso não haja dispositivos móveis para todos), sendo que cada dupla deve ter um dispositivo móvel (ou computador) e que, preferencialmente, todos os equipamentos utilizados tenham a mesma versão do jogo instalada. Destaca-se que há versões em que o jogo é programado para impossibilitar a derrota na primeira jogada (sendo essa a mais comum), então sugere-se que o professor responsável pela prática pesquise de antemão uma versão que seja de seu interesse. Quando a prática foi realizada pelos autores deste artigo, a busca pela expressão “Campo minado clássico” na loja de aplicativos Play Store resultou em uma versão que possibilitava escolher a quantidade de minas e de quadrados no tabuleiro, e nessa versão era possível perder já na primeira jogada.
Aconselha-se que o encontro formativo contemple pelo menos 4 aulas de 50 minutos, organizadas da seguinte forma: (1) explicação das regras, esclarecimento de dúvidas e momento para conhecer/experimentar o jogo (25 minutos); (2) pedir para que os participantes registrem as estratégias adotadas no espaço da “pergunta inicial” (10 minutos); (3) leitura, discussão e resolução da “Proposta de atividade 1” (25 minutos); (4) leitura, discussão e resolução da “Proposta de atividade 2” (40 minutos); (5) Formalização dos conceitos de probabilidade (100 minutos).
Diante do exposto, espera-se que a proposta de atividade corroborem com a proposição de espaços formativos em que a Probabilidade e a Estatística sejam tomadas como objeto de estudos, investigações e reflexões sobre a prática. Também é esperado que as discussões aqui realizadas contribuam para um processo de ensino e de aprendizagem da Probabilidade e da Estatística que supere a perspectiva pautada na memorização e aplicação de fórmulas.