Introducción
La visión multidimensional de la probabilidad no se encuentra en otras áreas y crea desafíos especiales para profesores y estudiantes (Batanero et al., 2016). La investigación en educación de la probabilidad ha ido en aumento, y se puede observar en los numerosos trabajos sobre este tema presentados en congresos como: el European Mathematics Education Conference (Jankvist; Van den Heuvel-Panhuizen; Veldhuis, 2019) en donde se reunieron en la mesa TWG05 Probability and Statistics Education investigadores internacionales para abordar temas que implican grandes desafíos para la educación estadística; y el International Conference on Teaching Statistics (2022), que en su última edición que se llevó a cabo en Argentina y abordó en el tópico 6 el tema overcoming challenges of teaching probability and risk in statistics education, donde se habló de la importancia del pensamiento probabilístico, el currículum y la el uso de situaciones aleatorias entre otras. Sin duda, contribuir a los indicios de estas investigaciones permite avanzar en el campo de la matemática educativa y de la educación estadística.
Algunos de los temas que se han sido objeto de estudio de estudio son los significados de la probabilidad (Batanero, 2005a, 2005b; Gómez; Contreras, 2013; Borovcnik; Kapadia, 2014), debido a la importancia que tienen en la enseñanza del currículum de estadística. El diseño curricular mejora la enseñanza de la estadística y la probabilidad en todos los niveles, y refuerza los contenidos durante toda la enseñanza obligatoria (Batanero; Gea; Arteaga, 2012). Para ello, es necesario educar en los componentes conceptual, procedimental y práctico de la estadística. Para Moreno (1998), esto incluye las ideas básicas sobre gráficos, diseño de experimentos, incertidumbre, probabilidad y riesgo. El autor menciona que, al avanzar la edad de los estudiantes, deben relacionar estas ideas con otras áreas y adquirir la comprensión de los conceptos y procesos implicados en el análisis y lectura de datos.
Por otra parte, Batanero (2005a) menciona que una mirada a la historia permite tomar conciencia de que los conceptos matemáticos son cambiantes. La autora hace énfasis al proceso que se desarrolla en el aprendizaje de los alumnos, quienes deben construir su conocimiento mediante un proceso gradual a través de errores, esfuerzo y añadir un elemento fundamental: la disciplina. Batanero (2005a) argumenta que, si el profesor que enseña probabilidad no es consciente de esta problemática, no podrá comprender las dificultades de los estudiantes, quienes, al igual que los docentes, se encuentran con las mismas situaciones contra intuitivas que surgieron durante el desarrollo histórico del cálculo de probabilidades.
En ese desarrollo, Batanero (2015) describe que el significado de aleatoriedad surge a la par de la probabilidad. La autora considera que, hasta ahora, no se ha encontrado una definición simple que se pueda usar sin ambigüedades para clasificar un evento o proceso dado como aleatorio o no, aunque hay reflexiones y aproximaciones de estadísticos, filósofos e investigadores en educación matemática. El concepto de aleatoriedad se encuentra asociado al significado de la probabilidad intuitiva y, por ende, al surgimiento de ésta como disciplina.
El significado intuitivo de probabilidad (Batanero, 2005a) relata la historia del concepto y el nacimiento de la teoría de la probabilidad. En esta investigación, se retoma el significado de la probabilidad intuitiva identificado en Batanero (2005a), y se analiza desde la triada semántica expuesta en Rico (2013). Esto permitirá identificar la estructura matemática, los registros de representación y los contextos que estuvieron alrededor de los significados de referencia de la probabilidad en el surgimiento de esta disciplina. La importancia del estudio de los significados de referencia radica en que sirven de marco para la identificación de los significados potenciados en las diferentes dimensiones del currículum – oficial, potencial, impartido y aprendido, descritos en Alsina (2000) – y sus posibles desconexiones o transformaciones.
Algunos autores, como Balcaza, Contretas y Font (2017), consideran que, para la determinación del significado de referencia, se requiere la realización de un estudio histórico-epistemológico sobre el origen y evolución del concepto en cuestión. Aunado a ello, para realizar un diseño curricular de un contenido matemático y estadístico en cualquier nivel educativo, es necesario considerar la diversidad de significados y su articulación progresiva, atendiendo a los grados de generalidad y formalización (Burgos; Godino, 2020). Además, este tipo de estudio contribuye al análisis de los recursos necesarios para la enseñanza de la probabilidad, como los libros de texto, que han ocupado un lugar importante en el proceso de enseñanza y aprendizaje y como organizadores del contenido y material de consulta (Vargas; Fernández-Plaza; Ruíz-Hidalgo, 2018).
Investigaciones sobre los significados de un concepto matemático para hacer una aproximación al significado de un concepto se han realizado en Vargas, Fernández-Plaza y Ruíz-Hidalgo (2020), o Hernández, Zamora, Lupiañez (2020), por mencionar algunos. Sin embargo, en ese escenario, aún son escasos los estudios con contenidos vinculados a la estadística y probabilidad (Vargas; Fernández-Plaza; Ruíz-Hidalgo, 2018) y más aún aquellos que consideren al plan de estudios como fuente principal de análisis. Por consecuencia, es necesario prestar atención a los problemas prácticos y pedagógicos derivados de la incorporación de temas probabilísticos en los planes de estudio (Vargas; Fernández-Plaza; Ruíz-Hidalgo, 2020).
Por tal motivo, el objetivo propuesto para el desarrollo de esta investigación es identificar los significados de referencia asociados al concepto de intuitivo de probabilidad que se encuentran en algunos documentos que se han analizado, iniciando su primera fase de desarrollo apoyado en el análisis didáctico y análisis del contenido descrito en Rico y Fernández-Cano (2013).
A la par, se observa el significado de un concepto matemático conformado por sus tres componentes: estructura conceptual; registros de representación; y fenomenología (Rico, 2013). Así, el presente estudio del significado intuitivo de la probabilidad propone articular los diferentes significados que se encuentran en el desarrollo de la probabilidad. La investigación permitirá no solo complementar los estudios en el mismo marco y robustecer el currículum. Además, es una propuesta diferente que ampliará la visión en un área que ha tomado gran importancia en los últimos años, respondiendo a la necesidad de realizar investigación en la educación probabilística. Aunado a ello, el problema que se pretende resolver al investigar los significados de referencia asociados al concepto intuitivo de probabilidad es continuar con un estudio transversal para el currículum escolar en la enseñanza de la probabilidad en los primeros años de estudio.
El momento histórico en el que se recoge la información de esta investigación es posterior a la Edad Media, cuando surgen ideas importantes sobre la probabilidad intuitiva mientras se practicaban juegos de azar. La historia afirma que ésta surgió a través de la correspondencia entre Fermat y Pascal, aunque los juegos daten de tiempos muy remotos (Mayer, 2015).
Se seleccionaron 5 documentos que acompañan este hecho histórico. La coincidencia de 2 artículos, 2 libros y un capítulo de libro con un mismo momento determinó la selección de la información. Los artículos son: La Historia de la Probabilidad (Restrepo; González, 2003); y Significados de la Probabilidad en la Educación Secundaria (Batanero, 2005a); los libros son: The Emergence of Probability (Hacking, 1975) y Rutas de Incertidumbre (Mayer, 2015); y el capítulo es del libro La Historia de la Probabilidad y su relación con la historia del surgimiento de la teoría de la decisión (Mateos; Morales, 2002).
Reseña del significado de probabilidad
En la historia, se hace un recuento de las primeras nociones de probabilidad al término de la Edad Media, comenzando por la correspondencia entre el matemático Blas Pascal y el abogado Pierre Fermat, donde se plantea la solución de problemas relacionados con el azar. A través del desarrollo de la teoría de la probabilidad, se encuentran también problemas planteados por Galileo, al Duque de Toscana, que están relacionados con el análisis combinatorio en un juego de dados. Estos planteamientos hicieron que varios matemáticos o apasionados de la ciencia, como Bernoulli, Abraham de Moivre, Thomas Bayes, Lagrange, entre otros, realizaran aportaciones que contribuyeron en la conformación de diferentes significados de la probabilidad a lo largo de estos años.
Las primeras nociones de probabilidad se encuentran al término de la época de la Edad Media (al final del año 1453) y al inicio del Renacimiento (s. XV-XVI), etapa que se caracterizó por la actividad artística, arquitectónica, intelectual y científica. A partir de esta era, con el avance de las matemáticas, se comienza a dar una explicación coherente a fenómenos que no seguían un patrón determinístico, sino aleatorio (Restrepo; González, 2003).
El desarrollo de la teoría probabilística se atribuye al médico italiano Gerolamo Cardano (1501-1576), escritor que, en el año de 1563, termina el primer libro de probabilidad llamado “Liber de ludo aleae”, que trata sobre el juego de los dados. No obstante, el primer indicio del desarrollo de la teoría de la probabilidad surge de la correspondencia sostenida por Blas Pascal (1623-1662, matemático francés) y Pierre Fermat (1601-1665, abogado de profesión y matemático por vocación), donde comparten un problema que surge cuando Blas hacía un viaje con un jugador apasionado por los dados y cartas conocido como el caballero Meré.
Al participar en un juego de dados, el caballero creyó que había encontrado una “falsedad” en los números, al observar que el comportamiento de los dados era diferente cuando se tiraba un dado que cuando se lanzaban dos. La “falsedad” radicaba en una comparación errónea entre la probabilidad de sacar un mismo número con un solo dado o con los dos. Para el jugador, debía existir una relación proporcional entre el número de jugadas que fueran necesarias para conseguir que sucediera el evento en un caso y en otro. El problema se centraba en que el caballero no tomaba en cuenta que, en el segundo caso, se estaba analizando una probabilidad compuesta por una combinación.
Posteriormente, en una de sus cartas, Pascal narra esta anécdota, donde dice a Fermat “[…] el caballero Meré tiene mucho talento, pero no es geómetra; esto es, como sabéis un gran defecto” (carta del 29 de julio de 1654). Aunque Pascal y Fermat no expusieron sus resultados por escrito, Chrisitaan Huygens, publicó en 1657 un breve tratado llamado “De Ratiocinnis in ludo aleae”, inspirado en la correspondencia sostenida entre Pascal y Fermat (Restrepo; González, 2003).
Si se analizan las cartas de Pascal a Fermat, se puede observar que Pascal emplea las palabras “valor”, “chance”, “combinación” para hacer referencia a objetos abstractos. Estas expresiones le sirven a Pascal como instrumentos para resolver algunas cuestiones propuestas por el caballero Meré (Batanero, 2005a). Posteriormente, uno de los problemas primitivos fue propuesto a Galileo por el Duque de Toscana en 1620. Este consistía en explicar por qué al lanzar dos dados, aunque las sumas 9 y 12 se pueden componer en el mismo número de veces, que las sumas de 10 y 11, por experiencia, los jugadores preferían apostar más por la segunda (Batanero, 2005a).
El problema expuesto por Blas Pascal sobre el caballero Meré y otros relacionados con el azar dieron origen al cálculo de las probabilidades. En consecuencia, diversos problemas probabilísticos se fueron planteando a través de la historia, y algunos matemáticos fueron interesándose en la solución de estas nuevas propuestas.
Los problemas que surgieron durante el desarrollo histórico de la teoría de la probabilidad son adecuados para analizar los significados en torno a este concepto. Según Batanero (2005a), en el caso de la probabilidad, existe una diferencia entre el conjunto de prácticas ligadas a la resolución del campo de problemas y el objeto matemático probabilidad, que ha surgido históricamente y sigue evolucionando como consecuencia de dichas prácticas. Por tal motivo, a lo largo del desarrollo histórico de la probabilidad, diferentes significados han sido asociados al concepto, tales como el significado intuitivo, laplaciano, frecuencial, subjetivo y matemático, que han sido descritos en Batanero (2005a). En la presente investigación, nos compete el significado intuitivo.
En cuanto al significado intuitivo de la probabilidad, los juegos de azar son comunes en todas las civilizaciones primitivas. Aparecen tanto en niños como en personas que no han estudiado probabilidades. Ellos utilizan frases y expresiones coloquiales para cuantificar los sucesos inciertos y expresar el grado de creencia en ellos (Batanero, 2005a). Estas ideas “[…] surgen ligadas a las apuestas, la esperanza, la ganancia en un juego y el concepto de juego equitativo, no se precisaron hasta que se trató de asignar números a estos grados de creencia para poder comparar la verosimilitud de diferentes sucesos” (Batanero, 2005a, p. 253).
Marco teórico y antecedentes
La historia es un concepto pedagógico transversal en el análisis didáctico en general y en el análisis del contenido en particular (Cañadas; Gómez; Pinzón, 2018). Es por ello que se hace una revisión del significado de probabilidad intuitivo a partir de las ideas de Pascal y Fermat, que es cuando surgen las primeras nociones de teoría de la probabilidad en Europa Occidental.
El significado intuitivo de probabilidad es definido por Alsina y Vásquez (2016) como aquél que utiliza términos de uso común para referirse a la incertidumbre y expresar el grado de creencia en relación a sucesos inciertos. Batanero (2005a) argumenta que las ideas intuitivas de probabilidad como grado de creencia personal es común encontrarlas en los juegos de azar. Para Gómez y Contreras (2013, p. 572), las primeras ideas intuitivas surgieron “ligadas a las apuestas, esperanza y ganancia en un juego, así como el concepto de juego equitativo y no se precisaron hasta que se trató de asignar números para poder comparar la verosimilitud de diferentes sucesos”.
La probabilidad intuitiva anticipa la realidad sin ser corroborada por la razón, y encaminar esa intuición de forma adecuada en los estudiantes de los primeros niveles educativos podría determinar un adecuado razonamiento probabilístico.
Ahora bien, la noción de significado de un concepto matemático escolar es propuesta por Rico (2012), quien considera tres componentes para el significado de un concepto matemático: la estructura conceptual, sistemas de representación y la fenomenología como elementos centrales para establecer los significados de un concepto matemático que se puede estudiar desde diferentes significados.
La estructura conceptual hace referencia a los conceptos, definiciones, propiedades, argumentos y proposiciones que de ahí se derivan, así como sus criterios y veracidad (Rico, 2012).
Los sistemas de representación son las distintas formas de representar el concepto y sus relaciones con otros conceptos (Gómez, 2007).
Finalmente, la fenomenología se refiere al contexto en donde es utilizado, la situación o problema en donde el concepto tiene un sentido (Gómez, 2007).
En este estudio, se toma la definición del significado propuesta por Rico (2012), con el objeto de identificar, organizar y caracterizar los significados de referencia asociados al concepto intuitivo de probabilidad mediante la metodología que se describe a continuación.
Metodología
La investigación se enmarca en un estudio cualitativo de carácter descriptivo, y el método adoptado es el análisis del contenido. Éste se utiliza en educación matemática como un método para establecer y estudiar la diversidad de significados escolares de los conceptos y procedimientos de las matemáticas que aparecen en un texto (Rico, 2013).
Al respecto, Rico (2013) menciona que las técnicas de análisis de contenido trabajan la naturaleza del mensaje-discurso para descubrir la estructura interna de la comunicación. Para el autor, dicho análisis incorpora una dimensión reductora, descomponiendo el contenido en unidades más simples, para lo cual utiliza la determinación de temas y la identificación de categorías. Según Rico (2013), la aplicación del análisis de contenido a la investigación educativa ayuda a:
Descubrir patrones en el discurso.
Contrastar una hipótesis previa.
Inferir significados interpretativos en un texto. De manera general, el procedimiento para realizar un análisis de contenido sigue unas determinadas etapas, a saber: determinar el corpus del contenido (texto, discurso, producción escrita) a analizar; concretar la unidad de análisis: palabra (nombre, verbo o adjetivo), frase o párrafo; localizar o inferir en el texto las unidades de análisis; denominar, definir e interpretar las categorías consideradas; evitar en lo posible la categoría “otros” para obviar indeterminaciones; codificar y cuantificar mediante frecuencias o rangos las unidades de análisis previamente adscritas al sistema de categorías predeterminado o inferir tal sistema de categorías sobre las unidades de análisis seleccionadas; relacionar entre sí e interpretar las categorías establecidas, considerando sus unidades de análisis adscritas; y relacionar el proceso de análisis de contenido con la cuestión que se indaga y con los agentes intervinientes (hablante/escritos u oyente/lector). (p. 17)
Las fases utilizadas para la presente investigación son las propuestas en Rico y Fernández-Cano (2013), y a continuación se presentan desde el contexto de este estudio.
Delimitar el corpus a analizar. Las fuentes de información que se han utilizado para el presente estudio se enuncian en la Tabla 1. Los números que acompañan a los autores fueron utilizados en la codificación de las unidades de análisis, que se presentan en la fase 3.
-
Denominar, definir e interpretar las categorías consideradas. Las categorías consideradas para analizar los significados en el desarrollo histórico de la probabilidad son las propuestas por Rico (2013, p. 18), y que se señalan a continuación:
Conceptual, que considera el momento histórico y el marco poblacional (el quién comunica y a quién comunica) donde se insertan.
Formal y estructural, que abarca los conceptos, definiciones y procedimientos, junto con la estructura formal, que proporcionan referencia a los contenidos utilizados.
Representacional, que comprende las notaciones gráficas, simbólicas, y sistemas de signos involucrados.
Fenomenológica, que aborda los fenómenos que dan origen a los conceptos, los contextos en los que se utilizan y aquellas situaciones en las que se presentan y en las cuales se aplican, que dotan de sentido a los contenidos en estudio.
Tabla 1 Fuentes de información para el desarrollo histórico.
| Autores | Año | Título | Tipo de documento |
|---|---|---|---|
| Luis F., Restrepo, B. y Julián González | 2003 | La historia de la probabilidad | Artículo |
| Carmen Batanero | 2005 | Significados de la probabilidad en la educación secundaria | Artículo |
| Ian Hacking | 1975 | The emergence of probability | Libro |
| Gregoria Mateos y Aparicio Morales | 2002 | Historia de la probabilidad y su relación con la historia de la Teoría de la decisión | Capítulo de Libro |
| Leticia Mayer Celis | 2003 | Rutas de incertidumbre | Libro |
Fuente: Elaboración propia (2023).
Además, se atiende a una clasificación cognitiva de los contenidos de las matemáticas escolares, considerando el campo conceptual que hace referencia a la sustancia del conocimiento: ¿qué es lo que lo compone? Y al campo procedimental que incluye los procedimientos y modos de actuación con respecto al conocimiento (Cañadas; Gómez; Pinzón 2018).
3) Codificar las unidades de análisis. En la parte superior de las fichas de registro presentadas en la Figura 1, tendrán un código de identificación. A continuación, se explica su lectura: por ejemplo, una ficha de código SI_01_83_01 SI corresponde a las siglas de significado intuitivo; 01 corresponde al autor al que se hace referencia en la Tabla 1; 83 es el número de la página donde se encuentra la cita textual; y 01 es el número del párrafo.
4) Relacionar entre sí e interpretar las categorías establecidas, considerando sus unidades de análisis.
5) Relacionar el proceso de análisis de contenido con la cuestión que se indaga. Esta fase se presenta a continuación conformándose en la fase de resultados de esta investigación.
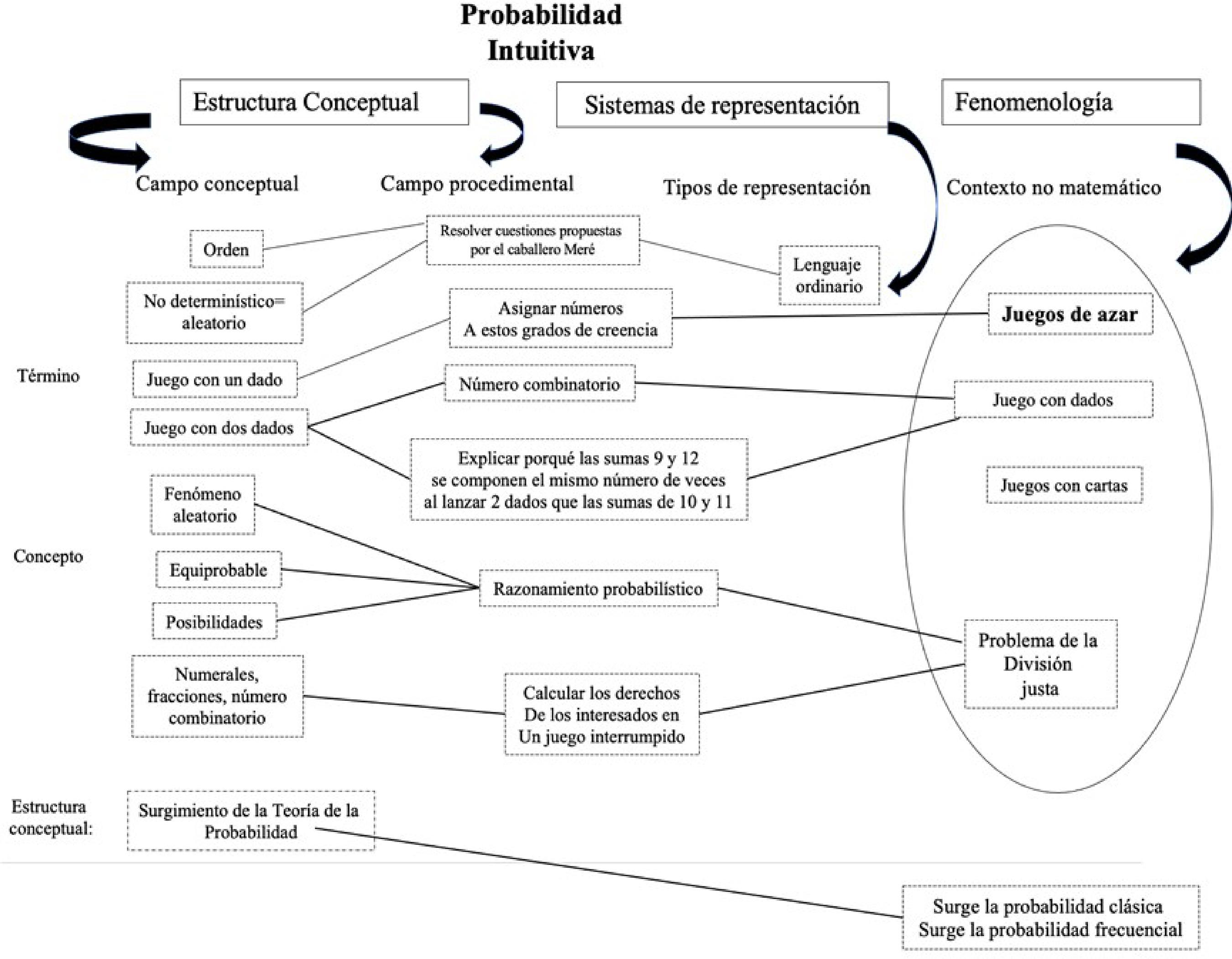
Fuente: elaboración propia (2023).
Figura 1 Mapa conceptual de los significados de la probabilidad intuitiva en su desarrollo histórico
Tabla 2 Ficha de registro de información SI_01_83_01, 2023.
| Código SI_01_83_01 | ||||
|---|---|---|---|---|
| Unidad de Análisis La edad media termina históricamente en el año 1453 con la caída de Constantinopla por parte de los otomanes, dando paso a la etapa conocida como renacimiento. A partir de esta etapa con el avance en las matemáticas y la filosofía, se empieza a dar una explicación coherente a muchos fenómenos que no seguían un patrón determinístico, sino aleatorio. (Restrepo, B. & González, J., 2003, p. 83). | ||||
| Etapa o fecha-precursor: Renacimiento | ||||
| Estructura conceptual | Sistemas de representación | Fenomenología | ||
| Campo conceptual: | Campo procedimental: | Tipos de representación | Contextos matemáticos | Contextos no matemáticos X |
| Nivel 1 Términos Determinístico No determinístico=aleatorio |
Nivel 1 Destrezas |
1. Lenguaje ordinario | Situación: | Situación: Dar una explicación coherente a muchos fenómenos |
| Nivel 2 Conceptos Fenómeno aleatorio |
Nivel 2 Razonamientos Explicar coherentemente fenómenos no determinísticos |
|||
| Nivel 3 Estructuras conceptuales |
Nivel 3 Estrategias |
|||
Fuente: Elaboración propia (2023).
Dentro de la estructura conceptual presente en la Tabla 2, en el primer nivel, se pueden encontrar los términos que son “[…] denominaciones o vocablos con los que se designan los conceptos o las relaciones entre conceptos” (Rico, 1995, p. 14). En el nivel dos, se encuentran los conceptos que son un conjunto de hechos, que suelen admitir un modelo o representación y, finalmente, las estructuras conceptuales que sirven para unir conceptos o sugerir formas de relación entre ellos (Rico, 1995).
En el campo procedimental, se encuentran las destrezas, los razonamientos y las estrategias; las primeras procesan hechos; los razonamientos se ejercen sobre los conceptos; y las estrategias se relacionan con las estructuras conceptuales y producen su manipulación (Rico, 1995).
Significado intuitivo de la probabilidad en la lectura de las fichas
En este apartado, se presentan los resultados que se obtienen del análisis del contenido, a través de las fichas donde se organizaron los significados intuitivos de la probabilidad, presentes en el desarrollo histórico del concepto. Se toma como base la revisión de los documentos de donde se sustrae la información. Una vez que se infieren significados interpretativos en los textos seleccionados, se han clasificado en las categorías de análisis propuestas por Rico (2013).
La Tabla 2 presenta un fragmento de Restrepo y González (2003) acerca del avance en las matemáticas y la filosofía en donde se comienza, dando una explicación a fenómenos que seguían un patrón aleatorio.
El fenómeno aleatorio que se encuentra en el nivel dos se considera dentro del campo conceptual, donde se intenta dar una explicación coherente a fenómenos no determinísticos en contextos no matemáticos.
A través del desarrollo intuitivo de la probabilidad, no se ha llegado al nivel de estructura, es decir, los significados asociados al concepto de probabilidad todavía no son considerados como una estructura matemática. Dentro de la tipología contemporánea de las probabilidades, ésta precede a las demás, lo que significa que el significado de probabilidad intuitiva fue el primero en la clasificación que se ha propuesto.
Cuando continuamos con el análisis del documento de Restrepo y González (2003), encontramos que los primeros términos que se ubican en el nivel uno, el juego de un dado y el juego con dos dados, surgen a partir de las ideas de Pascal, debido a su constante acompañamiento del caballero Meré, célebre por su afición a juegos de azar. El primer resultado arroja que el comportamiento del juego de los dados es diferente con uno que con dos dados. Hasta entonces, el caballero afirmaba que existía una relación proporcional entre el número de jugadas necesarias para conseguir el efecto deseado tanto con un dado como con dos, hipótesis que denominamos resultado falso.
Llama la atención, en el mismo documento, la afirmación del caballero Meré que Pascal pone en duda e intenta probar el desacuerdo junto con el jurista francés Pierre Fermat. Como resultado, se encuentra que, si los resultados son equiprobables, entonces existe una relación proporcional entre jugadas. Surge entonces el concepto que hemos caracterizado en el nivel dos: equiprobable, en el que se encuentra un sentido a la afirmación de Meré. Es cuando finalmente se empieza a formalizar la teoría de la probabilidad.
La equiprobabilidad que surge como concepto en el nivel dos se consideró un resultado erróneo encontrado por el caballero, ya que parte de que las combinaciones tenían la misma posibilidad de ocurrencia. Pero, para probar que estaba equivocado, en el campo procedimental, se encuentra que se buscaba explicar por qué las sumas de determinadas combinaciones se componían el mismo número de veces al lanzar dos dados, y Galileo responde correctamente a estos planteamientos.
En otro sentido, en la correspondencia que se realiza entre Fermat y Pascal, en el documento de Batanero (2005a), hemos identificado los términos numerales, letras y fracciones, y se introducen nuevos conceptos: esperanza matemática; posibilidades; número combinatorio; juego equitativo; frecuencia; y espacio muestral. Estos conceptos marcan la pauta del surgimiento de la probabilidad intuitiva, sin embargo, con los antecedentes descritos, no se ha definido con formalidad el concepto de probabilidad (Tabla 3).
Tabla 3 Ficha de registro de información SI_02_250_04, 2023.
| Código SI_02_250_04 | ||||
|---|---|---|---|---|
| Unidad de Análisis Si analizamos las cartas de Pascal a Fermat (Pascal, 1963/1654) podemos observar que Pascal emplea las palabras “valor”, “chance”, “combinación” para hacer referencia a objetos abstractos (esperanza matemática, posibilidades, número combinatorio); al mismo tiempo, tales expresiones, así como los numerales, letras, fracciones e incluso una representación del triángulo aritmético le sirven a Pascal como instrumentos al resolver algunas cuestiones propuestas por el caballero Meré” (Batanero, 2005a, p. 250). | ||||
| Etapa o fecha-precursor: Pascal y Fermat | ||||
| Estructura conceptual | Sistemas de representación | Fenomenología | ||
| Campo conceptual: | Campo procedimental: | Tipos de representación | Contextos matemáticos | Contextos no matemáticos X |
| Nivel 1 Términos Numerales, letras y fracciones |
Nivel 1 Destrezas Resolver cuestiones propuestas por el caballero Meré |
Representación del triángulo aritmético | Situación: | Situación: |
| Nivel 2 Conceptos, Objetos abstractos, Esperanza matemática, posibilidades, número combinatorio |
Nivel 2 Razonamientos |
Situación: palabras en el cotidiano (asociados a objetos abstractos) Valor Chance Combinación |
||
| Nivel 3 Estructuras conceptuales |
Nivel 3 Estrategias |
|||
Fuente: Elaboración propia (2023).
En el campo procedimental, se considera una destreza resolver cuestiones propuestas por el caballero Meré, o en otro contexto dar explicación al porqué las sumas 9 y 12 se pueden componer en el mismo número de veces al lanzar dos dados que las sumas 10 y 11 (problema propuesto a Galileo por el Duque de Toscana alrededor de 1620). Aunado a ello, como destreza, se intentaba asignar números a ciertos grados de creencia, encontrado también en fragmento de Batanero (2005a).
En el mismo documento, en el segundo nivel del campo procedimental, se encontró una situación muy interesante, que fue que tanto Pascal como Fermat y Galileo trataron de explicar, de forma coherente, fenómenos no determinísticos, además de comparar la verosimilitud de diferentes sucesos que estaban relacionados con el azar.
En Batanero (2005a), se encuentra que la ganancia es un término que toma importancia en los juegos de azar debido a la apuesta. Se plantearon la pregunta: ¿cómo dividir las apuestas de un juego incompleto? Es decir, qué pasaba si el juego no había terminado, cuál era la forma justa para ambos jugadores. Como en aquel tiempo estaban prohibidas las apuestas, era posible que, a mitad del juego o aun cuando fuera más avanzado, llegara alguna autoridad y lo suspendiera.
En el análisis del documento de Batanero (2005a), se registró que en el sistema de representación es identificado el uso de un lenguaje ordinario. En contextos no matemáticos, se utilizan palabras de manera cotidiana, como “chance” o “combinación”, que son identificadas en la correspondencia entre Fermat y Pascal. Este último intenta resolver los problemas planteados por el caballero Meré apoyado en el triángulo aritmético. Además, se ha identificado la importancia de ganar un juego relativo a la esperanza. La apuesta juega un papel importante en los juegos de azar, de ahí la importancia en realizar cálculos para tomar ventaja de un juego u otro. Se encuentran pocas situaciones en un contexto matemático. Sin duda, la situación que prevalece es un contexto no matemático, y se tienen en cuenta los juegos de azar, como dados o cartas, y la experiencia del jugador. Cabe mencionar que no se muestran todas las fichas, porque, para cada uno de los documentos de análisis, se muestra un ejemplo de ellas. En total, se analizaron 49 fragmentos de los textos.
Otro hallazgo en el análisis, es encontrado en el documento de Mayer (2015), donde coinciden en el nivel dos de conceptos y razonamientos la justicia distributiva para el campo conceptual y cómo calcular los derechos de los interesados en un juego interrumpido en el campo procedimental. Se identifica un contexto no matemático donde la situación es el juego interrumpido y, como fenómeno, se tiene el problema de la división justa (Tabla 4).
Tabla 4 Ficha de registro de información SI_05_231_01, 2023.
| Código SI_05_231_01 | ||||
|---|---|---|---|---|
| Unidad de Análisis Quizás el punto más interesante de esta correspondencia sea “el problema de la división justa”, que estos autores resolvieron en 1654. Éste resulta ser tanto un problema matemático como de la justicia distributiva, pues en principio se trata de calcular los derechos de los interesados en un juego interrumpido (Mayer, 2015, p. 231). | ||||
| Etapa o fecha-precursor: 1654-Pascal, Fermat | ||||
| Estructura conceptual | Sistemas de representación | Fenomenología | ||
| Campo conceptual: | Campo procedimental: | Tipos de representación | Contextos matemáticos | Contextos no matemáticos X |
| Nivel 1 Términos |
Nivel 1 Destrezas |
Situación: Problema matemático |
Situación: Juego interrumpido |
|
| Nivel 2 Conceptos Justicia distributiva |
Nivel 2 Razonamientos Calcular los derechos de los interesados en un juego interrumpido |
Fenómeno: Problema de la división justa | ||
| Nivel 3 Estructuras conceptuales |
Nivel 3 Estrategias |
|||
Fuente: Elaboración propia (2023).
Sin duda, el juego de dados toma un papel muy importante en este desarrollo histórico. A partir de las situaciones que surgían en el juego, se planeaban preguntas que en ese momento carecían de respuesta y donde iba de por medio la ganancia. Como un gran contemporáneo de Fermat y Pascal, Galileo Galilei plantea una situación, pero ahora con el lanzamiento de tres dados, situación encontrada en un fragmento de Mateos y Morales (2002), en un contexto no matemático. Se registró un nuevo término, el orden, y un resultado en el campo conceptual que consistía en mismo número de casos favorables a 9 o 10. Una destreza en el campo procedimental fue determinar los casos favorables al 9 9 (126, 135, 144, 225, 234, 333) y, del siguiente modo, los casos favorables al 10 (136, 145, 226, 235, 244, 343) (Tabla 5).
Tabla 5 Ficha de registro de información SI_04_4_02, 2023.
| Código SI_04_4_02 | ||||
|---|---|---|---|---|
| Unidad de Análisis El amigo que consulta a Galileo no tiene en cuenta el orden y enumera así los casos favorables al 9: 126, 135, 144, 225, 234, 333 y del siguiente modo los casos favorables al 10: 136, 145, 226, 235, 244, 343. De esta manera se obtenían el mismo número de casos favorables a 9 y a 10, en ambos casos seis. (Mateos; Morales, 2002, p. 4). | ||||
| Etapa o fecha-precursor: 1564-1642-Galileo Galilei | ||||
| Estructura conceptual | Sistemas de representación | Fenomenología | ||
| Campo conceptual: | Campo procedimental: | Tipos de representación | Contextos matemáticos | Contextos no matemáticos X |
| Nivel 1 Términos Orden Resultado mismo número de casos favorables a 9 y a 10 Hecho |
Nivel 1 Destrezas casos favorables al 9: 126, 135, 144, 225, 234, 333 y del siguiente modo los casos favorables al 10: 136, 145, 226, 235, 244, 343. |
Lenguaje ordinario | Situación: | Situación: Lanzamiento de tres dados |
| Nivel 2 Conceptos |
Nivel 2 Razonamientos |
|||
| Nivel 3 Estructuras conceptuales |
Nivel 3 Estrategias |
|||
Fuente: Elaboración propia (2023).
En el mismo documento, en otro fragmento, los autores continúan con la misma situación en un contexto no matemático que es el uso de dados. En el nivel dos del campo conceptual, se identifican como conceptos: combinación; casos posibles y número de casos posibles (VR6,3 = 63 = 216); casos favorables; orden; y resultados aleatorios.
Se destaca en el campo procedimental en el nivel uno como destreza los casos favorables al 9 y al 10. Los casos favorables al 9 serían la combinación 126 y en cualquier otro orden son P3 = 3! = 6 casos favorables. En total, son 6+6+6+3+3+1=25 casos favorables al 9. De la misma forma, calculó los casos favorables al 10, cambiando el orden de cada combinación distinta.
Las ideas de Pascal fueron retomadas por Huygens en 1967, fragmento encontrado en Hacking (1975), en donde se detectó en el campo procedimental en el nivel dos un razonamiento probabilístico (Tabla 6), que conduce a la primera estructura conceptual denominada teoría de la decisión. Anteriormente, se había observado, en las lecturas, que no se lograba alcanzar o concretizar el nivel de las estructuras conceptuales. Se puede inferir que se debía a que la idea de probabilidad no estaba pensada como una ciencia sino, más bien solo se pensaba en resolver situaciones relativas a tomar la ventaja en un juego de azar para obtener una ganancia.
Resultados
Aquí, presentaremos los resultados divididos en cada una de las componentes semánticas del significado para el concepto de probabilidad intuitiva:
Respecto a la estructura conceptual, el campo conceptual se concentra en el nivel dos correspondiente a los conceptos. Los conceptos asociados a la probabilidad intuitiva fueron: los fenómenos aleatorios; las posibilidades; los numerales; el número combinatorio; y la equiprobabilidad. Estos sientan las bases para el desarrollo de la teoría de la probabilidad, los cuáles nacen debido a los cuestionamientos que se hacen personajes como Pascal, Fermat y Galileo como consecuencia de la observación del comportamiento de los juegos de dados. El otro nivel es el de los hechos con términos como juego con un dado y juego con dos dados l, en donde el término “orden” desarrolla un papel importante, debido a que sirve como referente para resolver los cuestionamientos que fueron planteados por el caballero Merè, que se encontraron en el campo procedimental como lanzar un dado o lanzar dos dados en donde se encontraban resultados distintos. Algunos de las estrategias identificadas fueron usar las combinaciones, realizar una lista de los posibles resultados y observar los fenómenos probabilísticos en la práctica del juego.
En la lectura del mapa (Figura 1), se encuentra como tipo de representación un lenguaje ordinario, que se desarrolla de forma natural, en un contexto no matemático donde se jugaban dados y cartas no para contar o para hacer un planteamiento matemático, sino para obtener una ganancia.
A partir de ese momento, se desarrolla el razonamiento probabilístico, que fue encontrado en el nivel dos del campo procedimental. Este razonamiento intentó resolver de forma correcta las cuestiones probabilísticas planteadas en la historia para ganar de forma justa, y surge precisamente el problema de la división justa en un contexto no matemático, sobre todo si el juego era interrumpido súbitamente.
Finalmente, la fenomenología tuvo como referente principal los juegos de azar, pues fue en las situaciones de juego de dados, cartas o juegos interrumpidos los que dotaron de sentido a los términos y conceptos surgidos en las otras componentes y estuvieron presentes en todos los documentos analizados.
Una forma de organizar y sintetizar estas tres componentes para evidenciar los significados asociados a la probabilidad intuitiva se presenta en el mapa conceptual general de la Figura 1.
La estructura conceptual arroja el surgimiento de la teoría de la probabilidad que, a su vez, sentó las bases para la emergente probabilidad clásica y probabilidad frecuencial. La afirmación anterior se visualiza cuando se empiezan a formalizar los conceptos del nivel dos para pasar al nivel 3 de estructuras conceptuales (Tabla 6). La comunicación entre Fermat y Pascal, llevadas por la intuición y curiosidad, resuelve situaciones importantes de los juegos de azar y transita desde dar soluciones correctas a los planteamientos del caballero Meré hasta la formalización de las ideas.
Tabla 6 Ficha de registro de información SI_03_11_01, 2023.
| Código SI_03_11_01 | ||||
|---|---|---|---|---|
| Unidad de Análisis “In 1657 Huygens wrote the first probability textbook to be published. At about this time Pascal made the first application of probabilistic reasoning to problems other than games of chance, and thereby invented decision theory” (Hacking, 1975, p. 11). En 1657 Huygens escribió el primer libro de probabilidad para ser publicado. Por el mismo tiempo Pascal hizo la primera aplicación de razonamiento probabilístico a problemas que no fueran juegos de azar, y de este modo inventó la teoría de decisión. | ||||
| Etapa o fecha-precursor: 1657-Huygens-Pascal | ||||
| Estructura conceptual | Sistemas de representación | Fenomenología | ||
| Campo conceptual: | Campo procedimental: | Tipos de representación | Contextos matemáticos | Contextos no matemáticos X |
| Nivel 1 Términos |
Nivel 1 Destrezas |
Situación: | Situación: | |
| Nivel 2 Conceptos Objetos abstractos |
Nivel 2 Razonamientos Razonamiento probabilístico |
Situación: | ||
| Nivel 3 Estructuras conceptuales Teoría de decisión |
Nivel 3 Estrategias |
|||
Fuente: Elaboración propia (2023).
Se observa que no es un desarrollo lineal sino transversal, ya que elementos que se han encontrado en esta etapa de la probabilidad se entrelazan con conceptos, términos y procedimientos de las subsecuentes probabilidades. Realizar un análisis de la probabilidad clásica y la probabilidad frecuencial desde el análisis conceptual será un ejercicio muy interesante para poder describir a detalle dicha transversalidad.
Implicaciones
Los significados de referencia en la historia de la estadística son importantes para organizar el conocimiento, que surge del principal referente base encontrado en este estudio: los juegos de azar. A través de los diferentes significados encontrados, se puede ahondar en investigación que soporte los diferentes tipos de currículum en el área de probabilidad.
Además, este tipo de estudios coadyuvará en lo expuesto por Begué et al. (2017) sobre asegurar que los alumnos comprendan los diferentes enfoques de probabilidad, además de ayudarles a corregir posibles sesgos en su razonamiento que les dificulten poner en relación los diversos significados de la probabilidad.
Los significados de referencia encontrados toman sentido en el contexto de los juegos de azar, que deben estar presentes en el currículum desde el nivel preescolar, cuando los estudiantes desarrollan una intuición nata que los llevará posteriormente a formalizar un razonamiento probabilístico.















