Introdução
O currículo de ensino de Matemática Elementar tem como um de seus temas o trabalho com os números irracionais. Em contrapartida, Fischbein, Jehiam e Cohen (1995) enfatizam que este assunto é pouco trabalhado na Matemática Elementar.
Autores como Schubring (2004) e Palis (2005) relembram que se passou cerca de 2000 anos para que alguns pesquisadores fornecessem uma explicação matemática satisfatória sobre os números irracionais. Palis (2005) retrata que foi em meados do século XIX que se consolidou uma formulação mais precisa dos fundamentos dos números irracionais, devido a matemáticos como Dedekind em 1872 e Cantor em 1883.
Porém, no ensino básico, o trabalho com os números irracionais se encontra bem reduzido, principalmente no tocante ao significado e a importância deste tema. O estudo da história dos desdobramentos e dificuldades dos antigos povos com relação a este tópico pode nos revelar contribuições para o campo da educação, de modo a se aprimorar o entendimento dos números irracionais no ensino da Matemática Elementar.
Apesar da existência de uma infinidade de números irracionais, o número PI é um dos pouquíssimos casos comentados e utilizados como ferramenta na escolaridade básica, principalmente quando se trata de questões do perímetro e circunferência e, ainda, na trigonometria básica, pela relação entre ângulo e arco.
Boyer (1991) coloca que o número PI é, provavelmente, a mais antiga constante matemática que parece estar presente em aplicações pragmáticas de algumas civilizações antigas. Porém, o autor observa que não há indícios que em tais povos havia uma percepção explícita de sua natureza teórica.
Matthews (1995) destaca que muitos autores acreditam que a História da Matemática pode contribuir para o ensino, pois se constitui como uma forma real de contextualização que pode facilitar e enriquecer a compreensão conceitual, motivar, antecipar ou diagnosticar concepções e obstáculos dos alunos da escolaridade básica.
Autores como D’Ambrósio (1996), Miguel (1993;1997) e Schubring (2004) salientam a importância de conectar a Historiografia com diversas possibilidades de abordar o desenvolvimento de temas e ideias matemáticas em atividades de ensino e aprendizagem.
Pessoa Jr. (1996) aponta que o estudo da história pode aguçar o olhar para se perceber que certos objetos podem ser apresentados na escolaridade básica por diferentes modos. De modo complementar, Ginzburg (2001) sugere o ‘estranhamento’ como um modo ou metodologia para superar as aparências e alcançar uma compreensão mais profunda da realidade, num esforço para se enxergar outras possibilidades de se conhecer um objeto.
Embasados nestas sugestões é possível estender o olhar de modo complementar e crítico sobre certos conceitos, o que permite desvelar aspectos não presentes nos poucos documentos descobertos com relação aos conhecimentos matemáticos dos povos antigos.
Neste mote, o objetivo deste artigo foi apresentar e discutir a questão de aproximação em processos infinitos no entorno da História da Matemática como aporte para tecer uma possível abordagem significativa do número PI na escolaridade básica.
Referenciais Teóricos
Fischbein, Jehiam e Cohen (1995) apontam que um dos problemas com o ensino dos irracionais se deve a uma característica da Matemática Elementar: a ênfase excessiva em técnicas em detrimento da busca de significados dos objetos matemáticos.
Outro problema com o ensino dos números irracionais começa com a apresentação do tema nos anos finais do Ensino Fundamental. Autores como Santos (2014), Broetto (2016), Felix (2018), Jesus; Oliveira (2018) e Rocha (2018) relembram que, nesta faixa de ensino, os livros didáticos fazem a apresentação por meio de uma definição. As duas formas de definições mais usuais no material didático disponível são: “Qualquer número real que não possa ser expresso como a razão 𝑎/𝑏 de dois inteiros diz-se irracional” (NIVEN, 1984, p. 60) e “Números irracionais são aqueles que não possuem representação decimal periódica” (NIVEN, 1984, p. 62).
Porém, este tipo de abordagem causa dificuldades para os alunos da escolaridade básica. Uma forma alternativa de prover significado para este tema é apontada em Machado (1990), que destaca a questão da aproximação como um aporte para o estudo dos números irracionais. Ingenuamente, muitas vezes a questão da aproximação não é discutida em sala de aula, pois usualmente pensa-se que a Matemática é ligada exclusivamente aos aspectos exatos, um dos tipos de desvios apontado pelo referido autor.
A representação decimal dos números irracionais é infinita e não periódica. A abordagem das aproximações se constitui em uma conexão com os números racionais, pois os números irracionais somente existem no mundo pragmático através das sucessões de representações racionais. Machado (1990) destaca que esta propriedade está distante do entendimento do cidadão comum, pois não faz parte da rotina de nossas escolas.
Este elo entre os números irracionais e a aproximação para os números decimais finitos tem uma importante ambientação na informática. O computador representa uma máquina capaz de mobilizar algoritmos e cálculos com muita rapidez. O registro de dados na entrada, no processamento e na saída é viabilizado pelas memórias, onde é possível alocar uma quantidade finita de informação.
No caso dos cálculos envolvendo números irracionais, cuja representação decimal é não periódica e infinita, a máquina vai ter a disposição somente uma quantidade finita de dígitos, de modo a se efetivar uma aproximação. A cada cálculo realizado uma operação de aproximação é realizada. Após certo número de operações a precisão dos resultados pode não estar em conformidade com a necessidade de determinada atividade.
Esta configuração pragmática dos computadores requer testes para averiguar a confiabilidade da máquina. Neste processo, são utilizados algoritmos para obter o valor de certas constantes, que em geral acabam sendo certos números irracionais, pois é possível se efetuar uma comparação: quanto maior o número de casas decimais corretas entre o resultado da máquina com os resultados acumulados dos números irracionais melhor a confiabilidade do computador.
De modo similar, Lima (1985) destacou o problema do uso das calculadoras, onde o mostrador disponibiliza alguns dígitos, pois há uma limitação física de visualização dos dados. Deste modo, ao se digitar a tecla correspondente ao PI, o resultado apresenta uma representação decimal finita. Torna-se assim imprescindível se discutir que o resultado do mostrador pode ser aproximado para o número de casas decimais que as diversas aplicações do mundo físico necessitam.
No ensino da Matemática Elementar há de se ter o cuidado de que os alunos não confundam os números irracionais com uma aproximação racional de uma ou duas casas decimais, como relatado em pesquisas como em Lima (1985) e Pommer (2012).
A noção de aproximação é um eixo essencial para se de abordar os números irracionais na escolaridade básica. Para Beskin (1987), o conceito de aproximação remete à possibilidade de substituir um objeto por outro do mesmo tipo, mais simples e suficiente próximo do primeiro.
No universo desta pesquisa, a aproximação se constitui em uma operação matemática para substituir um número irracional por um número decimal finito, de acordo com o grau de precisão desejada.
Um importante trabalho com os números irracionais no enfoque das aproximações advém do modo como foram produzidos os conhecimentos matemáticos deste tema. Machado (1990) considera que o recurso a História da Matemática permite revelar uma continuidade com relação ao significado de temas tratados na escolaridade básica.
Kline (1976) indica que a História da Matemática pode envolver uma perspectiva globalizadora e relacional dos tópicos, pois uma observação desta área revela que o desenvolvimento dos conhecimentos se faz muitas vezes por tentativa e erro, com resultados que provém de variados caminhos, que se situam de acordo com as concepções dos diversos povos antigos.
Miguel (1993) caracteriza algumas funções da História da Matemática na sala de aula, onde se destacam a possibilidade de promover motivação, favorecer a significação e realçar a cultura dos povos antigos, que pode ser comparada com os conhecimentos mais atuais, fatores que certamente contribuem para o ensino desta disciplina.
Em outro texto, Miguel (1997) evidencia que um dos papéis da História da Matemática consiste em apontar analogias ou continuidades entre conceitos e processos matemáticos na ponte passado-presente. O referido autor destaca que uma das formas de trabalhar esta dimensão se faz por meio da resolução e apreciação de problemas históricos.
Neste universo, este texto adota por hipótese a retroação presente-passado em uma forma de diálogo com a epistemologia, o que viabilizaria uma conexão com diversos referenciais pedagógicos e recursos didáticos, o que oportuniza considerar algumas contribuições dos antigos povos para o ensino atual.
Ainda, uma abordagem envolvendo o desenvolvimento histórico dos números irracionais ao longo dos séculos permite realçar a essência dos números irracionais, que perpassa o conceito de infinito e das aproximações.
Eves (1992) aponta que Dedekind escreveu em 1888 o livro ‘O que são e para que servem os números’, no qual apresenta a construção formal dos números reais e irracionais. Neste livro há a abordagem dos números irracionais como o limite de sequências convergentes de números racionais, que o sucedem ou o antecedem, ou seja, as aproximações, por falta ou por excesso. Historicamente, o autor destaca que Arquimedes utilizou este processo para delimitar o intervalo
Referenciais Metodológicos
No tocante ao objetivo de discutir aportes para tecer uma abordagem significativa do número PI perante a questão de aproximação em processos infinitos recorremos a metodologia da pesquisa bibliográfica.
Para Lüdke e André (1986) as informações que podemos extrair e resgatar justifica o uso de documentos nas várias áreas das Ciências Humanas. O documento utilizado como fonte de pesquisa pode ter várias origens, como fontes escritas, verbais, iconográficas, dentre outros meios.
Sá-Silva, Almeida e Guindani (2009) alertam que até meados do século XIX a escola positivista havia privilegiado o registro escrito como meio oficial de pesquisa para os historiadores. Neste tipo de investigação o “[...] documento assumia o peso da prova histórica e a objetividade em garantia pela fidelidade ao mesmo” (p. 6).
Os referidos autores destacam que uma das formas de investigação com documentos é a pesquisa bibliográfica. A exploração desta tipologia na Educação possibilita ampliar o entendimento de objetos cuja compreensão necessita de contextualização histórica e sociocultural.
A natureza da pesquisa bibliográfica remete às contribuições de diferentes autores atentando para as fontes secundárias. Oliveira (2007) argumenta que a principal finalidade da pesquisa bibliográfica é proporcionar aos pesquisadores o contato com obras, artigos ou documentos que tratem do tema em estudo, de modo que se torna “[...] importante para quem faz opção pela pesquisa bibliográfica é ter a certeza de que as fontes a serem pesquisadas já são reconhecidamente do domínio científico” (p. 69).
Oliveira (2007) destaca que os documentos utilizados atuam como fontes de informações, indicações e esclarecimentos que, em seu bojo, podem elucidar certas questões, conjecturas ou esclarecer algum ponto que esteja na busca ou interesse de determinada pesquisa.
Sá-Silva, Almeida e Guindani (2009) pontuam que a pesquisa bibliográfica visa levantar um corpus satisfatório para coletar pistas capazes de fornecer informações interessantes ou importantes e para isto “[...] se utiliza de métodos e técnicas para a apreensão, compreensão e análise de documentos dos mais variados tipos” (p. 5).
Esta metodologia pode ser vista como constituída de duas etapas: a obtenção dos dados e a análise dos resultados. Para a etapa da obtenção de dados fez-se uso de artigos e livros envolvendo a História da Matemática.
Para a etapa da análise dos resultados seguiram-se as etapas de redução das informações deste material em confronto com o tema do número PI. Para a apresentação dos dados optou-se por se organizar os resultados em torno do grau de aproximação que estão imersas as aplicações dos povos antigos com relação ao tema dos números irracionais. Por último, as conclusões se fundamentaram no confronto dos referenciais teóricos com as informações desenvolvidas nas etapas de redução e apresentação.
Neste contexto, passamos a realizar algumas considerações envolvendo a história, a epistemologia e a didática em torno do número PI, obtidas em contato com artigos e livros envolvendo a História da Matemática.
Considerações históricas, epistemológicas e didáticas em torno do número PI
O símbolo de PI está associado à letra do alfabeto grego π (minúscula). Do ponto de vista da etimologia, o símbolo π foi utilizado pela primeira vez em 1706 por Welshman Willian Jones, matemático inglês que abreviou a palavra grega ‘περιφερεια’ (periferia), que representa o perímetro de um círculo de diâmetro unitário (Boyer, 1991). Em 1736, Euler passou a utilizar esta notação, que se estabeleceu como notação padrão. Daí se derivou uma primeira definição, apontada no Quadro 1.
Quadro 01: Definição usual do número PI em livros didáticos da escolaridade básica
|
|
Fonte: O autor.
Silveira (2001) entende que é possível definir o número PI a partir de outros três conceitos da Geometria Plana: área de um círculo, área da superfície esférica e volume da esfera, que estão sintetizados na Tabela 01.
TABELA 01: Três outras formas de definir o número PI
| Área do círculo | Área da esfera | Volume da Esfera |
|---|---|---|
|
|
|
|
Fonte: Adaptado de Silveira (2001)
Algumas pesquisas envolvendo o livro didático como em Borboleto (2008) e Pommer; Pommer (2011) revelam que a definição usual neste material é a primeira, ou seja, o número PI representa a relação entre o perímetro de uma circunferência e seu diâmetro.
A história do desenvolvimento matemático nas civilizações revela alguns episódios da vida cotidiana onde cálculos eram feitos por meio de regras práticas, geralmente situadas em modos de aproximação para números inteiros ou decimais finitos.
Com relação ao conhecimento empírico dos antigos povos, alguns historiadores fazem uso destes dados para calcular o valor de PI, de modo a traçar um percurso para o valor numérico associado. Este fato parece não ter sido a preocupação dos povos antigos, visto não haver indícios de tal atitude em nenhum documento encontrado até recentemente. “Com efeito, é difícil imaginarmos situações práticas reais onde, numa civilização incipiente, alguém tenha precisado calcular a circunferência de um círculo de diâmetro conhecido, ou vice-versa” (SILVEIRA, 2001, p. 2).
Acreditamos que o uso deste recurso torna possível resgatar uma série de conceitos e relações que permitem significar o número PI. Por questão de tradição, foi feita uma escolha para os livros didáticos trabalharem exclusivamente com o π associado ao perímetro da circunferência. Mas, em termos didáticos, é possível resgatar o percurso epistemológico envolvendo as ideias inerentes às várias possibilidades de definição do número PI.
Silveira (2001) destaca antigos documentos que foram encontrados tratando especificamente de π são tabletas mesopotâmicas (datadas de cerca de 2.000 a.C.), que utilizavam a aproximação inteira π = 3.
Outro exemplo disto pode ser encontrado no ‘Chui-Chang Suan-Shu’ (Nove Capítulos sobre a arte Matemática), de cerca de 250 a.C. Neste livro, Boyer (1991) argumenta que os chineses mencionam a seguinte regra: a área do círculo seria equivalente a três quartos do quadrado sobre o diâmetro que, indiretamente, resulta em π = 3, conforme o Quadro 2.
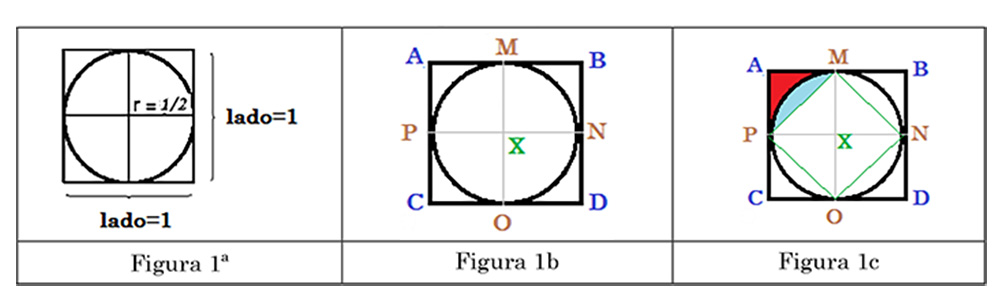
O cálculo permite obter uma primeira aproximação de PI para um inteiro, fato que oculta a natureza deste irracional. Na Figura 1 ilustramos as etapas de uma possível explicação para esta regra de aproximação. A Figura 1a mostra a situação inicial: um quadrado de lado unitário que circunscreve uma circunferência, de modo que o diâmetro da circunferência também é unitário. Podemos perceber que a área do círculo é menor que a área do quadrado circunscrito, ou seja, a área é menor que ‘1’.
Na Figura 1b fez-se um traçado dos eixos que passam pelo centro da circunferência (X) e foram demarcados os pontos M, N, O e P, intersecção destes eixos com as retas suporte das arestas do quadrado ABCD.
Na Figura 1c traça-se o quadrado MNOP que possui metade da área do quadrado ABCD, visto que os triângulos APM e MXP são congruentes (de modo análogo para os outros três triângulos que decompõe MNOP).
No Quadro 3 fizemos uma síntese dos resultados.
QUADRO 3: Comparação dos resultados
| Área do círculo inscrito | Média aritmética simples entre os extremos |
|---|---|
|
|
|
Fonte: O autor
Os livros de História da Matemática não justificam a regra do livro chinês. A média aritmética simples do Quadro 02 poderia ser uma dentre as possíveis justificativas, ficando esta ponderação especulativa uma abertura para favorecer um pensar matemático que envolve processos de aproximação, um tema pouco trabalhado na escolaridade básica.
Na Figura 1c percebe-se visualmente que as áreas em cor azul (segmento circular menor relativo ao ângulo
Outra aproximação racional de PI tem origem no antigo povo babilônico, de uma tableta de argila datada em cerca de 4000 mil anos. Segundo Boyer (1991), na tableta se encontra o valor 0;5736 (em notação sexagesimal) como resultado da razão entre o perímetro do hexágono regular e o perímetro do círculo circunscrito ao hexágono (Quadro 04).
QUADRO 04: O resultado da tableta Plipton 332
|
|
Fonte: O autor
Esta aproximação foi muito utilizada por diversos povos posteriores aos babilônios. O conhecimento empírico dos antigos babilônios conFigura uma aproximação racional de π com uma casa decimal correta.
Consideramos, a seguir, outra possibilidade de abordagem do número PI, em outro contexto histórico. Destacamos o trabalho de Ptolemeu, no livro Almagesto, do século II d.C, que se propôs a elaborar uma tábua de cordas trigonométricas na base sexagesimal. Esta Tabela permitiu, em um período posterior, se obter para π o valor de
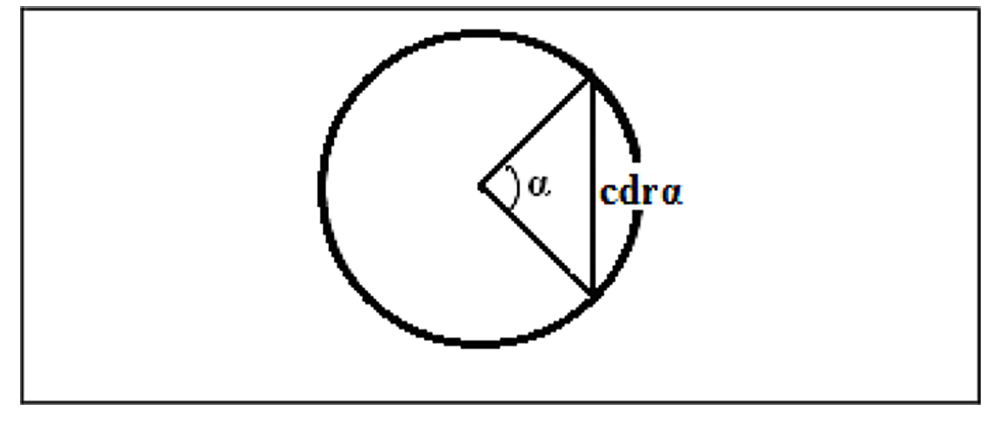
Para a elaboração da tábua, Ptolomeu reutilizou o processo geométrico de aproximação do perímetro de uma dada circunferência, considerando a sucessão de polígonos inscritos e circunscritos, devido a Arquimedes. Em um polígono de ‘n’ lados, cada lado corresponde a corda de um ângulo central α. A corda correspondente ao ângulo α é representada pelo segmento de reta cdr α, conforme ilustra a Figura 2.
A tábua de cordas trigonométricas de Ptolomeu foi elaborada no sistema sexagesimal, onde o raio do círculo trigonométrico valia 60 unidades. Na Tabela 2 optamos por colocá-la na base decimal.
TABELA 2: Parte da Tábua de Cordas de Ptolomeu (na base decimal)
| α | crd α |
|---|---|
| 0,5º | 0,5236 |
| 1º | 1,0472 |
| 1,5º | 1,5708 |
| 2º | 2,0944 |
| 2,5º | 2,6178 |
Fonte: Adaptado de Aaboe (1984).
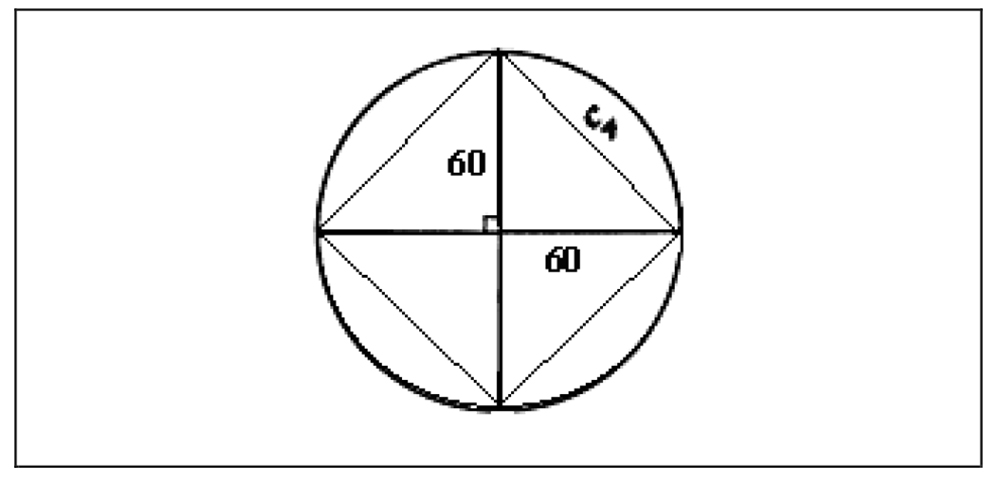
Utilizando-se da construção de Ptolomeu (Tabela 2), podemos obter uma aproximação do número PI pelo processo de determinar o perímetro dos polígonos inscritos a uma dada circunferência, através da leitura do valor de cdr α. Na Figura 3 apontamos o caso da corda associada ao ângulo de 90º.
Fonte: Aaboe (1984, p. 131).
Figura 3: Representação geométrica da corda que correspondente ao ângulo central de 90º.
O perímetro do polígono seria dado pela multiplicação do número de lados e a medida de cdr α. O valor aproximado de PI seria obtido por
Começamos pela obtenção do perímetro do quadrado inscrito (Figura 3), determinado pelo valor de cdr (90º) ou c4 multiplicado por 4. Aplicando-se Pitágoras, ou seja, c42 = 602 + 602 resulta
Para os demais polígonos sintetizamos os resultados no Quadro 05, onde cdrα é o valor da corda, cuja fonte é a Tabela completa de Ptolomeu que pode ser obtida em Aaboe (1984).
QUADRO 5: Valores aproximados de PI pelo método de Ptolomeu.
| Polígono inscrito | n: nº de lados | α | cdrα (Polomeu ) | Perímetro = n.cdrα |
|
|---|---|---|---|---|---|
| quadrado | 4 | 90º | 84;51,10 | 4. 84;51,10 = 339,41111 |
|
| Hexágono regular2 | 6 | 60º | 60 | 60.6 = 360 |
|
| Octógono regular | 8 | 45º | 45,9220 | 367,3760 | 3,0615 |
| Decágono regular | 10 | 36º | 37;4,55. | 10. 37;4,55 = 370,8194444 |
|
| Dodecágono | 12 | 30º | 31,0583 | 372,6996 | 3,1058 |
| - | 72 | 5º | 5,2344 | 376,8768 | 3,1406 |
| - | 360 | 1º | 1;2,50 | 360.1;2,50 = 360.1,0472222 = 377 |
|
Fonte: O autor.
Este processo permitiu se obter a aproximação 3,1417 por meio de uma rede de conexões intramatemáticas, considerando aspectos da Geometria, da Trigonometria e da Teoria dos Números.
Nota-se que, ao considerarmos os valores obtidos na última coluna do Quadro 5, há uma sequência finita de sete termos, (2,8284; 3; 3,0615; 3,0901; 3,1058; 3,1406; 3,1417), que contém valores aproximados para PI, considerando-se quatro casas decimais. Se extrapolarmos o caráter finito, a sequência de valores racionais está associada a uma das essências dos números irracionais, ou seja, em um processo infinito o número irracional é o valor convergente da sequência de aproximações.
Por último, buscaremos uma resposta para a questão: Como Arquimedes teria obtido o intervalo aproximado
Do ponto de vista da moderna historiografia, uma das possibilidades é buscarmos caminhos alternativos. Mas, do ponto de vista do ensino da Matemática, quais seriam as vantagens que tais especulações para abordar tal questão?
Uma possível projeção seria trilhar pelo viés da aproximação. Como não há registros do modo de aproximação que Arquimedes utilizou, estamos assumindo tais posições especulativamente.
O valor de PI fica confinado no intervalo:
Adotando-se para o raio da circunferência o valor r = ½, tal relação fica:
Perímetro do polígono inscrito < π > Perímetro do polígono circunscrito
Para a aplicação deste processo se faz necessário calcular o perímetro do hexágono inscrito e circunscrito a circunferência de raio ½. No Quadro 06 apontamos o cálculo do perímetro do hexágono inscrito e circunscrito a circunferência de raio ½.
QUADRO 6: Cálculo do perímetro do hexágono inscrito e circunscrito a circunferência de raio ½.
| Lado | pn (hexágono inscrito) | Pn (hexágono circunscrito) |
|---|---|---|
| 6 |
|
|
| p6=6.l6=3; |
|
Fonte: O autor
Tais cálculos se baseiam nas representações dadas na Figura 4.
A seguir, aplicam-se as expressões
Aplicado recursivamente, para os polígonos circunscritos e inscritos com o dobro de número de lados que o anterior, pode-se obter a aproximação de Arquimedes. Tais resultados estão expressos na Tabela 3.
Na questão da comparação da sequência de valores do perímetro inscrito dada por (3; 3,1058; 3,1326; 3,1294; 3,1410; 3,1414 3,1415; 3,1416) e a sequência de valores do perímetro do polígono circunscrito (3,4641; 3,2154; 3,1597; 3,1461; 3,1427; 3,1419; 3,1418; 3,1416) é possível observar que há uma convergência de valores para π ≅ 3,1416 que representa uma aproximação correta até a terceira casa decimal.
TABELA 3: Resultados dos perímetros dos polígonos inscritos e circunscritos.
| Número de lados | Perímetro do polígono inscrito | Perímetro do polígono circunscrito |
|---|---|---|
| 6 | 3 |
|
| 12 |
|
|
| 24 | 3,1326 | 3,1597 |
| 48 | 3,1394 | 3,1461 |
| 96 | 3,1410 | 3,1427 |
| 192 | 3,1414 | 3,1419 |
| 256 | 3,1415 | 3,1418 |
| 512 | 3,1416 | 3,1416 |
Fonte: O autor.
Poderíamos obter uma melhor aproximação para o número PI, até onde se deseje, desde que aumentemos o número de lados dos polígonos inscrito e circunscrito ao hexágono. Isto pode ser discutido com os alunos da escolaridade básica pelo acesso a uma planilha eletrônica, o que possibilita se obter mais casas decimais precisas e remete a uma ideia essencial do número PI: é a convergência das sequencias convergentes de números racionais, que o sucedem ou o antecedem, ou seja, as aproximações, por falta ou por excesso, conforme apontava Dedekind.
Considerações Finais
As situações descritas que envolveram o número PI se inserem na temática da resolução e apreciação de problemas históricos e representam um indicativo da multiplicidade de caminhos para se abordar as características de um número irracional, aos moldes do apontado em Miguel (1997).
Estas incursões históricas foram realizadas na confluência com a questão de aproximação, descrito em Beskin (1987), uma característica que favorece a caracterização conceitual dos números irracionais.
Ao acessar uma calculadora eletrônica, o aluno visualiza o número PI como um número com casas decimais finitas, ou seja, um número racional. Este instrumento empírico não é suficiente para mostrar a natureza teórica da natureza irracional do número PI, que esta ligada a questão da aproximação em sequências de valores, como foi o caso dos perímetros inscritos e circunscritos do processo ligado a Arquimedes.
Bonomi (2008) destaca que os recursos eletrônicos são instrumentos motivadores que permitem cálculos mais rápidos e com eficiência em certas tarefas e investigações, que facilitam caminhos para a construção de significado aos números irracionais.
Isto permite se ampliar o quadro de compreensão conceitual destacada em Matthews (1995), pois situa um espaço de significações pela possibilidade de caracterizar a essência dos números irracionais, definidos pela sequência de valores infinitos obtidas por falta e excesso.
Isto abre a oportunidade da atualização dos temas da matemática na escolaridade básica, que se enquadra no uso da História da Matemática em uma perspectiva globalizadora e relacional dos tópicos, apontada em Kline (1976). Isto é possibilitado pelo acesso ao número PI por meio das aproximações racionais em torno de aplicações pertinentes ao próprio universo matemático, mas circunstanciadas em situações pragmáticas dos antigos povos, fato que propicia um momento de estimular uma importante função da História da Matemática em sala de aula.
Uma análise das situações descritas pode se caracterizar como uma das possibilidades de estabelecer uma conexão passado-presente, de modo a se enxergar outras possibilidades de trabalho com os números irracionais, baseado nos pressupostos de Pessoa Jr. (1996) e Ginzburg (2001). Esta abordagem não usual constitui uma possível ponte entre os números irracionais e os números racionais.