Introdução

De acordo com o dicionário ^{Houaiss (2007}), Criar, do latim creare, significa “dar existência a; dar origem a; formar; imaginar”. Assim, falar sobre criatividade, a princípio, parece ser algo fácil, de conhecimento universal. De fato, a criatividade apresenta-se, para a maioria, como a qualidade de um ser que cria o inexistente, que é único, dotado de originalidade, um gênio. Contudo, alguns teóricos (^{SILVER, 1997}; ^{GONTIJO, 2007}; ^{VALE, 2015}) desmistificam estes e outros mitos que há por trás do que venha a ser a criatividade. Há ainda uma série de verbos que está associada à criatividade, isto é, fazer, planejar, construir, resolver, inventar, descobrir, pesquisar; teorizar, escrever, inovar, relacionar, adaptar, organizar; montar, integrar e interpretar. São todos indicadores de comportamento criativo, passíveis de serem usados tanto para a criatividade do dia-a-dia, quanto também para a criatividade ao mais alto nível.

Na Matemática, a criatividade pode ser amplamente promovida na população escolar em geral (alunos, professores, gestores) e pode ser desenvolvida pela maioria dos estudantes (^{SILVER, 1997}), sendo ela essencial no desenvolvimento do talento em Matemática e de difícil identificação e avaliação.

Cabe mencionar que a criatividade não ocorre apenas em uma área do conhecimento humano: ela pode, sim, emergir em qualquer ambiente, como afirma ^{Morais (2015}, p. 6), ao dizer que “a identificação e a promoção da criatividade devem acontecer em diferentes áreas de conhecimento, no desenho e no aproveitamento dos próprios currículos escolares”. Assim, percebe-se que

[...] é limitado associar a criatividade apenas com a pintura, a música, a escrita ou outra arte, pois a criatividade pode ser encontrada em qualquer atividade humana, desde as ciências, aos negócios, à educação, e todas necessitam de pessoas criativas para progredir (^{VALE, 2015}, p. 40).

Entretanto, será que existe um perfil de pessoas criativas? Todos podem ser criativos desde que haja um ambiente favorável? De acordo com ^{Vale (2015}), existe.

[...] uma visão estereotipada e redutora da pessoa criativa como sendo um gênio, louco, um artista incompreendido, ou então uma criança, pois estas são sempre criativas. Estes mitos não correspondem à realidade já que não é necessário ser gênio, louco ou criança para ser criativo (^{VALE, 2015}, p. 40)

Por um lado, ser criativo implica aptidões e estas, por sua vez, “refletem-se nos contornos dos nossos esforços criativos, não só na alta criatividade, mas também na manifestação criativa do quotidiano” (^{MORAIS, 2015}, p. 3).

A criatividade, por vezes, parece ser fruto de um momento único, podendo ser aflorada em qualquer pessoa. Tomando como exemplo um (a) professor (a) que se dedica a elaborar aulas diferenciadas, que promova de forma singular a aprendizagem em seus estudantes, este profissional fará inúmeras tentativas, algumas frustrantes, outras animadoras, potencializando-as até que, possivelmente, uma de suas aulas seja tão criativa que desperte o interesse dos estudantes, de modo que eles percebam algo de diferente, algo original.

Sendo assim, cabe à escola criar mecanismos que potencializem a criatividade de seus alunos, sobretudo na disciplina de Matemática, pois é um dos componentes curriculares que pode promover o desenvolvimento do pensamento criativo (^{GONTIJO, 2007}) pelo fato de que a formulação e a resolução de problemas são características da atividade criativa. “Tanto os processos como os produtos desta atividade podem ser avaliados de modo a determinar até que ponto é evidente a criatividade” (^{SILVER, 1997}, p. 76).

Dessa forma, faz-se necessária a prática de sala de aula onde se desenvolvam capacidades criativas dos alunos, permitindo-lhes uma participação ativa na sua aprendizagem de modo que possam fazer suas pesquisas e compartilhar suas descobertas.

Acreditando nessas ideias iniciais é que apresentamos este artigo como fruto de um trabalho de pesquisa cujo objetivo foi analisar e interpretar as dimensões da criatividade através de problemas matemáticos relacionados ao conceito de área.

O presente trabalho está organizado em três seções principais. Iniciamos apresentando os aportes teóricos sobre a relação entre a criatividade e a resolução de problemas, seguidos da metodologia da investigação e da coleta dos dados. Na quarta seção delineamos os problemas geradores, os procedimentos utilizados pelos alunos para solucioná-los, os resultados e discussão.

Criatividade e resolução de problemas: suas relações

Na literatura da Educação Matemática, muitos pesquisadores (^{SILVER, 1997}; ^{GONTIJO, 2007}; ^{VALE, 2015}; ^{AMARAL, 2016}) defendem a criatividade como um componente essencial para o desenvolvimento do talento e da competência em Matemática. É uma característica inerente ao próprio saber matemático embora esteja, muitas vezes, associada à genialidade ou a habilidades excepcionais, ela pode ser amplamente estimulada na população escolar de uma forma geral. Este ponto de vista sobre a criatividade está em concordância com a concepção Vygotskiana de desenvolvimento cognitivo e criativo, que postula que todos os indivíduos têm potencial criativo (^{AMARAL, 2016}).

A criatividade é uma capacidade transversal que depende menos dos conteúdos a explorar que da metodologia, das experiências e da cultura de interação na sala de aula. Ela é também coletiva quando, por exemplo, em uma atividade matemática interativa em sala de aula, os alunos estão trabalhando em conjunto: o primeiro aluno pode fazer uma afirmação, o segundo já acrescenta algo, o terceiro elabora o que foi dito anteriormente, e assim sucessivamente.

No entanto, nem sempre a criatividade é visível em contexto de sala de aula, “principalmente quando as atividades são focadas em exercícios rotineiros e mecanizados, que valorizam, sobretudo, rapidez e precisão, negligenciando o pensamento criativo” (^{AMARAL, 2016}, p. 42). Na maioria das vezes, os professores não têm consciência do pensamento espontâneo e intuitivo dos alunos, uma vez que nem sempre há espaço para atividades livres, bem como para reflexões informais que são importantes para desenvolver ideias espontâneas e do senso comum. Boa parte do pensamento matemático incentivado em ambiente escolar é focado na aprendizagem mecânica, memorização e domínio de inúmeras técnicas para resolver problemas específicos prescritos pelo currículo ou destinados a testes padronizados.

Segundo ^{Polya (2006} ), a arte de fazer Matemática é que contempla sempre algum grau de originalidade e criatividade e, se materializa na resolução de problemas com a produção de soluções únicas, inovadoras, e surpreendentes, sustentadas por pensamento matemático flexível, curiosidade e imaginação (^{Silver, 1997}).

Portanto, a resolução de problemas está intimamente relacionada com a criatividade matemática, contribuindo para que a Matemática seja vista pelos jovens como uma disciplina útil na vida diária (^{BOAVIDA et al., 2008}). As suas potencialidades são ilimitadas no que diz respeito ao desenvolvimento do pensamento criativo no domínio escolar (^{VALE, 2012}). Neste sentido, é pertinente contextualizar a criatividade no campo da resolução de problemas, tendo em conta o conhecimento e experiência prévios dos alunos, considerando-se o seu envolvimento livre na execução das tarefas, por meio de métodos e estratégias próprias de abordagem dos problemas.

A investigação sobre a Resolução de Problemas revela que esta atividade é pertinente em diversas perspectivas, dentre elas: visa um trabalho metodológico em sala de aula, bem como a construção de um novo conceito matemático, e essa metodologia pode também ser considerada como uma Filosofia de Educação Matemática, “dado ao seu alcance ao trabalho de alunos, professores, ensino, aprendizagem, avaliação, trabalho colaborativo e cooperativo, reflexão na ação e sobre a ação” (^{ANDRADE; ONUCHIC, 2017}, p. 457)

Há uma estreita relação entre a formulação de problemas e a criatividade (^{SILVER, 1997}; ^{PINHEIRO; VALE, 2013}), uma vez que a atividade criativa vê-se no jogo de formular, na tentativa de resolver, reformulando e resolvendo um problema (^{SILVER, 1997}). Além disso, o autor, numa perspectiva mais ampla, considera que a formulação de problemas se refere quer à criação de novos problemas quer à reformulação de um dado problema. “O importante desta atividade não é chegar à solução de um determinado problema, mas sim a criação de um novo problema” (^{SILVER, 1997}, p. 70).

Este tipo de pensamento, segundo alguns autores (^{SILVER, 1997}; ^{VALE; PIMENTEL, 2013}; ^{PINHEIRO; VALE, 2013}; ^{GONTIJO, 2015}) está na base da criatividade matemática e associada a três dimensões: a fluência, a flexibilidade e a originalidade, como componentes essenciais do pensamento criativo, além de serem características da resolução de problemas abertos.

^{Gontijo (2015}) ressalta que

[...] a capacidade criativa em Matemática também deve ser caracterizada pela abundância ou quantidade de ideias diferentes produzidas sobre um mesmo assunto (fluência), pela capacidade de alterar o pensamento ou conceber diferentes categorias de respostas (flexibilidade), por apresentar respostas infrequentes ou incomuns (originalidade) e por apresentar grande quantidade de detalhes em uma ideia (elaboração) (^{GONTIJO, 2015}, p. 17).

Das três dimensões referidas, a inovação ou originalidade é a mais amplamente reconhecida no fenômeno da criatividade, uma vez que se relaciona com a geração de ideias, abordagens e ações únicas (^{AMARAL, 2016}). Então, questionamos: Como os professores podem propiciar este ambiente de aprendizagem frente aos desafios já enfrentados diariamente na sala de aula?

Acreditamos que a Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas, tal como é apresentada por ^{Allevato e Onuchic (2014}), é uma metodologia diferente daquele trabalho em que regras de “como fazer” são privilegiadas. Trata-se de uma metodologia em que a construção de conhecimento se faz a partir de problemas (geradores) propostos como ponto de partida e orientação para o ensino e a aprendizagem de novos conceitos e conteúdos.

Dessa forma a Resolução de Problemas pode ser uma alternativa profícua para a realização de atividades que favoreçam o desenvolvimento da criatividade. Esta metodologia é um meio de se aprender Matemática, pois ela não valoriza a mecanização de conhecimentos e tem por finalidade ajudar os alunos a se tornarem criativos e investigadores perante uma situação desafiadora, um problema, de forma a compreender e questionar os conceitos de que irão necessitar para resolvê-lo.

É de consenso que o crescimento intelectual dos alunos não pode ser limitado. “Devemos incentivá-los a não fazer da Matemática uma ferramenta utilitarista, mas fazê-los pensar sobre a criatividade que ela pode despertar ao ponto de, utilizando conhecimentos prévios, poder construir novos conhecimentos” (^{HERMÍNIO, 2008}, p. 65).

O fato é que “a resolução de problemas deve ser vista como a principal estratégia de ensino, em que o trabalho de ensinar comece sempre com os alunos” (WALLE, 2009, p. 57) e que estes se sintam livres para pensar e definir diferentes estratégias de resolução, utilizando os conhecimentos prévios de que possuem e as habilidades peculiares de cada um, dentre elas a criatividade. É o que confirma ^{GONTIJO (2015}) ao referir que:

O desenvolvimento da criatividade em Matemática poderá ser potencializado quando são utilizados problemas que não podem ser resolvidos a partir da aplicação mecânica, [...] um verdadeiro problema implica que o sujeito não tenha acesso imediato à resposta somente pela sua memória, mas que está obrigado a pensar, a raciocinar, para encontrar os conhecimentos necessários que levam à resposta (^{GONTIJO, 2015}, p. 17).

Deste modo, percebe-se que a resolução de problemas matemáticos é um meio de potencializar o uso da criatividade por parte dos estudantes proporcionando a estes raciociocínios mais complexos e soluções diversas para um único problema matemático.

Metodologia de investigação

O estudo apresentado neste artigo segue uma metodologia de natureza qualitativa com abordagem descritiva e interpretativa (^{BOGDAN; BIKLEN, 1994}). A opção por esta abordagem metodológica incide no fato de que o estudo está relacionado com as cinco características indicadas pelos autores: (i) a fonte direta dos dados é o ambiente natural, constituindo-se o investigador o instrumento principal; (ii) é descritiva; (iii) o investigador interessa-se mais pelo processo do que pelos resultados ou produtos; (iv) a análise dos dados é feita de forma indutiva e (v) é importante conhecer o significado que os participantes atribuem às suas experiências com a implementação de inquéritos por questionários.

Analisamos as dimensões da criatividade através de problemas matemáticos relacionados ao conceito de área, numa classe com 25 alunos do 5o ano do Ensino Fundamental de uma escola pública do Estado da Bahia, por meio de uma intervenção pedagógica, fazendo uso da Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas. Esta metodologia defende o fato de que é preciso dar autonomia aos estudantes para que se apropriem do conhecimento que poderão construir e percebam que a Matemática não é um campo distante da sua realidade vivida cotidianamente.

Para a coleta dos dados, utilizou-se o Tangram que foi eficaz para o bom desenvolvimento das atividades, uma vez que os estudantes demonstraram mobilizados para resolver os problemas propostos, o que foi algo positivo. Mesmo tendo apresentando algumas dificuldades matemáticas os mesmos se divertiram enquanto buscavam compreender o problema e chegar às possíveis soluções.

É importante ter a visão de que compreender deve ser o principal objetivo do ensino, apoiados na crença de que o aprendizado de matemática, pelos alunos, é mais forte quando é autogerado do que quando lhes é imposto por um professor ou por um livro-texto. Quando os professores ensinam matemática através da resolução de problemas, eles estão dando a seus alunos um meio poderoso e muito importante de desenvolver sua própria compreensão (^{ONUCHIC, 1999}, p. 208).

Vale salientar que os alunos já conheciam o Tangram, por meio de tarefas de exploração e identificação das peças do objeto, permitindo-lhes descobrir diferentes possibilidades de combinar e agrupar as peças. Além disso, já desenvolviam atividades do tipo montar figuras geométricas (triângulo, quadrado, paralelogramo), a fim de estabelecer as relações e propriedades geométricas destas figuras.

Descrevemos nesse texto uma das intervenções realizada na turma mencionada anteriormente, mediada pelos dois primeiros autores deste trabalho com a presença da professora da turma. A tarefa apresentada tinha o propósito de que os estudantes compreendessem o conceito de área e desenvolvessem as dimensões da criatividade no contexto da resolução de problemas.

Para o início das atividades, tínhamos de escolher apenas um problema, respeitando o perfil da turma, o que, a princípio, aparentava ser algo fácil, mas que exigia prudência, porque o problema deveria ser o ponto inicial para se trabalhar com o modelo proposto por ^{Allevato e Onuchic (2014}), a Metodologia de Ensino-Aprendizagem-Avaliação de Matemática através da Resolução de Problemas. Por isso, o problema não poderia ser de difícil compreensão por parte dos alunos, pois os deixariam desestimulados e nem tampouco fácil, uma vez que não causaria empolgação em resolvê-lo, em consonância com a compreensão que ^{Onuchic (1999)} tem de problema, como sendo tudo aquilo que não se sabe fazer, mas que se tem interesse em resolver.

Ensinar Matemática, utilizando resolução de problemas como metodologia de ensino e aprendizagem, não é uma tarefa fácil, pois não basta apresentar um problema e “ficar sentado”, esperando que alguma mágica aconteça. Mas, também, não significa dizer que existe uma forma rígida para usufruir dessa metodologia nas aulas de Matemática.

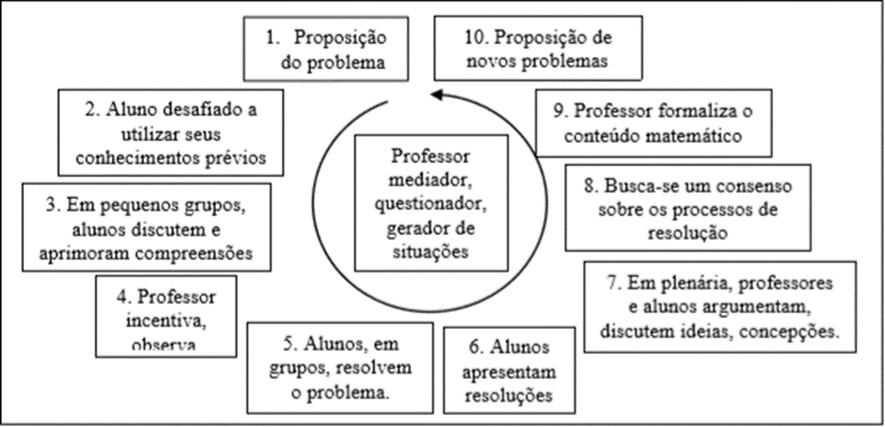
Para a resolução dos problemas propostos, durante a intervenção, recorremos as etapas sugeridas por ^{Allevato (2014}) para o seu desenvolvimento, apresentadas no esquema a seguir (quadro 1):

Fonte: ^{Vieira e Allevato (2014}).

Quadro 1: Etapas da resolução de problemas 

Os conteúdos matemáticos desenvolvidos dessa forma, segundo a autora, fazem sentido para o aluno, que passa a ser protagonista na construção de seu próprio conhecimento. Ao contrário de outras práticas em sala de aula, em que os problemas são propostos no final de cada conteúdo, com essa metodologia, os problemas são propostos aos alunos antes de lhes ter sido apresentado formalmente o conteúdo matemático e, desta forma, a aprendizagem se realiza a partir e no decorrer da resolução do problema.

Esse caminho para ensinar Matemática torna o ato de resolver problemas uma parte integrante no processo da aprendizagem matemática. Assim, os alunos aprendem matemática enquanto estão resolvendo problemas.

Outro aspecto importante a se considerar aqui, sobre a Resolução de Problemas, consiste em incluir um ensino que proporcione aos alunos um leque variado de problemas não rotineiros nos quais podem ser aplicadas diferentes estratégias, dentre elas, a visualização. Ela é “uma ferramenta poderosa no raciocínio matemático e que pode proporcionar algo mais profundo em Matemática do que apenas o uso de fórmulas” (^{VALE, 2017}, p. 139).

Segundo ^{Vale (2015}), o uso da visualização é um processo poderoso para resolver todos os tipos de problemas, inclusive àqueles em que o visual não é evidente. Desta forma, demos atenção nas atividades a problemas em contextos figurativos cuja resolução visual se recorre a desenhos, esquemas e propriedades matemáticas, ao utilizarmos o Tangram.

Os dados recolhidos durante a intervenção (produção dos alunos, notas de campo, observações realizadas, fotos) foram organizados e analisados de acordo com o problema de investigação: Quais as dimensões da criatividade apresentadas por alunos do 5o ano ao resolverem problemas relacionados ao conceito de área?

Os problemas apresentados aos alunos foram inspirados em Souza, ^{Diniz, Paulo e Ochi (1995}) e, ^{Toledo e Toledo (1997}) cuja intenção foi apresentar o Tangram como uma estratégia para desenvolver a noção de área usando unidades não padronizadas, neste caso as próprias peças do Tangram.

A seguir, no Quadro 2, são apresentados os problemas trabalhados durante a intervenção.

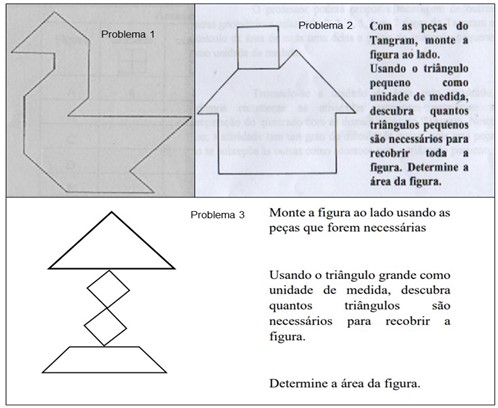
Fonte: Problema 1 (^{TOLEDO; TOLEDO, 1997}); Problemas 2 e 3 (^{DINIZ et al, 1995}).

Quadro 2: Problemas propostos aos estudantes 

Antes de propor os problemas, destinamos um tempo para que os estudantes pudessem explorar o material livremente e a apresentação do problema era feito oralmente com recurso a imagens ou ao material. Durante a resolução dos mesmos, procuramos seguir a metodologia de resolução de problemas proposta por ^{Allevato e Onuchic (2014}), da seguinte forma: observando e incentivando todos os estudantes, ouvindo atentamente as suas ideias e sugestões em seus grupos, por vezes questionando-os, desafiando-os para extensão do problema a outras situações mais exigentes. Depois, na plenária, foi promovida a discussão de modo a sintetizar as soluções; em seguida os pesquisadores registraram no quadro de maneira formal e organizada o conteúdo estudado no problema, ou seja, realizou a formalização do conteúdo que se pretendia para aquela atividade.

Resultados e discussão

Na perspectiva de estimular a criatividade nos estudantes, em todos os problemas propostos, solicitamos que os resolvessem de tantas maneiras diferentes quantas conseguissem, estimulando com isso capacidades criativas quanto a fluência, flexibilidade e originalidade.

Dentre as figuras a serem montadas “o pato” (Figura 1) foi a mais complexa. Os estudantes tentaram construí-la de muitas formas, no entanto, apenas um conseguiu montá-la, isto é, conseguiu visualizar como as peças, que compõem o Tangram, estão dispostas de tal maneira a formar ‘o pato’. Com esta resolução inferimos que esse aluno, ao tentar de várias maneiras chegar à figura do pato e pensar de modos diferentes sobre o mesmo problema, usando as peças de um único Tangram, atingiu uma das dimensões da criatividade em sua resolução, neste caso, a flexibilidade.

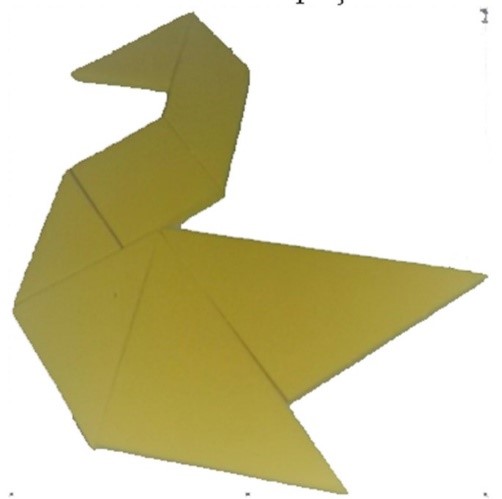
Fonte: Dados da pesquisa.

Figura 1: Representação de um pato montado com as peças de um único Tangram 

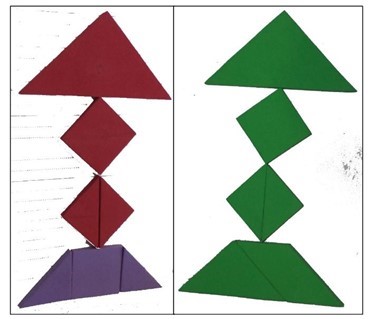
Na atividade seguinte, os estudantes precisavam encontrar a área de uma casa formada pelas peças do Tangram, tendo como unidade de medida não padronizada o triângulo pequeno.

Fonte: Dados da pesquisa.

Figura 2: Representação de casas montadas por alguns participantes 

Ao montarem a casa, sobrepondo as peças do Tangram, a maioria dos alunos respondeu conforme as Figuras 2A e 2B. Por outro lado, houve uma única resposta para as Figuras 2C e 2D. O número de soluções dadas apoiadas nas diferentes representações evidenciam, respectivamente, a flexibilidade e a fluência ao pensarem de modos diferentes e de produzirem um bom número de resoluções sobre o mesmo problema (^{VALE, 2015}).

Em continuidade a esta atividade, no cálculo da área da figura, tendo como unidade de medida o triângulo pequeno, foi necessária a nossa mediação, ou seja, pedimos aos alunos que descobrissem quantos triângulos pequenos caberiam no desenho da casa. A partir da resolução de um aluno, neste caso, a figura 2D, na qual ele pôde mostrar em sua resolução uma maior quantidade de triângulos pequenos, foi possível descobrir que eram necessários 16 triângulos pequenos para cobrir a casa, conforme diálogo a seguir:

PE: - E então João, quantos triângulos pequenos cabem no desenho de sua casa?

João: - Professora, eu sei que o quadrado (chaminé da casa) e o paralelogramo (parte do telhado) são formados por dois triângulos pequenos. No triângulo médio cabem dois triângulos pequenos e no grande cabem quatro triângulos pequenos… Daí, contando todos os triângulos, temos um total de 16.

Para que pudéssemos ampliar as discussões, propusemos aos alunos que calculassem a área da casa, agora usando como unidade de medida o quadrado. A princípio os alunos mostraram-se inseguros, contudo, com a nossa intervenção prosseguiram na procura da resolução da tarefa e, sem hesitar, chegaram à resposta de que era necessário utilizar 8 quadrados para construírem a casa. Para isso conduzimos o processo com alguns questionamentos, como: quantos triângulos pequenos cabem no quadrado? E no triângulo médio? E no grande?

A partir dessas atividades, iniciamos à formalização do conteúdo provocando uma discussão coletiva entre professor, alunos e os pesquisadores. Para isso, fizemos alguns questionamentos aos alunos relacionados às atividades realizadas e, complementávamos as respostas que recebíamos deles.

PE: - Qual a unidade de medida que utilizamos?

Os alunos responderam: o triângulo pequeno.

PE: - Como vocês fizeram para encontrar a área usando esta unidade?

A maioria disse que sobrepunha o triângulo pequeno sobre as demais figuras, encontrando quantos triângulos pequenos eram necessários para cobrir cada figura. Percebemos que os estudantes conseguiram compreender a construção que eles mesmos fizeram.

O último problema objetivava levar os alunos a perceberem o surgimento das frações para expressar o valor de determinadas áreas a partir da composição da figura em triângulos, ou seja, para resolver este problema, o aluno poderia usar todas as relações entre as peças que foram feitas nos problemas anteriores, comparando o triângulo grande com as demais peças.

A montagem da Figura 3 não foi difícil para eles, pois já estavam conseguindo perceber as relações entre o triângulo pequeno com as demais peças do Tangram. No entanto, mais uma vez, foi fundamental a nossa mediação na construção da figura.

Fonte: Dados da pesquisa.

Figura 3: Figura montada pelos participantes 

Cabe aqui, também, mencionar que durante as resoluções, os estudantes utilizaram a criatividade matemática, algumas vezes coletivamente, em duas de suas dimensões: a fluência e a flexibilidade, pois as questões induziam os participantes a produzir diversas ideias para o mesmo problema e, consequentemente, alteravam o pensamento e as respostas até encontrarem a mais adequada ou a “correta”.

Gerando uma discussão coletiva entre pesquisadores e alunos, para determinar a área, perguntamos:

PE: - Quantos triângulos pequenos são necessários para preencher um triângulo grande?

A resposta em “coro” foi: quatro triângulos.

PE: - E qual a fração corresponde a um de quatro triângulos pequenos?

Pensaram durante certo tempo, alguns estudantes disseram que não se lembravam, mas outros responderam que seria um quarto.

PE: - E qual a fração correspondente a dois destes quatro triângulos?

Os alunos responderam: São dois quartos.

A partir das discussões os alunos conseguiram responder que a área da figura seria dois triângulos grandes mais três quartos.

Percebe-se que não foi um trabalho com uma receita pronta e acabada, mas sim, um trabalho, no qual diversos fatores contribuíram para que o objetivo de introduzir o conceito de área pudesse ser alcançado, dentre eles: o interesse e envolvimento dos estudantes com os problemas, a promoção da criatividade, a compreensão do conceito de área com a utilização do Tangram para o nível de escolaridade dos alunos e a interação entre eles próprios, a professora e os pesquisadores.

Vale salientar que a professora teve uma participação singular e considerou a intervenção feita pelas pesquisadoras valiosa. Ao ter essa experiência matemática, a professora pode perceber o favorecimento na abordagem de tarefas que estimule a criatividade com base na resolução e formulação de problemas.

Nesse sentido, o professor deve estar atento e ser criativo nas estratégias a que recorrer, que lhe permita explorar esse potencial em cada um dos seus alunos e com cada uma das tarefas que utiliza, desafiando-os, também, a serem criativos e persistentes nas suas resoluções.

Considerações finais

O trabalho desenvolvido em torno da criatividade, com base na resolução de problemas, proporcionou variadas experiências, ricas e desafiantes. Destacamos a oportunidade de novas aprendizagens matemáticas, uma boa interação, socialização e discussão das estratégias utilizadas, pelos alunos, a partir de caminhos alternativos apoiados em suas intuições e conhecimentos prévios. Ademais, as pesquisadoras conseguiram interagir como mediadoras do processo, motivando os alunos nos momentos de suas dificuldades.

Por não ser algo tão comum, o desenvolvimento de atividades envolvendo a metodologia de ensino e aprendizagem através da resolução de problemas, parece difícil de ser praticada, mas, após a intervenção, observamos que o professor da turma mostrou-se satisfeito com a participação de seus alunos e interessado em trabalhar com a metodologia.

Durante a intervenção, percebemos o quão bem estruturada a proposta é para favocer um caminho rico para ser seguido pelos professores, porque

[...] quando os professores ensinam matemática através da resolução de problemas, eles estão dando a seus alunos um meio poderoso e muito importante de desenvolver sua própria compreensão. À medida que a compreensão dos alunos se torna mais profunda e mais rica, sua habilidade em usar matemática para resolver problemas aumenta consideravelmente (^{ONUCHIC, 1999}, p. 208).

Utilizar essa metodologia é uma maneira de propiciar aos alunos que eles sejam protagonistas do seu próprio conhecimento e que os professores podem orientá-los da melhor forma possível para que tomem gosto por essa forma de aprender e fazer Matemática. Mas, para que isso ocorra é necessário que o professor esteja preparado para utilizar esta metodologia. Outrossim, o ideal é que tivesse desde a sua formação inicial o conhecimento desta e de outras metodologias que possam ser utilizadas em sala de aula para o desenvolvimentos dos conteúdos matemáticos.

Na realização das tarefas pelos alunos as dimensões da criatividade foram afloradas. Ela se manifestou na fluência que adquiriram no momento de sobreporem as peças do Tangram para formar uma figura (por exemplo, as figuras do pato e da casa) e na exploração do conceito de área, ao utilizarem uma unidade de medida não padronizada. Pela flexibilidade que demonstraram ao pensarem visualmente de maneiras diferentes na composição das figuras, bem como no conceito de área com vistas a encontrarem diferentes resoluções. O uso do Tangram foi imprescindível para motivar os alunos nos momentos de interação, o que favoreceu também a criatividade coletiva.

Ademais, acreditamos que os professores devam incluir em suas práticas problemas que levem os alunos a serem criativos em suas resoluções de modo a melhorarem as suas capacidades matemáticas, pois eles precisam de oportunidade e de tempo para mostrar o seu potencial criativo.

Outro fator percebido nas resoluções dos problemas foi o uso da estratégia de visualização, sobretudo no problema de área de figuras. Um problema que permitiu justificar conclusões numéricas sem necessidade de recorrer a fórmula de área de figuras, estabelecendo uma relação com frações.

O uso de estratégias de criatividade pode ser uma maneira para os alunos desenvolverem o gosto pela Matemática, corroborando com ^{Silver (1997}) ao sugerir que o professor dê oportunidades aos estudantes de pensarem através de problemas desafiantes, abolindo os rotineiros e aborrecidos, pois, segundo ele, a criatividade só acontece se nos sentirmos atraídos e desafiados pelas situações que nos propõem.

Assim, este artigo buscou pontuar a confluência de duas linhas de raciocínio: a resolução de problemas e o desenvolvimento da criatividade e que poderá ser um caminho a descobrir e, assim, contribuir cada vez mais na aprendizagem dos estudantes.