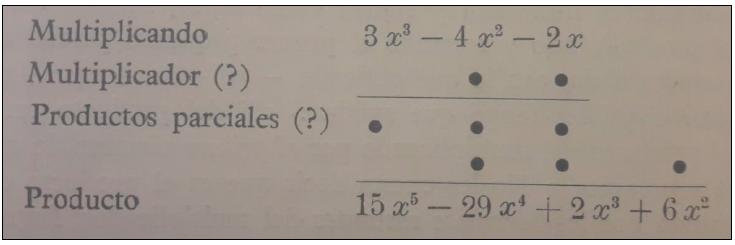Introducción

Desde el punto de vista de la historia de la educación matemática, uno de los aspectos que ofrecen más interés actualmente y para las generaciones futuras es el de la recuperación de textos antiguos o prácticas docentes del pasado que puedan tener plena actualidad en el momento actual con ciertas modificaciones. El legado que nos ofrecen profesores que tuvieron una amplia repercusión en su momento, que fueron innovadores y rompedores en cuanto a la forma de hacer matemáticas en las aulas, desde nuestro punto de vista debe ser recuperado y analizado con detalle para poder incorporarlo a las aulas de hoy en día.

Entre los matemáticos españoles que más repercusión han tenido tanto nacional como internacionalmente se encuentra el profesor Puig Adam (1900-1960). Su importancia tanto nacional como internacional así como las publicaciones que nos ha dejado deben ser objeto de estudio desde el punto de vista de la educación matemática para poder recuperar prácticas interesantes desde el punto de vista didáctico aunque deban ser actualizadas. Esto implica realizar un estudio en profundidad de sus obras, de los escritos que ha dejado y de las prácticas docentes que puedan ser de gran interés. En este sentido, nos ha llamado poderosamente la atención un libro publicado en 1956 en el que él mismo relata cómo llevaba a cabo la docencia en las aulas de educación secundaria, nos da una descripción bastante detallada de los materiales que utilizaba, de la dinámica practicada en el ejercicio profesional, del conocimiento que tenía de las dificultades de los alumnos y de los retos que suponía para ellos el aprendizaje de las matemáticas. Nuestro objetivo, por lo tanto ha sido analizar en profundidad, desde el punto de vista de la práctica docente, la descripción realizada por Puig Adam en el libro Didáctica Matemática Eurística de sus lecciones a la vez que se sitúa en el contexto de la época.

Antecedentes

Uno de los aspectos que la investigación en historia de la educación matemática ha abordado es el relativo a las contribuciones de algunos matemáticos singulares a la enseñanza de esta rama del conocimiento. En casi todos los países existen o han existido profesores de matemáticas que han marcado un antes y un después en la enseñanza y que, en su momento, fueron considerados como precursores de iniciativas novedosas que permitieron formar alumnos competentes en matemáticas y sirvieron de referencia para sus coetáneos así como para las siguientes generaciones. Además, su forma de pensamiento, su postura ante la enseñanza-aprendizaje, sus creencias acerca del proceso de enseñanza-aprendizaje y su impulso en favor de sus convicciones nos permiten comprender algunos de los cambios que se han producido en la historia de la educación de estos países. Esto ha producido contribuciones importantes de la investigación fundamentalmente en lo que se refiere a la enseñanza en la educación secundaria a principios del siglo XX.

Este es el caso del estudio sobre Euclides Roxo (1890-1950) realizado por ^{VALENTE (2004}) en el que se destaca el papel, desde el punto de vista historiográfico, que tienen los documentos del archivo personal de este profesor para entender el rumbo que tomó la enseñanza de las matemáticas en Brasil en la primera mitad del siglo XX. También hay que mencionar la contribución de Osvaldo Sangiorgi (1921-2017) a la segunda modernización de la enseñanza de la matemática en Brasil (VALENTE, 2010) mediante la introducción del movimiento de matemática moderna en este país (VALENTE, 2008) en el que estuvieron activamente involucrados muchos otros profesores como Martha Dantas según refleja ^{DIAS (2012}).

El movimiento de la matemática moderna tuvo sus protagonistas en diferentes países aunque la historiografía se encuentra en sus inicios como señalan ^{VANPAEMEL, DE BOCK y VERSCHAFFEL (2012}). Algunos investigadores se han centrado en “the main architecs of the reform, either in the form of tribute or as a commemorative text” (VANPAEMEL, DE BOCK y VERSCHAFFEL, 2012, p.487). En ese estudio, por ejemplo, se presenta el caso de Willy Servais (1913-1979) y su contribución a la modernización de la enseñanza de las matemáticas en Bélgica así como la influencia que tuvo George Papy en dicha reforma.

Entre los matemáticos influyentes en otros países en los dos primeros tercios del siglo XX, BJARNADOTTIR (2014) menciona a Ólafur Daníelsson (1877-1957) y su contribución a la educación matemática que duró hasta los setenta. Otros incluso llevaron su influencia más allá de ese periodo de tiempo e incluso de las fronteras de su país como fue Emma Castelnuovo (1913-2013) convirtiéndose en referentes internacionales.

En este mismo sentido ^{PARI (2011}) realizó una investigación sobre el profesor boliviano Jaime Escalante (1930-2010) utilizando como metodología la historia de vida. Por medio de entrevistas, observaciones y análisis de los documentos personales del profesor se muestra en este estudio la metodología que caracterizó su enseñanza en centros escolares de Los Ángeles donde un 95% de los alumnos eran latinos. Con esta misma metodología se ha comenzado un estudio (^{GONZÁLEZ, 2012}, 2013) sobre el profesor Norberto Cuesta Dutari cuyo archivo personal se encuentra en la biblioteca de la Universidad de Salamanca y que ha permitido analizar documentos como los cuadernos de los alumnos de este profesor. No vamos a hacer un listado de todos los profesores que en esa época tuvieron gran relevancia en sus países ya que la lista podría desbordar los objetivos de este documento. Los que han sido mencionados dan una idea de cierta línea de investigación que puede ser fructífera en el futuro.

Metodología

El libro que se va a analizar se titula: “Didáctica Matemática Eurística” (fig. 1).

Fuente: Elaboración propia.

FIGURA 1: Portada de libro. 

Fue publicado en Madrid en el año 1956 por el Instituto de Formación del Profesorado de Enseñanza Laboral y consta de 30 lecciones distribuídas en cuatro capítulos que agrupan las temáticas de una determinada rama de las matemática: Aritmética, Álgebra y Análisis, Geometría y, finalmente, Modelos matemáticos extraídos de la vida.

La distribución de las lecciones no es homogénea. Así, hay 10 lecciones de Aritmética, otras 10 de Álgebra y Análisis, 6 de Geometría y 4 de Modelos matemáticos.

Se trata de un libro innovador en el que se tratan de presentar técnicas didácticas novedosas ya que “los métodos y modos tradicionales de enseñanza de nuestra ciencia se consideraban fracasados y necesitados de reforma” (^{PUIG ADAM, 1956}, p. 5). La idea era una enseñanza basada en los procesos de aprendizaje haciendo del alumno un sujeto activo en este proceso. El adjetivo de eurística señala Puig Adam que se debe a que hay que tratar que el alumno “elabore por sí mismo los conceptos y onocimientos que haya que adquirir, mediante el acicate de situaciones hábilmente creadas ante él” (PUIG ADAM, 1956, p. 6).

Cada una de las lecciones está escrita en primera persona a modo de diario de lo que va haciendo el docente. No son un listado de contenidos y de actividades, sino una descripción de lo que ocurre en el aula, Así, se indica la metodología, los materiales usados, las agrupaciones de los estudiantes así como comentarios sobre la fundamentación matemática o didáctica de cada una de las actuaciones y una valoración de las dificultades con las que se encuentran los estudiantes para realizar las actividades.

Para realizar este trabajo se revisaron los planes de estudio publicados en España hasta mediados del siglo XX, seleccionándose aquellos que se correspondían según su publicación y vigencia con la fecha de publicación de las lecciones de Puig Adam. En dichos planes se buscaron los contenidos matemáticos impartidos y la distribución de las asignaturas según los diferentes cursos para conocer el tratamiento que se les daban a las matemáticas en la época.

En cuanto al libro analizado, después de una primera lectura de las lecciones se obtuvo un listado de ítems que hacían referencia a los aspectos tratados en las mismas. Tal es el caso de los siguientes: propiedades y reglas, relaciones, agrupamientos de alumnos, materiales y contextos, representaciones, definiciones, niveles de complejidad, juegos, ejemplos, problemas, flexibilidad, diversidad de interpretaciones, perspectivas futuras. Estos ítmes se han agrupado en tres categorías: contenido matemático, estrategias de enseñanza y conocimiento de los alumnos.

A través de una lectura posterior más profunda, se han ido entresacando evidencias de cada una de las categorías anteriores expuestas en el libro en cuestión que mostraban el tratamiento dado a dichos aspectos.

Contexto

Para entender la obra vamos a exponer algunas cuestiones sobre el momento histórico en el que se publicó tanto desde el punto de vista político, como educativo o social. Se trata de presentar este libro bajo los condicionantes en los que surgió, de forma que se puedan apreciar las características que hacen de él un libro innovador para la época. También mencionaremos algunos datos biográficos del autor pues son esenciales para entender el espíritu de esta obra.

A lo largo del siglo XX se sucedieron numerosas modificaciones y planes de estudio en la educación secundaria en España. Sobre todo los primeros años de este siglo fueron convulsos desde el punto de vista político y económico y ello influyó grandemente en las reformas realizadas en la enseñanza, fundamentalmente hasta los años 70.

En el año 1900 se creó el Ministerio de Instrucción Pública por Antonio García Alix. La enseñanza secundaria, organizada por Real Decreto de 20 de julio de 1901, intentó equilibrar las materias de carácter científico con las literarias para que esta etapa cumpliera una doble finalidad: dar una formación en cultura general y preparar a los alumnos para su ingreso en la universidad. La edad mínima de ingreso en los institutos se estableció a los 10 años y los estudiantes debían hacer un examen de ingreso en el que se valoraban sus conocimientos sobre Aritmética hasta la división inclusive y el sistema métrico decimal, así como nociones básicas sobre Geometría. La enseñanza se organizaba en seis cursos académicos habiendo asignaturas de matemáticas en los cuatro primeros.

El 6 de septiembre de 1903 se publicaba, siendo Ministro de Instrucción Pública D. Gabino Bugallal, el llamado “Plan del 3”. Este plan estuvo vigente de casi veinte años y mantuvo la distribución de asignaturas de matemáticas tal como estaba en el plan anterior.

En el año 1923 Miguel Primo de Rivera da un golpe de estado y en 1926 se publica un nuevo plan de estudios que organiza el Bachillerato en dos etapas: un Bachillerato Elemental de tres años de duración y un Bachillerato Universitario con un primer año común y en los siguientes dos especialidades: Letras y Ciencias.

Se volvió a retomar el plan de 1903 cuando el 14 de abril de 1931 se proclama la Segunda República española. Así el decreto de 13 de mayo de 1931 realiza algunas adaptaciones a este plan y en 1932 se publica un nuevo plan de estudios.

Este nuevo Plan tuvo escasa vigencia ya que en el año 1934, siendo Ministro Filiberto Villalobos, se estableció un nuevo Plan de estudios que sustituía a los anteriores (ESPAÑA, 1934). Las características de este plan de estudios vienen determinadas porque se mantiene la edad mínima de diez años para comenzar el Bachillerato, previo examen de ingreso y se establecen siete cursos para el Bachillerato dividiéndolo en dos ciclos: uno constituido por los tres primeros cursos y otro, por los cuatro últimos. Al finalizar los tres primeros cursos se hacía un examen de conjunto. Al terminar el séptimo curso se realizaba un ejercicio de reválida. En el primer ciclo, la enseñanza tenía un carácter elemental e intuitivo y el segundo ciclo se dividió en dos grados. En el primero (cuarto y quinto años) las disciplinas, desarrolladas de modo cíclico, tenían primordialmente un propósito formativo y en el segundo grado (sexto y séptimo curso) las disciplinas tenían un carácter propedéutico con el fin de acceder con posterioridad a los estudios universitarios.

Las Matemáticas estuvieron presentes en todos los cursos del nuevo Bachillerato siguiendo el método cíclico que se pone de manifiesto en los cuestionarios oficiales publicados en la Gaceta de Madrid de 21 de octubre de 1934. En los dos primeros cursos se introducen las primeras nociones de Aritmética y de Geometría intuitiva, recomendándose que se acentúe más el carácter intuitivo y práctico que tradicionalmente se daba a la enseñanza de estos conceptos. En el tercer año se vuelve sobre los conceptos de los años anteriores, iniciándose la presentación racional de la Aritmética y de la Geometría, sin que esto quiera decir que se explique de modo abstracto. En el cuarto año se continúa con esta presentación racional. En el quinto año se introduce el Álgebra y la Geometría del espacio. En el sexto año se inicia el estudio del Análisis con el número real, límites y continuidad de funciones; además se tratan los logaritmos, las progresiones aritméticas y geométricas, cuestiones de matemática comercial como el interés compuesto y se introducen los números complejos. Asimismo, en este curso se lleva a cabo el estudio de la Trigonometría. En séptimo curso se continúa con el Análisis y se inicia el trabajo con la Geometría analítica con la recta, circunferencia y cónicas.

Durante la guerra civil se continuó con la labor legislativa. En lo que respecta a la Enseñanza Secundaria, el Gobierno de la República no elaboró modificaciones ni nuevos Planes de Estudio durante la Guerra. En el bando del general Franco, el ministro Sainz Rodriguez preparó el Plan de Estudios de 20 de septiembre de 1938 que tendría vigencia hasta el año 1953, estableciéndose las bases organizativas de lo que pasó a denominarse Enseñanza Media. ^{UTANDE (1964}) calificaría este plan de estudios como una nueva enseñanza para un Estado nuevo (^{GONZÁLEZ y CODES, 2016}).

Dado que las lecciones que vamos a analizar se publicaron en 1953, pero que se han encontrado versiones anteriores muy similares en sendas publicaciones de los años 32 y 33: Aritmética y geometría, 1 ^er ciclo (^{REY PASTOR y PUIG ADAM, 1933}) y Lecciones de aritmética (REY PASTOR y PUIG ADAM, 1932), nos hemos centrado en los planes de estudio publicados en esas fechas para mostrar cómo era la enseñanza secundaria en España y las consideraciones que se establecían para la formación en matemáticas a los niños de aquellas generaciones.

El autor del libro, Pedro Puig Adam (1900-1960) fue uno de los matemáticos y profesores de matemáticas más relevantes en España y más reconocidos a nivel internacional durante el segundo tercio del siglo XX. Se formó tanto como matemático como ingeniero lo que repercutió en su forma de entender las matemáticas. Ocupó puestos docentes en diferentes instituciones tanto de educación secundaria como universitaria y estuvo ligado a la Institución Libre de Enseñanza con la que colaboró estrechamente.

Como señala ^{GONZÁLEZ (2008})

la contribución de Pedro Puig Adam a la didáctica de la matemática fue muy amplia y abarcó diferentes niveles y ámbitos del espectro educativo. Desde la publicación de textos escolares, la asistencia a Congresos, la formación de profesores, la publicación de artículos, el diseño de materiales o la colaboración con diversos organismos nacionales e internacionales dan debida cuenta del amplio interés que mostró por mejorar la práctica docente. (p. 99).

Desde el punto de vista internacional tuvo contacto con los grandes educadores del momento y con las figuras más sobresalientes de la educación matemática. Bien conocida por ejemplo fue su relación con Caleb Gategno a quien invitó a venir a España para dar a conocer sus regletas de color.

Fue miembro activo de la Comisión Internacional para el Estudio y la Mejora de la Enseñanza Matemática (CIEAEM) desde 1955 hasta su muerte. Desde 1956 formó parte del comité que presidido por Piaget redactó las Recomendaciones para la enseñanza de la Matemáticas. Además, Gattegno apoyó calurosamente su propuesta de que la XI Reunión de la CIEAEM se celebrase en Madrid. Dicha reunión se centró en el uso del material didáctico para la enseñanza de las matemáticas y tuvo una gran repercusión a nivel internacional (^{DE BOCK y VANPAEMEL, 2015}).

El legado del profesor Puig Adam ha sido muy amplio tanto en relación con los libros de texto que publicó para la enseñanza media tanto en solitario como los que hizo junto a su maestro Julio Rey Pastor, como sus conferencias y artículos en diversas revistas. En total se pueden contabilizar un centenar de publicaciones de diferente índole. Muchos de los artículos publicados estaban enmarcados en el mundo de la educación matemática y gran parte de estas publicaciones están dedicadas a la divulgación de prácticas asociadas al uso en el aula de material didáctico como son las que realizó en la revista Mathematica & Paedagogia (^{PUIG ADAM, 1957} y 1958), la primera de las cuales fue una traducción del discurso inaugural que pronunció en el 11 CIEAEM.

Uno de dichos libros que nos ha llamado poderosamente la atención, Didáctica Matemática Eurística (PUIG, 1956), recopila una colección de lecciones de los primeros cursos de enseñanza media, tal como él las impartía a sus alumnos. Este es el objeto de estudio del presente documento en el que nos hemos permitido analizar dichas lecciones desde el punto de vista de la investigación en didáctica de la matemática.

Contenido matemático

En las lecciones, Puig Adam persigue que los alumnos construyan algunas propiedades y reglas que tradicionalmente se aprenden de manera rutinaria, sin una manipulación previa que les dé sentido al resultado final. Para ello utiliza diferentes fenómenos y modos de representación. Por ejemplo, la propiedad conmutativa, que se refleja tanto en operaciones que la cumplen (producto de números naturales) como en operaciones que no la cumplen (resta de números naturales) se organiza a partir de la adivinación de un número con el que se obtiene otro restando/dividiendo o sumando/multiplicando por otro conocido. Este fenómeno también da sentido a las operaciones inversas de las dos primeras lecciones: resta respecto de la suma y división respecto de la multiplicación.

En ocasiones entremezcla propiedades con definiciones, como en la lección 2 en la que las definiciones de cociente y resto de una división se van combinando con las propiedades que cumplen ambos, siempre comenzando por casos sencillos: cociente de una división exacta y propiedad que cumple cuando se multiplican y dividen el dividendo y el divisor por un mismo número, para terminar con el caso más general: cociente de una división inexacta y propiedades del resto por defecto y por exceso.

Otro resto, el de la raíz cuadrada entera, también es protagonista en el algoritmo para la raíz cuadrada de un número de más de dos cifras: “Para que no se pueda formar un cuadrado mayor, el resto tiene, pues, que ser menor que ¿…?” (^{PUIG ADAM, 1956}, p. 20). El fenómeno que organiza esta operación consiste en completar el mayor cuadrado que se puede formar a partir de un número y, cuando el número de partida no sea un cuadrado perfecto, obtener el resto.

En el caso de las lecciones sobre fracciones, es destacable la variedad de fenómenos que justifican su significado y el de las operaciones aritméticas con fracciones. Por ejemplo, en el caso de la división de fracciones se establecen tres opciones: como inversa de la multiplicación o bien interpretando la fracción inversa “si una pieza de telamide 4/5 de metro, el metro mide 5/4 de la pieza” (^{PUIG ADAM, 1956}, p. 34).

Gran parte de las lecciones está dedicada a dar sentido a múltiples reglas aritméticas: la multiplicación de potencias de igual base, la multiplicación de una fracción por un mismo número, la suma o resta de fracciones que tienen distinto denominador, la división por una fracción, la inversión de signo, la obtención del m.c.m. y el m.c.d.,… Como se verá en el siguiente apartado, el método que emplea para que surjan estas reglas se aleja del método memorístico.

El contenido de las primeras lecciones se refiere a la aritmética elemental pues solo se trabaja con el conjunto de los naturales (operaciones aritméticas elementales, potencia y descomposición en factores primos y relación de congruencia) y con el conjunto de los racionales positivos con expresión decimal (raíz cuadrada y proporcionalidad) y con expresión fraccionaria (fracciones). Sin embargo, y a pesar de que no hay una intención de formalizar los conceptos matemáticos, más bien todo lo contrario, en ocasiones, el procedimiento heurístico que emplea “suministra una demostración intuitiva” (^{PUIG ADAM, 1956}, p. 23) de la regla que se pretende enseñar.

En cambio, las lecciones 9 y 10 tienen un claro carácter introductorio de conceptos que se estudian en cursos más avanzados. El caso de la lección sobre proporcionalidad, es un preámbulo para el tema de la proporcionalidad de segundo curso e introduce también la representación gráfica de funciones a través de una ingeniosa tarea en la que se entremezcla la manipulación de cuartillas de igual área y nociones matemáticas como área y lugar geométrico.

El contenido matemático de Geometría abarca conocimientos de todo el currículo de 1934, desde los primeros cursos hasta los más avanzados. Los conceptos de simetría, ángulos inscritos y posiciones relativas entre planos y rectas (la iniciación a la geometría del espacio) se dedican a los alumnos más jóvenes de entre 10 y 12 años, mientras que el estudio de los poliedros y la trigonometría los lleva a cabo con los adolescentes de entre 13 y 16 años.

En ocasiones, introduce a los alumnos de los dos primeros cursos algunos conceptos que en los cuestionarios aparecen en cursos superiores. Por ejemplo, el concepto de arco capaz está en los cuestionarios de tercer curso pero él lo introduce heurísticamente a alumnos de segundo curso a partir de la relación entre ángulos centrales e inscritos. Incluso introduce la invariancia de algunas relaciones entre ángulos centrales y entre ángulos inscritos a alumnos de primer curso, asentando así los cimientos para abordar en cursos superiores el “lugar de Thales” (^{PUIG ADAM, 1956}, p. 93).

En cuanto a las lecciones de álgebra y análisis trata de dar sentido a las expresiones literales y a las operaciones partiendo de situaciones cercanas al estudiante que poco a poco se van complicando. Así pasa de expresar cantidades de almendras a, bombones b y castañas c, a expresiones simbólicas como es el caso de 5x² - 8xy + 4y². Él mismo señala “Lo que es preciso evitar es que la regla preceda al dominio de lo que ella expresa, y no responda, por tanto, a un acto previamente ejercido por el alumno y expresado (bien o mal) por el mismo” (^{PUIG ADAM, 1956}, p. 49).

Las últimas lecciones del libro tratan acerca de modelos matemáticos extraídos de la vida. Con esta excusa, plantea cuatro lecciones: simetría en el espacio realizadas con una falleba, construcciones geométricas con un vidrio oscuro y matemática y arqueología. Las dos primeras están enfocadas en el estudio de simetrías bien sea en el espacio o en el plano. La tercera aborda cuestiones de reconstrucción de figuras rotas tanto planas como de tres dimensiones al modo que lo haría un arqueólogo, y una vez recompuestas utilizarlas para calcular áreas, perímetros, etc. Esta misma idea se utiliza para la realización de tareas de reconstrucción de fórmulas (fig. 3) en un contexto arqueológico.

Fuente: Extraído de Puig Adam 1956, p. 124

FIGURA 3: Reconstrucción de fórmulas 

De esta forma intenta no sólo motivar a los estudiantes sino que le permite observar si los estudiantes habían asimilado contenidos ya trabajados en el aula de forma no memorística.

La última de las lecciones aborda un tema más árido como es el del rigor y la lógica matemática como un “fenómeno de comunicación social” (^{PUIG ADAM, 1956}, p. 125). Se centra este tema en el asunto del lenguaje para lo cual realiza ejercicios con los alumnos en los que tiene que describir e interpretar descripciones hechas por los compañeros. Al mismo tiempo les inicia en las leyes de la lógica introduciendo situaciones a modo de anécdota y expresiones verbales de las que deben señalar su valor de verdad.

Estrategias de enseñanza

La forma de organizar las lecciones se realiza a través de juegos o modo de reto que se plantean a los alumnos con el fin de trabajar algún contenido matemático. Se plantea una situación inicialmente bastante sencilla pero que poco a poco se irá complicando. Por ejemplo para trabajar la reversibilidad entre la suma y la resta distribuye a los alumnos en grupos de tres de manera que uno piensa un número, otro alumno escribe un número que muestra a los otros dos y el primero debe dar la suma de tal forma que los que no hayan pensado el número inicial deben tratar de adivinarlo. Posteriormente se complica el juego, por ejemplo utilizando números muy grandes. Así para la lección mencionada pide a los alumnos que resuelvan ejercicios como x + 243 = 458 (^{PUIG ADAM, 1956}, p. 10). Finalmente se generaliza el tipo de situaciones utilizando expresiones algebraicas, por ejemplo en este caso sería x + a = m (PUIG ADAM, 1956, p. 10). Este esquema en tres pasos es utilizado por Puig Adam en varias de sus lecciones, constituyendo quizás su método de enseñanza. De esta forma se gradúa paso a paso la complejidad de los ejercicios pasando de situaciones muy concretas a aquellas que puedan ser más abstractas. Considera que de esta forma se conduce una lección eurísticamente (PUIG ADAM, 1956, p. 21).

Propone a los alumnos que enuncien problemas para dar sentido a las operaciones y a las expresiones algebraicas. Por ejemplo a partir de la expresión x + 6 - 3 = 5 un alumno propone “Tenía x, gana 6, pierde 3 y quedan 5 ¿cuántas tenía?” (^{PUIG ADAM, 1956}, p. 11). En este sentido trata de contextualizar o dar un significado en muchas ocasiones a las expresiones algebraicas para que no se queden los alumnos simplemente en un contexto matemático. Por ejemplo les propone el problema de la factura borrosa: “No recuerdo cuántos melones compré a siete pesetas, pero recuerdo que gasté 35 pesetas ¿cuántos melones compré?” (PUIG ADAM, 1956, p. 11). En otras parte de un problema enunciado por los alumnos para introducir un nuevo concepto para que los alumnos vean la analogía entre ambas situaciones. Así, les pide a los alumnos que enuncien un problema sobre la división a lo que dicen: “120 kilos valen 2400 pesetas ¿cuánto vale un kilo?” (PUIG ADAM, 1956, p. 33) a partir del que enuncia un problema sobre fracciones “Una barra de pan de 2/5 de kilo vale 9/4 de pesetas, ¿cuánto vale un kilo de pan”( PUIG ADAM, 1956, p. 33).

En otras ocasiones se vale de retos planteados desde un punto de vista estrictamente matemático pero procurando que se genere cierta motivación en los alumnos. Por ejemplo, plantea a los alumnos reconstruir la siguiente operación con polinomios:

Fuente: Extraído de Puig Adam 1956, p. 51

FIGURA 4: Multiplicación de polinomios 

Otra estrategia muy usada por Puig Adam es la de realizar preguntas a los alumnos para que reflexionen y sean conscientes tanto de los resultados obtenidos en los ejercicios como del proceso seguido en su solución. Por ejemplo, en la lección sobre la división les plantea la siguiente situación “Tocan a cuatro libros y sobran 21, la prueba confirma 15*4+21=81, pero ¿se conformarían los 15 niños entre los que se ha hecho el reparto? ¿Por qué?” (^{PUIG ADAM, 1956}, p. 13). A partir de aquí les introduce la terminología propia de la operación en cuestión, en este caso el término cociente y les ayuda a verbalizar el significado de los términos “Es el mayor número que….” (PUIG ADAM, 1956, p. 13). En otras ocasiones las preguntas le sirven a Puig Adam para hacer avanzar a los alumnos en el conocimiento. Así por ejemplo, a partir de una primera descomposición del número 36 en factores como puede ser 36 = 6 · 6, les pregunta por otras descomposiciones a partir de las que se obtiene 36 = 36·1 o haciéndoles reflexionar un poco más y pidiéndoles que lo descompongan en factores más pequeños y a partir de 6 = 3· 2, obtienen 36 = 6· 6 = 3· 2· 3· 2 con lo que obtienen finalmente la descomposición en factores primos. Mientras que en otras le sirve para entender el proceso de razonamiento seguido por los alumnos. Así en la lección sobre la proporcionalidad, una vez que los alumnos resuelven el reto propuesto, Puig Adam les pregunta para que le digan cómo han llegado a la solución. A partir de las respuestas de los alumnos llega a la conclusión de las estrategias usadas por ellos: “1) la igualdad de razones, entre pares de números de las dos series 2) la razón constante entre los números correspondientes de una y otra serie y 3) la correspondencia en la suma” (2 + 4 = 6 y 1 + 1,5 = 2,5) (PUIG ADAM, 1956, p. 36).

También recurre al cálculo mental para afianzar y progresar en el conocimiento. Así, después de introducir los cuadrados perfectos, la raíz cuadrada exacta y la raíz cuadrada entera les pregunta a los alumnos por la raíz cuadrada de algunos números como 21, 42, o 63.

Son numerosos los ejemplos que usa para justificar un concepto matemático, por ejemplo para dar sentido a la división por exceso plantea una situación de distribución de libros en estantes, pero también introduce otras como la compra de sellos o el uso del transporte. También en algún caso plantea un contraejemplo, como cuando hace ver a los niños que la potenciación no tiene la propiedad conmutativa y señala: “sólo en algún caso particular 2⁴ = 4²” (^{PUIG ADAM, 1956}, p. 14).

Recurre a diferentes materiales para que sirvan de puente entre los conceptos y el pensamiento de los niños. Así para introducir las potencias y las raíces cuadradas utiliza cartulinas que por aquel entonces vendían en las mercerías divididas en seis casillas con seis broches en cada casilla. Usa cuartillas que dobla para introducir las fracciones, sobre todo las mitades, cuartos, octavos,… Las balanzas le sirven para relaionar las ecuaciones con situaciones de equilibrio. Las cajas de mosaicos de colores con triángulos rectángulos isósceles entre sí, para introducir los irracionales cuadráticos. Rectángulos de papel de igual área pero de dimensiones diferentes para introducir la hipérbola o bien las regletas Cuisenaire para trabajar las congruencias y las clases residuales con alumnos de 3º de bachillerato (13 años):

Dispongo primero que los alumnos se numeren y ordenen, del 1 al 24, y empiezo el juego entregando al primero una regleta blanca, al segundo una roja, al tercero una verde, al cuarto una rosa, al quinto una amarilla, al sexto de nuevo una blanca, al séptimo de nuevo una roja, y aquí interrumpo las entregas que todos han visto. Pregunto al número 17 qué color de regleta le corresponderá. Acierta. Repito la pregunta al 24. Y finalmente ordeno que cada cual tome de la mesa una regleta del color que le corresponde. Ordeno que me enseñen y compruebo, haciendo que rectifiquen ellos mismos los aciertos, si los hay (^{PUIG ADAM, 1956}, p. 40).

El uso del material no significa que la lección se reduzca a ese uso. Una vez usado el material se introduce la terminología adecuada, por ejemplo, en este último caso la noción de números congruentes y posteriormente se trabaja sin utilizar el material, sólo manejando los números.

Puig Adam reconoce la importancia del uso de material para la enseñanza de la geometría. Material que en muchas ocasiones elaboran los propios alumnos para estudiar las simetrías, las cónicas y en cuanto a la geometría del espacio construyen con varillas modelos de los poliedros regulares. El uso del material además implica una participación active del alumno para adquirir el conocimiento matemático en cuestión. También recurre a recursos cotidianos para que los alumnos adquieran los conceptos matemáticos tal es el caso del uso del papel como modelo para estudiar el concepto de plano o las agujas de tricotar como modelo para las rectas.

Una de las estrategias que utiliza en sus lecciones es el recurso a las preguntas que le sirven para encauzar el razonamiento del alumno, para que anticipe soluciones, que reflexionen sobre los resultados que han obtenido o que vayan un poco más allá en el conocimiento matemático.

El juego es otra constante en su forma de enseñanza. Lo utiliza tanto como forma de motivación como desde el punto de vista formativo. Así, en relación con las simetrías propone el siguiente:

Señalando un eje vertical en el encerado, sitúo a un alumno a su derecha y otro a su izquierda, y propongo a uno de ellos que dibuje libremente y poco a poco una figura de trazos rectilíneos, ordenando al otro que vaya dibujando la figura simétrica (^{PUIG ADAM, 1956})

Procura que las actividades que realicen los alumnos en torno a un concepto contemple todas las variaciones posibles. Así en el estudio de la posición relativa de tres planos les pide a los alumnos que coloquen los tres planos paralelos entre sí, dos planos coincidentes y uno paralelo, tres planos coincidentes, planos que se corten,... y así continua incorporando poco a poco también las líneas rectas para estudiar su posición respecto del plano.

Cuando las clases son numerosas divide la clase en grupos y pone al frente de cada grupo a uno de los mejores alumnos que además cuentan con un ayudante:

Los jefes y ayudantes me presentaban primero sus soluciones a las cuestiones sucesivamente planteadas, y , con mis indicaciones sobre ellas, vigilaban y orientaban las osluciones tardías de los demás, con la consigna de dejar llegar al máximo la propia iniciativa de cada cual, y con mi superior vigilancia y decisión arbitral en los casos de dudas (^{PUIG ADAM, 1956}, p. 71).

Estas clases no deberían ser clases em las que imperara el silencio y la creatividad sino em las que se debatiera, se discutiera, se actuara.

La doble formación de Puig Adam, como matemático e ingeniero, también influye en el tipo de tareas. Así, por ejemplo, en relación con el cálculo de mínimos de una función plantea a sus alumnos un proyecto para construir un depósito cilíndrico con una capacidad determinada pero de forma que el gasto de chapa sea el mínimo. Para ello, además, los estudiantes deben hacer a escala una maqueta del depósito. Esto les sirve a los estudiantes de motivación “por el hecho de sentirse anticipadamente ingeniero” (^{PUIG ADAM, 1956}, p. 83).

Conocimiento del alumno

Las estrategias empleadas por Puig Adam muestran no solo su interés por llegar a todos los alumnos, sino un conocimiento profundo sobre sus limitaciones y capacidades (de los alumnos) según sus edades.

Una de las observaciones más interesantes a este respecto es la que expone a colación de la dificultad que surge al verbalizar la definición de cociente en una división inexacta:

Se confirma una vez más lo difícil que resulta a estas edades obtener definiciones concretas y hasta, simplemente, repetirlas una vez dadas, y creo que, aunque se den cuenta de la forma en que la definición traduce la idea, no son todavía capaces de reconstruir la definición hasta que la han memorizado (^{PUIG ADAM, 1956}, p. 13).

Y continúa lanzando una crítica constructiva a los métodos memorísticos:

Pero si son realmente capaces de aplicar bien un concepto, ¿Qué prisa hay en que lo enuncien correctamente de memoria? ¿No sería mejor esperar a que esta corrección resulte espontáneamente de un proceso de perfeccionamiento del lenguaje? Creo que estos interrogantes sirven para los profesores de Matemáticas que tanto se escandalizan por definiciones absurdas (prematuramente exigidas), sin que exista idea equivocada en el alumno, sino simplemente una dificultad de lenguaje (que no remedia una repetición memorística) (^{PUIG ADAM, 1956}, p. 13).

La postura de Puig Adam frente a la premura por formalizar conceptos y enseñar de manera mecánica procedimientos, se ve reforzada por las producciones de los alumnos. Tal es el caso de la descomposición en factores primos que realizan los alumnos “a quienes se había inculcado con anterioridad el esquema rutinario clásico” (^{PUIG ADAM, 1956}, p. 19), frente a los que la aprendieron con él que, según sus observaciones, es más natural, como se muestra en el ejemplo que se reproduce: 60 = 6· 10 = 2· 3· 2· 5 = 2²· 3· 5.

Puig Adam afirma en el prólogo de esta obra que “La didáctica es, ante todo, adaptación al alumno”, y para ello hay que saber escuchar no solo el lenguaje verbal, sino también el no verbal, el que no todos somos capaces de entender. En la transcripción de lo que acontecía en las clases hace varias referencias a estas cuestiones como cuando afirma: “noté fatiga en los niños” (p. 15), “reforcé el interés de los niños excitando su fantasía…” (^{PUIG ADAM, 1956}, p. 16) o “En vista de la desorientación general dejo que se explicaran las dos soluciones” (PUIG ADAM, 1956, p. 38).

Esa adaptación también la lleva a cabo adecuando las actividades a los distintos ritmos de trabajo: “Mientras los rezagados rectifican sus errores, he propuesto otras sucesiones para los más adelantados” (^{PUIG ADAM, 1956}, p. 36), y tratando de mantener el interés de sus alumnos para que estuvieran atentos en las clases: “Terminé la última sesión con un juego que ideé como premio al grupo” (p. 18), “Tengo que hacerles fijar la atención en que 6 es a la vez múltiplo de 2 y de 3” (PUIG ADAM, 1956, p. 29).

Para Puig Adam el conocimiento matemático se genera en un “doble juego de la percepción combinada con la acción (real o intuitiva)” (^{PUIG ADAM, 1956}, p. 84). Con esta idea como telón de fondo y con el conocimiento que posee de las capacidades de los estudiantes de Bachillerato, comienza las lecciones planteando a sus alumnos situaciones de las que sabe que se resolverán fácilmente para, progresivamente, aumentar el nivel de complejidad hasta llegar a la noción o propiedad que pretende. Es habitual leer en sus lecciones comentarios como “La respuesta y manipulación consiguiente les resulta fácil” (PUIG ADAM, 1956, p. 86), seguidas de “La dificultad empieza a presentarse cuando…” (PUIG ADAM, 1956, p. 87), que finalizan con el enunciado de la propiedad que han descubiertos los alumnos.

Las preguntas que realiza a los estudiantes no sólo tienen que ver con los contenidos matemáticos sino incluso con la preferencia de métodos. Así, al tratar la representación gráfica de funciones cuadráticas comienza con el método de completar cuadrados y luego el de identificar los coeficientes de la expresión algebraica y utilizar las reglas para obtener cortes con los ejes, máximo/mínimo,… Para finalizar les pregunta a los estudiantes qué método prefieren, indicando éstos que el de completar cuadrados, con lo que se siente satisfecho pues “han penetrado en el proceso estructural de la transformación” (^{PUIG ADAM, 1956}, p. 74).

Conclusiones

Las lecciones de Didáctica Matemática Eurística de Puig Adam representan un hito importante en la historia de la educación matemática en España, tanto por el contenido en sí de las lecciones, como por su intencionalidad. El deseo manifiesto de “ofrecer a los profesores sobre el modo de conducir eurísticamente lecciones determinadas” (^{PUIG ADAM, 1956}, p. 7) ha dejado un legado que no se puede dejar en el olvido.

El análisis de las lecciones ha desvelado tres dimensiones de la obra:

La exposición del método heurístico que ejemplifica en las distintas lecciones cubre una buena parte del contenido de los cursos de Bachillerato de la España de la primera mitad del siglo pasado. Además, manifiesta su vocación docente cuando se revela conocedor de las habilidades y los desaciertos de los alumnos, y paciente para lograr que los menos avispados alcancen el nivel de comprensión de los avanzados.

El análisis de esta obra nos ofrece una visión de la enseñanza que Puig Adam impartía a mediados del siglo pasado. El modo en que conduce las lecciones se apoya no solo en su ingenio para crear situaciones activas de aprendizaje, sino en un conocimiento profundo tanto de la materia como de los alumnos y del currículo. Actualmente, estos son temas de interés en las investigaciones sobre el conocimiento del profesor de matemáticas.