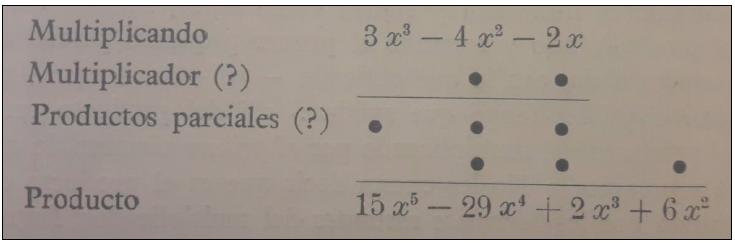Introdução

Do ponto de vista da história do ensino da matemática, uma das tendências com maior interesse atualmente e para as gerações futuras consiste na recuperação de textos antigos ou práticas docentes do passado que possam apresentar um carácter atual nos dias de hoje com as devidas modificações. Do nosso ponto de vista, o legado que nos foi deixado por professores que tiveram um vasto impacto na sua época, que foram inovadores ao romper com a tradição na forma de fazer matemática na sala de aula, deve ser recuperado e analisado em detalhe, de forma a poder ser incorporado nas salas de aula atuais.

Entre os matemáticos espanhóis com maior repercussão, tanto a nível nacional como internacional, está o professor Puig Adam (1900-1960). A sua importância nacional e internacional, bem como as publicações que nos deixou, devem ser objeto de estudo no contexto do ensino da matemática, no sentido de recuperar práticas interessantes a nível didático, ainda que necessitando da devida atualização. Tal implica realizar um estudo aprofundado das suas obras, de todo o material escrito que deixou e das práticas docentes que possam constituir maior interesse. Neste sentido, chamou-nos a atenção em especial uma obra publicada em 1956 na qual o próprio relata a sua prática docente nas aulas de ensino secundário, descrevendo de forma bastante detalhada os materiais que utilizava, as dinâmicas empregues no exercício da sua profissão, o conhecimento que tinha das dificuldades dos alunos e o desafio que constituía para eles a aprendizagem da matemática. Consequentemente, o nosso objetivo foi analisar em profundidade, desde o ponto de vista da prática docente, a descrição realizada por Puig Adam das suas aulas no livro Didáctica Matemática Eurística, com o devido enquadramento no contexto da época.

Antecedentes

Um dos aspetos abordados pela investigação na história do ensino de matemática consiste nos contributos de alguns matemáticos singulares para o ensino deste ramo do conhecimento. Em quase todos os países existem, ou existiram, professores de matemática que marcaram um antes e um depois no ensino e que, no seu momento, foram considerados como precursores de iniciativas inovadoras que permitiram formar alunos competentes em matemática, servindo de referência não só para os seus contemporâneos, como também para as gerações seguintes. Além disso, a sua forma de pensar, a sua postura perante o ensino-aprendizagem, as suas crenças sobre o processo de ensino-aprendizagem e o seu impulso a favor das suas convicções permitem-nos compreender algumas das mudanças que ocorreram na história da educação nestes países. Todos deixaram um contributo importante para a investigação, especialmente no que se refere ao ensino secundário no início do século XX.

É o caso do estudo sobre Euclides Roxo (1890-1950) realizado por ^{VALENTE (2004}), no qual se destaca o papel, do ponto de vista historiográfico, dos documentos do arquivo pessoal deste professor para compreender o caminho tomado pelo ensino da matemática no Brasil, na primeira metade do século XX. Cabe também mencionar o contributo de Osvaldo Sangiorgi (1921-2017) para a segunda modernização do ensino da matemática no Brasil (VALENTE, 2010), por meio da introdução do movimento da matemática moderna neste país (VALENTE, 2008), no qual estiveram ativamente envolvidos muitos outros professores, como Martha Dantas, segundo ilustrado por ^{DIAS (2012}).

O movimento da matemática moderna teve os seus protagonistas em diferentes países, embora a historiografia esteja ainda numa fase inicial, como referido por ^{VANPAEMEL, DE BOCK e VERSCHAFFEL (2012}). Alguns investigadores focaram-se nos “the main architects of the reform, either in the form of tribute or as a commemorative text” (VANPAEMEL, DE BOCK e VERSCHAFFEL, 2012, p.487). Neste estudo, por exemplo, é apresentado o caso de Willy Servais (1913-1979) e do seu contributo para a modernização do ensino da matemática na Bélgica, bem como a influência de George Papy nessa mesma reforma.

Entre os matemáticos influentes de outros países nos dois primeiros terços do século XX, BJARNADOTTIR (2014) menciona Ólafur Daníelsson (1877-1957) e o seu contributo para o ensino da matemática, que durou até aos anos setenta. Outros viram a sua influência ultrapassar inclusivamente este período de tempo e até as fronteiras do seu país, como foi o caso de Emma Castelnuovo (1913-2013), convertendo-se em referências internacionais.

No mesmo sentido, ^{PARI (2011}) conduziu uma investigação sobre o professor boliviano Jaime Escalante (1930-2010), utilizando como metodologia a história de vida. Recorrendo a entrevistas, observações e à análise dos documentos pessoais do professor, este estudo demonstra a metodologia que caracterizou o seu ensino nos centros escolares de Los Ángeles, onde 95% dos alunos eram latinos. Esta mesma metodologia foi utilizada para iniciar um estudo (^{GONZÁLEZ, 2012}, 2013) sobre o professor Norberto Cuesta Dutari, cujo arquivo pessoal se encontra na biblioteca da Universidade de Salamanca, em Espanha, e que permitiu analisar documentos como os cadernos dos alunos deste professor. No entanto, não iremos proceder a uma lista de todos os professores de grande relevância nos seus países nessa época, uma vez que essa mesma lista poderia ultrapassar os objetivos deste documento. Os acima mencionados ilustram já uma ideia de uma determinada linha de investigação que pode ser frutífera no futuro.

Metodologia

O livro que será alvo de análise intitula-se: Didáctica Matemática Eurística (fig. 1).

Fonte: Elaboração própria.

FIGURA 1: Capa do livro. 

Foi publicado em Madrid, no ano de 1956, pelo Instituto de Formación del Professorado de Enseñanza Laboral. Consta de 30 aulas distribuídas por quatro capítulos que agrupam os temas de um determinado ramo da matemática: Aritmética, Álgebra e Análise, Geometria e, por fim, Modelos matemáticos extraídos da vida.

A distribuição das aulas não é homogénea. Como tal, apresenta 10 aulas de Aritmética, outras 10 de Álgebra e Análise, 6 de Geometria e 4 de Modelos matemáticos.

Trata-se de um livro inovador no qual se apresentam técnicas didáticas novas, uma vez que “os métodos e modos tradicionais de ensino da nossa ciência foram considerados um fracasso, a necessitar de reforma” (^{PUIG ADAM, 1956}, p. 5). A ideia consistia num ensino baseado nos processos de aprendizagem que tornam o aluno um sujeito ativo neste processo. O adjetivo “heurística”, como assinalado por Puig Adam, surge no sentido de orientar o aluno para que “elabore por si mesmo os conceitos e conhecimentos que deve adquirir, ao ser estimulado pelo confronto com situações engenhosamente criadas” (PUIG ADAM, 1956, p. 6).

Cada uma das aulas está escrita na primeira pessoa em estilo de diário do que o docente ia fazendo. Não representa uma lista de conteúdos e atividades, mas antes uma descrição do que acontecia na sala de aula. É desta forma que indica a metodologia, os materiais usados, os grupos de alunos, assim como comentários sobre a fundamentação matemática ou didática de cada um dos processos e uma avaliação das dificuldades com as quais os alunos se deparavam ao realizar as atividades.

Para concretizar este trabalho procedeu-se à revisão dos planos de estudo publicados em Espanha até meados do século XX, selecionando os que correspondiam, segundo a sua publicação e vigência, com a data de publicação das aulas de Puig Adam. Nesses mesmos planos procurou-se também os conteúdos matemáticos lecionados e a distribuição das disciplinas segundo os diferentes anos curriculares, para conhecer qual a consideração dada às matemáticas na época.

Quanto ao livro analisado, após uma primeira leitura das aulas, elaborou-se uma lista de itens que faziam referência aos aspetos tratados nas mesmas. Foi o caso dos seguintes: propriedades e regras, relações, agrupamentos de alunos, materiais e contextos, representações, definições, níveis de complexidade, jogos, exemplos, problemas, flexibilidade, diversidade de interpretações, perspetivas futuras. Estes itens foram depois agrupados em três categorias: conteúdo matemático, estratégias de ensino e conhecimento dos alunos.

Através de uma leitura posterior mais aprofundada foi possível selecionar provas de cada uma das categorias anteriores expostas no livro em causa que demonstram o tratamento dado a ditos aspetos.

Contexto

Para uma melhor compreensão da obra serão expostas algumas questões relativamente ao momento histórico da sua publicação, tanto do ponto de vista político, como educativo ou social. Pretende-se, assim, apresentar este livro à luz das condicionantes em que surgiu, de forma a ser possível reconhecer as características que tornam este livro inovador para a época. De igual modo, serão mencionados alguns dados biográficos do autor considerados essenciais para entender o espírito desta obra.

Durante todo o século XX sucederam-se numerosas modificações e planos de estudo no ensino secundário em Espanha. Os primeiros anos deste século foram especialmente atribulados no âmbito político e económico, o que influenciou particularmente as reformas ocorridas no ensino, fundamentalmente até aos anos 70.

No ano de 1900, Antonio García Alix criou o Ministerio de Instrucción Pública (Ministério de Educação Pública). O ensino secundário, organizado pelo Real Decreto de 20 de julho de 1901, tentou equilibrar as matérias de carácter científico com as literárias para que esta etapa cumprisse uma dupla finalidade: providenciar uma formação em cultura geral e preparar os alunos para o ensino universitário. Estipulou-se uma idade mínima de acesso aos institutos de 10 anos e os estudantes tinham de fazer um exame de admissão no qual eram valorizados os seus conhecimentos sobre Aritmética até à divisão, inclusive, e o sistema métrico decimal, bem como noções básicas sobre Geometria. O ensino estava organizado em seis anos académicos, com disciplinas de matemática nos primeiros quatro anos.

A 6 de setembro de 1903 foi publicado, sob tutela do então Ministro de Educação Pública, D. Gabino Bugallal, o chamado “Plan del 3” (Plano do 3). Este plano esteve em vigor durante quase vinte anos e manteve a distribuição de disciplinas de matemática exatamente como no plano anterior.

No ano de 1923, Miguel Primo de Rivera liderou um golpe de estado e, em 1926, foi publicado um novo plano de estudos que organizou o ensino secundário chamado Bachillerato em duas etapas: um Bachillerato Elementar de três anos de duração e um Bachillerato Universitário com um primeiro ano comum e duas especialidades nos seguintes anos: Letras e Ciências.

O plano de 1903 foi, entretanto, retomado quando, a 14 de abril de 1931, foi proclamada a Segunda República espanhola. Assim, o decreto de 13 de maio de 1931 fez algumas adaptações a este plano e, em 1932, foi publicado um novo plano de estudos.

Este novo Plano teve uma vigência fugaz pois em 1934, sendo então Ministro Filiberto Villalobos, foi estabelecido um novo Plano de estudos que substituiu os anteriores (ESPAÑA, 1934). Este novo plano de estudos caracteriza-se pela manutenção da idade mínima de dez anos para iniciar o Bachillerato e do exame de admissão, estabelecendo, por outro lado, sete anos para o Bachillerato, dividido em dois ciclos: um constituído pelos três primeiros anos e o outro constituído pelos quatro últimos anos. No final dos três primeiros anos existia um exame conjunto. No final do sétimo ano era feito um exercício final. No primeiro ciclo, o ensino tinha um carácter elementar e intuitivo, enquanto o segundo ciclo foi dividido em dois graus. No primeiro (quarto e quinto anos), as disciplinas, desenvolvidas de modo cíclico, tinham primordialmente um propósito formativo. Já no segundo grau (sexto e sétimo ano), as disciplinas tinham um carácter propedêutico, com o objetivo de aceder, posteriormente, ao ensino universitário.

A matemática esteve presente em todos os anos do novo Bachillerato seguindo o método cíclico, como exposto nos questionários oficiais publicados na publicação periódica “Gaceta de Madrid”, de 21 de outubro de 1934. Nos dois primeiros anos eram introduzidas as primeiras noções de Aritmética e de Geometria intuitiva, recomendando-se frisar mais o carácter intuitivo e prático que tradicionalmente se dava ao ensino destes conceitos. O terceiro ano revia os conceitos dos anos anteriores, iniciando a apresentação racional da Aritmética e da Geometria, sem com isso implicar uma explicação de modo abstrato. No quarto ano dava-se continuidade a esta apresentação racional. No quinto ano era introduzida a Álgebra e a Geometria espacial. No sexto ano iniciava-se o estudo da Análise com o número real, limites e continuidade de funções; cobriam-se também os logaritmos, as progressões aritméticas e geométricas, questões de matemática financeira, como o interesse composto, e introduziam-se os números complexos. Neste mesmo ano também se estudava a Trigonometria. No sétimo ano dava-se continuidade à Análise e iniciava-se o trabalho com a Geometria Analítica com a reta, circunferência e cónicas.

Durante a guerra civil prosseguiram os processos legislativos. No que respeita ao Ensino Secundário, o Governo da República não fez modificações, nem novos Planos de Estudo durante a Guerra. Do lado do General Franco, o ministro Sainz Rodriguez preparou o Plano de Estudos de 20 de setembro de 1938, que ficaria em vigor até ao ano de 1953, estabelecendo assim as bases da organização do que passou a chamar-se Enseñanza Media (Ensino Secundário). ^{UTANDE (1964}) viria a qualificar este plano de estudos como um “novo ensino para um Estado novo” (^{GONZÁLEZ; CODES, 2016}).

Uma vez que as aulas que iremos analisar foram publicadas em 1953, mas foram encontradas versões anteriores muito semelhantes em duas publicações dos anos 32 e 33: Aritmética y geometría, 1 ^er ciclo (^{REY PASTOR e PUIG ADAM, 1933}) e Lecciones de aritmética (REY PASTOR; PUIG ADAM, 1932), focámo-nos nos planos de estudo publicados nessas datas para demonstrar como era o ensino secundário em Espanha e as considerações estabelecidas para a formação matemática das crianças dessa época.

O autor do livro, Pedro Puig Adam (1900-1960), foi um dos matemáticos e professores de matemática mais relevantes em Espanha, e mais reconhecido a nível internacional durante meados do século XX. Formou-se como matemático e engenheiro, o que se repercutiu na sua forma de entender a matemática. Ocupou cargos docentes em diferentes instituições, tanto de ensino secundário como universitário, e esteve ligado à Institución Libre de Enseñanza (Instituto de Ensino Livre) com a qual trabalhou em estreita colaboração.

Como referido por ^{GONZÁLEZ (2008}):

[...] o contributo de Pedro Puig Adam para a didática da matemática foi muito vasto e abrangeu diferentes níveis e âmbitos do espetro educacional. A publicação de textos escolares, participação em congressos, formação de professores, publicação de artigos, o desenho de materiais ou a colaboração com diversos organismos nacionais e internacionais refletem claramente o enorme interesse que demonstrou por melhorar a prática docente. (p. 99)³.

A nível internacional, teve contacto com os grandes educadores do momento e com as figuras mais proeminentes da educação da matemática. Era bem conhecida, por exemplo, a sua relação com Caleb Gategno, o qual convidou a ir a Espanha para dar a conhecer as suas barras de cor.

Foi membro ativo da Comissão Internacional para o Estudo e a Melhoria do Ensino da Matemática (CIEAEM) desde 1955 até à sua morte. A partir de 1956 fez parte do comité que, presidido por Piaget, redigiu as Recomendações para o Ensino da Matemática. Aliás, Gattegno apoiou de forma entusiasta a sua proposta de celebrar a XI Reunião da CIEAEM em Madrid. Essa reunião focou-se no uso do material didático para o ensino da matemática e teve uma grande repercussão a nível internacional (^{DE BOCK e VANPAEMEL, 2015}).

O legado do professor Puig Adam foi muito vasto, tanto a nível dos manuais que publicou para o ensino secundário, individualmente ou em conjunto com o Gatenho seu mentor Julio Rey Pastor, como a nível das conferências e artigos em diversas revistas. No total, é possível contabilizar uma centena de publicações de diferente índole. Muitos dos artigos publicados pertenciam ao âmbito do ensino da matemática e grande parte dessas publicações dedicou-se à divulgação de práticas associadas ao uso de material didático na sala de aula, como as que realizou na revista Mathematica & Paedagogia (^{PUIG ADAM, 1957} e 1958), a primeira das quais foi uma tradução do discurso inaugural que proferiu no 11 CIEAEM.

Um dos livros que nos chamou a atenção mais particularmente, Didáctica Matemática Eurística (PUIG, 1956), consiste na recompilação de uma coleção de aulas dos primeiros anos de ensino secundário, tal como o autor as lecionava aos seus alunos. Este é o objeto de estudo do presente documento, no qual tomámos a liberdade de analisar essas mesmas aulas a partir do ponto de vista da investigação da didática da matemática.

Conteúdo matemático

Nas suas aulas, Puig Adam tenta fazer com que os alunos construam algumas propriedades e regras que tradicionalmente se aprendem de forma rotineira, sem uma manipulação prévia que dê sentido ao resultado final. Para tal, utiliza diferentes fenómenos e modos de representação. Por exemplo, a propriedade comutativa, que se reflete tanto em operações que a cumprem (produto de números naturais), como em operações que não a cumprem (subtração de números naturais), é organizada a partir da adivinhação de um número com o qual se obtém outro subtraindo/dividindo ou somando/multiplicando por outro conhecido. Este fenómeno também dá sentido às operações inversas das duas primeiras aulas: subtração em relação à soma e divisão em relação à multiplicação.

Por vezes, mistura propriedades com definições, como na aula 2, quando as definições de quociente e resto de uma divisão se vão combinando com as propriedades que ambas cumprem, começando sempre por casos simples: quociente de uma divisão exata e propriedade que cumpre quando se multiplicam e dividem o dividendo e o divisor por um mesmo número, para terminar com o caso mais geral: quociente de uma divisão inexata e propriedades do resto por defeito e por excesso.

Outro resto, o da raiz quadrada inteira, também é protagonista no algoritmo para a raiz quadrada de um número de mais de dois algarismos: “Para que não se possa formar um quadrado maior, o resto tem, então, de ser menor do que…?” (^{PUIG ADAM, 1956}, p. 20). O fenómeno que organiza esta operação consiste em completar o maior quadrado possível de formar a partir de um número e, quando o número de partida não for um quadrado perfeito, obter o resto.

No caso das aulas sobre frações, destacamos a variedade de fenómenos que justificam o seu significado e o das operações aritméticas com frações. Por exemplo, no caso da divisão de frações estabelecem-se três opções: como inversa da multiplicação, ou interpretando a fração inversa “se uma peça de tecido mede 4/5 de um metro, o metro mede 5/4 da peça” (^{PUIG ADAM, 1956}, p. 34).

Grande parte das aulas dedica-se a dar sentido a múltiplas regras aritméticas: a multiplicação de potências de mesma base, a multiplicação de uma fração por um mesmo número, a soma ou subtração de frações com um denominador diferente, a divisão por uma fração, a inversão de sinal, a obtenção do MMC e do MDC, etc. Como se verá na secção seguinte, o método que emprega para fazer ver estas regras distancia-se do método da memorização.

O conteúdo das primeiras aulas refere-se à aritmética elementar pois só trabalha com o conjunto dos naturais (operações aritméticas elementares, potência e decomposição em fatores primos e relação de congruência) e com o conjunto dos racionais positivos com expressão decimal (raiz quadrada e proporcionalidade) e com expressão fracionária (frações). Contudo, e embora não haja uma intenção de formalizar os conceitos matemáticos, antes pelo contrário, por vezes, o procedimento heurístico que emprega “proporciona uma demonstração intuitiva” (^{PUIG ADAM, 1956}, p. 23) da regra que se pretende ensinar.

Pelo contrário, as aulas 9 e 10 têm um claro carácter introdutório de conceitos que são estudados em anos mais avançados. O caso da aula sobre proporcionalidade é um preâmbulo para o tema da proporcionalidade do segundo ano e introduz também a representação gráfica de funções através de uma engenhosa tarefa na qual se funde a manipulação de folhas de papel de área igual com noções matemáticas como área e lugar geométrico.

O conteúdo matemático de Geometria abrange conhecimentos de todo o currículo de 1934, desde os primeiros anos até aos mais avançados. Os conceitos de simetria, ângulos inscritos e posições relativas entre planos e retas (iniciação à geometria do espaço) destinam-se aos alunos mais jovens de entre 10 a 12 anos, enquanto o estudo dos poliedros e a trigonometria são orientados para adolescentes de entre 13 a 16 anos.

Por vezes, apresenta aos alunos dos dois primeiros anos alguns conceitos que, nos questionários, surgem apenas em anos mais avançados. Por exemplo, o conceito de arco capaz está nos questionários de terceiro ano, mas o autor apresenta-o de forma heurística a alunos do segundo ano a partir da relação entre ângulos ao centro e inscritos. Apresenta inclusive a invariância de algumas relações entre ângulos ao centro e entre ângulos inscritos a alunos do primeiro ano, lançando assim as bases para nos anos seguintes abordar o “lugar de Thales” (^{PUIG ADAM, 1956}, p. 93).

Quanto às aulas de álgebra e análise, tenta dar sentido às expressões algébricas e às operações partindo de situações próximas do estudante que, pouco a pouco, se vão complicando. Desta forma, passa de expressar quantidades de amêndoas a, bombons b e castanhas c, para expressões simbólicas, como o caso de 5x² - 8xy + 4y². Ele próprio refere: “O que é preciso evitar é que a regra preceda o domínio do que ela expressa, e não responda, portanto, a um ato previamente exercido pelo aluno e expressado (bem ou mal) pelo mesmo” (^{PUIG ADAM, 1956}, p. 49).

As últimas aulas do livro ocupam-se de modelos matemáticos extraídos da vida. Sob este mote, propõe quatro aulas: simetria no espaço realizadas com uma carmona, construções geométricas com um vidro escuro e matemática e arqueologia. As duas primeiras focam-se no estudo de simetrias, no espaço ou no plano. A terceira aborda questões de reconstrução de figuras partidas, tanto planas como de três dimensões, tal como o faria um arqueólogo, para depois de as recompor, utilizar para calcular áreas, perímetros, etc. Esta mesma ideia é utilizada para realizar tarefas de reconstrução de fórmulas (fig. 3) num contexto arqueológico.

Fonte: Extraído de Puig Adam 1956, p. 124

FIGURA 3: Reconstrução de fórmulas 

Desta forma, tenta motivar os estudantes e, simultaneamente, observar se assimilaram conteúdos já trabalhados na sala de aula sem ser pelo processo de memorização.

A última aula aborda um tema mais árido que consiste no rigor e na lógica matemática como um “fenómeno de comunicação social” (^{PUIG ADAM, 1956}, p. 125). Este tema concentra-se na questão da linguagem, que desenvolve através de exercícios com os alunos nos quais têm de descrever e interpretar descrições feitas pelos companheiros. Ao mesmo tempo, está a iniciá-los nas leis da lógica, introduzindo situações em forma de episódios e expressões verbais nas quais devem assinalar o seu valor de verdade.

Estratégias de ensino

A organização das aulas é realizada através de jogos ou modo de desafios colocados aos alunos com o objetivo de trabalhar algum conteúdo matemático. Começava por apresentar uma situação bastante simples, que lentamente se torna mais complicada. Por exemplo, para trabalhar a reversibilidade entre a soma e a subtração, distribuía os alunos por grupos de três, em que um pensava num número, outro aluno escrevia um número que mostrava aos outros dois e o primeiro devia dar a soma de tal forma a que os que não pensaram no número inicial o tentassem adivinhar. Posteriormente, o jogo ficava mais complicado, utilizando números muito grandes, por exemplo. Assim, para a aula mencionada, pedia aos alunos que resolvam exercícios como x + 243 = 458 (^{PUIG ADAM, 1956}, p. 10). Por fim, generalizava o tipo de situações utilizando expressões algébricas, que neste caso seriam, por exemplo: x + a = m (PUIG ADAM, 1956, p. 10). Este esquema em três passos é utilizado por Puig Adam em várias aulas suas, constituindo talvez o seu método de ensino. Desta forma, a complexidade dos exercícios aumenta de forma gradual, passando de situações muito concretas para outras que possam ser mais abstratas. Considerava que assim se leciona uma aula de forma heurística (PUIG ADAM, 1956, p. 21).

De igual modo, propunha aos alunos enunciar problemas para dar sentido às operações e às expressões algébricas. Por exemplo, a partir da expressão x + 6 - 3 = 5, um aluno propunha “Tinha x, ganha 6, perde 3 e ficam 5. Quantas tinha?” (^{PUIG ADAM, 1956}, p. 11). Ou seja, tentava muitas vezes contextualizar ou dar um significado às expressões algébricas para que os alunos não se limitassem apenas a um contexto matemático. Neste sentido, também lhes podia colocar o problema da fatura vaga: “Não me lembro de quantos melões comprei por sete pesetas, mas lembro-me de que gastei 35 pesetas. Quantos melões comprei?” (PUIG ADAM, 1956, p. 11). Noutras situações, partia de um problema enunciado pelos alunos para introduzir um novo conceito para que percebessem a analogia entre ambas as situações. Consequentemente, pedia aos alunos que enunciassem um problema sobre a divisão, ao que respondiam: “120 quilos valem 2400 pesetas. Quanto vale um quilo?” (PUIG ADAM, 1956, p. 33) e a partir deste enunciava um problema sobre frações: “Um cacete de pão de 2/5 quilo vale 9/4 de pesetas. Quanto vale um quilo de pão?”( PUIG ADAM, 1956, p. 33).

Noutras ocasiões, recorria a desafios colocados desde um ponto de vista estritamente matemático, mas procurando gerar uma certa motivação nos alunos. Por exemplo, propunha aos alunos reconstruir a seguinte operação com polinómios:

Fonte: Extraído de Puig Adam 1956, p. 51

FIGURA 4: Multiplicação de polinómios 

Outra estratégia muito utilizada por Puig Adam consistia em fazer perguntas aos alunos para que refletissem e fossem conscientes, tanto dos resultados obtidos nos exercícios, como do processo seguido para a sua solução. Por exemplo, na aula sobre a divisão, colocava a seguinte situação: “Distribui-se quatro livros a cada aluno e sobram 21, o teste confirma 15*4+21=81, mas será que as 15 crianças se conformariam com a distribuição? Porquê?” (^{PUIG ADAM, 1956}, p. 13). A partir daqui, introduzia a terminologia própria da operação em causa, neste caso o termo quociente, ajudando-os a verbalizar o significado dos termos: “O maior número é o que…” (PUIG ADAM, 1956, p. 13). Noutras situações, as perguntas ajudavam Puig Adam a fazer com que os alunos progredissem no conhecimento. Como tal, por exemplo, a partir de uma primeira decomposição do número 36 em fatores como 36 = 6 · 6, perguntava por outras decomposições a partir das quais se obtém 36 = 36·1, ou fazendo-os refletir um pouco mais, pedia-lhes que o decompusessem em fatores mais pequenos e a partir de 6 = 3· 2, obtêm 36 = 6· 6 = 3· 2· 3· 2 com o qual obtêm finalmente a decomposição em fatores primos. Já noutras situações, as perguntas ajudavam o autor a compreender o processo de raciocínio seguido pelos alunos. Assim, na aula sobre a proporcionalidade, após os alunos resolverem o desafio proposto, Puig Adam questionava-os para que dissessem como haviam chegado à solução. A partir das respostas dos alunos, concluía as estratégias que utilizavam: “1) a igualdade de razões, entre pares de números das duas séries; 2) a razão constante entre os números correspondentes de uma e outra série; e 3) a correspondência na soma” (2 + 4 = 6 e 1 + 1,5 = 2,5) (PUIG ADAM, 1956, p. 36).

Também recorria ao cálculo mental para reforçar e avançar no conhecimento. Assim, após introduzir os quadrados perfeitos, a raiz quadrada exata e a raiz quadrada inteira, perguntava aos alunos sobre a raiz quadrada de alguns números como 21, 42, ou 63.

São vários os exemplos que usava para justificar um conceito matemático. Para dar sentido à divisão por excesso, por exemplo, colocava uma situação de distribuição de livros em estantes, mas também introduzia outras como a compra de selos ou o uso de transportes. Em certos casos recorria ainda à contraposição de um exemplo, como quando expunha às crianças que a potenciação não tem a propriedade comutativa e assinalava: “só num caso particular 2⁴ = 4²” (^{PUIG ADAM, 1956}, p. 14).

Recorria igualmente a diferentes materiais para servirem de ponte entre os conceitos e o pensamento das crianças. Assim, para introduzir as potências e raízes quadradas utilizava cartolinas que, na altura, eram vendidas em mercearias, divididas em seis casas com seis botões de pressão em cada casa. Usava ainda folhas de papel (aproximadamente A5) que dobrava para introduzir as frações, sobretudo as metades, os quartos, oitavos, etc. As balanças serviam-lhe para relacionar as equações com situações de equilíbrio. As caixas de mosaicos de cores com triângulos retângulos e isósceles entre si eram usadas para introduzir os irracionais quadráticos. Retângulos de papel de área igual, mas de dimensões diferentes para introduzir a hipérbole ou as barras de Cuisenaire para trabalhar as congruências e as classes residuais com alunos de 3.º de bachillerato (13 anos):

Primeiro deixo que os alunos se enumerem e organizem, do 1 ao 24, e inicio o jogo entregando ao primeiro uma barra branca, ao segundo uma vermelha, ao terceiro uma verde, ao quarto uma rosa, ao quinto uma amarela, ao sexto de novo uma branca, ao sétimo de novo uma vermelha e aqui interrompo as entregas que todos viram. Pergunto ao número 17 qual será a cor da barra que lhe corresponderá. Acerta. Repito a pergunta ao número 24. E, por fim, dou instruções para que cada qual tire da mesa uma barra da cor que lhe corresponde. Peço que me mostrem e comprovo, fazendo com que retifiquem eles mesmos os acertos, se houver necessidade (^{PUIG ADAM, 1956}, p. 40).⁴

O uso do material não significa que a aula ficasse reduzida a esse uso. Após utilizar o material, introduzia a terminologia adequada, como por exemplo, neste último caso, a noção de números congruentes, trabalhando posteriormente sem utilizar o material, manipulando apenas os números.

Puig Adam reconhecia a importância do uso de material para o ensino da geometria. Esse mesmo material era, em muitas ocasiões, elaborado pelos próprios alunos para estudar as simetrias, as cónicas e, para a geometria do espaço, construíam modelos dos poliedros regulares com varetas. O uso do material implica, além do mais, uma participação ativa do aluno para adquirir o conhecimento matemático em causa. Recorria igualmente a recursos quotidianos para que os alunos adquirissem os conceitos matemáticos, como no caso do uso do papel como modelo para estudar o conceito de plano, ou das agulhas de tricotar como modelo para as retas.

Uma das estratégias que utilizava nas suas aulas era o recurso às perguntas para encaminhar o raciocínio dos alunos, de forma a que antecipassem soluções, refletissem sobre os resultados que obtinham, ou fossem, inclusive, um pouco mais além no conhecimento matemático.

O jogo era outra constante na sua forma de ensinar. Utilizava-o tanto como forma de motivação, como de formação. Como tal, em relação às simetrias, propunha o seguinte: “Assinalando um eixo vertical no quadro, coloco um aluno à sua direita e outro à esquerda, e peço que um deles desenhe livremente, fazendo pouco a pouco uma figura de traços retilíneos, enquanto o outro desenha a figura simétrica” (^{PUIG ADAM, 1956}).

Tentava que todas as atividades realizadas pelos alunos sobre um determinado conceito contemplassem todas as variações possíveis. No estudo da posição relativa de três planos, pedia aos alunos que colocassem os três planos paralelos entre si, dois planos coincidentes e um paralelo, três planos coincidentes, planos que se cortassem, etc., continuando assim a incorporar, pouco a pouco, também as linhas retas para estudar a sua posição relativamente ao plano.

Quando as turmas eram muito grandes, dividia-as em grupos, deixando um dos melhores alunos à frente de cada grupo, os quais contavam ainda com um ajudante:

Os chefes e ajudantes apresentavam-me primeiro as suas soluções para as perguntas colocadas sucessivamente e, segundo as minhas indicações correspondentes, vigiavam e orientavam as soluções tardias dos demais alunos, sob a orientação de deixar chegar ao máximo a iniciativa individual de cada um, recorrendo à minha vigilância e decisão arbitral em caso de dúvidas (^{PUIG ADAM, 1956}, p. 71).⁵

Estas aulas não deveriam ser, certamente, aulas onde reinasse o silêncio e a criatividade, sendo antes aulas onde havia debate, discussão e ação.

A dupla formação de Puig Adam, como matemático e engenheiro, também influenciou o tipo de tarefas. Consequentemente, no cálculo de mínimos de uma função, colocava aos seus alunos um projeto para construir um depósito cilíndrico com uma determinada capacidade, mas de forma a que o gasto de chapa fosse mínimo. Para tal, aliás, os estudantes deveriam fazer uma maquete do depósito à escala. Isto servia aos alunos como fator motivador “pelo facto de se sentir desde logo engenheiro” (^{PUIG ADAM, 1956}, p. 83).

Conhecimento do aluno

As estratégias empregues por Puig Adam mostram não só o seu interesse em chegar a todos os alunos, mas também um conhecimento profundo sobre as suas limitações e capacidades (dos alunos) segundo as suas idades.

Uma das observações mais interessantes neste respeito surge quando expõe claramente a dificuldade visível em verbalizar a definição de quociente numa divisão inexata:

Uma vez mais, confirma-se como é difícil nestas idades obter definições concretas e até, simplesmente, repeti-las após as receberem, e creio que, embora se apercebam de como a definição traduz a ideia, só são capazes de reconstruir a definição depois de a memorizarem (^{PUIG ADAM, 1956}, p. 13).⁶

E prossegue lançando uma crítica construtiva aos métodos de memorização:

Mas se são realmente capazes de aplicar bem um conceito, qual é a pressa para o enunciarem corretamente de memória? Não seria melhor esperar que esta correção resultasse espontaneamente de um processo de aperfeiçoamento da linguagem? Creio que estas interrogações servem para os professores de Matemática que ficam tão escandalizados com definições absurdas (prematuramente exigidas), sem que exista a ideia equivocada no aluno, mas antes apenas uma dificuldade a nível da linguagem (que não é remediada pela repetição de memorização) (^{PUIG ADAM, 1956}, p. 13).⁷

A postura de Puig Adam face à pressa em formalizar conceitos e ensinar procedimentos de forma mecânica é reforçada pelas produções dos alunos. Tal é o caso da decomposição em fatores primos realizada por alunos “a quem havia sido inculcado anteriormente o esquema de rotina clássico” (^{PUIG ADAM, 1956}, p. 19), por contraste aos que a aprenderam com o autor, que, segundo as suas observações, era mais natural, como demonstrado no exemplo que se reproduz: 60 = 6· 10 = 2· 3· 2· 5 = 2²· 3· 5.

Puig Adam afirma no prólogo desta obra que: “A didática é, acima de tudo, adaptação ao aluno”, e para tal há que saber escutar não só a linguagem verbal, mas também a não verbal, que nem todos somos capazes de entender. Na transcrição do que acontecia nas aulas fazia muitas referências a estas questões, como quando afirma: “notei cansaço nas crianças” (p. 15); “reforcei o interesse das crianças exercitando a sua imaginação…” (^{PUIG ADAM, 1956}, p. 16); ou “face à desorientação geral, deixo que se expliquem as duas soluções” (PUIG ADAM, 1956, p. 38).

Durante as atividades, empregava também essa adaptação aos diferentes ritmos de trabalho: “Enquanto os mais atrasados corrigem os erros, propus outras sucessões para os mais adiantados” (^{PUIG ADAM, 1956}, p. 36), e, no sentido de manter o interesse dos alunos para se manterem atentos nas aulas: “Terminei a última sessão com um jogo que idealizei como prémio para o grupo” (p. 18); “Tenho de fazer com que se apercebam que o 6 é ao mesmo tempo múltiplo de 2 e de 3” (PUIG ADAM, 1956, p. 29).

Para Puig Adam, o conhecimento matemático é criado num “duplo jogo de perceção combinada com a ação (real ou intuitiva)” (^{PUIG ADAM, 1956}, p. 84). Tendo esta ideia como pano de fundo, e com o conhecimento que possuía das capacidades dos estudantes de Bachillerato, começava as aulas apresentando aos seus alunos situações que sabia que resolveriam facilmente para, progressivamente, aumentar o nível de complexidade até chegar à noção ou propriedade que pretendia. Era habitual ler nas suas aulas comentários como: “A resposta e manipulação conseguintes são fáceis para eles” (PUIG ADAM, 1956, p. 86); seguidos de: “A dificuldade começa a surgir quando…” (PUIG ADAM, 1956, p. 87), que terminam com o enunciado da propriedade que os alunos acabavam por descobrir.

As perguntas feitas aos estudantes tinham não só a ver com os conteúdos matemáticos, mas também com a preferência de métodos. Assim, ao lecionar a representação gráfica de funções quadráticas, começava com o método de completar quadrados, depois usava o de identificar os coeficientes da expressão algébrica e a utilização das regras para obter cortes com os eixos, máximo/mínimo, etc. Para terminar, perguntava aos estudantes qual método preferiam, ao que respondiam o de completar quadrados, o que lhe trazia satisfação pois “penetraram no processo estrutural da transformação” (^{PUIG ADAM, 1956}, p. 74).

Conclusões

As aulas de Didáctica Matemática Eurística de Puig Adam representam um marco importante na história da educação matemática em Espanha, tanto pelo conteúdo das aulas em si, como pela sua intencionalidade. O desejo manifesto de “oferecer aos professores o modo de orientar determinadas aulas de forma heurística” (^{PUIG ADAM, 1956}, p. 7) deixou um legado que não se pode deixar cair no esquecimento.

A análise das aulas revelou três dimensões na obra:

A exposição do método heurístico que exemplifica nas diferentes aulas cobre uma boa parte do conteúdo programático dos anos de Bachillerato da primeira metade do século passado em Espanha. Adicionalmente, manifesta a sua vocação docente ao revelar-se conhecedor das capacidades e dos erros dos alunos, mas igualmente paciente para conseguir que os menos perspicazes alcançassem o nível de compreensão dos mais avançados.

A análise desta obra oferece-nos uma visão do ensino praticado por Puig Adam em meados do século passado. O modo como conduzia as aulas baseava-se não só na sua habilidade para criar situações ativas de aprendizagem, mas também num conhecimento profundo, tanto da matéria, como dos alunos e do currículo. Atualmente, estes são temas de interesse nas investigações sobre o conhecimento do professor de matemática.