1 INTRODUÇÃO

De uma forma global é comumente reconhecido que o foco nos Números e nas Operações é ainda prioritário nas tarefas propostas pelos professores desde a Educação Infantil. Essa priorização sustenta-se também pelo que se encontra expresso nos documentos oficiais (currículos e orientações), em que a unidade temática dos Números e Operações ocupa um lugar de destaque, desde os Anos Iniciais do Ensino Fundamental (^{BRASIL, 2018}), e prevalece, nesse contexto, o trabalho com os conteúdos envolvendo as denominadas quatro operações básicas (adição, subtração, multiplicação e divisão) com os números naturais (^{MANDARINO, 2009}; ^{MENDONÇA et al., 2007}).

Em particular, no âmbito das operações, a subtração é reconhecida como aquela em que os alunos começam a apresentar dificuldades (^{KAMII; LEWIS; KIRKLAND, 2001}). Porém, se por um lado há diferentes estudos focando o conhecimento dos alunos, suas capacidades e dificuldades no âmbito da subtração (^{BAROODY; TORBEYNS; VERSCHAFFEL, 2009}) e, de forma mais ampla, nas quatro operações básicas com números naturais, por outro lado, o papel que o conhecimento do professor relativamente a esse tópico exerce no processo de ensino e aprendizagem dos alunos é ainda pouco discutido, em comparação com o foco que, em termos de pesquisa, se tem dado nos alunos.

Considerando que esse conhecimento do professor assume um lugar de destaque entre os fatores (controláveis) que mais influenciam os resultados dos alunos - como demonstram, por exemplo, ^{Ball, Hill e Bass (2005}), ^{Boyd et al. (2009}), ^{Nye, Konstantopoulos e Hedges (2004}) -, é urgente que se busque uma melhoria desses resultados por via de um trabalho em que se tenha como objetivo principal a efetiva compreensão dos alunos acerca do que fazem e por que o fazem, em relação a cada um dos tópicos. Nesse contexto, e particularmente no caso da subtração, é essencial uma mudança de foco na pesquisa - dos alunos para o professor - que possibilite, de forma propositiva, pensar, estruturar e realizar formação com foco no que é efetivamente necessário (^{RIBEIRO; CARRILLO; MONTEIRO, 2009}), contribuindo para o desenvolvimento de práticas matemáticas que tenham efetiva intencionalidade de desenvolver os conhecimentos e as habilidades matemáticas dos alunos, desde a Educação Infantil.

Dentre os conhecimentos profissionais, que se espera, sejam comuns aos professores das diferentes áreas de conhecimento - que não consideram as especificidades dos tópicos a ensinar (os saberes apresentados por ^{Shulman e Tardiff} são exemplos dessas dimensões globais e que se consideram comuns a todos os professores) -, ao professor de matemática e que ensina matemática, cumprirá um conjunto de conhecimentos específicos para a sua prática profissional de ensinar matemática (^{BALL; THAMES; PHELPS, 2008}; ^{CARRILLO et al., 2018}; ^{JAKOBSEN; RIBEIRO; MELLONE, 2014}). Uma parte essencial desse conhecimento relaciona-se com as especificidades do conhecimento matemático que permitirá ao professor desenvolver uma prática matemática em que as discussões e as explorações com os alunos tenham como ponto de partida o que estes sabem, e como o sabem, ou seja, como organizam e apresentam seus raciocínios e argumentos. Isso demanda e implica que, como professores, sejamos detentores de um tipo de conhecimento que sustente o compreender e atribuir significado aos comentários dos alunos, interpretando-os de modo a possibilitar fornecer um feedback construtivo, tendo os comentários e o entendimento dos alunos como ponto de partida. Tal conhecimento é denominado de Conhecimento Interpretativo (^{DI MARTINO; MELLONE; RIBEIRO, 2019}; ^{JAKOBSEN; RIBEIRO; MELLONE, 2014}; ^{RIBEIRO; MELLONE; JAKOBSEN, 2013}).

Considerando que este Conhecimento Interpretativo é especializado, não se desenvolve pela mera prática de sala de aula e tampouco sem uma discussão intencional em âmbito de formação (^{JAKOBSEN; RIBEIRO; MELLONE, 2014}), torna-se essencial obter uma mais ampla compreensão de suas especificidades, de modo a, posteriormente, conceitualizar tarefas para a formação (^{RIBEIRO; ALMEIDA; MELLONE, 2019}) que contribuam de forma explícita para desenvolver esses elementos. Assim, neste artigo buscamos resposta para a seguinte questão de pesquisa:

Que dimensões do conhecimento especializado revelado por futuros pedagogos no tópico de subtração impactam no seu Conhecimento Interpretativo quando analisam produções de alunos envolvendo algoritmos para fornecerem um feedback construtivo?

2 ALGUMAS DIMENSÕES TEÓRICAS

Desde os Parâmetros Curriculares Nacionais (PCN) para os Anos Iniciais do Ensino Fundamental (^{BRASIL, 1997}) era possível encontrar, associada aos objetivos matemáticos, a proposta de trabalho com foco na construção de conhecimentos que permitiriam que os alunos pudessem “generalizar, projetar, prever e abstrair, favorecendo a estruturação do pensamento e o desenvolvimento do raciocínio lógico.” (^{BRASIL, 1997}, p. 24). Esses PCN sugeriam que o trabalho com as operações ocorresse a partir da compreensão dos diferentes significados de cada uma delas, buscando-se associar, a esse trabalho, o estabelecimento de relações entre as distintas operações, bem como um “estudo reflexivo do cálculo, contemplando diferentes tipos - exato e aproximado, mental e escrito.” (^{BRASIL, 1997}, p. 39). No entanto, esse documento reconhece que, em boa parte das vezes, esse trabalho é “iniciado pela obtenção de resultados básicos, seguido imediatamente pelo ensino de técnicas operatórias convencionais e finalizado pela utilização das técnicas em ‘problemas-modelo’.” (^{BRASIL, 1997}, p. 49). Essa falta de articulação envolvendo os sentidos e significados das operações pode ser considerada uma das causas das dificuldades para que os alunos possam efetivamente entender os procedimentos associados aos diferentes algoritmos. Isso ocorre porque, quando o foco do ensino está centrado no algoritmo em si, este será visto como um mero conjunto de passos sem sentido e que, portanto, não tem, com frequência, relação com o que se faz(fez) com o material concreto anteriormente.

Na Base Nacional Comum Curricular - BNCC (^{BRASIL, 2018}) também é reconhecida a necessidade de que “as habilidades matemáticas que os alunos devem desenvolver não podem ficar restritas à aprendizagem dos algoritmos das chamadas ‘quatro operações’.” (^{BRASIL, 2018}, p. 276). Assim, encontra-se na BNCC a sugestão de que o trabalho envolvendo os Números e as Operações, desde o 1º ano, inicie-se com a construção de fatos fundamentais da adição, seguido da abordagem de problemas envolvendo os significados da adição e subtração. De forma constante, a Base faz referências aos algoritmos até ao 5º ano e os números e as quatro operações básicas continuam a ocupar uma parte significativa dos documentos oficiais relativos aos Anos Iniciais, como já ocorria historicamente (^{MANDARINO, 2009}). Em particular, a operação de subtração é um dos temas críticos nessa etapa de ensino, já que este costuma ser o primeiro dos temas em que os alunos apresentam sérias dificuldades (^{KAMII; LEWIS; KIRKLAND, 2001}).

As investigações com foco nos números e nas operações continuam a atrair a atenção dos pesquisadores em todo o mundo. A maioria desses estudos têm como objeto de investigação os alunos e o seu entendimento, voltado, por exemplo, às estratégias de cálculo mental (^{CLARKE; CLARKE; HORNE, 2006}); à abordagem de estratégias de contagem relacionadas à adição e à subtração antes da apresentação do algoritmo convencional (^{ELLEMOR-COLLINS; WRIGHT, 2008}; ^{GERVASONI, 2006}); à construção e à argumentação de algoritmos não convencionais elaborados pelos alunos (^{MCCLAIN; COBB; BOWERS, 1998}). De todo modo, a maior parte das investigações no âmbito dos Números e das Operações possui foco no conhecimento e nas aprendizagens do aluno, deixando à margem as discussões a respeito do conhecimento - tanto matemático quanto pedagógico - do professor relativamente a este tópico.

Com efeito, é esperado que o professor de matemática e que ensina essa disciplina efetivamente reconheça a complexidade em torno de cada um dos conceitos e tópicos matemáticos, em particular da subtração, e busque ampliar o seu próprio conhecimento acerca dos distintos sentidos associados à subtração e das propriedades e dos procedimentos matemáticos presentes nos contextos dessa operação. Complementarmente, essa ampliação e conhecimento envolvem um entendimento efetivo, também, das técnicas e dos procedimentos associados aos algoritmos (convencionais e não convencionais), que permitam sustentar uma discussão mais profunda associada ao sentido do número e ao valor posicional no sistema de numeração decimal - a fim de que os alunos compreendam efetivamente, construam e ampliem seu próprio conhecimento matemático.

A problemática envolvendo o conhecimento do professor e as especificidades desse seu conhecimento vem sendo discutida, pelo menos, desde a década de 1980, essencialmente com os trabalhos iniciais de ^{Shulman e colegas (1986}, ¹⁹⁸⁷). Desse período até os dias atuais, essa abordagem global de Shulman - sem relação com uma área de conhecimento específica - tem sido considerada, em particular, no âmbito da Educação Matemática, o que resultou em distintos focos de atenção que têm ampliado a discussão e a compreensão dos aspectos inerentes às especificidades do conhecimento do professor de matemática e que ensina essa disciplina (^{BALL; THAMES; PHELPS, 2008}; ^{BAUMERT et al., 2010}; ^{CARRILLO et al., 2018}; ^{ROWLAND; HUCKSTEP; THWAITES, 2005}).

Das diversas conceitualizações do conhecimento do professor de matemática que ensina a disciplina, e dentre aquelas que, de alguma forma, consideram as especificidades desse conhecimento para o trabalho docente, assumimos, no contexto deste trabalho, a conceitualização do Mathematical Teachers´ Specialized Knowledge⁵ - MTSK - (^{CARRILLO et al., 2018}). Essa conceitualização foca-se nos aspectos especializados desse conhecimento, considerando que tal especialização não se restringe ao domínio do conhecimento pedagógico do conteúdo (Pedagogical Content Knowledge - PCK), mas se situa, também, no domínio do conhecimento do conteúdo - no caso, o matemático (Mathematical Knowledge - MK) -, incluindo neste escopo de especificidades, de forma inter-relacionada aos dois domínios anteriormente mencionados: as crenças dos professores sobre a matemática e sobre o ensino e a aprendizagem da matemática.

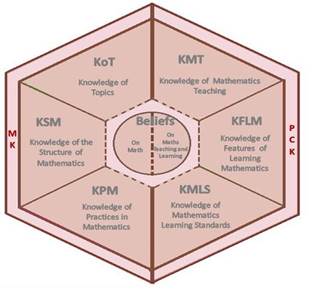
Fonte: ^{Carrillo et al. (2018}, p. 241)

Figura 1 Domínios do Mathematics Teachers’ Specialized Knowledge 

Focamos nossa atenção, neste estudo, nos três subdomínios do MK (ver epígrafe seguinte), uma vez que trataremos das especificidades do conhecimento matemático do professor que lhe permitem sustentar a atribuição de significado às produções dos alunos, relativamente ao tópico da subtração.

O Knowledge of Topics (KoT)⁶ inclui, entre outros elementos do conhecimento matemático do professor, aqueles associados aos conceitos que sustentarão os entendimentos do que se faz, de como se faz, e do porquê se faz de determinada forma. Inclui ainda o conhecimento de diferentes tipos de registro de representação e das características de um determinado resultado; e das múltiplas possíveis definições para um mesmo conceito. No contexto da subtração, aborda, por exemplo, um saber associado aos três distintos sentidos atribuídos a essa operação (retirar, completar e comparar) - como apontam, por exemplo, ^{Fuson et al. (1997}) -; os procedimentos (algoritmos) - standards ou não standards - para a determinação do resultado da operação de subtração (resto, excesso ou diferença); as propriedades que pautam o cálculo mental envolvendo a subtração - por exemplo, a associatividade, a compensação, a transitividade; as distintas formas de representação associadas ao cálculo da subtração - pictóricas, gráficas, aritméticas -, incluindo a modelação com recursos como o ábaco.

O Knowledge of the Structure of Mathematics (KSM) envolve o conhecimento matemático do professor sobre cada um dos tópicos, de forma ampla e profunda, que leve a assumir uma perspectiva da sua integração ao longo da escolaridade, bem como suas relações com estruturas mais amplas ou mesmo com outras estruturas consideradas auxiliares ao pensamento matemático. Tal conhecimento implica entender a matemática elementar de um ponto de vista superior e vice-versa (^{KLEIN, 1932}), possibilitando discussões posteriores com os seus alunos. Considera-se, de forma explícita e, portanto, aqui integrado, o conhecimento das conexões entre tópicos. Em relação à subtração, trabalha-se, por exemplo, no âmbito desta dimensão, o conhecimento do professor relativamente: às conexões entre esta operação e a de adição, quando associada ao sentido de completar ou de operações inversas; ou às conexões da subtração com a divisão, quando se associa a divisão à noção de retirar sucessivas parcelas iguais.

Incluído no Knowledge of Practices in Mathematics (KPM), considera-se o conhecimento do professor associado às formas (próprias) de fazer matemática. Entre elas está o conhecimento do que seja uma demonstração e das diferentes maneiras de se demonstrarem resultados matemáticos; dos critérios a estabelecer para que uma generalização seja válida; de sintaxes próprias da matemática; e de diferentes estratégias de resolução de problemas ou de modelagem matemática. No âmbito da subtração, por exemplo, podem-se considerar, como conteúdo do conhecimento do professor relacionado ao KPM, as (im)possibilidades de generalização dos procedimentos empregues em determinados processos para determinar o resultado da subtração, que permitirão considerá-los, ou não, como distintos algoritmos.

Essas dimensões do conhecimento especializado do professor, incluindo as crenças, sustentam uma atuação docente que busque desenvolver nos alunos os conhecimentos, as competências e as habilidades matemáticas, sem se limitar a uma “passagem” associada essencialmente/unicamente a um saber fazer. Mais especificamente, essa atuação docente pautada pelo conhecimento especializado do professor, possibilitará que ele não assuma o ensino de regras como ponto de partida - e nem exclusivamente como objetivo de chegada -, uma vez que, para desenvolver as competências matemáticas, é fundamental que os alunos ampliem suas capacidades e habilidades de estabelecer conexões entre conceitos, fundamentos e procedimentos. E elas não se desenvolvem, se os alunos forem “ensinados” a reproduzir regras sem compreensão, ainda (e mesmo) que tal ensino esteja sustentado em metodologias consideradas inovadoras e potentes para práticas perseguindo outros objetivos.

Portanto, essa atuação do professor que fomenta o entendimento matemático dos alunos deverá assumir como ponto de partida o que os alunos já conhecem e a forma como o conhecem. Isso requer do professor o que se denomina de Conhecimento Interpretativo (^{JAKOBSEN; RIBEIRO; MELLONE, 2014}), cujo conteúdo exerce um impacto direto no ensino e nas aprendizagens matemáticas dos alunos (^{DI MARTINO et al., 2016}). Esse é um conhecimento especializado, que permite ao professor atribuir sentido aos comentários e às produções dos alunos, mesmo que contenham erros ou inadequações matemáticas, sejam pautados por raciocínios não convencionais (não standards), ou se encontrem fora do que se denomina espaço solução do professor (^{JAKOBSEN; RIBEIRO; MELLONE, 2014}). O Conhecimento Interpretativo tem de ser desenvolvido no âmbito da formação de professores (inicial ou continuada), por meio de tarefas matemáticas (^{RIBEIRO; ALMEIDA; MELLONE, 2019}) intencionalmente desenhadas para esse fim, pois tal conhecimento não se desenvolve pela mera prática em sala de aula com os alunos (^{JAKOBSEN; RIBEIRO; MELLONE, 2014}).

Para efetivamente atribuir sentido/significado às produções dos alunos, e para implementar práticas que possam promover a construção do conhecimento matemático dos alunos, torna-se essencial que o professor detenha um conhecimento que lhe permita ativar “um real processo de interpretação, partindo de uma escuta avaliativa para uma forma mais flexível de escuta hermenêutica” (^{DI MARTINO et al., 2016}, p. 4, grifo nosso). Essa escuta avaliativa está associada a um processo de correspondência que o professor estabelece entre aquilo que o aluno comenta ou produz e o que o professor espera como resposta. A resposta esperada forma parte do espaço solução do professor para cada uma das situações. E a pesquisa mostra que o espaço solução do professor normalmente é composto por um número bastante reduzido de elementos - maioritariamente um único elemento (^{DI MARTINO et al., 2016}; ^{JAKOBSEN; RIBEIRO; MELLONE, 2014}) -, o que indica serem urgentes, no âmbito e na agenda das propostas de formação de professores, ações que considerem a sua ampliação.

Atendendo às ideias que sustentam uma escuta hermenêutica (^{DAVIS, 1997}), torna-se essencial considerar a flexibilidade do professor para redesenhar um caminho de aprendizagem matemática que incorpore os raciocínios e os conhecimentos dos alunos, expressos nas suas produções ou comentários, e para assumi-los como ponto de partida para a construção de novos conhecimentos matemáticos. O Conhecimento Interpretativo difere de outras conceitualizações do conhecimento do professor, por reconhecer como fundamentais - e desejáveis - os erros e os raciocínios não convencionais no processo de construção do conhecimento matemático dos alunos. Note-se, também, que essa noção de Conhecimento Interpretativo é algo que não permite que se analise apenas o erro dos alunos, ainda que essa análise seja parte do conhecimento do professor, pois demanda entender os motivos que podem sustentar esse erro - ou os raciocínios alternativos, mesmo que corretos - e tê-los como ponto de partida para desenhar as discussões posteriores com os alunos, as quais podem ser in situ ou simuladas, dependendo do contexto em que o professor se encontra.

Não basta, portanto, referir que o erro tem de ser considerado como fonte de aprendizagem, pois obviamente apenas essa enunciação não contribuirá para uma melhoria da prática matemática do professor. A propósito, cumpre aos formadores de professores e aos pesquisadores uma mais ampla e profunda discussão acerca do conhecimento requerido e implicado para que os erros e, particularmente, os raciocínios não convencionais dos alunos, sejam efetivamente tomados como um ponto de partida para o desenvolvimento de suas capacidades e aprendizagens. Assim, pode-se considerar que esse Conhecimento Interpretativo não corresponde à performance do professor e não corresponde, portanto, a um PCK. Mas é, sim, um conhecimento matemático especializado que sustenta a posterior efetivação de um feedback construtivo, que realmente auxilia os alunos a desenvolver o seu entendimento matemático - não se limitando, portanto, a fornecer um feedback de nível avaliativo, descritivo ou pessoal, mas, de fato, contributivo ( ^{GUALLEGUILLOS; RIBEIRO, 2019}).

Objetivando esse tipo de prática, há que considerar três dimensões no Conhecimento Interpretativo implicado e requerido para assumir as produções dos alunos e os conhecimentos e os raciocínios associados como ponto de partida. O conteúdo e as especificidades do conhecimento matemático do (futuro) professor tendem a possibilitar os três tipos de interpretação (^{MELLONE et al., 2017}): (i) interpretação avaliativa, quando o professor busca efetuar uma correspondência entre as produções dos alunos e as ideias que sustentam a forma de obter a resposta correta do próprio professor; (ii) interpretação que sustenta a prática letiva (design educacional), a forma como os professores desenham as etapas a desenvolver, tendo por base as produções dos alunos; (iii) interpretação como pesquisa, associada ao desejo e à habilidade do professor em rever a própria formalização matemática, de modo a garantir coerência com as produções dos alunos, mesmo em situações em que estas se possam encontrar em conflito com o que tradicionalmente se ensina na escola.

Assim, para que se possam (re)desenhar caminhos promotores de aprendizagens matemáticas dos alunos, o Conhecimento Interpretativo do professor exerce um papel fundamental na conceitualização (e modificação, sempre que for o caso) e na implementação das tarefas matemáticas, permitindo que se assumam, dentre outros focos, as produções dos alunos nessas tarefas como um dos elementos geradores para o desenvolvimento do conhecimento, das habilidades e das competências matemáticas dos resolutores. Embora existam várias pesquisas com olhar voltado para as tarefas matemáticas, como, por exemplo, ^{Charalambous (2010}), ^{Stein et al. (2000}) e ^{Swan (2007}), a maioria desses estudos tem como foco os alunos e os possíveis impactos de tais tarefas em suas aprendizagens e resultados. Nesse sentido, descuida-se do foco no conhecimento do professor para implementar tarefas matemáticas que mantenham, ampliem ou potencializem a qualidade matemática das discussões a ocorrer e o nível cognitivo (^{RIBEIRO; ALMEIDA; MELLONE, 2019}; ^{STEIN et al., 2000}).

Promover o desenvolvimento do conhecimento do professor - considerando-o especializado - implica uma formação de professores que persiga esse objetivo explicitamente. Portanto, dado o papel central das tarefas matemáticas na prática do professor, as tarefas para a formação de professores têm de possuir natureza, foco e objetivos específicos e complementares das tarefas para os alunos (^{RIBEIRO, 2016}; ^{RIBEIRO; ALMEIDA; MELLONE, 2019}; ^{RIBEIRO; MELLONE; JAKOBSEN, 2013}), características obviamente associadas ao modo como é entendida a própria formação de professores de matemática que ensinam a disciplina. Assim, a formação de professores que tem como objetivo último a melhoria das aprendizagens matemáticas dos alunos, por via da melhoria da prática matemática do professor através do incremento do seu conhecimento interpretativo e especializado, tem de considerar, necessariamente, a prática como ponto de partida e de chegada.

3 CONTEXTO E MÉTODO

Este trabalho é parte de um projeto mais amplo que objetiva conceitualizar tarefas - que denominamos formativas - para a formação de professores (^{RIBEIRO; ALMEIDA; MELLONE, 2019}) em vários tópicos matemáticos.⁷ Com esse intuito, em cada tópico desse trabalho, um dos momentos iniciais é o de desenvolver pesquisa que permita identificar as especificidades do conteúdo do conhecimento do professor (em atividade ou futuro) associado - implicado e requerido - em cada um desses tópicos, para lidar com as demandas de conhecimento que a pesquisa mostra serem essenciais para os alunos. Aqui focamo-nos no tópico de subtração e, em particular, no Conhecimento Interpretativo revelado por 26 futuros professores da Educação Infantil e dos Anos Iniciais, ao atribuírem significado a um conjunto de produções de alunos associadas à realização de 51-17, usando um algoritmo - enquanto trabalhavam em seis grupos (quatro de quatro elementos e dois de cinco). Estas informações foram coletadas na única disciplina no âmbito da Educação Matemática (60 horas) ofertada na Licenciatura em Pedagogia em uma universidade pública do Estado de São Paulo. O objetivo principal dessa disciplina é efetivar uma aproximação com a prática futura do professor, e as informações analisadas neste artigo decorrem das discussões efetuadas em uma das 15 aulas de quatro horas, onde se objetivava acessar o conteúdo do conhecimento especializado - e desenvolvê-lo - dos futuros professores no âmbito da subtração.

A tarefa proposta tinha como objetivos formativos principais desenvolver o conhecimento dos futuros professores, associado: (i) aos três distintos sentidos considerados para a subtração (retirar, comparar e completar); (ii) à possibilidade de se efetuar a subtração a partir de diferentes estratégias vinculadas, por exemplo, ao cálculo mental; (iii) à distintas formas de representação; (iv) à modelação da operação de subtração no material dourado e no ábaco, associada ao algoritmo convencional.

A tarefa tinha duas partes. A Parte I focava-se no que se entende por subtrair, na formulação de problemas distintos para a expressão 51-17 e na antecipação de possíveis respostas de alunos do 2.º e do 6.º anos para esses problemas. A Parte II da tarefa, que será o nosso foco aqui, voltava-se para o Conhecimento Interpretativo dos futuros professores e, com esse intuito, foi fornecido a eles um conjunto de produções de alunos associadas à determinação da solução de 51-17, e foi solicitado que comentassem cada uma dessas produções (oito, no total), atendendo à adequação e à correção matemática, e que elaborassem um feedback construtivo que permitisse desenvolver o entendimento de todos os alunos a partir de cada uma das respostas particulares - que não poderiam ficar, portanto, no nível do pessoal (“muito bem”, “bom esforço”, “lê outra vez”), nem da descrição (“fez isto”, “depois aquilo” e “terminou com esta outra coisa”).

Fonte: os autores

Figura 2 As oito produções incluídas na tarefa  

Aqui, iremos discutir somente as respostas dos futuros professores associadas às produções dos alunos “Diana” e “Edgar”. Note-se que a ordem pela qual as produções foram incluídas na tarefa é importante para potenciar o desenvolvimento do conhecimento dos futuros professores tanto no âmbito do conhecimento do conteúdo (subtração), que é o foco das respostas escritas que se buscam discutir, quanto no âmbito do conhecimento pedagógico para o ensino da subtração - pela exploração que se realiza durante a discussão em grande grupo. Assim, uma indicação para os futuros professores (e que é discutida posteriormente em termos dos objetivos formativos, mas não é foco de discussão neste artigo) é a de que devem considerar as produções dos alunos da esquerda para a direita e da primeira linha para a segunda.

A produção de Diana foi incluída na tarefa, com o objetivo de dar seguimento ao que terá sido o raciocínio e a argumentação dos futuros professores para as produções anteriores - se e sempre que possuírem um espaço solução com mais de um elemento ou quando forem detentores de um conhecimento que lhes permita ampliar esse espaço solução durante a discussão com os elementos do grupo (pois isso é algo essencial a desenvolver pela formação que ocorrerá posteriormente em grande grupo). Assim, é esperado que seja efetuado um paralelismo com o que teria ocorrido nas duas produções anteriores que forneceram uma resposta correta (retirar 11 ou adicionar três ao aditivo e ao subtrativo), mas que favoreça discutir posteriormente um raciocínio alternativo para obter os valores intermédios (40-6) e a possibilidade de não começar o cálculo pelas unidades; que se observe a correspondência entre o que se registra no algoritmo na vertical e o registro na escrita na horizontal, bem como as potencialidades desse tipo de raciocínio e exemplo para ampliar a discussão de envolver aspectos do Pensamento Algébrico (e da Álgebra) desde os Anos Iniciais.

A produção de Edgar foi incluída na tarefa de formação, pois, tipicamente, os (futuros) professores consideram a subtração somente no sentido de retirar, o que impossibilita atribuir significado à produção do aluno, já que a sua abordagem está baseada em ir completando, identificando quanto falta a 17 para chegar a 51. Em particular, esta abordagem encontra-se de forma explícita em alguns documentos oficiais de alguns países, o que permite discutir e ampliar também o conhecimento dos futuros professores no que concerne não apenas à BNCC, mas também a outros documentos que podem contribuir para desenvolver uma prática futura de forma matematicamente mais consciente e desafiadora.

Estas duas produções, para além de poderem ser associadas a distintos sentidos da subtração, foram incluídas por possuírem, também, potencialidades de promover discussões profícuas associadas a diferentes formas de representação, procedimentos, uso de recursos para a sua modelação, estratégias de cálculo mental e de conexões entre a operação de subtração e as outras operações (conexões no mesmo nível escolar), mas também com tópicos mais avançados, e essenciais, como a noção de distância, translação ou medida.

A análise foi efetuada primeiramente de forma separada pelos autores e posteriormente uniformizada - discutindo as dimensões em que não se verificava um acordo inicial. Esta abordagem metodológica busca garantir coerência e consistência interna e tem por objetivo fortalecer ainda as dimensões/categorias obtidas nessa análise, também objetivando o seu posterior uso na e para a melhoria da qualidade das tarefas propostas para a formação, de forma a potenciar, maximizar o desenvolvimento do Conhecimento Interpretativo dos resolutores.

Dado que a conceitualização da tarefa considera discutir especificamente diferentes subdomínios do conhecimento matemático do professor, a análise focou-se primeiramente no conteúdo desse conhecimento, tomando como lente teórico-analítica o MTSK, a partir dos três subdomínios relacionados ao Mathematical Knowledge (MK) e revelado nos comentários associados às interpretações fornecidas pelos futuros professores. Posteriormente, considerando as categorias teóricas do Conhecimento Interpretativo, foi feita uma análise com base nessas categorias, estressando-as em todos os momentos, buscando sempre a possibilidade de que pudessem ser ampliadas, tendo por base as especificidades das informações coletadas.

4 ANÁLISE E DISCUSSÃO

Todos os 26 estudantes consideravam a subtração apenas no sentido de retirar, e o único algoritmo que referiram conhecer era o de Alda, que, por essa razão, foi o primeiro a ser incluído na tarefa. Assim, o seu espaço solução para os sentidos da subtração era composto por um único elemento, ocorrendo o mesmo para os procedimentos para efetuar uma subtração: um único algoritmo - aquele que aprenderam enquanto alunos dos Anos Iniciais.

Todos os grupos de futuros professores apresentaram, para a produção de Diana, comentários que correspondem a uma descrição linear do que observam diretamente, sem qualquer questionamento sobre a possibilidade, ou não, de efetuar esse procedimento, permanecendo em um nível descritivo daquilo que inferem sobre o raciocínio matemático apresentado, ativando assim uma “escuta avaliativa” (^{DI MARTINO et al., 2016}).

Fonte: os autores

Figura 3 Comentários de três dos grupos de futuros professores para a produção de Diana 

Embora os futuros professores revelam (re)conhecer um possível procedimento matemático associado à produção de Diana (subtrair 11 unidades do minuendo e do subtraendo), os comentários não extrapolam o nível avaliativo, pois não apresentam argumentos sobre a adequação e/ou a validade matemática do procedimento utilizado, ficando assim no nível do saber fazer, ou, no caso, descrever o que se observa diretamente, sem qualquer questionamento sobre essa validade (KoT).

Ainda assim, apesar de a produção de Diana se associar, de forma intuitiva, a uma perspectiva de retirar a mesma quantidade ao aditivo e ao subtrativo, fazendo uso de uma propriedade do sistema de numeração decimal - essencialmente por se encontrar explícito na produção de Cláudia, que se encontra imediatamente antes (segundo as orientações que receberam de como olhar para as produções) -, nenhum dos grupos de futuros professores foi além de uma descrição do observável.

Já no que concerne à produção de Edgar, três dos grupos transpuseram a sua experiência anterior e sua forma de ver/escutar (escuta avaliativa) para esta situação e mantiveram a sua interpretação no nível descritivo. Essa interpretação descritiva, primeiro nível do conhecimento interpretativo (MELLONE; ^{RIBEIRO; JAKOBSEN, 2016}), está associada a um conhecimento dos tópicos (KoT) que se considera, no mínimo, do nível do aluno da etapa educativa em que esse tópico será abordado. E essa interpretação poderá estar associada ao fato de, neste caso, envolver um raciocínio matemático vinculado ao sentido de completar, que era desconhecido de todos os futuros professores, pois estes revelaram conhecimento da subtração somente como retirar (algo identificado pelas respostas dos futuros professores à primeira parte da tarefa para a formação).

Fonte: os autores

Figura 4 Comentários de três dos grupos futuros professores à produção de Edgar 

Para esses futuros professores o foco principal é o resultado (que está correto), e não a atribuição de sentido e significado ao raciocínio do aluno - essencialmente por este ser distinto do seu, já que demanda entender a subtração como completar e, portanto, o raciocínio associado se encontra fora do seu espaço solução. Esta tendência é revelada por outras pesquisas, e ela independe dos anos de experiência em sala de aula e, aparentemente, também dos contextos culturais em que os (futuros) professores se encontram, como demonstram, por exemplo, os estudos de ^{Ribeiro, Mellone e Jakobsen (2013}) e ^{Mellone, Ribeiro e Jakobsen (2016}). Isso salienta a centralidade do conhecimento do professor relativamente ao que é subtrair (nos diferentes subdomínios do conhecimento matemático especializado do professor - (^{CARRILLO et al., 2018}), para poder, posteriormente, mobilizar esse conhecimento na interpretação das produções dos alunos e possibilitar decidir, a partir dessa interpretação, quais as ações pedagógicas a tomar como recursos e forma de trabalho, para que os alunos entendam o que fazem e por que o fazem, a cada momento.

Por outro lado, o uso inadequado de expressões matemáticas como “decomposição” (para a expressão 17+3); “equação” (para as igualdades 17+3=20 e 20+31=51); “algarismos” (referindo-se ao minuendo, 51, e ao subtraendo, 17); “juntou os números”, associados a objetos matemáticos distintos daqueles a que tais termos estariam adequadamente relacionados, revelam o conhecimento dos futuros professores acerca de conceitos e definições de conceitos, envolvidos nos contextos da subtração (KoT), atrelado ao uso inadequado de uma linguagem matemática (KoT), já que o que é referido não encontra correspondência matemática (KPM). Essas interpretações revelam, também, a necessidade de que, pela formação, se desenvolva, de forma intencional, o conhecimento especializado dos futuros professores, no que se refere às definições, aos conceitos (KoT) e ao uso da sintaxe matemática (KPM), para que a prática (futura) possa ser implementada, perseguindo objetivos de aprendizagens matemáticas corretas e adequadas a todo o momento e para deixar a porta aberta para aprendizagens futuras, de forma sustentada.

O segundo comentário da Figura 4 destaca a ideia de estabelecimento de “relação entre os números encontrados”, que pode estar associada a uma noção de referencial, pois, ao indicarem as expressões [17+3=20] e [20+31=51], os futuros professores parecem assumir o “20” como um ponto de referência para o cálculo da diferença entre 17 e 51. Esse foco de atenção não permite atribuir significado à subtração como uma distância (completar), pois continuam no mesmo espaço de buscar enquadrar a sua forma de fazer em algo que o aluno fez e efetuam, assim, uma interpretação ainda no espaço avaliativo - apesar de, aqui, usar um passo intermediário que, à primeira vista, poderia sugerir uma interpretação mais profunda. Torna-se assim essencial ampliar, desenvolver e garantir um conhecimento matemático profundo, no que se refere, em particular, às formas de representação (KoT) dos processos matemáticos associados às expressões numéricas apresentadas; e efetuar uma relação com o sentido de completar atribuído à subtração (KoT), com conexões explícitas com a operação de adição (KSM), para além do fato de serem operações inversas.

Um comentário de um outro grupo merece destaque, tendo em vista que reforça a necessidade de que a formação se foque em aspetos que os alunos desde os Anos Iniciais têm o direito e dever de conhecer - tal como se encontra explícito na BNCC (^{BRASIL, 2018}), e que se refere a conhecer as diferenças entre o processo de decomposição de um número e a correspondente representação numérica dessa decomposição.

Fonte: os autores

Figura 5 Comentários de um dos grupos de futuros professores à produção de Edgar 

Este grupo também recorre à expressão “decomposição”, associada à adição de 3 a 17 (17+3 = 20), o que revela o seu conhecimento matemático vinculado aos conceitos e definições desses conceitos e ao uso adequado da linguagem matemática (KoT). É patente um conhecimento que leva a uma falta de correspondência entre o fazer matemático, o seu significado e a representação associada e que, portanto, necessita ser foco de discussão explícita na formação de professores.⁸ Tal dificuldade pode estar associada à correspondência com a linguagem natural e coloquial, em que decompor se associa, com frequência, apenas ao resultado final, e não se consideram os procedimentos e o raciocínio envolvidos. A interpretação efetuada pelo grupo não encontra uma correspondência matemática com a produção do aluno, já que aquela levaria à resposta de 31, e não 34 (KoT). Também neste caso, os futuros professores efetuaram uma interpretação sem efetivamente se colocar no lugar do aluno ( ^{MELLONE;RIBEIRO; JAKOBSEN, 2016}) e sem “escutar” o que este estaria a dizer (^{DAVIS, 1997}). Revelam, assim, um conhecimento matemático que lhes dificulta a flexibilidade para redesenhar um outro possível caminho de resolução da questão, que não o traçado por eles próprios. Essa busca demandaria olhar a produção, procurando entender o raciocínio associado, sem imposição do seu.

Já, ao serem convidados a fornecer um feedback construtivo, a maioria dos grupos (quatro em seis) permaneceu no nível da interpretação avaliativa, o que equivale a fornecer um feedback sustentado em uma interpretação que busca uma correspondência entre a produção do aluno e a forma específica dos elementos do grupo para resolver a questão. O feedback fornecido se encontra no mesmo espaço das respostas dos próprios futuros professores, quando solicitados a determinar o resultado de 51-17 usando um algoritmo. Apenas diferem porque pretendem ensinar o aluno a fazer da forma “correta”. O comentário que se afastou um pouco de uma linearização de correto/incorreto e se aproximou mais de uma iniciativa de “escuta hermenêutica” (^{DI MARTINO et al., 2016}), situa-se no espaço do que pode ser denominado um feedback instrutivo, em que o professor diz ao aluno o que deveria ter feito, mantendo o seu lugar de conhecimento e sem transcender para o lugar do aluno.

Fonte: os autores

Figura 6 Feedback de um dos grupos de futuros professores à produção de Diana 

O feedback fornecido pelos futuros professores apresenta leves traços de uma escuta hermenêutica, mas sem relação com o tópico matemático, associada a um reforço positivo e também desvinculada da questão (“você mostrou um bom raciocínio lógico” é algo que serve, aparentemente, para todas as situações). A sugestão dada de que “usar o 1 facilitaria na resolução”, corresponde a um feedback instrutivo. Caso tivesse sido validado pelos próprios futuros professores, por exemplo, com um novo registro matemático, poderia contribuir para que eles próprios pudessem reformular seu feedback.

5 ALGUNS COMENTÁRIOS FINAIS

Neste artigo, buscaram-se elementos que possibilitassem responder à seguinte questão: Que dimensões do conhecimento especializado revelado por futuros pedagogos no tópico de subtração impactam no seu Conhecimento Interpretativo quando analisam produções de alunos envolvendo algoritmos para fornecerem um feedback construtivo?

Com efeito, os resultados trazem à tona, neste contexto específico - e confirmam resultados de pesquisas realizadas em outros contextos culturais e sociais, como em ^{Di Martino et al. (2016}) e ^{Jakobsen, Ribeiro e Mellone (2014}) -, a existência de algo comum, no âmbito do conhecimento especializado do professor de matemática e que ensina a disciplina, que urge ser foco de discussão e desenvolvimento na formação de professores. Para que esses futuros professores possam avançar para o nível de uma escuta hermenêutica (^{DI MARTINO et al., 2016}), objetivando fornecer um feedback construtivo (^{JAKOBSEN; RIBEIRO; MELLONE, 2014}), e não meramente avaliativo ou associado a dimensões pessoais de reforço positivo, faz-se necessário entre as especificidades do seu conhecimento matemático, desenvolver, além de outros: os sentidos de subtrair, os procedimentos, as propriedades e os diferentes tipos de registros - quanto à sua validade e adequação matemática (KoT); as (im)possibilidades de generalização de determinados procedimentos para o caso particular da subtração (KPM). Apenas essa ampliação e o aprofundamento dessas especificidades do conhecimento matemático permitirão expandir o seu próprio espaço solução, de forma a possibilitar uma posterior prática pedagógica que tenha as produções e os raciocínios dos alunos como ponto de partida - o que estes sabem e como o sabem - para o desenvolvimento das discussões matemáticas.

Estas dificuldades reveladas pelos futuros professores em fornecer um feedback que supere uma descrição ou um reforço positivo pessoal, são um indicador da necessidade de uma mudança de foco na formação de professores, objetivando uma melhoria nessa direção. Tais dificuldades reforçam, também, a importância de se considerarem as tarefas de aprendizagem profissional (^{SMITH, 2001}), de modo a focar as especificidades do conhecimento do professor para a sua prática profissional de ensinar matemática (^{RIBEIRO; ALMEIDA; MELLONE, 2019}), pois elas abrem um espaço de reflexão e de trabalho diretamente relacionado com uma prática matemática considerada de qualidade - para as aprendizagens matemáticas dos alunos se tornarem efetivas, e com compreensão, para além de afetivas.

Assim, os resultados apontam, e reforçam, a necessidade de que a formação de professores de matemática e que a ensinam contribua para que os futuros professores deixem de ensinar como (acham que) foram ensinados (^{LORTIE, 1975}). Isso apenas será possível, se tiverem a oportunidade de vivenciar situações que se relacionem com a sua prática futura, para que, ao equacionar essas formas de fazer que “pensam conhecer”, sejam levados, de modo consciente e intencional, a pensar e fazer de forma diferente logo na formação inicial.

Estes resultados e o percurso realizado para a sua obtenção - abordagens metodológicas e teóricas consideradas - abrem, para um trabalho futuro, um conjunto de questões que podem guiar alguns processos de melhoria da formação, da prática e, obviamente, da pesquisa. Assim, algumas questões que emergem e que se relacionam de forma direta com o tópico aqui discutido, dizem respeito a, por exemplo: (i) que conhecimento revelam (futuros) professores, ao modelarem a subtração envolvendo os seus três sentidos?; (ii) quais os aspectos mais críticos no conhecimento de (futuros) professores que ensinam matemática, em cada um dos tópicos que têm de ensinar?; (iii) que conhecimento interpretativo mobilizam (futuros) professores que ensinam matemática, ao discutirem situações da prática (por exemplo, episódios de sala de aula, vinhetas, produções de alunos, vídeos) e em que dimensões do conhecimento sustentam a sua argumentação relativamente aos aspectos críticos identificados?; (iv) qual o conteúdo do conhecimento do formador de professores revelado durante a preparação e a implementação de tarefas formativas que tenham por objetivo promover o desenvolvimento do conhecimento interpretativo e especializado de (futuros) professores?; (v) qual a natureza e quais as especificidades das tarefas formativas para desenvolver as especificidades do conhecimento do professor em cada tópico?

Todas essas questões nos levam a que seja considerada, por um lado, no âmbito da pesquisa em Educação Matemática, uma mudança (ou ampliação) de foco nos aspectos que implicam diretamente nas aprendizagens dos alunos. E, como os resultados desta pesquisa evidenciaram, um desses aspectos refere-se às especificidades do conteúdo do conhecimento do professor para desenvolver a sua prática profissional. Por outro lado, do ponto de vista da formação de professores, essas questões evidenciam a necessidade de uma mudança de foco nos tipos de tarefas e discussões que habitualmente ocorrem com os futuros professores, ou os que já estão em atividade, que são relacionadas quase que estritamente às metodologias e usos de recursos didáticos, sem levar em conta a natureza e as particularidades do conhecimento matemático do professor e a necessidade de desenvolvimento desse conhecimento de forma propositiva e intencional.