1 INTRODUÇÃO
Atualmente tem‐se vindo a alargar o consenso de que a melhoria dos sistemas educativos não passa apenas por desenvolver currículos mais modernos e mais ajustados às atuais realidades mas que “There is a wide consensus that the complexity of education is increasing and with it the expectation towards teachers. Therefore, the quality of how teachers are prepared for their role has become a focus for policy attention.” (EUROPEAN COMMISSION, 2015, p. 10).
Estudos têm mostrado que o fator mais influente nos resultados obtidos pelos estudantes é a qualidade dos seus professores, especialmente nos primeiros anos de escolaridade (EUROPEAN COMMISSION, 2018).
Deste modo, considerando que o professor, em toda a sua globalidade, assume um papel de destaque nas aprendizagens dos alunos, e nas oportunidades de aprender que faculta (HIEBERT; GROUWS, 2007; NEWELL, 2011) assume-se como fundamental que possua, entre outros, um amplo e sólido conhecimento sobre os diferentes tópicos que lhe cumpre abordar, bem como das possíveis formas como estes se relacionam e evoluem ao longo da escolaridade. Inúmeras investigações (e.g., ELMORE, 2002; CHARALAMBOUS, 2016; HOOVER et al., 2016), têm mostrado que para ensinar matemática, os professores precisam de uma extensa base de conhecimento, habilidades técnicas de ensino e posturas epistemológicas, que devem ser metas de preparação dos professores e dos programas de desenvolvimento profissional. Nesse sentido, este amplo e sólido conhecimento matemático configura-se como essencial para assegurar um ensino eficiente da Matemática. Como refere Liping Ma (1999, p. 38): "o conhecimento limitado da matéria restringe a capacidade de um professor para promover uma aprendizagem conceptual entre os estudantes." Além disso, um conhecimento adequado para garantir a eficácia do ensino da Matemática depende não só́ de um sólido conhecimento matemático, mas também da natureza desse conhecimento. Os professores mais eficientes/competentes possuem uma melhor compreensão das interconexões entre os conceitos matemáticos (ASKEW et al., 1997).
O conhecimento do professor é, pois, inquestionavelmente, fulcral no processo de ensino e aprendizagem, na medida que determina o que se faz na sala de aula e a forma e o quê que o aluno aprende.
O caso dos professores dos primeiros anos (dos 6 aos 12 anos de idade) merece uma atenção especial. Existem muitas evidências de que os professores, em particular os professores do ensino fundamental, não possuem o conhecimento necessário para ensinar matemática de forma eficaz (JONES; TZEKAKI, 2016; HOURIGAN; LEAVY, 2017). Ora, apesar destes professores serem generalistas e, portanto, não serem especialistas em matemática, eles têm que ensinar matemática. Eles são os responsáveis pelo início de um período, mais ou menos longo, de aprendizagens matemáticas, com cada estágio altamente dependente do anterior e são eles que lidam com as ideias matemáticas básicas, mas fundamentais. Contudo, na formação dos professores dos primeiros anos, o conhecimento matemático geralmente é considerado trivial comparativamente à ênfase no conhecimento educacional. No entanto, assumindo que a matemática elementar é matemática fundamental no sentido defendido por Ma (1999), ou seja, embora seja apresentada num formato elementar ela contém os rudimentos de muitos conceitos importantes em ramos mais avançados da disciplina. Deste modo, é importante garantir conhecimentos matemáticos sólidos e eficientes nos futuros professores pois, como afirma o Conference Board of the Mathematical Sciences (CBSM) (2012, p. 24): “a strong understanding of the mathematics a teacher will teach is necessary for good teaching. Every elementary student deserves a teacher who knows, very well, the mathematics that the student is to learn.”
Neste artigo, após a apresentação do quadro teórico, serão apresentados e discutidos alguns resultados e problemáticas associadas a respostas dadas por futuros professores dos primeiros anos, a algumas questões sobre tópicos de Geometria. Com a referida discussão pretende-se contribuir para problematizar o foco da formação matemática de professores, a fim de permitir conceituar formas de melhorar essa formação, aumentando, dessa forma, o conhecimento matemático para ensinar dos professores.
2 CONHECIMENTO MATEMÁTICO DO PROFESSOR
Nas últimas décadas tem-se assistido a um crescente interesse dos investigadores pelo conhecimento do professor (FENNEMA; FRANKE, 1992; ASKEW et al., 1997; MA, 1999; BALL, 2003; DAVIS; SIMMT, 2006; SCHMIDT et al., 2011; ROWLAND, 2013). Um número considerável de teorias sobre o conhecimento do professor tem emergido e, apesar do reconhecimento unânime da relevância desse conhecimento, o seu estudo tem-se revelado uma tarefa difícil e complexa pois “esse conhecimento apresenta-se numa forma heterogénea, formado por diferentes componentes interligadas e difíceis de isolar.” (GOMES, 2003, p. 61).
Ainda que todos os tipos de conhecimento sejam relevantes e merecedores de atenção, verifica-se que o conhecimento relativo aos conteúdos a ensinar se apresenta como mais negligenciado nas investigações. De facto, as matérias a ensinar estiveram durante muito tempo, aparentemente ausentes da investigação, desempenhando um papel meramente contextual. Esta ausência levou a que Shulman (1986) e colegas a referissem como o problema do “paradigma perdido” e na opinião deste autor, o que faltava nas investigações eram questões acerca do conteúdo das lições, das questões postas, das explicações dadas. Shulman (1986) e os seus colegas revolucionaram as investigações sobre o conhecimento do professor, na medida em que se focaram e destacaram o estudo da percepção do conteúdo por parte do professor como uma forma especial de conhecimento que, segundo estes autores, determinaria a sua prática de ensino.
Referindo-se, em particular, ao conhecimento do conteúdo para os professores, Shulman (1986) considera três categorias: (a) conhecimento da matéria; (b) conhecimento pedagógico do conteúdo e (c) conhecimento curricular.
Muito trabalho tem sido feito desde então, nomeadamente no campo da Educação Matemática, esclarecendo e redefinindo diferentes categorias do conhecimento dos professores. Num desses trabalhos, realizado com professores dos primeiros anos, Ball (1990) considera que o entendimento necessário para ensinar matemática engloba não só́ o conhecimento substantivo da matemática como o conhecimento acerca da matemática. O conhecimento da Matemática é caracterizado por três critérios: (1) o conhecimento correto de conceitos e procedimentos, (2) o entendimento dos princípios e significados subjacentes e (3) o entendimento e apreciação das conexões entre ideias matemáticas. Quanto ao conhecimento acerca da Matemática ele inclui a compreensão acerca da natureza do conhecimento matemático e da Matemática como um campo científico.
Prosseguindo nas ideias de Shulman, Ball e colegas (e.g., BALL, 2003; BALL; THAMES; PHELPS, 2008; HILL; ROWAN; BALL, 2005) desenvolveram uma das conceptualizações mais conhecidas e influentes do conhecimento matemático do professor, o Mathematical Knowledge for Teaching (MKT). Este modelo será apresentado com detalhe na próxima secção.
3 CONHECIMENTO MATEMÁTICO PARA ENSINAR
A conceptualizações do Mathematical Knowledge for Teaching (MKT) centra-se na especificidade do papel que o professor tem de desempenhar. Nesta conceptualização são considerados dois domínios: subject matter knowledge (SMK, conhecimento do conteúdo) e pedagogical content knowledge (PCK, conhecimento pedagógico do conteúdo) subdivididos em três subdomínios cada (Figura 1).
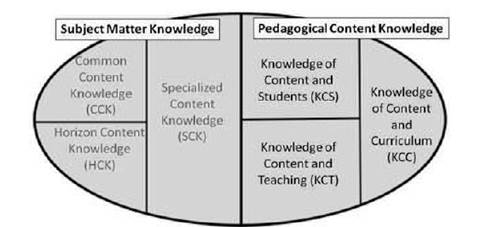
Fonte: Ball, Thames e Phelps (2008, p. 403)
Figura 1 Domínios do Mathematical Knowledge for Teaching
Neste artigo iremos centrar a nossa atenção no domínio do Conhecimento do Conteúdo (Subject Matter Knowledge) o qual, de acordo com este modelo, se divide em três componentes. Um destes componentes, do conhecimento comum do conteúdo (Common Content Knowledge, CCK), implica que o professor deverá ter um conhecimento matemático sobre factos básicos, associados ao saber fazer. Este é utilizado em situações diversas, não apenas relacionadas com o ensino e contempla um conhecimento que não envolve um questionamento sobre os porquês do que se faz nem sobre possíveis generalizações de determinados procedimentos. Este CCK corresponde, assim, a um conhecimento envolvido também noutras profissões que fazem uso da Matemática (HILL; BALL, 2004), numa perspectiva instrumental (SKEMP, 1976).
Para além desse componente do conhecimento do professor, surge um outro - denominado conhecimento especializado do conteúdo (Specialized Content Knowledge, SCK) - que demanda compreensão e raciocínios únicos, próprios do professor e que não é necessário noutras atividades profissionais. Este conhecimento inclui, entre outros, um conhecimento que permita preparar tarefas matematicamente desafiadoras, mantendo o seu elevado nível cognitivo (STEIN et al., 2000), atribuir sentido às respostas e produções dos alunos, usar representações matemáticas múltiplas recorrendo a uma linguagem matemática correta e adequada ou conhecer e saber como obter diferentes formas de definir um mesmo objeto geométrico.
Por último, a componente do conhecimento do conteúdo no horizonte (Horizon Content Knowledge, HCK) implica que os professores possuam uma visão simultaneamente global e local de como os distintos tópicos evoluem ao longo da escolaridade e se (inter)relacionam, mas numa perspectiva exterior ao currículo- conhecimento do conteúdo.
Assim, o MKT considera que o professor deve possuir um conhecimento substancial da matemática que se vai ensinar (tanto em profundidade como em extensão), uma capacidade de tornar acessíveis as ideias matemáticas ao ensino e um conhecimento do percurso escolar dos alunos, numa lógica de conexão com os conhecimentos matemáticos anteriores e com as aprendizagens futuras.
4 DOIS EXEMPLOS
Os exemplos que se apresentam nesta secção provêm de um projeto de pesquisa mais amplo que se focou no conhecimento matemático para ensinar (MKT) de futuros professores dos primeiros anos no qual se objetivou conceptualizar tarefas que permitissem incrementar esse conhecimento (GOMES et al., 2012). No âmbito dessa pesquisa foi elaborado um questionário com um conjunto de questões que pretendiam avaliar o conhecimento matemático dos futuros professores sobre vários tópicos de matemática.
Este questionário foi respondido por 40 futuros professores de uma Instituição de Ensino Superior portuguesa.
Neste artigo debruçámo-nos sobre as informações recolhidas a partir das respostas a duas questões relacionadas diretamente com Geometria. O foco da análise será o Conhecimento Matemático do Conteúdo pois considera-se fundamental, mas obviamente não exclusivo, que qualquer professor detenha um amplo conhecimento do conteúdo para que possa conjugar-se com os demais subdomínios, perspectivando um ensino de qualidade.
O primeiro exemplo escolhido centra-se no conhecimento dos futuros professores sobre representações, neste caso, de polígonos. A pergunta era (Figura 2):
Pretendia-se com esta questão identificar que tipo de representações os futuros professores associam ao conceito de polígono. Assumindo que a noção de polígono normalmente usada nos primeiros anos é a de “região plana limitada que incluiu a fronteira que é uma linha poligonal fechada” (FONSECA, 2004, p. 264) sendo que uma linha poligonal fechada é “formada por sucessivos segmentos de recta, tendo os segmentos consecutivos um extremo comum, não estando na mesma recta dois segmentos consecutivos e não tendo os segmentos de recta pontos comuns para além dos extremos” (FONSECA, 2004, p. 263), as respostas consideradas corretas seriam as representações C, D, F e H.
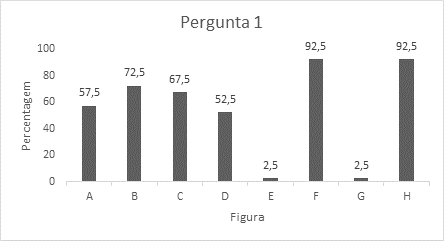
No Gráfico 1 apresentam-se as respostas dos participantes a esta pergunta. Como se pode ver na tabela, praticamente todos os participantes consideraram as figuras F e H como polígonos, e as figuras E e G como não polígonos.
Ainda que a maior parte dos participantes (57,5%) não apresente qualquer justificação para as suas opções, alguns referem que polígonos são figuras formadas por uma linha fechada ou por uma linha poligonal fechada. Curiosamente, todos os que apresentam uma destas justificações consideram, erradamente, a figura B (círculo) como polígono. Parece óbvio que desconhecem o significado de linha poligonal pois consideram que pode ser uma linha curva. No entanto, apenas 1 estudante considerou a figura G como polígono. Por outro lado, apenas 53% consideraram a figura D um polígono apesar de ser formada por uma linha (poligonal) fechada. Parece haver há uma tendência para considerar certas representações (protótipos, neste caso, F e H) como as representações de polígono.
Também 67,5% dos participantes consideraram a figura A como polígono. Isto pode acontecer porque consideram que nos polígonos podem existir “cruzamentos” ou veem a representação A não como um polígono, mas antes como dois triângulos unidos por um vértice.
Dos resultados obtidos parece poder concluir-se que uma ideia é comum a todos os estudantes: a de que um polígono é uma figura fechada. No entanto, o facto dessa linha ter que ser constituída por segmentos de reta já não é universal. Ora, sendo este um conceito geométrico básico que consta dos programas curriculares dos primeiros anos, esta falta de conhecimento dos participantes afigura-se grave uma vez que estes futuros professores deviam ter ideias claras sobre o que têm que ensinar.
O segundo exemplo escolhido centra-se no conhecimento dos professores sobre as definições e, em particular, sobre retângulos. A questão era (Figura 3):
Nenhum dos futuros professores apresentou uma definição matematicamente válida, ou seja, não foram capazes de elencar um conjunto de condições simultaneamente minimal, necessário e suficiente (WINICKI; LEIKIN, 2000). Os futuros professores forneceram apenas “pseudo-definições”, sendo que, alguns deles associam uma definição a uma listagem extensa de características (todas as que se recordam), como se considerassem que quantas mais propriedades tiver uma definição, melhor e mais completa ela é (Figura 4). Estes futuros professores parecem atribuir um papel descritivo e não normativo às definições, desvalorizando a característica da minimalidade.
Há respostas (47,5%) que assumem apenas os lados como elementos críticos. Ao considerarem como definição de retângulo uma figura com 4 lados iguais dois a dois (Figura 5), revela um conhecimento bastante incompleto sobre quadriláteros pois assumem que o retângulo é o único polígono com quatro lados que tem os lados iguais dois a dois.
Estes futuros professores não são capazes de reconhecer que a condição é necessária, mas não suficiente para definir um retângulo e ignoram quadriláteros como o losango ou o papagaio. Outras respostas (30%) baseiam-se numa classificação partitiva (DE VILLIERS, 1994; GOMES; RALHA, 2005) considerando, à partida, quadrados e retângulos pertencentes a conjuntos disjuntos (Figura 6).
Este tipo de lacunas, se não colmatadas, contribuirão para perpetuar um tipo de abordagem aos polígonos que considera somente uma sua classificação partitiva (por exemplo, DE VILLIERS, 1994; GOMES; RALHA, 2005; RIBEIRO, 2012) e restringindo o desenvolvimento de um conhecimento simultaneamente integrado e integrador.
Quanto às respostas que consideram como elementos críticos, para além dos lados, também os ângulos, é referido - tanto de forma explícita (Figura 7) como implícita (Figura 8) - que têm de ter quatro ângulos retos. Isto mostra que os futuros professores não detêm um conhecimento que lhes permita equacionar as condições da necessidade dessa referência, e os motivos matemáticos que sustentam tal condição.
Existem ainda estudantes que revelam, claramente, sustentar-se na sua imagem do conceito de retângulo para tentar construir a definição (Figura 9).
Esta definição, construída provavelmente por influência de alguns exemplos prototípicos, correspondendo a figuras cujos lados são paralelos aos lados de uma cercadura retangular, revela uma imagem conceptual de retângulo muito pobre mostrando o poder das propriedades figurativas na formação da imagem do conceito e as limitações do uso de representações pouco variadas para os conceitos.
5 DISCUSSÃO
Como se pode constatar pelos exemplos apresentados, são várias as carências de conhecimento reveladas por estes estudantes, futuros professores.
No que diz respeito à 1ª questão, ela envolve sobretudo um conhecimento comum de conteúdo (CCK) já que era pedida a identificação de representações de um conceito elementar (polígono). Como se verificou, há muitos futuros professores que têm noções completamente erradas de polígono. Esta falta de conhecimento do professor a nível do Conhecimento do Conteúdo compromete o conhecimento Pedagógico do conteúdo uma vez que, ao não possuir uma imagem mais completa e um conhecimento mais sólido do conceito, não conseguirá identificar exemplos e contraexemplos do conceito nem apreciar as representações elaboradas pelos seus alunos.
As respostas dadas à 2ª pergunta, relativas à definição de retângulo, ilustram importantes deficiências no conhecimento dos professores e mostram-nos a necessidade de uma atenção redobrada ao papel das definições. Com efeito, o papel das definições, particularmente em geometria, é crucial, uma vez que elas organizam dedutivamente as propriedades de um objeto, relacionam-no com todos os outros, construindo assim um sistema orgânico de definições e uma rede encadeada de conceitos e subconceitos. Vinner (1991) defende que o conhecimento da definição formal é fundamental, em particular, na identificação de exemplos, contraexemplos e não exemplos de um conceito, na resolução de problemas e nas demonstrações. Configura-se assim, como essencial que os professores detenham uma profunda compreensão da natureza das definições (SCK), do seu papel e das suas características. Entre outros, pressupõe-se que o professor saiba o que se entende por definir (condições necessárias e suficientes, e minimais); que definir e enumerar propriedades correspondem a coisas diferentes; seja conhecedor da coexistência de várias definições alternativas para um mesmo conceito e entenda que a opção por uma delas tem consequências em termos de organização dos conceitos. Não ser capaz de percepcionar os quadriláteros numa perspectiva hierárquica pode ser visto como uma deficiência no CK que terá consequências no PCK.
Só com este tipo de conhecimento estarão os professores aptos a proporcionarem aos seus alunos atividades significativas, que desenvolvam os conceitos de forma não limitada (MA, 1999).
5 EM JEITO DE CONCLUSÃO
Os exemplos apresentados são paradigmáticos porquanto ilustram algumas das dificuldades e das lacunas do conhecimento de futuros professores. Este défice de conhecimento, nomeadamente Conhecimento do Conteúdo (CK) pode comprometer o desenvolvimento do conhecimento pedagógico do conteúdo (PCK) e, consequentemente, ter efeitos negativos sobre a instrução e o progresso dos alunos (por exemplo, HILL; ROWAN; BALL, 2005; HILL et al., 2007, 2008; BAUMERT et al., 2010). Deste modo, parece adequado afirmar que o conhecimento do conteúdo desempenha um papel crucial no ensino e ainda que não seja suficiente para garantir um ensino eficiente, é certamente necessário.
Ao serem identificadas as dificuldades dos futuros professores em lidar com os conceitos, estamos a identificar fragilidades e pontos críticos onde deverá incidir a formação destes profissionais. Isto coloca-nos uma enorme responsabilidade na medida em que a formação que oferecemos deve ser de qualidade e contribuir para que estes estudantes possam vir a tornar-se professores matematicamente competentes (tal como é defendido em Conference Board of the Mathematical Sciences (2012) e European Commission (2018)).
Nesse sentido, a formação que oferecemos tem uma importância fulcral e deverá ter, necessariamente, em conta os diferentes aspetos do conhecimento do professor. Em particular, estes exemplos indicam que o conhecimento do conteúdo (CK) deve merecer uma atenção especial na formação inicial e na pratica letiva. Terá que ser uma formação vá mais além de um conhecimento matemático de nível elementar, no sentido do conhecimento comum do conteúdo (CCK) (HILL; BALL, 2004). Este conhecimento comum tem sido, até ao momento, e com demasiada frequência, o conhecimento explorado (e exigido) aos futuros professores, o que se configura como uma dificuldade para que estes possam entender, efetivamente, o que fazem e porque o fazem. É, pois, necessário um conhecimento que permita a compreensão das ideias, dos porquês, das suas conexões e das diferentes formas de serem representadas. É também um conhecimento que tem que ter em conta a especificidade da ação docente. Os problemas matemáticos genuínos, centrais no trabalho de ensino envolvem representar conceitos de várias formas, escolher uma definição utilizável, desenvolver explicações alternativas. Além disso, o conhecimento matemático necessário para o ensino, particularmente no nível elementar, não é menos exigente nem mais simples do que o conhecimento de um matemático, tendo, isso sim, contornos singulares em função da complexidade do currículo que tem de implementar.
Assim, a formação inicial deverá, por um lado, centrar-se em tópicos nos quais os futuros professores revelam maiores dificuldades e, por outro, ter em conta a especificidade da ação docente e do conhecimento envolvido num ensino com e para a compreensão, de modo a possibilitar que os professores possam ir desenvolvendo o seu MKT de forma continuada.
É, assim, necessária mais investigação que permita entender de forma mais ampla os aspetos mais críticos do conhecimento do professor e possibilite desenhar uma formação que tenha em consideração as especificidades desse conhecimento.