Notion of perpendicularity based on the instrument configuration

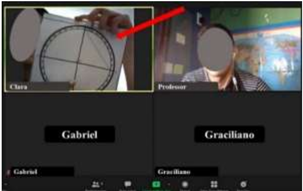
At the beginning of the practice, as already mentioned, the students received as a guide only the student's sheet of paper, which described the guidelines for the practice and Pedro Nunes' instructions for the construction of the instrument jacente no plano. In this document, it was not available a figure that showed the physical configuration of the apparatus, this fact, added to just a first reading of the excerpts from the Cosmographer, made it possible to raise the following question “[...] teacher, we have to draw a triangle on top of the print?” (Clara, 2021, Audio recording Room 3). This same interpretation appears in other rooms, and in this regard, we have (Figure 4).

In response to Clara's questioning and representation, the group was instructed to read the excerpts again in more detail, so that they could reach a conclusion closer to the correct positioning of the triangle. Given the new reading, a member of the group states: “[...] I understand, I understand, since he wants to be perpendicular, it is as if the triangle was standing on the thing, is it standing on the paper, you know? He wants it perpendicular to the circumference! Is it right, teacher? (Gabriel, 2021, Audio recording Room 2). Here the expression “was standing on the thing” appears, which indicates that this idea of standing is one of the meanings he attributes to the concept of perpendicularity.

Taking into account that the teaching material must serve as a mediator to benefit the teacher/student/knowledge relationship in the construction of knowledge (^{Passos, 2012}), then, as a way of encouraging group work using the instrument, Gabriel's question is passed on to the other members of the group, one of them then responds: “[...] I understood, here's the thing, you build the triangle and then bounce it on top of the plane, then raise the triangle, it will serve as a base to build the triangle and lift it up to be perpendicular to the plane, [...] as if it were a raft” (Graciliano, 2021, Audio recording Room 2). Given this interpretation, Flora (2021) states “[...] that was what you were saying Gabriel”. Gabriel concludes his thought by highlighting that:

That! [...] it’s to build the triangle using this circumference, because you will use the two radii as if they were two catheti. Then, using this as if it were a kind of ruler, then you just leave the little triangle standing up, then this triangle that is standing up has to be above the center, because it will be measured in relation to the Sun, right. It is going to be like a sundial (Gabriel, 2021, Audio recording Room 2).

Source: Authors’ archive (Room 2, 2021).

Figure 4 Positioning the isosceles right triangle. 

In the speech of these participants, it is possible to observe that in order to understand the configuration of the instrument they attribute meaning to the notion of perpendicularity based on already known concrete objects. The raft, as well as the Sundial, in fact have an upright structure on a base that may indicate perpendicularity. This association made by students from something concrete to the abstract indicates that they still do not have an effective understanding of the concept of perpendicularity, because “[...] for people who have already conceptualized these objects, when they hear the name of the object, it flows in their minds the idea corresponding to the object, without needing the initial support they had from the attributes size, color, movement, shape, and weight” (^{Lorenzato, 2012}, p. 22). What can be seen in the students' speech is that the aforementioned concept is still closely linked to the support of a concrete nature.

In Primary and Secondary Education textbooks, it is possible to observe the appreciation given to concrete support. To start dealing with the topic, in the particular case of perpendicularity, in volume two of the 2016 collection 'Conexões com a matemática' - which means Connections with Mathematics” - from the publisher Moderna, they highlight the gnomon (a stick stuck in the ground to mark shadows) and the plumb line to build walls (^{Leonardo, 2016}). This allusion to concrete supports seen in this collection is in accordance with what ^{Lorenzato (2012}) argues, in which these initial supports are seen as elements to awaken a first conceptualization of the objects.

Still on moments of the meeting that allude to the notion of perpendicularity, see Figure 5.

Source: Authors’ archive (Room 5, 2021).

Figure 5 Gestural representation of the notion of perpendicularity. 

Focusing on what Luiza says about perpendicularity, it is noted that she brings yet another meaning to compose the concept, since it is known that “[...] geometric representations can be given through drawings, constructed objects, gestures, through language, among other manifestations” (^{Passos, 2000}, p. 39). From what she says, if the triangle is slightly inclined it is not perpendicular to the base, she then uses her hands to represent her argument. The positioning given to the hands actually references the notion of perpendicularity, as it is known that “[...] two straight lines are perpendicular when they intersect forming four congruent angles; each of them is called a right angle” (^{Lima, Carvalho, Wagner, & Morgado, 2016}, p. 177). Her speech also corroborates this fact, since it is said that the angle made by the triangle with the board is 90º.

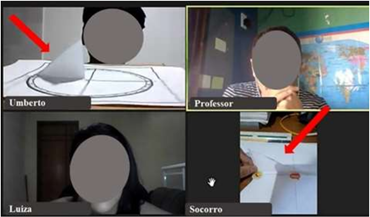
Given these discussions about perpendicularity based on the configuration of the instrument, students arrive at the representation in Figure 6.

Source: Authors’ archive (Room 5, 2021).

Figure 6 Configuration of the instrument jacente no plano perceived by the students. 

As it can be seen, by reading Pedro Nunes' excerpts, the students were able to understand how the triangle should be positioned. However, it is interesting to note that even though they were in the same group (Room 5), they still positioned the triangle differently on the circumference. Note that Umberto places the 90º angle of the isosceles right triangle close to the center of the circle, while Socorro places it at a point on the circumference. When asked about the reason for this impasse, one of the students replies, in a tone of affirmation “Socorro, you put the sides of the triangle wrong” (Luiza, 2021, Audio recording Room 5). It is known according to the excerpts from Pedro Nunes that the way Socorro did it was correct, however, instead of saying that one was right and the other wrong, the students were instructed to do a new reading of the text available on the student’s worksheet.

In the next category, emphasis is given to the way students thought about constructing the triangle.

Construction of the isosceles right triangle

As already mentioned in the previous category, the students' first initiative was to draw the triangle on the graduated circumference. After understanding that the triangle should be perpendicular, they thought about using the circumference “[...] to build the triangle [...], because you will use the two radii as if they were two catheti. Then using this as if it were some kind of ruler” (Gabriel, 2021, Audio recording Room 2). As justification for this, they state “[...] we said that the semidiameter would be the radii and we formed the isosceles right triangle” (Flora, 2021, Audio recording in the main room with all students).

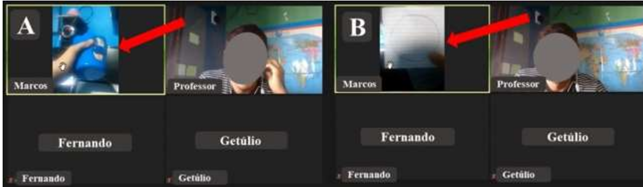
Still in the same direction, another student highlights that “[...] I saw that the most correct method was to draw a straight line (a string) from zero to ninety on the circumference” (Marcos, 2021, Audio recording at main room with all students). However, one of the students' difficulties in using the circumference as a kind of template, as they perceived, was the fact that some students did not have the material previously requested for practice. In order to alleviate this ‘problem’, one of the students uses a sheet and a cylindrical-shaped object to construct the circumference (Figure 7).

In Figure 7 (A) there is the cylindrical object and in Figure 7 (B) the created circumference. Regarding this construction, Marcos (reporter from room 4) highlights that “[...] I built this circle here, with a circular object, I don’t know if it was deformed, but I built it and supposedly drew the diagonals because there is no way to guarantee it” (Marcos, 2021, Audio recording in the main room with all students). The incorporation of the cylindrical object for the construction of the instrument jacente no plano was not foreseen for this practice, however, it is known that “[...] materials need to be integrated into situations that lead to reflection and systematization, so that it starts a formalization process” (^{Base Nacional Comum Curricular [BNCC], 2018}, p. 276).

Source: Authors’ archive (Room 4, 2021).

Figure 7 Construction of the circumference. 

In these terms, it is understood that the cylindrical object played an important role in the fulfillment of the proposed activity, since in the student's speech it is observed that he is aware of the possible inaccuracy of the material used, and that from it he may not have constructed an exactly circular figure and it is difficult to determine its center to trace the diameters.

Faced with this possible inaccuracy, in order to get closer to something exact, a student asks for the floor and declares that “[...] the construction of the triangle, we make by taking the compass, making a quarter of a circle that is 90º, then the little 90º vertex of the triangle is exactly at what would be the center of the circumference” (Luiza, 2021, Audio recording in the main room with all students). This construction, it seems, involved the transport of angles, as the 90º angle (quadrant) was possibly constructed from the measurements of the semidiameter of the circumference placed on the board (^{Carvalho, 1958}), as this is a very viable construction that we recurrently observed in books on geometric constructions.

Another strategy for constructing the isosceles right triangle, still associated with the circumference, refers to the use of a rigid material designed by the students in Room 1 (Figure 8).

Source: Authors’ archive (Main Room, 2021).

Figure 8 Proposal for constructing the isosceles right triangle. 

In this case, it is noted that to construct the triangle, students start from the idea of perpendicularity as a 90º angle. The use of a sheet of paper, a rigid material illustrated with the corners of a notebook, indicates that the students possibly visualize a rectangle on the sheet/cover of the material, which they certainly know has four right internal angles. According to ^{Pais (1996}), when taking intuitive, experimental, and theoretical aspects of geometric knowledge as a basis, which are central in an epistemological theory of geometry, it is understood that this notebook serves as a first representation of the concept in the process of apprehending the object.

In the main room, still discussing the construction of this triangle, Marcos asks for the floor to highlight that:

[...] There was a discussion in my group, we had difficulties regarding what an isosceles triangle was, I had understood that they were two equal sides and one smaller, but in fact it is just two equal sides, the other not necessarily smaller or larger, because been isosceles has nothing to do with angles, it has to do with the size of the side, right (Marcos, 2021, Audio recording in the main room with all students).

In this regard, it is noted that the discussion possibly helped them reflect on the concept of isosceles triangle. As the first idea for constructing the triangle was associated with the graduated circle, in this case the triangle formed has one larger side (hypotenuse) and two smaller sides (radii). However, if it were not a right-angled, and only isosceles, then the triangle could have had a pair of congruent larger sides and a smaller one, as Marcos points out.

Given the reflections conducted so far, it is understood that the students had the possibility of reconfiguring and/or expanding the mathematical knowledge mobilized, as the situations promoted the communication of mathematical ideas and the exchange of ideas through group work. (^{Rêgo & Rêgo, 2012}).

Positioning the triangle perpendicular to the board

During the discussions in the main room, with the return of all groups of students, it became clear that Pedro Nunes' instruction to position the triangle perpendicular to the board was the most difficult for them. The proof of this is that only one team managed to present a strategy that was exposed and refined to all participants in the laboratory practice. When presenting the idea, the reporter from Room 5 highlights that:

To ensure that the triangle was perpendicular, we even thought of an argument, but we do not know if it's quite correct. The board has these two diameters here where each one forms 90º [...] then the triangle is on one of these lines, these diameters, on the other diameter we draw a plane, for example if we glued a sheet, we would have to ensure that this angle here is 90º, so it would be perpendicular to it, and we also guarantee this by comparing the angle of the triangle that we know it is 90º with this angle, we will determine that it is equal using the compass (Luiza, 2021, Audio recording in the main room with all students).

At the heart of this strategy, it is noted that the group proposes to work based on the diameters of the circumference. As auxiliary resources, they include the incorporation of a sheet of paper representing a plane and a compass to ensure a 90º angle responsible for the perpendicularity of the isosceles right triangle. In this regard, we have the Figure 9.

Source: Authors’ archive (Room 4, 2021).

Figure 9 Construction of the circumference. 

In Figure 9, the student represents the triangle with her hand and with a sheet of paper the supposed plane that her team suggested as a strategy. In the words of the reporter “[...] here is the triangle and the other plane that you drew, which is not the board, this plane is on top of the board, you guarantee that it is perpendicular because it is exactly on the other diameter of the board” (Luiza, 2021, Audio recording in the main room with all students). It can be seen that the students are working with perpendicular planes, one represented by the triangle and the other represented by the sheet of paper. In this way, in fact, it is possible to ensure that the triangle would be perpendicular, as the intersection of these planes is a straight line that intersects the board in at least two right angles (one from the triangle and the other from the sheet), which is enough to ensure perpendicularity.

Explaining the idea of Room 5, the student also highlights that “[...] so, we actually have three planes, we have the board, [...] this triangle is contained in another plane too, right, we want to prove that the plane that contains the triangle” (Luiza, 2021, Audio recording in the main room with all students). When asked if the triangle could be considered a plane, Marcos says:

If we considered the piece of paper to be a plane (the graduated circumference) the triangle can also be considered a plane. [...] there are two points of it in a plane and a third is not contained in it, so it means that they form a secant plane, [...] because the straight line is in one and the straight line is outside (Marcos, 2021 , Audio recording in the main room with all students).

In fact, the student's justification is pertinent and acceptable. Pedro Nunes does not provide any information in this regard. He only says that an isosceles right triangle must be constructed in a hard material. It is understood that the cosmographer only refers to the representation of what a triangle would be, as it is evident that whatever material the triangle is constructed from, it will always be, in fact, a right triangular prism and the instrument board a rectangular parallelepiped, this due to the dimensions that indicate spatiality (length, width, and height).

After a request from some colleagues, the reporter of Group 5 returns to talk about her room's strategy. About this, in Figure 10, we seek to detail the student's speech through images.

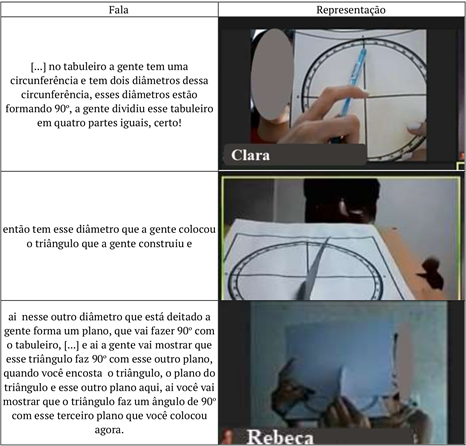
Source: Authors’ archive (Main room, 2021).

Figure 10 Representation of the student's speech about the strategy used. 

Given this situation, the idea and validity of the strategy adopted can be clearly observed. It is possible to see the secant planes highlighted previously by Marcos, one of them represented by the triangle and the other by the sheet of paper incorporated to achieve the desired positioning. However, it is worth noting that this construction highlighted by the reporter in Room 5 maintains a mistake, already observed previously, even when they were in internal activity in the group, which is the positioning of the right triangle on the semidiameter. It is known that the 90º vertex of the triangle must be on the circumference, and not at the center. This problem was resolved through a new reading of Pedro Nunes' excerpts and through the reporter's dialogue with the other students from the other groups.

Still on this strategy thought up by the participants in Room 5, concerned about one of the resources used, a student expresses her impression:

- I understand until when she talks about the plane, right. But the idea of the compass confuses me at the end (Rebeca).

- The idea of the compass is just to ensure that the triangle is 90º, because when you have a compass, you form a circumference. And then, let's suppose, if I draw from here to here, I'm drawing the value of an angle, this here is an angle when I draw on the compass. If I take the compass and instead of drawing a whole circle I draw a quarter of a circle, I am drawing a 90º angle. So, I'm going to use the compass to show that I can draw an angle of exactly 90º making a quarter of a circle, did you understand (Luiza).

- But you draw it on another plane? (Rebeca).

- That! (Luiza) (Dialogue among students in the main room, 2021).

In these terms, it is understood that the idea of the compass is to construct a quarter circle in the plane represented by the sheet of paper. This quarter circle, according to the reporter, does not necessarily need to have its sides congruent to the semidiameter of the circumference, as it is mandatory for the triangle that must be placed perpendicular. Given this, it is clear that it would also be valid to just build another triangle and cut it out of the sheet of paper. As for a possible student learning about the concepts covered, the dialogues indicate that this has possibly been achieved, since according to ^{Lorenzato (2012}), one of the main triggers for this to happen is the mental activity. In this laboratory activity, learning was present at all times, proof of this are the speeches and actions of the participants in their attempt to comply with Pedro Nunes' instructions. Given this strategy, another idea arises for the positioning of the isosceles right triangle, in relation to it, we have Figure 11.

Source: Authors’ archive (Dialogue among students in the main room, 2021).

Figure 11 Dialogue on the strategy that incorporates the parabolic movement. 

In this idea, the student uses the pen as a way to represent the triangle. Thus, it is clear that the student is attributing another meaning to the concept of perpendicularity. Here it appears associated with the highest point of a parabolic movement curve. Furthermore, they also enable them to mobilize/articulate different concepts, not just internal to mathematics itself. Due to time, this strategy was not explored with the students and the activity ended with a brief review of the students' observations presented in order to formalize the triangle positioning strategy.

Considering the students' strategies and actions in order to solve the practical problem driven by Pedro Nunes' instructions, we agree with ^{Pereira and Saito (2019}) when they highlight that working with mathematical instruments enables relationships and geometric concepts synthesized in the apparatus gain even more meaning for students.

Thus, thinking about the training of undergraduate Mathematics Education students, it is understood that this practice may have contributed to their understanding that “[...] Geometry involves the study of a broad set of concepts and procedures necessary to solve problems in the physical world and in different areas of knowledge” (^{BNCC, 2018}, p. 271), as some concepts were mobilized in a practical and articulated way.

Considering the theoretical and methodological fundaments, it is understood that the BPU developed possibly favored student learning, as it was permeated by constant exploration and investigation, as predicted by ^{Lorenzato (2012}) for the activities that take place within the MTL. The BPU also enabled students to observe mathematical knowledge in practical terms, a potential that meets what was proposed by ^{Miguel and Mendes (2010}).