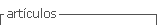Introdução

Aprendizagem significativa é uma expressão que tem sido utilizada com certa frequência e destaque, principalmente por professores das diversas áreas do conhecimento, em especial pelos da área de Ciências e Matemática. Há, no entanto, um certo desconhecimento, por parte de alguns que utilizam tal expressão, quanto aos fundamentos da teoria na perspectiva de seu autor.

Muitos autores construíram suas teorias no campo do desenvolvimento cognitivo numa concepção de aprendizagem significativa, como é destacado em ^{Moreira (1997)} que elencam alguns, tais como: David ^{Ausubel (1963}, ¹⁹⁶⁸), Jean ^{Piaget (1971}, ¹⁹⁷³, ¹⁹⁷⁷), George ^{Kelly (1963)}, Lev ^{Vygotsky (1987}, ¹⁹⁸⁸), Philip ^{Johnson-Laird (1983)}, dentre outros.

No presente artigo, a abordagem principal será tratar um pouco sobre a Teoria da Aprendizagem Significativa na perspectiva de David Ausubel, tentando identificar alguns de seus elementos numa atividade realizada em sala de aula, que se utilizou modelos matemáticos para trabalhar alguns conteúdos fundamentais de Matemática numa disciplina de Pré-Cálculo para uma turma composta por estudantes de vários cursos de graduação numa universidade pública do Estado do Pará.

O estudo de funções elementares no Ensino Médio é um dos temas fundamentais, além de motivadores no ensino de Matemática, pois os estudantes têm a oportunidade de lidar diretamente com aplicações práticas da matemática, tanto em problemas do dia-a-dia como em problemas de outras ciências como a Física, Química, Biologia, Economia, dentre outras.

Nesse sentido, é particularmente importante o estudo das funções exponenciais e logarítmicas, quando se utiliza ferramentas de apoio no processo de ensino e aprendizagem como as calculadoras científicas e os softwares de simulação.

Baseado em experiências desenvolvidas em sala de aula com estudantes de vários cursos de graduação, em disciplinas de Pré-Cálculo, onde a ementa básica era o estudo de funções elementares, pretende-se apresentar uma proposta de ensino de alguns modelos exponenciais por meio de simulação, utilizando a planilha eletrônica Excel.

Os modelos a serem discutidos neste trabalho são: o modelo de crescimento ou decaimento exponencial; o modelo de crescimento limitado ou inibido; e o modelo de crescimento logístico.

De acordo com a sequência de exposição do tema nas aulas de Pré-Cálculo, neste artigo, serão apresentadas também, além de uma breve visão da teoria de Aprendizagem Significativa, as principais características desses modelos e alguns exemplos de aplicações destes. Na sequência, ao relatar a experiência realizada em sala de aula, serão listados alguns problemas ou situações-problema, no contexto de alguns cursos de graduação onde a disciplina é ministrada, além de procurar descrever as reações mais relevantes dos estudantes sobre a atividade.

Aprendizagem significativa na perspectiva de Ausubel

David Paul Ausubel nasceu em 25 de outubro de 1918, no Brooklin, Nova Iorque, Estados Unidos. Era filho de uma família judia, imigrantes da Europa Central. Estudou Psicologia (1939) na Universidade da Pensilvânia (Filadélfia) e Medicina (1943) na Universidade de Middlesex (Londres). Na Universidade de Colúmbia (Nova Iorque) obteve seu doutorado em Psicologia do Desenvolvimento (1950). Atuou como professor na Universidade de Nova Iorque por muito tempo, onde também foi diretor no Departamento de Psicologia Educacional, sendo por isso homenageado pela American Psychological Association em 1976, logo após sua aposentadoria. Mais tarde voltou para sua prática como psiquiatra, no Rockland Children's Psychiatric Center, e em 9 de julho de 2008 vem a falecer, aos 90 anos de idade.

O contexto histórico onde Ausubel nasceu e teve sua formação inicial foi marcante, pois nasce no final da primeira grande guerra, num país que lograva o status de maior potência mundial em termos financeiros e industrial, mas que sofreria em todos os setores como consequência da crise econômica internacional instaurada logo após a guerra, e perduraria pelas duas décadas seguintes. Ausubel teve grande motivação (negativa) externa para buscar alternativas de melhoria no campo educacional. Se mostra bem insatisfeito com a educação que teve em sua formação inicial, marcada por uma educação punitiva e humilhadora, violenta e reacionária, segundo ele mesmo afirmava.

A teoria da Aprendizagem Significativa ou teoria de Assimilação é uma teoria cognitivista que procura explicar os mecanismos internos que ocorrem na mente humana com relação ao aprendizado e à estruturação do conhecimento. Essa teoria quando foi apresentada por Ausubel em 1963, as ideias behavioristas eram predominantes no processo de aprendizagem do sujeito. A ênfase era dada à análise do comportamento dos estudantes por meio de respostas e estímulos, que eram influenciados por situações externas. Assim, não era considerado aquilo que os estudantes já sabiam, de tal forma que estes só poderiam aprender se fossem ensinados por alguém.

Na perspectiva de Ausubel, a concepção de ensino e aprendizagem segue um caminho oposto às ideias behavioristas. Para haver aprendizagem, segundo ele, o elemento mais importante a ser considerado é a estrutura cognitiva, onde se tem o conteúdo total e organizado de ideias, conceitos e proposições de um indivíduo. Assim, a aprendizagem significativa ocorre quando há a ampliação da estrutura cognitiva do indivíduo por meio da incorporação de novas ideias a ela. Portanto, para Ausubel conforme Moreira et al (1997, p.19) “Aprendizagem significativa é o processo através do qual uma nova informação (um novo conhecimento) se relaciona de maneira não arbitrária e substantiva (não literal) à estrutura cognitiva do aprendiz”.

A maneira não arbitrária de relacionar as informações, significa que ocorre de uma forma lógica e não imposta. Já a maneira substantiva, significa que o estudante consegue explicar o novo conhecimento de formas diferentes com linguagem sinônima.

A estrutura existente específica que se relaciona com a nova informação ou novo conhecimento é denominada por Ausubel de subsunçores. Trata-se de conceitos, ideias ou proposições já existentes na estrutura cognitiva (conhecimentos prévios) do aprendiz que serve de ponto de ancoragem para uma nova informação, permitindo ao indivíduo atribuir-lhe significado. Para que ocorra aprendizagem significativa, segundo Ausubel, duas condições são essenciais: 1) o material a ser aprendido deve ser relacionável, isto é, precisa ser potencialmente significativo; 2) o estudante precisa estar disposto a aprender, a relacionar à sua estrutura cognitiva. O material a ser aprendido não é significativo em si mesmo, é o estudante que dá o significado próprio ao mesmo e o incorpora à sua estrutura.

Três tipos básicos de aprendizagem são apresentados por Ausubel. São eles: representacional, por conceitos e proposicional. De acordo com ^{Moreira (1999)}, a aprendizagem representacional é a aprendizagem de símbolos individuais (tipicamente palavras) ou aprendizagem do que eles representam. A aprendizagem por conceitos é um caso particular de aprendizagem representacional, que também são representados por símbolos individuais, mas que indicam representações genéricas ou de categorias. Primeiro se aprende o conceito indicado por uma certa palavra, em seguida se aprende o significado desse conceito. Esse tipo de aprendizagem pode ocorrer tanto na formação do indivíduo, por meio do contato e da interação, como na assimilação dos conceitos a partir da ampliação de seu vocabulário. Em terceiro lugar, a aprendizagem proposicional, que pode ser entendida como a combinação e relação de várias palavras e conceitos, de forma a produzir nova proposição. Tanto a aprendizagem por conceito como a proposicional dependem diretamente da representacional.

Em todos esses casos, a percepção de que houve aprendizagem significativa de conceitos ou proposições, segundo Ausubel, “implica a posse de significados claros, precisos, diferenciados e transferíveis” (^{MOREIRA; MASINI, 1982}, p.14). Nesse sentido, para que o processo de aquisição e organização de significados na estrutura cognitiva do indivíduo se torne mais claro e preciso, Ausubel introduz o que chama de princípio da assimilação.

O princípio da assimilação, conforme Ausubel, é um processo que ocorre quando uma nova informação, conceito ou proposição, potencialmente significativa, se relaciona a um conceito subsunçor existente na estrutura cognitiva e assimilada pelo indivíduo na forma de uma ideia ou conceito mais inclusivo, isto é, o processo de interação produz um subsunçor modificado, ampliado. Tal ampliação significa que a nova informação possibilita a extensão, a elaboração ou a qualificação de conhecimentos anteriores existentes na estrutura cognitiva do indivíduo (^{MOREIRA; MASINI, 1982}, p.15).

Para Ausubel, a aprendizagem significativa ocorre de três formas: subordinada, superordenada e combinatória. Na forma subordinada, a nova informação é uma particularidade de um conceito mais geral (subsunçor) que vai sendo progressivamente diferenciado em termos de detalhes e especificidade. Na forma superordenada, ocorre o inverso, isto é, a nova informação é um conceito geral que vai sendo integrado à partir de ideias ou conceitos particulares (subsunçores). Nas duas formas de aprendizagem, tanto na subordinada como na superordenada, existe uma relação de dependência entre a nova informação e os subsunçores. É diferenciada, partindo do geral ao particular, ou é integrada, partindo do particular ao geral. Já na terceira forma de aprendizagem, a combinatória, não há uma relação de dependência, nesse caso, a nova informação pode ser assimilada por meio elementos comparativos, por analogia.

De uma forma simples, ^{Ausubel (1968)} resume sua teoria afirmando que: “Se eu tivesse que reduzir toda a psicologia educacional a um único princípio, diria isto: o fato isolado mais importante que influencia a aprendizagem é aquilo que o aprendiz já conhece. Descubra o que ele sabe e baseie nisso os seus ensinamentos”.

No entanto, fundamentar todo o processo educativo somente nesse princípio pode inibir o desenvolvimento pleno do estudante. A interatividade, a busca pelo conhecimento, a experimentação, o questionamento, o protagonismo, todos esses elementos se constituem facetas para uma aprendizagem significativa. Além disso, conforme ^{Moreira (2000)} o estudante precisa aprender de forma crítica, o que eleva a aprendizagem significativa a um nível mais abrangente e firma “o aprendiz” como sujeito realmente participativo da sua própria aprendizagem, bem como um sujeito ativo na sociedade em que está inserido.

Nesse sentido, ^{Barbosa (2003)} no campo do ensino de Matemática, principalmente no contexto da Modelagem e no uso de modelos matemáticos, defende que estes devem ser analisados numa perspectiva sociocrítica¹⁶ da Modelagem Matemática, isto é, discutir o papel e a natureza dos modelos matemáticos na sociedade, apoiando-se na Educação Matemática Crítica (^{SKOVSMOSE, 1994}). Para Barbosa, os modelos matemáticos têm uma “função social” quando destaca que estes desenvolvem um papel na sociedade como balizadores de decisões, de modo que “faz-se necessário ultrapassar as dimensões técnicas da Modelagem e realizar uma análise crítica do papel dos modelos matemáticos na vida social” (^{BARBOSA, 2001}, p. 19).

A Educação Matemática Crítica, de acordo com ^{Skovsmose (2000}, p. 2), pode ser sintetizada ao afirmar que:

[...] inclui o interesse pelo desenvolvimento da educação matemática como suporte da democracia, implicando que as micro-sociedades de salas de aulas de matemática devem também mostrar aspectos de democracia. [...] enfatiza que a matemática como tal não é somente um assunto a ser ensinado e aprendido (não importa se os processos de aprendizagem são organizados de acordo com uma abordagem construtivista ou socio-cultural). A Matemática em si é um tópico sobre o qual é preciso refletir. (^{SKOVSMOSE, 2000}, p. 2)

Nota-se a ênfase no aspecto sócio-cultural da Matemática, pois de acordo com ^{Barbosa (2004}, p. 2), esse argumento “[...] está diretamente conectado com o interesse de formar sujeitos para atuar ativamente na sociedade e, em particular, capazes de analisar a forma como a matemática é usada nos debates sociais”. Nessa perspectiva, o interesse aqui é, conforme ^{Barbosa (2003}, p.7), “envolver os alunos na reflexão sobre a presença da matemática na sociedade, a organização e condução das atividades”.

Portanto, quanto às implicações para a aprendizagem significativa de forma crítica dos conteúdos matemáticos, é acertada a afirmação de ^{Barbosa (2001}, p.22): “Mais do que informar matematicamente às pessoas, é preciso educar criticamente através da matemática. Essa dimensão ultrapassa os limites intrínsecos da matemática e volta-se para a preocupação do ser-sujeito pela matemática”.

Descrição geral dos modelos exponenciais estudados

Percebe-se, no decorrer da História, que o desenvolvimento do conhecimento humano quase sempre passou pela necessidade de se encontrar resposta para um problema real. Na Matemática essa percepção é notória. A maioria do ferramental matemático foi desenvolvido com o propósito de resolver e generalizar problemas oriundos de situações reais, de tal forma que modelos simbólicos pudessem expressar e resolver tais problemas, auxiliando na tomada de decisões adequadas.

O objetivo fundamental do “uso” da matemática é de fato extrair a parte essencial da situação-problema e formalizá-la em um contexto abstrato onde o pensamento possa ser absorvido com uma extraordinária economia de linguagem. Desta forma, a matemática pode ser vista como um instrumento intelectual capaz de sintetizar ideias concebidas em situações empíricas que estão quase sempre camufladas num emaranhado de variáveis de menor importância (^{BASSANEZZI, 2002}, p. 18).

Diversos fenômenos naturais e sociais apresentam problemas e situações-problema que podem ser traduzidos por meio de modelos, cuja representação matemática são funções exponenciais.

Nesse contexto, devido a relação da matemática com outras ciências, o ensino e a aprendizagem ganham significativo sentido como parte relevante do currículo, tanto do Ensino Médio como nos cursos de graduação em disciplinas como Pré-Cálculo.

Além do mais, essa relação oportuniza ao estudante perceber a importância do conteúdo trabalhado de modo que a contextualização se torna uma importante ferramenta no processo de ensino e aprendizagem para resolver problemas reais.

Diante dessa perspectiva, serão consideradas a seguir algumas características de três tipos de funções exponenciais, a saber, o modelo típico de crescimento (ilimitado) e decrescimento (ou decaimento) exponencial; o modelo de crescimento limitado (ou inibido); e, o modelo de crescimento logístico.

Em primeiro lugar, considera-se a função f:ℝ→ℝ+ , definida pela expressão y=fx=Aerx , chamada função exponencial, onde r e A são chamados parâmetros. Se r é um número real positivo tem-se um crescimento exponencial, e se r é um número real negativo tem-se um decrescimento ou decaimento exponencial. O número real r é a taxa de crescimento (se r>0 ) ou de decaimento (se r<0 ). Também A é uma constante positiva e representa o valor inicial da função y=fx , isto é, y0=f0=A . Ver Figura 11(b).

Fonte: Elaborado pelos autores, adaptado de ^{Bassanezi (2015)}.

Figura 1 Modelos Exponenciais 

De modo semelhante, a função f:ℝ→ℝ+ , definida pela lei y=fx=B−Ae−kx é chamada função de crescimento exponencial limitado ou inibido, onde A , B e k são os parâmetros. O número real positivo k é a taxa de crescimento, mas é decrescente como função da variável de estado. Os parâmetros A e B são números reais positivas, sendo B−A>0 o valor inicial da função y=fx , isto é, y0=f0=B−A , e a constante B representa o valor limitante ou inibidor da função. Ver Figura 1(c).

Por fim, a função f:ℝ→ℝ+ definida pela expressão y=fx=A1+Be−kx é chamada função de crescimento exponencial logístico, onde A , B e k são os parâmetros. O número real positivo k é a taxa de crescimento, que cresce ou decresce como função da variável de estado, conforme passa pelo ponto de inflexão¹⁷. Os parâmetros A e B são números reais positivos, sendo A1+B>0 o valor inicial da função fx , isto é, y0=f0=A1+B , a constante A representa o valor limitante ou inibidor da função, e B=Ay0−1 . Ver Figura 1(d)

De acordo com ^{Bassanezi (2015}, p. 89), os gráficos representados pelas figuras acima e que traduzem as funções exponenciais em destaque “servem para modelar fenômenos em que as taxas de crescimento (ou decrescimento) das variáveis de estado positivas são funções das próprias variáveis”, de modo que se as taxas de variação são constantes (positiva ou negativa), as curvas para esse caso são os das Figuras 11(b), se porém, “a taxa de crescimento é decrescente como função da variável de estado”, as curvas para esses casos são os das Figuras 11(d).

Uma experiência na utilização dos modelos em sala de aula

A descrição a seguir se refere a uma atividade desenvolvida na disciplina Pré-Cálculo, no estudo de funções elementares. A atividade consistiu na construção/aplicação e análise de modelos exponenciais do tipo descrito anteriormente. O grupo participante da atividade foi composto por 23 estudantes de vários cursos, advindos das Ciências Biológicas, Química, Engenharia Florestal, Farmácia e Ciências Econômicas. A disciplina ministrada foi em uma universidade pública do Estado do Pará.

Na primeira aula, sobre o estudo específico de funções exponenciais, foram apresentadas cinco situações-problema, distribuídas para cada dupla uma cópia digitada das questões, solicitando que eles lessem e respondessem até o final da aula, conforme sua compreensão.

A primeira situação-problema foi sobre o Crescimento de um investimento aplicado a juros compostos com taxa fixa, descrita da seguinte forma: Um investimento de R$ 1000,00 é aplicado a uma taxa de juros fixos de 13,5% anualmente. Descreva os valores acumulados em cada ano (nos próximos 6 anos) e represente graficamente esses dados num sistema de coordenadas cartesianas.

A segunda situação-problema foi sobre a Concentração de um medicamento no organismo, descrito como segue: O antibiótico GENTAMICINA é administrado em um paciente de forma injetável. A concentração C (em ml/L) desse medicamento no organismo do paciente, em função do tempo t (em horas), está representado na Tabela 2. Represente os pontos t,C num sistema cartesiano de coordenadas.

O terceiro problema proposto foi sobre a Eficiência no Trabalho, descrito como segue: Segundo os especialistas da área de Administração e da Psicologia, a rapidez com a qual um funcionário dos correios, por exemplo, separa a correspondência é função da experiência. O chefe administrativo de uma agência dos correios, por 12 meses observando o trabalho dos funcionários, registrou na tabela x uma estimativa da eficiência média deles quanto ao número de cartas que conseguem separar por hora, conforme sua experiência. Com base nessa tabela, represente os pontos t,n em um sistema de coordenadas cartesianas, onde t é o tempo (em meses) de experiência no trabalho e n é o número de cartas que consegue separar por hora.

A quarta situação-problema foi sobre Crescimento Bacteriano, descrito da seguinte forma: A bactéria E. coli é comumente encontrada no intestino humano. Sob condições ideais, uma célula de E. coli dobra a cada 20 minutos, aproximadamente. Sabendo que existe uma relação entre o número inicial de células e o número de células após um período de tempo de crescimento, descreva esse crescimento durante 4 horas e represente os dados, t,n , num sistema de coordenadas.

Por fim, o quinto problema proposto foi sobre o Crescimento da mosca das frutas, no qual também foi apresentado dados empíricos, conforme a descrição: Uma população p de moscas-das-frutas (Drosophila) cresceu durante um experimento que durou 48 dias. O número de moscas foi contado a intervalos regulares e os valores obtidos foram representados na tabela abaixo conforme o tempo de contagem. Represente esses pontos num sistema cartesiano de coordenadas.

Ao final da primeira aula, quase todas as duplas haviam concluído a tarefa, e como a aula seguinte seria uma semana depois, foi proposto para essa aula, que fizessem a mesma atividade utilizando agora uma planilha, como o Excel, e tentassem descobrir qual o modelo matemático apropriado para cada situação. Além disso, para o problema quatro, foi solicitado que pesquisassem sobre as fases do crescimento bacteriano.

Para a apresentação dos resultados na aula seguinte, a turma foi dividida em 5 grupos¹⁸, ficando cada grupo responsável por um dos problemas, de acordo com a afinidade temática.

Na segunda aula, cada grupo apresentou o seu problema, exibindo seus respectivos gráficos. Os grupos G1 e G4 não tiveram dificuldades em reconhecer e expressar de forma explícita a função exponencial como sendo o modelo matemático que representava os dados dos seus problemas. O grupo G3 teve dificuldade para exibir a forma explícita do modelo, mas conseguiu pesquisar e reconhecer que era um tipo de função exponencial. Os grupos G2 e G5, porém, com um pouco mais de dificuldades, conseguiram apenas representar os dados na planilha do Excel na forma de um gráfico de dispersão.

Em seguida, cada grupo relatou a experiência que teve para desenvolver o trabalho e como se deu a busca pelas informações, principalmente as dificuldades quanto ao uso da planilha do Excel. Destacaram a importância que a Matemática pode ter nas outras áreas do conhecimento, além da necessidade de se conhecer mais sobre as ferramentas da informática, como o Excel.

Ao final dessa segunda aula, o professor da disciplina comentou de forma geral sobre o tipo de função que estavam trabalhando e como esses modelos matemáticos aparecem de forma natural em várias situações e podem ser utilizadas para resolver problemas práticos das mais diversas áreas do conhecimento. Finalizou, lembrando que na aula seguinte iriam detalhar um pouco mais o tema e o uso do Excel (e do GeoGebra) no contexto dos problemas propostos, estudando os tipos de modelos matemáticos exponenciais representados por estes.

Na terceira aula foram retomados os problemas inicialmente propostos, identificando-os e formalizando os três tipos de modelos que emergiram a partir dos dados. O professor teve a oportunidade de fazer uma exposição dialogada mais formal sobre esses modelos ao definir, apresentar outros exemplos de aplicação e propor a análise destes. A exposição contou também com um breve comentário sobre o uso do Excel (e do GeoGebra) para representar graficamente os dados de cada problema, e principalmente para evidenciar explicitamente os modelos por meio de suas respectivas equações. Percebeu-se que os estudantes, a partir desse momento, mostraram-se ainda mais interessados em realizar outras atividades semelhantes.

Para finalizar a terceira aula, foi proposta para cada grupo uma atividade composta por três novos problemas (diferentes para cada grupo), que continham dados empíricos os quais deveriam ser representados na planilha do Excel ou GeoGebra, construído o gráfico e exibido o modelo matemático y=fx . Além desses problemas, foi proposto que pesquisassem dados empíricos de alguma situação-problema que representassem um modelo exponencial assintótico ou um modelo logístico. O trabalho de cada grupo deveria ser compartilhado com a turma na aula seguinte, sendo apresentado na forma de slides.

A quarta aula, portanto, foi dedicada exclusivamente para as apresentações. Todos os grupos demonstraram segurança e compreensão no processo de representação dos dados, construção dos gráficos e determinação dos modelos nos problemas propostos a priori. Com exceção de um grupo (G2), todos os outros conseguiram encontrar dados relativos a algum problema ou situação-problema que representavam um modelo exponencial assintótico (G5) ou um modelo logístico (G1, G3 e G4).

A aprendizagem significativa na atividade com modelos matemáticos

Ao concluir a quarta aula, havia a sensação de que o tema trabalhado daquela forma tinha sido considerado significativo pelos estudantes, pois além dos seus depoimentos percebeu-se a apropriação dos conceitos, da linguagem e até mesmo das ferramentas da informática (Excel e GeoGebra). Isso foi percebido no depoimento dado pelos estudantes¹⁹ ao final da aula.

O estudante E3 destaca: estudei esse tipo de função no 2^o grau, mas não sabia que podia ser usada em outras áreas. Acho que se o meu professor do 2^o grau tivesse me ensinado desse jeito eu teria gostado mais de Matemática. Outro estudante, E20, também enfatizou a aplicabilidade desse tipo de função ao declarar que a Matemática, a gente pensa que é só um monte de fórmulas, mas não, ela tem também aplicações em outros campos. Nota-se que os conhecimentos prévios trazidos do Ensino Médio, além de ampliados, são vistos de modo significativo, pois agora conseguem perceber não só como algo estático, seco, sem sentido, mas como algo dinâmico e aplicável.

Com relação às ferramentas da informática, o estudante E12, relatando sobre a experiência de trabalhar com a planilha Excel, afirmou: eu não sabia que o Excel poderia ser usado nos problemas de Matemática.

Outros disseram que nunca haviam nem usado uma planilha, como se percebeu no relato de outros estudantes: nunca gostei muito de computador. Usava às vezes na escola só o Word pra escrever algum trabalho, mas esse aí [Excel] já tinha ouvido falar, mas nunca usei, destacou o estudante E17, e completou E9, eu também só sabia de ouvir falar, mas com a ajuda do meu colega, eu consegui aprender como usar.

Observa-se que, não só conteúdos matemáticos se tornam significativos para os estudantes, mas também as ferramentas da informática. Para muitos deles, ferramentas como Word, Excel, PowerPoint, GeoGebra, e outras não faziam parte, na prática, da sua realidade. Com o desenvolvimento da atividade, essas ferramentas passaram a ser significativas para esses estudantes, de acordo com a experiência que cada um teve.

De um modo geral, todos os estudantes que participaram da atividade sinalizaram a importância da Matemática para as várias áreas do conhecimento, destacando que o uso de dados empíricos para a construção e análise de modelos são motivadores para o desenvolvimento de um trabalho investigativo. Além disso, é importante também ter à disposição para o desenvolvimento desse tipo de trabalho ferramentas da informática que auxiliem no tratamento dos dados, o que ajuda na compreensão dos fenômenos em estudo, e portanto, facilita a aprendizagem de modo significativa.

Considerações finais

Ao propor a atividade com as funções exponenciais, foi possível perceber que o trabalho com modelos matemáticos pode se tornar significativo para os estudantes e ser enriquecido quando se utiliza dados empíricos de situações práticas da realidade ou do contexto acadêmico/profissional dos estudantes, de modo que esses dados possibilitam o desenvolvimento de atividades experimentais. Para isso, fazer uso de ferramentas “simples” e “comuns” da informática, como a planilha do Excel ou o GeoGebra, é uma prática que se torna cada vez mais apropriada num processo onde a aprendizagem significativa é o alvo principal.

Assim, a construção e análise de modelos matemáticos que emergem nesse processo apresentam-se como elementos motivadores para introdução e aprofundamento no estudo de conteúdos que fazem parte do currículo de uma disciplina, como a que foi usada para aplicar a atividade com modelos (a disciplina Pré-Cálculo).

Portanto, a utilização de dados empíricos referentes a algum problema real, processados num ambiente informatizado, como o Excel ou o GeoGebra, possibilitam que conteúdos matemáticos estudados desde o Ensino Básico até o Ensino Superior apresentem-se mais úteis nas aplicações e análises de situações-problema, permitindo que os estudantes possam dar mais significado ao que estudam, ao percebê-los em diversos contextos da sua realidade.