Introdução

Proliferaram-se nas quatro últimas décadas as investigações visando contribuir para a melhoria do processo de ensino e aprendizagem em Matemática e, nesse sentido, em diferentes contextos, os teóricos têm pesquisado o assunto e defendido os modelos de ensino a partir das concepções psicológicas, sociopolíticas e pedagógicas que adotam.

Neste estudo, de natureza teórica, tratamos especificamente de possibilidades de ensino e aprendizagem em Matemática nos anos iniciais do ensino fundamental na vertente da teoria da educação desenvolvimental. Para isso, definimos como objetivo discutir os pressupostos da teoria da educação desenvolvimental, a qual concebemos como um movimento dialético entre o ensinar e o aprender, e como construir conhecimentos matemáticos nos anos iniciais do ensino fundamental por meio da atividade de estudo. Ancoramo-nos em referenciais teóricos da teoria histórico-cultural e da teoria da educação desenvolvimental construídos a partir dos estudos de Vigotskii (2000, 2001), Leontiev (2001, 2004), Davidov (1982, 1987, 1988), Davidov e Márkova (1987) e Repkin (2014).

Tem sido bastante difundida no contexto da educação matemática a ideia de que a didática dessa ciência se ocupa de “como ensinar” uma vez que se tenha definido “o que ensinar”. Subjacente a este modo de pensar, a ideia de que os conteúdos matemáticos existem por si, são únicos, havendo todavia diversas formas para a sua abordagem. Sob esse modo de compreender o problema didático, a Matemática parece deixar de se constituir como objeto de problematização, ainda que se considere que o sejam as formas pelas quais se consolida o seu desenvolvimento como ciência. Essa forma de se conceber o ensino e aprendizagem da Matemática colocam-na como um fato natural, de existência autônoma, o que se contrapõe à visão dessa ciência como um constructo teórico, social e cultural.

Na formulação do artigo, primeiramente apresentamos posições teóricas acerca da educação desenvolvimental, em seguida, damos destaque a como os conhecimentos matemáticos são construídos a partir da atividade de estudo e argumentamos sobre o potencial dessa teoria para a construção sólida dos conhecimentos matemáticos nos primeiros anos escolares.

Considerações sobre os pressupostos teóricos da educação desenvolvimental

Um grupo de estudiosos russos e ucranianos, baseados na teoria histórico-cultural preconizada por Vygotski (1896-1934) e na teoria da atividade de Leontiev (1903-1979) logrou desenvolver um tipo de educação que fosse capaz de promover a produção e construção do pensamento teórico nos educandos. O grupo russo foi liderado primeiramene por Elkonin e depois Davidov. Já o grupo ucraniano era liderado por Repkin (PUENTES; AMORIM; CARDOSO, 2019).

Os estudos que deram origem à teoria da educação desenvolvimental partem da crítica feita à educação tradicional que, segundo esses estudiosos, estava instaurada no sistema da educação russa (antiga União soviética). A educação tradicional é entendida por esses estudiosos como um sistema de educação que basicamente produz apenas a formação do pensamento empírico nos educandos não promovendo a formação do pensamento teórico. Davidov (1987) assevera que a educação russa, nessa época, tinha como objetivo a formação em massa da população e a educação primária era empirista-utilitária, o que massificava a formação do pensamento empírico em detrimento da formação do pensamento teórico. Cabe salientar que conforme escrito por Libâneo (2008, p. 61) o pensamento teórico é “uma ação mental peculiar pela qual se efetua uma reflexão sobre um objeto que, ao mesmo tempo, é um meio de reconstrução mental desse objeto no pensamento”, ou seja, o pensar teórico “é desenvolver processos mentais pelos quais chegamos aos conceitos e os transformamos em ferramentas para fazer generalizações conceituais e aplicá-las a problemas específicos” (LIBÂNEO, 2008, p. 61).

Na perspectiva do conceito de educação desenvolvimental é preciso entender que o conhecimento é produzido de forma coletiva e que a principal função da educação é propiciar ao educando a apropriação do conhecimento histórico e culturalmente construído pela humanidade. Assim, nas palavras de Vigotskii (2001), a boa educação é aquela que precede o desenvolvimento, e, para o sucesso de tal fim, o professor deve atuar na zona de desenvolvimento proximal do sujeito, ou seja, deve atuar nas funções que ainda não estão totalmente formadas no sujeito, mas que já encontram-se em estado embrionário. Segundo o autor, atuar nessa zona é fundamental para “nos delinear o futuro imediato da criança e seu estado dinâmico de desenvolvimento, propiciando o acesso não somente ao que já foi atingido através do desenvolvimento, como também àquilo que está em processo de maturação” (VYGOTSKI, 2007, p 58).

Segundo Davidov (1987), para poder alcançar uma educação que promovesse o desenvolvimento era preciso reorganizar o sistema de ensino construindo novos princípios porque “[...] os programas da escola tradicional estão elaborados em correspondência com as exigências lógico-formais sobre o pensamento humano” (DAVIDOV, 1999, p. 5). Ainda, segundo o autor, com a análise do material desses programas é possível identificar que em seu desenvolvimento o pensamento do educando é levado à análise das propriedades externas do objeto por meio da observação de elementos de igualdade e semelhanças em relação a outros objetos. Deste modo “[...] o «conhecimento geral» é assimilado pelos alunos como resultado da comparação dos fenômenos particulares. O pensamento dos alunos vai do «particular para o geral»” (DAVIDOV, 1999, p. 5, grifos do autor).

Assim, essa educação forma no educando noções e conceitos empíricos. O pensamento empírico é importante para o ser humano para orientar-se em sua vida cotidiana e resolver situações corriqueiras, mas esse tipo de pensamento não é suficiente para construir o conhecimento teórico (Davidov, 1988). A construção ou produção do conhecimento teórico passa pelo conhecimento empírico e avança para além dele.

Por isso Davidov propõe uma nova organização do ensino que pode ser feita seguindo os seguintes princípios:

1) todos os conceitos que compõem a disciplina escolar dada ou seus principais capítulos devem ser assimilados pelas crianças através do exame das condições de origem, graças aos quais esses conceitos se tornam indispensáveis [...]; 2) a assimilação dos conhecimentos de caráter geral e abstrato precede a familiarização com conhecimentos mais específicos e concretos; estes últimos devem ser separados do abstrato como sua única base [...]; 3) no estudo das fontes de objetais-materiais de um ou de outros conceitos os alunos devem, sobretudo, descobrir a conexão geneticamente inicial, geral, que determina o conteúdo e a estrutura do campo de conceitos dados [...]; 4) é necessário reproduzir essa conexão em modelos simbólicos objetivos, gráficos ou especiais que permitam estudar suas propriedades de forma pura [...]; 5) em especial, há que se formar nos alunos ações objetivas de tal natureza que permitam que possam compreender o material do estudo e reproduzir nos modelos a conexão essencial do objeto e assim estudar suas propriedades (por exemplo, para compreender a conexão que está na base dos conceitos de números inteiros, números fracionais e reais é necessário formar nos alunos uma ação especial para determinar a característica da divisibilidade e multiplicidade das magnitudes); 6) os alunos devem passar gradualmente e no devido tempo das ações objetais a sua realização no plano mental (DAVIDOV, 1987, p. 153-154, tradução nossa).

Para o autor, seguindo os princípios supracitados, é possível proporcionar ao educando a apropriação do conhecimento teórico. Percebe-se que a base desses princípios se constitui na compreensão dialética do pensamento, ou seja, na lógica dialética na qual o pensamento movimenta-se do geral para o particular. A construção do conhecimento parte do observável e da análise das propriedades externas do objeto e se movimenta passando pela abstração, generalização e análise da essência do objeto voltando em movimento ao concreto agora pensado (KOPNIN, 1978).

Davidov (1999) dá um exemplo do programa de ensino que defende usando a construção do conceito de número pela criança. Nele o autor descreve:

Preliminarmente as crianças são apresentadas ao conceito de grandeza (esta é determinada por três relações de diferenças: а = b, a < b, a > b). Baseando-se neste conceito, as crianças podem efetuar a igualação direta das grandezas físicas. Por exemplo, utilizando uma amostra de qualquer pedaço de madeira, as crianças podem fazer com uma grande tábua muitos desses pedaços pequenos. Porém há casos em que a igualação das grandezas só pode ser feita por meios indiretos. Por exemplo, em um balde de uma certa conformação é preciso despejar tanta água quanto se tem em um balde de outra conformação. Para resolver este problema, a pessoa deve saber medir grandezas com o auxílio do número. Conforme nosso programa, o professor passa para os alunos uma tarefa que exija medição. As crianças adivinham que para executar essa tarefa é preciso achar um meio especial (por exemplo, uma pequena caneca, se for para medir a água), e também dominar regras especiais de sua utilização (por exemplo, a regra de como encher essa caneca d'água). As crianças com a ajuda do professor encontram o meio de medição, aprendem as regras de sua utilização e descobrem que o próprio ato de medição é uma busca de uma relação de multiplicidade das grandezas, que implica neste ou naquele número. Os alunos podem imediatamente escrever na forma verbal a fórmula geral dessa relação. А b = N (А — é a grandeza medida; b — é o meio de medição; N — é a relação de multiplicidade, fixada por um número como expressão do resultado da ação da medição). Tendo assimilado o significado geral dessa fórmula, as crianças podem então efetuar quaisquer tipos de medições particulares, podem obter números concretos, baseando-se nos quais podem realizar uma igualação indireta (por exemplo, resolver um problema de igualação da água em baldes de diferente conformação) (DAVIDOV, 1999, p. 5-6, grifos do autor).

A citação é longa, mas esclarecedora. Fica evidente que nesse processo primeiro o educando parte do sensorial-visual, faz a generalização e abstração por meio de diferentes modelos, com a generalização analisa suas singularidades e particularidades, compreende a essência do objeto e constrói o conceito. Davidov (1988, p. 133), preceitua que “o pensamento teórico idealiza os aspectos experimentais da produção dando-lhes, inicialmente, a forma de experimento cognitivo objetal-prático e, depois, de experimento mental, realizado em forma de conceito e por meio deste”. Assim, por meio desse processo chega-se ao pensamento teórico.

Sem embargo, “o pensamento teórico não surge e nem se desenvolve na vida cotidiana das pessoas, ele se desenvolve somente em uma tal instrução, cujos programas se baseiam na compreensão dialética do pensamento” (DAVIDOV, 1999, p. 6). Desta forma, para os teóricos da educação desenvolvimental o principal papel da escola é proporcionar ao educando a construção do pensamento teórico apropriando-se dos conhecimentos historicamente produzidos pela humanidade.

Nesse sentido, o autor estabelece que o conhecimento humano se constitui em unidade com suas ações mentais de abstração e generalização, ou seja, o conhecimento não surge à margem da atividade cognitiva do sujeito e não se consolidam a priori.

A atividade de estudo: implicações pedagógicas para a constituição de sujeitos de aprendizagem na educação matemática

Pensar a constituição efetiva de sujeitos de aprendizagem em Matemática tem como pressuposto inicial que o conhecimento didático-pedagógico produzido nesta área do conhecimento permite sustentar que o oferecimento ao aluno de vivências e experiências desafiadoras contribui para a construção de um autoconceito um tanto mais valorizado de si mesmo. Criar esse ambiente adequado de aprendizagem impõe propor situações de estudo as quais, embora possam ser complexas, não são impossíveis de realização, se o sujeito é motivado a interagir com os seus pares e com o objeto de conhecimento, a poder questionar para avançar, a se permitir o erro e superar os obstáculos de aprendizagem, de quaisquer naturezas.

No entanto, como sugere Snyders (1988), a escola, em sua vertente considerada tradicional, adia a felicidade. Raramente o aluno estuda para ser feliz no momento da aprendizagem; ele estuda para ser feliz amanhã. Os alunos são instados apenas esporadicamente a se posicionarem na escola relativamente ao que já sabem, aos saberes que se constituem da experiência do viver, cultivados pela curiosidade, pelos desejos e necessidades; pela cultura primeira, como define o autor.

Embora a cultura primeira traga alguma satisfação, ela não supre as necessidades de desenvolvimento intelectual no atual contexto de sociedade tecnológica, em transformação, impondo-se que os saberes da experiência inicial sejam incorporados ou superados por conceitos novos a cada dia, formulações as quais consolidam o que o autor denomina de cultura elaborada. Na sala de aula na qual há o prazer de aprender vislumbra-se o porvir, o desenvolvimento da personalidade, da psique e a constituição verdadeira de sujeitos de aprendizagem e de ensino. Em comunhão, aprendendo não para nos adaptarmos, mas para intervirmos na realidade, recriando-a, como diria Freire (2009):

A nossa capacidade de aprender, de que decorre a de ensinar, sugere ou, mais do que isso, implica a nossa habilidade de apreender a substantividade do objeto aprendido. A memorização mecânica do perfil do objeto não é aprendizado verdadeiro do objeto ou do conteúdo. Neste caso, o aprendiz funciona muito mais como paciente da transferência do objeto ou do conteúdo do que como sujeito crítico, epistemologicamente curioso, que constrói o conhecimento do objeto ou participa de sua construção (FREIRE, 2009, p. 69, destaques do autor).

Assim, ensinar e aprender Matemática exige muito mais uma pedagogia da autonomia do que uma pedagogia das competências. Observe-se, também, que apesar da proeminência e a confluência de posições teóricas sobre o trabalho educativo, de diferentes autores, situados em diferentes contextos históricos, as condutas pedagógicas pouco se alteram na escola básica. Destaque-se ainda, porque são muito interessantes nas aulas de Matemática, quando ocorrem, os questionamentos dos alunos sobre a origem, a utilidade e os motivos para apropriação dos conceitos matemáticos. As respostas aos alunos giram em torno da utilidade do conhecimento matemático na vida cotidiana, da sua dimensão prático-utilitária, para uso no trabalho, para realização de concursos e, por vezes, para continuidade dos estudos e realização de exames vestibulares. Decididamente, aprender Matemática para ser feliz amanhã.

A despeito da importância da aprendizagem matemática para o futuro, o fato é que essas justificativas não satisfazem aos alunos haja vista que a maioria não vai prestar exames vestibulares, não pensa em trabalho ainda e os que pensam têm consciência da dificuldade de ingresso em um mercado de trabalho com mais de treze milhões de desempregados. Essas justificativas se mostram para eles, muito distantes. Os motivos são desconectados das necessidades, no limite das concepções da psicologia histórico-cultural. Mas as justificativas dos professores, geralmente aceitas pelos estudantes por conta da autoridade docente, nem sempre convencem e revelam indícios de inadequação do método de ensino. Se esse não é o único determinante para os problemas pedagógicos, certamente é um dos mais relevantes.

Urge, para além desses motivos de aprendizagem, situar os alunos em contexto de atividade de estudo em Matemática pela necessidade e o prazer da descoberta do conceito matemático, pelo jogo mental que proporciona aos que dela se apropriam, pelo favorecimento que proporciona ao desenvolvimento intelectual e pelo alcance de sua perspectiva de aplicação para encaminhamento da solução de problemas imediatos, mas, também, no respaldo ao incomensurável desenvolvimento tecnológico observado, modificando os modos de ser e estar no mundo, pelas transformações decorrentes da microeletrônica e das tecnologias digitais de informação e comunicação.

No modelo pedagógico ainda predominante, observa-se um processo de transmissão do conhecimento matemático no qual os docentes, de forma geral, exploram procedimentos algorítmicos, nem sempre bem compreendidos pelos discentes, sob a forma de uma definição previamente apresentada, exercícios-modelos e problemas de aplicação. Prevalece no processo a informação em detrimento da efetividade da formação.

Preocupado com a apropriação significativa de conceitos, Davidov (1988) aponta para o equívoco pedagógico de se considerar os alunos dos anos iniciais de escolarização como capazes de adquirir apenas um nível de formação de conceitos fundamentais ou elementares, resultantes de experiências vivenciadas de forma similar às atividades desenvolvidas anteriormente ao ingresso na escola, no contexto da atividade do jogo e da ludicidade e no cotidiano de práticas desenvolvidas. E destaca como principal característica dos programas de ensino tradicionais o entendimento segundo o qual o pensamento dos alunos evolui mediante observação de fenômenos particulares, distinguindo neles aspectos gerais ou semelhantes, ou seja, o pensamento dos alunos evolui do particular para o geral.

Uma perspectiva de educação desenvolvimental em Matemática considera a necessidade de formulação de um vocabulário fundamental da Matemática a partir de observação, comparação e estabelecimento de regularidades em situações matemáticas envolvendo noções de número, conceitos geométricos ou medidas e grandezas situadas em contexto de articulações entre o vivido, o percebido e o concebido, isto é, o movimento se estabelece do geral e amplo para o particular e específico.

Davidov (2019) procede a uma análise exaustiva relativamente aos problemas de pesquisa sobre a atividade de estudo. Começa por definir a aprendizagem funcional como instância de esforço pessoal do sujeito para assimilar determinado conteúdo, marcada sobejamente pela reprodução de modelos, mesmo quando pré-determinados pelos docentes, e a aprendizagem desenvolvimental como atividade que carece da participação dos professores e pedagogos para a organização, coordenação e controle desse processo de aprendizagem funcional dos indivíduos. Para ele, a aprendizagem desenvolvimental pode ser compreendida como uma correlação entre o estudo e atividade pedagógica, mas destaca enfaticamente que a atividade de estudo dos alunos se revela mais ativa e significativa quando há um motivo expresso, um sistema de ação e o controle dessa atividade, avançando de tarefas reprodutivas para tarefas criativas. Por isso, a necessidade de se explorar pedagogicamente

(...) os vínculos específicos das ações de estudo individuais com os vários componentes do pensamento teórico; a conexão de tais componentes com as peculiaridades do conhecimento teórico que as crianças absorvem durante a resolução de tarefas de estudo. Contudo, é necessário investigar as conexões desses componentes com as peculiaridades do conhecimento teórico assimilado por meio da resolução de tarefas de estudo; bem como compreender os mecanismos psicológicos da influência real da Atividade de Estudo no desenvolvimento dos processos cognitivos dos alunos (DAVIDOV, 2019, p. 284).

Retomemos como referência a noção de número. Em geral, ela é abordada na escola apenas como quantidade de elementos de um conjunto de grandezas discretas: a expressão de uma coleção de figurinhas; uma quantidade de dinheiro, sem referência, de início, à possibilidade de fracionamento de sua unidade, de seu inteiro; ou, de um agrupamento de frutas. Prevalece a preocupação com a representação simbólica dessas quantidades, em detrimento dos sentidos de aprendizagem de significados do número.

Pouco aparecem, na escolarização matemática inicial, situações didáticas envolvendo as idades das crianças; as suas datas de nascimento; as suas massas corporais; as suas alturas; as localizações das suas residências; os seus telefones; ou, os números dos documentos de identificação, RG ou CPF, de seus pais ou deles próprios. Imaginem que nessa idade elas têm como compreender o significado de R$ 2,38 ou que o colega meça 1,15 m, é dito de imediato na escola quando isso é discutido. E se esquece de que apesar de não reconhecerem, possivelmente, a representação simbólica da quantidade, sabem que esse valor em dinheiro é pouco maior que uma nota que não permite comprar um bombom de boa qualidade. Ou que a altura do seu colega é pouco maior que o metro sanfonado, em bambu, que seu pai usa para trabalhar na construção civil.

Tais considerações, em seu conjunto, indicam que o número não é apenas expressão de quantidade (quantos?), mas pode envolver também noção de ordem, ou seja, o lugar ocupado em uma sequência ou a localização de um apartamento em um prédio (qual?) ou, ainda, um código como o número do telefone ou a senha do banco. De igual modo, a expressão da quantidade de determinadas grandezas exige o seu fracionamento.

A propósito, durante uma ação de intervenção na realidade escolar, em função de uma brincadeira das crianças do 2º ano ao somar suas idades, agrupando e trocando notas de dinheiro simbólico em papel e moedas de um real, solicitei a elas que somassem a minha idade à de outra professora, parceira no projeto. De imediato, um aluno saiu com essa: “Puxa, vai dar uma pessoa mais velha que o meu avô!!!”.

Indaguei quantos anos tinha o avô, acreditando na mera manifestação de um jargão popular, e ele respondeu: 80 anos. Enfatizei que fizera uma estimativa muito boa, que a soma precisa das idades era 82. Ele respondeu: “É que neste ano, a idade do meu avô é igual à soma da idade de minha mãe que tem 38 anos com a idade de meu pai, de 42 anos. São quatro amarelinhas, juntas”.

As amarelinhas eram as notas de 20 reais em dinheiro simbólico, usadas para resolver problemas do tipo: “Quantas notas de 20 reais são necessárias para formar 100 reais?” “Quantas notas de 20 reais cabem em 75 reais?” “Sobra dinheiro? Qual a forma de compor essa quantia usando o menor número possível de notas?”. O aluno construíra formulações desta natureza porque envolviam situações de aprendizagem significativas para ele; motivos e necessidades de aprendizagem eram articulados. Provavelmente tenha internalizado que 40 são duas amarelinhas, as notas de 20 reais, sendo que com os 2 reais que sobraram formou outro agrupamento de 40, ou seja, duas amarelinhas.

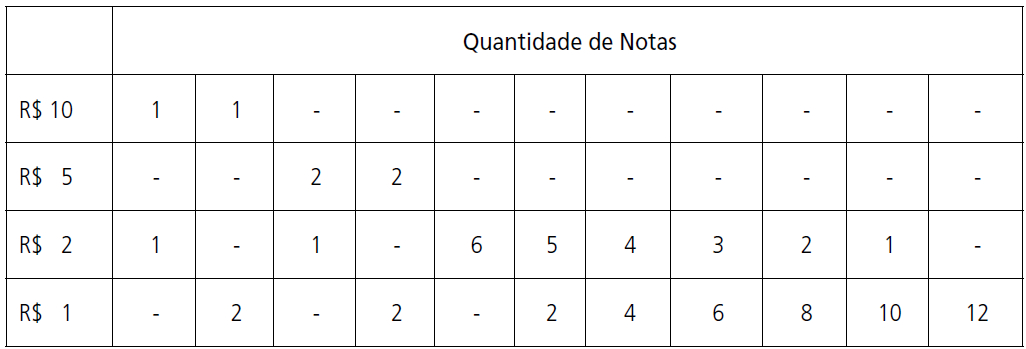
Avançando com formulações desta natureza, a resolução de problemas do tipo “enunciar diferentes maneiras de formar 12 reais usando moedas de 1 real e notas de 2, 5 e 10 reais” possibilitarão coordenação de ações mentais envolvendo raciocínio aditivo; de início, de forma aleatória, podendo esquecer algumas combinações, e, a posteriori, organizando essas ideias em uma tabela, em ordem decrescente (ou crescente) de notas de modo que as combinações totalizem R$ 12,00 em todas as colunas:

Fonte: Arquivo dos pesquisadores

Quadro 1 Composição com notas 

O número não é a mera expressão quantitativa de dados da realidade empírica, nomeados simbolicamente, mas uma construção teórica que, não prescindindo da abordagem de dados da realidade empírica, exige o estabelecimento de relações, o reconhecimento de regularidades existentes ou não entre elas e a tirada de conclusões. Sua constituição envolve, de fato, as operações lógicas de classificação, ordenação e inclusão hierárquica, passa pelas relações de igualdade, diferença e transitividade, mas exige, inexoravelmente, a compreensão pela criança da função social do número nos seus aspectos de quantidade, ordem e código.

Isso se deve ao primeiro princípio expresso por Davidov (1987) para a constituição do conhecimento teórico, qual seja, os conceitos devem ser assimilados pelas crianças mediante análise das condições de sua origem, as quais fazem com que esses conceitos sejam necessários. Igualmente, defende Davidov (1987, p. 153), “a assimilação dos conhecimentos de caráter geral e abstrato precede a familiarização com conhecimentos mais específicos e concretos; estes últimos devem ser separados do abstrato como sua única base”.

Por isso, não parece fazer sentido que a escolarização inicial pouco se refira a situações matemáticas envolvendo números racionais, a julgar pelo fato de as crianças já lidarem com situações-problema envolvendo esses conceitos. Uma extensão da tabela anteriormente construída poderia sistematizar questões do tipo “enunciar diferentes maneiras de pagar uma compra no valor de R$ 2,75 usando moedas de R$ 1,00; R$ 0,50 ou R$ 0,25”.

Como sugerido anteriormente, inicialmente as crianças devem recorrer à estimativa, ao cálculo mental, a esquemas de tentativa e erro, para depois serem conduzidos à organização dos dados como, por exemplo, em uma tabela na qual as combinações expressas nas colunas sempre totalizam R$ 2,75:

Fonte: Arquivo dos pesquisadores

Quadro 2 Composição com moedas 

Seja no quadro anterior, seja neste, é fundamental explorar situações que permitam às crianças perceberem algumas regularidades: quanto maior o valor das notas, menor a quantidade de notas necessárias; à medida que se aumenta a quantidade de uma das notas, necessariamente se reduz das outras, proporcionalmente aos valores envolvidos em cada troca.

Permitem ainda explorar, em momento pedagógico oportuno, o conceito de expressão numérica, geralmente apresentado às crianças destituído de significação. Por exemplo: 1,00 + 2 X 0,50 + 3 X 0,25 na quarta coluna, ou 3 X 0,50 + 5 X 0,25 na nona coluna devem resultar em R$ 2,75 em ambas as formulações.

Essas formulações aritméticas constituem, ainda, a base para a articulação pedagógica de ideias relativas ao desenvolvimento do pensamento algébrico se convencionarmos que X é o número de moedas de R$ 1,00; Y o número de moedas de R$ 0,50 e Z, o total de moedas de R$ 0,25, de forma tal que as expressões aritméticas anteriores poderiam ser representadas algebricamente como X + 2Y + 3Z = 2,75 e 3Y + 5Z = 2,75, ou ainda, que X + Y = 1,50 e 3X + 2Y = 4,00.

Ao argumento de que as crianças têm dificuldades com as combinações, vale lembrar que, na maioria dos casos, ao iniciar o ensino fundamental elas já detém algumas relações fundamentais, tais como: 0,50 + 0,50 = 1; 0,25 + 0,25= 0,50; 0.50 + 0,25 = 0,75. E, se não detém, cabe à escola dar o encaminhamento, já que lidar com essas situações é condição necessária para o alfabetismo pleno, preparando o sujeito para o exercício da cidadania, tal como se registra nos Parâmetros Curriculares Nacionais, Matemática, Anos Iniciais:

(...) fazer observações sistemáticas de aspectos quantitativos e qualitativos do ponto de vista do conhecimento e estabelecer o maior número possível de relações entre eles, utilizando para isso o conhecimento matemático (aritmético, geométrico, métrico, algébrico, estatístico, combinatório, probabilístico); selecionar, organizar e produzir informações relevantes, para interpretá-las e avaliá-las criticamente (BRASIL, 2000, p. 51).

Esta preocupação também se nota na Base Nacional Comum Curricular ao abordar a perspectiva do letramento em Matemática:

O Ensino Fundamental deve ter compromisso com o desenvolvimento do letramento matemático, definido como as competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente, de modo a favorecer o estabelecimento de conjecturas, a formulação e a resolução de problemas em uma variedade de contextos, utilizando conceitos, procedimentos, fatos e ferramentas matemáticas. É também o letramento matemático que assegura aos alunos reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo e perceber o caráter de jogo intelectual da matemática, como aspecto que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso (fruição) (BRASIL, 2018, p. 264).

Mas isso não se obtém pelo tratamento das competências e habilidades matemáticas como se isoladas fossem. Assim, é inarredável que os professores e as equipes técnicas das secretarias de educação, responsáveis pela elaboração do currículo, sem desconsiderar essas ideias, não se prendam ao discurso da dita pedagogia das competências, resvalando, seja para os exageros na busca de exploração das estruturas lógico-matemáticas (aritméticas, topológicas, algébricas, projetivas ou de ordem) tal como já se observou na ênfase exagerada na teoria dos conjuntos em passado não muito distante, seja relativizando o papel da Matemática no currículo do ensino fundamental no que se refere ao respaldo dos processos de leitura e escrita.

Pensar a educação matemática nos anos iniciais do ensino fundamental não deve abdicar da ideia de desenvolvimento nos educandos da “capacidade individual de formular, empregar e interpretar a matemática em uma variedade de contextos” (PISA, 2012), isto é, de que eles se inserem desde muito cedo em uma perspectiva de letramento matemático. Isso exige a familiarização, ao longo da escolarização fundamental, com diversas formas de organização de ideias matemáticas situadas no contexto de análises de situações da vida cotidiana, nas interfaces com outras áreas do conhecimento e da própria matemática.

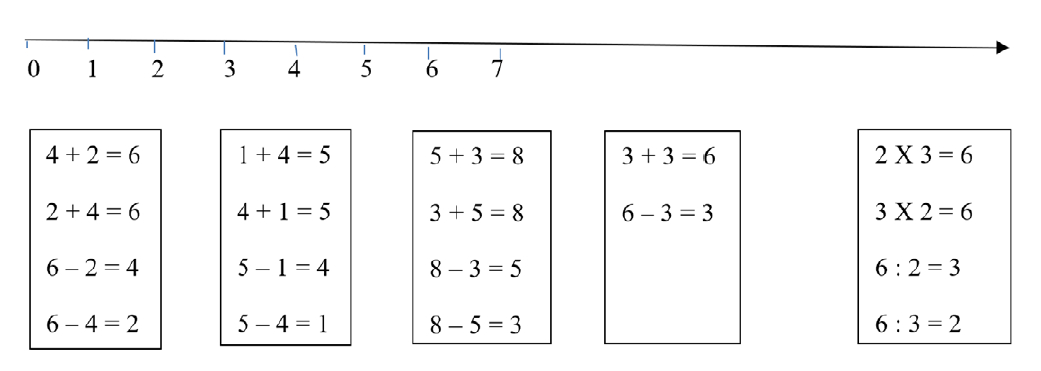
A exploração desse universo conceitual pode avançar para a abordagem de situações matemáticas envolvendo as noções de operações fundamentais, de medida e de número, articulando essas ideias e criando condições para a coordenação de ações. Por exemplo, abordando fatos fundamentais das operações elementares em uma reta numerada ou uma régua, com base nas ideias matemáticas de juntar ou reunir; tirar; repartir igualmente e medir:

Progressivamente, se o professor estabelece que um segmento X é igual a 5 e que outro segmento Y seja igual a 2 o aluno pode concluir que X + Y = 7, ou que X – Y = 3, o que pode permitir, novamente, a exploração das estruturas algébricas como mencionada no texto da BNCC, a qual causa preocupação em parte do professorado por compreendê-las, em função de lacunas na formação, como conceitos estanques e desarticulados.

Essa conduta pedagógica de explorar diferentes situações matemáticas, tanto as de natureza empírica, quanto as representações semióticas e ferramentas para resolução de problemas, encontra respaldo em diversas correntes teóricas e confluem efetivamente para uma situação de construção de uma perspectiva de educação matemática desenvolvimental.

Vergnaud (1996) avança na compreensão neopiagetiana do problema didático em debate ao enfatizar, com base na sua teoria dos campos conceituais, as estruturas aditivas e as estruturas multiplicativas. Como se sabe, o próprio autor reconhece as interfaces do seu pensamento com o legado teórico de Vygotsky, atribuindo relevância a questões como interação social, linguagem e simbolização no domínio progressivo de determinado campo conceitual por parte das crianças em situação escolar, bem como ao destacar como tarefa fundamental do docente o provimento de oportunidades para os educandos desenvolverem seus esquemas na zona de desenvolvimento proximal.

Desse modo, um campo conceitual configura-se em um amplo espectro, informal, heterogêneo e diversificado de problemas, situações, relações, conteúdos, estruturas, postulados e teoremas, enfim, operações de pensamento interligadas durante todo o processo de elaboração. Esse debate já vem de longa data, mas se mostra longe de uma solução:

A linguagem exige a escrita. Só ela poderá fixar, de modo duradouro, a impressão fugidia da palavra esquiva. Ela cria ordem, clareza e possibilidade de supervisão. Mas, se os homens conseguiram inventar relativamente cedo uma escrita capaz de reproduzir de um modo adequado a sua linguagem, seja sob a forma de figuras como os hieróglifos, seja sob a forma de caracteres como os nossos, longos, muito longos períodos haveriam de ser necessários para dominar o reino dos números, aparentemente tão bem ordenado, de modo a satisfazer suas finalidades (KARLSON, 1961, p. 13).

Desde muito cedo, antes mesmo do início da escolarização em nível fundamental, as crianças já lidam com alguma forma de representação ou registro para comunicarem aspectos numéricos, ainda que não tenham se apropriado das ideias que envolvem a noção de número. É pela necessidade de comunicação que a criança mostra a sua idade erguendo três dedos da mão, o que, em geral, aprende com um adulto.

Por isso, uma perspectiva de educação matemática desenvolvimental deve considerar dois movimentos dialeticamente articulados: relacionar observações do mundo real com representações (símbolos, esquemas, tabelas, figuras) e relacionar tais representações com princípios e conceitos matemáticos. Trata-se de estimular a comunicação, conduzindo os estudantes a se expressarem nas formas falada e escrita, lidando com representações gráficas, desenhos, esquemas, construções e aprendendo a organizar e tratar dados conforme também a defende Duval (2007, 2011).

Daí, pensar a transformação do cotidiano das aulas de Matemática em uma perspectiva de educação inclusiva, e não apenas para algumas mentes privilegiadas, implica em produzir coletivamente sentidos de aprendizagem matemática, o que, por sua vez, nos conduz a pensar na negociação de significados dessa ciência. Isso nos parece fundamental porque ao ingressar na escola os alunos trazem em sua bagagem cultural ideias e noções matemáticas que desenvolveram, ainda que forma parcial e fragmentada, as quais não podem ser desconsideradas se pretendemos que a escola seja um espaço no qual os estudantes possam aprender a produzir e desfrutar da cultura.

Produzir sentidos e negociar significados matemáticos deve ter como como pressupostos que os alunos são capazes de aprender, situando o docente e os discentes em um vínculo de intercâmbio cultural no qual todas as ideias dos sujeitos envolvidos podem ter um valor para a apropriação e veiculação do conceito matemático. A ênfase docente neste intercâmbio cultural concebe que os educandos se colocam no mundo em contexto mais amplo, para além do âmbito matemático, ato que carrega em si grande valor educativo implícito.

Considerar esse princípio significa ter na devida conta que o conhecimento humano se desenvolve na unidade com a atividade intelectual situada no contexto de abstrações, generalizações e aplicações do apreendido, vale dizer, à medida que aprende é que o sujeito se desenvolve, estabelecendo relações entre as ideias e conceitos e tirando conclusões sobre eles. Dessa forma, o conhecimento matemático não se desenvolve aprioristicamente, isto é, ele expressa o resultado do pensamento, da reflexão sobre a realidade e das ações mentais para a sua obtenção. Trata-se de uma construção mental cuja natureza é primordialmente histórica, em articulação com suas implicações lógicas, ou seja, as ideias matemáticas evoluem historicamente e a sua organização lógica decorre das relações que o sujeito consegue estabelecer com os fatos sobre os quais se debruça no fazer humano.

Em outras palavras, pela atividade de estudo, os alunos devem retratar o processo real pelo qual a humanidade desenvolveu os conceitos matemáticos, os quais resultam de retificações sucessivas, em um amplo movimento dialético e histórico de afirmação, negação e síntese. Desse modo, não parece razoável ensinar Matemática desconsiderando-se o processo histórico de sua evolução, a experiência inicial dos alunos com as ideias matemáticas e as dificuldades que eles enfrentam para a sua apropriação, as quais têm, em geral, explicações de natureza epistemológica, isto é, se referem a questões relacionadas à forma como o conhecimento matemático se constitui.

Considerar a atividade de estudo em Matemática tem, portanto, uma primeira consequência didática, implicando no fato de que a organização dos programas de ensino não deveria se constituir pela sequenciação de natureza meramente lógica, mas por uma organização histórico-lógica. Isso significa que o desenvolvimento humano, o desenvolvimento científico e a cultura se articulam, ocorrendo uma integração entre a filogênese, a evolução da espécie; a ontogênese, a evolução do sujeito histórico; e a cultura na qual essas relações se constituem. E coloca em xeque a ação didática na qual a Matemática é apresentada como coisa pronta, definitiva, bastando uma boa explanação docente para a efetiva apropriação pelos estudantes.

A resultante desse processo na tradição escolar brasileira é sobejamente conhecida: os alunos tentam incorporar procedimentos algorítmicos, em geral, sem compreensão, não conseguindo aplicá-los de forma efetiva na resolução de problemas. Todos os indicadores de avaliação externa apontam para essa dificuldade, estabelecendo a necessidade de uma transformação subjetiva das rotinas de estudo, permeada pelo trabalho intelectual do sujeito que aprende.

Assim é que para definir uma proposta de educação desenvolvimental, Elkonin (2019), Davidov (2019) e colaboradores elaboraram princípios teóricos consistentes sobre a atividade de estudo. Mas, o que é a atividade de estudo? Para respondermos a essa pergunta partiremos primeiramente do conceito de atividade elaborado por Leontiev (2004). O conceito de atividade na teoria de Leontiev está relacionado com a ideia do princípio do caráter objetal da atividade, ou seja, a atividade parte sempre do manejo de algum objeto. Isso constitui a essência da teoria psicológica da atividade (DAVYDOV, 1988). Cabe salientar que o objeto aqui é entendido “como algo com que o ser vivo se relaciona, como o objeto da sua atividade, seja ela externa ou interna” (DAVYDOV, 1988, p. 29).

Por questões similares, dentre tantas outras, Leontiev (2001) esclarece que entende como atividade o processo psicológico no qual estão presentes os seguintes fatores: necessidade, motivo e objetivo. A necessidade é um elemento essencial para a atividade. Porém, segundo Repkin (2014, p. 92), “a necessidade em si não é suficiente para produzir atividade. O encontro com um objeto deve acontecer. Esse objeto, que é capaz de satisfazer a necessidade, é o estímulo direto. Na psicologia, isso é chamado de motivo”. Assim a atividade está ligada a um motivo. O motivo deve coincidir com o objetivo e ao final do processo deve ocorrer uma mudança no sujeito.

O objetivo é o determinante direto que produz atividade e determina as suas formas e meios, isto é, é o mecanismo psicológico para sua regulação. O objetivo deve ser atingido ou concretizado sob certas condições definidas, que incluem conhecimento e habilidades do sujeito, as características especiais do objeto da ação, e assim por diante. Na psicologia, chamamos de tarefa o agregado das condições em que um objetivo é definido. Uma tarefa é um objetivo nas condições concretas de sua realização. Por essa razão, qualquer atividade é um processo de resolução de tarefas (REPKIN, 2014, p. 92).

Para a realização das tarefas de estudos os teóricos da educação desenvolvimental enumeraram um conjunto de ações que devem ser desenvolvidas pelo educando. Essas ações são:

• transformação dos dados da tarefa a fim de revelar a relação universal do objeto estudado;

• modelação da relação diferenciada em forma objetivada, gráfica ou por meio de letras;

• transformação do modelo da relação para estudar suas propriedades em forma pura;

• construção do sistema de tarefas particulares que podem ser resolvidas por um procedimento geral;

• controle da realização das ações anteriores;

• avaliação da assimilação do procedimento geral como resultado da solução da tarefa de aprendizagem dada (DAVIDOV, 1988, p. 173).

Nesse modo de pensar a educação, um amplo movimento dialético entre ensinar e aprender, organizar o trabalho pedagógico em Matemática impõe a necessidade de exploração de situações matemáticas significativas, produzindo sentidos de aprendizagem; exige propiciar condições para que os estudantes sejam conduzidos a estabelecer relações entre as ideias matemáticas; formar conjecturas; sugerir soluções para as questões apresentadas; buscar maneiras eficientes para validação de resultados; refletir sobre representações semióticas voltadas à contribuição para obtenção de respostas adequadas ao problema; encaminhar progressivamente a argumentação dedutiva; e, reformular e reorganizar os conhecimentos adquiridos com vistas à generalização.

Nesse modo de conceber a educação matemática, mais que o de formulador de problemas, o papel do professor é de instigar os alunos a propor e refletir sobre situações matemáticas que emergem da atuação específica do alunado, por ele mediada com referência na atividade matemática. Essa interação entre os atores sociais, professor e alunos, exige do sujeito mais experiente, o docente, atitude de busca de maior precisão nas formulações dos aprendizes, reorganizando os questionamentos, discutindo e intervindo sempre que se fizer necessário de modo a guiar o processo de desenvolvimento. Fazer valer a perspectiva da teoria de Vygotsky (2000) de que é a aprendizagem que provoca o desenvolvimento e não o contrário.

Em outro sentido, assumir a tarefa de estudo na qual a reconstrução da Matemática se revela um projeto pessoal é ao que se deve motivar e esperar dos alunos. Tratar suas resoluções como objeto de reflexão, com vistas ao desenvolvimento do pensamento teórico, em um ambiente no qual possam revisar e modificar ideias matemáticas antes elaboradas, aperfeiçoando-as, e tomando consciência de suas apropriações, desenvolvendo a capacidade de resolver problemas com base em ideias anteriores as quais possam contribuir para a melhor abordagem, enquanto sujeito que tem modos próprios de sentir, pensar e agir intelectualmente.

Se é fato que as representações semióticas consolidam uma forma de registrar em expressão escrita o fato matemático pensado, igualmente se deve considerar que a representação de uma dada situação matemática envolve tanto a construção da própria representação como a possibilidade de se operar com ela, conforme transformações concretizadas no contexto de leis dos registros nos quais de sustenta.

Em suma, tais transformações exercem um papel na produção de novas relações, no reconhecimento de regularidades e na formulação de novas significações para relações anteriormente estabelecidas.

Considerações finais à guisa de conclusão

Ao longo do presente artigo, buscamos evidenciar que as ideias matemáticas, bem como os conceitos, estratégias, ferramentas, regras e modos de representação, não existem de forma independente das práticas a elas associadas. A rigor, um conceito matemático não se caracteriza apenas por uma mera definição e nem por representação de modelo único.

Por isso, pensar a educação matemática em perspectiva desenvolvimental implica em considerar o exercício de ações didático-pedagógicas que se situam em amplo movimento dialético entre ensinar e aprender. Consideramos, então, que a apropriação do conhecimento matemático envolve um conjunto de formulações teóricas com implicações específicas para o ensino e a aprendizagem. Nesse sentido, envolve não apenas o ato de (re)conhecer, mas exige também a criação a partir da produção de sentidos e de estabelecimento de relações entre significados matemáticos.

Trata-se de atividade humana de conhecimento que deve ser concebida para além de uma simples ferramenta, de conhecimento instrumental, enfatizando no processo de sua apropriação o seu poder reflexivo, de análise e de questionamento, um produto da evolução mental em seu processo histórico-cultural, com implicações decisivas para o desenvolvimento científico como um todo articulado e com consequências para o desenvolvimento da sociedade. Isso se nota com muita clareza, por exemplo, no fantástico estágio de desenvolvimento das tecnologias digitais de informação e comunicação, sustentado a partir de articulações possíveis com base em modelos matemáticos.

Desse modo, não basta aos alunos o conhecimento das origens dos fatos matemáticos e suas influências sobre a sociedade; menos ainda, a reprodução das ideias matemáticas assimiladas em sua forma final de apresentação ou difusão. Em perspectiva desenvolvimental, os alunos precisam aprender como essa ciência se desenvolve, bem como a construir novos modelos para a representação de ideias matemáticas, em sintonia com os seus modos de pensar, sentir e agir frente a realidade.

Trata-se de concretizar um movimento dialético entre ensinar e aprender no qual o processo de apropriação do conhecimento matemático é regido pela produção de sentidos de aprendizagem e pela negociação de significados de tal modo que os conceitos matemáticos devem ser apresentados de maneira contextualizada, mas buscando a generalização própria dos conhecimentos científicos, tendo como pressupostos fundamentais:

a) a atuação efetiva dos alunos na construção dos conceitos, em lugar de memorização mecânica de informações desligadas de suas vivências e destituídas de significação;

b) percepção dos fatos matemáticos como instrumentos para a resolução de problemas da realidade;

c) desenvolvimento da capacidade de utilização integrada de conceitos da Matemática e de outras áreas do conhecimento na resolução de problemas;

d) desenvolvimento de capacidades e atitudes para enfrentar desafios, criando suas próprias estratégias, interagindo e atuando colaborativamente com o outro;

e) apropriação da noção de que alguns conceitos matemáticos têm a função de fundamentação da construção de outras ideias científicas úteis para a resolução de problemas e para o incremento do desenvolvimento intelectual.

Por isso, imperativo é considerar que as práticas matemáticas envolvem uma gama ampla de atividades, as quais se desdobram em função dos conceitos, sendo elas os seus determinantes.

Daí, os problemas que geram seu aparecimento, as comparações entre diferentes formas de resolução, as discussões que suscitam, as conjecturas formuladas, as relações estabelecidas e os novos problemas que podem surgir como resultantes do confronto de ideias, bem como as formas de representação de significados, são os elementos constitutivos de um conceito matemático.

Sem esse movimento dialético entre ensinar e aprender, coeso e articulado, não há que se falar em educação matemática desenvolvimental. Menos ainda, em autonomia, autoformação ou alegria na escola.