Introdução
O presente trabalho teve como objetivo analisar a abordagem do ensino de Grandezas e Medidas nos Parâmetros Curriculares para a Educação Básica do Estado de Pernambuco. Para isso, nos sustentamos em Lima e Bellemain (2010), por apresentarem um quadro teórico importante, acerca dos processos de ensino e de aprendizagem das Grandezas e Medidas.
Assim, durante toda a investigação, buscamos identificar se essa proposta curricular analisada estava de acordo com o marco teórico adotado neste artigo, visto que é considerado uma referência nacional ao se abordar questões pertencentes às Grandezas e Medidas.
Mesmo com o desenvolvimento e homologação da Base Nacional Comum Curricular - BNCC, que consiste em um documento normativo do currículo a ser desenvolvido ao longo das etapas e modalidades da educação básica no país (BRASIL, 2017; 2018), os Parâmetros Curriculares para a Educação Básica do Estado de Pernambuco ainda são as orientações preconizadas e utilizadas como referência nos processos de ensino e de aprendizagem das aulas de Matemática na referida unidade da federação.
Por esse motivo, ou seja, devido ao fato de não ter ocorrido, ainda, uma adequação das propostas curriculares estaduais às orientações da BNCC, optamos por analisar o documento que está em vigência e vem sendo utilizado nos últimos anos como documento norteador do trabalho dos professores nas aulas de Matemática da educação básica em Pernambuco.
Vale salientar que as Grandezas e Medidas podem ser encontradas em diversas situações do mundo real, todavia, nem sempre as percebemos de forma clara. Ao pararmos para refletir sobre esse aspecto, é possível perceber a presença desse saber matemático nas práticas sociais, na conexão com outras áreas do conhecimento e também com outros campos da própria Matemática. Desse modo, notamos a necessidade desse campo da matemática para o pleno exercício da cidadania.
Durante muito tempo, as Grandezas e Medidas foram consideradas como tópicos pertencentes ao campo da Geometria, sendo trabalhados na escola, com esse status, por muitos professores de Matemática. Tal fato acabava impedido, por exemplo, que os estudantes considerassem o conceito de área como uma grandeza associada à figura geométrica (PEREIRA DA COSTA e ROSA DOS SANTOS, 2015).
Além disso, como o campo geométrico era pouco abordado no livro didático e quase nunca ensinado nas aulas de Matemática, em decorrência do Movimento da Matemática Moderna, consequentemente, o trabalho com as questões referentes às Grandezas e Medidas era praticamente inexistente na educação básica.
Com o intuito de tentar reverter esse cenário, os Parâmetros Curriculares Nacionais - PCN de Matemática (BRASIL, 1997), com base em diversas pesquisas educacionais nacionais e internacionais (DOUADY; 1983; CHAMORRO PLAZA e BELMONTE GÓMEZ, 1988; SEGOVIA, CASTRO, CASTRO e RICO 1989; DOUADY e PERRIN-GLORIAN, 1989; BALTAR e COMITI, 1994; LIMA, 1995; BALTAR, 1996; entre outros), reconheceu às Grandezas e Medidas não mais como ramo da Geometria, mas como um campo matemático autônomo. Essa distinção fez com que os conteúdos pertencentes a este eixo tivessem maior destaque e importância para serem abordados durante a educação básica.
Entretanto, mesmo com essas alterações para dar maior destaque aos conteúdos pertencentes ao campo das Grandezas e Medidas, em muitos casos, ainda é possível constatarmos uma ênfase exacerbada na aplicação de expressões matemáticas (as chamadas “fórmulas”), com forte uso da linguagem algébrica, e nas conversões de unidades de medidas. Consequentemente, as discussões em torno desse campo são deixadas de lado e não recebem a devida atenção.
Essa visão limitada na forma em se abordar os conteúdos pertencentes a este campo da Matemática acarreta na omissão de um aspecto importante no estudo desse campo matemático, que é a compreensão das grandezas associadas às figuras geométricas. Logo, a discussão conceitual e epistemológica do conceito continua sendo deixada de lado.
Tal realidade vivenciada por vários estudantes do ensino básico é o oposto do que aponta Carvalho e Almeida (2010). Segundo esses autores, deve-se discutir a importância dos conteúdos ligados às Grandezas e Medidas nas práticas cotidianas, salientando que o seu ensino não pode limitar-se apenas a conversão de unidades de medidas e nem ao uso das “fórmulas” com foco algébrico.
Infelizmente, esse fenômeno não se restringe somente ao ensino básico, pois até mesmo nos cursos de formação de professores de Matemática, pouco se discute sobre os aspectos relativos à aprendizagem e ao ensino das Grandezas e Medidas. Isso faz com que os professores tenham uma formação fragilizada no que diz respeito a discussão conceitual, histórica, epistemológica, sóciocognitiva e didática de conhecimentos pertencentes a esse campo.
Além disso, devemos estar vigilantes ao papel que os documentos curriculares oficais possuem no ambiente escolar, servindo de orientação e base aos professores, com o propósito de melhorar o ensino e, consequentemente, a aprendizagem. Nessa direção, nos questionamos: Qual é a abordagem do ensino de Grandezas e Medidas nos documentos curriculares oficiais do Estado de Pernambuco?
Para tanto, buscando respostas para essa questão, traçamos o seguinte objetivo de pesquisa: analisar a abordagem do ensino de Grandezas e Medidas nos documentos curriculares oficiais da educação básica no Estado de Pernambuco. Especificamente, identificar quais as grandezas a serem abordadas em cada nível escolar, verificar as orientações didático-metodológicas dos aspectos privilegiados nos documentos e comparar as relações dessas orientações com as discussões apresentadas por Lima e Bellemain (2010).
O Ensino das Grandezas e Medidas
Como dito anteriormente, os conceitos pertencentes ao campo das Grandezas e Medidas estão presentes em diferentes situações do nosso dia a dia, mesmo que, incosciemente, algumas vezes não percebamos isso. Além disso, os seus conhecimentos estão ligados às atividades humanas desde as mais simples, até as mais complexas.
Com base nos Parâmetros Curriculares Nacionais - PCN (BRASIL, 1997), as grandezas exercem papel importante no currículo escolar, uma vez que apresentam ao aluno, de maneira clara, a utilidade do conhecimento matemático em contextos do cotidiano.
Em síntese, a importância de estudar na escola básica o campo das Grandezas e Medidas se justifica, pois, pela forte presença constante nas práticas sociais, pela articulação com os outros campos da Matemática e conexão com outras áreas do conhecimento (LIMA e BALTAR BELLEMAIN, 2010).
Geralmente, o ensino das Grandezas e Medidas nos anos iniciais do ensino fundamental tem dado ênfase à apresentação de unidades de medidas padronizadas de comprimento, massa, tempo, área e capacidade, na conversão destas unidades e, em alguns casos, na aplicação de expressões matemáticas (“fórmulas”) de área e perímetro de figuras planas.
Contudo, essa abordagem não é considerada a mais adequada para essa modalidade de ensino, visto que pode gerar problemas conceituais nos estudantes. Então, deve-se primeiro trabalhar o conceito da grandeza para que os estudantes compreendam com o que estão trabalhando e, somente, após essa abordagem inicial, é que o conceito deve começar a ser sistematizado, abordando-o em diferentes situações que dão sentido a ele, tais como: comparação, medição, ordenação e estimação.
Exigir uma formalização precoce, com uso excessivo de cálculos e de linguagem algébrica, pode ocasionar dificuldades em aprendizagens futuras (MASOLA e ALLEATO, 2019). Isso se justifica, pois embora as crianças já cheguem a escola com algum conhecimento sobre grandezas, elas não apresentam entendimento do seu significado. Por exemplo, uma criança sabe que a medida do comprimento de uma avenida é de três quilômetros, entretanto, não possui compreensão do comprimento equivalente a um quilômetro (PERNAMBUCO, 2008).
Logo, é importante que a sistematização das unidades de medidas convencionais seja realizada após a compreensão do significado da grandeza estudada e, também, de unidades de medida não convencionais. A exploração de expressões matemáticas (as chamadas “fórmulas”) deve ser deixada para os anos finais do ensino fundamental e para o ensino médio.
Como mencionado no parágrafo anterior, o trabalho com unidades de medida não convencionais é um importante aspecto na compreensão dos processos de medições e no entendimento das unidades de medida convencionais. Essa abordagem tem um forte apelo articulador com outras disciplinas escolares como, por exemplo, história, e auxilia o estudante a compreender a necessidade em trabalhar com unidades de medida convencionais.
Nessa perspectiva histórica, o que hoje é abordado como objeto de estudo no campo das Grandezas e Medidas serviu, há muito tempo atrás, no Egito Antigo, como uma forma organizada do rei cobrar impostos dos egípcios. Sobre este aspecto, Caraça (1951, p. 32) ao citar o trabalho de Heródoto apresenta que:
[...] disseram-me que este rei (Sesóstis) tinha repartido todo o Egigto entre os egípcios, e que tinha dado a cada um uma porção igual e rectangular de terra, com a obrigação de pagar por ano um certo tributo. Que se a porção de algum fosse diminuída pelo rio (Nilo), ele fosse procurar o rei e lhe expusesse o que tinha acontecido à sua terra. Que ao mesmo tempo o rei enviava medidores ao local e fazia medir a terra, a fim de saber de quanto ela estava diminuída e de só fazer o tributo conforme o que tivesse ficado de terra.
Com esse exemplo, é possível perceber além do forte apelo prático, que acompanhou a história da humanidade e sua evolução, que os conceitos das Grandezas e Medidas relacionam-se com outros campos da Matemática, pois o tributo (valor monetário) era cobrado de forma proporcional ao pedaço de terreno de cada egípcio. Desse modo, a ideia de proporcionalidade estava relacionada diretamente a área do terreno que, por sua vez, implica na quantidade de tributo a ser pago por suas terras.
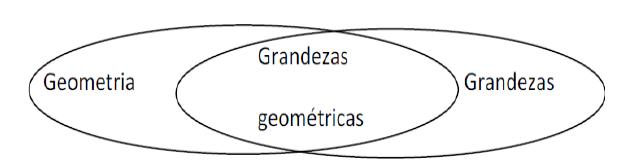
O campo das Grandezas e Medidas possui fortes relações com outras áreas da Matemática. Tal relação pode ser evidenciada ao abordarmos, por exemplo, o estudo das grandezas geométricas. Esse tópico é composto pelas grandezas comprimento, área, volume e abertura de ângulo. Como ilustrado na Figura 01, o estudo dessas grandezas é uma forma de promover uma articulação entre o campo das Grandezas e Medidas e o campo geométrico (LIMA e CARVALHO, 2010).
Se fizermos um levantamento de pesquisas desenvolvidas nas últimas três décadas sobre as Grandezas e Medidas, podemos encontrar diversos estudos, realizados com alunos ou com livros didáticos, em especial, a respeito das grandezas geométricas4 no Brasil e na França, dentre eles destacamos os trabalhos sobre área (DOUADY e PERRIN-GLORIAN, 1989; TELES, 2007; ROSA DOS SANTOS, 2015; BARROS, 2016) e volume (FIGUEIREDO, 2013; MORAIS, 2013).
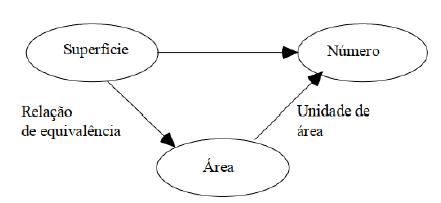
No trabalho com a grandeza área destaca-se o modelo didático proposto por Douady e Perrin-Glorian (1989). Para essas autoras, o conceito de área é uma grandeza autônoma, sobre a qual é estabelecida a distinção de três quadros: o geométrico, numérico e o das grandezas. Nessa direção, Bellemain (2000) elaborou um esquema que relaciona esses quadros, conforme ilustrado pela Figura 02.
O quadro geométrico é composto pelas superfícies planas, o das grandezas é composto pelas classes de equivalência de mesma área, e o quadro numérico é composto por números reais positivos. Esse modelo didático foi utilizado em diversas pesquisas que abordaram as grandezas (comprimento, área e volume), inclusive nas citadas anteriormente.
Rosa dos Santos (2015, p.82) destaca que os quadros acima:
[...] apesar de serem distintos, são imbricados entre si e apresentam alguns dos principais elementos de base para o desenvolvimento de estudos sobre o conceito de área. Por exemplo, a relação de equivalência, ou seja, ter mesma área, é o objeto que permite passar do quadro geométrico ao das grandezas. Da mesma forma, as unidades de medida de área que admitem passar do quadro das grandezas ao das medidas, e as funções que permitem passar do quadro geométrico ao numérico.
O trabalho com área foi marcado durante muito tempo pela ênfase na aplicação de expressões matemáticas (“fórmulas”) de figuras geométricas e na conversão de unidades de medidas de área. Por essa razão, diversas dificuldades como a confusão entre área e perímetro, podem ser geradas. As equações possuem um papel relevante, entretanto, para desempenhar esse papel é preciso que sejam utilizadas com compreensão e significado (LIMA e BELLEMAIN, 2010).
Procedimentos Metodológicos
Este trabalho apresenta uma abordagem qualitativa e, ainda, um caráter documental, no qual empregamos o aporte teórico de Lima e Bellemain (2010) para analisar o ensino das Grandezas e Medidas nos Parâmetros Curriculares para a Educação Básica de Pernambuco.
Para tanto, a apreciação do documento foi realizada em quatro momentos. No primeiro momento, foram identificadas as grandezas indicadas para serem trabalhadas em cada nível de ensino; no segundo momento, verificamos os aspectos privilegiados no documento; no terceiro, identificamos as propostas metodológicas para esse campo; e no quarto e último momento, procuramos estabelecer relações entre as propostas do documento e o texto de Lima e Bellemain (2010).
O documento a ser analisado
Os Parâmetros Curriculares para a Educação Básica do Estado de Pernambuco (PC-PE) foi publicado no ano de 2012 e contou com a colaboração de diversos consultores e especialistas na área de Matemática. Esse documento curricular se fundamentou na Base Curricular Comum para as Redes Públicas de Ensino de Pernambuco (PERNAMBUCO, 2012).
Nos PC-PE, são apresentados os conteúdos da Educação Básica a serem abordados nos anos iniciais do ensino fundamental, nos anos finais do ensino fundamental e no ensino médio. Suas propostas são baseadas nas atuais matrizes de referência de avaliação, como o Sistema de Avaliação da Educação Básica (SAEB), Sistema de Avaliação da Educação Básica de Pernambuco (SAEPE), do Exame Nacional do Ensino Médio (ENEM) e do Programa para o Vestibular da Universidade de Pernambuco (UPE).
De modo resumido, o documento traz discussões a respeito da importância de se refletir sobre o ensino e a aprendizagem, apresentando três concepções sobre esses dois processos. A primeira concepção aborda o ensino como sendo um processo vinculado a construção e reconstrução de conhecimentos. A segunda concepção defende que o processo de aprendizagem se desenvolve com base na fragmentação do conhecimento. A última concepção apresenta que, durante os processos de ensino e de aprendizagem, o estudante é o autor principal da construção do saber.
Em relação as orientações metodológicas para o ensino e à aprendizagem dos conceitos matemáticos, esse documento apresenta as estratégias de resolução de problemas com base em diferentes tendências em Educação Matemática, tais como: a modelagem matemática, as tecnologias no ensino de Matemática, história da Matemática, jogos matemáticos na sala de aula e os projetos de trabalho, como sendo alternativas para auxiliar o professor em sua prática pedagógica.
No que diz respeito às expectativas de aprendizagem, os PC-PE as organiza de acordo com as três etapas de escolarização da educação básica (anos iniciais do ensino fundamental, anos finais do ensino fundamental e ensino médio). Essas expectativas são apresentadas em cada um dos cinco eixos temáticos dos conteúdos da Matemática: Geometria, Estatística e Probabilidade, Álgebra e Funções, Grandezas e Medidas e Números e Operações.
Resultados e Discussão
Essa análise dos resultados será organizada em dois momentos, a saber: (a) identificação das grandezas em cada nível de ensino; e (b) aspectos privilegiados no documento analisado. A seguir, apresentamos a análise relativa à primeira etapa.
a) Identificação das grandezas em cada nível de ensino
Ao analisarmos o documento em questão, buscamos identificar quais são as grandezas abordadas em cada nível de ensino. Um aspecto interessante observado, durante essa etapa, foi a organização das informações fornecidas pelo próprio documento. Antes de detalhar as expectativas de aprendizagem por ano de escolarização, os PC-PE apresentam um quadro que sintetiza as grandezas contempladas em cada nível de ensino, conforme ilustrado a seguir na Figura 03.
Tal quadro facilita a observação do que se deve trabalhar ao longo da escolarização, e como evoluir na abordagem dos conceitos pertencentes ao campo das Grandezas e Medidas.
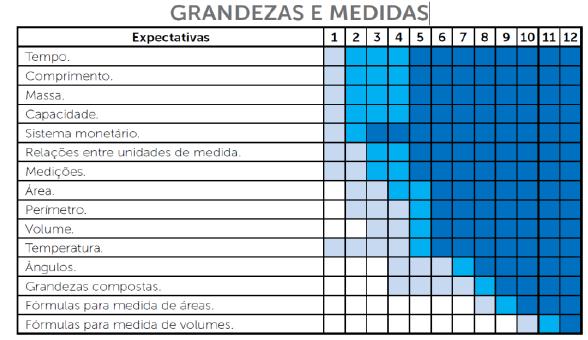
FONTE: Pernambuco, 2012, p.47.
FIGURA 03: Abordagem das grandezas e medidas ao longo da escolarização em Pernambuco
Contudo, ao analisarmos as expectativas de aprendizagens e ao compararmos com o quadro, percebemos que as grandezas área e temperatura são introduzidas no 2º ano do ensino fundamental e a grandeza “ângulo” no 4º ano aparecem como expectativa no quadro, mas não é apresentada ao detalhar as expectativas em cada bimestre do ano escolar.
Chamamos atenção para o fato que de os PC-PE estão considerando ângulo como grandeza. Na verdade, ângulo é uma figura geométrica formada por duas semirretas, distintas e não opostas, com a mesma origem (PEREIRA DA COSTA, 2016). Como as semirretas são infinitas, então, é impossível medir seus comprimentos. Desse modo, a grandeza associada a esse objeto geométrico é a abertura, que pode ser comparada, medida, estimada e ordenada (LIMA e BELLEMAIN, 2010).
Para sintetizar as grandezas abordadas nos Parâmetros para a Educação Básica do Estado de Pernambuco - Parâmetros Curriculares de Matemática para o Ensino Fundamental e Médio, organizamos as informações em um quadro (Quadro 01).
QUADRO 01: Resumo das Grandezas abordadas durante a educação básica nos: Parâmetros para a Educação Básica do Estado de Pernambuco: Parâmetros Curriculares de Matemática para o Ensino Fundamental e Médio.
| Anos Iniciais do EF | Anos Finais do EF | Ensino Médio |
|---|---|---|
| Abertura de ângulo | Abertura de ângulo | |
| Área | Área | Área |
| Capacidade | Capacidade | |
| Comprimento | Comprimento | |
| Massa | Massa | |
| Perímetro | Perímetro | Perímetro |
| Sistema Monetário | Grandezas Compostas | Grandezas Compostas |
| Temperatura | Temperatura | |
| Tempo | Tempo | |
| Volume | Volume | Volume |
FONTE: Elaborado pelos autores.
Após identificar quais as grandezas abordadas nas diferentes etapas do ensino, percebemos algumas particularidades, que o quadro acima apresentado nos ajuda a evidenciar. Por exemplo, analisando os anos iniciais e os anos finais do ensino fundamental, percebemos a grande relação entre as grandezas a serem abordadas nestas etapas (uma totalidade de 10 grandezas diferentes).
Assim, praticamente todas as grandezas são abordadas na primeira etapa do ensino fundamental, sendo também constatado na segunda etapa. As únicas exceções são: a grandeza “sistema monetário”, abordada somente nos anos iniciais do ensino fundamental; e as “grandezas compostas” abordadas somente nos anos finais do ensino fundamental.
A abordagem dessa diversidade de grandezas, a partir de diferentes situações, ajudará o estudante a compreender esse conceito como características de objetos que podem ser comparados a outros semelhantes do ponto de vista da igualdade ou desigualdade (PEREIRA DA COSTA e ROSA DOS SANTOS, 2015). Nesse sentido, comprimento, área, volume e abertura de ângulo são grandezas geométricas, associadas a objetos geométricos, enquanto tempo e temperatura são grandezas físicas, vinculadas à fenômenos do mundo físico (LIMA e BELLEMAIN, 2010).
Ao observar a proposta de conteúdos para o ensino médio, evidenciamos uma diferença na quantidade de grandezas a serem trabalhadas nesta etapa do ensino. Isto não significa que, nessa fase, os alunos estudem menos conteúdos relacionados ao campo das Grandezas e Medidas. A redução ocorre pois se espera que, ao chegar no ensino médio, os alunos já tenham consolidado o estudo com as demais grandezas. Assim, nesse nível escolar, são contempladas somente as grandezas geométricas (comprimento/perímetro, área e volume) e as grandezas compostas.
É notável que o documento segue um padrão na organização e seleção das grandezas a serem abordadas em cada etapa da escolarização. Além disso, observamos também uma maior evidência ao trabalhar área, perímetro e volume durante toda a educação básica.
b) Aspectos privilegiados no documento analisado
Neste tópico, foram observadas as ideias centrais a respeito das expectativas de aprendizagem no campo das Grandezas e Medidas para cada etapa da escolarização. Por questão de organização, dividimos essa análise em três momentos: anos iniciais do ensino fundamental, anos finais do ensino eundamental e ensino médio.
i) Anos Iniciais do Ensino Fundamental
Nesta etapa da escolarização, as crianças chegam a escola com conhecimentos matemáticos produzidos a partir da sua interação social. Desse modo, é importante que o professor saiba utilizar esses conhecimentos para que possa abordar situações que façam significado para as crianças e as ajudem a construir conhecimentos mais elaborados (PERNAMBUCO, 2012).
No que diz respeito à abordagem das grandezas, em específico, podemos constatar as seguintes propostas para os anos iniciais do ensino fundamental: compreensão do significado de algumas grandezas e trabalho sobre capacidade de estimativa; construção da ideia de medição; compreensão que as grandezas podem ser medidas e comparadas; trabalho com unidades de medida não padronizadas (após a construção dos significados das grandezas); trabalho com grandezas geométricas; comparação de grandezas (sem recorrer às medidas); ordenação e sequenciamento de eventos com base nas grandezas; distinção entre figura e grandeza; e compreensão de número associado à medida.
Com base nessas orientações, percebemos que o foco nos anos iniciais é o estudo das grandezas e medidas a partir das seguintes situações: estimação, comparação, ordenação e sequenciamento. Logo, o uso de expressões matemáticas não é recomendado para esse nível. Isso é importante para o estudante possa perceber que grandezas são características de objetos (geométricos ou do mundo físico) e não se resumem a um número, a uma medida. Esse tipo de abordagem é baseado nas discussões de Lima e Bellemain (2010).
Uma prática importante ao trabalhar com o estudo das grandezas, como já apresentado anteriormente, são as unidades de medida não padronizadas. Para os autores, com o uso dessas unidades de medida, os estudantes podem procurar soluções próprias para as situações propostas pelo professor em sala de aula. O aluno também pode pode perceber que ao alterar a unidade de medida, a grandeza não sofre alteração, mas a medida sim.
A discussão sobre a distinção entre figura geométrica e grandeza nesse nível é importante pois a um mesmo objeto geométrico é possível relacionarmos diversas grandezas. Por exemplo, para um paralelepípedo podemos associar a sua capacidade (volume de seu interior), a sua área (relativa às suas faces), o seu comprimento (referente às suas arestas).
ii) Anos Finais do Ensino Fundamental
Esta etapa da escolarização exerce um papel de continuação da etapa anterior, tendo em vista que os processos iniciados anteriormente devem ser ampliados e consolidados nesta fase. Para isso, é imprescindível que o professor consiga diagnosticar a aprendizagem que os alunos desenvolveram nos anos anteriores e, a partir dela, possa criar estratégias para melhor abordar os conceitos pertencentes ao campo das Grandezas e Medidas (PERNAMBUCO, 2012).
As principais propostas desta etapa são: ampliação da ideia de medição; ênfase no emprego de unidades padronizadas de medida; introduzir unidades agrárias, unidades relacionadas a informática, e iniciar a relação de duas grandezas; trabalho com grandezas geométricas; dissociação entre as figuras; grandezas associadas à figura; número associado à medida dessas grandezas; e sistematização de algumas fórmulas (cálculo da medida das grandezas).
Em relação à etapa anterior, percebemos avanços na abordagem dos anos finais. O estudo das unidades de medidas não convencionais não é mais recomendando. Há a introdução do estudo das unidades de medidas vinculadas à sociedade contemporânea, como por exemplo, as de informática.
Um aspecto novo no trabalho dos conteúdos pertencentes ao campo em questão é o estudo das relações entre duas ou mais grandezas,como um tópico importante para a aprendizagem dos estudantes, auxiliando-nos na compreensão das noções de de função, razão e proporção. Tais conceitos são construídos a partir da relação entre grandezas e abre espaço para a introdução de um trabalho em conexão com a disciplina de Ciências.
Nessa etapa, o aluno é introduzido ao uso de expressões matemáticas (as chamadas “fórmulas”) para o cálculo da medida de grandezas. Segundo Lima e Bellemain (2010), isso é importante, visto que há situações que comparar, estimar, ordenar e sequenciar não dão conta. Mas, esse uso é recomendado quando o estudante reconhece as grandezas como atributos, que podem ser medidos, comparados, estimados, ordenados, sequenciados e construídos.
É importante que sejam vivenciadas situações que contribuam para a dissociação entre a grandeza abordada e as unidades de medida que podem ser utilizadas em suas medições. Desse modo, o aluno poderá compreender que o uso das expressões matemáticas (“fórmulas”) não é o foco do conceito, mas um artifício que pode ser utilizado durante sua abordagem.
iii) Ensino Médio
Nesta etapa da escolarização é entendida como a fase de consolidação das etapas anteriores e como um momento de reforçar as articulações da Matemática com outros campos do saber (PERNAMBUCO, 2012).
Em síntese, podemos dizer que esta etapa visa: consolidação da ideia de grandeza, a partir das articulações com a Física e com a Química; foco nas grandezas compostas; consolidação das grandezas geométricas; e consolidação do uso das fórmulas.
No ensino médio, percebemos que o foco é a consolidação de algumas abordagens iniciadas nas etapas anteriores, como por exemplo, a utilização de expressões matemáticas (“fórmulas”) e o estudo das grandezas geométricas no âmbito da Matemática.
Além disso, há uma ênfase no estudo das grandezas compostas, tais como, velocidade, aceleração, densidade, potência, pressão, entre outras, que são importantes no estudo de diferentes fenômenos da Física e da Química. Nessa direção, fica mais evidente a articulação entre as grandezas e medidas e essas diferentes disciplinas do currículo escolar, como sinalizam Lima e Bellemain (2010).
Considerações Finais
Analisando as propostas contidas nos Parâmetros Curriculares para a Educação Básica do Estado de Pernambuco, a respeito das expectativas de aprendizagem relativas às Grandezas e Medidas, e comparando-as às discussões de Lima e Bellemain (2010), constatamos que ambas as propostas convergem nas discussões de como se trabalhar os conceitos desse campo no ensino básico.
Percebemos a forte influência das articulações das Grandezas e Medidas com outras áreas da Matemática e com outras disciplinas escolares, juntamente com a relevância social, como as principais justificativas para se abordar o ensino das grandezas no documento curricular analisado.
Embora não tenha sido o foco de análise deste trabalho, ao compararmos a abordagem do campo das Grandezas e Medidas apresentada nos Parâmetros para a Educação Básica do Estado de Pernambuco com as normatizações apresentadas na Base Nacional Comum Curricular, mesmo com a distância temporal de cinco anos entre os documentos, pode-se verificar que os PC-PE apresentam discussões que também são apresentadas na BNCC. Além disso, há situações, nas quais essas propostas divergem quanto as orientações para o ensino de alguns conceitos.
Nessa comparação, inclusive, pode-se destacar que o campo das Grandezas e Medidas recebe um maior destaque no documento estadual de Pernambuco, do que no documento nacional. Em geral, essa diferença ocorre pois nos PC-PE há uma maior riqueza de informações que auxiliam o embasamento didático-pedagógico dos professores da educaçação básica. Assim, percebe-se que na BNCC, as discussões sãos mais sucintas e superficiais.
Outra diferença a ser mencionada entre as duas propostas curriculares, em especial, no que diz respeito a abordagem dos conteúdos pertencentes às Grandezas e Medidas, é a exploração precoce proposta no documento nacional para situações relativas às transformações entre unidades de medidas convencionais.
Mesmo não sendo o foco, a BNCC recomenda a possibilidade de abordar as transformações entre unidades de medidas convencionais mais usuais ainda nos anos iniciais do ensino fundamental. Contudo, tal pespectiva não é verificada nos PC-PE, assim como em Lima e Bellemain (2010), ao explicitarem que essa abordagem deve ser deixada para os anos finais do ensino fundamental.
A justificativa para essa escolha se sustenta no fato de que os estudantes ainda estão se apropriando da ideia de unidades de medidas (convencionais ou não) e das grandezas a elas associadas. Ao se abordar o processo de transformações entre essas unidades já nos anos iniciais do ensino fundamental, tal fenômeno pode comprometer a aprendizagem relativa à noção de grandeza.
Recomendações como essas servem para corroborar que, mesmo após cinco anos de sua publicação em relação à BNCC, as situações apresentadas Parâmetros Curriculares para a Educação Básica do Estado de Pernambuco ainda são bastante atuais e pertinentes para auxiliar o trabalho dos professores durante as aulas de Matemática.
No seu trabalho com o campo das Grandezas e Medidas, os PC-PE apresentam uma proposta que tem como base a evolução na construção dos conceitos. Para isso, inicialmente, deve-se abordar situações que deem significado ao conceito de grandeza. Atividades de construir, comparar, medir, estimar, ordenar e sequenciar as grandezas são muito importantes não somente nos anos iniciais do ensino fundamental, mas em todas as outras etapas da escolarização.
Uma situação que deve ser evitada é a exploração das expressões matemáticas, as chamadas “fórmulas”, e padronizações nos anos iniciais do ensino fundamental, pois é importante que o aluno compreenda o conceito, utilize unidades de medidas não padronizadas e saiba realizar estimativas. A formalização é uma etapa importante, mas que só deve ser abordada posteriormente.
Ao se trabalhar as grandezas geométricas é importante proporcionar atividades que desenvolvam no estudante a capacidade de distinguir e articular tais grandezas, e que saibam identificar o objeto geométrico, as grandezas e as medidas.
Desse modo, é possível concluir que os pressupostos apresentados por Lima e Bellemain (2010) estão contemplados nos PC-PE, e que essa convergência contribui para criar situações pedagógicas propícias, para que os processos de ensino e de aprendizagem das Grandezas e Medidas, na educação básica do estado de Pernambuco, sejam vivenciados de forma adequada.