INTRODUÇÃO
O Exame Nacional do Ensino Médio (Enem) é uma prova aplicada em larga escala, tem caráter multidisciplinar e os seus resultados têm sido utilizados por muitas instituições de ensino superior (IES) brasileiras como principal critério de seleção aos cursos de graduação. Assim, é necessário que as provas sejam elaboradas de forma que forneçam resultados confiáveis e possibilitem a seleção justa dos candidatos. Nesse sentido, a psicometria auxilia na elaboração de testes que apresentem boa capacidade de realizar medidas. Entre as características necessárias de um teste educacional estão a validade e a fidedignidade, ou seja, deve apresentar boas evidências de que realiza o que se pretende e de forma precisa (TOFFOLI et al., 2016).
Por muito tempo, a Teoria Clássica dos Testes (TCT) foi e continua sendo utilizada na análise da qualidade métrica de instrumentos de medida nas avaliações educacionais (SARTES; SOUSA-FORMIGONI, 2013; SOUSA; BRAGA, 2020). No entanto, nos últimos anos, tem ganhado destaque a Teoria da Resposta ao Item (TRI) em avaliações em larga escala, sob a justificativa de oferecer vantagens como estabilidade e comparabilidade dos resultados, algo não oferecido pela TCT (ANDRADE; LAROS; GOUVEIA, 2010). Ainda assim, considera-se que o modelo TRI não tem substituído totalmente a TCT, mas complementa as suas análises (SARTES; SOUSA--FORMIGONI, 2013).
A TCT, para alguns autores (ANDRADE; TAVARES; VALLE, 2000; KLEIN, 2013; SARTES; SOUSA-FORMIGONI, 2013), apresenta problemas, como a dependência da amostra, ou seja, do particular conjunto de sujeitos avaliados, dessa forma o teste apresenta escores diferentes para grupos diferentes de avaliados; a dependência do teste e dos itens, pois escores distintos são obtidos se um grupo de sujeitos é avaliado com diferentes testes sobre o mesmo conhecimento; e, em decorrência disso, os testes não permitem a comparabilidade dos resultados, sendo, dessa forma, instáveis.
Para propor alternativas a esses problemas, surge a TRI, que alega proporcionar estabilidade dos resultados, ou seja, os sujeitos terão os mesmos escores, ou notas, mesmo que sejam utilizados testes com itens diferentes. Isso se torna possível porque o parâmetro de análise é o item, em que, independentemente dos avaliados, terá sempre os mesmos parâmetros. Por apresentar essa invariabilidade, os resultados tornam-se comparáveis (PASQUALI, 2009; VALLE, 2000).
Diante disso, a partir de 2009, o Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inep) passou a utilizar a TRI na validação dos itens e na análise dos resultados do Enem. O exame utiliza o modelo logístico de três parâmetros, em que considera dificuldade, discriminação e probabilidade de acerto casual do item (BRASIL, 2011). Assim, acreditamos que a mudança de método de análise pode influenciar na confiabilidade da medida realizada, pois o modelo mais convencional da TRI exige a unidimensionalidade dos itens, algo muito difícil de ser obtido. Algumas críticas questionam a coerência metodológica do exame (TAVARES, 2013). Entre as discussões, Tavares (2013) indaga a possibilidade de cumprir o pressuposto, já que o conhecimento humano é multideterminado, ou seja, depende de vários fatores. Questionou-se também a validade das medidas realizadas, já que um modelo unidimensional não consegue explicar uma realidade multidimensional, embora se advogue por uma “unidimensionalidade essencial” (STOUT, 1990).
Como possibilidade de um modelo de melhor ajuste a essa realidade surgem os modelos de TRI multidimensional (RECKASE, 2009). No entanto, esses modelos ainda são pouco implementados nas avaliações educacionais em larga escala.
Com base nisso, considerando que o Enem é uma prova multidisciplinar, questionamos a sua validade como um instrumento unidimensional. Embora o exame apresente áreas de avaliação bem determinadas, como Linguagens e Códigos (LC), Matemática (MT), Ciências da Natureza (CN) e Ciências Humanas (CH), cada área é composta por conhecimentos de diferentes disciplinas. Por exemplo, na prova de LC há itens referentes aos conhecimentos de Língua Portuguesa, Língua Estrangeira, Artes e Educação Física. Embora possamos compreender que todas essas áreas constituem uma linguagem, cada uma resguarda a sua especificidade que a diferencia das outras.
Em estudos anteriores, evidências desse problema têm sido apontadas. Ao analisar o Enem 2012 como prova única de 180 itens por meio da TRI multidimensional, foram identificadas quatro dimensões, no entanto, os itens não foram relacionados com as áreas de conhecimento que constituem a prova, gerando dificuldade de interpretação semântica do exame (VIEIRA, 2016). Nesse sentido, a divisão dos itens nas quatro áreas de conhecimento do exame não apresenta estrutura fatorial consistente com os conteúdos dos itens. Em outro estudo, a mesma análise foi realizada com o certame de 2016, em que foram identificados dois fatores (PICCIRILLI; SOUZA, 2018). Na interpretação dos autores, sugere-se que essas duas dimensões estão relacionadas a interpretação de texto e raciocínio lógico.
Modelos com duas dimensões para as provas de CH e MT, com três dimensões para a prova de CN com uma estrutura diferente da originalmente proposta, foram mais bem ajustados em análises fatoriais exploratórias e confirmatórias para o exame realizado em 2010 (MUNER, 2013). Nesse mesmo estudo, por meio de uma análise semântica por juízes independentes, identificou-se a presença das habilidades de inteligência cristalizada, conhecimento quantitativo, inteligência fluida e leitura e escrita, em que a sua estrutura interna apresentou validade de construto, mas de forma convergente para uma reorganização dos itens de acordo com o modelo hierárquico da inteligência de Catell-Horn-Carroll (CHC).
Presença de um segundo fator também foi identificada na prova de MT do exame realizado em 2015, utilizando análise de componentes principais dos resíduos a partir do ajuste do modelo de Rasch, em que considera apenas o parâmetro de dificuldade dos itens (PRIMI; CICCHETTO, 2018). Nesse estudo foi observado que itens difíceis dessa prova compunham uma dimensão secundária e que uma quantidade significativa de 183.450 participantes com nota geral baixa apresentava bom desempenho nesses itens. Como o modelo de TRI unidimensional de três parâmetros, que leva em conta o parâmetro de acerto casual (ou “chute”) utilizado pelo exame, exige coerência nas respostas por penalizar os candidatos que acertam itens difíceis quando erram itens fáceis, esses participantes são prejudicados em sua pontuação final quando a prova não cumpre o pressuposto da unidimensionalidade.
No entanto, em outro estudo (TRAVITZKI, 2017), ao utilizar a análise paralela para a verificação da dimensionalidade do Enem, técnica também utilizada nesta pesquisa, o autor considera que a estrutura unidimensional para as provas do Enem de 2009 e 2011 é suficiente para explicar a variabilidade das respostas aos itens. Por outro lado, o autor também identifica a existência de um segundo fator significativo, mas que considera de menor importância. Ao analisar a qualidade psicométrica da prova de MT de 2018, verificou a presença do pressuposto da unidimensionalidade a partir da análise paralela, mas pelo menos quatro itens apresentaram problemas de ajuste e foram excluídos para prosseguimento da análise (SOARES; SOARES; SANTOS, 2020). Em estudo (SOUSA; PONTES JUNIOR; BRAGA, 2020) que analisa a estrutura fatorial da prova de LC dos anos de 2009 a 2014 com base na análise de componentes principais, é identificada a presença de uma dimensão dominante nas provas, exceto para a prova do ano de 2014. No entanto, esse estudo indica que o percentual de variância explicada das provas é muito baixo, sendo a maior para a prova do ano de 2011, com 14,71% de variância explicada pelo primeiro fator.
Problemas na estrutura fatorial dos itens do Enem podem ser identificados ainda em fase de análises preliminares do exame por meio de alguns parâmetros psicométricos como fidedignidade, dificuldade e discriminação dos itens. Travitzki (2017) analisa a fidedignidade das provas do Enem como inadequado para a prova de MT e aceitável, mas próximo do limiar inferior, para as provas de CN. Problemas de fidedignidade também são encontrados em estudo que analisa o Enem 2011 por meio de um modelo bifatorial (GOMES; GOLINO; PERES, 2018). Nesse estudo, os autores, apoiados em Hogan (2013 apud GOMES; GOLINO; PERES, 2018), consideram que em exames de alto impacto (high stake) os índices de fidedignidade deveriam ser superiores a 0,95. Com base nisso, índices de fidedignidade inadequados foram encontrados para as quatro provas do exame. No entanto, em um modelo bifatorial, o fator geral, denominado no estudo de desempenho escolar geral (DEG), apresenta fidedignidade aceitável. Diante desses dados, os autores consideram que “a operacionalização da matriz de referência por meio dos itens que compõem as provas do Enem parece não ser capaz de avaliar especificamente cada domínio isoladamente. No entanto, os quatro domínios contribuem para a formação do DEG” (p. 341). Ressaltam ainda que isso indica que o Enem consiste em um modelo multidimensional.
Além de problemas de fidedignidade identificados em provas do Enem, alguns estudos indicam problemas nos itens do exame. Travitzki (2017), com base em critérios como correlação, correlação bisserial, discriminação e o índice de ajuste, identifica 33% dos itens de CN na prova de 2009, e 29% na prova de 2011 foram considerados ruins ou duvidosos. Para a prova de MT, chegou a 49% em 2009 e 18% com essa classificação. Da mesma forma, estudo aponta qualidade desejável da prova de MT do Enem 2015 quando se considera parâmetros de TCT e TRI (TOFFOLI, 2019). Nesse estudo, a prova possuía muitos itens com índices de discriminação muito baixos (< 0,3), ou seja, não apresentam a capacidade de diferenciar candidatos de baixa e alta habilidade, e não apresentavam itens considerados fáceis, quando analisados pela TCT. Quando analisados pela TRI, muitos itens apresentaram baixa discriminação ou discriminação negativa, e itens com parâmetros de dificuldade muito altos, fora do intervalo entre -3 e + 3, considerados adequados. Problemas dessa natureza podem indicar má elaboração dos itens e podem influenciar na sua correlação com a área de conhecimento e consequentemente em sua dimensionalidade.
Diante disso, as evidências dessas pesquisas indicam que os itens do exame não se ajustam bem a um modelo unidimensional. Dessa forma, esta pesquisa está pautada no seguinte problema e questões decorrentes: os itens das provas do Enem 2017 são unidimensionais? Diante disso, este estudo teve o objetivo de analisar a dimensionalidade das provas das quatro áreas do Enem (LC, MT, CN e CH) por meio da análise paralela e da análise fatorial de informação plena.
MÉTODO
População e amostra
A população-alvo deste estudo é constituída de 6.731.341 candidatos de todas as regiões e estados do Brasil que realizaram o Enem 2017. Foram excluídos os candidatos que não estiveram presentes no exame e os que não responderam a nenhum dos itens do exame, permanecendo 4.426.755 candidatos.
A amostra final desta pesquisa é formada por 10.000 participantes do Enem de 2017 que estiveram presentes em todas as provas do exame. Esses participantes foram selecionados por amostragem aleatória simples. Esse número reduzido da amostra em relação ao quantitativo total dos participantes se deu pela capacidade limitada de processamento dos computadores utilizados nesta pesquisa. O volume muito grande de dados não foi suportado pela capacidade operacional, gerando instabilidade no processamento das máquinas. Considerando o tamanho populacional, o erro estimado foi menor que 1% para um intervalo de confiança de 95%.
Caracterização do exame
O Enem é um exame que busca avaliar competências e habilidades desenvolvidas pelos alunos no decorrer da educação básica, sendo orientado por uma matriz de referência especificamente construída.
A matriz de referência atualmente possui cinco eixos cognitivos comuns a todas as áreas, a saber: i) dominar linguagens; ii) compreender fenômenos; iii) enfrentar situações-problemas; iv) construir argumentação; e v) elaborar propostas. Suas competências e habilidades são divididas em quatro grandes áreas do conhecimento: Linguagens e Códigos, que contempla os conhecimentos de Português, Educação Física, Artes, Língua Estrangeira Moderna e Tecnologia da Informação e Comunicação; Ciências da Natureza, que abrange a Biologia, Química e Física; Ciências Humanas, envolvendo a História, Geografia, Sociologia e Filosofia; e Matemática.
O exame é constituído de 180 itens de múltipla escolha com cinco alternativas, sendo 45 itens para cada grande área e uma redação.
Destacamos que utilizamos apenas um dos quatro cadernos de prova de cada área. Para LC e CN, utilizou-se o caderno azul, para CH, o caderno amarelo, e para MT, o caderno cinza. A seleção da amostra foi realizada para cada caderno de prova separadamente, ou seja, a amostra de candidatos de um caderno não é a mesma de outra. Para o caderno de LC, o candidato opta por Língua Inglesa ou Espanhola. Este estudo foi realizado com os candidatos que escolheram a segunda opção de Língua Estrangeira. Todas as escolhas foram realizadas por seleção aleatória simples, ou seja, por sorteio.
Os microdados dos resultados das provas e as respostas de cada candidato, nos itens do Enem 2017, estão disponíveis no site do Inep e são de livre acesso ao público.
Tratamento para dados ausentes
Entre os participantes da amostra deste estudo, ocorreu ausência de respostas a determinados itens das provas. No entanto, em nenhuma delas a quantidade de valores ausentes ultrapassou 1%. Para não eliminar os participantes das análises posteriores, optou-se por substituir os valores ausentes pelo método de imputação múltipla.
O método de imputação múltipla consiste na substituição dos valores ausentes por meio de várias simulações até chegar a uma aproximação estatística ótima. Esse método é bastante robusto quando os valores ausentes são completamente aleatórios (NEWMAN, 2014) e em casos de dados binários ou dicotômicos (BÉLAND et al., 2018). Para a aplicação desse método, utilizamos o software SPSS 20.0.
Análise estatística
Para todas as análises realizadas neste trabalho, foi utilizado o software R, programa livre e amplamente usado pelos pesquisadores para implementação de análises estatísticas. Esse software incorpora uma ampla possibilidade e flexibilidade nas análises.
Inicialmente foram obtidas a discriminação dos itens com base na TCT. Foram estimados os parâmetros de discriminação por meio da correlação ponto bisserial, uma vez que os itens foram dicotomizados em certo e errado (PASQUALI, 2009). Para essas análises, foi utilizado o pacote “ltm” (RIZOPOULOS, 2006). Itens com discriminação muito baixa (r pb < 0,15) foram excluídos da análise, pois indicam baixa correlação do item com o escore total. Inicialmente a discriminação foi utilizada com finalidade de analisar sua adequação para a realização da análise fatorial exploratória.
Para uma análise exploratória da dimensionalidade, submeteram-se os dados a um teste de Análise Paralela. Para aplicação desse teste, utilizou-se o pacote “psych” (REVELLE, 2017). Essa análise consiste na comparação dos eigen value dos dados reais com os de um conjunto de dados simulados gerados aleatoriamente com igual número de variáveis e de mesmo tamanho amostral (HAYTON; ALLEN; SCARPELLO, 2004). O critério para a determinação do número de fatores a serem retidos se baseia na comparação dos eigen value dos dados reais e dos dados gerados. Retêm-se os fatores no momento em que o valor eigen dos dados reais é menor que o dos dados simulados. Para a análise da existência de uma dimensão dominante nos dados, realizou-se uma comparação do primeiro eigen value com o segundo (Eigen1/Eigen2). O scree plot também foi analisado na definição do número de fatores.
Outra análise utilizada para verificar o pressuposto da unidimensionalidade foi a Análise Fatorial de Informação Plena (FIFA - Full Information Factor Analysis), um modelo baseado na TRI, considerada mais adequada em situações de itens dicotômicos (BARTHOLOMEW, 1980) típicos de testes educacionais, como é o caso deste trabalho, que utiliza os dados da prova do Enem. Para essa análise, foi utilizado o pacote estatístico “mirt” (CHALMERS, 2012).
O ajuste dos modelos foi realizado com base nas medidas do Root-Mean-Square Error of Approximation (RMSEA), Standardised Root Mean Square Residual (SRMSR), Tucker-Lewis Index (TLI) e Comparative Fit Index (CFI). São considerados desejáveis para um bom ajuste dos modelos valores de RMSEA e SRMSR abaixo de 0,05. Já para os valores de TLI e CFI são considerados como indicativos de bom ajuste os valores acima de 0,95. Para essas análises, foi utilizado o pacote estatístico “mirt” (CHALMERS, 2012).
Também foram analisados os valores dos índices de ajuste dos modelos com base no Critério de Informação de Akaike (AIC - Akaike’s Information Criterion) e o Critério de Informação Baysiano (BIC - Bayesian Information Criterion) (NYLUND; ASPAROUHOV; MUTHÉN, 2007). O modelo que produz menores valores de ambos os critérios é o de melhor ajuste. No entanto, o AIC tende a superestimar a quantidade de dimensões e o BIC, a subestimar. O índice considerado neste estudo foi o BIC, pois é avaliado como mais consistente que o índice AIC por meio de estudos de simulação Monte Carlo (NYLUND; ASPAROUHOV; MUTHÉN, 2007).
A análise do ajuste do modelo também foi realizada com base no Índice de Dimensionalidade (ID) considerando as recomendações de Nojosa (2002). Consiste, inicialmente, em obter os valores de ajuste do modelo com um fator (M1). Posteriormente estima-se os modelos com dois (M2), três fatores (M3) e assim sucessivamente, e então são comparados entre si.
Ao comparar os modelos, obtêm-se um valor com uma distribuição qui-quadrado (X2). No entanto, esse valor é superestimado. Recomenda-se então dividir esse valor por dois ou por três para um ajuste mais adequado (NOJOSA, 2002). Esse valor será denominado nesta pesquisa de qui-quadrado corrigido (X2corr). Ele, então, é dividido pelos graus de liberdade (gl). Nojosa (2002) ressalta que esse valor não é interpretável diretamente, pois só a diferença do valor X2 entre os modelos deve ser considerado. Esse valor obtido será denominado de ID. Na comparação de dois modelos, M1 x M2, um ID com valor positivo maior que 2,0 indica que o segundo modelo é melhor, se o valor for menor que 2,0, o primeiro modelo é preferível. Nesse sentido, espera-se que, se os itens forem unidimensionais, a comparação entre os modelos 1 (M1) e 2 (M2) forneça um ID positivo menor que 2,0.
RESULTADOS E DISCUSSÃO
Análise descritiva dos itens pela teoria clássica
Para compreender melhor o comportamento dos itens, foram estimados os parâmetros com base na teoria clássica. O objetivo foi analisar a discriminação dos itens por meio do coeficiente de correlação ponto bisserial de modo a identificar o quanto o item se correlaciona com o escore total do conjunto de itens. Os valores estão dispostos na Tabela 1.
TABELA 1 Parâmetros clássicos dos itens do Enem 2017
| ÁREA | LC | MT | CN | CH | ||||
|---|---|---|---|---|---|---|---|---|
| ITEM | r pb | d | r pb | d | r pb | d | r pb | d |
| 1 | 0,34 | 0,31 | 0,31 | 0,29 | 0,29 | 0,25 | 0,48 | 0,30 |
| 2 | 0,30 | 0,46 | 0,33 | 0,64 | 0,22 | 0,25 | 0,47 | 0,55 |
| 3 | 0,36 | 0,45 | 0,22 | 0,27 | 0,23 | 0,55 | 0,16 | 0,23 |
| 4 | 0,15 | 0,29 | 0,27 | 0,17 | 0,35 | 0,49 | 0,37 | 0,53 |
| 5 | 0,30 | 0,33 | 0,33 | 0,43 | 0,15 | 0,16 | 0,40 | 0,49 |
| 6 | 0,36 | 0,65 | 0,09 | 0,11 | 0,29 | 0,16 | 0,39 | 0,59 |
| 7 | 0,34 | 0,37 | 0,31 | 0,12 | 0,40 | 0,46 | 0,47 | 0,35 |
| 8 | 0,24 | 0,41 | 0,22 | 0,22 | 0,16 | 0,19 | 0,12 | 0,23 |
| 9 | 0,36 | 0,50 | 0,44 | 0,40 | 0,23 | 0,60 | 0,51 | 0,35 |
| 10 | 0,27 | 0,26 | 0,25 | 0,24 | 0,13 | 0,12 | 0,26 | 0,49 |
| 11 | 0,45 | 0,61 | 0,00 | 0,12 | 0,14 | 0,17 | 0,39 | 0,44 |
| 12 | 0,26 | 0,20 | 0,31 | 0,30 | 0,19 | 0,32 | 0,22 | 0,23 |
| 13 | 0,20 | 0,19 | 0,21 | 0,25 | 0,30 | 0,42 | 0,50 | 0,58 |
| 14 | 0,44 | 0,37 | 0,30 | 0,25 | 0,18 | 0,16 | 0,21 | 0,36 |
| 15 | 0,23 | 0,50 | 0,29 | 0,28 | 0,21 | 0,35 | 0,46 | 0,41 |
| 16 | 0,27 | 0,33 | 0,29 | 0,31 | 0,18 | 0,19 | 0,29 | 0,54 |
| 17 | 0,36 | 0,51 | 0,34 | 0,30 | 0,40 | 0,25 | 0,41 | 0,31 |
| 18 | 0,26 | 0,23 | 0,14 | 0,16 | 0,21 | 0,28 | 0,28 | 0,31 |
| 19 | 0,50 | 0,58 | 0,13 | 0,19 | 0,43 | 0,37 | 0,19 | 0,36 |
| 20 | 0,23 | 0,13 | 0,29 | 0,27 | 0,33 | 0,37 | 0,39 | 0,36 |
| 21 | 0,31 | 0,66 | 0,11 | 0,13 | 0,06 | 0,47 | 0,19 | 0,23 |
| 22 | 0,33 | 0,37 | 0,22 | 0,29 | 0,38 | 0,23 | 0,37 | 0,43 |
| 23 | 0,39 | 0,57 | 0,35 | 0,43 | 0,13 | 0,21 | -0,05 | 0,21 |
| 24 | 0,33 | 0,28 | 0,25 | 0,38 | 0,22 | 0,24 | 0,30 | 0,29 |
| 25 | 0,10 | 0,15 | 0,25 | 0,17 | 0,15 | 0,26 | 0,04 | 0,25 |
| 26 | 0,21 | 0,41 | 0,40 | 0,59 | 0,13 | 0,23 | 0,38 | 0,48 |
| 27 | 0,46 | 0,65 | 0,37 | 0,50 | 0,17 | 0,18 | 0,50 | 0,42 |
| 28 | 0,23 | 0,54 | 0,31 | 0,27 | 0,19 | 0,15 | 0,31 | 0,30 |
| 29 | 0,05 | 0,14 | 0,15 | 0,06 | 0,36 | 0,46 | 0,34 | 0,39 |
| 30 | 0,26 | 0,30 | 0,24 | 0,28 | 0,10 | 0,14 | 0,04 | 0,20 |
| 31 | 0,48 | 0,46 | 0,33 | 0,34 | 0,25 | 0,21 | 0,39 | 0,38 |
| 32 | 0,45 | 0,39 | 0,29 | 0,30 | 0,09 | 0,08 | 0,32 | 0,32 |
| 33 | 0,00 | 0,17 | 0,24 | 0,11 | 0,33 | 0,36 | 0,52 | 0,49 |
| 34 | 0,39 | 0,77 | 0,13 | 0,23 | 0,10 | 0,13 | 0,20 | 0,24 |
| 35 | 0,13 | 0,25 | 0,38 | 0,37 | 0,07 | 0,09 | 0,52 | 0,31 |
| 36 | 0,05 | 0,25 | 0,05 | 0,23 | 0,35 | 0,51 | 0,06 | 0,27 |
| 37 | 0,35 | 0,51 | 0,25 | 0,27 | 0,20 | 0,16 | 0,15 | 0,27 |
| 38 | 0,29 | 0,30 | 0,24 | 0,15 | 0,26 | 0,20 | 0,26 | 0,23 |
| 39 | 0,08 | 0,18 | 0,37 | 0,12 | 0,31 | 0,27 | 0,40 | 0,45 |
| 40 | 0,37 | 0,41 | 0,11 | 0,17 | 0,20 | 0,11 | 0,19 | 0,22 |
| 41 | 0,22 | 0,31 | 0,14 | 0,16 | 0,27 | 0,29 | 0,47 | 0,45 |
| 42 | 0,36 | 0,41 | 0,20 | 0,28 | 0,24 | 0,33 | 0,29 | 0,38 |
| 43 | 0,34 | 0,53 | 0,27 | 0,24 | 0,40 | 0,29 | 0,30 | 0,31 |
| 44 | 0,35 | 0,35 | 0,12 | 0,23 | 0,12 | 0,23 | 0,20 | 0,14 |
| 45 | 0,26 | 0,19 | 0,15 | 0,23 | 0,31 | 0,25 | 0,15 | 0,11 |
Fonte: Elaboração dos autores (2020).
Legenda: r bp : correlação ponto bisserial; d: dificuldade do item.
Nota: Destaque em negrito para as correlações ponto-bisserial abaixo de 0,15.
A partir disso, sete itens de LC (4, 25, 29, 33, 35, 36 e 39), dez itens de MT (6, 11, 18, 19, 21, 34, 36, 40, 41 e 44), dez itens de CN (10, 11, 21, 23, 26, 30, 32, 34, 34 e 44) e cinco itens da prova de CH (8, 23, 25, 30 e 36) apresentaram discriminação abaixo de um valor minimamente aceitável (> 0,15). Portanto, esses itens foram excluídos das análises seguintes. Esse procedimento é recomendado na análise inicial da qualidade dos itens (COSTA; FERRÃO, 2015). Esse valor de discriminação também foi utilizado como parâmetro para exclusão de itens da análise fatorial no estudo de Ferreira (2009).
Diante disso, observam-se problemas em muitos itens das provas do Enem de 2017. Muitos itens apresentam discriminação muito baixa. Isso indica que esses itens não têm boa correlação com o escore total da prova (MUÑIZ, 1994). Do ponto de vista prático, isso demonstra que o item não está conseguindo diferenciar candidatos de escore total mais alto daqueles com escore total mais baixo (MUÑIZ, 1994; VIANNA, 1976), ou seja, ambos tiveram probabilidade de acertar o item bem próximo (ANDRADE; LAROS; GOUVEIA, 2010). Dito de outra forma, o item não está discriminando os examinados eficazes e os ineficazes em um teste (ANDRIOLA, 1998; MUÑIZ, 1994). Itens com problema de discriminação devem ser rejeitados (VIANNA, 1976).
Esse tipo de problema é uma tarefa que pode ser resolvida pelos elaboradores de itens. Comumente, problemas de clareza e objetividade do item causam dificuldades em sua interpretação, o que pode induzir candidatos de bom desempenho ao erro. Em um estudo foi identificado que itens com formulação complexa e enunciado confuso apresentam baixa discriminação (CANÇADO; CASTRO; OLIVEIRA, 2013). Por outro lado, o mesmo estudo indicou que os itens simples, objetivos e claros apresentam boa qualidade discriminativa.
Diante disso, verifica-se um problema importante na estruturação da prova. Pois considerando um exame que objetiva, atualmente, a seleção de candidatos para os cursos de graduação oferecidos pelas IES, é desejável que apresentem boa qualidade discriminativa. Após essa avaliação inicial, foi realizada a análise da dimensionalidade com base na análise paralela e a FIFA, com o objetivo de compreender a estrutura fatorial dos itens.
Análise da dimensionalidade das provas do Enem 2017
Nesta seção foi conduzida uma análise paralela com a verificação de componentes principais com base em uma matriz de correlações tetracóricas. Na Tabela 2 estão dispostos os valores próprios (eigen value) para as cinco primeiras dimensões de cada prova do Enem 2017.
TABELA 2 Eigen value da análise de componentes principais, Enem 2017
| FATORES | LC | MT | CN | CH | ||||
|---|---|---|---|---|---|---|---|---|
| c.p | d.s | c.p | d.s | c.p | d.s | c.p | d.s | |
| 1 | 6,80 | 1,12 | 5,04 | 1,11 | 4,52 | 1,11 | 8,09 | 1,12 |
| 2 | 1,52 | 1,10 | 1,81 | 1,10 | 1,61 | 1,1 | 1,48 | 1,11 |
| 3 | 1,23 | 1,10 | 1,17 | 1,09 | 1,17 | 1,09 | 1,11 | 1,10 |
| 4 | 1,11 | 1,09 | 1,15 | 1,08 | 1,14 | 1,08 | 1,09 | 1,09 |
| 5 | 1,06 | 1,08 | 1,11 | 1,07 | 1,13 | 1,07 | 1,07 | 1,08 |
| 6 | 1,05 | 1,07 | 1,07 | 1,07 | 1,10 | 1,07 | 1,05 | 1,08 |
| 7 | 1,03 | 1,07 | 1,03 | 1,06 | 1,06 | 1,06 | 1,04 | 1,07 |
| 8 | 1,00 | 1,06 | 1,02 | 1,05 | 1,05 | 1,05 | 1,03 | 1,06 |
| 9 | 0,98 | 1,06 | 1,01 | 1,05 | 1,03 | 1,05 | 0,99 | 1,06 |
| 10 | 0,98 | 1,05 | 0,99 | 1,04 | 1,02 | 1,04 | 0,96 | 1,05 |
| 11 | 0,96 | 1,04 | 0,97 | 1,04 | 1,00 | 1,04 | 0,95 | 1,05 |
| 12 | 0,94 | 1,04 | 0,95 | 1,03 | 0,98 | 1,03 | 0,93 | 1,04 |
| Eigen1/Eigen2 | 4,47 | 2,78 | 2,80 | 5,47 | ||||
Fonte: Elaboração dos autores (2020).
Legenda: c.p: eigen values dos componentes principais; d.s: eigen values dos dados simulados.
Nota: Destaque para eigen values dos dados reais quando é menor ou igual aos eigen values dos dados simulados.
Ao submeter os dados de cada prova à análise paralela, esperava-se a existência ou predominância de um fator, ou seja, que os itens fossem unidimensionais, considerando que esse é o pressuposto do modelo de TRI utilizado no exame. No entanto, nas comparações dos eigen value dos dados reais com os simulados, o teste indicou a existência de quatro fatores para a prova de LC, cinco fatores para as provas de MT, seis fatores para a prova de CN e três fatores para a prova de CH.
Entretanto, há um certo consenso no entendimento de que é suficiente admitir a existência de uma dimensão dominante, uma “dimensionalidade essencial” (STOUT, 1990). Diante disso, apenas duas provas parecem apresentar uma dimensão dominante. A prova de LC apresentou a razão entre o eigen1 e eigen2 de 4,47, ou seja, cerca de quatro vezes maior que o segundo, e a prova de CH com valor 5,47, ou seja, o eigen1 é cinco vezes maior que o eigen2. Para as provas de MT e CN, o eigen1 é apenas duas vezes maior que o eigen2.
Para melhor visualização da magnitude dos eigen value das provas, foi construído um scree plot dos valores de cada fator dos dados reais e dos dados simulados (Figura 1).
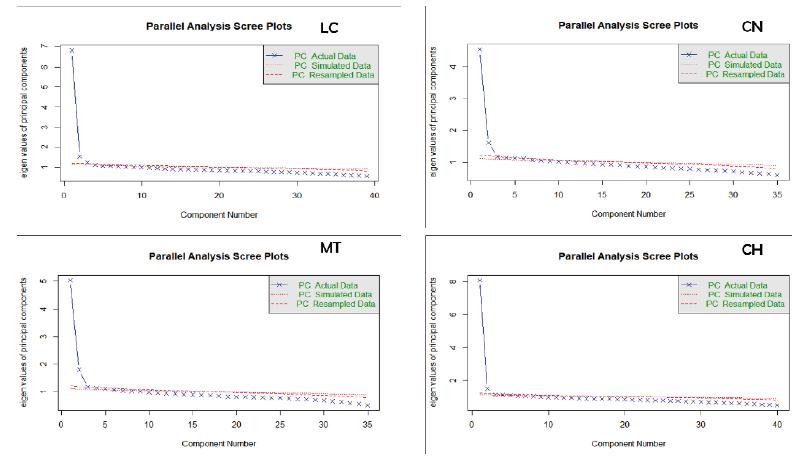
Fonte: Elaboração dos autores (2020).
FIGURA 1 Scree plot da análise paralela das provas do Enem 2017
Nesses gráficos, torna-se mais evidente a existência de uma dimensão dominante nas provas de LC e CH. No entanto, nas provas de MT e CN, evidencia-se, de forma mais acentuada, a presença de uma segunda dimensão.
Após uma análise exploratória inicial da dimensionalidade dos dados por meio da correlação ponto bisserial e da análise paralela, submetemos os itens a uma FIFA. Uma primeira análise foi realizada com os valores de ajuste dos modelos com base nas medidas do RMSEA, SRMSR, TLI e CFI. Os valores desses índices podem ser observados para cada prova na Tabela 3.
TABELA 3 Índice de ajuste dos modelos estimados para as provas do Enem 2017
| PROVAS | MODELOS | RMSEA | SRMSR | TLI | CFI |
|---|---|---|---|---|---|
| LC | 1 | 0,011 | 0,014 | 0,987 | 0,988 |
| 2 | 0,009 | 0,013 | 0,991 | 0,992 | |
| 3 | 0,008 | 0,012 | 0,993 | 0,994 | |
| 4 | 0,007 | 0,011 | 0,993 | 0,995 | |
| MT | 1 | 0,009 | 0,014 | 0,983 | 0,985 |
| 2 | 0,009 | 0,013 | 0,984 | 0,987 | |
| 3 | 0,008 | 0,013 | 0,988 | 0,990 | |
| 4 | 0,007 | 0,012 | 0,989 | 0,992 | |
| CN | 1 | 0,009 | 0,014 | 0,977 | 0,980 |
| 2 | 0,009 | 0,013 | 0,980 | 0,983 | |
| 3 | 0,008 | 0,012 | 0,984 | 0,988 | |
| 4 | 0,008 | 0,012 | 0,984 | 0,988 | |
| CH | 1 | 0,010 | 0,013 | 0,992 | 0,993 |
| 2 | 0,009 | 0,012 | 0,994 | 0,995 | |
| 3 | 0,008 | 0,011 | 0,995 | 0,996 | |
| 4 | 0,007 | 0,010 | 0,996 | 0,997 |
Fonte: Elaboração dos autores (2020).
Como foi constatado na Tabela 3, os valores de ajuste para todas as provas estimados para os modelos de 1, 2, 3 e 4 parâmetros mostraram-se adequados. Os valores do RMSEA e SRMSR se mantiveram abaixo de 0,05 e os valores do TLI e CFI acima de 0,95. Esses índices não conseguiram identificar com precisão o modelo fatorial mais adequado para esses itens. Isso pode ter ocorrido porque esses índices são sensíveis a grandes amostras.
Também foram analisados os valores dos índices de ajuste dos modelos com base nos valores de AIC e BIC. Os dados dessa análise estão dispostos na Tabela 4.
TABELA 4 Critério de Informação Baysiano (BIC) e Critério de Informação de Akaike (AIC) dos modelos estimados para as provas do Enem, 2017
| DIMENSÕES | LC | MT | CN | CH | ||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | AIC | BIC | |
| 1 | 469439,3 | 470282,9 | 380552,8 | 381309,9 | 387059,2 | 387816,3 | 468863,2 | 469728,4 |
| 2 | 469253,3 | 470370,9 | 380444,1 | 381446,3 | 387063,7 | 388065,9 | 468714,5 | 469861,0 |
| 3 | 469121,0 | 470505,4 | 380366,6 | 381606,8 | 386936,4 | 388176,6 | 468616,5 | 470037,0 |
| 4 | 469059,6 | 470703,5 | 380355,4 | 381826,4 | 386892,6 | 388363,5 | 468608,2 | 470295,4 |
Fonte: Elaboração dos autores (2020).
O índice de ajuste do AIC, como apresentado na literatura, tende a ser mais permissivo quanto ao número de fatores (NYLUND; ASPAROUHOV; MUTHÉN, 2007), o que ocorreu nesta pesquisa. Os valores decrescem à medida que são acrescentados mais fatores ao modelo. Indicando, por esse índice, que quatro ou mais fatores se ajustam bem.
Ao verificar os índices de ajuste oferecidos pelo BIC, observamos que o menor valor, portanto, o modelo mais bem ajustado, foi o dos modelos unidimensionais das provas. Notamos também que, à medida que são acrescentados mais fatores, os valores do BIC aumentam. Isso indica que se perde qualidade no ajuste ao estimar modelos com mais de uma dimensão. No entanto, embora o BIC tenha sido considerado mais consistente na indicação do número de dimensões a serem retidas na análise fatorial, o teste é considerado como conservador, ou seja, valoriza modelos com menos dimensões.
Também foi analisado o ID por meio da comparação entre os modelos. Os ID das comparações dos modelos estão dispostos na Tabela 5.
TABELA 5 Índice de dimensionalidade das provas do Enem 2017
| PROVAS | COMPARAÇÃO | X2 | X2CORR | GL | ID |
|---|---|---|---|---|---|
| LC | M1 - M2 | 262,002 | 87,334 | 38 | 2,298 |
| M2 - M3 | 206,238 | 68,746 | 37 | 1,858 | |
| M3 - M4 | 133,464 | 44,488 | 36 | 1,235 | |
| MT | M1 - M2 | 176,698 | 58,899 | 34 | 1,732 |
| M2 - M3 | 143,442 | 47,814 | 33 | 1,499 | |
| M3 - M4 | 75,188 | 25,063 | 32 | 0,783 | |
| CN | M1 - M2 | 63,559 | 21,186 | 34 | 0,623 |
| M2 - M3 | 193,233 | 64,411 | 33 | 1,952 | |
| M3 - M4 | 107,810 | 35,937 | 32 | 1,123 | |
| CH | M1 - M2 | 226,643 | 75,547 | 39 | 1,937 |
| M2 - M3 | 173,993 | 57,998 | 38 | 1,526 | |
| M3 - M4 | 82,315 | 27,438 | 37 | 0,741 |
Fonte: Elaboração dos autores (2020).
Em todas as comparações realizadas para as provas de MT, CN e CH, os valores de ID foram positivos menores que 2,0. Dessa forma, o ID indica que essas provas são unidimensionais. No prosseguimento das comparações, a prova de LC se ajustou melhor ao modelo de dois fatores. As demais provas tiveram melhor ajuste ao modelo unidimensional. Diante disso, esses resultados corroboram os apresentados pelo critério BIC.
No prosseguimento das análises, as cargas fatoriais de cada item também são indicativos da dimensionalidade destes, já que consistem na correlação do item com o fator. Dessa forma, espera-se que se os itens das provas, especialmente da prova de LC, são unidimensionais, cargas fatoriais altas, 0,30 ou mais, sejam identificadas. Optamos por realizar sucessivas análises das cargas fatoriais dos itens até se obter itens com cargas satisfatórias. As cargas fatoriais dos itens para o modelo unidimensional estão na Tabela 6.
Tabela 6 Cargas fatoriais dos itens com um fator do Enem 2017
| ITENS | LC | MT | CN | CH | ||||
|---|---|---|---|---|---|---|---|---|
| 1º EXTRAÇÃO | 2º EXTRAÇÃO | 3º EXTRAÇÃO | 1º EXTRAÇÃO | 1º EXTRAÇÃO | 2º EXTRAÇÃO | 1º EXTRAÇÃO | 2º EXTRAÇÃO | |
| i1 | 0,54 | 0,52 | 0,51 | 0,79 | 0,74 | 0,74 | 0,78 | 0,77 |
| i2 | 0,69 | 0,69 | 0,69 | 0,63 | 0,38 | 0,36 | 0,68 | 0,67 |
| i3 | 0,51 | 0,49 | 0,49 | 0,82 | 0,46 | 0,45 | 0,41 | 0,38 |
| i4 | 0,40 | 0,41 | 0,41 | 0,86 | 0,48 | 0,48 | 0,44 | 0,44 |
| i5 | 0,65 | 0,65 | 0,65 | 0,83 | 0,64 | 0,64 | 0,59 | 0,58 |
| i6 | 0,45 | 0,45 | 0,45 | * | 0,82 | 0,81 | 0,48 | 0,48 |
| i7 | 0,57 | 0,56 | 0,56 | 0,92 | 0,63 | 0,63 | 0,81 | 0,81 |
| i8 | 0,24 | ** | ** | 0,57 | 0,87 | 0,87 | * | * |
| i9 | 0,46 | 0,46 | 0,45 | 0,76 | 0,26 | ** | 0,77 | 0,76 |
| i10 | 0,50 | 0,49 | 0,48 | 0,88 | * | * | 0,28 | ** |
| i11 | 0,59 | 0,59 | 0,59 | * | * | * | 0,47 | 0,47 |
| i12 | 0,44 | 0,43 | 0,43 | 0,87 | 0,60 | 0,60 | 0,68 | 0,67 |
| i13 | 0,54 | 0,53 | 0,53 | 0,81 | 0,63 | 0,63 | 0,76 | 0,76 |
| i14 | 0,77 | 0,78 | 0,77 | 0,78 | 0,95 | 0,95 | 0,25 | ** |
| i15 | 0,23 | ** | ** | 0,86 | 0,69 | 0,69 | 0,73 | 0,73 |
| i16 | 0,44 | 0,44 | 0,44 | 0,79 | 0,86 | 0,86 | 0,32 | 0,32 |
| i17 | 0,41 | 0,41 | 0,41 | 0,60 | 0,76 | 0,76 | 0,82 | 0,82 |
| i18 | 0,60 | 0,59 | 0,59 | * | 0,67 | 0,67 | 0,77 | 0,76 |
| i19 | 0,67 | 0,66 | 0,66 | * | 0,81 | 0,81 | 0,18 | ** |
| i20 | 0,77 | 0,77 | 0,77 | 0,89 | 0,43 | 0,43 | 0,50 | 0,49 |
| i21 | 0,36 | 0,36 | 0,36 | * | * | * | 0,62 | 0,60 |
| i22 | 0,58 | 0,58 | 0,57 | 0,67 | 0,87 | 0,87 | 0,53 | 0,53 |
| i23 | 0,46 | 0,46 | 0,46 | 0,57 | * | * | * | * |
| i24 | 0,59 | 0,58 | 0,58 | 0,34 | 0,78 | 0,78 | 0,35 | 0,35 |
| i25 | * | * | * | 0,84 | 0,12 | ** | * | * |
| i26 | 0,19 | ** | ** | 0,72 | * | * | 0,50 | 0,50 |
| i27 | 0,63 | 0,63 | 0,63 | 0,52 | 0,68 | 0,66 | 0,74 | 0,74 |
| i28 | 0,23 | 0,23 | *** | 0,81 | 0,81 | 0,80 | 0,78 | 0,78 |
| i29 | * | * | * | 0,86 | 0,67 | 0,67 | 0,55 | 0,55 |
| i30 | 0,44 | 0,44 | 0,45 | 0,76 | * | * | * | * |
| i31 | 0,66 | 0,66 | 0,66 | 0,60 | 0,87 | 0,87 | 0,67 | 0,66 |
| i32 | 0,71 | 0,71 | 0,70 | 0,85 | * | * | 0,81 | 0,81 |
| i33 | * | * | * | 0,72 | 0,82 | 0,81 | 0,85 | 0,85 |
| i34 | 0,59 | 0,59 | 0,61 | * | * | * | 0,48 | 0,48 |
| i35 | * | * | * | 0,66 | * | * | 0,87 | 0,86 |
| i36 | * | * | * | * | 0,73 | 0,75 | * | * |
| i37 | 0,40 | 0,40 | 0,40 | 0,65 | 0,63 | 0,63 | 0,70 | 0,71 |
| i38 | 0,59 | 0,59 | 0,58 | 0,91 | 0,86 | 0,85 | 0,55 | 0,54 |
| i39 | * | * | * | 0,92 | 0,68 | 0,70 | 0,59 | 0,58 |
| i40 | 0,67 | 0,68 | 0,68 | * | 0,89 | 0,89 | 0,71 | 0,71 |
| i41 | 0,33 | 0,33 | 0,33 | * | 0,75 | 0,76 | 0,73 | 0,72 |
| i42 | 0,47 | 0,48 | 0,48 | 0,78 | 0,86 | 0,86 | 0,66 | 0,65 |
| i43 | 0,39 | 0,39 | 0,39 | 0,73 | 0,86 | 0,85 | 0,71 | 0,70 |
| i44 | 0,74 | 0,74 | 0,73 | * | * | * | 0,86 | 0,86 |
| i45 | 0,80 | 0,80 | 0,79 | 0,74 | 0,89 | 0,89 | 0,63 | 0,62 |
| %Var | 29,5 | 31,2 | 31,8 | 58,1 | 52,4 | 55,0 | 40,9 | 43,0 |
Fonte: Elaboração dos autores (2020).
Notas: a) *Itens excluídos por baixa discriminação (< 0,15). **Itens excluídos por baixa carga fatorial na primeira extração (< 0,30). ***Itens excluídos por baixa carga fatorial na segunda extração (< 0,30).
b) Destaque em negrito para cargas fatoriais menores que 0,30.
Ao analisar as cargas fatoriais dos itens das provas do Enem 2017, apenas os itens da prova de MT apresentaram adequação já na primeira extração, com cargas fatoriais variando entre 0,34 e 0,92. O modelo final apresentou um percentual de variância explicado de 58,1%. Durante o processo de ajuste de um modelo fatorial para essa prova, 10 de 45 itens foram excluídos por baixa discriminação, permanecendo 35 itens.
Para os itens da prova de LC, foram necessárias três extrações para a obtenção de um modelo fatorial satisfatório. No modelo final, dez itens também foram excluídos, inicialmente por baixa discriminação e ao aplicar o critério da carga fatorial durante o ajuste do modelo, permanecendo 35 itens. As cargas fatoriais desses itens variaram entre 0,33 e 0,79. O percentual de variância explicado foi de 31,8%.
Para os itens da prova de CN, foram necessárias duas extrações para a obtenção de um modelo fatorial adequado. No modelo final 12 itens foram excluídos por baixa discriminação e baixas cargas fatoriais, permanecendo 33 itens no modelo final. As cargas fatoriais variaram entre 0,36 e 0,95. O percentual de variância explicado foi de 55%.
Por último, os itens da prova de CH se ajustaram também na segunda extração. Inicialmente foram excluídos cinco itens por baixa discriminação e depois mais três itens por baixa carga fatorial na primeira extração. O modelo final resultou em 37 itens como cargas fatoriais entre 0,32 e 0,86 e percentual de variância explicado de 43%.
Na Tabela 7 estão os itens excluídos durante o processo de análise fatorial para cada prova do exame.
TABELA 7 Itens excluídos durante a análise fatorial exploratória, Enem 2017
| PROVAS | TOTAL DE ITENS | r pb < 0,15 | 1ª EXTRAÇÃO >0,30 | 2ª EXTRAÇÃO >0,30 | TOTAL DE ITENS EXCLUÍDOS |
|---|---|---|---|---|---|
| LC | 45 | 25, 29, 33, 35, 36 e 39 | 8, 15 e 28 | 28 | 10 |
| MT | 45 | 6, 11, 18, 19, 21, 34, 36, 40, 41 e 44 | - | - | 10 |
| CN | 45 | 10, 11, 21, 23, 26, 30, 32, 34, 35, e 44 | 9 e 25 | - | 12 |
| CH | 45 | 8, 23, 25, 30 e 36 | 10, 14 e 19 | 8 |
Fonte: Elaboração dos autores (2020).
Durante a análise fatorial exploratória, foram excluídos dez itens da prova de LC e MT, 12 itens de CN e oito itens de CH. Esperávamos que as análises indicassem que todos os itens apresentassem unidimensionalidade. No entanto, isso não ocorreu, o que demonstra problemas métricos dos itens das provas. Investigações mais aprofundadas são necessárias para analisar o impacto desses problemas na estimação das habilidades dos sujeitos. Supomos, inicialmente, que esses problemas podem prejudicar os candidatos no processo de seleção para os cursos de graduação das IES.
Para todas as provas do exame, foi possível ajustar um modelo unidimensional, no entanto, após a exclusão de muitos itens (ver Tabela 8). Embora seja parcimonioso um modelo unidimensional, considerando apenas uma dimensão dominante (STOUT, 1990), essa dimensão não conseguiu explicar a variabilidade dos outros itens. Provavelmente esses itens podem ser explicados pela existência de outras dimensões. Nesse caso, modelos de TRI multidimensionais são mais adequados (RECKASE, 2009).
Os pressupostos dos modelos de TRI unidimensionais, o mesmo utilizado no Enem, têm sido fortemente criticados. Tavares (2013, p. 69) faz o seguinte questionamento sobre esse ponto: “Se pensarmos em um exame específico utilizado em larga escala em nosso país, como o Enem, podemos assegurar que a TRI baseada em um modelo logístico unidimensional de três parâmetros é a melhor opção metodológica para esse caso?”. Ainda acrescenta apontando a perspectiva interdisciplinar do exame como um de seus diferenciais, o que torna mais difícil essa ideia.
Uma das saídas apontadas para esse problema da dimensionalidade do Enem e seu caráter interdisciplinar não comportado pelo modelo de TRI unidimensional é a utilização de modelos multidimensionais (OLIVEIRA, 2015). Esse problema da estrutura fatorial do exame foi testado empiricamente em algumas pesquisas.
Alguns estudos que realizam uma análise da estrutura fatorial dos itens para a compreensão dos construtos medidos por esse exame têm sido realizados. Em uma pesquisa se analisou o Enem de 2010 por meio da análise fatorial exploratória e confirmatória (MUNER, 2013). Nesse estudo, a autora conseguiu ajustar um modelo unidimensional com explicação de 30% da variância apenas para a prova de LC, mas após a exclusão de alguns itens. Na prova de CH e MT, foi ajustado um modelo bidimensional, ambos com 40% de variância explicada, e na prova de CN, um modelo com três dimensões e 50% de variância explicada. A estrutura fatorial dessas provas foi ratificada pela análise fatorial confirmatória com bons valores de ajuste do modelo.
Resultados que corroboram os deste estudo foram encontrados em outro que analisa o Enem, mais especificamente a prova de MT de 2015 (PRIMI; CICCHETTO, 2018). Nessa pesquisa, os autores implementaram uma análise de componentes principais sobre os resíduos obtidos no ajuste do modelo de TRI de Rasch. Com essa análise foi identificada a existência de um fator secundário importante indicando sistematicidade no acerto de participantes considerados como de baixa habilidade em itens difíceis.
Em outro estudo analisou-se as quatro provas do Enem de 2012 tomadas com prova única com 180 itens sob a ótica da TRI uni e multidimensional (VIEIRA, 2016). As análises indicaram que um modelo unidimensional se ajustou bem. O modelo multidimensional com quatro fatores também apresentou bom ajuste, mas não sugeriu que os itens estavam relacionados com suas respectivas áreas de conhecimento, o que dificulta a interpretação semântica dos fatores.
Embora Vieira (2016) tenha evidenciado que um modelo unidimensional se ajusta bem aos itens das quatro áreas, torna-se ainda mais complicada a interpretação desse fator e recai nas discussões apresentadas por Tavares (2013), de que é difícil compreender que apenas um fator latente é responsável pelas respostas aos itens de um teste educacional, ainda mais se tratando do Enem.
Por outro lado, uma outra pesquisa, ao analisar a estrutura fatorial de todos os 180 itens do Enem de 2016 por meio do método de análise fatorial de informação plena, identificou a existência de pelo menos duas dimensões (PICCIRILLI; SOUZA, 2018). Ao realizar a interpretação dos itens, os autores sugerem que os dois fatores medidos pelos itens são interpretação de texto e raciocínio lógico.
Também foram realizadas análises psicométricas da estrutura fatorial das provas do exame antes de 2009, quando o Enem ainda utilizava técnicas de psicometria clássica na análise dos resultados. Em estudo realizado com o Enem de 1999 (NOJOSA, 2002) e 2001 (COSTA, 2015), foi possível ajustar um modelo de TRI multidimensional com cinco fatores. Nojosa (2002) ressalta que esse modelo seria o mais adequado para a análise do exame considerando suas características de conteúdo.
Os resultados indicaram que alguns itens das provas do exame não atenderam ao pressuposto de unidimensionalidade, pois só foi possível ajustar um modelo unidimensional após a exclusão de alguns itens. Na prova de MT, por exemplo, um modelo unidimensional foi ajustado após a exclusão de 12 dos 45 itens da prova. Com base nessas evidências ainda não é possível realizar conclusões fortes sobre a dimensionalidade do Enem.
Não obstante, o exame apresenta algumas inadequações quanto à sua proposta inicial (ANDRADE, 2012): i) para que os resultados sejam comparados, é necessário que haja alguns itens em comum, no entanto, não é possível que se apliquem itens já utilizados em outros exames, já que é um teste de seleção e suas provas são divulgadas na íntegra; ii) para a validação dos itens, é necessário que eles sejam pré-testados em uma amostra do universo de participantes, quando isso ocorre alguns possíveis candidatos têm acesso aos itens anteriormente; iii) uma das justificativas para a utilização da TRI é que ela tem foco na análise do item, assim é possível atribuir pesos distintos para os itens, algo que também é possível e legítimo com a TCT, com a qual se solucionariam os problemas da dificuldade de interpretação dos resultados do exame pelos candidatos, de modo que estes não têm como estimar o seu resultado.
Além desses problemas apresentados, há uma outra questão que precisa ser levantada. Segundo uma nota técnica publicada pelo Ministério da Educação (MEC),1 a utilização da TRI no Enem tem duas finalidades principais: i) permitir a comparabilidade entre os anos; ii) permitir a aplicação do exame várias vezes ao ano.
Em relação ao primeiro objetivo apresentado, cabe uma reflexão. A comparabilidade entre os resultados é particularmente importante quando se quer acompanhar a evolução do aprendizado de um determinado grupo (ANDRADE; LAROS; GOUVEIA, 2010), com vistas à tomada de decisão ao redirecionamento de políticas e recursos. No entanto, o objetivo principal do Enem atualmente é ser parâmetro de seleção para os cursos de graduação nas universidades, institutos federais e instituições privadas de ensino superior. Dessa forma, os resultados têm como foco o desempenho individual dos candidatos para fins de classificação, que não necessariamente são estudantes. Assim, resultados comparáveis para tomada de decisão e definição de políticas públicas educacionais já são oferecidos por outras provas, como as realizadas no âmbito do Sistema de Avaliação da Educação Básica (Saeb) (KLEIN, 2009).
Quanto ao segundo objetivo alegado pelo Inep, este não tem se concretizado na prática, pois o exame ainda é aplicado uma única vez ao ano. Além desses dois principais objetivos, aponta-se também a possibilidade de se aplicarem provas distintas, ou seja, com itens diferentes, sem, contudo, alterar o nível de dificuldade da prova. Esse procedimento também não tem sido realizado. Atualmente são aplicados cadernos de prova com cores diferentes, em que há apenas a alteração da posição dos itens em cada caderno.
Com base nisso, acredita-se que os resultados desta pesquisa podem contribuir para a discussão da utilização do modelo de TRI unidimensional no Enem, considerando a falta de evidência sobre a sua estrutura latente. No entanto, ressalta-se a necessidade de mais estudos empíricos que possibilitem melhores informações sobre essa questão, sobretudo, debates e reflexões em relação à real necessidade desse modelo para os atuais objetivos do exame. Também ressaltamos a necessidade de pesquisas que analisem se a ordem dos itens interfere na dimensionalidade do exame; e o impacto da falta de ajuste ao modelo unidimensional na pontuação dos participantes. Aspectos esses que não são abordados nesta pesquisa.
Como discutido, não é apenas uma questão de modelo matemático, mas de adequação a pressupostos que, se violados, podem prejudicar milhões de candidatos que almejam uma vaga nas IES de todo o país.















