Introdução
O cálculo mental está presente em diversas situações do cotidiano como, por exemplo, ao calcular o troco de uma compra no supermercado, ou para o cálculo da porcentagem de um desconto em determinada compra, ou ainda para o cálculo da melhor forma de realizar um investimento ou aplicação financeira. Além disso, considera-se que o cálculo mental é importante para a aprendizagem da Matemática, tendo em vista que permite desenvolver a flexibilidade com os números e o senso numérico.
É muito comum a associação do cálculo mental a respostas rápidas e exatas, por meio de respostas memorizadas. Porém, o cálculo mental está associado à escolha da melhor estratégia para resolver uma operação, permitindo aproximações e estimativas.
O cálculo mental é apontado por muitos pesquisadores como uma alternativa para auxiliar o ensino e a aprendizagem de Matemática. Segundo eles, o cálculo mental é uma forma de promover o sentido numérico, pois encoraja a procura por processos mais fáceis embasados nas propriedades dos números e das operações (Reys, 1984; Parra, 1996; Abrantes, Serrazina, & Oliveira, 1999; Maclellan, 2001) e, ao mesmo tempo, o sentido de número está altamente relacionado com a habilidade do cálculo mental (Markovits & Sowder, 1994). Segundo Thompson (1999b), devemos ensinar metodicamente o cálculo mental pois:
A maioria dos cálculos na vida real é feita na cabeça, e não no papel; O cálculo mental promove o pensamento criativo e independente; Contribui para o desenvolvimento de melhores habilidades de resolução de problemas; Desenvolve senso de número sonoro; É uma base para o desenvolvimento de habilidades de estimativa (Thompson, 1999b, p. 179, tradução nossa).1
Os benefícios do cálculo mental descritos por estes e outros autores, indicam que o cálculo mental é uma forma de potencializar a aprendizagem de conteúdos matemáticos, principalmente da aritmética, base de toda a Matemática. Entendemos o cálculo mental como
[...] aqueles exatos ou aproximados, que são efetuados mentalmente, ou com anotações para apoiar o raciocínio, que não dependem, exclusivamente, do uso de algoritmos e da contagem. São aqueles que utilizam estratégias, raciocínio lógico numérico, que derivam resultados de outros memorizados e tem suas ações validadas pelas propriedades numéricas e operacionais (Zancan & Sauerwein, 2017, p. 311).
Observa-se que o cálculo mental se desenvolve por meio de estratégias, que são debatidas historicamente e apresentadas por diferentes autores, em manuais pedagógicos como de Backheuser (1933) e de Albuquerque (1951), em relatos de pesquisas ou em artigos científicos como Beishuizen (1993), Thompson (1999a), Threlfall (2002), Boaler (2020) e Parra (1996). A própria definição de cálculo mental não é consenso entre diferentes autores. Por exemplo, cada um dos autores Parra (1996), Buys (2008), Reys (1984), Zancan e Sauerwein (2017) trazem uma definição diferente para cálculo mental. Entretanto, é consenso a relevância do cálculo mental no ensino das operações e o benefício para o ensino de Matemática.
Ao observar as indicações das estratégias para o ensino de cálculo mental, surgem os questionamentos: ‘Como ensinar essas estratégias de cálculo mental?’, ou ‘Quais conhecimentos necessários para as estratégias de cálculo mental?’, ou ainda, ‘Que tipo de atividades podem potencializar o cálculo mental?’.
Neste artigo nos propomos a analisar as estratégias de cálculo mental descritas por estes autores e elencar os conhecimentos necessários a cada uma delas, de modo a compreender o que é preciso saber para formular uma estratégia. Para além disso, apresentamos sugestões de atividades que podem ser ampliadas, aprofundadas e implementadas na rotina escolar, possibilitando a construção dos conhecimentos identificados como básicos para o cálculo mental.
Estratégias de cálculo mental na bibliografia
Nesse estudo realizamos, por meio da pesquisa bibliográfica, uma investigação teórica para conhecer, compreender e analisar as estratégias de cálculo mental referidas por diferentes autores. Neste texto vamos apresentar os autores que se destacam no estudo das estratégias de cálculo mental. A pesquisa bibliográfica, considerada o primeiro passo de qualquer pesquisa científica (Marconi & Lakatos, 2020) nos auxiliou a encontrar as estratégias de cálculo mental mais usuais. A pesquisa utilizou fontes secundárias, especialmente manuais, livros e artigos sobre cálculo mental.
Paralelamente, fizemos um estudo a respeito da recomendação do cálculo mental na Base Nacional Comum Curricular (BNCC), documento de caráter normativo que define o conjunto de aprendizagens essenciais que todos os alunos devem desenvolver ao longo das etapas e modalidades da Educação Básica. No documento, encontramos dez competências específicas da Matemática, onde uma delas descreve que o aluno deve ser capaz de “Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo” (Brasil, 2018, p. 269). Bem como orientações detalhadas dos ‘objetos de conhecimento’ e ‘habilidades’ que devem ser desenvolvidas em cada ‘unidade temática’. Garantindo, assim, que todos os alunos tenham assegurados seus direitos de aprendizagem e desenvolvimento, em conformidade com o que preceitua o Plano Nacional de Educação (PNE).
A BNCC, relacionada ao Ensino Fundamental, possui 247 habilidades, com média de 27 itens para ano escolar, contemplando as unidades temáticas: álgebra (15%), probabilidade e estatística (15%), geometria (17%), grandezas de medidas (21%) e número (32%). Notamos que, praticamente 1/3 das unidades temáticas estão associadas ao ‘número’. Uma avaliação das Habilidades, descritas na unidade temática ‘número’, mostra que estas se baseiam em ler, escrever, contar, estimar, comparar, ordenar quantidades, compor e decompor números, construir fatos básicos relacionados às quatro operações, assim como resolver e elaborar problemas com números, de naturais a reais, envolvendo as quatro operações, bem como construir fatos básicos. O ‘cálculo mental’ aparece em 12 habilidades e as ‘estratégias de cálculo’ em seis, na sua grande maioria antecedidas da palavra ‘utilizando’ e seguidas da palavra ‘escrita’. Assim, a BNCC normatiza que os alunos devem desenvolver habilidades relacionadas ao número e suas operações, sugerindo, para isso, a utilização do cálculo mental e escrito ou estratégias de cálculo. Entretanto, em nenhum momento, traz explicitamente que o ‘cálculo mental’ deve ser ensinado. Percebemos que ele permeia as habilidades, sempre associado ao escrito.
Na escolha das fontes bibliográficas para análise, priorizamos materiais que abordassem estratégias de cálculo mental pois, assim como descreve Manzo (1971, p. 32), as fontes bibliográficas são “[...] meios para definir, resolver, não somente problemas já conhecidos, como também explorar novas áreas, onde os problemas ainda não se cristalizaram suficientemente”. Na Tabela 1 apresentamos as bibliografias selecionadas e analisadas, que versam, em seu conteúdo, sobre estratégias de cálculo mental para a adição.
Tabela 1 Fontes consultadas.
| Obra | Autor | Ano |
| A Aritmética na escola nova | Everardo Backheuser | 1933 |
| Como se ensina aritmética | Everardo Backheuser | 1946 |
| Metodologia da matemática | Irene de Albuquerque | 1951 |
| Metodologia do ensino primário | Afro do Amaral Fontoura | 1961 |
| Mental strategies and materials or models for addition and subtraction up to 100 in Dutch second grades. | Meindert Beishuizen | 1993 |
| Didática da matemática: reflexões psicopedagógicas | Cecília Parra | 1996 |
| Mental calculation strategies for addition and subtraction | Ian Thompson | 1999a |
| Issues in teaching numeracy in primary schools | Ian Thompson | 1999b |
| Flexible mental calculation | John Threlfall | 2002 |
| Estrategias cognitivas para el cálculo mental | Gálvez et al. | 2011 |
| Mentes sem barreiras: as chaves para destravar seu potencial ilimitado de aprendizagem | Jo Boaler | 2020 |
Fonte: As autoras (2021).
Conforme notamos na Tabela 1, as fontes consultadas são heterogêneas, contemplando de manuais didáticos à artigos científicos. Sabemos que existem indícios do cálculo mental na literatura bem antes de 1933, porém foi necessário escolher algumas fontes, e esta escolha deu-se considerando o tipo de estratégias de cálculo mental descritas.
A análise das fontes selecionadas mostra que alguns autores que mencionam estratégias de cálculo mental em seus escritos, não nominam as estratégias, como Jo Boaler (2020) e Grecia Gálvez et al. (2011). Outros autores destacam-se por dar nome a elas. Por exemplo, Everardo Backheuser (1946) referência uma estratégia de subtração denominada Método Austríaco, que consiste em
[...] completar o subtraendo até igualar o minuendo. Este método é considerado, atualmente, como uma estratégia de ensino da subtração, que consiste em transformar a subtração em uma adição para chegar na resposta. Por exemplo 37 - 18 = __. O raciocínio utilizado é o seguinte: 18 até 20 = 2 e 20 até 37 = 17, então a resposta é 2+17 = 19 (Berticelli & Novaes, 2021, p. 727).
Meindert Beishuizen (1993) se refere à duas estratégias de adição como 1010 e N10. A estratégia 1010 consiste em somar, primeiramente, as dezenas de ambos os números e, após, as unidades. Por exemplo, 35+23=(30+20)+(5+3)=50+8=58. Enquanto a estratégia N10, consiste em somar primeiro as dezenas da segunda parcela e depois as unidades. Por exemplo, 35+23=(35+20)+3=55+3=58.
Ian Thompson (1999a, p. 3) descreve oito estratégias para adição e subtração, as quais nomeia como: “Fatos duplos, Quase dobro, Subtração como o inverso da adição, Usando cinco, Fazendo uma ponte pelo dez, Compensação, Balanceamento”. Para o autor, ‘fatos duplos’ são aquelas operações que envolvem dobros, por exemplo, 18-9, 14-7. ‘Quase dobros’ são aquelas com valores próximos ao dobro, por exemplo, 7+8, calculada fazendo 7+7+1. ‘Subtração como o inverso da adição’ consiste em resolver subtrações por meio de resultados memorizados da adição, como saber que 8-2 é 6, porque 6+2=8. ‘Usar o cinco’ é a estratégias de decompor os números em 5+__ , por exemplo, 6+8=5+1+5+2 =5+5+3=10+3. A ‘ponte pelo 10’ é a estratégia de completar a dezena mais próxima, por exemplo, 8+5=8+2+3=10+3. A ‘compensação’ consiste em pensar em um resultado memorizado e compensar, por exemplo, para resolver 9+7, pensar que 10+7=17, então 9+7=16. Por fim, o ‘balanceamento’ é quando retiramos de uma parcela e acrescentamos na outra, como pensar que 9+7=10+6. O autor destaca que as estratégias mais importantes são: “[...] fazer uma ponte pelo dez, para cima e para baixo, decompor números de um dígito e usar a compensação em adições e subtrações que envolvam o número 9” (Thompson, 1999a, p. 4, tradução nossa).2
A publicação de John Threlfall (2002) é uma revisão bibliográfica sobre cálculo mental, donde o autor seleciona artigos de pesquisadores que versam sobre estratégias de cálculo mental. Dentre eles estão citados Thompson (1999a) e Beishuizen (1993).
A análise das estratégias de cálculo mental para a adição, indicadas pelos autores consultados permitiu estabelecer categorias e, assim, inferir os conhecimentos necessários a cada uma destas estratégias. Como Severino (2016), entendemos que no processo de análise do objeto buscamos transformar aquilo que era composto e complexo em algo simples, ou seja, analisamos cada estratégia para compreendê-la e em seguida inferir em quais conhecimentos ela se fundamenta. Em outras palavras, usamos o processo de "[...] decompor, dissecar, interpretar, estudar [...]" (Severino, 2016, p. 74) que é apresentado por Severino (2016), no sentido de analisar a estratégia e compreender os conhecimentos necessários para elas. Salientamos que existem estratégias de cálculo mental para as quatro operações, porém, para este texto, optamos em analisar e trazer estratégias apenas para adições, pois entendemos que esta é a base para as demais operações.
Na sequência, avaliamos estes conhecimentos a luz das habilidades apontadas na BNCC e finalizamos com sugestões de atividades para construir estes conhecimentos na prática, em qualquer nível de ensino.
Estratégias de cálculo mental e conhecimentos para estas estratégias
Nesta seção vamos exemplificar cinco estratégias de cálculo mental para a adição e inferir os conhecimentos necessários para elas. Estes exemplos foram estratificados da bibliografia apresentada no Tabela 1.
Exemplo 1: 8+6=8+2+4=10+4=14
Para realizar esta adição acionou-se a estratégia de completar o 10, ou Ponte pelo 10, descrita por Thompson (1999a). Esta estratégia necessita dos seguintes conhecimentos:
Saber que o 10 pode ser decomposto em 10=1+9=2+8=3+7=4+6=5+5= 6+4=7+3=8+2=9+1; e neste caso, escolher 8+2=10;
Saber que o 6 pode ser decomposto em 6=1+5=2+4=3+3=4+2=5+1, e neste caso, escolher 6=2+4;
Ter compreendido as composições numéricas, neste caso, que 10+4=14;
Ter senso numérico para saber que pode pensar que do 8 para o 10 faltam 2 unidades, que o 6=2+4, que pode trocar operação 8 + 6 pela operação equivalente 8+2+4= 10+4.
A partir deste exemplo percebemos que esta estratégia é construída com conhecimento de composição e decomposição numérica. As composições principais que devem estar memorizadas são as que têm resultado 10 (exemplificadas no item i), juntamente com as memórias de resultados de adições em que o 10, ou múltiplos de 10, é uma das parcelas (exemplificada no item iii). Todo este processo é permeado pelo senso numérico, entendido como a capacidade de interagir com os números de maneira flexível e conceitual (Boaler, 2018).
Os mesmos conhecimentos podem ser utilizados para adições com parcelas maiores que 10. Por exemplo, para calcular 27+16 acionamos que: 27+3=30 e que 16=3+13. Em seguida, o senso numérico possibilita a mudança da expressão 27+16, por 27+3+13 e por 30+13. Para resolver a adição 30+13 novamente é acionada a decomposição do 13 como 10+3, assim, com o senso numérico efetua-se 30+10+3=43. Ou seja, todos os conhecimentos acima citados permitiram substituir 27+16 por 27+3+10+3, facilitando a obtenção do resultado sem o uso da contagem ou do algoritmo da adição.
Exemplo 2: 7+6=6+1+6=6+6+1=12+1=13
Para realizar esta adição acionou-se a estratégia da memória dos dobros descrita por Thompson (1999a). Esta estratégia necessita dos seguintes conhecimentos:
Saber que 6+6 =12;
Saber que o 7 pode ser decomposto em 7=1+6=2+5=3+4=4+3=5+2=6+1;
Ter senso numérico para saber que pode as igualdades 6+7=6+(6+1)=(6+6)+1=12+1 são válidas;
Ter memorizado que 12+1=13.
A partir deste exemplo, percebemos que esta estratégia é construída com base nas memórias dos dobros dos números e na decomposição numérica. Novamente, todo este processo é permeado pelo senso numérico, que permite obter expressões equivalentes.
Este mesmo exemplo pode ser resolvido partindo da memória do dobro de 7: 7+6=7+7-1=14-1=13. Nesta resolução usou-se o conhecimento que 7+7=14 e que 6=7-1.
Exemplo 3: 15+14=10+5+10+4=10+10+5+4=20+9=29
Nesta adição acionou-se a estratégia da decomposição numérica denominada 1010 por Beishuizen (1993). Esta estratégia necessita dos seguintes conhecimentos:
Saber que 15 e 14 são compostos por dezenas e unidades, da forma 10+5 e 10+4, respectivamente;
Ter senso numérico para saber que 15+14=(10+5)+(10+4)=10+10+5+4;
Ter memória do resultado de 5+4=9;
Ter compreendido as composições numéricas, neste caso, que 10+10=20 e que 20+9=29;
Este exemplo indica que, para esta estratégia, são necessários conhecimentos de composição e decomposição em dezenas e unidades, associadas a memórias de alguns resultados de adição e senso numérico.
Exemplo 4: 16+13=16+10+3=26+3=29 ou 16+13=13+16=13+10+6=23+6=29
Nesta adição acionou-se a estratégia de decomposição em dezenas e unidades de uma das parcelas, denominada de N10 por Beishuizen (1993). Esta estratégia necessita dos seguintes conhecimentos:
Saber que 13=10+3 ou 16=10+6;
Saber que 13+10=23 ou 16+10=26;
Ter compreendido as composições numéricas e saber que 23+6=29 ou 26+3=29.
Exemplo 5: 26+19=26+20-1=46-1=45
Nesta adição acionou-se a estratégia de arredondamento para a dezena mais próxima a uma das parcelas descrita por Thompson (1999a). Esta estratégia necessita dos seguintes conhecimentos:
Saber que 26+20=46;
Saber que 19+1=20, e que 19=20-1;
Ter senso numérico para saber que 26+19=26+20-1;
Este exemplo indica que, para esta estratégia, são necessárias memórias de alguns resultados de adição com múltiplos de 10, aqui 26+20. Além disso, saber que 19=20-1, permitindo usar o 20-1 ao invés do 19.
Os exemplos sugerem que na mesma adição pode ser resolvida por diferentes estratégias. Assim como Threlfall (2002), acreditamos que a escolha da estratégia está relacionada aos conhecimentos prévios do indivíduo, pois o cálculo mental oferece um “[...] modelo flexível que enfatiza o conhecimento pessoal como um determinante de como um caminho de solução emerge no contexto de cálculos particulares, por meio do que é percebido pelo indivíduo sobre os números no cálculo” (Threlfall, 2002, p. 45, tradução nossa),3
Observe as estratégias que podem ser acionadas para obter a solução da adição 18+17=35:
Estratégia 1: Completando o 10 ou um de seus múltiplos (Exemplo 1)
18+17=18+2+15=20+15 ou 18+17=17+18=17+3+15=20+15
Estratégia 2: Utilizando a memória de dobros (Exemplo 2)
18+17=18+18-1=36-1 ou 18+17=17+17+1=34+1
Estratégia 3: Somando as unidades e depois as dezenas de cada número (Exemplo 3)
18+17=10+10+8+7=20+15 ou 18+17=8+7+10+10=15+20
Estratégia 4: Decompondo um dos números em dezena e unidade e somando (Exemplo 4)
18+17=18+10+7=28+7 ou 18+17=18+7+10=25+10
Estratégia 5: Arredondamento para a dezena mais próxima (Exemplo 5)
18+17=17+18=17+20-2=37-2
A análise mostrou que estas estratégias são permeadas por conhecimentos relacionados à memória de fatos básicos, decomposição de um número em adições ou subtrações, memória dos dobros e propriedades numéricas. De posse destes conhecimentos, fica fácil elaborar uma estratégia de cálculo mental.
Conhecimentos necessários para adições por cálculo mental
Identificamos que os conhecimentos necessários ao cálculo mental para adições podem ser agrupados em quatro grupos, os quais denominamos: Fatos Básicos, Decomposição, Dobros e Rede de Relações Numéricas do 10 (RRN do 10). A seguir descrevemos nossa definição acerca destes conhecimentos:
- Fatos básicos: São aquelas operações de adição ou subtração cujo resultado não ultrapassa a dezena mais próxima, ou seja, a soma é dada apenas pela alteração da unidade das parcelas. Por exemplo: 5+3; 7+2; 14+5; 21+8; 32+7.
- Decomposição: Este fato consiste em ter memorizadas todas as possíveis decomposições, em somas, dos números menores que 10. Ou seja, todas as combinações mostradas abaixo:
2=1+1;
3=1+2;
4=1+3=2+2;
5=1+4=2+3;
6=1+5=2+4=3+3;
7=1+6=2+5=3+4;
8=1+7=2+6=3+5=4+4;
9=1+8=2+7=3+6=4+5
- Dobros: Algumas estratégias requerem a memorização dos dobros, os mais frequentes são os dobros dos números de 1 a 20. Assim como a operação inversa. Ou seja, saber que 7+7=14 e que, consequentemente, 14-7=7. Por exemplo, 12+12=24;24-12=12; 15+15=30;30-15=15.
- Rede de relações numéricas do 10 (RRN do 10): Neste grupo estão todos os conhecimentos que envolvem o 10 nas parcelas ou no resultado, bem como os múltiplos de 10. Vejamos alguns exemplos:
10=1+9=2+8=3+7=4+6=5+5;
10-1=9;10-2=8;10-7=3;…;10-9=1;
10+1=11;10+2=12;10+3=13;…;10+9=19;
10=11-1=12-2=13-3=14-4…;
20+1=21;20+2=22;20+3=23…;
20=21-1=22-2=23-3=24-4…
11+10=21;10+15=25; 30+14=44…;
13-10=3;25-10=15 …
Para acionar qualquer estratégia de cálculo mental, além de um mínimo de conhecimento matemático, é necessário ter senso numérico, ou seja, possuir “[...] uma mentalidade matemática focada em dar sentido a números e quantidades" (Boaler, 2020, p. 33). O senso numérico permite a interação com os números de maneira flexível e conceitual (Boaler, 2020), o que auxilia na memorização de resultados. Essa flexibilidade com os números possibilita o desenvolvimento de um pensamento matemático ativo, onde o estudante busca compreender e dar sentido às operações. Com isso, consegue acionar estratégias de cálculo mental, de forma autônoma e segura, pois “[...] a eficiência em uma estratégia reside no pensamento e no entendimento de cada aprendiz individualmente. Nenhuma estratégia será suficiente para um estudante que ainda não a entende” (Humphreys & Parker, 2019, p. 42).
Desta forma, apropriando-se dos conhecimentos acima descritos, o indivíduo pode fazer cálculo mental pois, a partir deles, juntamente com propriedades numéricas, pode pensar em estratégias e obter resultados de operações de adição sem utilizar algoritmos ou contagem. Com a utilização de estratégias, alguns resultados são memorizados mais facilmente, construindo novos conhecimentos, o que auxilia na construção de novas estratégias. Assim inicia um movimento cíclico entre conhecimentos e estratégias, que aperfeiçoa o senso numérico e a flexibilidade com os números. Por meio da repetição, este movimento gera memórias.
Por outro lado, um indivíduo necessita de alguns conhecimentos básicos, pois, mesmo que tenha interesse, não conseguirá construir qualquer estratégia de cálculo mental. Sem conhecimento e sem estratégia, o senso numérico e a flexibilidade não provocam a construção de novos conhecimentos.
Além disso, entendemos que o professor é uma peça importante e indispensável, pois é ele quem inicia todo o processo. Uma vez que tenha tomado a decisão de inserir o cálculo mental na rotina dos alunos, este inicia a dinâmica da construção de conhecimento, construção de estratégias e assim por diante. Cada nova memória, cada novo conhecimento, permite novas estratégias, que resultam em mais flexibilidade e senso numérico, e assim, com tempo e prática, o cálculo mental se desenvolve.
O professor, fortemente intencionado a construir cálculo mental, necessita de atividades planejadas que construam os conhecimentos que são necessários, os quais foram descritos acima. Na próxima sessão exemplificamos algumas atividades que podem ser utilizadas para iniciar o movimento em busca do cálculo mental.
Sugestões de atividades para a construção do cálculo mental
A partir de nossa experiência com cursos de formação de professores e das pesquisas que temos realizado sobre este tema, acreditamos que o requisito inicial para um ensino de cálculo mental bem-sucedido é a intenção, ou seja, o professor - um dos protagonistas da sala de aula (Berticelli & Zancan, 2021) - deve estar decidido a inserir o cálculo mental em sua prática. A decisão provoca uma mudança de concepção em relação ao ensino de Matemática, no discurso, na forma como este vai direcionar o pensamento dos alunos, incentivando-os a buscar diferentes maneiras de resolução, buscando desenvolver o raciocínio, estimulando o uso de estratégias e procurando deixar de lado o uso de algoritmos em operações que podem ser resolvidas por estratégias de cálculo mental. Além disso, os alunos precisam saber que estão aprendendo cálculo mental, de modo que o professor precisa criar momentos de conversas sobre as diferentes formas de resolver a mesma operação. Para isso, o professor deve ter clareza e deixar claro para os alunos o porquê de determinadas atividades, bem como quais os conhecimentos em que estas estão construídas.
Com relação às atividades a serem propostas para os alunos, a primeira sugestão é primar pela flexibilidade quanto à forma de apresentação das adições. Em geral uma adição é apresentada da forma a + b = ____, onde o aluno tem apenas uma resposta. Nesse sentido propomos que a mesma adição a + b = c seja alternada dentre as doze possibilidades diferentes, apresentadas no Tabela 2:
Tabela 2 Diferentes formas de apresentar a adição.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fonte: Elaborado pelas autoras (2021).
Essa variação na apresentação da operação permite exercitar a flexibilidade do aluno para com os números, assim ele se familiariza com diferentes apresentações para a tradicional 6+4=___; que pode variar como ___=6+4 , 10=__+4 ou 10=6+___. Esta abordagem influencia fortemente no entendimento da álgebra, quando o aluno entende a equação 10=x+4 como equivalente a x+4=10.
Outra sugestão está relacionada ao grau de dificuldade das atividades, que deve apresentar-se de forma gradativa, com atividades agrupadas e nomeadas, permitindo que o estudante tenha entendimento sobre como deve proceder o pensamento. Nos exemplos abaixo apresentamos extratos de tarefas, recortes, que devem ser variadas e ampliadas para serem utilizadas em sala de aula.
Na Figura 1, exemplificamos as primeiras tarefas que devem ser agrupadas por conhecimento, envolvendo números inteiros de 1 a 10.
O segundo bloco de atividades deve conter números menores que 20 em suas operações, exceto no bloco decomposição, que deve se manter em números menores que 10, conforme percebemos na Figura 2:
Estas tarefas abordam resultados de 1 a 20, que desejamos que sejam memorizados pelos alunos, o qual provocamos por meio da repetição. Por isso, quem determina por quanto tempo elas devem ser repetidas são os alunos. Na sequência, exploramos a forma de apresentação das adições (Figura 3):
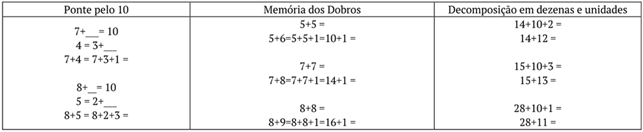
Quando os resultados das adições agrupadas aqui por: Fatos Básicos, Decomposição, Memória dos Dobros e a RRN do 10, para números menores que 20, estiverem memorizadas, o indivíduo estará em condições de inserir estratégias de cálculo mental em sua rotina e iniciar a dinâmica do cálculo mental. Estas estratégias podem ser induzidas por meio de atividades projetadas para este fim. Abaixo mostramos exemplos de atividades em que nominamos as estratégias (Figura 4) e, com o estímulo do professor, podem começar a ser trabalhadas em sala. Apenas depois de memorizados os resultados para adições com números até 20, passamos para números maiores.
Nas Figuras 5 e 6 apresentamos atividades com números menores que 30 e menores que 40, respectivamente, que exploram estratégias de cálculo mental. Importante atentar que toda vez que queremos que o aluno acione determinada estratégia, precisamos apresentar adições onde as parcelas sejam constituídas por números que facilitem ou até induzam a estratégia que queremos que o aluno utilize, pois, os números apresentados favorecem a escolha de determinada estratégia. Explicando de modo mais claro, se a intenção é explorar a ponte pelo 10, devemos apresentar situações que favoreçam esta escolha, como por exemplo 8+5 = ____, ao invés de 8+8 = ___.
Além destas, existem outras estratégias que podem ser acionadas e que não estão exemplificadas neste texto. Aqui abordamos aquelas que consideramos as primordiais. Defendemos que, independentemente do nível de ensino, a construção dos conhecimentos deve seguir a sequência das sugestões acima. O tempo demandado para a construção dos conhecimentos pode variar de acordo com o nível de ensino, a intenção do professor, a quantidade de atividades realizadas na rotina escolar e os momentos de conversas sobre o pensamento escolhido.
Reforçamos que, com a apropriação destes conhecimentos e memorização destes resultados, o indivíduo pode ou não construir qualquer estratégia de cálculo mental. Porém, temos clareza de que, ao realizar as atividades acima, o indivíduo tem possibilidades de desenvolver os conhecimentos necessários para formular uma estratégia de cálculo mental. Entretanto, sem estes conhecimentos, nenhuma estratégia de cálculo metal, por mais simples que seja, poderá ser construída. Ressaltamos que estas atividades têm a finalidade de complementar as demais atividades já desenvolvidas em sala de aula.
Considerações finais
A possibilidade de várias combinações entre estratégias faz com que cada indivíduo escolha aquela que lhe for mais conveniente, a partir dos sentidos e significados dos números por ele estabelecidos. A escolha de diferentes estratégias está relacionada às memórias, tornando o cálculo mental algo particular. Considerando estas memórias, fica claro que não tem sentido ensinar estratégias de cálculo mental sem antes ensinar os conhecimentos necessários a elas e tê-los compreendido e memorizado, visto que, sem eles as estratégias não acontecem. Em outras palavras, entendemos que, para trabalhar as estratégias de cálculo mental em sala de aula, devemos primeiramente nos ocupar em ensinar os quatro grupos de conhecimentos listados acima: ‘fatos básicos’, ‘decomposição’, ‘dobros’ e ‘Rede de relações numéricas do 10’, de forma que o indivíduo aprenda, compreenda e os memorize.
Muitas das estratégias descritas aqui aparecem em livros didáticos do Ensino Fundamental I, inseridas em exemplos sem explicações detalhadas, donde o autor considera que o professor tem habilidade para compreendê-las. Entretanto, a realidade da sala de aula pode não ser esta. Quando o professor não sabe, ele deixa de explorar o cálculo mental e, com isso, está impedindo a flexibilização do pensamento, que pode ser aplicada tanto para os números, como para qualquer outra situação.
De posse dos conhecimentos necessários para a escolha de estratégias de adição, o indivíduo já tem a base construída para desenvolver as estratégias de subtração, multiplicação e divisão, visto que a adição é a condição primordial, considerada a base de todo o cálculo mental. Neste estudo defendemos que é necessário, primeiramente, ensinar os conhecimentos elencados neste texto, por meio de atividades preparadas com esta finalidade. Em um segundo momento, motivar os indivíduos a fazerem uso das estratégias de cálculo mental. Com os conhecimentos e com a construção das primeiras estratégias o processo inicia e se retroalimenta, ou seja, quanto mais utiliza estratégias, mais conhecimentos são construídos e memorizados, com mais conhecimentos, mais estratégias, e assim por diante. Com isso, o cálculo mental se constrói e, com ele, uma melhor relação com a Matemática.











 texto em
texto em