Introduction

Rational numbers, whether represented as fractions, decimals, or percentages, are not only infinite but also ubiquitous. In daily life, they are inescapable in rural, suburban, and urban environments; at home and work; in commerce, sports, and recreation. Whether one is engaged in quotidian or academic pursuits, rational numbers are also useful. The academic and the quotidian utility of rational numbers are connected. Fractions did not originate as an abstract algebraic structure such as an Abelian group with the addition operation¹ or as a commutative field with a unit.² Instead, they emerged to answer questions concerning “how much?”. To answer such a question in practical and material terms, as ^{Gillings (1972/1982)} recounts, in Ancient Egypt, land surveyors used rods, poles, and knotted cords of rope to measure lengths and the end-to-end distance of the property. Such measures rarely, if ever, were an exact multiple of the rod, pole, or distance between two knots on a cord; that is, of the unit of measure. We can imagine that at first the measure as approximations to natural numbers was acceptable. However, later, to pay and collect taxes, for instance, more precise measurements were undoubtedly required.

In quotidian and academic endeavors alike, rational numbers are moreover essential. In educational settings, they are so critical that procedural and, especially, conceptual knowledge of fractions are linchpins for success with higher mathematics. For achievement in mathematics beyond the elementary school years, an emerging body of empirical studies in mathematics education is documenting the importance of competence with fractions (^{Siegler et al., 2011}; ^{Bailey et al., 2012}; ^{Siegler et al., 2012}). However, despite their importance, current research also indicates that students and their teachers indistinguishably lack flexible and conceptual knowledge of fractions (^{Lamon, 2012}; ^{Olanoff et al., 2014}).

Conceptual knowledge of mathematics is critical for pleasurable and successful participation in school mathematics and recreational mathematics as well as in fields such as science, technology, and engineering. Policy makers, psychologists, mathematicians, and mathematics education researchers alike recognize both anecdotally and empirically that conceptual knowledge of fractions and, in general, rational numbers constitute a necessary condition for participation and high performance in advanced mathematics (^{Wu, 2001}; ^{Lamon, 2007}; ^{National Mathematics Advisory Panel, 2008}; ^{Wu, 2009}; ^{Bailey et al., 2012}; Lamon, 2012; ^{Siegler et al., 2012}; ^{Maher e Yankelewitz, 2017}). Students who experience conceptual difficulties with fractions not only incorrectly order and operate on them (^{Maher e Yankelewitz, 2017}) but also have poor mathematics achievement and unsuccessful experiences learning higher mathematical topics such as algebra, probability, and calculus (^{Lamon, 2001}; ^{Bailey et al., 2012}; ^{Booth e Newton, 2012}; ^{Siegler et al., 2012}; ^{Depaepe et al., 2015}; ^{Torbeyns et al., 2015}).

The conceptual deficiency in fraction knowledge among teachers and students coexists with current curriculum standards and textbooks grounded in known ineffective an epistemological notion about fractions that they represent parts of a whole equipartitioned (^{Ni e Zhou, 2005}; ^{Alajmi, 2012}). This part/whole notion and its corresponding pedagogical practices are based on an ontological view of fractions.

Fractions are conceptual objects. Their existence in mathematics, that is, their ontology is owed to a theorization of specific human actions that are part of a material historical, cultural practice. There can be different ontological perspectives about a mathematical concept. In the case of fractions, there are mainly two perspectives: partitioning and measurement. From the partitioning perspective, the existence of fractions emerges from the division of divisible things, a unit equally subdivided and a certain number of them distinguished. Whereas, from a measurement perspective, the ontology of fractions arises from problems of measuring quantities, which is the multiplicative comparison of pairs of magnitudes. Moreover, based on its ontological commitment, each perspective defines fractions differently.

The dominant perspective in school mathematics is the partitioning view that privileges a so-called part/whole notion or subconstruct (Lamon, 2012). Within the partitioning perspective, researchers generally agree that there are four other subconstructs—quotient, ratio, operator, and measure—and that constitute a complete knowledge of fractions (^{Kieren, 1980}; ^{Behr et al., 1983}; ^{Freudenthal, 1983}; ^{Vergnaud, 1983}; ^{Kieren, 1993}; ^{Lamon, 2001}). Despite decades of reforms in mathematics education policy, curriculum standards, and textbooks, students still have serious difficulties conceptualizing fractions and rational numbers (^{Martin et al., 2007}; ^{National Mathematics Advisory Panel, 2008}; ^{Alajmi, 2012}; ^{Lin et al., 2013}; ^{Siegler e Lortie-Forgues, 2015}; ^{Maher & Yankelewitz, 2017}).

Contributing to difficulties in learning fraction is its multifaceted construct. For instance, a fraction 34 can be conceived as a part of a whole (three out of four equal parts), as a quotient (three divided by four), an operator (three quarters of a quantity), a ratio (three objects to four objects), and finally as a measure (iterating the unit fraction, 14 , three times on a number line). Historically and currently, one ontological approach has dominated: the view that fractions are parts of wholes (^{Davydov & Tsvetkovich, 1991}; ^{Morris, 2000}). That is, the symbol, a/b , represents parts of a whole, where b indicates the number of equal parts into which a whole has been partitioned, and a designates the number of parts of interest. Given a part/whole interpretation, the fraction, 34 , is understood to be three parts out of four parts. Relying only on this interpretation of fractions limits students’ understanding (Lamon, 2012). For instance, in Figure 1, do the shaded portions represent 32 of 1, 32 of 2, 34 of 1, or something else?

(Source: ^{Gattegno e Hoffman, 1976})

Figure 1 What fraction do the shaded portions represent? 

Given the dominant part/whole ontological interpretation of fractions, as ^{Gattegno and Hoffman (1976)} argue with presenting Figure 1, can students be faulted for thinking that the shaded circles in Figure 1 represent 32 of 2? Students who only work with limited types of visual representations, for example, area models like circles divided into equal-sized pieces, may develop limited strategies, such as counting the number of pieces rather than assessing the relationship of the part(s) to a whole or unit. Moreover, conceiving of fractions as “parts of a whole,” students have difficulty making sense of the fractions where the numerator is larger than the denominator such as 74 and conceding that a fraction is a number, not just part of something (^{Tucker, 2008}).

Corroborating observations of other researchers about the dominant ontological perspective (for example, ^{Kerslake, 1986}; ^{Behr et al., 1992}; ^{Tzur, 1999}; Wu, 2009), ^{Lamon (2001)} emphasizes that “mathematically and psychologically, the part/whole interpretation of fraction is not sufficient as a foundation for the system of rational numbers” (p. 150). Nevertheless, a critical gap in the knowledge base persists concerning what alternative subconstruct or ontological perspective overcomes the insufficiency of the dominant perspective and facilitates robust conceptual understanding of fractions.

A complete theory and effective framework for teaching and learning rational numbers are needed (Lamon, 2007). This is especially true since “students’ knowledge of fractions … predicts their mathematics achievement in high school, above and beyond the contributions of their knowledge of whole-number addition, subtraction, and multiplication; verbal and nonverbal IQ; working memory; family education; and family income” (^{Siegler et al., 2012}, p. 695).

In mathematics education, research on students’ learning of fractions and operations on fractions has been based on two ontological perspectives: partitioning and measurement. The partitioning perspective views a fraction as a relation established between parts of a whole equipartitioned. This ontological perspective is rooted in a belief that counting is the basis for arithmetic and has led to the commonly accepted part/whole conception of fractions (^{Schmittau, 2004}). Indeed, it is how the Common Core State Standards (^{National Governors Association Center for Best Practices e Council of Chief State School Officers, 2010}) suggests introducing factions in the elementary school grades. Nevertheless, research indicates that this perspective seriously limits the robustness of students’ understanding of fractions (^{Kerslake, 1986}). It tends to support the erroneous idea that a positive fraction is composed of two different natural numbers and impedes understanding of improper fractions (^{Tzur, 1999}). While research on fraction knowledge within the partitioning perspective has yielded valuable insights into cognitive issues of fraction learning (see for example, ^{Dienes, 1967}; ^{Kieren, 1976}; 1980; ^{Behr et al., 1984}; ^{Mack, 1990}; Kieren, 1993; ^{Mack, 1995}; ^{Behr et al., 1997}; ^{Tzur, 1999}; Lamon, 2007; 2012; ^{Hunt et al., 2016}; ^{Patahuddin et al., 2017}), a critical limitation to fractions research has been its ontological foundation, the partitioning perspective. Little sustained research has investigated the known alternative ontological basis for fraction knowledge, the measurement perspective.

Reaching back historically

Before indicating research on the measurement ontology, it is instructive to consider why the partitioning perspective has dominated curricular approaches to fraction knowledge. As ^{Schmittau (2003)} explains the World is full of things which are countable and, interacting in the World, children participate in inherited cultural practices that involve counting. Consequently, children begin formal schooling with knowledge of counting and properties of counting numbers. In Vygotskian terms, through their counting practices, children develop spontaneous rather than scientific knowledge of counting numbers and their properties. Since dominant educational theory suggests, as ^{Schmittau (2003)} notes, that “children must construct their own concepts, what better basis could there be on which to build future mathematical understanding than children’s own spontaneous counting concepts?” (p. 226). Counting does generate positive integers but not fractions or irrational numbers. Formally, mathematics defines fractions as the quotient of two integers, a/b , such that b≠0 . Since this understanding of fractions is not an entry point to fraction knowledge for children, educators devise physical and visual representations such as area models and equipartition the models to illustrate fractions as the ratio of the positive integers formed. However, its formal mathematical definition and the pedagogical practices of constructing equipartitioned visual models are unrelated conceptually to the material origin of fractions.

Fractions emerged 4,000 years or more ago in the social practice of measuring quantities. In a chapter on the essential nature of mathematics, the Soviet-era mathematician, physicist, and philosopher, A. D. Aleksandrov³ (¹⁹⁶³), locates the origin of fractions in the early interaction between geometry and arithmetic.

In general, the measurement of any magnitude combines calculations with some specific operation which is characteristic of this sort of magnitude.… But in the process of measurement it turns out, generally speaking, that the chosen unit is not contained in the measured magnitude an integral number of times, so that a simple calculation of the number of units in not sufficient. It becomes necessary to divide up the unit of measurement in order to express the magnitude more accurately by parts of the unit; that is, no longer by whole numbers but by fractions. It was in this way that fractions actually arose, as is shown by an analysis of the historical and other data. They arose from the division and comparison of continuous magnitudes; in other words, from measurement. The first magnitudes to be measured were geometric, namely lengths, areas of fields, and volumes of liquids or friable materials, so that in the earliest appearances of fractions we see the mutual action of arithmetic and geometry. This interaction leads to the appearance of an important new concept, namely fractions, as an extension of the concept of number from whole numbers to fractional numbers…. Fractions did not arise, and could not arise from the division of whole numbers, since only whole objects are counted by whole numbers. Three men, three arrows, and so forth, all these make sense, but two-thirds of a man and even two-thirds of an arrow are senseless concepts; even three separate thirds of an arrow will not kill a deer, for this it is necessary to have a whole arrow. (p. 24-25; original emphasis)

Aleksandrov argues that the historical emergence of fractions is neither connected to the idea of whole number division nor multiples of unit fractions. His argument hinges on the fundamental distinction between a unit used for counting and for measuring. He writes: “only whole objects are counted by whole numbers” (my emphasis). That is, when counting, the chosen unit is indivisible; whereas, when measuring, the chosen unit is divisible. This critical conceptual difference notwithstanding, the ontological presentation of fractions as emerging from the quotient of whole numbers—parts of an equipartioned whole—or as multiples of unit fractions displayed on a numberline are the bases of contemporary proposals for introducting fractions (See, for example, Common core state standards for mathematics, ^{Common Core State Standards Initiative, 2010}). Instead, Aleksandrov posits that the specific interaction between arithmetic and geometry from which the need for fractions emerged was the social practice of measuring magnitudes of lengths, areas, and volumes. These practices were part of the social life of ancient Africans in Egypt.⁴ For instance, they employed them to construct pyramids more than 1000 years (5000 years ago) before the famous Ahmes and Moscow papyri were scribed (^{Struik, 1967/1948}; ^{Resnikoff & Wells Jr., 1984/1973}), both of which evidence Egyptians’ invention of fractions and operations on fractions. Fractions arising from measuring practices are intertwined with land surveying. According to Herodotus, a Greek historian, who wrote the nine-volume magnum opus, The Histories, in the fifth century BCE, the Egyptian practice of land surveying gave rise to ‘geometry,’ a derivative of an Ancient Greek word meaning measuring the earth (^{Roque, 2012}). The ancient Egyptian measuring practices that begot fractions and geometry simultaneously caused geometry and fractions to be mutually constituted.

Though fractions continued to be used in later civilizations such as Mesopotamia, Greece, China, and India, as ^{Davydov and Tsvetkovich (1991)} note, it was only in the 12^th century CE, just 900 years ago, that they were considered as numbers and then finally, in the 19^th century CE, laws for operating with fractions were formally elaborated. By the time rules for operating with fractions were established, fractions had become (1) conceptually distant from their concrete “object source” in measuring quantities and (2) an abstract number equal in status with natural numbers (^{Courant & Robbins, 1996/1941}; ^{Davydov e Tsvetkovich, 1991}).

From a Vygotskian or cultural-historical perspective, understanding the ontology of a mathematical concept starts with considering its historical origin in social practices and the conscious mathematical theorization that led to its development. Measurement as the source for fraction knowledge has been the object of limited research efforts. As the material source of both whole numbers and fractions, measurement has been theoretically and pedagogically investigated by Brousseau (^{Brousseau et al., 2004}) as well as Davydov and others who have adapted Davydov’s curriculum (^{Davydov & Tsvetkovich, 1991}; ^{Morris, 2000}; ^{Schmittau & Morris, 2004}; ^{Dougherty e Venenciano, 2007}). Different from “children’s spontaneously constructed counting structures, the [Davydov] curriculum develops the concept of a number as the ratio of some quantity to another quantity that is used as the unit” (^{Morris, 2000}). ^{Morris (2000)} investigated the adoption of this approach to fraction learning with a group of fourth-graders (9- to10-year olds) who were learning about fractions as numbers. Two results of her analysis are particularly important. First, “literal symbolism proved to be unproblematic for the children. It appears to assist the instructor in changing the focus of instruction from numerical computation to reasoning about quantitative relationships” (^{Morris, 2000}). Second, “working only with graph paper and a pencil [, children derived their own] representations … [that] assisted them in keeping track of abstract relationships, and forced them to re-think these relationships with each new application” (^{Morris, 2000}). It is possible to provide students with manipulative materials, such as Cuisenaire rods (described below), so that when writing about relations among their measured lengths, they use “literal symbolism.” Moreover, learners will use the manipulative materials to talk about relations they perceive, abstract, and talk about and later indicate those relations in writing.

Davydov (^{Davydov & Tsvetkovich, 1991}), ^{Morris (2000)}, ^{Schmittau and Morris (2004)}, Brousseau (^{Brousseau et al., 2004}), and others (^{Dougherty & Venenciano, 2007}) have contributed to knowledge about affordances of a measurement perspective for whole number and fraction knowledge. Their work raises questions about how to use this perspective to teach fraction knowledge so that students, younger than fourth graders, develop number sense about fractions that in turn will provide a conceptual scaffold for students to learn subsequently about fractions as numbers and operations on fractions.

Looking forward ontologically and epistemologically

In response to this conceptual gap in the literature, we propose that a measurement perspective shapes positively early elementary students’ (6 to 8 year olds) development of number sense about fractions through studying fractions as measures and issues of magnitude, order, and equivalence. Informed by theoretical work of ^{Davydov and Tsvetkovich (1991)}, developed and implemented during the era of the Union of Soviet Socialist Republics, we propose particular ways to conceptualize the ontology of fractions and the epistemology of fraction knowledge. We distinguish two different levels of abstraction to arrive at whole numbers and fractions. First, whole number knowledge requires abstracting quantity from the qualitative characteristics of objects and later being concerned with magnitude, order, equality, and inequality of these quantities. Second, knowledge of fractions requires another level of abstraction. It necessitates abstracting quantitative relations between quantities followed by recognizing magnitude, order, equality, and inequality of these quantitative relations. This second level of abstraction is the cognitive challenge and opportunity of our perspective on fraction learning.

The ontological perspective of our measurement perspective posits the following:

Based on this ontological perspective, we posit the following epistemological position about how fraction knowledge can emerge:

Fractional number sense is a special case of number sense. In general, number sense emerges before children begin formal schooling (^{Jordan et al., 2010}); in contrast to those who do not, children who possess foundational knowledge of whole numbers are positioned to benefit from mathematical experiences and instruction of elementary school (^{Baroody et al., 2006}). ^{Kalchman et al. (2001)} provide the following list of characteristics what number sense includes: “(a) fluency in estimating and judging magnitude, (b) ability to recognize unreasonable results, (c) flexibility when mentally computing, (d) ability to move among different representations and to use the most appropriate representations” (p. 2). Knowledge of number concepts and skills with mathematics procedures appear to be mutually supportive, each facilitating the development of the other area (^{Rittle-Johnson et al., 2001}). In contrast to whole number knowledge, students of early elementary school age (5- to 9-years old) have relatively underdeveloped fractional number sense. By the time instruction in fraction begins in third grade (8- to 9-years old), students, at most, have ideas of one-half, one-third, and perhaps one-fourth. Linguistically, in English, they have difficulty pronouncing fractional numbers, not hearing or producing the ordinal endings for unit and non-unit fractions. For instance, for the fraction, 24 , instead of two-fourths, students erroneously say “two fours.”

In addition to the need to develop oral fluency with fractional names, early elementary students would benefit from developing number sense about the magnitude, order, equivalence, and inequality of fractions, starting with fractions-as-measures. To implement our ontological and epistemological perspective that we presented penultimate paragraph requires tools such as manipulative materials that have an extensive attribute that can be used to compare the attribute among different instantiations of the tool. We have chosen to use Cuisenaire rods (see Figure 2). The ingenious inventor of these rods, Emile-Georges Cuisenaire (1891-1975), a Belgian schoolteacher, imbued them with functional and interesting correspondences between color and length. Rods of the same color are the same length and, conversely, rods of the same length have the same color. A length that is the double of another is also darker in tone. The smallest rod is a neutral color, usually referred to as “white.” Rods that are equivalent in length to two, four, and eight white rods have pigments with an affinity to the red family (purple and brown). Rods equivalent in length to 3, 6, and 9 white rods are colored respectively green, dark green, and blue, while rods equivalent to 5 and 10 white rods are yellow and orange. The rod whose length has the distinction of being relatively prime to rods of all other lengths in the set is colored black. Interestingly, the two primary colors, red and yellow, mix to make orange, which parallel the fact that the two nontrivial factors of the orange rod (equivalent in length to 10 white rods) are the red rod (equivalent in length to 2 white rods) and yellow rod (equivalent in length to 5 white rods).

Figure 2 Cuisenaire rods, ten different sizes and colors, arranged in a “staircase” formation. 

The Cuisenaire rods are a simple but inventive collection of physical materials (wooden or, now, plastic parallelepipeds) or manipulatives with which children can quickly become familiar. Being familiar with manipulatives in mathematics learning is an important first step in their effective use (^{Willingham, 2009}). To become familiar with Cuisenaire rods and relations among them, children need to engage in both free play and structured tasks in which they attend to two characteristics of the rods: the tangible (length) and the visible (color). Because of their simplicity, while students work on mathematics tasks, Cuisenaire rods do not generate high extraneous cognitive load (^{Sweller, 1994}; ^{Sweller et al., 1998}). As such, they allow students to focus mainly on acquiring awarenesses about relations among the rods, which yield ideas about whole numbers, fractions, and operations on them. However, as ^{Meira (1998)} underscores, instructional representations such as Cuisenaire rods have no inherent transparency, they are “meaningful only with respect to learners’ activities.”

With Cuisenaire rods, students can build mathematical meaning and mental images about fractions and operations on fractions. Teachers direct their students’ attention to simple but powerful visualizations of fractions: measuring lengths of Cuisenaire rods and identifying relations among the rods. The rods are straightforward, physical, and cognitive models of fractions. Students can evoke images them to think about fractions, relations among fractions, and operations on fractions. They enable students to build personal and, therefore, meaningful ideas about fractions and connect them to other mathematical ideas (^{Ma, 1999}). Students can connect different mathematical ideas when their understanding builds on basic ideas and when they use simple, manipulative models systematically (^{Ma, 1999}; ^{Willingham, 2009}).

To understand fractions and other topics of school mathematics, there are two necessary approaches to the idea of number and operations on numbers: partitioning and measurement. First, the partitioning approach involves counting, the naming of an ordered sequence of numerals or using these numerals to label, without omission or duplication, separate and distinct items of a collection such as children on a soccer field or turtles on a beach. Second, the measurement approach involves measuring, comparing a continuous quantity to a standard unit such as determining the straight-line distance from one end of a soccer field to its other end or the yearly amount of rainwater collected in a barrel. Counting is used to answer the question, “How many?”; while measuring answers the question, “How much?”

Looking forward pedagogically

To avoid epistemological flaws and inadequacies of the partitioning perspective, we use an approach based on measurement (^{Davydov & Tsvetkovich, 1991}; ^{Gattegno, 2009/1960}). A prime example of an extensive quantity is length. With this, then, how does one teach about fractions from a measurement approach, using Cuisenaire rods? This is the subject an instructional model that we propose, the 4A-Instructional Model. Table 1 below presents the model, which consists of four phases for implementing a pedagogical approach, the subordination of the teaching of mathematics to students’ learning⁵, using Cuisenaire rods. In this approach, an instructional unit is often longer than a single class meeting. The sequence consists of a coherent, flexible sequence of tasks intended to enable students to educate their awareness about ideas of a mathematical topic.

The criterion for moving from one phase to another is students’ fluent facility with the manipulative actions, verbal and symbolic language, mental actions, and ideas of an instructional phase. That is, for a given instructional objective, while working in the Actual Actions phase as soon as students evidence that they are comfortable with the associated rod manipulations, talking about what they are doing and perceiving, and can perform actions nearly without the rods, then it is time to move to the second phase Virtual Actions. Once in this phase, when students exhibit their ability to respond mentally and fluently to tasks from the actual actions phase without physically manipulating rods, then it is appropriate to transition to the Actions-Written phase, where they will work symbolically on actions with which they already have both actual and virtual facility.

The fourth phase, Actions Formalized, is a culminating phase where the mathematical ideas that students constructed in the first three phases are discussed and written using formal, symbolic language. This is the phase, for example, where students use algorithms to represent formally what have done in the previous three phases. In this way, an algorithm is experienced as an encapsulation or symbolic trace of meaningful mathematical actions (^{Schmittau, 2003}).

Each of the four phases of our instructional model occasions opportunities for formative and summative assessments. In each phase, teachers hear and observe what students do and say and, in response to either form of evaluation, adjust their instructional intentions.

Theoretical and empirical underpinnings of the 4A-Instructional Model

It is crucial to reveal the research basis for the epistemological perspective that informs the 4A-Instructional Model. The model assumes that individuals construct knowledge by actively relating of new information to their personal experience and their current frameworks for making sense of that experience (^{Gattegno, 1973}). It also presupposes that though individuals construct their own knowledge, it is accomplished through activities carried out socially (^{Vygotsky, 1978/1930}). In the first phases of the 4A-Instructional Model, oral language and talk are given primacy over symbolic writing. As ^{Oakes et al. (1997)} note, talk “is the medium in which meaning is most readily and ubiquitously negotiated” (p. 2). Mathematics learning happens through communication in a social context about objects and relations among the objects (^{Gattegno, 1987}). The activity of doing mathematics involves employing speech genres (explanation, argumentation, and so on) and mathematical inscriptions (numerals, operators, graphs, geometric figures, notations, and so forth). Our 4A-Instructional Model suggests that for mathematics learning, speaking and writing need to occur at distinct moments. In the trajectory of human history and development, hearing and talking precede reading and writing. Similarly, for mathematics instruction, reading and writing mathematics should follow facility with hearing and talking mathematically (Gattegno, 1973; ^{Bezuk & Cramer, 1989}; ^{Moses & Cobb, 2001}). Intentionally and distinctly, our instructional model first works on hearing and talking mathematically (Actual and Virtual Actions) and then on reading and writing mathematics (Actions Written and Formalized). This approach also minimizes the cognitive load (^{Sweller, 1994}) of recalling and attending to mathematical conventions when expressing mathematical ideas in written form before having a secure understanding of these ideas. We recognize that written mathematical numerals and symbols are not mathematical ideas but rather merely written expressions of such ideas. In the first two phases, students first engage with building their conceptual ideas and then, in the latter two phases, approach how to express their ideas in writing and finally encapsulated symbolically or as a definition.

In the first two phases, spoken words for fractions and mathematical operations such as “five-fourths of,” “five-fourths of four-ninths,” and “five-ninths” are used and only in the third phase are written symbols like 54× , 54×49 , and 59 introduced. There are several reasons for this pedagogical perspective. Students learn by interacting with themselves and others mediated by natural language—talking, listening, and observing (Gattegno, 1973; ^{Vygotsky, 1978/1930}; ^{Zack & Graves, 2001}). It is critical for students to talk and use mathematical language to appropriate the words and the associated ideas. It is important for students to discuss tasks and ideas and to question one another, negotiate meaning, clarify their understanding, and make their ideas comprehensible to their partners. During collaborative tasks, students practice and use mathematical language. Their understanding grows as they express themselves to their partners and, thereby, reflect on their ideas and learning. To encourage students to talk with partners, teachers use several classroom collaborative structures, such as reciprocal teaching, solve and discuss, partner discussions, and so on, Moreover, talking before writing reduces cognitive load. Students work first on talking about actions and perceptions related to their rod manipulations and, once they have fluency with their articulation, then they can focus on using notational and other symbolic forms to represent what they already know and can do.

What students can already do meaningfully and comfortably is evidenced as they transition from the Actual-Actions phase into and throughout the Virtual-Actions phase. In this phase, without manipulating the rods, students express to themselves and others actions they performed previously in the Actual-Actions phase. ^{Gattegno (1957)} emphasizes the importance of this phase when he observes that if students “are to become mathematicians the actual actions must be replaced by virtual ones” (p. 14). Corroborating this position, ^{Davydov (1990)} notes that “students should pass gradually and in good time from object-related actions to performing them on a mental plane” (p. 174). To support students’ object-related actions being performed mentally, Virtual-Actions replace Actual-Actions. Virtual mental actions may lead students to develop visuospatial strategies. Such strategies resorting to imaginary rods and rod configurations may be the mechanism that underlies students’ ability to create mentally and articulate orally valid fractional statements about fractions-as-measure magnitudes, order, equivalence, and inequalities.⁷ Achieving facility in this Virtual-Actions phase is the foundational underpinning for the two subsequent phases, Written and Formalized Actions. Without this facility, the sustainable construction of, for example, the Actions-Written phase is compromised and, instead of relational understanding, students inevitably must rely on memory and procedural mechanisms.

Teachers implement our 4A-Instructional Model in educational settings. These settings are shaped by society’s social, political, and economic context. Within this multifaceted context, students interact verbally in mathematical activity using informal and academic language to make sense of mathematical objects and relations among these objects (see Figure 3). As students interact, they are supported to use academic language to describe to themselves and others what they notice as they manipulate Cuisenaire rods as well as to explain and provide evidence of relations they notice. They are also encouraged to use academic language to justify consequences of the relations and investigate conjectures. This phase is the Actual-Action phase and serves as a foundation for all the other phases (see Figure 3). Before moving to the second phase, students need to develop a secure understanding of how to perform specific actions on rods and relate that to mathematical relations and ideas. Also, students need to acquire fluent ways to talk about these mathematical actions, relations, and ideas.

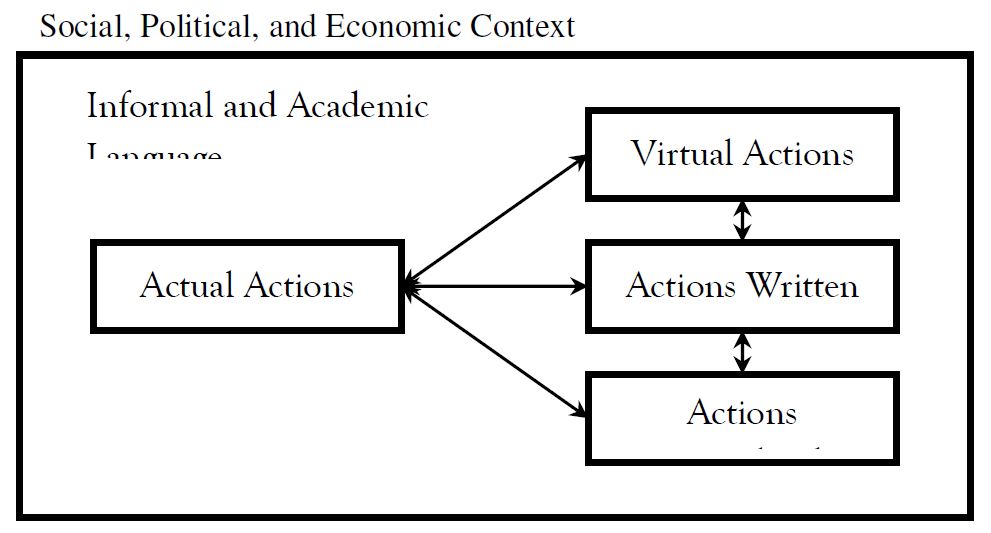
Figure 3 The 4A-Instructional context and process of students’ unfolding mathematical activities facilitated by the subordination of teaching to learning. 

During the last three phases, students limit their use of physical objects while investigating mathematical ideas. In the second phase, Virtual Actions, they start with visualizing their actions on rods and, in the third and fourth phases, Actions Written and Actions Formalized, use mathematical symbols and notation to write about actions they know how to perform and then formalize these actions in symbolic or definitional form. Nevertheless, during these last three phases, it is imperative to allow students to revisit the Actual-Action phase and work with rods to investigate certain ideas. When students find it necessary to revisit the Actual-Action phase, it does not mean that they are regressing, it indicates that they are making sense of new situations or differently of familiar ones (^{Carpenter et al., 2015}). Teachers may also invite students to use rods to investigate and talk about certain mathematical ideas so that students perceive or work on connections between the Actual-Actions phase and other phases.

Other instructional strategies ask students to represent their ideas in writing early, while they are manipulating objects and trying to make sense of mathematical ideas. This strategy does not allow students to immerse fully in the mathematical relations embodied in their manipulations of objects. Other instructional strategies do not allow students to act on objects before writing; students are asked to manipulate symbols in writing. In this type of mathematics instructional strategy, students do not learn about mathematical ideas and relations among them. Instead, they memorize rules for manipulating symbols and how to express their results in ways that are acceptable by their teache